工程力学(静力学和材料力学)第2版课后习题答案_范钦珊主编_第2章_力系的简化[2]

合集下载

工程力学教程第二版课后习题答案

工程力学教程第二版课后习题答案工程力学是一门应用力学原理研究工程结构和材料力学性能的学科。

作为工程学的基础课程之一，工程力学的学习对于培养工程师的分析和解决实际工程问题的能力至关重要。

而工程力学教程第二版是一本经典的教材，其中的课后习题是帮助学生巩固所学知识的重要辅助材料。

本文将为读者提供工程力学教程第二版课后习题的答案，帮助读者更好地理解和掌握工程力学的知识。

第一章：静力学1. 问题：一根长度为L，截面为矩形的梁，其宽度为b，高度为h。

梁的两端分别固定在支座上，中间有一个集中力P作用在梁上。

求梁在P作用下的最大弯矩和最大剪力。

答案：根据静力学原理，我们可以通过平衡力和力矩来求解该问题。

首先，根据平衡力的原理，梁在P作用下的最大剪力等于P。

其次，根据力矩的原理，梁在P作用下的最大弯矩等于P乘以梁的长度L的一半。

因此，最大弯矩为PL/2。

第二章：动力学1. 问题：一个质量为m的物体以速度v沿着水平方向运动，突然撞击到一个质量为M的静止物体上。

求撞击后两个物体的速度。

答案：根据动量守恒定律，撞击前后两个物体的总动量保持不变。

设撞击后质量为m的物体的速度为v1，质量为M的物体的速度为v2。

由动量守恒定律可得mv = mv1 + Mv2。

另外，根据能量守恒定律，撞击前后两个物体的总动能保持不变。

设撞击前质量为m的物体的动能为1/2mv^2，撞击后质量为m的物体的动能为1/2mv1^2，质量为M的物体的动能为0（静止）。

由能量守恒定律可得1/2mv^2 = 1/2mv1^2 + 0。

综上所述，可以解得v1 = (m - M)v / (m + M)，v2 = 2m / (m + M)。

第三章：应力分析1. 问题：一个长方体的尺寸为a×b×c，其材料的杨氏模量为E，泊松比为v。

求该长方体在x、y、z方向上的应力分量。

答案：根据应力分析的原理，我们可以通过应力的定义和杨氏模量、泊松比的关系来求解该问题。

工程力学(范钦珊-蒋永莉-税国双-著)-清华大学出版社.pdf

工程力学——课后练习题讲解教师张建平第一章静力学基础课后习题：1. P32习题1-12. P32习题1-23. P33习题1-8图a和b所示分别为正交坐标系Ox解：图（）：F分力：图与解图，两种情形下受力不同，二者的1-2a解图示压路机的碾子可以在推力或拉力作用下滚过）：θ解图第二章力系的简化课后习题：1. P43习题2-12. P43习题2-23. P44习题2-4由作用线处于同一平面内的两个力F和习题图所示一平面力系对A(30)，B(0，图示的结构中，各构件的自重都略去不计。

1图2-4解习题）中的梁∑0,F0,1m习题3-3图解：根据习题3-3第三章附加习题课后习题：1. P69习题3-52. P69习题3-63. P70习题3-74. P71习题3-135. P71习题3-143-14 图示为凸轮顶杆机构，在凸轮上作用有力偶，其力偶矩确定下列结构中螺栓的指定截面Ⅰ－Ⅰ上的内力分量，，产生轴向拉伸变形。

，产生剪切变形。

如习题4-2图所示直杆A、C、B在两端A、B处固定，在C解：首先分析知，该问题属于超静定问题，受力图如图所示：试用截面法计算图示杆件各段的轴力，并画轴力图，单解：(a)题题－3一端固定另一端自由的圆轴承受四个外力偶作用，如5-3解：将轴划分为四个截面扭矩平衡方程im m 扭矩平衡方程+m3-3扭矩平衡方程5-5 试写出图中所示各梁的剪力方程、弯矩方程图3建立坐标系并确定两个控制面，如图左侧为研究对象：−=）取根据力平衡方程和弯矩平衡方程得出4ql弯矩方程：1解建立坐标系，并取两个控制面，如图ql ql1Q。

工程力学(工程静力学与材料力学)第二版答案(完整资料).doc

(a) (b)习题1-1图【最新整理，下载后即可编辑】1－1 图a 、b 所示，Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。

试将同一方F 分别对两坐标系进行分解和投影，并比较分力与力的投影。

解：（a ），图（c ）：11 sin cos j i F ααF F +=分力：11 cos i F αF x = ， 11 sin j F αF y = 投影：αcos 1F F x = ， αsin 1F F y =讨论：ϕ= 90°时，投影与分力的模相等；分力是矢量，投影是代数量。

（b ），图（d ）：1y F x xF 1y Fα1xF y F（c ）2F2y F2y2x 2x F2y FF（d ）(a) (b)习题1－2图F DR AC BD AxF AyF(a-1)Ay F FB C A AxF 'F C(a-2) C DF DR(a-3)AxFF A C BD AyF (b-1) 分力：22)tan sin cos (i F ϕααF F x -= ，22sin sin j FϕαF y =投影：αcos 2F F x = ， )cos(2αϕ-=F F y 讨论：ϕ≠90°时，投影与分量的模不等。

1－2 试画出图a 、b 两情形下各物体的受力图，并进行比较。

比较：图（a-1）与图（b-1）不同，因两者之F R D 值大小也不同。

1－3 试画出图示各物体的受力图。

习题1－3图F AxFAyF D C BABF或(a-2)FB AF DCA(a-1)BF AxF AAyF C(b-1)WF BD CF FCBBF AACBF(f-1)(e-3)'A(f-2)1O(f-3)c FF AF DF BF AF A习题1－4图1－4 图a所示为三角架结构。

力F1作用在B铰上。

杆AB 不计自重，杆BD杆自重为W。

试画出图b、c、d所示的隔离体的受力图，并加以讨论。

工程力学(工程静力学和材料力学)第二版答案

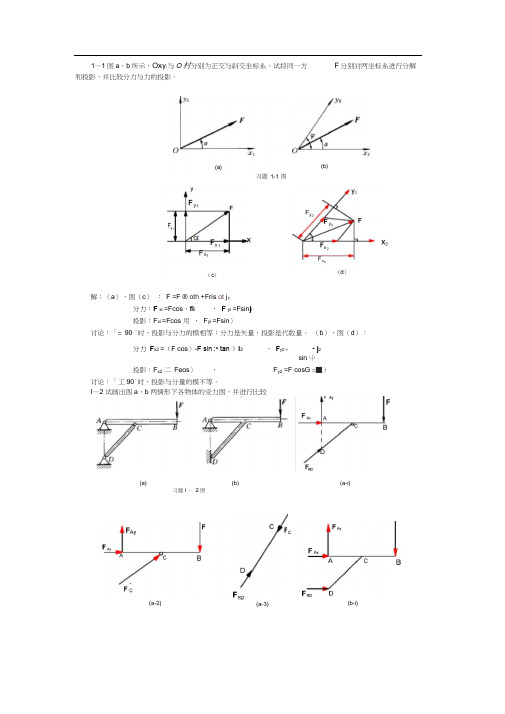
1—1图a、b所示，Ox i y i与O村分别为正交与斜交坐标系。

试将同一方F分别对两坐标系进行分解和投影，并比较分力与力的投影。

解：（a），图（c）： F =F ® oth +Fris ot j1分力：F xi =Fcos、fi i ， F yi =Fsin j i投影：F xi =Fcos 用，F yi =Fsin〉讨论：「= 90 °时，投影与分力的模相等；分力是矢量，投影是代数量。

（b），图（d）：分力F x2 =（F cos〉-F sin :• tan ）i2 ，F y2 = - j2sin屮投影：F x2二Feos〉，F y2 =F cosG =■）讨论：「工90°时，投影与分量的模不等。

I—2试画出图a、b两情形下各物体的受力图，并进行比较(a) (b) (a-i)习题i —2图(a-2)(a-3)(b-i)(b)a-1 ）与图（b-1 ）不同，因两者之F R D值大小也不同试画出图示各物体的受力图。

AA Wi 丄A A 加习题1-3图F比较：图1-31-4图a所示为三角架结构。

力F i作用在B铰上。

杆AB不计自重，杆BD杆自重为W。

试画出图b、c、d所示的隔离体的受力图，并加以讨论。

(b)A B A B/p/ /D(c)(d)(d-1)B F B1------ A习题1-4图(b-1)i(b-3)F AFB1F'FF' B2yBBF' B2y(d-2)F1 1-5(s)W习题1-5图(C)1— 6图示刚性构件F 沿其作用线移至点 D 或点 E （如图示），是否会改变销钉解：由受力图1— 6a , 1- 6b 和1— 6c 分析可知，F 从C移至E , A 端受力不变，这是因为力 F 在自身刚体ABC 上滑移；而F 从C 移至D ,则A 端受力改变，因为 HGC F CX! F Cy(b-3)在构件的点C 作用有一水平力F 。

(完整版)工程力学习题答案范钦珊蔡新着工程静力学与材料力学第二版

比较：图(a-1)与图(b-1)不同，因两者之1 - 3试画出图示各物体的受力图。

1 - 1图a 、b 所示，Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。

试将同一方 F 分别对两坐标系进行分解和投影，并比较分力与力的投影。

解：(a)，图(c ):分力：投影：=90 ° 时, (d )： F cos i 1 FX 1F y1 F sin F y1 F sinj l讨论：(b ),图F X 1 F cos投影与分力的模相等；分力是矢量, X 2投影是代数量。

F sinsin分力: j2BD(b)D(b-1)(a-3)投影：工90°时, F X 2 F cos ，投影与分量的模不等。

讨论：1 -2试画出图a 、b 两情形下各物体的受力图，并进行比较。

F y2 F cos(F X 2 (F cos F sin tan )i 2 F y2(a)l F AyF A X1F RD 值大小也不同。

a5A■dFBFF CABB(a-1)(b-1)BC DBCBCWDAy或(b-2)(c-1)(d-1)DCABCDFt D或(d-2)(e-2)(e-1)CO iOyBFA(f-3)(e-3)IV2[fW(f-1)(c)习题1—3图F BF BF AxF AF DB FF cW(f-2)AOAF A力 F i 作用在,并加以讨论。

----------------- :B 铰上。

杆AB 不计自重，杆BD 杆自重为 W 。

试画出图1 —4图a 所示为三角架结构 b 、c 、d 所示的隔离体的受力图 A zz ” X Xzr 'i/A1rC[------------DF AxAB虾F 或(a_2)1 — 6图示刚性构件 ABC 由销钉A 和拉杆GH 支撑，在构件的点C 作用有一水平力F 。

试问如果将力 F 沿其作用线移至点 D 或点E （如图示），是否会改变销钉 A 的受力状况。

工程力学(第二版)习题册答案

一、填空题
1. 相对滑动相对滑动趋势接触面的切线相反 2. 10N 20N 30N 30N 30N 3. 100N 竖直向上平衡 4. 平稳无冲击自锁
阻碍物体相对滑动
相对滑动趋势
二、选择题
1. A
三、简答题
1. ①问题中含有可能发生相对滑动的摩擦面，因此，存在摩擦力； ②受力图中要画出摩擦力，摩擦力总是沿着接触面的切线方向并与物体相对滑
7.
8.
9.
第二章平面力系
第一节共线力系的合成与平衡
一、填空题
1. 在同一条直线上
2. FR Fi FR 0
二、计算题
设向右为正方向。则 FR=120+40-80-200=-120N 方向：水平向左
第二节平面汇交力系的合成
一、填空题
1. 作用于同一平面内且各力作用线相交于一点的力系共线力系力的作用点 2. -F 或 F 0 0 -F 或 F 3. 合力在任一坐标轴上的投影各分力在同一轴上投影的代数和 4. F4 F3 5. 自行封闭 6. 所有各力在 x 轴上投影的代数和为零所有各力在 y 轴上投影的代数和为零 Fx 0 Fy 0
3. 后轮：摩擦力向前前轮：摩擦力向后
4. 不下滑，处于自锁状态
四、计算题
FT 60 18 3N
五、应用题
1. （提示）从摩擦力与 F 对 B 点的力矩大小的比较进行考虑
第三章空间力系第一节力在空间坐标轴上的投影与合成
一、填空题
1. 力的作用线不都在同一平面内呈空间分布的力系 2. 一次投影法二次投影法
二、选择题
1. A 2.B
它所限制物体
三、简答题
1.柔性体约束只能承受拉力，不能承受压力。 2.被约束物体可以沿约束的水平方向自由滑动，也可以向离开约束的方向运动，但不能向垂直指向约束的方向运动。 3.剪刀的两半部分可以绕销钉轴线相对转动，但不能在垂直销钉轴线的平面内沿任意方向做相对移动。 4.木条不能沿圆柱销半径方向移动，但可以绕销轴做相对转动。 5.固定端约束既限制物体在约束处沿任何方向的移动，也限制物体在约束处的转动。

工程力学(静力学和材料力学)第2版课后习题答案范钦珊主编 .

eBook工程力学（静力学与材料力学）习题详细解答（教师用书）(第7章)范钦珊唐静静2006-12-18第7章弯曲强度7－1 直径为d的圆截面梁，两端在对称面内承受力偶矩为M的力偶作用，如图所示。

若已知变形后中性层的曲率半径为ρ；材料的弹性模量为E。

根据d、ρ、E可以求得梁所承受的力偶矩M。

现在有4种答案，请判断哪一种是正确的。

习题7－1图(A) M＝Eπd 64ρ64ρ (B) M＝Eπd4Eπd3(C) M＝32ρ32ρ (D) M＝Eπd34 正确答案是。

7－2 关于平面弯曲正应力公式的应用条件，有以下4种答案，请判断哪一种是正确的。

(A) 细长梁、弹性范围内加载；(B) 弹性范围内加载、载荷加在对称面或主轴平面内；(C) 细长梁、弹性范围内加载、载荷加在对称面或主轴平面内；(D) 细长梁、载荷加在对称面或主轴平面内。

正确答案是 C _。

7－3 长度相同、承受同样的均布载荷q作用的梁，有图中所示的4种支承方式，如果从梁的强度考虑，请判断哪一种支承方式最合理。

l 5习题7－3图正确答案是7－4 悬臂梁受力及截面尺寸如图所示。

图中的尺寸单位为mm。

求：梁的1－1截面上A、 2B两点的正应力。

习题7－4图解：1. 计算梁的1－1截面上的弯矩：M=−⎜1×10N×1m+600N/m×1m×2. 确定梁的1－1截面上A、B两点的正应力：A点：⎛⎝31m⎞=−1300N⋅m 2⎟⎠⎛150×10−3m⎞−20×10−3m⎟1300N⋅m×⎜2My⎝⎠×106Pa=2.54MPa(拉应力)σA=z=3Iz100×10-3m×150×10-3m()12B点：⎛0.150m⎞1300N⋅m×⎜−0.04m⎟My⎝2⎠=1.62×106Pa=1.62MPa(压应力)σB=z=3Iz0.1m×0.15m127－5 简支梁如图所示。

工程力学课后习题答案_范钦珊(合订版)

Fw
习题 1—9 图
FT1
F Fw
T2
FN
习题 1—9 解图
7
1 一 10 图示压路机的碾子可以在推力或拉力作用下滚过 100mm 高的台阶。假定力 F 都是沿着杆 AB 的方向，杆与水平面的夹角为 30°，碾子重量为 250 N。试比较这两种情形下，碾子越过台阶所需力 F 的大小。
习题 1－10 图
即 (d + 3) sinθ = 2(4.5 − d ) sinθ 2 d +3=9−d
d =3
（2）
y
4 G
C
E
θ2
Dθ d −4.5 F O
FR
3
Ax
2
习题 2－2 解图
∴ F 点的坐标为（-3, 0）合力方向如图所示，作用线过 B、F 点；
tan θ = 4 3
AG = 6 sinθ = 6 × 4 = 4.8 5
nb2返回总目录下一章11ebook工程力学静力学与材料力学习题详细解答教师用书第2章范钦珊唐静静200612181第2章力系的简化21由作用线处于同一平面内的两个力f和2f所组成平行力系如图所示
eBook
工程力学
（静力学与材料力学）
习题详细解答
（教师用书） (第 1 章)
范钦珊唐静静
2006-12-18
FC C
A FA
习题 1－3e 解 1 图
C
BF
FB
FAx A
FAy
习题 1－3b 解 1 图
A FA
FB
α C
B
D
FD 习题 1－3d 解 1 图
D
F
C
F'c
B

工程力学(第二版)课后答案

1－1五个力作用于一点O，如图示。

图中方格的边长为10mm 。

试求此力系的合力。

解题思路：（1）由式（1－13）求合力在直角坐标轴上的投影；（2）由式（1－14）求合力的大小；（3）由式（1－15）求合力的方向。

答案：F R ＝669.5N , ∠(F R，i )＝34.901－2如图示平面上的三个力F1＝100N，F2＝50N，F3＝50N，三力作用线均过A点，尺寸如图。

试求此力系的合力。

解题思路：（1）由式（1－13）求合力在直角坐标轴上的投影；（2）由式（1－14）求合力的大小；（3）由式（1－15）求合力的方向。

答案：F R ＝161.2N , ∠(F R，F i)＝29.701－3试计算下列各图中的力F对点O之矩。

解题思路：各小题均由式（1－16）求力矩。

答案：略1－4如图所示的挡土墙重G 1＝75 kN ，铅直土压力G 2＝120 kN ，水平土压力F p ＝90 kN 。

试求三力对前趾A 点之矩的和，并判断挡土墙是否会倾倒。

解题思路：（1）由式（1－16）求三力对前趾A 点之矩的代数和；（2）若其值为负（顺时针转），则挡土墙不会翻倒。

答案：∑M A ＝－180kN.m ，不会倾倒。

1－5如图所示，边长为a 的正六面体上沿对角线AH 作用一力F 。

试求力F 在三个坐标轴上的投影，力F 对三个坐标轴之矩以及对点O 之矩矢。

解题思路：（1）由式（1－13）、（1－14）、（1－15）求合力的大小和方向；（2）由式（1－25）求力对三个坐标轴之矩；（3）由式（1－26）求力对坐标原点之矩。

答案：M x ＝0，Fa M y 33＝，Fa M 33z ＝－, k Fa j Fa M O 3333-＝1－7试画出下列各图中物体A ，构件AB 的受力图。

未画重力的物体重量不计，所有接触面均为光滑接触。

解题思路：（1）画出研究对象的轮廓形状；（2）画出已知的主动力；（3）在解除约束处按约束的性质画出约束力。

理论力学第2版范钦珊陈建平主编第二章力系的等效与简化

MO(F) (r F) (xi yj zk )(Fxi Fy j Fzk ) (yFz zFy )i (zFx xFz ) j (xFy yFx )k 力对点 O的矩在三个坐标轴上的投影为
MOx (F) yFz zFy
MOy (F) zFx xFz MOz (F) xFy yFx
M F rBA sin F d
（2）方向：转动方向；
与rBA转到F方向一致。
（3）作用面：力偶作用面。
也是rBA和F所在的平面。
rBA
二、力偶的表示方法：
1、用组成力偶的两个力F, F。
2、用力偶矩矢 M。 3、用力偶作用面内的旋转箭头。
无论用哪种方法表示，都应该能清楚的反映出力偶的三个要素。
MOz (F) xFy yFx
方法二：
设作用在刚体上的力F 的作用点为A，将力 F分解为两个力，其中 Fz // oz ，另一分力 Fxy
在过A且垂直于oz轴的平面xy内，则：
M z (F) Mo (Fxy ) Fxyd
方法三
先将空间力向直角坐标系的各坐标轴投影，将这些投影视为分力，分别确定这些分力对同一坐标轴之矩，然后取其代数和。
新作F用点的矩. B
MB MB (F) rBA F
F′
B
F″ B
F＝
F＝
A
A
说明：
F′ MB
A
①力平移的条件是附加一个力偶m。
②力的平移定理是力系简化的理论基础。
力向一点的平移定理实例
（a）
（b）
三.一般力系的简化
Fi Fi Mi MO (Fi )
汇交力系与力偶系等效代替一般任意力系.
3i
4
j
12k 9 j 12i

理论力学课后问题详解(范钦珊)

C(a-2)DR(a-3)(b-1)DR第1篇工程静力学基础第1章受力分析概述1－1 图a 、b 所示，Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。

试将同一力F 分别对两坐标系进行分解和投影，并比较分力与力的投影。

习题1－1图解：（a ）图（c ）：11 s i n c o s j i F ααF F +=分力：11 cos i F αF x = ， 11 s i n j F αF y =投影：αcos 1F F x = ， αs i n 1F F y =讨论：ϕ= 90°时，投影与分力的模相等；分力是矢量，投影是代数量。

（b ）图（d ）：分力：22)cot sin cos (i F ϕααF F x -= ，22sin sin j F ϕαF y = 投影：αcos 2F F x = ， )cos(2αϕ-=F F y讨论：ϕ≠90°时，投影与分量的模不等。

1－2 试画出图a 和b习题1－2图比较：图（a-1）与图（b-1）不同，因两者之F R D 值大小也不同。

（c ）2x（d ）1－3 试画出图示各物体的受力图。

习题1－3图B或(a-2)(a-1)(b-1)F(c-1) 或(b-2)(e-1)F(a)1－4 图a 所示为三角架结构。

荷载F 1作用在铰B 上。

杆AB 不计自重，杆BC 自重为W 。

试画出b 、c 、d 所示的隔离体的受力图，并加以讨论。

习题1－4图1－5 图示刚性构件ABC 由销钉A 和拉杆D 支撑，在构件C 点作用有一水平力F 。

试问如果将力F 沿其作用线移至D 或E （如图示），是否会改为销钉A 的受力状况。

解：由受力图1－5a ，1－5b和1－5c 分析可知，F 从C 移至E ，A 端受力不变，这是因为力F 在自身刚体ABC 上滑移；而F 从C 移至D ，则A 端受力改变，因为HG 与ABC 为不同的刚体。

1(f-1)'A(f-2)1(f-3)F F'F 1(d-2)AF yB 21(c-1)F A B1FDx y(b-2)1(b-3)F yB 2 F A B1B F习题1－5图AxF'(b-3)E D(a-3)B(b-2)(b-1)F 'CDDF EFBC(c)AxF1－6 试画出图示连续梁中的AC 和CD 梁的受力图。

范钦珊版材料力学习题全解第2章拉伸与压缩杆件的应力变形分析与强度计算

习题 2－2 习题 2－4 习题 2－6 习题 2－8 习题 2－10 习题 2－12 习题 2－14 习题 2－16 习题 2－18
2
材料力学习题详细解答之二第 2 章拉伸与压缩杆件的应力变形分析与强度计算
2－1 两根直径不同的实心截面杆，在 B 处焊接在一起，弹性模量均为 E＝200 GPa，受力和尺寸等均标在图中。
习题 2－8 图
解：由图(a)：
8
∑ F y = 0 ， F3 =
3 FP 5
4 5 4 3
∑ Fx = 0 ， F1 = − F3 = − FP
由图(b)：
∑ Fx = 0 ， F4 = 4 F3 = 4 FP
5 3
5 ∑ F y = 0 ， F2 = − F3 = − FP 3
| F1 |>| F2 |
m2，l=2
习题 2－4 图
解：根据已知条件，用截面法求得
5
FNA = 40 kN, FNB = 20 kN, FNE = 30 kN FNA 40 × 10 3 = = 200 MPa （1） σ A = A 2.0 × 10 − 4 F σ B = NB = 100 MPa A F NE σE = = 150 MPa A （2） σ max = σ A = 200 MPa（A 截面）
σa =
2． σ s =
FNa Ea FP =− Aa b0 hEs + 2b1hEa
− 200 × 109 × 385 × 103 0.03 × 0.05 × 200 × 109 + 2 × 0.02 × 0.05 × 70 × 109
= −175 MPa（压）
σa =
−175E a 70 = −175 = −61.25 MPa（压） Es 200

工程力学第2版课后习题答案_范钦珊主编_第1章_静力学基础

工程力学第2版课后习题答案_范钦珊主编_第1章_静力学基础
1.静力学研究的对象是（）
A、物体
B、流体
C、物质
D、刚体
2.两个大小为3N、4N的力合成一个力时,此合力最大值为（）
A、5N
B、7N
C、12N
D、1N
3.在研究拉伸与压缩应力应变时,我们把杆件单位长度的绝对变形称为（）
A、应力
B、线应变
C、变形
D、正应力
4.质点动力学基本方程为（D）
A、W=FS
B、P=MV
C、I=FT
D、F=ma
5.以下关于截面上内力的大小的结论哪一个是正确的?（）
A、与截面的尺寸和形状无关
B、与截面的尺寸有关,但与截面的形状无关
C、与截面的尺寸和形状有关
D、与截面的形状有关,但与截面的尺寸无关
6.当作用在质点系上外力系的主矢在某坐标轴上的投影为零时,则质点系质心的()
A．速度一定为零
B．速度在该轴上的投影保持不变
C．加速度在该轴上的投影一定不为零
D．加速度在该轴上的投影保持不变
7.一空间力系中各力的作用线均平行于某一固定平面,而且该力系又为平衡力系,则可列独立平衡方程的个数是()
A．6个
B．5个
C．4个
D．3个
8.已知点的运动方程为x=2t3+4,y=3t3－3,则其轨迹方程为()
A.3x+4y－36=0
B.3x－2y－18=0
C.2x－2y－24=0
D.2x－4y－36=0。

工程力学课后习题答案第二版

工程力学课后习题答案第二版工程力学是一门应用力学原理研究工程结构力学性质和变形规律的学科。

在学习这门课程时，课后习题是巩固和加深对知识的理解和掌握非常重要的一环。

本文将为大家提供工程力学课后习题第二版的答案，帮助大家更好地学习和应用这门学科。

第一章：力的基本概念和力的作用效果1. 一个力的大小和方向完全由它的作用点、作用方向和作用线的位置决定。

第二章：力的合成与分解1. 合力的大小等于各个力的矢量和的大小，方向与矢量和的方向一致。

2. 分解力是将一个力分解为两个或多个力，使其合力等于原力。

第三章：力的平衡1. 在力的平衡条件下，合力和合力矩均为零。

2. 平衡条件可以用来计算物体上未知力的大小和方向。

第四章：力的传递与支持1. 力的传递是指力在物体内部的传递和传递路径。

2. 支持是指物体受力后的支撑和承受能力。

第五章：力的作用点的变化1. 力的作用点的变化会改变物体的力学行为和受力情况。

2. 力的作用点的变化可以改变物体的平衡状态和变形情况。

第六章：力的矩1. 力的矩是力对某一点产生的力矩。

2. 力的矩可以用来计算物体的平衡条件和受力情况。

第七章：力的偶力系统1. 偶力系统是指力对称分布在物体上的力系统。

2. 偶力系统的合力为零，合力矩不为零。

第八章：力的等效1. 等效力是指具有相同外力效果的力。

2. 等效力可以用来简化力的计算和分析。

第九章：力的图解法1. 力的图解法是一种通过力的图示来计算和分析力的方法。

2. 力的图解法可以帮助我们更直观地理解和应用力的知识。

第十章：力的应用1. 力的应用是指将力的原理和方法应用于实际工程问题的过程。

2. 力的应用可以帮助我们解决各种力学问题和优化工程结构。

通过对工程力学课后习题第二版的答案的学习和理解，我们可以更好地掌握和应用这门学科。

同时，通过解答习题，我们可以提高自己的分析和解决问题的能力，培养工程思维和创新能力。

希望本文提供的答案能够帮助大家更好地学习和掌握工程力学知识。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

eBook
工程力学
（静力学与材料力学）
习题详细解答
（教师用书）
(第2章)
范钦珊唐静静
2006-12-18
习题2－2图
第2章力系的简化
2－1 由作用线处于同一平面内的两个力F 和2F 所组成平行力系如图所示。

二力作用线之间的距离为d 。

试问：这一力系向哪一点简化，所得结果只有合力，而没有合力偶；确定这一合力的大小和方向；说明这一合力矢量属于哪一类矢量。

解：由习题2－1解图，假设力系向C 点简化所得结果只有合力，而没有合力偶，于是，有
∑=0)(F C M ，02)(=⋅++−x F x d F ，
d
x =∴，F F F F =−=∴2R ，
方向如图示。

合力矢量属于滑动矢量。

2－2 已知一平面力系对A (3，0)，B (0，4)和C (－4.5，2)三点的主矩分别为：M A 、M B 和M C 。

若已知：M A ＝20 kN·m 、M B ＝0和M C ＝－10kN·m ，求：这一力系最后简化所得合力的大小、方向和作用线。

解：由已知M B = 0知合力F R 过B 点；
由M A = 20kN ·m ，M C = -10kN ·m 知F R 位于A 、C 间，且
CD AG 2=（习题2－2解图）
在图中设
OF = d ，
则
θcot 4=d
CD AG d 2)sin 3(==+θ （1） θθsin )2
5.4(sin d CE CD −== （2）
即
θθsin )2
5.4(2sin )3(d
d −
=+ d d −=+93 3=d
习题2－1图
习题2－1解图
R
∴ F 点的坐标为（-3, 0）
合力方向如图所示，作用线过B 、F 点； 3
4tan =
θ 8.45
4
6sin 6=×
==θAG 8.4R R ×=×=F AG F M A kN 6
258.420R ==
F 即 )kN 310,25(R
=F 作用线方程：43
4
+=
x y 讨论：本题由于已知数值的特殊性，实际G 点与E 点重合。

2－3三个小拖船拖着一条大船，如图所示。

每根拖缆的拉力为5kN 。

试求：(1)作用于大船上的合力的大小和方向。

(2)当A 船与大船轴线x 的夹角θ为何值时，合力沿大船轴线方向。

解：（1）由题意知 kN 5T T T ===C B A F F F 。

由习题2－3解图，作用于大船上的合力在x 、y 轴上的投影的大小分别为：
kN
19.1)45sin 10sin (sin40kN 5kN 12.3)cos45cos10(cos40kN 5R R =−⋅==++⋅=D
D
D
D D D y x F F
所以，作用于大船上的合力大小为：
kN 4.2119.112.3222R 2R R =+=+=y x F F F
合力与x 轴的夹角为： D 53.53
.1219
.1arctan
arctan
R R ===x
y F F α （2）当要使合力沿大船轴线方向，即合力R F 沿轴线x ，则0R =y F 0)45sin 10sin (sin kN 5R =−⋅=D D θy F 88.0sin =θ，
T T
A
F B F C
T F y
R
F
习题2－3解图
习题2－3图
所以，解得D 61=θ
2－4 齿轮受力F P ＝lkN ，压力角D 20=α，节圆直径D =160mm 。

试求力F P 对齿轮轴心O 的力矩。

解：力F P 对齿轮轴心O 的力矩为：
m
kN 075.002
cos )(P P ⋅−=+⋅
−=D F M O αF
2－5 胶带轮所受胶带拉力N 200T1=F ,N 100T2=F ，胶带轮直径D =160mm 。

试求力T1F ,T2F 对O 点的力矩。

解：力T1F ,T2F 对O 点的力矩为：
m
N 82
16
.0)100200(2)()(T2T1⋅=⋅−=⋅
−=D F F M O F
2－6 钢柱受到一偏心力l0kN 的作用，如图所示。

若将此力向中心线平移，得到一力(使钢柱压缩)和一力偶(使钢柱弯曲)。

已知力偶矩为800N·m ，求偏心距d 。

解：偏心距d 为：
80mm m 08.010kN 10m N 8003
==×⋅==
F M d
2－7 在设计起重吊钩时，要注意起吊重量F 对n-n 截面产生两种作用力，一为作用线与F 平行并过B 点的拉力，另一为力偶。

已知力偶矩为4000 N·m ，求力F 的大小。

解：力F 的大小为：
40kN N 104010
0mm 10m N 400033-=×=×⋅==
d M F
上一章返回总目录下一章
T1
F T2
F
习题2－5图
习题2－6图
习题2－7图
P
F
习题2－4图。