重庆市涪陵五中2009届高三上学期期末综合复习数学试题(理)
重庆市涪陵五中高级高三期末复习题数学文

重庆市涪陵五中高级高三期末复习题数学文 TTA standardization office【TTA 5AB- TTAK 08- TTA 2C】重庆市涪陵五中高2009级高三(上)期末复习题 数学试题(文)一.选择题(每小题5分,共60分,在每小题的四个选项中,只有一个符合题目要求)1.如果0,0><b a ,那么下列不等式中正确的是( )A .ba 11< B .b a <- C .22b a < D .||||b a > 2.直线1=y 与直线2y x =-的夹角为( )A . 12π B .6π C .4π D .3π 3.过点)3,1(-且垂直于直线032=+-y x 的直线方程为( )A . 012=-+y xB . 052=-+y xC .052=-+y xD .072=+-y x4.不等式组221030x x x ⎧-<⎨-<⎩的解集是( ) A . {}11x x -<< B .{}13x x -<< C .{}01x x << D .{}03x x <<5.抛物线2ax y =的准线方程是2=y ,则a 的值为 ( )A . 81B .81- C .8 D .8- 6.若4log log 33=+N M ,则N M +的最小值是( ) A .4 B .18 C .34 D .97.双曲线的两条准线将实轴三等分,则它的离心率为( )A .23B .3C .34D. 38.不等式)(},12|{0)(2x f y x x c x ax x f -=<<->--=则函数的解集为的图象( )9.过点)2,1(A 的直线l 将圆4)2(22=+-y x 分成两段弧,当劣弧所对的圆心角最小时,直线l 的斜率k 的值为( )A .21 B .22 C .23 D .3 10.已知点A )2,3(,F 是抛物线x y 22=的焦点,点P 是抛物线上一动点,则||||PF PA +取得最小值时的坐标是( )A .)0,0(B .)1,1(C .)2,2(D .)1,21(11.设12F F ,分别是双曲线1922=-y x 的左、右焦点.若点P 在双曲线上,且021=⋅PF PF=+( )AB. CD.12.若不等式012≥++ax x 对一切]21,0(∈x 成立,则a 的最小值为( ) A.0 B.2- C.52- D.3- 二.填空题(每小题4分,共16分,把答案填在题中所给的横线上)13.已知两条直线12:330,:4610.l ax y l x y +-=+-=,若12//l l ,则a =____14.在平面直角坐标系中,不等式组⎪⎩⎪⎨⎧≥≥+-≤-+00202y y x y x 所表示的平面区域的面积是___________15.将一张坐标纸折叠一次,使点)2,0(A 与)0,4(B 重合,且点)3,7(C 与点),(n m D 重合,则n m 2+的值为___________16.设12F F ,是椭圆()222210x y a b a b+=>>的两个焦点,以1F 为圆心,且过椭圆中心的圆与椭圆的一个交点为M ,若直线2MF 与圆1F 相切,则该椭圆的离心率是__________三.解答题(本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤)17.(本小题13分)求经过点)1,2(-A ,和直线1x y +=相切,且圆心在直线2y x =-上的圆的方程.18.(本小题13分)已知函数21(0)()21(1)x c cx x c f x c x -+<<⎧⎪=⎨⎪+<⎩ ≤满足29()8f c =. (1)求常数c 的值;(2)解不等式()18f x >+. 19.(本小题12分) 已知双曲线的方程是22169144.x y -=(1)求该双曲线的焦点坐标、离心率和渐近线方程;(2)设1F 、2F 是双曲线的左右焦点,点P 在双曲线上,且1232PF PF ⋅=,求12F PF ∠的大小.20.(本小题12分)某村计划建造一个室内面积为8002m 的矩形蔬菜温室.在温室内,沿左、右两侧与后侧内墙各保留1m 宽的通道,沿前侧内墙保留3m 宽的空地.当矩形温室的边长各为多少时?蔬菜的种植面积最大,最大种植面积是多少?21.(本小题12分)设椭圆()222210x y a b a b+=>>的左焦点为1(2,0)F -,左准线1l 与x 轴交于点(3,0)N -,过点N 且倾斜角为30︒的直线l 交椭圆于A 、B 两点.(1)求直线l 和椭圆的方程;(2)求证:点1(2,0)F -在以线段AB 为直径的圆上.22.(本小题12分)动直线m 的倾斜角是45,若m 与抛物线22(0)y px p =>交于A ,B 两点,且A ,B 两点的纵坐标之和为2(1)求抛物线的方程;(2)设直线1//m m ,直线1m 过抛物线的准线与x 轴的交点,M 为抛物线上一动点,求M 到直线1m 的最小距离;(3)线段AB 的中垂线交x 轴于P 点,当P 关于直线m 的对称点落在抛物线上时,求直线m 的方程。
重庆市2009届高三数学模拟试题分类汇编——立体几何
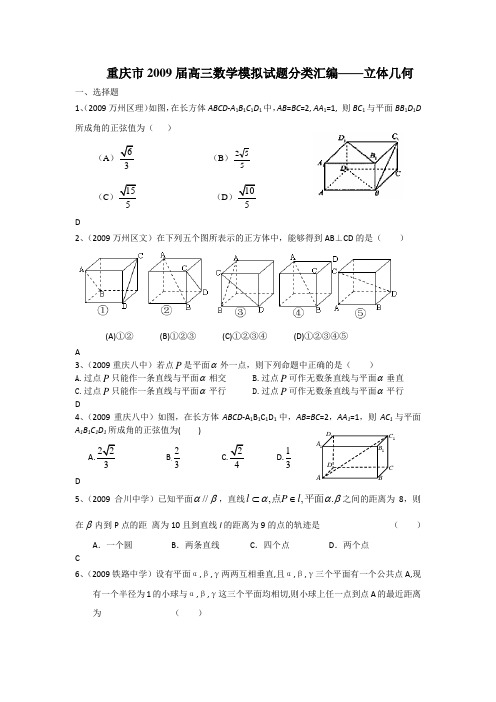
重庆市2009届高三数学模拟试题分类汇编——立体几何一、选择题1、(2009万州区理)如图,在长方体ABCD -A 1B 1C 1D 1中,AB =BC =2, AA 1=1, 则BC 1与平面BB 1D 1D 所成角的正弦值为( )(A )63(B )552(C )155 (D )105D2、(2009万州区文)在下列五个图所表示的正方体中,能够得到AB ⊥CD 的是( )(A)①② (B)①②③ (C)①②③④ (D)①②③④⑤ A3、(2009重庆八中)若点P 是平面α外一点,则下列命题中正确的是( )A.过点P 只能作一条直线与平面α相交B.过点P 可作无数条直线与平面α垂直C.过点P 只能作一条直线与平面α平行D.过点P 可作无数条直线与平面α平行 D4、(2009重庆八中)如图,在长方体ABCD -A 1B 1C 1D 1中,AB=BC =2,AA 1=1,则AC 1与平面A 1B 1C 1D 1所成角的正弦值为( ) A.223 B 23 C.24D.13D5、(2009合川中学)已知平面βα//,直线βαα.,,平面点l P l ∈⊂之间的距离为8,则在β内到P 点的距 离为10且到直线l 的距离为9的点的轨迹是 ( )A .一个圆B .两条直线C .四个点D .两个点C6、(2009铁路中学)设有平面α,β,γ两两互相垂直,且α,β,γ三个平面有一个公共点A,现有一个半径为1的小球与α,β,γ这三个平面均相切,则小球上任一点到点A 的最近距离为( )1A ABC D 1D1C 1BA .21 B .22 C .3 D .2-1C二、填空题1、(2009重庆八中)14.已知各顶点都在一个球面上的正四棱柱底面边长为1,体积为2,则这个球的表面积是________________ 4π2、(2009重庆八中)已知三棱锥P ABC -的三条侧棱PA 、PB 、PC 的长分别为a 、b 、c ,且两两垂直,并满足22()6a b c += ,当三棱锥体积最大时,侧面PAB 与底面ABC 成060,则三棱锥体积最大时a =__________________ 13、(2009合川中学)已知正四面体的棱长为6,则这个正四面体的外接球的体积是 .29π4、(2009合川中学)已知直线α⊂a ,直线l 与平面α所成的角为3π,则两直线a 、l 所成的角的范围是 .]2,3[ππ 5、(2009铁路中学) 现有4个条件:(其中a,b 表示不同的直线,α,β,γ表示不同的平面)①γ⊥α,γ⊥β ②a //b ,a ⊥α,b ⊥β③a ,b 异面,a ⊂α,b ⊂β,且a //β,b//α④α内距离为d 的两平行直线在β内的射影仍为两条距离为d 的平等行线其中能推出 α//β的条件是 (写出所有满足题意的条件的序号) ②③三、解答题 1、(2009重庆八中)17.如图,在四棱锥O ABCD -中,底面ABCD 是边长为2的菱形,OA ABCD ⊥底面, 2OA =,M 为OA 的中点,N 为BC 的中点,060ABC ∠= (1)证明:直线MN OCD 平面‖; (2)求异面直线AB 与MD 所成角的余弦值; (3)求点B 到平面OCD 的距离。
2009年重庆市高考数学试卷(理科)及答案

2009年重庆市高考数学试卷(理科)一、选择题(共10小题,每小题5分,满分50分)1.(5分)直线y=x+1与圆x2+y2=1的位置关系为()A.相切B.相交但直线不过圆心C.直线过圆心D.相离2.(5分)已知复数z的实部为﹣1,虚部为2,则=()A.2﹣i B.2+i C.﹣2﹣i D.﹣2+i3.(5分)(x+2)6的展开式中x3的系数是()A.20 B.40 C.80 D.1604.(5分)已知||=1,||=6,•(﹣)=2,则向量与向量的夹角是()A.B.C.D.5.(5分)不等式|x+3|﹣|x﹣1|≤a2﹣3a对任意实数x恒成立,则实数a的取值范围为()A.(﹣∞,﹣1]∪[4,+∞)B.(﹣∞,﹣2]∪[5,+∞)C.[1,2] D.(﹣∞,1]∪[2,+∞)6.(5分)锅中煮有芝麻馅汤圆6个,花生馅汤圆5个,豆沙馅汤圆4个,这三种汤圆的外部特征完全相同.从中任意舀取4个汤圆,则每种汤圆都至少取到1个的概率为()A.B.C.D.7.(5分)设△ABC的三个内角A,B,C,向量,,若=1+cos(A+B),则C=()A.B.C. D.8.(5分)已知,其中a,b∈R,则a﹣b的值为()A.﹣6 B.﹣2 C.2 D.69.(5分)三个互不重合的平面把空间分成六个部份时,它们的交线有()条.A.1 B.2 C.3 D.1或210.(5分)已知三角函数f(x)=sin2x﹣cos2x,其中x为任意的实数.求此函数的周期为()A.2πB.πC.4πD.﹣π二、填空题(共5小题,每小题5分,满分25分)11.(5分)若A={x∈R||x|<3},B={x∈R|2x>1},则A∩B=.12.(5分)若f(x)=a+是奇函数,则a=.13.(5分)将4名大学生分配到3个乡镇去当村官,每个乡镇至少一名,则不同的分配方案有种(用数字作答).14.(5分)设a1=2,,b n=,n∈N+,则数列{b n}的通项公式b n=.15.(5分)已知双曲线的左、右焦点分别为F1(﹣c,0),F2(c,0),若双曲线上存在一点P使,则该双曲线的离心率的取值范围是.三、解答题(共6小题,满分75分)16.(13分)设函数.(Ⅰ)求f(x)的最小正周期.(Ⅱ)若y=g(x)与y=f(x)的图象关于直线x=1对称,求当时y=g (x)的最大值.17.(13分)某单位为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为和,且各株大树是否成活互不影响.求移栽的4株大树中:(1)两种大树各成活1株的概率;(2)成活的株数ξ的分布列与期望.18.(13分)设函数f(x)=ax2+bx+k(k>0)在x=0处取得极值,且曲线y=f(x)在点(1,f(1))处的切线垂直于直线x+2y+1=0.(Ⅰ)求a,b的值;(Ⅱ)若函数,讨论g(x)的单调性.19.(12分)如图,在四棱锥S﹣ABCD中,AD∥BC且AD⊥CD;平面CSD⊥平面ABCD,CS⊥DS,CS=2AD=2;E为BS的中点,CE=,求:(Ⅰ)点A到平面BCS的距离;(Ⅱ)二面角E﹣CD﹣A的大小.20.(12分)已知以原点O为中心的椭圆的一条准线方程为,离心率,M是椭圆上的动点(Ⅰ)若C,D的坐标分别是,求|MC|•|MD|的最大值;(Ⅱ)如题(20)图,点A的坐标为(1,0),B是圆x2+y2=1上的点,N是点M 在x轴上的射影,点Q满足条件:,、求线段QB的中点P 的轨迹方程.21.(12分)设m个不全相等的正数a1,a2,…,a m(m≥7)依次围成一个圆圈,(Ⅰ)若m=2009,且a1,a2,…,a1005是公差为d的等差数列,而a1,a2009,a2008,…,a1006是公比为q=d的等比数列;数列a1,a2,…,a m的前n项和S n(n≤m)满足:S3=15,S2009=S2007+12a1,求通项a n(n≤m);(Ⅱ)若每个数a n(n≤m)是其左右相邻两数平方的等比中项,求证:a1+…+a6+a72+…+a m2>ma1a2a m.2009年重庆市高考数学试卷(理科)参考答案与试题解析一、选择题(共10小题,每小题5分,满分50分)1.(5分)(2009•重庆)直线y=x+1与圆x2+y2=1的位置关系为()A.相切B.相交但直线不过圆心C.直线过圆心D.相离【分析】求出圆心到直线的距离d,与圆的半径r比较大小即可判断出直线与圆的位置关系,同时判断圆心是否在直线上,即可得到正确答案.【解答】解:由圆的方程得到圆心坐标(0,0),半径r=1则圆心(0,0)到直线y=x+1的距离d==<r=1,把(0,0)代入直线方程左右两边不相等,得到直线不过圆心.所以直线与圆的位置关系是相交但直线不过圆心.故选B2.(5分)(2009•重庆)已知复数z的实部为﹣1,虚部为2,则=()A.2﹣i B.2+i C.﹣2﹣i D.﹣2+i【分析】由题意求出复数z,代入,复数分子、分母同乘分母的共轭复数,化简为a+bi(a,b∈R)的形式,可得选项.【解答】解:因为由条件知z=﹣1+2i,则=,故选A.3.(5分)(2009•重庆)(x+2)6的展开式中x3的系数是()A.20 B.40 C.80 D.160【分析】利用二项展开式的通项公式求出通项,令x的指数为3求出展开式中x3的系数.【解答】解:设含x3的为第r+1,则Tr+1=C6r x6﹣r•2r,令6﹣r=3,得r=3,故展开式中x3的系数为C63•23=160.故选D.4.(5分)(2009•重庆)已知||=1,||=6,•(﹣)=2,则向量与向量的夹角是()A.B.C.D.【分析】利用向量的运算法则及向量模的平方即是向量的平方求出,再利用向量的数量积公式求出向量的夹角余弦,求出向量夹角.【解答】解:∵==2.又,∴=3.即cos<a,b>=3=1×6cos<a,b>,得cos<a,b>=,∴a与b的夹角为,故选项为C.5.(5分)(2009•重庆)不等式|x+3|﹣|x﹣1|≤a2﹣3a对任意实数x恒成立,则实数a的取值范围为()A.(﹣∞,﹣1]∪[4,+∞)B.(﹣∞,﹣2]∪[5,+∞)C.[1,2] D.(﹣∞,1]∪[2,+∞)【分析】利用绝对值的几何意义,求出|x+3|﹣|x﹣1|的最大值不大于a2﹣3a,求出a的范围.【解答】解:因为|x+3|﹣|x﹣1|≤4对|x+3|﹣|x﹣1|≤a2﹣3a对任意x恒成立,所以a2﹣3a≥4即a2﹣3a﹣4≥0,解得a≥4或a≤﹣1.故选A.6.(5分)(2009•重庆)锅中煮有芝麻馅汤圆6个,花生馅汤圆5个,豆沙馅汤圆4个,这三种汤圆的外部特征完全相同.从中任意舀取4个汤圆,则每种汤圆都至少取到1个的概率为()A.B.C.D.【分析】本题考查的知识点是古典概型,我们计算出总的滔法种类,再计算满足条件“从中任意舀取4个汤圆,则每种汤圆都至少取到1个”所包含的基本事件个数,然后代入古典概型公式计算,即可得到答案.【解答】解:因为总的滔法C154,而所求事件的取法分为三类,即芝麻馅汤圆、花生馅汤圆、豆沙馅汤圆,取得个数分别按1,1,2;1,2,1;2,1,1三类,故所求概率P==.故选C.7.(5分)(2009•重庆)设△ABC的三个内角A,B,C,向量,,若=1+cos(A+B),则C=()A.B.C. D.【分析】利用向量的坐标表示可求=1+cos(A+B),结合条件C=π﹣(A+B)可得sin(C+=,由0<C<π可求C【解答】解:因为=又因为所以又C=π﹣(B+A)所以因为0<C<π,所以故选C.8.(5分)(2009•重庆)已知,其中a,b∈R,则a﹣b的值为()A.﹣6 B.﹣2 C.2 D.6【分析】先通分得,然后由极限的性质知,由此可以求出a﹣b的值.【解答】解:∵已知==2,∴,∴a=2,b=﹣4;∴a﹣b=6.故选D.9.(5分)(2009•重庆)三个互不重合的平面把空间分成六个部份时,它们的交线有()条.A.1 B.2 C.3 D.1或2【分析】三个互不重合的平面把空间分成六个部份有两种情形:一是其中两个平面平行,第三个平面都与它们相交;二是三个平面交于一条直线,考虑到两类即可解决.【解答】解:分两类:①当两个平面平行,第三个平面与它们相交时,有两条交线;②当三个平面交于一条直线时,有一条交线,故选D10.(5分)(2009•重庆)已知三角函数f(x)=sin2x﹣cos2x,其中x为任意的实数.求此函数的周期为()A.2πB.πC.4πD.﹣π【分析】首先由题目中已知三角函数f(x)=sin2x﹣cos2x求周期,需要把函数化为标准型,然后根据周期公式求解即可得到答案.【解答】解:因为f(x)=sin2x﹣cos2x=,所以函数的周期T=,故答案选择B.二、填空题(共5小题,每小题5分,满分25分)11.(5分)(2009•重庆)若A={x∈R||x|<3},B={x∈R|2x>1},则A∩B={x|0<x<3} .【分析】要求A与B的交集,先要求出两个集合的区间,解出绝对值不等式得到集合A,根据指数函数的增减性得到集合B,然后取两集合的公共部分即可得到交集.【解答】解:由|x|<3解得﹣3<x<3;由2x>1=20,根据指数函数y=2x为增函数得到x>0∴A={x|﹣3<x<3},B={x|x>0},则A∩B={x|0<x<3}.故答案为:{x|0<x<3}12.(5分)(2009•重庆)若f(x)=a+是奇函数,则a=﹣.【分析】充分不必要条件:若奇函数定义域为R(即x=0有意义),则f(0)=0.或用定义:f(﹣x)=﹣f(x)直接求a.【解答】解:函数的定义域为R,且为奇函数,则f(0)=a+=0,得a+=0,得a=﹣,检验:若a=﹣,则f(x)=+=,又f(﹣x)==﹣=﹣f(x)为奇函数,符合题意.故答案为﹣.13.(5分)(2009•重庆)将4名大学生分配到3个乡镇去当村官,每个乡镇至少一名,则不同的分配方案有36种(用数字作答).【分析】由题意知将4名大学生分配到3个乡镇去当村官,每个乡镇至少一名,需要先从4个人中选出2个作为一个元素看成整体,再把它同另外两个元素在三个位置全排列,根据分步乘法原理得到结果.【解答】解:∵将4名大学生分配到3个乡镇去当村官,每个乡镇至少一名,∴先从4个人中选出2个作为一个元素看成整体,再把它同另外两个元素在三个位置全排列,共有C24A33=36.故答案为:3614.(5分)(2009•重庆)设a1=2,,b n=,n∈N+,则数列{b n}的通项公式b n=2n+1.【分析】由题设条件得b n====2b n,由此能+1够导出数列{b n}的通项公式b n.【解答】解:由条件得:b n====2b n+1且b1=4所以数列{b n}是首项为4,公比为2的等比数列,则b n=4•2n﹣1=2n+1.故答案为:2n+1.15.(5分)(2009•重庆)已知双曲线的左、右焦点分别为F1(﹣c,0),F2(c,0),若双曲线上存在一点P使,则该双曲线的离心率的取值范围是(1,).【分析】不防设点P(x o,y o)在右支曲线上并注意到x o>a.利用正弦定理求得,进而根据双曲线定义表示出|PF1|和|PF2|代入求得e 的范围.【解答】解:不防设点P(x o,y o)在右支曲线上并注意到x o>a.由正弦定理有,由双曲线第二定义得:|PF1|=a+ex o,|PF2|=ex o﹣a,则有=,得x o=>a,分子分母同时除以a2,易得:>1,解得1<e<+1故答案为(1,)三、解答题(共6小题,满分75分)16.(13分)(2009•重庆)设函数.(Ⅰ)求f(x)的最小正周期.(Ⅱ)若y=g(x)与y=f(x)的图象关于直线x=1对称,求当时y=g (x)的最大值.【分析】(1)利用两角差的正弦公式及二倍角公式及化简三角函数;再利用三角函数的周期公式求出周期.(2)在y=g(x)上任取一点,据对称行求出其对称点,利用对称点在y=f(x)上,求出g(x)的解析式,求出整体角的范围,据三角函数的有界性求出最值.【解答】解:(1)f(x)===故f(x)的最小正周期为T==8(2)在y=g(x)的图象上任取一点(x,g(x)),它关于x=1的对称点(2﹣x,g(x)).由题设条件,点(2﹣x,g(x))在y=f(x)的图象上,从而==当时,时,因此y=g(x)在区间上的最大值为17.(13分)(2009•重庆)某单位为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为和,且各株大树是否成活互不影响.求移栽的4株大树中:(1)两种大树各成活1株的概率;(2)成活的株数ξ的分布列与期望.【分析】(1)甲两株中活一株符合独立重复试验,概率为,同理可算乙两株中活一株的概率,两值相乘即可.(2)ξ的所有可能值为0,1,2,3,4,分别求其概率,列出分布列,再求期望即可.【解答】解:设A k表示甲种大树成活k株,k=0,1,2B l表示乙种大树成活1株,1=0,1,2则A k,B l独立.由独立重复试验中事件发生的概率公式有P(A k)=C2k()k()2﹣k,P(B l)=C21()l()2﹣l.据此算得P(A0)=,P(A1)=,P(A2)=.P(B0)=,P(B1)=,P(B2)=.(1)所求概率为P(A1•B1)=P(A1)•P(B1)=×=.(2)解法一:ξ的所有可能值为0,1,2,3,4,且P(ξ=0)=P(A0•B0)=P(A0)•P(B0)=×=,P(ξ=1)=P(A0•B1)+P(A1•B0)=×+×=,P(ξ=2)=P(A0•B2)+P(A1•B1)+P(A2•B0)=×+×+×=,P(ξ=3)=P(A1•B2)+P(A2•B1)=×+×=.P(ξ=4)=P(A2•B2)=×=.综上知ξ有分布列ξ01234P从而,ξ的期望为Eξ=0×+1×+2×+3×+4×=(株).解法二:分布列的求法同上,令ξ1,ξ2分别表示甲乙两种树成活的株数,则ξ1:B(2,),ξ2:B(2,)故有Eξ1=2×=,Eξ2=2×=1从而知Eξ=Eξ1+Eξ2=.18.(13分)(2009•重庆)设函数f(x)=ax2+bx+k(k>0)在x=0处取得极值,且曲线y=f(x)在点(1,f(1))处的切线垂直于直线x+2y+1=0.(Ⅰ)求a,b的值;(Ⅱ)若函数,讨论g(x)的单调性.【分析】(Ⅰ)因为”函数在x=0处取得极值“,则有f'(0)=0,再由“曲线y=f(x)在(1,f(1))处的切线与直线x﹣2y+1=0相互垂直”,则有f'(1)=2,从而求解.(Ⅱ)由(Ⅰ)可得到:,令g'(x)=0,有x2﹣2x+k=0,因为还有参数k,由一元二次方程,分三种情况讨论,(1)当△=4﹣4k<0,函数g (x)在R上为增函数,(2)当△=4﹣4k=0,g(x)在R上为增函数(3)△=4﹣4k>0,方程x2﹣2x+k=0有两个不相等实根,则由其两根来构建单调区间.【解答】解:(Ⅰ)因f(x)=ax2+bx+k(k>0),故f'(x)=2ax+b又f(x)在x=0处取得极值,故f'(x)=0,从而b=0,由曲线y=f(x)在(1,f(1))处的切线与直线x+2y+1=0相互垂直可知该切线斜率为2,即f'(1)=2,有2a=2,从而a=1(6分)(Ⅱ)由(Ⅰ)知:、令g'(x)=0,有x2﹣2x+k=0(8分)(1)当△=4﹣4k<0,即当k>1时,g'(x)>0在R上恒成立,故函数g(x)在R上为增函数(10分)(2)当△=4﹣4k=0,即当k=1时,,K=1时,g(x)在R上为增函数(12分)(3)△=4﹣4k>0,即当0<k<1时,方程x2﹣2x+k=0有两个不相等实根当是g'(x)>0,故g(x)在上为增函数当时,g'(x)<0,故g(x)在上为减函数当时,g'(x)>0,故g(x)在上为增函数(14分)19.(12分)(2009•重庆)如图,在四棱锥S﹣ABCD中,AD∥BC且AD⊥CD;平面CSD⊥平面ABCD,CS⊥DS,CS=2AD=2;E为BS的中点,CE=,求:(Ⅰ)点A到平面BCS的距离;(Ⅱ)二面角E﹣CD﹣A的大小.【分析】(Ⅰ)根据线面平行的判定定理可知AD∥平面BCS,则从而A点到平面BCS的距离等于D点到平面BCS的距离,从而DS为点A到平面BCS的距离,在Rt△ADS中求出DS即可;(Ⅱ)过E点作EG⊥CD,交CD于点G,又过G点作GH⊥CD,交AB于H,根据二面角平面角的定义可知∠EGH为二面角E﹣CD﹣A的平面角,过E点作EF ∥BC,交CS于点F,连接GF,在Rt△FEG中,求出此角即可.【解答】解:(Ⅰ)因为AD∥BC,且BC⊂平面BCS,所以AD∥平面BCS,从而A点到平面BCS的距离等于D点到平面BCS的距离.因为平面CSD⊥平面ABCD,AD⊥CD,故AD⊥平面CSD,从而AD⊥SD,由AD∥BC,得BC⊥DS,又由CS⊥DS知DS⊥平面BCS,从而DS为点A到平面BCS的距离,因此在Rt△ADS中(Ⅱ)如图,过E电作EG⊥CD,交CD于点G,又过G点作GH⊥CD,交AB于H,故∠EGH为二面角E﹣CD﹣A的平面角,记为θ,过E点作EF∥BC,交CS于点F,连接GF,因平面ABCD⊥平面CSD,GH⊥CD,易知GH⊥GF,故.由于E为BS边中点,故,在Rt△CFE中,,因EF⊥平面CSD,又EG⊥CD故由三垂线定理的逆定理得FG⊥CD,从而又可得△CGF~△CSD,因此而在Rt△CSD中,,在Rt△FEG中,可得,故所求二面角的大小为20.(12分)(2009•重庆)已知以原点O为中心的椭圆的一条准线方程为,离心率,M是椭圆上的动点(Ⅰ)若C,D的坐标分别是,求|MC|•|MD|的最大值;(Ⅱ)如题(20)图,点A的坐标为(1,0),B是圆x2+y2=1上的点,N是点M 在x轴上的射影,点Q满足条件:,、求线段QB的中点P 的轨迹方程.【分析】(Ⅰ)由题设条件知焦点在y轴上,故设椭圆方程为(a>b >0).设,由准线方程.由此能够求出椭圆方程.从而得到点M的坐标为(±1,0)时上式取等号,|MC|•|MD|的最大值为4.(Ⅱ)设M(x m,y m),B(x B,y B)Q(x Q,y Q).因为,故x Q=2x N,y Q=y M,x Q2+y Q2=(2x M)2+y y=4.因为,(1﹣x Q﹣y Q)•(1﹣x N﹣y n)=(1﹣x Q)(1﹣x N)+y Q y N=0,所以x Q x N+y Q y N=x N+x Q﹣1.由此可导出动点P的轨迹方程为.【解答】解:(Ⅰ)由题设条件知焦点在y轴上,故设椭圆方程为(a>b>0).设,由准线方程得.由得,解得a=2,c=,从而b=1,椭圆方程为.又易知C,D两点是椭圆的焦点,所以,|MC|+|MD|=2a=4从而|MC|•|MD|,当且仅当|MC|=|MD|,即点M的坐标为(±1,0)时上式取等号,|MC|•|MD|的最大值为4.(II)如图(20)图,设M(x m,y m),B(x B,y B)Q(x Q,y Q).因为,故x Q=2x N,y Q=y M,x Q2+y Q2=(2x M)2+(y M)2=4 ①因为,(1﹣x Q,﹣y Q)•(1﹣x N,﹣y N)=(1﹣x Q)(1﹣x N)+y Q y N=0,所以x Q x N+y Q y N=x N+x Q﹣1.②记P点的坐标为(x P,y P),因为P是BQ的中点所以2x P=x Q+x B,2y P=y Q+y B由因为x N2+y N2=1,结合①,②得===故动点P的轨迹方程为21.(12分)(2009•重庆)设m个不全相等的正数a1,a2,…,a m(m≥7)依次围成一个圆圈,(Ⅰ)若m=2009,且a1,a2,…,a1005是公差为d的等差数列,而a1,a2009,a2008,…,a1006是公比为q=d的等比数列;数列a1,a2,…,a m的前n项和S n(n≤m)满足:S3=15,S2009=S2007+12a1,求通项a n(n≤m);(Ⅱ)若每个数a n(n≤m)是其左右相邻两数平方的等比中项,求证:a1+…+a6+a72+…+a m2>ma1a2a m.【分析】(1)利用等比数列的性质,用a1、d表示出a2009、a2008,结合已知,列方程即可解出a1、d,进而求出a n.(2)通过探求数列的周期性或利用反证法求解.【解答】解:(I)因a1,a2009,a2008,a1006是公比为d的等比数列,从而a2009=a1d,a2008=a1d2,由S2009=S2007+12a1得a2008+a2009=12a1,解得d=3或d=﹣4(舍去).∴d=3,又S3=3a1+3d=15.解得a1=2从而当n≤1005时,a n=a1+(n﹣1)d=2+3(n﹣1)=3n﹣1当1006≤n≤2009时,由a1,a2009,a2008,a1006是公比为d的等比数列得a n=a1d2009﹣(n﹣1)=a1d2010﹣n(1006≤n≤2009)因此(II)由题意a n2=a n﹣12a n+12(1<n<m),a m2=a m﹣12a12,a12=a m2a22得有①得④由①,②,③得a1a2a n=(a1a2a n)2,故a1a2a n=1.⑤又,故有.⑥下面反证法证明:m=6k若不然,设m=6k+p,其中1≤p≤5若取p=1即m=6k+1,则由⑥得a m=a6k+1=a1,而由③得,得a2=1,由②得,而④及⑥可推得a n=1(1≤n≤m)与题设矛盾同理若P=2,3,4,5均可得a n=1(1≤n≤m)与题设矛盾,因此m=6k为6的倍数由均值不等式得由上面三组数内必有一组不相等(否则a1=a2=a3=1,从而a4=a5═a m=1与题设矛盾),故等号不成立,从而a1+a2+a3++a6>6又m=6k,由④和⑥得a72++a m2=(a72++a122)++(a6k﹣52++a6k2)=(k﹣1)(a12++a62)=因此由⑤得a1+a2+a3++a6+a72++a m2>6+6(k﹣1)=6k=m=ma1a2a3a m。
2009年全国高考重庆卷(数理)试题

2009年全国高考重庆卷(数理)试题shuli一、单项选择题:(本题共6小题,每小题3分,共18分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.两个大小分别为F1和F2(F1<F2)的力作用在同一质点上,它们的合力的大小F满足答案:C2.一根容易形变的弹性导线,两端固定。
导线中通有电流,方向如图中箭头所示。
当没有磁场时,导线呈直线状态:当分别加上方向竖直向上、水平向右或垂直于纸面向外的匀强磁场时,描述导线状态的四个图示中正确的是答案:D3.两刚性球a和b的质量分别为ma和mb、直径分别为da和db (da>db )。
将a、b球依次放入一竖直放置、内径为的平底圆筒内,如图所示。
设a、b两球静止时对圆筒侧面的压力大小分别为f1和f2,筒底所受的压力大小为F.已知重力加速度大小为g。
若所以接触都是光滑的,则A.F=(ma+mb)g,f1=f2B.F=(ma+mb)g,f1≠f2C.mag<F<(ma+mb)g,f1=f2D.mag<F<(ma+mb)g,f1≠f2答案:A4.一长直铁芯上绕有一固定线圈M,铁芯右端与一木质圆柱密接,木质圆柱上套有一闭合金属环N,N可在木质圆柱上无摩擦移动。
M连接在如图所示的电路中,其中R为滑线变阻器,E1和E2为直流电源,S为单刀双掷开关。
下列情况中,可观测到N向左运动的是A.在S断开的情况下,S向a闭合的瞬间B.在S断开的情况下,S向b闭合的瞬间C.在S已向a闭合的情况下,将R的滑动头向c端移动时D.在S已向a闭合的情况下,将R的滑动头向d端移动时答案:C5.一平行板电容器两极板间距为d、极板面积为S,电容为ε0s/d,其中ε0是常量。
对此电容器充电后断开电源。
当增加两板间距时,电容器极板间A.电场强度不变,电势差变大B.电场强度不变,电势差不变C.电场强度减小,电势差不变D.电场强度较小,电势差减小答案:A6.近地人造卫星1和2绕地球做匀速圆周运动的周期分别为T1和T2,设在卫星1、卫星2各自所在的高度上的重力加速度大小分别为g1、g2,则答案:B二、多项选择题:(本题共4小题,每小题4分,共16分,在每小题给出的四个选项中,有二个或三个选项是符合题目要求的。
重庆市涪陵五中高2009级数学期末综合复习题(理科)

重庆市涪陵五中高2009级数学期末综合复习题(理科)一.选择题(每小题5分,共60分,在每小题的四个选项中,只有一个符合题目要求) 1.三条直线两两相交,可确定的平面个数是( )A .1B .1或3C .1或2D .32.若点),4(a P 到直线0134=--y x 的距离不大于3,则a 的取值范围是( ) A .)10,0[ B .]10,0( C .]10,0[ D .]10,1[3.某气象站预报天气的准确率是8.0,那么两次中恰有一次预报准确的概率是( ) A .96.0 B .64.0 C .32.0 D .16.04.五个同学坐在五个不同的座位上,但甲同学不坐其中某个座位,那么不同的坐法总数是( )A .48B .72C .96D .120 5.已知直线m l ,和平面α,则m l //的一个必要不充分条件是( )A .m l ,与α成等角B .αα⊥⊥m l ,C .αα⊂m l ,//D .αα//,//m l 6.若011212222)32(a x a x a x a x x n n n n n ++++=+--- ,则 ++-222n n a a 02a a ++等于( )A .n2 B .n3 C .)26(21n n - D .)26(21n n + 7.已知0)2(2)5(2=++--m x m x m 有一个正根和一个负根,且负根的绝对值大于正根,则m 的取值范围是( )A .94->m B .594<<-m C .50<<m D .52<<-m 8.设P 是060的二面角βα--l 内一点,⊥PA 面α,⊥PB 面β,B A ,分别为垂足,3,4==PB PA ,则AB 的长是( )A .32B .52C .37D .249.设21,F F 是双曲线22221(00)x y a b a b-=>>,的两个焦点,P 在双曲线上,若ac PF PF PF 2||||,02121=⋅=⋅(c 为半焦距),则双曲线的离心率为( )A .231+ B .251+ C .2 D .213- 10.在一个盒子里盛有若干个均匀的红球和白球,从中任取一个球,取到红球的概率为31,若从中任取两个球,取到的全是红球的概率为111,则盒子里一共有红球和白球( ) A .6 个 B .9个 C .12个 D .24个11.在北纬045圈上有B A ,两地,它们分别在东经050与东经0140圈上,则B A ,两地的球面距离是( )A .R π21B .R π31 C .R π41 D .R π22 12.甲乙独立解决同一问题,甲解决这个问题的概率是1P ,乙解决这个问题的概率是2P ,那么恰好有一人解决这个问题的概率是( )A .21P PB .)1()1(1221P P P P -+-C .211P P -D . )1)(1(121P P --- 二.填空题(每小题4分,共16分,把答案填在题中所给的横线上)13.圆1)1(22=-+y x 上的动点),(y x M 使不等式0≥++c y x 恒成立,则c 的取值范围是___________。
2009届重庆高三学生学业质量调研抽测一理

2009届重庆市高三学生学业质量调研抽测(一)数学试卷(理科)第I 卷(选择题,共50分)一、选择题:(本大题10个小题,每小题5分,共50分)在每小题给出的四个备选项中,只有一项是符合题目要求的.1.函数sin cos y x x =⋅的最小正周期为( )A .2π B .π C .2π D .4π 2.已知全集,U R =集合{}{}2,1,A x x B x x =>=≤则()()U U A C B B C A =( )A .∅B .{}12x x x <≥或C .{}12x x ≤<D .{}12x x <≤3.函数22(0)y x x x =-<的反函数为( )A .11)y x =≥-B .10)y x =+>C .11)y x =+≥D .10)y x =->4.若0,0,a b >>且1,a ≠则log 0a b >是(1)(1)0a b -⋅->的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件5.将直线1:2l y x =绕原点逆时针旋转60得直线2l ,则直线2l 到直线3:230l x y +-=的角为( )A .30B .60C .120D .1506.已知点P 在抛物线24x y =上,且点P 到x 轴的距离与点P 到焦点的距离之比为13,则点P 到x 轴的距离为( )A .12B .1C .14D .2 7.将函数()cos y f x x =的图象按向量(,1)4a π=平移得到22sin y x =的图象,那么函数()f x 可以是( )A .sin xB .cos xC .2sin xD .2cos x8.若点P 为共焦点的椭圆1C 和双曲线2C 的一个交点,1F 、2F 分别是它们的左右焦点.设椭圆离心率为1e ,双曲线离心率为2e ,若120PF PF ⋅=,则221211e e +=( ) A .1 B .2 C .3 D .49.在平行四边形ABCD 中,11,,34AE AB AF AD ==CE 与BF 相交于G 点.若,,AB a AD b ==则AG =( )A .2177a b +B .2377a b +C .3177a b +D .4277a b + 10.如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横纵坐标分别对应数列{}*()n a n N ∈的前12项,如下表所示:按如此规律下去,则200920102011a a a ++=( )A .1003B .1005C .1006D .2011第II 卷(非选择题,共100分)二.填空题:(本大题共6小题,每小题4分,共24分)将每小题正确的答案填在相应的横线上.11.函数()f x =________________________.12.方程2222210x y mx my m m +++++-=表示圆,则m 的取值范围是___________;13.已知数列{}n a 是等比数列,且45678910128,a a a a a a a ∙∙∙∙∙∙=则21510________;a a a ∙= 14.已知实数,x y 满足1210x x y x y m ≥⎧⎪-+≤⎨⎪+≤⎩,如果目标函数y Z x =的最大值为2,则实数___________m =;15.定义在实数集R 上的偶函数()f x 满足(1)(1)f x f x -=+.当[]2,3x ∈时,()f x x =,则[]2,0x ∈-时,()____________f x =;16.如图,以AB 为直径的圆有一内接梯形ABCD ,且//AB CD .若双曲线1C 以A 、B 为焦点,且过C 、D 两点,则当梯形的周长最大时,双曲线的离心率为_____________.三、解答题:(本大题共6小题,共76分).解答应写出文字说明,演算步骤或证明过程.17.(13分)已知33(cos ,sin ),(cos ,sin ),2222x x a x x b ==-若2().f x a b a b =⋅-+ (I )求函数()f x 的单调减区间;(II )若,,34x ππ⎡⎤∈-⎢⎥⎣⎦求函数()f x 的最大值和最小值. 18.(13分)设数列{}n a 满足12323...2(*).n n a a a na n N ++++=∈(I )求数列{}n a 的通项;(II )设2,n n b n a =求数列{}n b 的前n 项和n S .19.(13分)某厂家拟在2009年举行促销活动,经调查测算,该产品的年销量(即该厂的年产量)x 万件与年促销费用(0)t t ≥万元满足4(21k x k t =-+为常数)。
高一数学期末综合复习题(理科)

重庆市涪陵五中高级数学期末综合复习题(理科)选择题(每小题5分,共60分,在每小题的四个选项中,只有一个符合题目要求) 1.三条直线两两相交,可确定的平面个数是( )A .1B .1或3C .1或2D .32.若点),4(a P 到直线0134=--y x 的距离不大于3,则a 的取值范围是( ) A .)10,0[ B .]10,0( C .]10,0[ D .]10,1[3.某气象站预报天气的准确率是8.0,那么两次中恰有一次预报准确的概率是( ) A .96.0 B .64.0 C .32.0 D .16.04.五个同学坐在五个不同的座位上,但甲同学不坐其中某个座位,那么不同的坐法总数是( )A .48B .72C .96D .120 5.已知直线m l ,和平面α,则m l //的一个必要不充分条件是( )A .m l ,与α成等角B .αα⊥⊥m l ,C .αα⊂m l ,//D .αα//,//m l 6.若11212222)32(a x a x a x a x x n n n n n ++++=+--- ,则++-222n n a a 02a a ++等于( )A .n2 B .n3 C .)26(21nn - D .)26(21n n +7.已知0)2(2)5(2=++--m x m x m 有一个正根和一个负根,且负根的绝对值大于正根,则m 的取值范围是( )A .94->m B .594<<-m C .50<<m D .52<<-m8.设P 是060的二面角βα--l 内一点,⊥PA 面α,⊥PB 面β,B A ,分别为垂足,3,4==PB PA ,则AB 的长是( )A .32B .52C .37D .249.设21,F F 是双曲线22221(00)x y a b a b -=>>,的两个焦点,P 在双曲线上,若ac PF PF PF PF 2||||,02121=⋅=⋅(c 为半焦距),则双曲线的离心率为( )A .231+B .251+C .2D .213-10.在一个盒子里盛有若干个均匀的红球和白球,从中任取一个球,取到红球的概率为31,若从中任取两个球,取到的全是红球的概率为111,则盒子里一共有红球和白球( )A .6 个B .9个C .12个D .24个11.在北纬045圈上有B A ,两地,它们分别在东经050与东经0140圈上,则B A ,两地的球面距离是( )A .R π21B .R π31C .Rπ41D .R π2212.甲乙独立解决同一问题,甲解决这个问题的概率是1P ,乙解决这个问题的概率是2P ,那么恰好有一人解决这个问题的概率是( )A .21P PB .)1()1(1221P P P P-+- C .211P P - D . )1)(1(121P P --- 二.填空题(每小题4分,共16分,把答案填在题中所给的横线上)13.圆1)1(22=-+y x 上的动点),(y x M 使不等式0≥++c y x 恒成立,则c 的取值范围是___________。
2009年普通高等学校招生全国统一考试数学理试题(重庆卷,解析版)讲解

2009年普通高等学校招生全国统一考试数学理(重庆卷,解析版)本试卷满分150分,考试时间120分钟第Ⅰ卷考生注意:1.答题前,务必将自己的姓名、准考证号、填写清楚 ,并贴好条形码.请认真核准条形码上的准考证号、姓名和科目.2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.在试题卷上作答无效.3.本卷共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.4.所有题目必须在答题卡上作答,在试题卷上答题无效. 5.考试结束后,将试题卷和答题卡一并交回. 参考公式: 如果事件A B ,互斥,那么 ()()()P A B P A P B +=+如果事件A B ,相互独立,那么 ()()()P A B P A P B =如果事件A 在一次试验中发生的概率是P ,那么n 次独立重复试验中恰好发生k 次的概率()(1)(01,2)k kn k n n P k C P P k n -=-=,,,以R 为半径的球体积:34π3V R =一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个备选项中,只有一项是符合题目要求的。
1.直线1y x =+与圆221x y +=的位置关系为( ) A .相切 B .相交但直线不过圆心 C .直线过圆心D .相离【答案】B【解析】圆心(0,0)为到直线1y x =+,即10x y -+=的距离d ==,而01<<,选B 。
2.已知复数z 的实部为1-,虚部为2,则5iz=( ) A .2i - B .2i + C .2i -- D .2i -+【答案】A【解析】因为由条件知12z i =-+,则55(12)5102(12)(12)5i i i i i z i i ---+===--+--,所以选A 。
3.282()x x+的展开式中4x 的系数是( ) A .16B .70C .560D .1120【答案】【解析】设含4x 的为第2616316621,()()2rrr r r rr r T C x C xx--++==,1634r -= 所以4r =,故系数为:44621120C =,选D 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重庆市涪陵五中2009届高三上学期期末综合复习数学试题(理)
一.选择题(每小题5分,共60分,在每小题的四个选项中,只有一个符合题目要求)
1.三条直线两两相交,可确定的平面个数是( )
A .1
B .1或3
C .1或2
D .3
2.若点),4(a P 到直线0134=--y x 的距离不大于3,则a 的取值范围是( )
A .)10,0[
B .]10,0(
C .]10,0[
D .]10,1[
3.某气象站预报天气的准确率是8.0,那么两次中恰有一次预报准确的概率是( )
A .96.0
B .64.0
C .32.0
D .16.0
4.五个同学坐在五个不同的座位上,但甲同学不坐其中某个座位,那么不同的坐法总数是( )
A .48
B .72
C .96
D .120
5.已知直线m l ,和平面α,则m l //的一个必要不充分条件是( )
A .m l ,与α成等角
B .αα⊥⊥m l ,
C .αα⊂m l ,//
D .αα//,//m l
6.若011212222)32(a x a x a x a x x n n n n n ++++=+--- ,则 ++-222n n a a 02a a ++等于( )
A .n 2
B .n 3
C .)26(21n n -
D .)26(2
1n n + 7.已知0)2(2)5(2=++--m x m x m 有一个正根和一个负根,且负根的绝对值大于正根,则m 的取值范围是( )
A .94->m
B .59
4<<-m C .50<<m D .52<<-m 8.设P 是060的二面角βα--l 内一点,⊥PA 面α,⊥PB 面β,B A ,分别为垂足,3,4==PB PA ,
则AB 的长是( )
A .32
B .52
C .37
D .24
9.设21,F F 是双曲线22
221(00)x y a b a b
-=>>,的两个焦点,P 在双曲线上,若ac PF PF PF PF 2||||,02121=⋅=⋅(c 为半焦距)
,则双曲线的离心率为( ) A .231+ B .251+ C .2 D .2
13- 10.在一个盒子里盛有若干个均匀的红球和白球,从中任取一个球,取到红球的概率为
31,若从中任取两个球,取到的全是红球的概率为11
1,则盒子里一共有红球和白球( ) A .6 个 B .9个 C .12个 D .24个
11.在北纬045圈上有B A ,两地,它们分别在东经050与东经0140圈上,则B A ,两地的球面距离是( )
A .R π21
B .R π31
C .R π41
D .R π2
2 12.甲乙独立解决同一问题,甲解决这个问题的概率是1P ,乙解决这个问题的概率是2P ,那么恰好有一人解决这个问题的概率是( )
A .21P P
B .)1()1(1221P P P P -+-
C .211P P -
D . )1)(
1(121P P --- 二.填空题(每小题4分,共16分,把答案填在题中所给的横线上)
13.圆1)1(22=-+y x 上的动点),(y x M 使不等式0≥++c y x 恒成立,则c 的取值范围是___________。
14.已知∈∆A ABC ,平面α,090,6,//=∠=BAC BC BC α,AC AB ,与平面α分别成0045,30角,则BC 到平面α的距离为___________。
15.92)1(x
x +的展开式中的常数项为___________。
(用数字作答) 16.粒子A 位于数轴0=x 处,粒子每隔1秒向左或向右移动一个单位,设向右移动的概率为
32,向左移动的概率为3
1,则3秒后,粒子在1=x 处的概率为___________。
三.解答题(本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题13分)在一次口试中,要从20道题中随机抽出6道题进行回答,全部答对或答对5道题就获得优秀,答对其中的4道题就获得及格。
某考生会回答20题中的8道题,试求:
(1)他获得优秀的概率是多少? (2)他获得及格与及格以上的概率是多少?
18.(本小题13分)一圆与y 轴相切,圆心在直线03=-y x 上,在x y =上截得的弦长为72,求圆的方程。
19.(本小题12分)设甲、乙两人每次射击命中目标的概率分别为
43和5
4,且各次射击相互独立 (1)若甲、乙各射击一次,求甲命中但乙未命中目标的概率;
(2)若甲、乙各射击两次,求两人命中目标次数相等的概率。
20.(本小题12分)椭圆()22
2210x y a b a b
+=>>与直线01=-+y x 交于N M ,两点,且以MN 为直径的圆经过原点
(1)求
2211b a +的值;(2)若椭圆离心率在]22,33[上变化时,求椭圆长轴长的取值范围。
21.(本小题12分)如图:在四棱锥ABCD P -中,底面ABCD 是正方形,侧棱⊥PD 底面ABCD ,DC PD =,E 是PC 的中点,作PB EF ⊥交PB 于点F
(1)证明://PA 平面EDB ; (2)证明:⊥PB 平面EFD ;
(3)求二面角D PB C --的大小。
22.(本小题12分)如图:棱柱中111C B A ABC -,C A B A AA 111,,都与平面ABC 所成的角相等,a B A AB AC CAB ====∠10,90,D 为BC 上的点且//1C A 平面1ADB
求:(1)C A 1与平面1ADB 的距离;
(2)二面角C AB A --1的大小;(3)1AB 与平面ABC 所成角的大小。
参考答案
一.选择题:BCCCA ,DCCBC ,BB
二.填空题:13:12-≥
c 14:6 15:84 16:9
4 三.解答题:
17.解:
(1) 设他获得优秀的概率为1P ,则193835620
11258681=+=C C C C P (2) 设他获得及格或及格以上的概率为2P ,则9691331620212482=+=P C C C P 答:略
18.解:设该圆的标准方程为2
22)()(r b y a x =-+-,则由题意知: ()
⎪⎪⎪⎩⎪⎪⎪⎨⎧=⎪⎭⎫ ⎝⎛-+==-2
222||7||03r b a r
a b a ,解之得⎪⎩⎪⎨⎧===313r b a 或⎪⎩⎪⎨⎧=-=-=313r b a ,故所求圆的标准方程为: 9)1()3(22=-+-y x 或9)1()3(22=+++y x
19.解:(1)设甲命中但乙未命中目标的概率为1P ,则203)541(431=-⋅=P
; (2)设两人命中目标次数相等的概率为2P , 则400
193)54()43()541(54)431(43)54
1()43
1(221212222=⋅+-⋅⋅⋅-⋅⋅+-⋅-=C C P
20.解:设),(),,(2211y x N y x M ,由已知ON OM ⊥,故0=⋅
即02121=+y y x x ,而N M ,在直线01=-+y x 上,故有0)1)(1(2121=+-+-+x x x x 即01)(22121=++-x x x x …①,联立
⎩⎨⎧=-++-=0
1222222b a y a x b x y ,得02)(2222222=-+-+b a a x a x b a 所以2
22
222122221,2b a b a a x x b a a x x +-=+=+,将其代入①式有: 01222
22
22222=++-+-b a a b a b a a ,化简得21122=+b a (2)因为21122=+b a 且222c b a +=,所以有211222=-+c
a a
即2112222=-+e a a a ,所以2222)1(21e
e a --=,而]22,33[∈e 2a ≤≤ 21.解:
(1)证明:连接AC BD ,,设AC 与BD 的交点为O ,则O 是AC 的中点,又因为E 是PC 的中点 所以BDE PA BDE EO EO PA 面面且⊄⊂,,//,故EDB PA 面//;
(2)证明:又已知PB EF ⊥,而DC PD =,E 是PC 的中点,则PC DE ⊥
又因为⊥PD 底面ABCD ,ABCD BC 面⊂,所以PD BC ⊥,且DC BC ⊥,C PC DC =⋂ 故PCD BC 面⊥,而PCD DE 面⊂,所以BC DE ⊥
又因为B PB BC =⋂,所以PBC DE 面⊥,故PB DE ⊥,又因为E EF DE =⋂
所以⊥PB 平面EFD ;
(3)由(2)可知,EFD ∠为二面角D PB C --的平面角,设a DC PC 2== 则a EF a PB a BD a DE 66,32,22,2====,a PB BD PD DF 3
62=⋅= 在三角形EFD 中,8
32cos 222=⋅-+=∠DE DF DE EF DF EFD ,故83arccos =∠EFD 。
22.解:(1)a 21 (2)2arctan (3)552arctan。
