悬臂梁系统的脉冲控制
哈密顿原理推导悬臂梁的横向自由振动微分方程

一、概述悬臂梁是工程中常见的结构,其横向自由振动微分方程的推导是理解结构动力学的重要环节。
哈密顿原理是一个物理学上的基本原理,能够提供系统的最小作用量原理。
本文将利用哈密顿原理来推导悬臂梁的横向自由振动微分方程,旨在深入探讨结构动力学中的基本原理,为工程研究提供理论支持。
二、背景知识1. 悬臂梁悬臂梁是一种常见的结构形式,其特点是其中一端固定,另一端悬挂。
悬臂梁在工程中广泛应用,如桥梁、建筑、机械等领域。
2. 哈密顿原理哈密顿原理是经典力学中的一个基本原理,它描述了系统的最小作用量原理。
哈密顿原理是拉格朗日原理的推广,它通过最小化系统的作用量来描述系统的运动方程。
三、悬臂梁的横向自由振动悬臂梁的横向自由振动是指在无外界力的情况下,悬臂梁自身由于外界扰动而产生的振动。
我们可以利用哈密顿原理来推导悬臂梁的横向自由振动微分方程。
四、哈密顿原理推导1. 系统的广义坐标我们需要确定系统的广义坐标。
悬臂梁的横向自由振动可以使用横向位移作为广义坐标来描述。
假设悬臂梁的长度为L,质量为m,弹性系数为k,则系统的横向位移可以用函数y(x, t)来表示。
2. 系统的作用量系统的作用量S可以表示为积分形式,即S = ∫L dt其中L为拉氏量,表示系统的动能T和势能V的差值。
在悬臂梁的横向自由振动中,系统的动能可以用动能函数T表示,系统的势能可以用势能函数V表示。
则拉氏量可以表示为L = T - V其中动能函数T可以表示为T = ∫0L 1/2 * m * (∂y/∂t)^2 * dx势能函数V可以表示为V = ∫0L 1/2 * k * y^2 * dx3. 哈密顿原理的应用根据哈密顿原理,系统的作用量S在运动的路径上取极值。
我们可以通过变分法来求解作用量S的极值问题。
假设横向位移y(x, t)在固定边界条件下使得作用量S取得极值,则可以得到横向位移函数y(x, t)满足的运动方程。
五、悬臂梁的横向自由振动微分方程通过哈密顿原理的推导,我们可以得到悬臂梁的横向自由振动微分方程。
悬臂梁一阶固有频率及阻尼系数测试

说明:在下面的数据处理中,如1A,11d T,1δ,1ξ,1n T,1nω:表示第一次实1验中第一、幅值、对应幅值时间、变化率、阻尼比、无阻尼固有频率。
第二次和和三次就是把对应的1改成2或3.由于在编缉公式时不注意2,3与平方,三次方会引起误会,请老师见谅!!Ap0308104 陈2006-7-1 实验题目:悬臂梁一阶固有频率及阻尼系数测试一、实验要求以下:1. 用振动测试的方法,识别一阻尼结构的(悬臂梁)一阶固有频率和阻尼系数;2. 了解小阻尼结构的衰减自由振动形态;3. 选择传感器,设计测试方案和数据处理方案,测出悬臂梁的一阶固有频率和阻尼根据测试曲线,读取数据,识别悬臂梁的一阶固有频率和阻尼系数。
二、实验内容识别悬臂梁的二阶固有频率和阻尼系数。
三、测试原理概述:1,瞬态信号可以用三种方式产生,有脉冲激振,阶跃激振,快速正弦扫描激振。
2,脉冲激励用脉冲锤敲击试件,产生近似于半正弦的脉冲信号。
信号的有效频率取决于脉冲持续时间τ,τ越小则频率范围越大。
3.幅值:幅值是振动强度的标志,它可以用峰值、有效值、平均值等方法来表示。
频率:不同的频率成分反映系统内不同的振源。
通过频谱分析可以确定主要频率成分及其幅值大小,可以看到共振时的频率,也就可以得到悬臂梁的固有频率4、阻尼比的测定自由衰减法: 在结构被激起自由振动时,由于存在阻尼,其振幅呈指数衰减波形,可算出阻尼比。
一阶固有频率和阻尼比的理论计算如下:113344423.515(1)2=210;70;4;285;7800;,1212,, Ix= 11.43 cm Iy= 0.04 cm 0.004 2.810,,1x y y f kg E pa b mm h mm L mm mab a bI I I m m E L πρρ-----------⨯======⨯=⨯固x y =式惯性矩:把数据代入I 后求得载面积:S =bh=0.07m 把S 和I 及等数据代入()式,求得本41.65()HZ 固理悬臂梁理论固有频率f =阻尼比计算如下:2221111220,2,........ln ,,22;n d n n nd n d n T ii i j ji i i i j i i i j i n d i jn d n d d d d x dx c kx dt dtc e A A A A A T A T T ξωξωωξωωωξωωηηδξωωωωωπδπξ++-++++++++=++===≈==⨯⨯⨯==≈2二阶系统的特征方程为S 微分方程:m 很少时,可以把。
悬挂运动控制系统设计报告
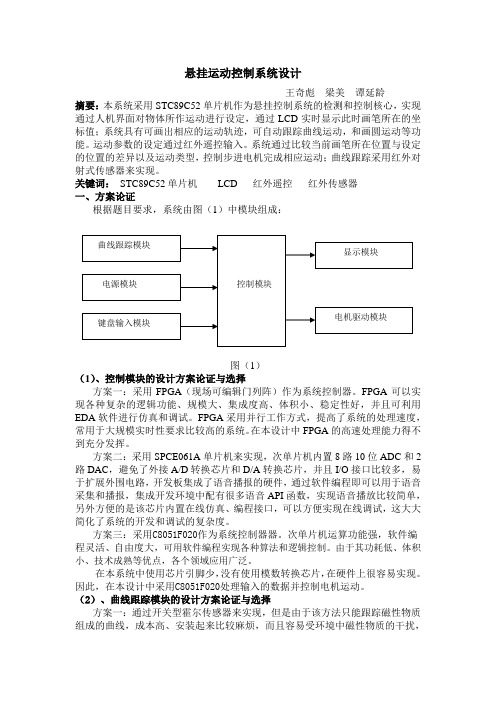
悬挂运动控制系统设计王奇彪 梁美 谭延龄摘要:本系统采用STC89C52单片机作为悬挂控制系统的检测和控制核心,实现通过人机界面对物体所作运动进行设定,通过LCD 实时显示此时画笔所在的坐标值;系统具有可画出相应的运动轨迹,可自动跟踪曲线运动,和画圆运动等功能。
运动参数的设定通过红外遥控输入。
系统通过比较当前画笔所在位置与设定的位置的差异以及运动类型,控制步进电机完成相应运动;曲线跟踪采用红外对射式传感器来实现。
关键词: STC89C52单片机 LCD 红外遥控 红外传感器一、方案论证根据题目要求,系统由图(1)中模块组成:图(1)(1)、控制模块的设计方案论证与选择方案一:采用FPGA (现场可编辑门列阵)作为系统控制器。
FPGA 可以实现各种复杂的逻辑功能、规模大、集成度高、体积小、稳定性好,并且可利用EDA 软件进行仿真和调试。
FPGA 采用并行工作方式,提高了系统的处理速度,常用于大规模实时性要求比较高的系统。
在本设计中FPGA 的高速处理能力得不到充分发挥。
方案二:采用SPCE061A 单片机来实现,次单片机内置8路10位ADC 和2路DAC ,避免了外接A/D 转换芯片和D/A 转换芯片,并且I/O 接口比较多,易于扩展外围电路,开发板集成了语音播报的硬件,通过软件编程即可以用于语音采集和播报,集成开发环境中配有很多语音API 函数,实现语音播放比较简单,另外方便的是该芯片内置在线仿真、编程接口,可以方便实现在线调试,这大大简化了系统的开发和调试的复杂度。
方案三:采用C8051F020作为系统控制器器。
次单片机运算功能强,软件编程灵活、自由度大,可用软件编程实现各种算法和逻辑控制。
由于其功耗低、体积小、技术成熟等优点,各个领域应用广泛。
在本系统中使用芯片引脚少,没有使用模数转换芯片,在硬件上很容易实现。
因此,在本设计中采用C8051F020处理输入的数据并控制电机运动。
(2)、曲线跟踪模块的设计方案论证与选择方案一:通过开关型霍尔传感器来实现,但是由于该方法只能跟踪磁性物质组成的曲线,成本高、安装起来比较麻烦,而且容易受环境中磁性物质的干扰,控制模块 曲线跟踪模块 电源模块键盘输入模块 显示模块 电机驱动模块抗干扰性能不好。
双脉冲前馈防摇摆控制原理

双脉冲前馈防摇摆控制原理
双脉冲前馈防摇摆控制是一种用于抑制系统振荡或摇摆的控制方法。
它基于双脉冲信号的原理,在系统输入中引入特定的脉冲信号来改变系统的动力学特性,从而实现对系统振荡或摇摆的抑制。
双脉冲前馈防摇摆控制的原理如下:
振荡或摇摆现象的分析:首先需要对系统的振荡或摇摆现象进行分析,包括振荡或摇摆的频率、幅度和相位等特性。
这有助于确定抑制振荡或摇摆所需的控制信号特性。
双脉冲信号生成:根据系统的振荡或摇摆特性,在控制系统中生成两个相位差为180度的脉冲信号。
这两个脉冲信号通常具有相同的幅度和宽度,但相位差使得它们的作用方向相反。
双脉冲信号的作用:将生成的双脉冲信号作为控制信号添加到系统的输入中。
由于双脉冲信号的相位差,它们会引起对系统动力学特性的改变。
其中一个脉冲信号对振荡或摇摆产生抑制作用,而另一个脉冲信号对其产生放大作用。
控制效果评估和调整:通过实时监测系统的响应和振荡或摇摆程度,对双脉冲信号的幅度和宽度进行调整,以达到最佳的抑制效果。
可以使用自适应控制算法或其他参数调整方法来实现对双脉冲信号的优化调整。
双脉冲前馈防摇摆控制通过引入相位差的双脉冲信号,
改变系统的动力学特性,从而抑制系统的振荡或摇摆现象。
这种控制方法通常应用于需要精确控制和抑制振荡或摇摆的系统,例如飞行器的姿态控制、机械臂的运动控制等。
悬臂梁冲击试验机使用方法

悬臂梁冲击试验机使用方法摘要:一、悬臂梁冲击试验机简介二、悬臂梁冲击试验机使用步骤1.设备开机及校准2.试样准备与安装3.设定试验参数4.开始试验5.试验结果分析三、注意事项与维护四、安全操作规程正文:悬臂梁冲击试验机是一种测试材料抗冲击性能的仪器设备,广泛应用于航空航天、汽车、建筑、材料科学研究等领域。
本文将详细介绍悬臂梁冲击试验机的使用方法,以帮助用户更好地掌握设备操作和试验技巧。
一、悬臂梁冲击试验机简介悬臂梁冲击试验机主要由主机、控制系统、数据采集系统等部分组成。
主机部分包括悬臂梁、摆锤、底座等部件,控制系统用于控制试验过程,数据采集系统用于实时记录试验数据。
试验时,将试样安装在悬臂梁上,通过摆锤施加冲击力,检测试样在冲击载荷下的破坏强度、能量吸收能力等性能指标。
二、悬臂梁冲击试验机使用步骤1.设备开机及校准在使用悬臂梁冲击试验机前,首先检查设备各部件是否完好,然后按照以下步骤进行开机和校准:(1)连接电源,开启主机电源,设备进入工作状态。
(2)操作控制系统,使摆锤上升至最高点,然后释放,观察摆锤是否能自由摆动,以确保设备正常运行。
(3)使用校准工具对设备进行校准,确保试验数据的准确性。
2.试样准备与安装根据试验标准和要求,制备合适的试样,并安装到悬臂梁上。
注意确保试样与悬臂梁的紧密接触,以避免试验过程中试样脱落。
3.设定试验参数根据试验需求,在控制系统上设置试验参数,如冲击速度、冲击次数等。
确保设置的参数符合试验标准。
4.开始试验确认试验参数无误后,启动试验。
控制系统将按照设定的参数进行试验,同时数据采集系统将实时记录试验数据。
5.试验结果分析试验结束后,根据数据采集系统记录的数据,分析试验结果,评估材料的抗冲击性能。
三、注意事项与维护(1)试验过程中,操作人员应密切关注试验情况,确保设备运行正常。
(2)定期对设备进行保养,保持设备清洁,检查各部件连接是否牢固,润滑部件,确保设备正常运行。
一种基于悬臂梁结构的微冲量测量方法

一种基于悬臂梁结构的微冲量测量方法王大鹏;叶继飞;李南雷;王青;王健博【摘要】为了对星载微推力器的单脉冲冲量进行非接触测量,提出了一种基于悬臂梁结构的测量方法.基于悬臂梁动力学模型,确定了测量系统传递函数,得到测量系统在结构上等效为无穷多个欠阻尼二阶子系统的并联.分析得到一阶子系统脉冲响应的最大位移与脉冲力冲量大小为线性关系,线性系数大小由一阶子系统的增益值、阻尼比及固有振动频率决定,在此基础上确定了冲量测量方法:对系统脉冲响应低通滤波得到一阶子系统脉冲响应后求取最大位移,结合标定得到线性系数即可求解冲量大小.线性系数的标定中,根据系统增益值与位移测量位置的刚度系数为倒数关系的特征,确定了一阶子系统增益值的标定方法,依据自由振动法确定了阻尼比及固有振动频率的标定方法.通过实验验证了测量方法的正确性,分析得到测量误差为7.287%.【期刊名称】《仪表技术与传感器》【年(卷),期】2019(000)003【总页数】6页(P39-44)【关键词】微推力器;微冲量测量;悬臂梁;参数标定;误差分析【作者】王大鹏;叶继飞;李南雷;王青;王健博【作者单位】航天工程大学,激光推进及其应用国家重点实验室,北京 101416;西安卫星测控中心,陕西西安 710043;航天工程大学,激光推进及其应用国家重点实验室,北京 101416;航天工程大学,激光推进及其应用国家重点实验室,北京 101416;西安卫星测控中心,陕西西安 710043;西安卫星测控中心,陕西西安 710043【正文语种】中文【中图分类】TH823;V4390 引言基于多颗微小卫星的编队、集群、星座,可承担更为复杂的空间任务[1],是未来卫星技术发展的趋势之一[2]。
微推力器是微小卫星的关键部件,其推进性能直接影响航天器空间任务的完成[3]。
单脉冲冲量是衡量微推力器推进性能的重要参数之一,大小通常在10-8~10-3 N·s量级,需要在工程应用前对其进行精确测量。
基于模糊神经PID控制器的掘进机悬臂运动控制系统

基于模糊神经PID控制器的掘进机悬臂运动控制系统刘国鹏【摘要】掘进机悬臂机构的负载变化具有很强的随机性.为能实现悬臂运动的精确控制和提高巷道成形质量,设计了将模糊神经PID控制器应用于掘进机悬臂运动的控制系统,即该控制器将控制掘进机悬臂液压缸运动的电液比例阀工作电流偏差e 和偏差变化率ec作为输入变量.重点介绍了控制器的结构组成、网络模型和学习过程.该系统利用Matlab/Simulink对电液比例阀的模型进行了仿真,结果表明该控制器不仅具有较强的鲁棒性,而且在被控对象参数发生较大变化时能自适应地调整PID参数,基本满足了掘进机悬臂运动控制的要求.【期刊名称】《煤矿机电》【年(卷),期】2015(000)004【总页数】5页(P1-4,8)【关键词】掘进机悬臂运动;模糊神经PID控制器;控制系统【作者】刘国鹏【作者单位】中煤科工集团太原研究院有限公司,山西太原030006【正文语种】中文【中图分类】TD63+2.20 引言掘进机悬臂动作机构是断面截割和巷道成形的主要执行机构,悬臂运动的精确控制是保证巷道成形效果和实现自动掘进或无人掘进的关键技术。
由于掘进断面煤岩分布的随机性和掘进机空间坐标原点与巷道中心轴线相对位置的时变性,要建立悬臂运动控制系统的数学模型十分困难[1]。
对于一般的非线性系统,模糊PID 控制器具有鲁棒性强、PID参数可自动调整和控制精度高等优点,但模糊结构一经确定,模糊规则和隶属函数就被确定下来,对于具有严重的时变性和不确定性的掘进机悬臂运动控制系统,其模糊PID 的控制效果不是很理想。
为此,本文提出将自适应模糊PID 控制器与神经网络控制器结合起来,既解决了PID 控制器参数的在线调整,又可有效地掌握模糊控制规则和隶属度函数[2],期望能实现对扰动及被控对象变化的快速平稳调节,控制掘进机悬臂在预定的巷道边界内按预定轨迹运动,提高巷道成形效率和成形质量。
1 掘进机悬臂运动控制系统系统框图如图1 所示,主要包括悬臂摆动速度的控制和悬臂边界定位的控制。
轴向运动悬臂梁横向振动的磁力控制

Na j g,2 0 1 ,Chn ) ni n 10 6 ia
第4 2卷 第 5期 21 0 0年 1 O月
南
京
航
空
航
天
大
学 学 报
V o1 4 o.5 . 2N
A t on utc J u n l fNa j gUnv r i fAe o a t s& s r a i s o r a ni iest o r n u i o n y c
OC .2 1 t 00
轴 向运 动悬 臂 梁 横 向振 动 的磁 力控 制
王 亮 陈怀 海 贺旭 ቤተ መጻሕፍቲ ባይዱ 游伟 倩
( 京 航 空 航 天 大学 振 动 工 程 研 究 所 , 京 ,1 0 6 南 南 201)
摘 要 : 究 了使 用 永 磁 铁 对 铁 质 轴 向运 动 悬 臂 梁 进 行 横 向振 动 的主 动 控 制 ; 立 了 自由 端 带 有 集 中质 量 的 轴 向 研 建 运 动 悬臂 梁 的 振 动 理论 模 型 , 通 过 振 动 实验 进 行 了修 正 。 过 理 论 分 析 和 实验 研 究 , 到 了 非接 触 磁 力 对 铁 质 并 通 得
悬臂 梁 的 作 用 规律 , 立 了使 用 非 接 触 磁 力 进 行 横 向振 动控 制 方 法 。对 上 述 控 制 方 法进 行 了模 拟 计 算 和 实 际 实 建 验, 结果 表 明 , 拟 计 算 与 实验 完全 吻 合 , 的振 动 得 到 了有 效 抑 制 。 模 梁 关键 词 : 向运 动 悬 臂 粱 ; 动 控 制 ; 轴 振 主动 控 制 ; 力 ; 接 触 磁 非 中 图分 类 号 : 2 O3 8 文献 标 识 码 : A 文 章 编 号 :0 52 1 (0 0 0— 580 10 —6 5 2 1 )50 6 —6
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第32卷第2期 、,ol-32 No.2 辽宁工程技术大学学报(自然科学版)
Journal of Liaoning Technical University(Natural Science) 2013年2月
Feb. 20l3 文章编号:1008.0562f2o13)o2.0241—04
悬臂梁系统的脉冲控制
李红武,李鑫 (南阳师范学院数学与统计学院,河南南阳473061) 摘要:为解决悬臂梁碰撞系统的混沌控制问题,利用脉冲微分系统理论和数值模拟技术,对悬臂粱系统的混沌 控制进行了研究.结果表明:当悬臂梁碰撞系统出现混沌现象时,若在满足一定条件的时间点上对该系统施加脉 冲信号,系统的混沌状态将会得到有效控制.利用龙格一库塔方法对施加了脉冲信号的系统进行了数值模拟,模拟 结果表明:在固定时间点处系统的混沌状态得到了有效控制,验证了脉冲控制方法的可行性与有效性.该方法对 研究建筑物的动力学行为具有一定的参考价值. 关键词:混沌控制;悬臂梁系统;非光滑系统;分岔;脉冲微分系统;脉冲控制;龙格一库塔方法;数值模拟 中图分类号:O 221 文献标志码:A
Impulsive control of cantilever beam system LI Hongwu.Li Xin (School of Mathematics and Statistics,Nanyang Normal University,Nanyang 473061,China) Abstract:In order to solve the chaos control problem in cantilever beam system,using the theory of impulsive differentia1 system and numerical method.the chaos control problem in cantilever beam system iS investigated in this study.The results show that when the chaos occurs in the cantilever beam system.at the time satisfying some conditions,if the impulsive signals are input into the system,the chaos of the system can be controlled.In addition, the numerical simulation on the system is conducted using Runge—Kutta method.The simulation results also show that the chaos in the system is controlled on a certain time.which demonstrates the feasibility and effectiveness of impulsive method.The proposed method is useful for future study on buildings’dynamic behavior. Key words:chaos control;cantilever beam system;non-smooth system;bifurcation;impulsive diferential system; impulsive control;Runge.Kutta method;numerical simulation
混沌控制与混沌同步是动力学研究的热点和 难点问题.混沌控制与混沌同步的方法很多:周期激 励控制法、常数激励控制法、随机噪声控制法、延 迟反馈控制法[1】、自适应控制法【2 4。、连续变量反馈 法、脉冲变量反馈法等.脉冲控制法以其控制所需能 量少,响应速度快,较强的抗噪声能力和鲁棒稳定 性,特别适用于经不起长期外部信号作用或外部信 号昂贵的项目.脉冲控制是在某些时间点上给系统 以外部控制信号,使得系统在极短时间内出现突然 的改变或干扰,从而使系统的运动状态发生改变. 脉冲信号作用下的动力系统总体上来说属于 一种非光滑系统,它会使系统的运动方程发生突然 的跳跃.冯进钤【5J利用Chebyshev多项式研究了带有 约束的随机Duffing系统的倍周期分岔问题,王林
泽[ 利用外加正弦驱动抑制了一类分段光滑系统的 混沌,Emans[ 考察了图1中一类带悬臂梁的碰振
.. 季 < 7— 图1悬臂梁碰撞系统 Fig.1 cantilever beam system
收稿日期:2012.08.20 基金项目:河南省自然科学基金资助项目(102300410219);河南省教育厅自然科学基金资助项目(2010B110018) 作者简介:李红武(1978-),男,河南淅川人,讲师,主要从事系统分析与应用数学方面研究. 本文编校:曾繁慧
g
,l1一口 242 辽宁工程技术大学学报(自然科学版) 第32卷 系统的分岔与混沌,用非线性和线性两种不同的方 法来描述系统的恢复力.脉冲控制方法以其独特的 优点,受到了众多学者的青睐:Yang ljJ等通过建 立脉冲系统的稳定性比较定理来判断系统是否是 稳定的,从而断定系统能否利用脉冲方法实现稳定 控制或者实现同步,为脉冲控制及同步理论奠定了 基础,大大推动了脉冲微分系统的发展.本文在此基 础上考察见图1悬臂梁碰撞系统的混沌控制问题. 见图1:长方体的质量为 悬臂梁的长度为 , 悬臂粱的弯曲弹性系数为 ,弹簧的弹性系数为k.M 受到大小为F(t')= COS(60t1的激励, 的位移为 X,M与弹性支撑面的距离为g.该系统广泛存在于现 实生活中,最常见的,该系统可作为建筑物的模拟, 用于研究建筑物的动力学行为.文献[7,14]考察了参 数变化对系统动力学行为的影响,并发现了该系统 的混沌吸引子.本文将在上述文献基础上,考察该悬 臂梁系统的脉冲控制问题,在满足X≥g时,对系 统施加外部脉冲控制信号,将系统由混沌状态控制 到周期运动状态. 1 悬臂梁系统的分岔与混沌 悬臂梁{亚瑾系统满足如卜刀程 ^ +c文+ ( )+ H( )( —g)=F0 cos(cot),(1) 式中,c是内部弹性系数, )是Heaviside步函数, )= . 恢复力S(x1描述为非线性形式, 厂( )=丁12EI + 432 EI 3・ 于是,式(1)可描述为一阶微分方程组 I =z, cos( 一( + 刮 ) 2
式中, = x, : c,
6= , = k
Y , = ,季=寺・’g ‘
文献[7,14]发现了系统的混沌吸引子,当参数取 a=0.038,季=0.6,e=20.0, =0.42,0.5≤d≤1.5 时,画出关于参数d的分岔图,见图2.
图2式(2)的分岔 Fig.2 bifurcation diagram of system(2) 取d=1.3,画出相应的相图和时间历程图,见图3, 系统处于混沌运动状态. 由于混沌及其复杂性和特有的“蝴蝶效应”, 往往会导致系统运动状态的不可预测性,可能导致 系统失控,甚至是彻底崩溃.在这种情况下,抑制混 沌,使系统运行到各种正常的有序状态,这就是混 沌控制的最初设想.下面将采用脉冲控制方法,将系 统由混沌运动状态控制到规律的周期运动状态.
.2 —1.5 .1 .0.5 0 0.5 1 JUU j) X fa1相图 图3式(2)在 1.3时的相图和相应的时间历程 Fig.3 phase portrait and time history as d=-I.3 400 450 500 f (b)时间历程
550
2 5 . 第2期 李红武,等:悬臂梁系统的脉冲控制 243 2 悬臂梁系统的脉冲控制 式中,k为控制参数
脉冲微分系统[15-18]一般可以表示为微分方程 J =厂( , ), (f, )芒M, (3) I ( )=F(f, (f)),(f, (f))
式中,,’:R× R , cR 为一开集.McRx.Q, F:M--) .定义脉冲发生时刻的跳跃量为 (f)= ( )一 ( ),其中 ( ) 姆 (f+ ),
( )= ( + )・从而有 ( )= (f, ( )) ( )+ (f),设集合M可以表示为Rx.Q中的
={(f, )lf= ( ), ), M= , 其中 ( )< ( )<…< ( )<…, ( )表示脉冲发生的时 刻,对任意 ∈ ,有lim ( ): ,则式(3)可 表示为 jX=厂(f, ) (辟 (X),k=1,2,…),(4) 【 ( )= ( )+ (f) ( ),Ji}:1,2,…)
式(4)第一个方程描述了系统连续渐变过程,称 作连续部分,是用微分方程描述的;第二个式子刻 画了系统的脉冲效应,称为脉冲部分,是用差分方 程描述的.f ( 1决定了脉冲发生的时间,称作脉冲 时刻;AX(t1描述了脉冲跳跃的强度,称为脉冲函 数.其中的 f 1如果是 的函数,则称式(4)为 变时刻脉冲微分系统;若其中的 f 1是随机发生 的,则称式(4)为随机时刻脉冲微分系统.特别地, 如果ff(X)三ri, 是一常数,则式(4)表示为 j =厂(f,X) (f≠ ,k=1 2一), (5) I ( )= (,一)+ (f)(f k=1 2。‘)
称式(5)为固定时刻脉冲微分系统.目前讨论得较 充分的结果主要集中在固定脉冲时刻的脉冲微分 式(5),对变脉冲时刻的脉冲微分系统和随机时刻 脉冲微分系统的结果并不多见,研究方法上仍然缺 乏有效手段.为此,采用脉冲控制方法,对悬臂梁式 (2)进行脉冲控制,具体如下: 当Y<季时, f 一 : (6) os(cot)一 ]
当Y≥季时, f=z ,一 { : c。s( )一 一 ( + 36 3)一 ( 一季)。
J z=(1一k)z
3 系统脉冲控制的数值模拟 为验证上述脉冲方法的混沌控制效果,利用四 阶龙格一库塔方法对施加脉冲信号的悬臂梁式(7) 进行动力学行为数值模拟.在上述参数取值
=0.038,季=0.6,e=20.0,CO=0.42,d=1.3相同的条 件下,取0≤k≤0.1,画出Y随k变化图形见图4.
0 0.02 O.04 0.06 0.08 0.1 k 图4 Y随k变化
(a)相图 300 310 320 330 340 350 360 370 380 390 400 f (b)时间历程 图5 k=O.05时的相图和时间历程 Fig.5 phase portrait and time history as七=0.05
