异面直线所成的角练习题
异面直线所成的角专题训练
异面直线所成的角专题训练1.在正方体ABCD-A1B1C1D1中，异面直线AC和XXX所成的角为多少度？答案：90度。
2.在正方体ABCD-A1B1C1D1中，AB的中点M，DD1的中点N，则异面直线B1M与CN所成的角是多少度？答案：60度。
3.在正方体ABCD-A1B1C1D1中，E为线段AC的中点，则异面直线DE与B1C所成角的大小为多少度？答案：无法确定，题目中缺少信息。
4.在三棱锥ABC-A1B1C1中，底面为正三角形，侧棱垂直于底面，AB=4，AA1=6.若E是棱BB1上的点，且BE=B1E，则异面直线A1E与AC1所成角的余弦值为多少？答案：1/3.5.在三棱锥P-ABC中，△ABC为等边三角形，△PAC为等腰直角三角形，PA=PC=4，平面PAC⊥平面ABC，D为AB的中点，则异面直线AC与PD所成角的余弦值为多少？答案：-1/2.6.在棱长为1的正方体ABCD-A1B1C1D1中，M和N分别为A1B1和BB1的中点，直线AM与CN所成角的余弦值是多少？答案：-3/5.7.在直三棱柱ABC-A1B1C1中，AC⊥BC，且CA=CC1=10，则直线B1C与直线AB1所成角的余弦值为多少？答案：5/13.8.在直三棱柱ABC-A1B1C1中，AA1=2，A1B1=2，AB⊥BC，点M是AC1的中点，则异面直线MB与AA1所成角的余弦值为多少？答案：-1/3.9.正三棱锥A-PBC的侧棱两两垂直，D，E分别为棱PA，BC的中点，则异面直线PC与DE所成角的余弦值为多少？答案：-3/5.10.在正方体ABCD-A1B1C1D1中，点E为BC的中点，点F为B1C1的中点，则异面直线AF与C1D所成角的大小为多少度？答案：无法确定，题目中缺少信息。
中，ABCD是正方形，E是AD的中点，F是BC的中点，异面直线EF与AC所成的角的正弦值为(。
)A．12B．13C．23D．110.在正方体ABCD A1B1C1D1中，E是AD的中点，F是BC的中点，异面直线EF与直线AC所成的角的正切值为(。
人教A版高中数学必修第二册强化练习题-8.6.1直线与直线垂直(含答案)
人教A版高中数学必修第二册8.6 空间直线、平面的垂直8.6.1 直线与直线垂直基础过关练题组一 求异面直线所成的角1.(2024安徽六安期中)如图,已知正四棱锥P-ABCD的所有棱长均为2,E为棱PA的中点,ABCD-A1B1C1D1中,E,F与直线AD1所成角的大小为在正方体ABCD-A(1)求异面直线CD1与BC1所成的角;(2)求证:MN∥平面ABCD.题组二 空间两条直线所成角的应用5.(多选题)(2024山东德州夏津第一中学月考)已知E,F 分别是三棱锥P-ABC 的棱PA,BC 的中点,且PC=6,AB=8.若异面直线PC 与AB 所成角的大小为60°,则线段EF 的长可能为( )A.7B.13C.5D.376.在长方体ABCD-A 1B 1C 1D 1中,底面ABCD 是边长为1的正方形,异面直线AB 与A 1C 所能力提升练在正四面体S-ABC 中3.4.(2024贵州凯里第一中学模拟)平面α过直三棱柱ABC-A 1B 1C 1的顶点B 1,平面α∥平面ABC 1,平面α∩平面BB 1C 1C=l,且AA 1=AB=BC,AB ⊥BC,则A 1B 与l 所成角的正弦值为( )A.32 B.22 C.12 D.335.已知正三棱柱ABC-A 1B 1C 1的侧面积为12,当其外接球的表面积取最小值时,异面直线AC 1与B 1C 所成角的余弦值为 .题组二 异面直线所成角的应用6.(2024上海青浦高级中学期末)在棱长为1的正方体ABCD-A 1B 1C 1D 1中,P 为底面ABCD 内(包括边界)的动点,满足直线D 1P 与CC 1所成角的大小为π6,则线段DP 扫过的面积为( )A.π12B.π6C.π3D.π27.(2024广东阳江期末)在四面体A-BCD 中,AB=CD=1,BC=2,且AB ⊥BC,CD ⊥BC,异面直线AB 与CD 所成的角为π3,则该四面体外接球的表面积为 .8.(2022河南濮阳第一高级中学月考)在四棱柱ABCD-A 1B 1C 1D 1中,侧面都是矩形,底面ABCD 是菱形且AB=BC=23,∠ABC=120°,若异面直线A 1B 和AD 1所成的角为90°,求AA 1的长度.答案与分层梯度式解析8.6 空间直线、平面的垂直8.6.1 直线与直线垂直基础过关练1.B2.C3.A 5.BD 6.DPC,EO=1PC=1,在所以BB1∥平面AEF,平面DBB1,所以BB1又与直线AD1所成的角为连接B N,CN,因为点M为A1B1的中点,A1B1=AB,所以MB1=AN,又MB1∥AN,所以四边形ANB1M为平行四边形,所以AM∥B1N,所以异面直线AM与B1C所成的角为∠CB1N(或其补角),设∠CB1N=θ,在正△ABC中,由AB=4,可得CN=23,在直角△BNB1中,BB1=3,BN=2,所以B1N=22+32=13,在直角△BCB1中,BC=4,BB1=3,所以B1C=42+32=5,在△B 1CN 中,由余弦定理的推论可得cos θ=B 1C 2+B 1N 2-C N 22B 1C·B 1N=52+(13)2-(23)22×5×13=135.故选A.4.解析 (1)连接A 1B,A 1C 1,因为A 1D 1=BC 且A 1D 1∥BC,所以四边形A 1D 1CB 为平行四边形,所以CD 1∥A 1B,则∠A 1BC 1或其补角为异面直线CD 1与BC 1所成的角,易知A 1C 1=A 1B=BC 1,所以△A 1C 1B 为等边三角形,所以∠A 1BC 1=60°,所以异面直线CD 1与BC 1所成的角为60°.(2)证明:连接C 1D,BD,则N 为C 1D 的中点,又M 为BC 1的中点,所以MN ∥BD,又MN ⊄平面ABCD,BD ⊂平面ABCD,所以MN ∥平面ABCD.5.BD 如图,取AC 的中点H,连接EH,FH,因为E,F 分别为PA,BC 的中点,PC=6,AB=8,所以AB ∥HF,HE ∥PC,HF=4,HE=3,所以异面直线PC 与AB 所成的角即为∠EHF(或其补角),所以∠EHF=60°或∠EHF=120°.当∠EHF=60°时,根据余弦定理的推论得cos ∠EHF=HE 2+H F 2-E F 22HE ·HF =9+16−EF 224=12,解得EF=13;当∠EHF=120°时,根据余弦定理的推论得cos ∠EHF=HE 2+H F 2-E F 22HE ·HF =9+16−EF 224=-12,解得EF=37.故选BD.易错警示 通过立体图形无法直接判断∠EHF是锐角还是钝角,因此∠EHF可能是异面直线所成的角,也可能是其补角,所以需要进行分类讨论.6.D ∵AB∥DC,∴∠A1CD(或其补角)即为异面直线AB与A1C所成的角,由图可知∠A1CD为.锐角,∴∠A1CD=π3设DD1=x,连接A1D,则A1C=12+12+x2=2+x2,A1D=x2+1.在∴∴7.垂直于上底面于点D,则ADD∥O2A,1∴或其补角,当在当在Rt△ABD中,AB=BD2+A D2=2.综上,AB=2或AB=2.能力提升练1.A2.A3.C4.A 6.A1.A 取SM的中点E,连接EN,AE,如图,∵N是SB的中点,∴EN∥MB,EN=12MB,∴∠ANE或其补角即为异面直线BM与AN所成的角.设正四面体的棱长为4,∵M是SC的中点,N是SB的中点,△SAB和△SBC均为正三角形,∴BM⊥SC,AN⊥SB,且BM=AN=23,∴EN=3,在△ASE中,由余弦定理得AE2=SA2+SE2-2SA·SE·cos∠ASE=16+1-2×4×1×12=13,在△ANE中,由余弦定理的推论得cos∠ANE=AN2+N E2-A E22AN·NE =12+3−132×23×3=16,∴异面直线BM与AN所成角的余弦值为16.故选A.2.A 如图,过点A作AN∥OM,交圆O于点N,连接ON,PN,则∠PAN或其补角即为异面直线OM与AP所成的角,设AO=ON=1,易知∠OAN=∠ONA=∠AOM=30°,则AN=3,因为轴截面PAB为等腰直角三角形,所以PN=PA=2,在△APN中,由余弦定理的推论得cos∠PAN=PA2+A N2-P N22PA·AN =2+3−226=64,所以异面直线OM与AP所成角的余弦值为64.故选A.3.C 如图,连接AD1,AP,易得AD1∥BC1,所以∠AD1P(或其补角)即为异面直线D1P与BC1所成的角.设正方体的棱长为1,DP=x,x∈[0,1],在△AD 1P 中,AD 1=2,AP=D 1P=1+x 2,故cos ∠AD 1P=(2)2+(1+x 2)2-(1+x 2)222·1+x 2=221+x 2,∵x ∈[0,1],∴cos ∠AD 1P=221+x2∈又∠AD 1P 是△AD 1P 的内角,∴∠AD 1P 故选C.B 1则ABC 1,所以B 1C 2∥平面⊂由小题速解 因为平面α∥平面ABC 1,平面α∩平面BB 1C 1C=l,平面ABC 1∩平面BB 1C 1C=BC 1,所以l ∥BC 1,则A 1B 与l 所成的角为∠A 1BC 1(或其补角),下同解析.5.答案 514解析 设正三棱柱的底面边长为a,高为h,外接球的半径为R,由题意知3ah=12,即ah=4,易得△ABC 外接圆的半径r=a2sin π3=a3,则R 2=r 2+ℎ24=a 23+ℎ24≥aℎ3=43,当且仅当a=32h 时取等号,此时外接球的表面积最小.将三棱柱补成一个四棱柱,如图,连接DB 1,DC,则AC 1∥DB 1,∴∠DB 1C(或其补角)为异面直线AC 1与B 1C 所成的角,易得B 1C=DB 1=a 2+ℎ2,DC=3a,∴cos ∠DB 1C=2(a 2+ℎ2)-3a 22(a 2+ℎ2)=514.解题技法 补形平移是常用的一种作平行线的方法,一般是补一个相同形状的几何体,构成一个特殊的几何体,方便作平行线,如此题将三棱柱补成一个四棱柱.6.A 因为DD 1∥CC 1,所以直线D 1P 与CC 1所成的角即为DD 1与D 1P 所成的角,易知DD 1⊥PD,所以DD 1与D 1P 所成的角为∠DD 1P,即∠DD 1P=π6,故tan ∠DD 1P=DPDD 1=33,即DP=33,所以点P 的轨迹是以D 为圆心,33为半径的圆的四分之一,故线段DP 扫过的面积为14π×=π12.故选A.7.答案 16π3或8π解析 由题意,可以将四面体A-BCD 补成一个直三棱柱,如图所示.∵CD∥BE,∴直线AB与CD所成的角为∠ABE或其补角,∵异面直线AB与CD所成的角为π3,∴∠ABE=π3或∠ABE=2π3.设△ABE外接圆的半径为r,当∠ABE=π3时,AE=BE=AB=1,则2r=1sinπ3,解得r=33;当∠ABE=2π3时,AE=3,则则8.BC且A1D1=BC,所以A1B∥CD1,所成的角为∠AD1C,故∠AD1均为矩形,设在故。
空间角(异面直线所成角,线面角,二面角)
第四讲 空间角（异面直线所成角线面角二面角）A 组题一、选择题1.下面正确的序号是①两直线的方向向量所成的角就是两条直线所成的角.②直线的方向向量和平面的法向量所成的角就是直线与平面所成的角. ③两个平面的法向量所成的角是这两个平面所成的角.④两异面直线夹角的范围是(00,90⎤⎦，直线与平面所成角的范围是0090⎡⎤⎣⎦，，二面角的范围是[0，1800] ( ).A.①B.②C.③D.④【答案】D【解析】对于①，因为两异面直线夹角的范围是(00,90⎤⎦，而两直线的方向向量所成的角可能为钝角. 所以①错. 对于②，直线的方向向量和平面的法向量所成的角是直线与平面所成的角或其补角. 所以②错.对于③，两个平面的法向量所成的角是这两个平面所成的角是这两个平面所成的角或其补角. 所以③错. 故选D .2.如图，在正方体ABCD －A′B′C′D′中，AB 的中点为M ，DD′的中点为N ，则异面直线B′M 与C N 所成的角是( ). A.90° B.75° C.60° D.45°【答案】A【解析】取AA′的中点Q ，连接QN ，B Q ，且B Q 与B′M 相交于点H ，则QN 綉AD 綉BC ，从而有四边形NQ BC 为平行四边形，所以N C ∥Q B ，则有∠B′H B 为异面直线B′M 与C N 所成的角. 又∵B′B ＝BA ，∠B′B M ＝∠BA Q ＝90°，B M ＝A Q ，∴△B′B M ≌△BA Q ， ∴∠M B′B ＝∠Q B M .而∠B′M B ＋∠M B′B ＝90°，从而∠B′M B ＋∠Q B M ＝90°，∴∠MH B ＝90°.故选A. 3.如图，在四棱锥P －ABCD 中，∠ABC ＝∠BAD ＝90°，BC ＝2AD ，△P AB 和△P AD 都是等边三角形，则异面直线CD 与P B 所成角的大小为( ) A.90° B.75° C.60° D.45°【答案】 A【解析】如图，过点B 作直线B E ∥CD ，交DA 的延长线于点E ，连接PE .∴∠P B E (或其补角)是异面直线CD 与P B 所成角.∵△P AB 和△P AD 都是等边三角形，∴∠P AD ＝60°，DA ＝P A ＝AB＝P B ＝A E ，∴∠P A E ＝120°.设P A ＝AB ＝P B ＝A E ＝a ，则PE .又∠ABC ＝∠BAD ＝90°，∴∠BA E ＝90°，∴B E a ，∴在△P B E 中，P B 2＋B E 2＝PE 2，∴∠P B E ＝90°.即异面直线CD 与P B 所成角为90°.故选A.4.已知直四棱柱ABCD －A 1B 1C 1D 1中，底面ABCD 为正方形，AA 1＝2AB ，E 为AA 1的中点，则异面直线B E 与CD 1所成角的余弦值为( )B.15 D.35【答案】C【解析】如图，连接BA 1,因为BA 1∥CD 1，所以∠E B A 1是异面直线B E 与CD 1所成角，设AB ＝1,则111,EB A E A B ===,作EF ⊥BA 1, 11A E AB EF A B ⋅==FB =∠E B A 1.选C.5. 如图，三棱锥P —ABC 中， P C ⊥平面ABC ，P C ＝AC ＝2，AB ＝BC ，D 是P B 上一点，且CD ⊥平面P AB, 则异面直线A P 与BC 所成角的大小； A.90°B. 60°C. 75°D.45°【答案】B【解法】∵P C ⊥平面ABC ，⊂A B 平面ABC ， ∴P C ⊥AB ．∵CD ⊥平面P AB ，⊂A B 平面P AB ， ∴CD ⊥AB ．又C CD PC = ， ∴AB ⊥平面P CB ．过点A 作A F //BC ，且A F ＝BC ，连结PF ，C F ． 则 PAF ∠为异面直线P A 与BC 所成的角．由（Ⅰ）可得AB ⊥BC ，∴C F ⊥A F ，得PF ⊥A F ．则A F ＝C F ＝2，PF ＝6 CF PC 22=+，在PFA Rt ∆中， tan ∠P A F ＝26AFPF=＝3，∴异面直线P A 与BC 所成的角为60°．选B.6. 如图,正方形ABCD 所在平面与正方形，AB EF 所在平面成60ο角,求异面直线AD 与B F 所成角的余弦值. A.42 B.2C. 3D.【答案】A 【解析】∵CB ∥AD, ∴∠CB F 为异面直线AD 与B F 所成的角.连接C F 、C E 设正方形ABCD 的边长为α,则B F ＝a 2∵CB ⊥AB, E B ⊥AB ∴∠C E B 为平面ABCD 与平面AB EF所成ABC DPE F的角,∴∠CB E ＝∠60ο ∴C E ＝a F C ＝a 2 ,∴cos ∠CB F ＝42,选A. 7. 如图，已知棱柱1111D C B A ABCD -的底面是菱形，且⊥1AA 面ABCD ， 60=∠DAB ，1AA AD =，F 为棱1AA 的中点，M 为线段1BD 的中点，则面1BFD 与面ABCD 所成二面角的大小． A ．30° B ．45° C ．60° D ．90°【答案】C【解析】 底面是菱形， BD AC ⊥∴ 又⊥B B 1 面ABCD ，⊂AC 面ABCD B B AC 1⊥∴，⊥∴AC 面11B BDD 又AC MF // ⊥∴MF 面11B BDD 延长F D 1、DE 交于点E ，F 是A A 1的中点且ABCD 是菱形AB AE DA ==∴ 又 60=∠DAB 90=∠∴DBE ∴BE B D ⊥1 BD D 1∠∴为所求角 在菱形ABCD 中， 60=∠DAB BD BC 3=∴ 3t a n 11==∠BDDD BD D 601=∠∴BD D ,选C .8.在一个45°的二面角的一个面内有一条直线与二面角的棱成45°，则此直线与二面角的另一个面所成的角为( ) A ．30° B ．45° C ．60° D ．90° 【答案】A【解析】如图，二面角α－l －β为45°，β，且与棱l 成45°角，过A 作A O ⊥α于O ，作A H ⊥l 于H .连接OH 、O B ，则∠A HO 为二面角α－l －β的平面角，∠AB O 为AB 与平面α所成角．不妨设A HRt △A OH 中，易得A O ＝1；在Rt △AB H 中，易得AB ＝2.故在Rt △AB O 中，sin ∠AB O ＝12AO AB =，∴∠AB O ＝30°，为所求线面角．选A. 二、填空题9. 如图所示，在正四面体S －ABC 中，D 为S C 的中点，则BD 与S A所成角的余弦值是A BC DA 1B 1C 1D 1F MOE________．【解析】取AC 中点E ，连接D E ，B E ，则BD 与D E 所成的角即为BD 与S A 所成的角．设S A ＝a ，则BD ＝B Ea ，D E ＝2a .由余弦定理知cos ∠BD E.10. 如图，在正四棱柱1111D C B A ABCD -中，底面ABCD 的边长为3，1BD 与底面所成角的大小的正切为23，则该正四棱柱的高等于____________．【答案】【解析】由题意得11122tan 33DD DBD DD BD ∠===⇒=. 11. A 、B 是直二面角α－l －β的棱l 上的两点，分别在α，β内作垂直于棱l 的线段AC ，BD ，已知AB ＝AC ＝BD ＝1，那么CD 的长为【解析】如图，由于此题的二面角是直角，且线段AC ，BD 分别在α，β内垂直于棱l ，AB ＝AC ＝BD ＝1，作出以线段AB ，BD ，AC 为棱的正方体，CD 即为正方体的对角线，由正方体的性质知，CD三、解答题 12. 如图，三棱锥P —ABC 中， P C ⊥平面ABC ，P C ＝AC ＝2，AB ＝BC ，D 是P B 上一点，且CD ⊥平面P AB ．(1) 求证：AB ⊥平面P CB ；(2 求异面直线A P 与BC 所成角的大小；（3π） 【解析】(1) ∵P C ⊥平面ABC ，⊂A B 平面ABC ，BDPE∴P C ⊥AB ．∵CD ⊥平面P AB ，⊂A B 平面P AB ， ∴CD ⊥AB ．又C CD PC = ， ∴AB ⊥平面P CB ．(2) 过点A 作A F //BC ，且A F ＝BC ，连结PF ，C F ．则 PAF ∠为异面直线P A 与BC 所成的角．由（Ⅰ）可得AB ⊥BC ，∴C F ⊥A F ．由三垂线定理，得PF ⊥A F ．则A F ＝C F ＝2，PF ＝6 CF PC 22=+，在PFA Rt ∆中， tan ∠P A F ＝26AF PF =＝3， ∴异面直线P A 与BC 所成的角为3π．13.如图所示，在多面体111A B D DCBA 中，四边形11AA B B，11,ADD A ABCD均为正方形，点E 为11B D的中点，过点1A ，D ，E 的平面交1CD 于点F .（1）求证：1//EF B C ；(2)求二面角11EA DB ﹣﹣余弦值.【解析】（1）证明：由题可得1//AD B C ，又因为1A D ⊄平面11B CD ，1B C ⊂平面11B CD ，所以1//A D 平面11B CD ．又平面1A DEF平面11B CD EF =，所以1//A D EF ．又因为11//A D B C ，所以1//EF B C ．（2）将原图形补全成正方体，如图所示，则平面1A CD 即为平面1A EFD ，所以求二面角11E A D B --的余弦值可以转化为求二面角111C A D B --的余弦值。
考点18 异面直线所成的角-庖丁解题2019学年高一数学人教版(必修2)(解析版)
原创精品资源学科网独家享有版权，侵权必究！
1
异面直线所成的角
1．定义：已知两条异面直线a ，b ，经过空间任一点O 作直线a ′∥a ，b ′∥b ，我们把a ′与b ′所成的锐角或直角叫做异面直线a 与b 所成的角或夹角．
2．异面直线所成的角θ的取值范围：(090]︒︒，
3．当θ＝o 90时，a 与b 互相垂直，记作a b ⊥．
【例】设P 是直线l 外一定点，过点P 且与l 成30°角的异面直线（ ）
A ．有无数条
B ．有两条
C ．至多有两条
D ．有一条
【答案】A
【规律总结】异面直线所成的角的大小与O 点的位置无关，即O 点位置不同时，这一角的大小是不会改变的．
1．如图所示，在长方体1111ABCD A B C D -中，AB 11BC CC ==，则异面直线11AC BB 与所成角的大。
异面直线所成的角专题训练
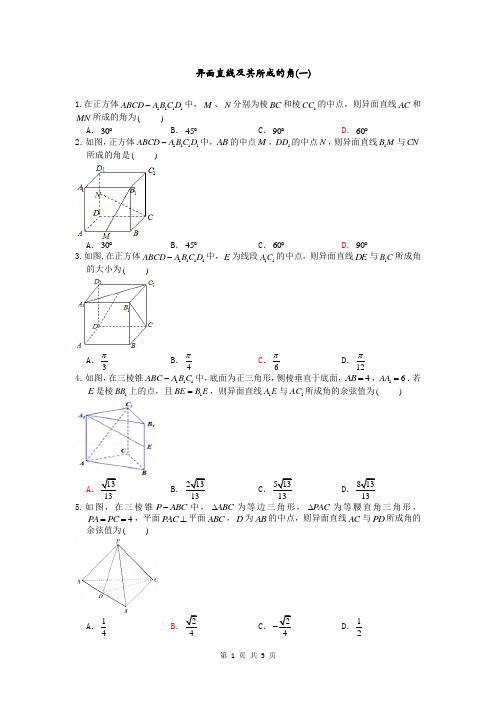
异面直线及其所成的角(一)1.在正方体1111ABCD A B C D -中，M 、N 分别为棱BC 和棱1CC 的中点，则异面直线AC 和MN 所成的角为( ) A ．30︒ B ．45︒ C ．90︒ D ．60︒ 2．如图，正方体1111ABCD A B C D -中，AB 的中点M ，1DD 的中点N ，则异面直线1B M 与CN 所成的角是( )A ．30︒B ．45︒C ．60︒D ．90︒ 3.如图,在正方体1111ABCD A B C D -中，E 为线段11AC 的中点，则异面直线DE 与1B C 所成角的大小为( )A ．3π B ．4π C ．6π D ．12π 4．如图，在三棱锥111ABC A B C -中，底面为正三角形，侧棱垂直于底面，4AB =，16AA =．若E 是棱1BB 上的点，且1BE B E =，则异面直线1A E 与1AC 所成角的余弦值为( )A 13B 213C 513D 8135.如图，在三棱锥P ABC -中，ABC ∆为等边三角形，PAC ∆为等腰直角三角形，4PA PC ==，平面PAC ⊥平面ABC ，D 为AB 的中点，则异面直线AC 与PD 所成角的余弦值为( )A ．14B 2C ．2D ．126．在棱长为1的正方体1111ABCD A B C D -中，M 和N 分别为11A B 和1BB 的中点，那么直线AM 与CN 所成角的余弦值是( ) A ．25- B ．25C ．35D ．10 7．如图，直三棱柱111ABC A B C -，AC BC ⊥，且12C A C C C B==，则直线1BC 与直线1AB 所成角的余弦值为( )A ．5 B ．5 C ．25 D ．358．在直三棱柱111ABC A B C -中，1111122AA A B B C ==，且AB BC ⊥，点M 是11AC 的中点，则异面直线MB 与1AA 所成角的余弦值为( )A ．13B ．22C ．32D ．129.正三棱锥A PBC -的侧棱两两垂直，D ，E 分别为棱PA ，BC 的中点，则异面直线PC 与DE 所成角的余弦值为( )A ．3 B ．5 C ．3 D ．6 10.如图所示，在正方体1111ABCD A B C D -中，若点E 为BC 的中点，点F 为11B C 的中点，则异面直线AF 与1C E 所成角的余弦值为( )A ．23B 5C 5D 2511．在三棱柱111ABC A B C -中，ABC ∆是等边三角形，1AA ⊥平面ABC ，2AB =，12AA =，则异面直线1AB 和1BC 所成角的正弦值为( )A ．1B 7C ．12D 312．在正方体1111ABCD A B C D -中，E 为BC 的中点，F 为11B C 的中点，则异面直线AF 与1C E 所成角的正切值为( )A 5B ．23C 25D 5异面直线及其所成的角(二)1.正四棱锥的侧棱与底面边长都相等,E 是SB 的中点,则AE 与SD 所成角的余弦值为( )A ．13BC ．23D 2.如图,在直三棱柱111ABC A B C -中，90ACB ∠=︒，12AA =，1AC BC ==，则异面直线1A B 与AC 所成角的余弦值是( )3.四棱锥P ABCD -中,底面ABCD 为正方形,且PA ⊥平面ABCD ,PA AB =,则直线PB 与直线AC 所成角的大小为( )A.6π B.4π C.3π D.2π 4.如图,在四棱锥P ABCD -中,底面ABCD 是矩形,PA ⊥底面ABCD ,E 是PC 的中点,2AB =,AD =,2PA =,则异面直线BC 与AE 所成的角的大小为( )A.6π B.4π C.3π D.2π 5.在如图所示的正方体1111A B C D ABCD 中,E 是11C D 的中点，则异面直线DE 与AC 夹角的余弦值为( )A. B.120- C.1206.正方体1111ABCD A B C D -中,E 是AD 的中点,则直线1C E 与BC 所成的角的余弦值是( )C.137.如图,在正四面体ABCD 中,E 为AB 的中点,F 为CD 的中点,则异面直线EF 与AC 所成的角为( )A.90︒B.60︒C.45︒D.30︒ 8.在正方体1111ABCD A B C D -中,P 为11AC 的中点,则直线1DC 与AP 所成角的余弦值为( )C.129.在长方体1111ABCD A B C D -中,1AB BC ==,12AA =,则异面直线1AD 与1DB 所成角的余弦值为( )C.1510.已知直三棱柱111ABC A B C -,120ABC ∠=︒,2AB =,11BC CC ==,则异面直线1AB 与BC 所成角的余弦值为( )A.1511.如图,在三棱锥A BCD -中,三条棱DA 、DB 、DC 两两垂直,且DA DB DC ==,M 、N 分别是棱BC 、AD 的中点,则异面直线AM 与BN 所成角的余弦值为( )A.1212.如图,在正方体1111ABCD A B C D -中,M ,N 分别为11C D 和1CC 的中点,则异面直线AM 与BN 所成角的余弦值为( )13.三棱柱ABC A B C ''-'的所有棱长都等于2，并且AA '⊥平面ABC ,M 是侧棱BB '的中点,则直线MC '与A B '所成的角的余弦值是( )异面直线及其所成的角(一)答案1-6 DDCABB 7-12 ABDBAC异面直线及其所成的角(二)答案1-6 DDCBDC 7-13 CDABDAA。
利用空间向量求异面直线所成角及直线与平面所成角
第三节 利用空间向量求异面直线所成角及直线与平面所成角 一、异面直线所成角设AB 、CD 为异面直线，所成角为θ则=θcos练习：如图，在棱长为2的正方体ABCD —A 1B 1C 1D 1中，O 是底面ABCD 的中心，E 、F 分别是CC 1、AD 的中点，则OE 和FD 1所成角的余弦值为________.探讨：如图,正四面体A-BCD 中，E 、F 分别是BC 、AD求AE 和CF 所成角的余弦值。
例1、如图，ABCD-A 1B 1C 1D 1是正四棱柱，（1）求证BD ⊥平面ACC 1A 1 （2）若二面角C 1-BD-C 的大小为︒60，求异面直线BC1与AC 所成角大小 。
（06北京文）二、直线与平面所成角1、法向量：如表示向量→a 的有向线段所在直线垂直于平面α，则称这个向量垂直于平面α，记作α⊥→a 。
如果α⊥→a ，那么向量→a 叫平面α的法向量。
例2，如图所示，ABCD 是直角梯形AD //BC ，︒=∠90ABC SA ⊥平面ABCD ，SA=AB=BC=1 ，AD=21， （1） 求平面SBC 的一个法向量； （2） 求平面SCD 的一个法向量； （3） 求平面SAD 的一个法向量；D 1 C 1ABC DA 1B 1（4）求平面ABCD的一个法向量。
2，若AB是平面α的一条斜线，→n是α的一个法向量，设AB与α所成角为θ，则sinθ。
例3，如图，正三棱柱ABC-A1B1C1中，AB=AA1，求AC1与平面BB1C1C所成角。
练习：在正方体ABCD-A1B1C1D1中，M、NB 1C1、AD的中点，求直线A1D1与平面BMD1N的余弦值。
例4，如图，AB⊥平面BCD，BC⊥CD，AB=BC，AD 平面BCD所成角为30°。
（1）求AD与平面ABC所成的角；（2）AC与平面ABD所成角。
作业：1.如图，在长方体ABCD-A1B1C1D1中BC=22，214=CD ，51=DD ，求A 1C 和B 1D 1所成角的 大小。
异面直线所成的角
异面直线所成的角专题—异面直线所成的角求法异面直线所成角的大小，是由空间任意一点分别引它们的平行线所成的锐角（或直角）来定义的．准确选定角的顶点，平移直线构造三角形是解题的重要环节．本次课对此类题的解题方法做了一些归纳和总结，仅供参考．例1：在正方体ABCD -A 1BC 11D 1中，E , F 分别为AD , AA 1的中点 (1)求直线AB 1和CC 1所成角的大小 (2)求直线AB 1和EF 所成角的大小E ,F 分别为AB 和的中点，例2：在正方体ABCD -A 求异面直线B 1C 与EF 所1BC 11D 1中，成的大小一、异面直线的定义：把不同在任何一个平面内的两条直线叫异面直线（即既不相交也不平行的直线）; 从而空间中直线与直线的位置关系分三种：平行、相交、异面二、异面直线所成角的概念（画法）：如图，已知两条异面直线a , b ，经过空间任意一点O 作直线a ' //a , b ' //b ，我们把a ' 与b ' 所成的锐角（或直角）叫做异面直线a 与b 所成的角（或夹角）例3：如图:正四面体S －ABC 中，如果E ，F 分别是SC ，AB 的中点，求异面直线EF 与SA 所成的角Bθ角的取值范围：(00,900] 三、异面直线所成的角求解步骤：1. 恰当选点，作两条异面直线的平行线，构造平面角θ；2. 证明这个角θ就是异面直线所成角；3. 解三角形，求出所构造角θ的三角函数值，得出度数；异面直线所成的角求法简记为：一作、二证、三求；例4：如图，AB 和CD 是两条异面直线，AB =CD =3，AE BF 1=E , F 分别为线段AD , BC 上的点，且=, ED FC 2EF =7，求AB 和CD 所成的角。
异面直线测试题一．选择题：1．直线a , b 是异面直线是指① a ∩b =?, 且a 与b 不平行；② a ?面α，b ?面β，且平面α∩β=?；③ a ?面α，b ?面β，且a ∩b =?；④ 不存在平面α，能使a ?α且b ?α成立。
异面直线所成角详解
E
B
D
M F
C
平移法
㈡.利用平行线分线段成比例的推论平移 例3.空间四边形ABCD中，AB＝CD＝3，E、F分别是AD、BC上的点， 且AE∶ED＝BF∶FC＝1∶2，
EF＝ 7 ，求异面直线AB和CD所成的角
A
E M
B F
D C
平移法
㈢.利用平行四边形平移
例4.正方体AC1中若E、F分别为AB和BB1的中点， 求A1E与CF所成角的余弦
【求异面直线所成角的步骤】
（1)"作",即用"平移法"过空间一点作两条异面直线的平行线,平移过程多用 到中位线、平行四边形的性质,操作过程会因选择的构造角度不同出现角的位 置不同,常用方法如下: ①过一条直线上的点,作另一条直线的平行线.特别是某些特殊点处,例如"端 点"或"中点"处 （2)"证"即证明所作平面角符合异面直线所成的角或补角的定义 （3）"求"即通过解三角形,计算所作的角的大小
OB1与A1C1所成的角的度数为
900
B1 A1
C1 D1
D O
A
C B
平移法
在正四面体S-ABC中，SA⊥BC, E, F分别为SC、AB 的 中点，那么异面直线EF 与SA 所成的角等于（ B ）
(A)300
(B)450
(C)600
S
(D)900
E A
D
F
C
B
平移法
（解法二）
S
E
A
G
D C
F B
D (1)以E为特殊点
G.
E
C
B
F A
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
A B C S
E F A B C D D 1
C 1 B 1 A 1
M
N
N M
F
E D
C
B A
高二数学练习（二）
一、选择题
1．分别和两条异面直线都相交的两条直线一定是 （ ） （A ）不平行的直线 （B ）不相交的直线
（C ）相交直线或平行直线 （D ）既不相交又不平行直线
2．已知EF 是异面直线a 、b 的共垂线，直线l ∥EF ，则l 与a 、b 交点的个数为 （ ） （A ）0 （B ）1 （C ）0或1 （D ）0，1或2
3．两条异面直线的距离是 （ ） （A ）和两条异面直线都垂直相交的直线 （B ）和两条异面直线都垂直的直线 （C ）它们的公垂线夹在垂足间的线段的长 （D ）两条直线上任意两点间的距离
4．设a, b, c 是空间的三条直线，下面给出三个命题：① 如果a, b 是异面直线，b, c 是异面直线，则a, c 是异面直线；② 如果a, b 相交，b, c 也相交，则a, c 相交；③ 如果a, b 共面，b, c 也共面，则a, c 共面．上述命题中，真命题的个数是 （ ） （A ）3个 （B ）2个 （C ）1个 （D ）0个
5．异面直线a 、b 成60°，直线c ⊥a ，则直线b 与c 所成的角的范围为 （ ）
（A ）[30°，90°] （B ）[60°，90°]
（C ）[30°，60°] （D ）[60°，120°]
6．如图:正四面体S －ABC 中，如果E ，F 分别是SC ，AB 的中点，那么异面直线EF 与SA 所成的角等于 （ ） （A ）90°（B ）45°（C ）60°（D ）30° 7．在棱长为1的正方体ABCD －A 1B 1C 1D 1中，M 和N 分别为A 1B 1和的
中点，那么直线AM 与CN 所成角的余弦值是 （ ） （A ）23（B ）1010（C ）5
3（D ）54
8．右图是正方体的平面展开图，在这个正方体中，
①BM 与ED 平行； ②CN 与BE 是异面直线； ②③CN 与BM 成 60角；④DM 与BN 垂直．
以上四个命题中，正确命题的序号是 （ ） （A ）①②③ （B ）②④ （C ）③④ （D ）②③④
9．梯形ABCD 中AB//CD ，AB ⊂平面α，CD ⊄平面α，则直线CD 与平面α内的直线的位置关系只能是
（ ）（A ）平行 （B ）平行和异面 （C ）平行和相交 （D ）异面和相交 10．在空间四边形ABCD 中，E 、F 分别为AB 、AD 上的点，且AE ：EF ＝AF ：FD
＝1 ：4，又H 、G 分别为BC 、CD 的中点，则 （ ） （A ）BD//平面EFGH 且EFGH 是矩形 （B ）EF//平面BCD 且EFGH 是梯形
（C ）HG//平面ABD 且EFGH 是菱形 （D ）HE//平面ADC 且EFGH 是平行四边形
二、填空题 11．如图，在正三角形ABC 中，D 、E 、F G ，H ，I ，J 分别为AF ，AD ，BE ，DE DE ，EF ，DF 折成三棱锥以后，GH 与IJ
12．在四面体ABCD 中，若AC 与BD 成60°角，且AC ＝BD ＝a ，则连接AB 、BC 、CD 、DA 的中点的四边形面积为 ．
B
A C
D A
F E P C B
A N M D
C B
A D C
B
A
P Q
D 1
C 1
B 1
A 1
13．在长方体ABCD －A 1B 1C 1D 1中，AB ＝BC ＝3，AA 1＝4，则异面直线AB 1与 A 1D 所成的角的余弦值
为 ．
14．把边长为a 的正方形ABCD 沿对角线BD 折起， 使A 、C 的距离等于a ，如图所示，则异面直线AC 和BD 的距离为 ．
三、解答题
15．已知AB 、BC 、CD 为不在同一平面内的三条线段，AB ，BC ，CD 的中点P 、Q 、R 满足PQ ＝2，QR
PR ＝3，求AC 与BD 所成的角．
16．已知P 为△ABC 所在平面外的一点，PC ⊥AB ，PC ＝AB ＝2，E 、F 分别为PA 和BC 的中点． （1）求证：EF 与PC 是异面直线； （2）EF 与PC 所成的角；
（3）线段EF 的长．
17．如图，AB 和CD 是两异面直线，BD 是它们的公垂线，AB ＝CD ，M 是BD 的中点，N 是AC 的中点． （1）求证：MN ⊥AC ； （2）当AB ＝CD ＝a ，BD ＝b ，AC ＝c 时，求MN 的长．
18．（如图）已知P 、Q 是棱长为a 的正方体ABCD －A 1B 1C 1D 1的面AA 1D 1D 和A 1B 1C 1D 1的中心．
（1）求线段PQ 的长； （2）证明：PQ ∥AA 1B 1B ．。