06 项目一 任务三 流体力学基本方程的应用(伯努利方程)
伯努利流体方程

伯努利流体方程
伯努利方程(Bernoulli's equation)是流体力学基本方程之一,常用于描述静止流体或运动流体在流经不同位置时,压力、速度、高度等物理量的变化关系。
伯努利方程最早由瑞士数学家和物理学家伯努利(Daniel Bernoulli)在1738年提出,被称
为伯努利定理,也称作伯努利方程或伯努利流体方程。
伯努利方程的数学形式为:
P + 1/2ρv^2 + ρgh = constant
其中,P表示流体的压力,ρ表示流体的密度,v表示流体的
速度,g表示重力加速度,h表示流体的高度,constant表示一个常数。
伯努利方程可以表达出一个流体在液体静压力、动能和势能三者之间的平衡状态。
在一个理想的流体中,如果流体穿过一段水管,那么在这段水管的任何位置,液体静压力、动能和势能总和相等。
应用伯努利方程,可以计算液体在不同位置的压力、速度和高度等物理量的变化。
伯努利方程可以应用在气体、液体等不同介质的流体力学问题中,如风力发电机、水压机等。
浅谈伯努利方程在流体力学中的应用

浅谈伯努利方程在流体力学中的应用作者:张丽来源:《教育教学论坛》2016年第28期摘要:伯努利方程是流体力学的重要理论基础,它为我们计算工程数据及解释日常生活中的一些现象,如管道总水头的计算、香蕉球的形成原理等,提供了重要的理论依据。
关键词:伯努利方程;流体力学;研究中图分类号:G642 文献标志码:A 文章编号:1674-9324(2016)28-0207-02作为力学的一个重要分支,流体力学以流体为主要研究对象,是研究流体平衡和运动规律的科学。
流体力学在许多工业科技中有着广泛的应用。
水利工程的建设、造船工业的迅速发展都离不开水静力学和水动力学的建立和研究,航空事业则离不开气体动力学的深入发展。
一、伯努利方程的推导伯努利方程只能应用于一条流线上的不同点,且必须是不可压缩理想流体在重力场中做定常流动。
二、伯努利方程的应用(一)当流体为液体时,伯努利方程的应用(二)当流体为气体时,伯努利方程的应用能量方程④的适用条件是:流动绝热但并不要求等熵,流动可以有摩擦。
即使通过强间断面,能量方程仍然使用。
伯努利方程⑤的适用条件是:无黏性,因而无机械能损失,流动过程有无热量的输入都不影响它的应用。
只有在等熵的流动中④和⑤才能相等[3]。
三、结语在生活中的很多方面都有伯努利方程的应用,工程中有很多这样的例子,如矿山通风机工况点确定[4]、都江堰修建等,都需要很多关于流体的计算来保证工程的安全,伯努利方程就在其中起了很大的作用。
参考文献:[1]孔珑.工程流体力学[M].第三版.中国电力出版社,2007.[2]刘仁隆.故事物理学[M].科学出版社,1980:52-58.[3]刘大有.伯努利方程应用中的若干问题[J].力学与实践,1991,(4).[4]赵昌友.伯努利方程及应用[J].池州学院学报,2014,28(6):。
流体力学伯努利方程公式

流体力学伯努利方程公式
流体力学伯努利方程是物理学中最基本且重要的方程之一。
它是关于流体运动的一组非线性方程,用于以数学方法描述流体运动,它被用于解决流动问题,如气体动力学、湍流流动和热流动。
伯努利方程由英国数学家兼流体力学家约翰·尼科(John von Neumann)在1946年初提出,它是一个具有三个未知量的非线性方程组,同时反映了运动的流体的动量、动能和动量守恒的特性。
伯努利方程的首要用途是计算几何体内流体的参数,它刻画了由于抗力矢量和动量耦合而引起的湍流运动流场。
伯努利方程指定了一个n维流体中特定目标位置上物体的物理参数,它具有一个参数向量,即,流速,流体密度,力学压力,温度和能量密度。
基本伯努利方程可以写成:
∇·(ρu)=0,
∇·u=0,
∇·P+ρ∂u/∂t=ρS,
其中ρ是流体的密度,u是流速,P是静压力,t是时间,S代表的是外力。
伯努利方程被广泛地应用于可解决多维流动,如水流、风流、温度场、抗静电场和对流传输等。
在主动低频技术中,伯努利方程还用于解决超声成像,超声测量和声学设计方面的应用。
它通常被用于数值分析,以解决流动问题的复杂性,并根据实验数据预测流体的行为。
因此,伯努利方程在现代物理学中扮演着一个重要的角色,它不仅可以帮助人们更好地理解流体的行为,还可以帮助我们更特别的设计有效的模拟和预测流体的行为。
伯努利方程

伯努利方程伯努利方程是描述理想流动的基本方程之一,它是在瑞士数学家伯努利(James Bernoulli)在1738年发表的一篇论文中提出的。
该方程对于理解流体力学以及飞行、水力、空气动力学等领域具有重要的应用。
伯努利方程是基于质量守恒定律、动量守恒定律和能量守恒定律推导而来的方程。
该方程表达式为:P + ½ρv² + ρgh = 常数其中,P为流体的压力,ρ为流体的密度,v为流体的速度,h为流体的高度,g为重力加速度。
伯努利方程是在假设部分没有粘性损失的情况下成立的,也就是无黏性流动。
在实际的情况下,流体会存在一定的粘性损失,因此伯努利方程只适用于无粘流体,但在低速流动下,伯努利方程可近似地应用于粘性流体。
对于伯努利方程,我们可以从以下角度来解释其中的每个项:① P:压力项,它表示了流体在流动过程中所受到的压力。
当流体速度增加时,压力往往会降低,例如在突缩管中,当管道的截面积变小时,流体的速度会增加,而压力会降低。
②½ρv²:动能项,它表示了流体的动能。
在流体的流动过程中,当速度增加时,动能也会增加,例如在水力发电站中,当水流的速度增加时,水的动能也会增加,从而推动水轮发电。
③ρgh:势能项,它表示了流体的势能。
当流体在重力作用下流动时,流体会从高处向低处移动,势能也随之降低。
例如当我们用pump把水从低处抽到高处时,水的势能就会增加。
由于伯努利方程中的常数在同一条流线上保持不变,因此可以利用伯努利方程来分析流体在不同位置的流速、压力和高度之间的关系。
这在飞行、水利及空气动力学等领域的设计和应用中具有重要的作用。
伯努利方程的应用十分广泛。
例如在空气动力学领域中,伯努利方程被用来解释飞机起飞、飞行、着陆过程中的颤振等现象。
在水利工程领域中,伯努利方程被用来计算水流在不同地方的速度、压力和高度等因素,对于设计水坝、水龙头、流量计等工程设施具有重要的作用。
总之,伯努利方程作为理解流体力学基本方程之一,不仅在理论研究中具有广泛的应用,也在实际的设计和应用中具有十分重要的意义。
流体力学 伯努力方程
测流速原理该点在水面下的深度为d故该处的压强pgdb点在管口之前流速v根据伯努利方程所以在实际应用时上式须修正为其中c为比多管的修正系数由实验来确定
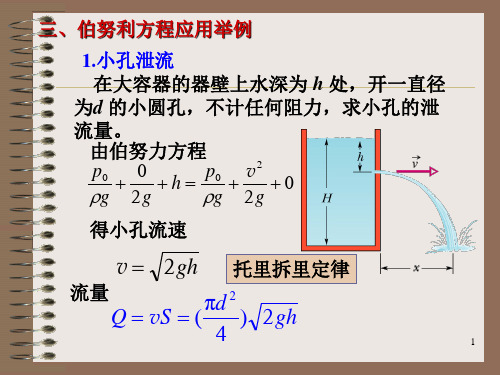
三、伯努利方程应用举例 1.小孔泄流 在大容器的器壁上水深为 h 处,开一直径 为d 的小圆孔,不计任何阻力,求小孔的泄 流量。 由伯努力方程 p0 p0 v 2 0 h 0 g 2 g g 2 g
h1
B
C A
pC p0 gh1
h2
其中p0为大气压
11
(2)当虹吸管下端开启时, h1 下端和A处的压强仍为:
p下 端 p0 , pA p0
B
C A
h2
而vB vc v下端 , v A 0 . 所以 pB p0 g( h2 h1 ) , pC p0 gh2
(2)取1-2-4的一个流线,由伯努利方程
P1 1 2 1 1 v1 P2 v 2 P4 v2 2 4 2 2 2 P4 P0
1 2 2 P1 P0 v 4 v1 P0 100, P1 -P0 100Pa 2 1 2 2 P2 P0 v 4 v 2 P0 , 2 P3 =P0 P2 P0 0 P3 P0 0
Qv v1S1 v2 S2
2( 汞 )g hS1 S 2
2 2
( S1 S 2 )
2 2
6
H
1 1 2 2 p1 v1 p2 v2 2 2
v1S1 v2 S2
v1 主管 细管 v2
p p1 p2 gh
•
Q v1S1 S1S2
例题2 在如图所示的虹吸管装置中,已 知 h1 和 h2 ,试问:(1)当截面均匀的虹吸管 下端被塞住时,A、B和C处的压强各为多大? (2)当虹吸管下端开启时,A、B和C处的压 强又各为多大? 这时水流出虹吸管的速率为 多大?
伯努利方程的应用(例题)

将以上各值代入(b)式,可求得输送碱 液所需的外加能量:
We
18.59.81
2.452 2
29.4 103 1100
30.8
242.0
j
/
kg
碱液的质量流量:
qm
4
d 2 2u2
0.785 0.072
2.451000
10.37kg
/
s
泵的有效功率:
Ne Weqm 24210.37 2510W 2.51kW
2019/7/29
Z3 1m,Z4 0.2m,
P4 0(表压),P3 ? 1000kg / m3
将已知数据代入柏努利方程式得:
g p3 1.96
P3 11770Pa(表压)
计算塔前管路,取河水表面为1-1’截面,喷头内侧为2-2’ 截面,在1-1’和2-2’截面间列柏努利方程。
截面2-2’处压强为 :
P2 gh 10009.810.5 4905Pa(表压)
流经截面1-1’与2-2’的压强变化为:
P1 P2 (101330 3335) (10330 4905)
P1
(101330 3335)
0.079 7.9% 20%
u2
qV A
qV
d2
5
3600 0.0332
1.62m / s
4
4
由连续性方程 u1 A1 u2 A2 ∵A1>>A2,
因为u1<<u2, 所以:u1≈0
已知:We=0 ,
R 30J / kg
第3章2_流体动力学基础-伯努利方程的应用(1)

【例3-7】图示为一抽水装置,利用喷射水流在吼道断面 上造成的负压,可将M容器中的积水抽出。已知:H、b、 h。试分析:吼道有效断面面积A1与喷嘴出口断面面积A2 之间应满足什么样的条件能使抽水装置开始工作(不计能 量损失)?
32
【解】 以1-1为基准面,列0-0、1-1断面的能量方程:
uA 2 g
pA p0
uA c 2 g
校正系数c由实验 确定,一般约为 0.95-1.0
pA p0
21
双孔测速管
皮托-普朗特管 把测压管和测速管结 合在一起制成的,原 理与单孔测速管相同。 经过试验,如果按图 示尺寸制造,其校正 系数c=1,使用方便。
22
【例3-5】水从立管下端泄出,立管直径为d=50mm, 射流冲击一水平放置的半径R=150mm的圆盘,若水层 离开盘边的厚度δ=1mm,求流量Q及汞比压计的读数 Δh (不计水头损失) 。
11
2、节流式流量计
工业上常用的节流式流量计主要有三种类型,即孔板、喷嘴和 圆锥式(又叫文丘里管)。 节流式流量计 特点:装置中断面逐渐 收缩
12
基本原理: 当管路中液体流经节流装置时,液流断面收缩,在收缩断面处 流速增加,压强降低,使节流装置前后产生压差。在选择一定 的节流装置的情况下,液体流量越大,节流装置前后压差也越 大,因而可以通过测量压差来计算流量大小。
p1
p真
0.2 13.6 2.72m水柱
出水口通大气,水池液面通大气,p2=p0=0。 对断面1-1、2-2列能量方程:
p1
V12 p2 V22 H2 2g 2g
A d 50 V22 V12 1 V12 1 V12 0.198V12 A2 d 2 75
伯努利方程及其应用

1.2 伯努利方程的应用
• 设理想流体在管内作稳定流动,在水平粗、细管
等高点处的截面积、压强、流速分别为 SA、PA、vA
和 SB、PB、vB,竖直毛细管内液面高度差为 h。将 流量计水平连接到被测管路中,应用伯努利方程
得
PA
1 2
2 A
PB
1 2
B2
再根据连续性方程 SAA SBB Q
可得A 点的流速
1
'
,S2 流 ,S 2 ' 处的
截面积、压强、流速、高度等都保持不变。
流体元 S1S2在流动过程 中,受两端的大气压力 和重力作用,在 ∆t时 间段内, 相当于流体元
S根1 S据1'连流续动性到原S理2 S,2 ' 处两,个
流体元 的质量相等,
设为 m 。
1.1 伯努利方程
• 大气压力P1S1 做正功,P2S2 做负功,总功为
两截面的流速和截面SA 的压强(忽略水的可压缩性 和黏性)。
• 解:根据连续性方程 SAA SBB Q
•得
A
Q SA
0.12 100 104
12(m / s)
B
Q SB
0.12 60 104
20(m / s)
1.1 伯努利方程
• 因为在水平管中流动,h1=h2 ,再根据理想流体的伯 努利方程可知
大学物理
伯努利方程及其应用
1.1 伯努利方程 1.2 伯努利方程的应用
1.1 伯努利方程
• 博学的荷兰科学家丹尼尔•伯努利在研究流体运动 时,提出了理想流体作稳定流动时遵循的基本方 程——
• 伯努利方程。
• 下面我们从 • 功能原理的 • 角度进行推导。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
教案分页
授课章节或
项目名称
项目一 任务三 流体力学基本方程的应用(伯努利方程)
授课周次、时
间、次序
第一周 月 日星期 第 节(总第 次课)
本次授课
类型
☑理论 □实验 □实训 □理实一体 □
本次授课
场地
□一般教室 □多媒体教室 ☑实训室 □室外 □
教学方法 视频演示法、讨论法、双向交流、分组操作
教学目标
知识目标
1、熟知伯努利方程的两种形式及式中各部分的含义;
技能目标
1、会应用伯努利方程解决实际问题,进行简单计算;
教学重点、
难点及
解决方法
重点:
1.伯努利方程
难点:
1.实际应用、计算
解决方法:
视频演示、双向交流、分组操作、总结讲评
教学
活动
组织
实施
本单元教学内容及设计
教学手段及
时间分配
教学内容简要回顾、教学任务导入(或案例解析):
通过找学生上黑板默写公式的形式,对上节课所讲内容:流
体力学基本方程、连续性方程进行回顾,并用一句谚语“人往高
处走,水往低处流”导入课程内容。
教学过程(含教学内容、师生互动、教学重点解决、难点突破):
一、组织教学,整顿课堂秩序,点名
二、微思课
观看视频《大国工匠》记录片
2
三、导入新课
同学们,上节课我们学习了流体密度、压强、流量和流速、
黏度的表达方式,还掌握流体静力学基本方程和连续性方程的应
用,对流体在静止及运动过程中的一些规律有所了解,这节课我
们讨论一下流体在流动的过程中涉及的能量交换。
四、新课内容
四、伯努利方程及应用
同学们都知道一句谚语:“人往高处走,水往低处流。”为什
么会产生这种现象呢?(引导学生开始讨论,回顾初中、高中物
理所学知识,得出结论) 同学们说的没错,因为能量转换,高处
的水因为具有重力势能,只要存在高度差,水的重力势能就会自
发的转化为水的动能,这就是我们平时最常见的现象“水往低处
流”的原因啦。那么今天我们所讲的流体也具有这样的性质,我
们一起讨论一下,流动的流体都具有哪些能量?各能量之间又发
生了怎样的转换呢?
1.流动流体所具有的机械能
(1)位能
流体受到重力作用在不同高度处所具有的能量称为位能。(从
这个概念上,同学们就发现了就是我们所熟悉的重力势能,只是
我们给他换了名字)。
位能是一个相对值,计算位能时应先规定一个基准是平面。
质量为m kg的流体的位能为mgZ,其单位为J;
(2)动能
流体以一定速度流动所具有的能量,称为动能。
质量为m kg,速度为u m/s流体的动能为1/2mu2,其单位为
J。
(3)静压能
进入截面后的流体,因克服静压强而具有的能量称为静压能。
(概念上比较抽象,首先让学生明白什么是静压强,如何体现克
服静压强做功这一现象)
我们一起看看书中P25页下面这段话,理解以上两个问题。
质量为m kg流体的静压能为 ,其单位为J。
因此,m kg流体在某截面上的总机械能为:
1kg流体在某截面上的总机械能为:
mp
mpmumgz221
pugz221
3
2.伯努利方程式
(1)理想流体的伯努利方程式
首先构建分析模型,利用书中P26图1-27系统的两个截面处
的能量进行分析,当理想流体在某一密闭管路中作稳定流动时,
由能量守恒定律可知,进入管路系统的总能量应等于从管路系统
带出的总能量。忽略流动阻力和一切能量损失,得出:
①以单位质量流体为基准的理想流体的伯努利方程
②以单位重量流体为基准的理想流体的伯努利方程
上式等式两边同除g,
注意:两式所选基准不同,公式形式也不相同。
(2)实际流体的伯努利方程式
在流动过程中存在阻力,克服阻力需要消耗一部分机械能,
称为能量损失或阻力损失,用ΣW
f
表示,单位为J/kg。从流体输
送机械所获得的外加功,用We表示,单位为J/kg。
①以单位质量流体为基准的理想流体的伯努利方程
②以单位重量流体为基准的理想流体的伯努利方程
同学们注意,式中各项的称谓也有所变化,位压头、静压头、
动压头、有效压头、损失压头。
(3)伯努利方程式的讨论
当系统中流体静止时,伯努利方程变为
此式为流体静力学基本方程的另一种形式。
3.伯努利方程式应用
同学们,碰到实际问题,我们如何用伯努利方程式解决的?
22221
2
11
212
1pugzp
ugz
gugpzgugpz22
22222
11
1
fhgugpzHegugpz2222222111
feWpugzWpugz22221211
212
1
221
1
pgzp
gz
4
(1)作图
(2)截面的选取 确定衡算范围
(3)基准水平面的选取
(4)单位必须一致
下面我们一起看看书中P29例题1-9、1-10,具体按照以上步
骤,如何利用伯努利方程式解决实际问题的。
指导学生阅读题目,黑板上作图演示,根据题目找出已知量、
未知量,分析讨论,与伯努利方程式相对应,带入已知数值,得
出答案。
教学内容简要小结:今天学习的主要内容为伯努利方程及其应用,
针对理想流体、实际流体,选择基准不同(单位质量、单位重量),
一共有四种形式的伯努利方程式,请同学们下去之后仔细思考,
融汇贯通,另外我们还讲解了利用伯努利方程解决实际问题的步
骤和例题,希望大家再看一看,不明白的地方及时问。
作业布置
教学反思
