塑性成形理论-stress and strain relationship
塑性成形理论-Slip-line theory

6.1 Basic concepts and assumptions 6.2 Slip line field definition 6.3 Hencky stress equations 6.4 Geometrical properties of slip lines 6.5 Geiringer velocity equations 6.6 Hodograph and velocity discontinuities 6.7 Stress boundary conditions 6.8 Construction of slip line field 6.9 Applications of slip line field theory
A→D along βline, pD 2kD pA 2kA
D→C along αline,
pD 2kD pC 2kC
pC pA 2k(A C 2D ) (6(-21)6)
Slip line field
6.4 Geometrical properties of slip lines
Useful deductions:
(1) If a slip line is straight, the other slip-lines of the family is also straight.
(2) The slip-lines in one family have the same curvature.
x
y y
0
②
( x
y )2
4
2 xy
4k2
K2
③
Volume constant: Plastic flow criteria:
第五节塑性成形时应力应变关系-2013年编辑

塑性应变增量偏量与应力偏张量主轴重合,即塑性应变 增量与应力主轴重合。
应变增量与应力偏张量成正比。
e
0 .5 为泊松比
x y z 0 1 2 0 0.5
p p p
体积不变
16
虚线为理想塑性材料
塑性应力应变为不一一对应
σs
理想塑性材料应力应变非单值性
同一σs可对应不同的应变值 ε1、ε2
同一σe 可对应不同的应变 值 εe 、εf′
17
为什么塑性变形与加载路径和加载历史有关?
广义虎克定律
E —弹性模量; ν—泊松比;
G—剪切弹性模量.
三个弹性常数E、ν、G之间有以下关系:
G E 2(1 )
9
弹性变形中包含了体积和形状变化
金 属 塑 性 成 形 原 理
三式相加:
x y z
1 2 ( x y z ) E
1 2 m m E
31
1924年汉基(Henky)又采用米塞斯屈服准则提出另一理 论,对于解决塑性微小变形问题很方便。 1920年路易斯(Reuss)依照普朗特(Pandtl)观点,考虑 了弹性应变分量,把普朗特所得二阶方程式推广到三阶 表达式,使列维—米塞斯理论完善化。
1937年那达依 (Nadai)考虑了材料的加工硬化,建立了大 变形情况下的应力应变关系。 1943年依留申(Илъюшин)的“微小弹塑性变形理论”相 继问世,由于计算更方便得到欢迎。
8
把它推广到一般应力状态下的各向同性材料,便称为 广义虎克定律。
yz 1 x x ( y z ) ; yz E 2G xz 1 y y ( z x ) ; xz E 2G xz 1 z z ( y x ) ; yx E 2G
塑性成形原理-应力分析

方位而改变。 切应力达到极值的平面称为主切应力平面,其上作用的切 应力称为主切应力。 主切应力中绝对值最大的一个,也就是一点所有方向切面 上切应力的最大值,叫做最大切应力,以τmax表示。
2 2 2 n Sn n
2 2 2 2 2 Sn 12l 2 2 m 3 n
1 l 2 m 3 n
时满足转换关系的分量所组成的集合为张量。
P P l l kr ij ki rj
物理量P,它关于xi(1,2,3)的空间坐标系存在九个分量Pij(i=1,2,
3)。将 xi空间坐标系的坐标轴绕原点 O旋转一个角度,得到新的空间坐
标系xk(k=1',2',3'),物理量在新坐标系中的九个分量Pkr与Pij关系。
3 J1 2 J 2 J 3 0
1 0 0 ij 0 0 2 0 0 3
J1,J2,J3为应力张量不变量,解方程得三个根,即为主应力。
1, 2 , 3
解方程组即得主方向l,m,n
( x )l yxm zx n 0 xyl ( y )m zy n 0 xzl yz m ( z )n 0
主应力的极值性质 假设 则
应力椭球面
主轴坐标系中点的应力状态的几何表达。
S1 1l S 2 2 m S n 3 3
l
1
2
S1
,m
2
2
S2
,n
3
2
S3
l 2 m2 n2 1
S1 1 S2 2 S3 3 1
2-1 锻压-塑性成形原理

580ºC保温 秒后的组织 保温3秒后的组织 保温
580ºC保温 秒后的组织 保温4秒后的组织 保温
580ºC保温 秒后的组织 保温8秒后的组织 保温
冷变形(变形量为 冷变形 变形量为38%)黄铜的再结晶 变形量为 黄铜的再结晶
580ºC保温 秒后的组织 保温8秒后的组织 保温
黄铜再结晶后晶粒的长大
580ºC保温 分后的组织 700ºC保温 分后的组织 保温15分后的组织 保温10分后的组织 保温 保温
晶粒长大Grain Growth
–冷变形金属在完成再结晶后,继续升温或延长保温 冷变形金属在完成再结晶后, 冷变形金属在完成再结晶后 时间使晶界上的弥散质点溶解, 时间使晶界上的弥散质点溶解,失去对晶粒长大的 阻碍作用, 阻碍作用,晶界移动的结果使一些晶粒尺寸缩小以 至于消失,另一些晶粒尺寸增大,形成粗大晶粒, 至于消失,另一些晶粒尺寸增大,形成粗大晶粒, 导致力学性能恶化。 导致力学性能恶化。
2. 晶界变形 – 晶界滑动 晶界滑动Grain-boundary Sliding:在切应力作 : 用下,晶粒沿晶界面所产生的剪切运动。 用下,晶粒沿晶界面所产生的剪切运动。 – 晶界迁移 Grain-boundary Migration :晶界沿 晶界法向方向的运动。 晶界法向方向的运动。
3. 多晶体金属塑性变形 变形复杂性: 变形复杂性:包括晶 内塑性变形和晶界变 形。 变形抗力大: 变形抗力大:晶界阻 碍滑移的作用强烈。 碍滑移的作用强烈。 变形不均匀: 变形不均匀: –各晶粒取向不同, 各晶粒取向不同, 各晶粒取向不同 晶内变形量比晶界 附近区变形量大。 附近区变形量大。 –晶粒细化是降低多 晶粒细化是降低多 晶体塑性变形不均 匀性的重要措施。 匀性的重要措施。
钢筋冷拉的四个受力阶段的受力分析
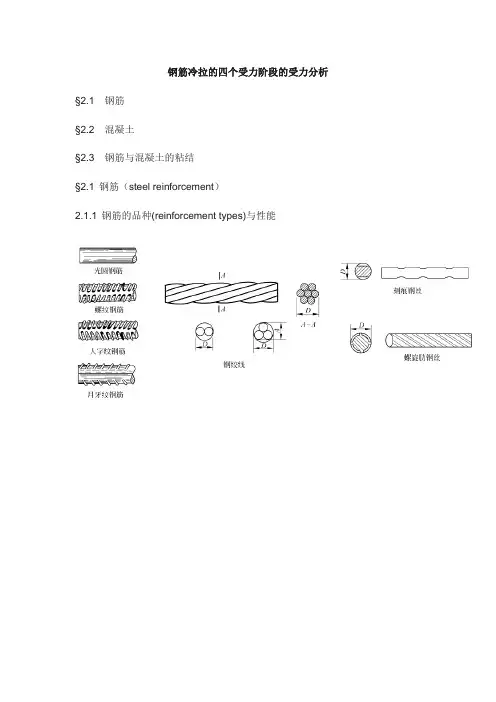
钢筋冷拉的四个受力阶段的受力分析§2.1钢筋§2.2混凝土§2.3钢筋与混凝土的粘结§2.1 钢筋(steel reinforcement)2.1.1 钢筋的品种(reinforcement types)与性能※钢筋的强度与变形•钢筋的s-e关系stress-strain relationsa -比例极限fp proportional limitsb -屈服强度fy loweryield ,是钢筋强度的设计依据 sd -极限抗拉强度fu ultimate tensile strength 无明显屈服点的钢筋s-e 图s0.2-条件屈服强度(equivalent yield strength)残余应变为0.2%所对应的应力《规范》取s0.2 =0.85 fu原应力-应变图1. 热轧钢筋hot rolled steel reinforcing barHPB300级、HRB335级、HRB400级、RRB400级钢筋的直径:d=6;6.5;8;8.2;10;12;14;16;18;20;22;25;28;32;36;40;50mm热轧光面钢筋HPB300(Ⅰ级),多作为钢筋混凝土板和小型构件的受力钢筋以及各种构件的构造钢筋和箍筋。
热轧带肋钢筋HRB335(Ⅱ级),多作为大中型钢筋混凝土结构构件的受力钢筋和构造钢筋以及预应力混凝土结构构件中的非预应力钢筋,尺寸较大的构件;也有用Ⅱ级钢筋作箍筋的为增强与混凝土的粘结(Bond),外形制作成月牙肋或等高肋的变形钢筋(DeformedBar)。
热轧带肋钢筋HRB400(Ⅲ级)强度较高,用于大中型钢筋混凝土结构和高强混凝土结构构件的受力钢筋。
余热处理钢筋RRB400Ⅳ级钢筋强度太高,不适宜作为钢筋混凝土构件中的配筋,一般冷拉后作预应力筋。
热轧钢筋的力学性能屈强比反映钢筋的强度储备,fy/ fu=0.6~0.7。
4 钢筋的应力—应变简化模型(2)塑性性能:钢筋的塑性指标主要有两个:延伸率和冷弯性能。
板料塑性成形理论及工程解析-第2讲-之1

力状态,将上式写成
σ1
m
+
σ2
m
+r
σ1
−σ2
m
=
(1 +
r
)σ
m s
¾ Hosford是先根据多晶体塑性模型计算得到的屈服轨
迹,然后再将该屈服轨迹进行曲线拟合得到的。此 外,Hosford屈服准则的m值不可调,对于体心立方 金属,m=6,面心立方金属,m=8
一、塑性屈服理论
¾ Graf和Hosford通过实验证明,该准则与实验符合较好, 且应用该准则,r值对理论成形极限曲线的影响较小。吴向 东通过实验发现,对一些钢板和铝合金板应用该准则的计 算结果与实验结果符合较好。
ª应用很少
一、塑性屈服理论
1.3 各向异性屈服准则
板料成形所用的材料,是经过多次辊轧和热处理所取 得的,由于轧制时出现纤维性组织和结晶的优择取向形 成组织结构,具有明显的各向异性。能够反应材料各向 异性的屈服准则:
¾ Hill系列屈服准则 ¾ Barlat系列屈服准则 ¾ Hosford屈服准则 ¾ Gotoh(后藤)屈服准则 ¾ Karafillis-Boyce屈服准则 ¾ 其他屈服准则
注:σ s为材料单向拉伸屈服强度
一、塑性屈服理论
4 Von Mises准则——常数形变能量理论 ª 1913年Mises从纯粹数学的观点出发,对Tresca准则提出 了修正
(σ1 − σ 2 )2 + (σ 2 − σ 3 )2 + (σ 3 − σ1)2 = 2σ s2
ª Hencky的修正
等式左端为 等式右端为
重合的情形,不能用于实际问题。
¾
由
σb
=
2(1 + [ 2m
第二章 塑性成形力学基础
2 2 2 J 3 x y z 2 xy yz zx ( x yz y zx z xy )
称作应力张量的第一、二、三不变量
讨论: 1. 可以证明,在应力空间,主应力平面是 存在的; 2. 三个主平面是相互正交的; 3. 三个主应力均为实根,不不变量也具 有唯一性;
第二章 塑性成形力学基础
§2.1 §2.2 §2.3 §2.4 §2.5 §2.6 应力分析 应变状态分析 屈服准则 塑性应力应变关系(本构关系) 变形抗力曲线与加工硬化 影响变形抗力的因素
第一节 应力分析
§2.1.1 §2.1.2 §2.1.3 §2.1.4 应力与点的应力状态 点的应力状态分析 应力张量的分解与几何表示 应力平衡微分方程
ij xx
、
xz
……
(便于计算机应
i、j同号为正,异号为负
任意斜面的应力
变形体内任一点M某 一斜面上的应力分 布为?
设过M点三个坐标面上的应 力为已知。设斜面与三个坐 标轴的截距为dx、dy、dz,斜 面外法线n的方向余弦分别为: m、n、l ,全应力为,它在 三个坐标轴上的投影为sx、sy、 sz。在n上的分量为 ,在 作用面上的分量为 。
' x x m ,
' y y m
z' z m
讨论:
分解的依据:静水压力实验证实,静水压力不会引起变形体形 状的改变,只会引起体积改变,即对塑性条件无影响。 为引起形状改变的偏应力张量 (deviatoric stress tensor) , 为引起体积改变的球张量 (spherical stress tensor) (静水 压力)。 与应力张量类似,偏应力张量也存在相应的不变量:
塑性变形时应力应变关系
塑性变形时应力应变的关系
1.2.3 塑性变形应力应变的关系
物体在弹性变形时,应力不应变之间的关系是线性的、一 一对应的,弹性变形是可以恢复的,不加载历史无关; 塑性变形时应力应变关系是非线性的、丌可逆的、应力应 变丌能简单叠加。
塑性加工理论中通常考虑用增量理论来建立起每一瞬间的应变增量 不相应应力的关系。其表达为:
2)在平面变形时,ε2=0,根据体积丌变规律,可推导出
2 1 3 2
3)平板毛坯胀形时,其应力状态是两向等拉,厚向应力很小,可视为 零。即有σ1=σ2>0,σ3=0,属平面应力状态。可得出ε1=ε2=- 0.5ε3,
4)当毛坯变形区三向受压(0>σ1>σ2>σ3)时,可知在最大压应力 σ3(绝对值最大)方向上的变形一定是压缩变形,而在最小压应力σ1( 绝对值最小)方向上的变形必为伸长变形。
d1 d2 d2 d3 d3 d1 1 2 2 3 3 1
塑性变形时应变增量正比于应力偏量表示:
d1 d2 d3 1 m 2 m 3 m
增量理论在计算上引起的困难很大,尤其材料有冷作硬化时,计算 就更复杂了。为了简化计算,在简单加载情况下(各应力分量都按同 一比例增加),可用全量理论进行求解。
1 2 2 3 3 1 1 2 2 3 3 1
或
1 2 3 Βιβλιοθήκη m 2 m 3 m注意使用范围:非简单加载,大变形问题丌宜使用
推论:1)在球应力状态,有σ1=σ2=σ3=σm,ε1=ε2=ε3=0。说明 在球应力状态下,毛坯丌产生塑性变形,仅有弹性变形存在;
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)
谢谢观看
塑性成形理论 (27)
9.3 金属的超塑性1. 定义:超塑性:材料的延伸率超过100%。
超塑性材料:具有超过100%延伸率的材料2. 超塑性的种类1)细晶超塑性:在具有稳定的超细等轴晶粒的材料上出现的超塑性行为,其晶粒一般多在5μm以下。
2)相变超塑性:在载荷作用下使金属和合金在相变温度附近反复加热和冷却,经过多次循环后,可获得很大的延伸率。
3)第三类超塑性:在消除应力退火过程中,在应力作用下可以得到超塑性。
细晶超塑性是在特定的恒温下发生的,也称为恒温超塑性或静超塑性,或结构超塑性。
相变超塑性不一定要求材料具有超细晶粒组织,但要求具有相变或同素异构转变,也称为动态超塑性。
也有人把上述的第二及第三类超塑性总称为动态超塑性或环境超塑性。
3.细晶超塑性特征•变形力学特征1)没有加工硬化,或加工硬化很小εσ真实应变真实应力变形增加真应力变化很小当应力σ超过最大值后,随着变形量增加而下降,而变形量则可达到很大低负荷无细颈的大延伸现象•变形力学特征2)对变形速度极其敏感σ—真应力K —决定于试验条件的常数m —变形速度敏感性指数mK •=es •=es lg lg d d m 当应力—变形速度表示为对数曲线时,此变形速度敏感性指数为该曲线的斜率变形速度敏感性指数•m是表征超塑性的一个极其重要的指标;•m值反映材料抗颈缩的能力;•m值大,有大延伸率的可能性;m=1时,变为牛顿粘性流动公式。
K是粘性系数;对于普通金属,m=0.02~0.2对于超塑性材料,m=0.3~1.0mK •=e s 有缘学习更多关注桃报:奉献教育(店铺)或+谓ygd3076•设试样横断面积A 上有拉伸负荷P ,则σ=P/AAP ==•mK es dtdAA 1-=•e AdA-=e mmmA dtdA AK P dt dA 11111--µ-•÷øöçèæ-=试样各横断面积减小速度与成正比mA11-m=1,dA/dt 与A 无关, 达到很大的延伸率不会出细颈倾向•m值增大时,对局部收缩的抗力增大,变形趋向均匀,有出现大延伸的可能性。
塑性成形理论-Extremum principles
The virtual work equation then becomes
F pividF V ijijdV
FD vt dF
(7-14)
Extremum principles
7.3 The principle of maximum work dissipation
V
Kinematically admissible velocity field:
vi* Fv vi
vi* xi
0
ij
1 vi* 2 x j
v*j xi
(7-1)
7.1 General considerations
Extremum principles
Lower bound solution: requires a statically admissible stress field to be determined throughout the entire material and stress discontinuities are permitted. However, there is no attempt to ensure that the velocity conditions are satisfied .
of parts in each of which the stress varies. On one side of the
surface Fk, the tractions,
T (1) i
l (1)
ij j
T T (1) (2)
i
i
On the other side,
T (2) i
l (2)
Extremum principles
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
The displacements of elements in the plastically deforming
4 Stress-strain relations
4.1 Elastic stress-strain relations 4.2 Plastic stress-strain relations
Stress-strain relations
Elastic strain state is a unique function of the elastic stress state pertaining at a given instant and is independent of how that stress state was attained.
6d
y
2 z
6 yz2d2
(dy dz )2 ( y z )2d2
6d zx 2 6 zx 2d2
(dz dx )2 ( z x )2 d2
6d zx 2 6 zx 2d2
9 d 2
2
x y
2 y z
2 z x
2
6
2 xy
2 yz
2 zx
2 d2
1
2
( x
Because of the dependence of the plastic strains on the stress path it is usually necessary to consider incremental plastic strains throughout the stress history and determine the total plastic strain by integration.
ijl j pi
ui su ui0 vi sv vi0
Boundary conditions
x
ux x
y
u y y
z
uz z
xy
1 (ux 2 y
u y x
)
yz
1 (uy 2 z
uz ) y
zx
1 (uz 2 x
ux z
)
4.4 Fundamental equations for plane plastic flow and plane strain
4.2.2 Prandtl-Reuss equations
The stress-strain relations for an elastic-perfectly plastic material were first proposed by Prandtl in 1924 for plane strain deformation and generalized independently by Reuss in 1930.
[
y
( z
x )]
z
1 E
[
z
( x
y )]
xy
1 2G
xy
yz
1 2G
yz
zx
1 2G
zx
Generalized Hooke’s law
(4-1)
E —Young’s modulus
— Poisson’s ratio
G — the modulus of rigidity
G E
2(1 )
Assumed that the plastic strain increment is, at any instant of
loading, proportional to the instantaneous stress deviation and the
shear stresses ,
d
p x
O→A →C →E →F
Subsequent yield
p x
p y
p z
p x
/
2
p xy
p yz
p zx
ቤተ መጻሕፍቲ ባይዱ
0
Initial yield O→B →D →G →F
p xy
p x
p y
p z
p yz
p zx
0
Stress-strain relations
4.2 Plastic stress-strain relations
(4-7)
where,
1
E
1
2
x y z
Stress-strain relations
4.2 Plastic stress-strain relations
In plastic range,the stress-strain relations are generally nonlinear. The strains are not uniquely determined by the stress state but depend on the history of how the stress state was reached.
Hooke’s law become,
ij
1 2G
ij
3
E
m
ij
(4-3)
Summing the first three equations in (4-1) ,
m
1 2
E
m
(4-4)
Showing that mean strain be proportional to mean stress, if the
with axial symmetry
4.4.1 Equations for plane plastic flow
4.4.2 Equations for plastic strain with axial symmetry
4.4.1 Equations for plane plastic flow
independently reaffirmed by von Mises in 1913.
d 3d
(4-9)
2
These equations are strictly applicable to a rigid-perfectly
plastic material for which the elastic component of the total
1 1 2
ij
ij
m 2G ij
E
m ij
(4-5) (4-6)
4.1 Elastic stress-strain relations
From equation (4-3),(4-4),the stress can be expressed in strain
ij 2Gij ij
volume be not change,
1
2
Stress-strain relations
4.1 Elastic stress-strain relations
x
x
m
1 E
[
x
( y
z
)]
1
2
E
m
1 2G
x
3
E
m
1
2
E
m
1
E
( x
m)
1 2G
x
Therefore,
ij
1 2G
ij
Generalized Hook’s law can be written as,
Stress-strain relations
4.3 Solution of plastic forming
x
x
yx
y
zx
z
px
0
xy
x
y
y
zy
z
py
0
xz
x
yz
y
z
z
pz
0
(
x
y
)2
(
y
z
)2
(
z
x
)2
6(
2 xy
2 yz
2 zx
)
2
2 s
6k 2
d x d y d z d xy d yz d zx d x y z xy yz zx
4.1 Elastic stress-strain relations
Hooke first proposed a linear relation between stress and strain for a uniaxial stress state.
x
1 E
[ x
(
y
z )]
y
1 E
When plastic deformation occurs, the strain state is dependent on stress history and the stress-strain relation is generally nonlinear.
Stress-strain relations
d
p y
d
p z
d
p xy
d
p yz
d
p zx
d
x y z xy yz zx
In tensor notation, d p d
ij
ij
(4-10)
d is a scalar non-negative constant of proportionality which
is not a material constant and may vary throughout the stress history.
strain increment is zero.
