黑体辐射实验数据处理
黑体辐射实验

黑体辐射实验实验十八黑体辐射实验一、实验目的1.了解黑体和一般发光体辐射强度的关系;2.掌握测量一般发光光源的辐射能量曲线的方法3.验证普朗克辐射定律;4.验证斯忒藩一波耳兹曼定律;5.验证维恩位移定律;二、黑体辐射和实验基本理论1.黑体辐射任何物体,只要绝对不为零,就会向周围发射辐射,这称为热辐射。
黑体是一种完全的热辐射体,即,任何非黑体所发射的辐射通量都小于同温度下的黑体发射的辐射通量。
在热平衡下,黑体的辐射能力则仅与温度有关。
黑体的辐射亮度在各个方向都相同,即黑体是一个完全的余弦辐射体。
辐射能力小于黑体,但辐射的光谱分布与黑体相同的温度辐射体称为灰体。
2.黑体辐射定律(1)黑体辐射的光谱分布——普朗克辐射定律普朗克提出,在空腔辐射体中电磁辐射的能量是量子化的。
根据这一假定,在某一温度下达到平衡时,黑体的光谱辐射度可表示为: )1e (C )1e (1hc 2E T 2C kT hc 51552T -λ=-λλπ=λλλ(瓦/米3)(18-1)式中c 为光速,h 为普朗克常数,C 1 = 3.74×10-16 (瓦米2)、常数C 2 = 1.4398⨯10-2(米开尔文)。
黑体光谱辐射亮度由下式给出: π=λλT TE L (瓦/米3球面度) (18-2)图18-1 黑体的频谱亮度L λT 随波长变化图2-1 给出黑体的频谱亮度随波长的变化,其中每一条曲线上都标出黑体的绝对温度。
与诸曲线的最大值相交的对角直线表示维恩位移定律。
(2)黑体的积分辐射——斯忒藩—波尔兹曼定律此定律用辐射度表示为,40T T T d E E δ=λ=⎰∞λ(瓦特/米2)(18-3)T 为黑体的绝对温度,δ为斯忒藩—波尔兹曼常数,δ =2345c h 15k 2π= 5.670×10-8 (瓦/米2•开尔文4) (18-4)其中,k 为波尔兹曼常数,h 为普朗克常数,c 为光速。
由于黑体辐射是各向同性的,所以其辐射亮度与辐射度有关系π=TE L(18-5)于是,斯忒藩—波尔兹曼定律也可以用辐射亮度表示为4T L πδ=(瓦特/米2•球面度)(18-6)(3)维恩位移定律光谱亮度的最大值的波长 λmax 与它的绝对温度T 成反比,T Amax =λ(18-7)A 为常数,A=2.896⨯10-3 (米×开尔文)。
2 实验二 黑体辐射实验

实验二黑体辐射实验概述WGH-10型黑体实验装置专门用于进行黑体辐射能量的测量和任意发射光源的辐射能量的测量。
可以记录出发光源的辐射能量曲线。
在实验时,通过改变光源的温度,分别进行扫描,可以从记录的光谱辐射曲线直接看到维恩位移定律的现象,并能够对普朗克定律、斯忒藩-波尔兹曼定律进行较精确的验证。
WGH-10型黑体实验装置的控制系统采用WINDOWS界面,在WINDOWS 95/98系统下均能适用,功能强大、操作简便。
控制软件中,根据普朗克公式可以计算出任意温度下的绝对黑体的理论曲线,用户可以根据需要提取。
WGH-10型黑体实验装置所配的光源是溴钨灯,溴钨灯的谱线大致类似于黑体,但是由于钨的发射系数不是1,所以需要进行修正。
软件可以对不同温度下溴钨灯的曲线进行发射系数 (仅限于溴钨灯)的修正。
此外WGH-10型黑体实验装置还可作为光谱区间在800-2500nm范围的光栅光谱仪使用,进行其它实验。
1.规格与主要技术指标1.1 规格、参数:相对孔径 D/F=1/7焦距 302.5 mm色散元件 300L光栅狭缝 0-2 mm连续可调,示值精度0.01mm/格,最大高度20mm主机尺寸 360×300×160mm1.2 主要技术指标:波长范围 800—2500nm波长精度±6 nm波长重复性 3 nm杂散光≤0.3%T2.黑体的基本理论2.1 黑体辐射任何物体,只要其温度在绝对零度以上,就向周围发射辐射,这称为温度辐射。
黑体是一种完全的温度辐射体,即,任何非黑体所发射的辐射通量都小于同温度下的黑体发射的辐射通量;并且,非黑体的辐射能力不仅与温度有关,而且与表面的材料的性质有关。
而黑体的辐射能力则仅与温度有关。
黑体的辐射亮度在各个方向都相同,即黑体是一个完全的余弦辐射体。
辐射能力小于黑体,但辐射的光谱分布与黑体相同的温度辐射体称为灰体。
2.2黑体辐射定律2.2.1 黑体辐射的光谱分布——普朗克辐射定律此定律用光谱辐射度表示,其形式为:)1(251-=TC e C E T λλλ(瓦特/米3)式中:第一辐射常数C 1 = 3.74×10-16 (瓦×米2)第二辐射常数C 2 = 1.4398⨯10-2(米×开尔文)黑体光谱辐射亮度由下式给出:πλλT T E L =(瓦特/米3.球面角)图2-1 给出了T L λ随波长变化的图形。
黑体辐射实验
实验十 黑体辐射实验实验者:头铁的小甘引言:任何物体,只要温度大于绝对零度,就会向周围发生辐射,这称为温度辐射。
黑体是指能够完全吸收所有外来辐射的物体,处于热平衡时,黑体吸收的能量等 于辐射的能量,由于黑体具有最大的吸收本领,因而黑体也就具有最大的辐射本 领。
这种辐射是一种温度辐射,辐射的光谱分布只与辐射体的温度有关,而与辐 射方向及周围环境无关。
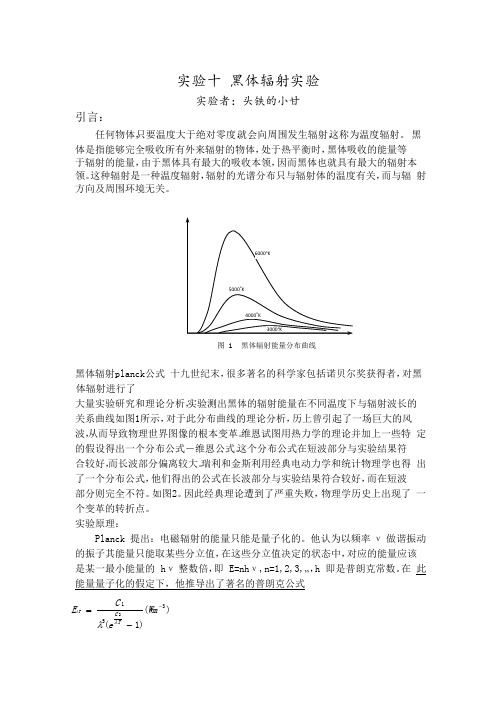
6000o K5000o K4000o K3000o K图 1 黑体辐射能量分布曲线黑体辐射 p lanck 公式 十九世纪末,很多著名的科学家包括诺贝尔奖获得者,对黑体辐射进行了大量实验研究和理论分析,实验测出黑体的辐射能量在不同温度下与辐射波长的 关系曲线如图 1 所示,对于此分布曲线的理论分析,历上曾引起了一场巨大的风 波,从而导致物理世界图像的根本变革。
维恩试图用热力学的理论并加上一些特 定的假设得出一个分布公式-维恩公式。
这个分布公式在短波部分与实验结果符 合较好,而长波部分偏离较大。
瑞利和金斯利用经典电动力学和统计物理学也得 出了一个分布公式,他们得出的公式在长波部分与实验结果符合较好,而在短波 部分则完全不符。
如图 2。
因此经典理论遭到了严重失败,物理学历史上出现了 一个变革的转折点。
实验原理:Planck 提出:电磁辐射的能量只能是量子化的。
他认为以频率ν做谐振动 的振子其能量只能取某些分立值,在这些分立值决定的状态中,对应的能量应该 是某一最小能量的 h ν整数倍,即 E=nh ν,n=1,2,3,…,h 即是普朗克常数。
在 此能量量子化的假定下,他推导出了著名的普朗克公式)()1(3512--=Wm eC E TC T λλλπ第一辐射常数C 1=8πhc =3.74×10-16(Wm 2),第二辐射常数C 2=1.4388×10-2(mK )。
它与实验结果符合得很好。
Planck 提出的能量量子假说具 有划时代的意义,标志了量子物理学的诞生。
黑体辐射试验

黑体辐射实验
三、实验内容(续) 2. 仪器的光学系统 光学系统采用C-T型,光学原理图如下所示:
M1反射镜、M2准光镜、M3物镜,M4反射镜、M5 深椭球ቤተ መጻሕፍቲ ባይዱ G平面衍射光栅、S1入射狭缝、S2,S3出射狭缝、T调制器
三、实验内容(续)
黑体辐射实验
光学系统的入射狭缝、出射狭缝均为直狭缝,宽度连续可调,光源 发出的光束从入射狭缝S1处进入系统,S1位于反射式准光镜M2的焦面 上,通过S1射入的光束经M2反射成平行光束投向平面光栅G上,衍射 后的平行光束经物镜M3成象在S2上。经M4、M5会聚在光电接受器D上。 各部件的规格如下: M2、M3 焦距302.5mm 光栅G 每毫米刻线300条 闪耀波长1400nm滤光片 工作区间: 第一片 800-1000nm 第二片 1000-1600nm 第三片 1600-2500nm 3. 仪器的机械传动系统 仪器采用如图12-4(a)所示“正弦机构”进行波长扫描,丝杠 由步进电机通过同步带驱动,螺母沿丝杠轴线方向移动,正弦杆由弹 簧拉靠在滑块上,正弦杆与光栅台连接,并绕光栅台中心回转,如图 12-4(b),从而带动光栅转动,使不同波长的单色光依次通过出射 狭缝而完成“扫描”。
三、实验内容(续)
黑体辐射实验
4. 溴钨灯光源 标准黑体应是黑体实验的主要设置,但标准黑体其价格很高, 所以本实验装置采用稳压溴钨灯作光源,溴钨灯的灯丝是用钨丝 制成,钨是难熔金属,它的熔点为3665°K。钨丝灯是一种选择 性的辐射体,它产生的光谱是连续的,它的总辐射本领RT可由下 式求出。 式中为温度T时的总辐射系数,它是给定温度 钨丝的辐射强度与绝对黑体的辐射强度之比,因此 -4 或 式中B为常数,B=1.47×10 钨丝 灯的辐射光谱分布Rλ T为
黑体热辐射实验结果的修正与拟合

激光与非线性光学实验室—— 李立 2011-7-4一、 实际物体热辐射与绝对黑体辐射绝对黑体辐射可由普朗克定律描述,给出了光谱辐射强度随温度和波长的依赖关系,251/(,)1b c T c E T e λλλ−=− (1)其中λ是波长(m ),T 是黑体温度(K ),c 1 为第一辐射常数:3.742×10-16 W ⋅m2,c 2为第二辐射常数:1.4388×10-2 W ⋅K 。
黑体是指能吸收投入到其面上的所有热辐射能的物体,是一种科学假想的物体,现实生活中是不存在的,但却可以人工制造出近似的人工黑体。
与绝对黑体类似,灰体也是一种假象的理想物体,其特征是光谱吸收比与波长无关的物体。
同温度下,黑体的表面辐射能力最强,实际物体的表面辐射能力都比同温度下的绝对黑体要弱,而且热辐射光谱也要发生一定程度的变化。
实际物体的热辐射由下式描述,(,)(,)(,)b L T T E T λελλ= (2)其中ε (T , λ)代表实际物体的光谱发射率(或称黑度),它依赖于实际物体的物质种类、表面温度和表面情况,而与外界条件无关。
通常光谱发射率是温度和辐射波长的函数,在一定范围内变化,而且小于1。
比如钨丝灯(溴钨灯,黑体色温2800-3300K 之间的某一值)的发射率在0.2~0.5之间变化。
E b (T , λ)为同温度下的绝对黑体辐射。
二、 实际物体辐射谱的校正利用钨丝灯可以校正测量仪器得到的辐射光谱能量分布。
假定测量系统的光谱响应为R (λ),钨丝灯的标准辐射谱为L (T , λ),钨丝灯的仪器测量谱为I (T , λ),则有如下关系,(,)()(,)I T R L T λλλ= (3)因此,如果已知标准辐射谱L (T , λ),就可以获得测量系统的响应谱R (λ),(,)()(,)I T R L T λλλ= (4)标准灯的绝对辐射谱可以有制造商提供,或者到国家的计量检定测试机构进行标定。
实验七 黑体辐射

实验七 黑体辐射Black-body Radiation任何物体,只要其温度在绝对零度以上,就向周围发射辐射,这称为温度辐射;只要其温度在绝对零度以上,也要从外界吸收辐射的能量。
处在不同温度和环境下的物体,都以电磁辐射形式发出能量,而黑体是一种完全的温度辐射体,即任何非黑体所发射的辐射通量都小于同温度下的黑体发射的辐射通量;并且,非黑体的辐射能力不仅与温度有关,而且与表面的材料的性质有关,而黑体的辐射能力则仅与温度有关。
在黑体辐射中,存在各种波长的电磁波,其能量按波长的分布与黑体的温度有关。
实验目的(experimental purpose)1.了解黑体实验的发展历史,明确光谱辐射曲线的广泛应用;2.了解黑体实验仪器组件,明确测量过程与分析要素;3.明确黑体实验设计思想,掌握黑体辐射原理与定律。
实验原理(experimental principle)任何物体都具有不断辐射、吸收、发射电磁波的本领。
辐射出去的电磁波在各个波段是不同的,也就是具有一定的谱分布。
这种谱分布与物体本身的特性及其温度有关,因而被称之为热辐射。
为了研究不依赖于物质具体物性的热辐射规律,物理学家们定义了一种理想物体——黑体(black body),以此作为热辐射研究的标准物体。
所谓黑体是指入射的电磁波全部被吸收,既没有反射,也没有透射( 当然黑体仍然要向外辐射)。
显然自然界不存在真正的黑体,但许多地物是较好的黑体近似( 在某些波段上)。
黑体不仅仅能全部吸收外来的电磁辐射,且发射电磁辐 射的能力比同温度下的任何其它物体强。
黑体辐射指黑体发出的电磁辐射。
黑体辐射能量按波长的分布仅与温度有关。
对于黑体的研究,使得自然现象中的量子效应被发现。
我们换一个角度来说:所谓黑体辐射其实就是当地的状态光和物质达到平衡所表现出的现象:物质达到平衡,所以可以用一个温度来描述物质的状态,而光和物质的交互作用很强,而如此光和光之间也可以用一个温度来描述(光和光之间本身不会有交互作用,但光和物质的交互作用很强)。
实验七 黑体辐射

实验七 黑体辐射Black-body Radiation任何物体,只要其温度在绝对零度以上,就向周围发射辐射,这称为温度辐射;只要其温度在绝对零度以上,也要从外界吸收辐射的能量。
处在不同温度和环境下的物体,都以电磁辐射形式发出能量,而黑体是一种完全的温度辐射体,即任何非黑体所发射的辐射通量都小于同温度下的黑体发射的辐射通量;并且,非黑体的辐射能力不仅与温度有关,而且与表面的材料的性质有关,而黑体的辐射能力则仅与温度有关。
在黑体辐射中,存在各种波长的电磁波,其能量按波长的分布与黑体的温度有关。
实验目的(experimental purpose)1.了解黑体实验的发展历史,明确光谱辐射曲线的广泛应用;2.了解黑体实验仪器组件,明确测量过程与分析要素;3.明确黑体实验设计思想,掌握黑体辐射原理与定律。
实验原理(experimental principle)任何物体都具有不断辐射、吸收、发射电磁波的本领。
辐射出去的电磁波在各个波段是不同的,也就是具有一定的谱分布。
这种谱分布与物体本身的特性及其温度有关,因而被称之为热辐射。
为了研究不依赖于物质具体物性的热辐射规律,物理学家们定义了一种理想物体——黑体(black body),以此作为热辐射研究的标准物体。
所谓黑体是指入射的电磁波全部被吸收,既没有反射,也没有透射( 当然黑体仍然要向外辐射)。
显然自然界不存在真正的黑体,但许多地物是较好的黑体近似( 在某些波段上)。
黑体不仅仅能全部吸收外来的电磁辐射,且发射电磁辐 射的能力比同温度下的任何其它物体强。
黑体辐射指黑体发出的电磁辐射。
黑体辐射能量按波长的分布仅与温度有关。
对于黑体的研究,使得自然现象中的量子效应被发现。
我们换一个角度来说:所谓黑体辐射其实就是当地的状态光和物质达到平衡所表现出的现象:物质达到平衡,所以可以用一个温度来描述物质的状态,而光和物质的交互作用很强,而如此光和光之间也可以用一个温度来描述(光和光之间本身不会有交互作用,但光和物质的交互作用很强)。
黑体辐射实验

电科专业实验报告实验名称黑体辐射实验班级姓名学号一、实验目的:1.掌握黑体辐射的基本理论。
2.掌握黑体辐射能量的测量和任意发射光源的辐射能量的测量。
3.学会利用相同的装置验证黑体的辐射定律。
二、实验原理:1.黑体辐射基本理论:任何物体都会以电磁辐射的形式发射和接收能量。
辐射能与温度和表面性质都有关系。
辐射体的辐射性质,可以有一定的温度下,辐射体表面单位面积的辐射能量随波长的分布曲线,即单色辐射度曲线表示。
实际物体的单位辐射度依赖于辐射源的组成部分,是辐射波长的连续光谱,人的肉眼只能看到其可见光的部分。
相同温度下的黑体均发出同样的形式的光谱,不受其组成的影响。
有三个辐射定律:斯特藩-波尔兹曼定律、维恩位移定律、普朗克辐射定律。
2.黑体实验装置的原理:主机部分由单色器狭缝、接受单元光学系统以及光栅驱动系统等。
本实验选用硫化铅为光信号接收器,从单色仪出缝射出的单色光信号经过调制器,调制成50HZ的频率信号被PBS接收。
三、实验步骤:1、按要求正确连接电路。
检查无误后,打开溴钨灯电源预热;打开主机电源,连接好USB数据线。
2、建立传递函数曲线。
(1)、将标准光源电流调整为“溴钨灯的色温”表中,色温为2940K 时电流所在位置;(2)、预热20分钟后,在系统上记录该条件下全波段图谱;该光谱曲线包含了传递函数的影响;(3)、点击“验证黑体辐射定律”菜单,选“计算传递函数”命令,将该光谱曲线与已知的光源辐射能量线时,测量结果即扣除了仪器传递的影响。
3、修正为黑体。
任意发光体的光谱能量辐射本领与黑体辐射都有一系数关系,系统软件提供了钨的发射系数,并能通过将菜单栏的“修正成为黑体”点击为选定,进行修正。
测量溴钨灯的辐射能量曲线即自动修正为同温度下黑体的曲线。
4、验证黑体辐射定律。
将菜单栏中的“传递函数”和“修正成为黑体”均点击为选定后,扫描纪录溴钨灯曲线。
设定不同的色温多次测试,并选定不同的寄存器(最多可选择5个寄存器)分别将测试结果存入待用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五、数据记录与数据处理
测得不同光源色温下的三条黑体辐射曲线:
1.验证普朗克辐射定律。
(1)在光源色温为2860K的曲线上取波长为1264nm的一点,测得辐射度为2108.4W/mm2,理论值为2212.1 W/mm2。
相对误差为Δ相对=4.69%。
(2)在光源色温为2670K的曲线上取波长为1146nm的一点,测得辐射度为1733.1W/mm2,理论值为1737.4W/mm2。
相对误差为Δ相对=0.25%。
(3)在光源色温为2450K的曲线上取波长为1238nm的一点,测得辐射度为1131.3W/mm2,理论值为1132.6W/mm2。
相对误差为Δ相对=0.11%。
2.验证斯忒藩-波耳兹曼定律。
测量结果如图:
根据斯忒藩-波耳兹曼定律,一个黑体表面单位面积在单位时间内辐射出的总能量与黑体本身的热力学温度T的四次方成正比,其比例系数称为斯忒藩-波耳兹曼常数。
因此要验证斯忒藩-波耳兹曼定律,只需把测得的斯忒藩-波耳兹曼常数与公认值相比较。
由测量结果可以看出,光源色温为2450K的那组数据算得的结果很明显有问题。
舍去这组数据,重新计算测得的斯忒藩-波耳兹曼常数平均值为δ平均=5.5497×10-14W/(mm2K4),与公认值相比,相对误差为Δ相对=2.12%。
3.验证维恩位移定律。
测量结果如图:
根据维恩位移定律,黑体的温度与辐射本领最大值相对应的波长的乘积为一常数A。
为了验证维恩位移定律,只需把测得的常数A与公认值相比较。
从3组实验数据,计算得到A平均=2.836mm·K,与公认值的相对误差为Δ相对=2.07%。
