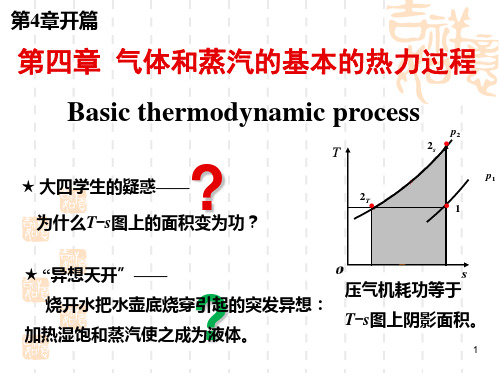
工程热力学 第四章 气体和蒸汽的基本热力过程.
工程热力学沈维道第4章 习题提示和答案
题 4-12 附图
提示和答案： 在 p − v 图和 T − s 图上， 随顺时针移动， n 增大。 可逆绝热膨胀 Δs1− 2s = 0 ， 定温膨胀 Δs = 0.462kJ/(kg ⋅ K) ，多变膨胀 Δs = 0.1923kJ/(kg ⋅ K) 。 4-14 试证明理想气体在 T − s 图（如图 4-20）上的任意
可见温度变化范围很大时按定值比热容计算误差太大。
23
第四章 气体和蒸汽的热力过程
4-10
一体积为 0.15 m 3 的气罐，内装有 p1 = 0.55 MPa，t1 = 38 °C 的氧气，今对氧气
加热，其温度、压力都将升高，罐上装有压力控制阀，当压力超过 0.7 MPa 时阀门自动打 开，放走部分氧气，使罐中维持最大压力 0.7 MPa 。问当罐中氧气温度为 285 ℃时，共加 入多少热量？设氧气的比热容为定值， cV = 0.667 kJ/(kg ⋅ K) ， c p = 0.917 kJ/(kg ⋅ K) 。 提示和答案： 初终态氧气氧气的质量 m1 =
wt , s =
4-6
1 M
( H m,1 − H m,2 ) = −138.21 × 103 J/kg 。
3 kg 空气从 p1 = 1 MPa 、 T1 = 900 K ，可逆绝热膨胀到 p2 = 0.1 MPa 。设比热
容为定值，绝热指数 κ =1.4，求： （1）终态参数 T2 和 v2 ； （2）过程功和技术功； （3） ΔU 和
的技术功
wt = − ∫ vdp = ∫ pdv + ( p1v1 − p2 v2 ) ，将过程功 ∫ pdv 的各关系式代入， p v v
v2
1
p2
1
v2
工程热力学第四章理想气体热力过程教案
第四章 理想气体的热力过程概 述热能⇔机械能的相互转化是靠工质在热力设备中吸热、膨胀、压缩等状态变化的过程来实现的，这个状态变化的过程就是热力过程，那么，在前面第一章研究的平衡状态，第二章研究理想气体的性质以及第三章研究分析开、闭口系热力状态变化的工具——热力学第一定律都是为这一章打基础。
前面第三章已提到过相同的工质在相同的温度下，不同的热力过程，能量转化的状况是不同的。
P V q q >，00v p w w ==膨技，，因此工程上实际过程多种多样、复杂、多变，不是可逆过程，据传递能量的工质不一不可能一一加以研究，何况逐个研究不总结规律性的知识用途也不大。
因此，我们仍采用热力学常用的方法，对复杂多样的热力过程进行合理化的假设。
认为是理想气体的可逆过程，这就是我们下面要研究的理想气体○V ○P ○T ○S 。
○P ：例如各种环热设备，工质一面流动一面被加热，流动中克服阻力的压力降与其压力相比小很多，故认为压力不变。
○V ：汽油机工作时，火花塞一点火，气缸内已被压缩的可燃混合气即燃烧，在一瞬间烧完，这期间气缸与外界无质量交换，活塞移动极微，可近似定容过程。
○T ：如往复式压气机，气体在气缸中被压缩时温度升高，为了省功气缸周围有冷却水套，若冷却效果好，气缸中温度几乎不变，可近似定温过程。
○S ：例气缸中燃烧产物在气缸中膨胀对外作功过程，由于工质与外界交换的热量很少可略去不计，认为是定熵过程。
上述过程实际上是略去次要因素后的一个等同特征，就是过程中有一个状态参数不变，对理想气体()u f t = ()h f t =这研究起来就方便很多，而且只有实际意义。
4—1 研究热力过程的目的及方法一． 目的1．实现预期的能量转化，合理安排热力过程，从而来提高功力装置的热经济性。
2．对确定的过程，也可预计热→功之多少。
二．解决的问题1．根据过程特点，寻找过程方程式 2．分析状态参数在过程中的变化规律3．确定热功转化的数量关系，及过程中,,u h s ∆∆∆的变化 4．在P —V ，T —S 图上直观地表示。
04工程热力学第四章-整幅显示
（4-43） （4-45）
显见
wt w
绝热过程工质对外的作功全部来自工质自身的热力学能（或焓）
六、变比热容定熵过程的图表计算法
• 300～600K时，用定比热容计算精确度较高 • 600K以上时，热力过程采用变比热容计算比定比热容要精确得多！ 1. 计算方法（p1、v1 → p2、v2）
w pdv pv
图4-5 定温过程
（4-29） （4-31）
传热量: qT u w w Rg T ln
v2 v p p1v1 ln 2 p1v1 ln 2 wt （4-30） v1 v1 p1
定温过程的加热量用于全部对外作功
4–5 绝热过程 （可逆的绝热过程=定熵过程）
s c p
1
2
p dT Rg ln 2 0 T p1
T2 p2 dT Rg ln cp f (T ) p1 T1 T
(b)
s cv
1
2
v dT Rg ln 2 0 T v1
T1 p2 1 T2 dT dT ln c c p p p1 Rg T0 T T0 T
（4-1）
1、初、终态参数的关系
p1v1 p2v2
n n
p2 v ( 1 )n p1 v2
（4-1） （4-2） （4-3）
T1 v1
n 1
T2v2
n 1
2. 多变指数
n
T2 v ( 1 ) n 1 T1 v2 1 T2 p2 nn ( ) T1 p1
ln p2 ln p1 ln( p2 / p1 ) ln v2 ln v1 ln(v2 / v1 )
工程热力学第四章理想气体热力过程
03
CHAPTER
等容过程
等容过程是指气体在变化的整个过程中，其容积保持不变的过程。
定义
特点
适用场景
气体在等容过程中，气体温度和压力会发生变化，但容积保持不变。
等容过程常用于高压、高温或低温等极端条件下的气体处理。
03
02
01
等容过程定义
在等容过程中，气体吸收的热量等于气体所做的功和气体温度升高所吸收的热量之和。
多变过程的具体形式取决于气体所经历的压力和温度的变化规律。
多变过程定义热力学第一定律 Nhomakorabea热力学第二定律
理想气体状态方程
热效率
多变过程的热力学计算
01
02
03
04
能量守恒定律，用于计算多变过程中气体吸收或释放的热量。
熵增原理，用于分析多变过程中气体熵的变化。
描述气体压力、体积和温度之间的关系，可用于多变过程的计算。
衡量多变过程能量转换效率的指标，通过比较输入和输出的热量来计算。
提高热效率的方法
优化多变过程参数，如压力和温度的变化规律，以减少不可逆损失和提高能量转换效率。
热效率与熵增的关系
根据熵增原理，不可逆过程会导致熵的增加，从而降低热效率。因此，减少不可逆损失是提高多变过程热效率的关键。
热效率计算公式
$eta = frac{Q_{out}}{Q_{in}}$，其中$Q_{out}$为输出热量，$Q_{in}$为输入热量。
计算公式
通过优化气体的初态和终态，以及选择合适的加热和冷却方式，可以提高等容过程的热效率。同时，也可以通过改进设备结构和操作方式来提高热效率。
提高热效率的方法
等容过程的热效率
04
CHAPTER
工程热力学第4章气体和蒸汽的基本热力过程
(isothermal process; constant temperature process)
n pv const. 定熵（可逆绝热）过程
(isentropic process; reversible adiabatic process)
n v const. 定容过程
1
1
T1 p1 T2 p2
理想气体，定比热，可逆绝热过程。
13
二、过程的 p – v 图及T - s 图
p v
p v
cp cV
p v
(n 0) 0
p n p v n v
p
(n 1)
(n )
n
p v
p
v
.
n=0
n↑
n=1
n=±∞ n=κ
o
v
T T s cs
h cp
T2 T1
T2 T1
2
Tds
1
w
2
pdv
1
2 1
pvdv v
RgT1 ln
v2 v1
wt
2
vdp
1
2 1
vpdv p
RgT1
ln
p2 p1
q u w h wt q w wt 12
4–3 理想气体等比熵（可逆绝热）过程
一、过程方程
Tds δq dh vdp 0 vdp dh cpdT
4–1 研究热力过程的目的及一般方法
一、基本热力过程 (fundamental thermodynamic process)
近似直线
在ln p-lnV 图上有 ln p = -nlnV + c pvn 常数 4
工程热力学复习重点及简答题
工程热力学复习重点2 0 1 2 . 3 绪论[1] 理解和掌握工程热力学的研究对象、主要研究内容和研究方法[2] 理解热能利用的两种主要方式及其特点[3] 了解常用的热能动力转换装置的工作过程1．什么是工程热力学从工程技术观点出发，研究物质的热力学性质，热能转换为机械能的规律和方法，以及有效、合理地利用热能的途径。
2．能源的地位与作用及我国能源面临的主要问题3. 热能及其利用[1] 热能：能量的一种形式[2] 来源：一次能源：以自然形式存在，可利用的能源。
如风能,水力能,太阳能、地热能、化学能和核能等。
二次能源：由一次能源转换而来的能源，如机械能、机械能等。
[3] 利用形式：直接利用：将热能利用来直接加热物体。
如烘干、采暖、熔炼（能源消耗比例大）间接利用：各种热能动力装置，将热能转换成机械能或者再转换成电能，4．.热能动力转换装置的工作过程5．热能利用的方向性及能量的两种属性[1] 过程的方向性：如：由高温传向低温[2] 能量属性：数量属性、,质量属性（即做功能力）[3] 数量守衡、质量不守衡[4] 提高热能利用率：能源消耗量与国民生产总值成正比。
第1 章基本概念及定义1. 1 热力系统一、热力系统系统：用界面从周围的环境中分割出来的研究对象，或空间内物体的总和。
外界：与系统相互作用的环境。
界面：假想的、实际的、固定的、运动的、变形的。
依据：系统与外界的关系系统与外界的作用：热交换、功交换、质交换。
二、闭口系统和开口系统闭口系统：系统内外无物质交换,称控制质量。
开口系统：系统内外有物质交换,称控制体积。
三、绝热系统与孤立系统绝热系统：系统内外无热量交换（系统传递的热量可忽略不计时，可认为绝热）孤立系统：系统与外界既无能量传递也无物质交换=系统+相关外界=各相互作用的子系统之和=一切热力系统连同相互作用的外界四、根据系统内部状况划分可压缩系统：由可压缩流体组成的系统。
简单可压缩系统：与外界只有热量及准静态容积变化均匀系统：内部各部分化学成分和物理”性质都均匀一致的系统，是由单相组成的。
工程热力学第4章
29
4-7 理想气体过程综述
一、各种过程在p-v图和T-s图上的相对位置
定容、定压、定温和定熵（可逆绝热）四个典型过 程都可以理解为多变过程的特例。其在p-v图上和T-s图 上的斜率如下：
( n 0)
0 p v
T cp 0 T cV
30
p p n v v n
Tc Tb
考虑过程等压 c
hc hb
a
q p ha hc 面积amnca
ha hb 面积amnca
38
p-v,T-s图练习（1）
压缩、升温、放热的过程，终态在哪个区域？
p
T
v
39
s
p-v,T-s图练习（2）
膨胀、降温、放热的过程，终态在哪个区域？
p
T
v
40
s
p-v,T-s图练习（3）
1 2
wt vdp 0
1
2
q p h wt h c
T2 p T1
T2 T1 1 Tds
2
四、Δu、 Δh、Δs和c
u c
T2 V T1
T2 T1
h c
T2 p T1
T2 T1
11
s
2
1
T2 dT cp s c p ln T T1
三、 定容过程的功量和热量
因为dv = 0，所以膨胀功为零，即
2
w pdv 0
1
注意和p-v 图对应
技术功： t vdp v( p1 p2 ) Rg (T1 T2 ) w
1
2
热量：
q Tds cV dT
工程热力学第4章 气体与蒸汽的热力过程
cv R(k1)
可逆绝热：ds = 0
p(v b)k 定值
例4：将理想气体在可逆绝热过程中所作技术功的 大小，表示在T-s图上。
[分析]：
绝热过程技术功：
wt cp(T1T2)
cp(T1T2)
1 T
2' 2
q12
＝面积1ba2’1
a
bS
五、多变过程
❖ 工程实际中有些热力过程，p、v、T有明显变化， 且系统与外界交换的Q不可忽略。则不能用上述4种 基本热力过程来描述。
定v： T2 / T1 = p2 / p1
p2 =0.987MPa
V=0.15m3 p1=0.55MPa
t=38℃, m1
定v V=0.15m3
定p
p2=0.7MPa
t2=123℃, m1
V=0.15m3 p3=0.7MPa
t3=285℃, m3
V=0.15m3 p1=0.55MPa
t=38℃, m1
QpT T 23mpd cT T T 23p R2VT cpdT = 126.2kJ
需加热量：Q = Qv + Qp = 56.3+126.2=182.5 kJ
例2： 1kg空气：t1=100℃、p1=2bar； t3=0℃ 、
p3=1bar，其中1-2为不可逆绝热膨胀过程，其熵变为 0.1kJ/kg·K，2-3为可逆定压放热过程，
nk n 1
cV
(T2
T1 )
qcv nn1k(T2T1) wnR1(T1T2)
q kn w k 1
或： nkqk1
w
若q/w不是恒定，则n是变化的。为便于分析计算， 常用一个与实际过程相近似的n不变的多变过程来 代替，该多变指数称为平均多变指数。
北京科技大学研究生考试初试-871工程热力学大纲
考试科目名称:871工程热力学《工程热力学》考试大纲工程热力学课程是热能与动力工程、建筑环境与设备专业的一门重要技术基础课，它的教学目的与任务是：让学生学习关于能量守恒与转换的理论基础，使学生牢固地掌握工程热力学的基本理论、基本知识和相应的热工分析、计算能力，并进一步得到基本技能的训练。
为学习专业课提供充分的理论准备，也为学生以后解决生产实际问题和参加科学研究打下必要的理论基础。
其考试大纲内容如下：一、第一章基本概念要求熟练掌握：系统，平衡状态和状态参数，温度温标，压力，状态方程，准静态过程和可逆过程，循环，功和热量；透彻理解以下的基本概念：热力系统，热力学状态、平衡状态、准静态过程、可逆过程和不可逆过程、功与热量。
二、第二章热力学第一定律要求熟练掌握热力学第一定律基本表达式——基本能量方程，总能，热力学能，焓，膨胀功，技术功，热力学第一定律的第一解析式和稳定流动能量方程式及其应用，循环功之间及循环净功与循环净热量之间关系，循环热效率概念与计算公式；透彻理解以下概念：热力学第一定律的实质—能量守衡与转换定律在热现象中的应用，能量方程的内在联系与共性，热变功的实质。
会进行功和热量的计算，以及功和热量在p-v图和T-s图上的表示。
三、第三章气体和蒸汽的性质要求熟练掌握理想气体和实际气体的概念、理想气体状态方程、理想气体的比热容和热力学能、焓、熵的定义、计算；水蒸气的性质：水蒸气的饱和状态、饱和温度、饱和压力、饱和湿蒸汽、干度、三相点，水蒸气状态的确定。
四、第四章气体和蒸汽的基本热力过程要求熟练掌握理想气体的基本热力过程：定温、定压、定容、定熵和多变过程的过程方程、参数变化和过程中功及热量的计算及其p-v图和T-s图。
水的定压加热汽化过程及其在p-v图和T-s上的表示；会计算水蒸气定压过程的热量，水蒸气绝热过程的功。
五、第五章热力学第二定律熟练掌握热过程的方向性、热力学第二定律的表述；卡诺循环和卡诺定理、克劳修斯积分不等式、熵流和熵产、熵方程、孤立系统的熵增原理；作功能力、作功能力损失与熵产和火用平衡方程。
工程热力学 第4章
2
2
p
dT，s
1
2
dq T
pdv，w
vdp q ，
Tds
5
二、四个基本热力过程
(一)、定容过程（dv=0）
工质在变化过程中容积保持不变的热力过程。 1.过程方程式： v = Const。 2.基本状态参数间的关系式：
p2 T2 v1 v2及 p1 T1
dq Tds
dq cn dT
T T T n s n cn cV
n 1
30
p
p p n v v n
(n 0)
0
T
( n 1) (n )
p v
T cp
s
v
p v
T T s n cn
p1v1 - p2 v2
nRg n 1
T1 T2
nw
25
5.理想气体 n q的计算
q u w cv T2 T1
Rg n 1
T2 T1
k - 1cv T T cv 2 1 n 1
q=
n cV T2 T1 n 1
n
ln p2 / p1 ln v1 / v2
cn c p n 等。 cV n 或由 cn n 1 cn cV
28
四、多变过程的能量关系w / q
w
Rg n 1
T1 T2
1
n 1
cV T1 T2
n q cV T2 T1 n 1
n
w 1 q n
1 0 n 1 0 n
《工程热力学》第四章-工质的热力过程
u2 u1 cv dT
1
s2 s1
2
q
T
1
● 能量转换
膨胀功
w pdv
1
2
2
1
p1v1n p1v1n 1n 1n 1 dv v2 v1 n 1 p1v1 p2v2 n v 1 n
n 1 v n1 n R R p2 R (T1 T2 ) T1 1 T1 1 1 n 1 n 1 p1 n 1 v2
● 能量转换
膨胀功 w 1 pdv 1
2
2
2
v2 p1 dv RT RT ln RT ln v v1 p2
2
p1 v2 dp RT ln RT ln 技术功 wt 1 vdp 1 RT p p2 v1
热
量
q u w w h wt wt
★ 若透平的效率为ηT=0.9，则终态温度和膨胀透平
的功率又为多少？
例3：如图所示，两端封闭而且具有绝热壁的气缸，被可移 动的、无摩擦的、绝热的活塞分为体积相同的A、B两部分， 其中各装有同种理想气体1kg。开始时活塞两边的压力、温 度都相同，分别为0.2MPa，20℃，现通过A腔气体内的一个 加热线圈，对A腔气体缓慢加热，则活塞向右缓慢移动，直 至pA2=pB2=0.4MPa时，试求： ① A，B腔内气体的终态容积各是多少？ A B ② A，B腔内气体的终态温度各是多少？ ③ 过程中供给A腔气体的热量是多少？ ④ A，B腔内气体的熵变各是多少？ ⑤ 在p-v图、T-s图上，表示出A，B腔气体经过的过程 设气体的比热容为定值：c p 1.01kJ /(kgK), cv 0.72kJ /(kgK)
工程热力学--第四章整理知识点第三版
工程热力学第三版沈维道蒋智敏童钧耕合编第四章理想气体的热力过程定容过程的熵变量可简化为可见定值比热容时定容过程在T - s 图上是一条对数曲线。
由于比体积不变,d v = 0,定容过程的过程功为零,过程热量可根据热力学第一定律第一解析式得出:定容过程中工质不输出膨胀功, 加给工质的热量未转变为机械能, 而全部用于增加工质的热力学能, 因而温度升高, 在T - s 图上定容吸热过程线1 - 2指向右上方,是吸热升温增压过程。
反之, 定容放热过程中热力学能的减小量等于放热量, 温度必然降低, 定容放热过程线1 - 2′指向左下方, 是放热降温减压过程。
上述结论直接由热力学第一定律推得,故不限于理想气体, 对任何工质都适用。
在p - v 图上定压过程线为一水平直线。
定压过程的熵变量可简化为因而定值比热容时定压过程在T - s 图上也是一条对数曲线。
但定压线较定容线更为平坦些,这一结论可由如下分析得出。
和分别是定容线和定压线在T - s 图上的斜率。
对于任何一种气体, 同一温度下总是c p > c V ，<即定压线斜率小于定容线斜率,故同一点的定压线较定容线平坦。
理想气体的气体常数R g 数值上等于1 kg 气体在定压过程中温度升高1 K所作的膨胀功, 单位为J /(kg · K).过程热量可根据热力学第一定律第一解析式得出:即任何工质在定压过程中吸入的热量等于焓增, 或放出的热量等于焓降。
定压过程的热量或焓差还可借助于比定压热容计算,即定压过程的技术功理想气体定温稳定流经开口系时技术功w t 与过程热量q T 相同, 由于这时p 2 v 2 = p 1 v 1 ,流动功( p 2 v 2 - p 1 v 1 )为零, 吸热量全部转变为技术功。
绝热过程是状态变化的任何一微元过程中系统与外界都不交换热量的过程,即过程中每一时刻均有δq = 0.当然,全部过程与外界交换的热量也为零, 即q = 0根据熵的定义,, 可逆绝热时δq rev = 0, 故有ds= 0, s = 定值。
工程热力学课件第4章
κ=
cp cv
pv κ = 常数
∴κ > 1
Qc p > cv
2、初、终状态参数关系 、
p 2 v1 = p1 v 2
κ
pvκ = 常数
pv = RT
T2 v1 = T1 v2 κ −1 T2 p2 κ = T1 p1
1 1
2
2
κ
dp
1
=κ
R (T1 − T2 ) = κw κ −1
pκ
κ ( p1v1 − p 2 v 2 ) = κ −1
2）热量 ）
q=0
∆s = 0
∆u + w = 0 或 ∆u = − w ∆ h + wt = 0 或 ∆ h = − wt
4-3 多变过程的综合 分析
多变过程
1、 过程方程： pv n 、 过程方程：
pc dT pc dp sc − sb = ∫ cp − ∫ R = −R ln T T pb p pb
T
Qsc > sb
∴pc < pb
sb sc
s
定压线向左水平移动， 定压线向左水平移量转换 、 1）过程功 dp= 0 ∴wt = −∫1 vdp = 0 ） 2）热量 ）
2
2
v
4
3
wT = wt ,T
2）热量 ）
T
∆h = c p (t2 − t1) = 0
2’ 1 2
∆u = cv (t2 − t1) = 0
v2 p1 p1 q = w = wt = RT ln = RT ln = p1v1 ln v1 p2 p2
s
4
工程热力学第4章
工程热力学第4章第4章理想气体热力过程及气体压缩4．1 本章基本要求熟练掌握定容、定压、定温、绝热、多变过程中状态参数p、v、T、?u、?h、?s的计算，过程量Q、W的计算，以及上述过程在p-v 、T-s图上的表示。
4．2 本章重点结合热力学第一定律，计算四个基本热力过程、多变过程中的状态参数和过程参数及在p-v 、T-s图上表示。
本章的学习应以多做练习题为主，并一定注意要在求出结果后，在p-v 、T-s图上进行检验。
4．3 例题例1．2kg空气分别经过定温膨胀和绝热膨胀的可逆过程，如图4.1，从初态p1=9.807bar,t1=300?C膨胀到终态容积为初态容积的5倍，试计算不同过程中空气的终态参数，对外所做的功和交换的热量以及过程中内能、焓、熵的变化量。
图4.1 解：将空气取作闭口系对可逆定温过程1-2，由过程中的参数关系，得p2?p1v11?9.807??1.961bar v25RT1=0.1677m3/kg p1按理想气体状态方程，得v1?—30—v2?5v1=0.8385m3/kgT2?T1=573K t2=300?C气体对外作的膨胀功及交换的热量为WT?QT?p1V1lnV2=529.4kJ V1过程中内能、焓、熵的变化量为?U12=0 ?H12=0 ?S12=或?S12=mRlnQT=0.9239kJ /K T1V2=0.9238kJ /K V1对可逆绝热过程1-2′, 由可逆绝热过程参数间关系可得'p2?p1(v1k) 其中v2'?v2=0.8385m3/kg v21故p2'?9.807()1.4=1.03bar 5T2'?p2'v2'R=301K t2'=28?C气体对外所做的功及交换的热量为Ws?11(p1V1?p2V2)?mR(T1?T2')=390.3kJ k?1k?1Qs'?0过程中内能、焓、熵的变化量为?U12'?mcv(T2'?T1)??390.1kJ或?U12'??W2??390.3kJ?H12'?mcp(T2'?T1)??546.2kJ ?S12'=0例2. 1kg空气多变过程中吸取41.87kJ的热量时，将使其容积增大10倍，压力降低8倍，求：过程中空气的内能变化量，空气对外所做的膨胀功及技术功。
第四章 理想气体和蒸汽的
n称为多变过程的多变指数
基本过程是多变过程的特例
2009-10 Henan Polytechnic University
《工程热力学》
六、多变过程的p-v图及T-s图曲线的斜率 1) p-v图 p
v n
pv c
n
T 2) T-s图 s n
p p n v v n
n 1 T1 T2 p1v1 p2v2 T1 T2 Rg Rg
二、在p – v 图及T – s 图上表示
p1 v1 p2v2
n 1
p p v v T
T T 0 s T cT
cT
qT
dT
2009-10 Henan Polytechnic University
Rg n 1
2
2
(T1 T2 )
2
C 2 vC (n)v n1dv wt vdp vd n 1 1 1 v
nCv dv n pdv nw
n 1 1
2
2
wt nw
2009-10 Henan Polytechnic University
2
t2
1
cv t Rg
t2
1
q p (cv t Rg )(t2 t1 )
h c p
T2 T1
u cV
s
T2
T2 T1
T2 T1
T2 T1
T1
T2 dT p2 dT T2 cp Rg ln s c p c p ln T1 T p1 T T1
c p n v
p ncv ( n 1) v
工程热力学思考题参考答案,第四章
工程热力学思考题参考答案,第四章Company number：【WTUT-WT88Y-W8BBGB-BWYTT-19998】第四章气体和蒸汽的基本热力过程 试以理想气体的定温过程为例，归纳气体的热力过程要解决的问题及使用方法解决。
答：主要解决的问题及方法：(1) 根据过程特点（及状态方程）——确定过程方程(2) 根据过程方程——确定始、终状态参数之间的关系(3) 由热力学的一些基本定律——计算,,,,,t q w w u h s ∆∆∆(4) 分析能量转换关系（P —V 图及T —S 图）（根据需要可以定性也可以定量）例：1)过程方程式：T =常数（特征）PV =常数（方程）2)始、终状态参数之间的关系：12p p =21v v 3)计算各量：u ∆=0、h ∆=0、s ∆=21p RInp -=21v RIn v 4)PV 图，TS 图上工质状态参数的变化规律及能量转换情况对于理想气体的任何一种过程，下列两组公式是否都适用答：不是都适用。
第一组公式适用于任何一种过程。
第二组公式21()v q u c t t =∆=-适于定容过程,21()p q h c t t =∆=-适用于定压过程。
在定容过程和定压过程中，气体的热量可根据过程中气体的比热容乘以温差来计算。
定温过程气体的温度不变，在定温过程中是否需对气体加入热量如果加入的话应如何计算答：定温过程对气体应加入的热量过程热量q 和过程功w 都是过程量，都和过程的途径有关。
由理想气体可逆定温过程热量公式2111v q p v In v =可知，故只要状态参数1p 、1v 和2v 确定了，q 的数值也确定了，是否q 与途径无关 答：对于一个定温过程，过程途径就已经确定了。
所以说理想气体可逆过程q 是与途径有关的。
在闭口热力系的定容过程中，外界对系统施以搅拌功w δ，问这v Q mc dT δ=是否成立答：成立。
这可以由热力学第一定律知，由于是定容过2211v v dv w pdv pvpvIn RTIn v v v ====⎰⎰为零。
工程热力学.4理想气体热力过程及气体压缩G
v2 pv dv RgT1 ln v v1
2 1
wt vdp
p2 vp dp RgT1 ln p p1
q u w h wt
q w wt
4.2.2可逆绝热过程——定熵过程
q 0 Tds ds 0 s const
一、过程方程 理想气体
Tds q dh vdp 0 vdp dh cpdT
( A)
Tds q du pdv 0 pdv du cV dT
(B)
A B
取定比热容，积分
v dp dp dv 0 p dv p v
又因为是闭口系，m不变，而V2=2V1
2v1 s12 Rg ln Rg ln 2 0 v1 即s2 s1
δq 2) ds T
s2 s1 Rg ln 2
s12 ds
1 2 2
0
1
δq ?0 T
上述两种结论哪一个对？为什么？ 既然 δq 0
q0
0 2 0 1
1kg空气从初态p1=0.1MPa，t1=100℃，经历某种变 化后到终态 p2=0.5MPa，t2=1000℃， 取 1）定比热 容 ；2）变比热容, 求：熵变 解： 1）
s12 s2 s1 c p ln T2 p Rg ln 2 T1 p1
(1000 273)K 0.5MPa 1.004kJ/(kg K) ln 0.287kJ/(kg K) ln (100 273)K 0.1MPa 0.78kJ/(kg K)
T2 u2 2 1 T1 u1
u cv t (T2 T1 )
工程热力学第四版思考题答案
工程热力学第四版沈维道思考题完整版第 1 章基本概念及定义1. 闭口系与外界无物质交换，系统内质量将保持恒定，那么，系统内质量保持恒定的热力系一定是闭口系统吗? 答：否。
当一个控制质量的质量入流率与质量出流率相等时(如稳态稳流系统)，系统内的质量将保持恒定不变。
2. 有人认为，开口系统中系统与外界有物质交换，而物质又与能量不可分割，所以开口系不可能是绝热系。
这种观点对不对，为什么? 答：不对。
“绝热系”指的是过程中与外界无热量交换的系统。
热量是指过程中系统与外界间以热的方式交换的能量，是过程量，过程一旦结束就无所谓“热量”。
物质并不“拥有”热量一个系统能否绝热与其边界是否对物质流开放无关。
3•平衡状态与稳定状态有何区别和联系，平衡状态与均匀状态有何区别和联系？答：“平衡状态”与“稳定状态” 的概念均指系统的状态不随时间而变化，这是它们的共同点；但平衡状态要求的是在没有外界作用下保持不变；而平衡状态则一般指在外界作用下保持不变，这是它们的区别所在。
力计算公式4•倘使容器中气体的压力没有改变，试问安装在该容器上的压力表的读数会改变吗？在绝对压P P b P e (P P b )；P P b P v (P P b )中，当地大气压是否必定是环境大气压?答：可能会的。
因为压力表上的读数为表压力，是工质真实压力与环境介质压力之差。
环境介质压力，譬如大气压力，是地面以上空气柱的重量所造成的，它随着各地的纬度、高度和气候条件不同而有所变化，因此，即使工质的绝对压力不变，表压力和真空度仍有可能变化。
“当地大气压”并非就是环境大气压。
准确地说，计算式中的P b 应是“当地环境介质”的压力，而不是随便任何其它意义上的“大气压力”，或被视为不变的“环境大气压力”。
5•温度计测温的基本原理是什么？答：温度计对温度的测量建立在热力学第零定律原理之上。
它利用了“温度是相互热平衡的系统所具有的一种同一热力性质”，这一性质就是“温度”的概念。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2、多变过程的过程方程式(polytropic process)
pvn 定值 ln p n ln v 定值 即多变过程在 ln p ln v 图上为直线，斜率为n 。
■初、终状态参数之间的关系
定温线在p-v图上是等轴双曲线，在T-s图上是水平线
p
2′
T
1 2
2′ 1
2
O
vO
s
1-2：吸热减压膨胀；1-2′：放热增压压缩
q du pdv pdv Tds
■热量、过程功、技术功
u cV (T2 T1) 0 h cp (T2 T1) 0
பைடு நூலகம்
qT w wt T s
■过程方程式 v 定值
如汽油机气缸中的燃烧过程。 ■初、终状态参数之间的关系
p2 / p1 T2 / T1
即定容过程压力与温度成正比。
■在p-v图和T-s图上的表示
n (p / v)v np / v
nk cn n 1 cV cV (T / s)v T / cV
/
kg
(h)v
(h)p
cp
(t 400℃
100℃ 2
t1) 310.6kJ / kg
定容过程：
s cV
400℃ 100℃
ln
T2 T1
0.4414kJ /(kg K)
q u 224.5kJ / kg
w0
wt v( p1 p2v ) 86.1kJ / kg
●可以取(, ) 之间的所有数。 n v 定值（定容过程）
n 0 p 定值（定压过程）
n 1 T 定值 （定温过程）
n k
（绝热过程）
四个基本热力过程是多变过程的特例。
●实际过程中，n 值是变化的，可用平均值代替；或者
把实际过程分作几段，每段的值保持不变。
w0
wt v( p1 p2v ) 86.1kJ / kg
定压过程： s
cp
ln T2 T1
0.5925kJ /(kg K)
q h 301.2kJ / kg
w p(v2p v1) 86.1kJ / kg wt 0
（2）利用平均比热容表计算 查附表5，得到：
dp cp dv dp dv 0
p cV v p v
若比热容取定值，积分得：
ln p ln v 定值 pv 定值 指数常用定熵指数 k（绝热指数，adiabatic exponential） 表示，即： k，
pvk 定值
■定熵指数 k
温度越高，值越小。
4-5 绝热过程
■过程方程式
q 0 q 0
如内燃机气缸中的膨胀和压缩过程、叶轮式压气 机中的压缩过程、汽轮机和燃气轮机中的膨胀过程。 ●可逆绝热过程（定熵过程）
ds qrev / T 0 s 定值
q du pdv cV dT pdv 0 q dh vdp cpdT vdp 0
（2）多变压缩
k 1.4 ，cV 0.717kJ / (kg K) ，cp 1.004kJ / (kg K)
T2 ( p2 / p1)(n1)/ nT1 433.71K
h cp (T2 T1) 129.22kJ / kg
s
cp
ln T2 T1
Rg
n( n 1
p1v1
p2v2 )
n n 1
Rg
(T1
T2
)
nw
即技术功是过程功的n倍。
■热量
q
u
w
cV
(T2
T1 )
k n
1 1 cV
(T1
T2
)
nk n 1
cV
(T2
T1 )
■多变过程的比热容
cn
q /(T2
T1)
nk n 1
cV
4-2 定容过程
(s)v
cV
ln
T2 T1
定容线在p-v图上是垂直线，在T-s图上是对数曲线。
p
2
T
2
1
1
2′
2′
O
v
s
1-2：吸热升温增压；1-2′：放热降温减压
■过程功
2
w 1 pdv 0
■技术功
2
wt 1 vdp v( p1 p2 )
■热量
qv u
即定容过程吸收的热量全部用于增加热力学能。
p1v1n p2v2n
T2
/ T1
(v1
/
v2 )n1
( p2
/
p )(n1)/n 1
即多变过程温度与比体积的 n 1次方成反比，与
压力的 (n 1) / n 次方成正比。
3、多变指数 n (polytropic index) n ln( p2 / p1) ln(v2 / v1)
ln
p2 p1
0.1084kJ /(kg K)
n wt n 1 Rg (T1 T2 ) 168.87kJ / kg
Pt qm wt 2.03kW nk
q n 1 cV (T2 T1) 39.55kJ / kg
qQ qmq 1708.6kJ/h
kav (k1 k2 ) / 2
说明：当终温 t2未知时，要先假定 t2 ，反复试算，且
结果为近似值。
●变比热容时终温的确定（气体热力性质表）
已知：初态（ p1、T1 ）（或（ v1、T1）），终态 p2
（或 v2），求终温 T2。
（1）按定值比热容计算
初、终温相同，(u)v (u) p cV (t2 t1) 215.1kJ / kg
(h)v (h) p cp (t2 t1) 301.2kJ / kg
定容过程： s
cV
ln T2 T1
0.4231kJ /(kg K)
q u 215.1kJ / kg
4、多变过程的p-v图和T-s图 pvn 定值 ln p n ln v 定值 dp n dv 0
pv (p / v)n np / v （p-v图的斜率）
q cndT Tds (T / s)n T / cn（T-s图的斜率）
5、多变过程的过程功、技术功及热量
u1 h1 RgT1 268.67kJ / kg
u2 h2 RgT2 493.21kJ / kg
(u)v (u) p u2 u1 224.5kJ / kg
(h)v (h) p h2 h1 310.6kJ / kg
定容过程：
s s20 s10 Rg ln
●比热容取定值
单原子气体：k 1.67 双原子气体：k 1.4 多原子气体：k 1.29
●比热容取平均值 （1）先确定平均比定压热容和平均比定容热容，
k c / c t2
t2
av
p t1 V t1
（2）先确定各温度下的比定压热容和比定容热容，
k1 cp1 / cV1 k2 cp2 / cV 2
第四章 气体和蒸汽的基本热力过程
4-1 理想气体的可逆多变过程 4-2 定容过程 4-3 定压过程 4-4 定温过程 4-5 绝热过程 4-6 理想气体热力过程综合分析 4-7 水蒸汽的基本过程 ＊4-8 非稳态流动过程
4-1 理想气体的可逆多变过程
1、气体的基本热力过程(Basic thermodynamic process) 定容过程(isometric process, constant volume process) 定压过程(isobaric process, constant pressure process) 定温过程 (isothermal process, constant temperature process) 绝热过程(isentropic process, reversible adiabatic process)
cp
100℃ 0℃
1.006kJ /(kg K)
cp
400℃ 0℃
1.028kJ /(kg K)
cV
100℃ 0℃
cp
100℃ 0℃
Rg
0.719kJ /(kg K)
cV
400℃ 0℃
cp
400℃ 0℃
Rg
0.741kJ /(kg K)
cp
c 400℃
p
100℃
p2v p1
0.44kJ / (kg K)
q u 224.5kJ / kg
w0
wt v( p1 p2v ) 86.1kJ / kg
定压过程：
s s20 s10 0.6093kJ /(kg K) q h 310.6kJ / kg
w p(v2p v1) 86.1kJ / kg wt 0
(s) p
cp
ln
T2 T1
定压线在p-v图上是水平线，在T-s图上是对数曲线。
p
2′ 1
2
T
2′
2 1
O
v
s
1-2：吸热升温膨胀；1-2′：放热降温压缩
cV cp (T / s)v (T / s) p T