工程热力学-第四章 习题
工程热力学(第五版)第4章练习题

第4章 理想气体热力过程及气体压缩4.1 本章基本要求熟练掌握定容、定压、定温、绝热、多变过程中状态参数p 、v 、T 、∆u 、∆h 、∆s 的计算,过程量Q 、W 的计算,以及上述过程在p -v 、T -s 图上的表示。
4.2 本章重点结合热力学第一定律,计算四个基本热力过程、多变过程中的状态参数和过程参数及在p -v 、T -s 图上表示。
本章的学习应以多做练习题为主,并一定注意要在求出结果后,在p -v 、T -s 图上进行检验。
4.3 例 题例1.2kg 空气分别经过定温膨胀和绝热膨胀的可逆过程,如图4.1,从初态1p =9.807bar,1t =300C ο膨胀到终态容积为初态容积的5倍,试计算不同过程中空气的终态参数,对外所做的功和交换的热量以及过程中内能、焓、熵的变化量。
图4.1解:将空气取作闭口系对可逆定温过程1-2,由过程中的参数关系,得bar v v p p 961.151807.92112=⨯==按理想气体状态方程,得111p RT v ==0.1677kg m /3 125v v ==0.8385kg m /312T T ==573K 2t =300C ο气体对外作的膨胀功及交换的热量为1211lnV V V p Q W T T ===529.4kJ 过程中内能、焓、熵的变化量为12U ∆=0 12H ∆=0 12S ∆=1T Q T=0.9239kJ /K 或12S ∆=mRln12V V =0.9238kJ /K 对可逆绝热过程1-2′, 由可逆绝热过程参数间关系可得kv v p p )(211'2= 其中22'v v ==0.8385kg m /3 故 4.12)51(807.9'=p =1.03barRv p T '''222==301K '2t =28C ο气体对外所做的功及交换的热量为)(11)(11'212211T T mR k V p V p k W s --=--==390.3kJ 0'=s Q过程中内能、焓、熵的变化量为kJ T T mc U v 1.390)(1212''-=-=∆或kJ W U 3.390212'-=-=∆kJ T T mc H p 2.546)(1212''-=-=∆ '12S ∆=0例2. 1kg 空气多变过程中吸取41.87kJ 的热量时,将使其容积增大10倍,压力降低8倍,求:过程中空气的内能变化量,空气对外所做的膨胀功及技术功。
《工程热力学》第四章 总结及例题
U13 Q13 W13 649.4kJ 316.62kJ 965.52kJ
H13 nCpm T3 T1 U pV 965.52kJ 299.855 619.393 kPa 2m3 1604.6kJ
S13
n CVm
ln
T3 T1
R ln V3 V1
500mol 3 4.1868J/(mol K) ln 144.26K 4.56kJ/K 298K
Pa
10
1-2过程:由25 ℃,2m3 可逆绝热膨胀到1 atm 2-3过程:定温可逆压缩回到2 m3
理想气体等温过程 :热量=膨胀功=技术功
Q
Q12
Q23
Q23
WT 23
nRT
ln
V3 V2
500
mol 8.314
5
J/(mol K) 144.26
K ln
2 m3 5.906 m3
649.4 kJ
7
q h wt wt q h wt q (ha hb )
考虑过程等压 c a
a
q h c vdp
q ha hc
技术功:
wt q (ha hb )
8
例2 0.5 kmol某种单原子理想气体 ,由25 ℃,2m3 可逆绝热膨 胀到1 atm,然后在此状态的温度下定温可逆压缩回到2 m3。1) 画出各过程的p-v图及T-s图;2)计算整个过程的Q,W,ΔU, Δ H 及ΔS。
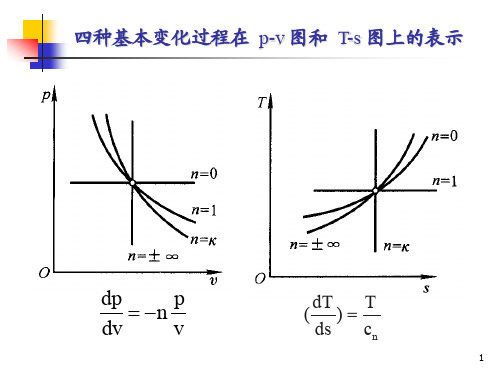
四种基本变化过程在 p-v 图和 T-s 图上的表示
dp n p dv v
dT T ( )
ds cn
1
p-v图和T-s图上的曲线簇
2
u,h,w,wt,q在p-v,T-s图上的变化趋势
u↑,h ↑(T ↑) w ↑(v ↑) wt ↑(p ↓) q ↑(s ↑)
工程热力学与传热学习题(英文版):第四章 热力学第二定律

must be obtained or discarded into the river ?
3. Heat rejection by a refrigerator
The food compartment of a refrigerator, shown in Fig 4-2, is maintained at 4℃ by removing heat from it at a rate of 360 kJ/min. If the required power input to the refrigerator is 2 kW, determine (a) the coefficient of performance of the refrigerator and (b) the rate of heat rejection to the room that houses the refrigerator.
allowed process.
12. The concept of lost work
If 1000 kJ of energy is transferred from a work reservoir to a heat at 373K, determine (a) the amount of entropy generation and (b) amount of lost work with the environment at 300K.
The
power output of the heat engine is 180 kW. Determine the
reversible power and the irreversibility rate for this process.
《工程热力学》第四章 思考题

n0
wt>0
n 1 wt>0
nk
n
n 1
q>0
n
v
nk s5
确定过程中工质状态参数的变化规律分析过程中的能量转换关系
思考题4-1:
(1)任务:确定过程中工质状态参数的变化规律, 分析过程中的能量转换关系。
(2)使用方法:
a) 热力学第一定律表达式
稳定流动
q du w dh wt
q
h
1 2
c2
gz
ws
h
wt
1
b)可逆过程
q du pdv q dh vdp对于定容Fra bibliotek - 1v 过程:
q u w q u21v u1v u2 cv (T1v T2 ) cv (T1 T2 )
上述推导有何问题?
思考题4-13:
u↑,h ↑(T ↑) w ↑(v ↑) wt ↑(p ↓) q ↑(s ↑)
p
h>0 u>0
q>0
w>0
T
h>0
w>0
n0
u>0
p f (v),T f (v),T f ( p)
2)根据已知参数和过程方程式,确定未知参数;
3)在p-v图和T-s图上表示过程中状态参数的变化 规律;
4)求热力过程中热力学能、焓和熵的变化
5)确定过程的功量(膨胀功和技术功)和热量。
3
思考题4-12:
q u w 0 w u12 u1 u2 cv (T1 T2 )
c) 理想气体状态方程式 u f (T) h f (T)
pv RgT cp cv Rg k cp / cv
2
u 1 cvdT
工程热力学第四章 习题解答

第四章 习题解答4-1 多变指数:()()2112ln ln 0.1250.9ln ln 0.1p p n v v ===()210.9 1.4110.91v n n q c T T u u n n κκ---=-=∆=∆---∴11408 kJ/kg 55u q ∆==⨯=40832 kJ/kg w q u =-∆=-=()21 1.4811.2 kJ/kg p h c T T u κ∆=-=⋅∆=⨯= 4011.228.8 kJ/kg s w q h =-∆=-=2211ln ln 1.01ln100.732ln 0.1250.822 kJ/kg Kp v v ps c c v p ∆=+=⨯+⨯=⋅ 4-2 ⑴1 1.4112 1.410.287423110.21 1.41 111.9 kJ/kg RT p w p κκκ--⎡⎤⎛⎫⎛⎫⨯⎢⎥=-=- ⎪ ⎪⎢⎥--⎝⎭⎝⎭⎢⎥⎣⎦= 0s ∆=⑵ ()()120.72342330088.25v w u c T T =-∆=-=⨯-=kJ/kg22113000.1lnln 1.0045ln 0.287ln 4230.5 0.117 kJ kg p T p s c R T p ∆=-=⋅-⋅=⑶1120.5ln 0.287ln195.4 kJ kg 0.2p w RT p ==⋅= 120.5ln 0.287ln 0.462 kJ kg K 0.2p s R p ∆==⨯=⋅⑷1112210.287423110.267.1121n n RT p w n p -⎡⎤⎡⎤⎛⎫⨯⎢⎥=-=-= ⎪⎢⎥⎢⎥--⎝⎭⎣⎦⎢⎥⎣⎦kJ/kg2221ln ln 1.005ln 0.723ln 0.20.35 kJ kg Kp v v ps c c v p ∆=+==-⋅4-3 ⑴ 21ln8.314373ln107140.6 kJ kmol v w RT v ==⨯= 21ln8.314ln1019.14 kJ K v s R v ∆==⨯=⋅ ⑵ 0w =21ln8.314ln1019.14 kJ K v s R v ∆==⨯=⋅ 4-4 210.12ln 50.2598ln 2.091 kJ K 0.6v S mR v ∆==⨯=-()303 2.091633.6 kJ Q W T S ==∆=⨯-=-0, 0H U ∆=∆=4-5 2211201.3286568.3 K 101.3p T T p ⎛⎫==⨯= ⎪⎝⎭()()210.287568.3286202.6 kJ kg 1.41v u c T T ∆=-=-=-()()21 1.40.287568.3286283.6 kJ kg 1.41p h c T T ⨯∆=-=-=-210.287586.3ln ln 0.493 kJ kg K 1.41286v T s c T ∆===⋅-4-6 ⑴ 21303 K T T ==120.3ln 60.287303ln 573.2 kJ 0.1p Q W mRT p ===⨯⨯⨯=⑵ 1 1.411.422110.1303221.4 K 0.3p T T p κκ--⎛⎫⎛⎫==⨯= ⎪ ⎪⎝⎭⎝⎭ , 0Q = ()()120.2876303221.4351.3 kJ 1 1.41R W m T T κ=-=⨯-=--⑶ 1 1.211.222110.1303252.3 K 0.3n np T T p --⎛⎫⎛⎫==⨯= ⎪ ⎪⎝⎭⎝⎭()()120.2876303252.3436.5 kJ 1 1.21R W m T T n =-=⨯-=--()()21 1.2 1.40.2876252.33031 1.21 1.41 218.3 kJv n Q m c T T n κ--=-=⨯⨯⨯----=4-7 ()()()()1221ln ln 0.60.12 1.30ln ln 0.8150.236p p n v v ===1116000.236493.4 K 0.287p v T R ⨯===2221200.815340.8 K 0.287p v T R ⨯===()()120.287493.4340.8146 kJ 1 1.31R w T T n =-=-=--()()21 1.3 1.40.287340.8493.411 1.31 1.4136.5 kJ/kgn R q T T n κκ--=⋅-=⋅⋅-----= ()()210.723340.8493.8109.5 kJ kg v u c T T ∆=-=⨯-=- ()()21 1.01340.8493.4154.1 kJ kg p h c T T ∆=-=⨯-=-22120.8150.12ln ln 1.01ln 0.723ln0.2360.6 0.089 kJ kg Kp v v p s c c v p ∆=+=⋅+⋅=⋅4-8 40200160 kJ kg u q w ∆=-=-=-211600.533 kJ kg K 373673v u c T T ∆-===⋅--()()()()()2121122112ln ln ln 16 1.491673ln ln ln 6373p p p p n v v p T p T ====⎛⎫⋅ ⎪⎝⎭()()121 1.4912000.327 kJ/kg K 673373n w R T T --⨯===⋅-- 0.5330.3270.86 kJ kg K p v c c R =+=+=⋅4-9 10.412122933454.7 K v T T v κ-⎛⎫==⨯= ⎪⎝⎭()()1120.287293454.7116 kJ 1 1.41R w T T κ=-=-=---2221ln 0.287454.7ln 3143.4 kJ vw RT v ==⨯⨯=12116143.427.4 kJ w w w =+=-+=4-10 ⑴ 333100 1.73583 K 0.2968p v T R ⨯=== 11.413232 1.735831265 K 0.25v T T v κ--⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭22120.296812651.5 MPa 0.25RT p p v ⨯====11227730.250.153 MPa 1265T v v T ==⨯=⑵ 定压过程:()()210.29681265773365 kJ kg 1 1.41R u T T κ∆=-=-=--()()210.29681265773146 kJ kg w R T T =-=⨯-=定熵过程:()()320.29685831265506 kJ kg 1 1.41R u T T κ∆=-=-=---506 kJ kg w u =-∆=4-11 ⑴ 31110.2875730.274 m 600RT v p ⨯===321330.2740.822 m kg v v ==⨯=11.4112121573369 K 3v T T v κ--⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭2220.2873690.129 MPa 0.822RT p v ⨯===310.274 v v ==3m kg223330.1290.387 MPa p v p v ==⨯= 32369T T ==K⑵ ()()1120.287573369146.41 1.41R w T T κ=-=-=--kJ kg32221ln 0.287369ln 116.43v w RT v ==⨯⨯=-kJ kg()1.293146.4116.438.8 kJ W mw ==⨯-=4-12 1112101.3ln101.3150ln 59250 kJ 5000p Q pV p ==⨯⨯=- 4-13 101.3256000.21550.2872733600pV mRT ⨯===⨯⨯ kg/s 1,120.1ln 0.21550.287293ln 37.8 kW 0.8s T p W mRTp ==⨯⨯=- 112,1 1.411.4111.40.2872930.8 0.2155151.3 kW 1.410.1s SRT p W m p κκκκ--⎡⎤⎛⎫⎢⎥=- ⎪⎢⎥-⎝⎭⎢⎥⎣⎦⎡⎤⨯⨯⎛⎫⎢⎥=⨯-=-⎪⎢⎥-⎝⎭⎣⎦4-14 1600 kg/h kg/s 6m== ⑴定温压缩11210.1ln 0.287293ln 25.1 kW 60.6s T p W mRTp ⋅==⨯⨯=- ⑵定熵压缩112,1 1.411.4111 1.40.2872930.6 132.8 kW 6 1.410.1s SRT p W m p κκκκ--⎡⎤⎛⎫⎢⎥=- ⎪⎢⎥-⎝⎭⎢⎥⎣⎦⎡⎤⨯⨯⎛⎫⎢⎥=⨯-=-⎪⎢⎥-⎝⎭⎣⎦⑶多变压缩 112,1 1.2211.22111 1.220.2872930.6 129.6 kW 6 1.2210.1n n s nnRT p W m n p --⎡⎤⎛⎫⎢⎥=- ⎪⎢⎥-⎝⎭⎢⎥⎣⎦⎡⎤⨯⨯⎛⎫⎢⎥=⨯-=- ⎪⎢⎥-⎝⎭⎣⎦4-15 压缩比2160.160p p ==,应采用二级压缩20.775 MPa p == ∵13322n nT p T p -⎛⎫= ⎪⎝⎭,2120T T '==℃ (冷却至初温)∴1 1.2511.2533226293441.90.775n np T T p --'⎛⎫⎛⎫==⨯= ⎪⎪⎝⎭⎝⎭K3168.8t =℃ 4-16 ()()()()()2121122112ln ln ln 0.50.1 1.130.5289ln ln ln 0.1348p p p p n v v p T p T ====⎛⎫⋅ ⎪⎝⎭111100400482.3 kg/min 8.04 kg/s 0.287289p V mRT ⨯====⨯ ()()12 1.130.2878.042893481 1.1311183 kWs nR W mnwm T T n ⨯==-=⨯---=- ()()21 1.13 1.48.040.7233482891 1.131 712.3 kW 42738 kJ/minv n Q m c T T n κ--=-=⨯⨯⨯---=-= 4-17 12111v p c p λ⎡⎤⎛⎫⎢⎥=-- ⎪⎢⎥⎝⎭⎣⎦⑴ n =1.4,11.40.510.0610.870.1v λ⎡⎤⎛⎫=--=⎢⎥ ⎪⎝⎭⎢⎥⎣⎦⑵ n =1.25,11.250.510.0610.840.1v λ⎡⎤⎛⎫=--=⎢⎥ ⎪⎝⎭⎢⎥⎣⎦ ⑶ n =1.0,11.00.510.0610.760.1v λ⎡⎤⎛⎫=--=⎢⎥ ⎪⎝⎭⎢⎥⎣⎦4-18 ()21w pw a n m c t m c T T ∆=--111100250297.3 kg/h 0.08258 kg/s 0.287293a p V m RT ⨯====⨯ ()()()2112 4.186846514297.3293423 0.705 kJ/kg Kw pw w pw n a a m c t m c t c m T T m T T ∆∆⨯⨯=-==--⨯-=-⋅111n v n n Rc c n n κκκ--==--- 1.40.2870.7051.411 1.200.2870.7051 1.41nn Rc n R c κκκ⨯+---===-+--1.211.2122114230.10.905 MPa 293n n T p p T --⎛⎫⎛⎫==⨯= ⎪⎪⎝⎭⎝⎭()()1211.20.2870.0825829342318.48 kW1.21s a s a anRW m w m nw m T T n ===--⨯=⨯-=-。
工程热力学复习参考题-第四章

第四章 理想气体热力过程一、选择题1.在定容过程中,理想气体的内能变化Δu =D A .⎰21dT c p B .⎰21pdvC .⎰21vdpD .⎰21dT c v2.在定熵过程中,理想气体的内能变化Δu =BDA .⎰21dT c p B .-⎰21pdv C .-⎰21vdp D .⎰21dT c v3. 在定压过程中,理想气体的内能变化Δu =D A .⎰21dT c p B .⎰21pdvC .⎰21vdpD .⎰21dT c v4.在定熵过程中,理想气体的焓的变化Δh =AC A .⎰21dT c p B .⎰21pdvC .⎰21vdpD .⎰21dT c v5.理想气体定容过程中,焓的变化Δh =B A .c v ΔT B .c p ΔT C .u+pv D .w t6.理想气体定温过程的热量q 等于BCD A .c n ΔT B .w t C .T Δs D .w 7.理想气体等温过程中,q ,w ,w t 间的关系为DA .q> w t >wB .q=w< w tC .q>w= w tD .q=w= w t8.理想气体绝热过程初终态温度,压力的关系为A A .12T T =κκ112-⎪⎪⎭⎫ ⎝⎛p pB . 21T T = κκ112-⎪⎪⎭⎫ ⎝⎛p pC .12p p = κκ112-⎪⎪⎭⎫ ⎝⎛T T D .21p p = κκ112-⎪⎪⎭⎫⎝⎛T T9.理想气体多变过程内能变化Δu 等于B A .c n ΔT B .c v ΔT C .c p ΔT D .R ΔT 10.理想气体多变过程焓的变化Δh 等于C A .c n ΔT B .c v ΔT C .c p ΔTD .R ΔT二、填空题1.Rg=0.297kJ/(kgK)的1kg 双原子理想气体在定压下吸热3349kJ ,其内能变化Δu = 。
2.Rg=0.26kJ/(kgK)、温度为T =500K 的1kg 理想气体在定容下吸热3349kJ ,其熵变Δs = 。
工程热力学第4章习题答案

4-12 一个气缸活塞系统如图 4-19 所示,活塞的截面积为 40cm2,活塞离气缸底部 10cm, 重物 20kg,初始状态温度 300K,大气压力 101325Pa。求
(1)如果使缸内空气温度升高 5℃的同时使重物升高 2cm 需要加入多少热量; (2)然后当可逆绝热情况下使活塞回到原位置,需要再加上多少重物。
4-6 空气的初参数为 p1=0.5MPa 和 t1=50℃,此空气流经阀门发生绝热节流作用,并使空 气容积增大到原来的 2 倍。求节流过程中空气的熵增,并求其最后的压力。
解:对于理想气体 ∆h = cp∆T ,可得 h2 − h1 = cp (T2 − T1 ) ,绝热节流前后焓值相等,因此
T1 = T2 ,因此对于理想气体绝热节流前后温度也相等
4-3 某理想气体动力循环由这样 4 个过程构成,先从状态 a 定温膨胀到状态 b,后绝热 膨胀到状态 c,再定压放热到状态 d,最后绝热压缩回到状态 a,在 p-v 图、T-s 图上表示该 循环。已知吸热量 q1 和各点的焓,列出放热量、功和循环热效率的计算式。
解:由 T-s 图,c-d 过程是定压放热过程,放热量 q2 = ∆h + wt = ∆h = hd − hc < 0
= 0.789kJ/ (kg ⋅ K)
由理想气体状态方程可得
p1V1 T1
=
p2V2 T2
,而V2
= 2V1 ,可得
p2 p1
= 0.379
κ −1
绝热过程 T2 T1
=
⎛ ⎜ ⎝
p2 p1
⎞ ⎟ ⎠
κ
,可得绝热指数κ = 1.4
因此 cp = κ cV = 1.4× 0.789 = 1.105kJ/ (kg ⋅ K )
工程热力学(第五版)第4章练习题

第4章 理想气体热力过程及气体压缩4.1 本章基本要求熟练掌握定容、定压、定温、绝热、多变过程中状态参数p 、v 、T 、∆u 、∆h 、∆s 的计算,过程量Q 、W 的计算,以及上述过程在p -v 、T -s 图上的表示。
4.2 本章重点结合热力学第一定律,计算四个基本热力过程、多变过程中的状态参数和过程参数及在p -v 、T -s 图上表示。
本章的学习应以多做练习题为主,并一定注意要在求出结果后,在p -v 、T -s 图上进行检验。
4.3 例 题例1.2kg 空气分别经过定温膨胀和绝热膨胀的可逆过程,如图4.1,从初态1p =9.807bar,1t =300C 膨胀到终态容积为初态容积的5倍,试计算不同过程中空气的终态参数,对外所做的功和交换的热量以及过程中内能、焓、熵的变化量。
图4.1解:将空气取作闭口系对可逆定温过程1-2,由过程中的参数关系,得bar v v p p 961.151807.92112=⨯== 按理想气体状态方程,得111p RT v ==0.1677kg m /3125v v ==0.8385kg m /312T T ==573K 2t =300C气体对外作的膨胀功及交换的热量为1211lnV V V p Q W T T ===529.4kJ 过程中内能、焓、熵的变化量为12U ∆=0 12H ∆=0 12S ∆=1T Q T=0.9239kJ /K 或12S ∆=mRln12V V =0.9238kJ /K 对可逆绝热过程1-2′, 由可逆绝热过程参数间关系可得kv v p p )(211'2= 其中22'v v ==0.8385kg m /3 故 4.12)51(807.9'=p =1.03barRv p T '''222==301K '2t =28C气体对外所做的功及交换的热量为)(11)(11'212211T T mR k V p V p k W s --=--==390.3kJ 0'=s Q过程中内能、焓、熵的变化量为kJ T T mc U v 1.390)(1212''-=-=∆或kJ W U 3.390212'-=-=∆kJ T T mc H p 2.546)(1212''-=-=∆ '12S ∆=0例2. 1kg 空气多变过程中吸取41.87kJ 的热量时,将使其容积增大10倍,压力降低8倍,求:过程中空气的内能变化量,空气对外所做的膨胀功及技术功。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、在p-v图和T-s图上画出定比热容理想气体的(1) 可逆定容加热过程、可逆定压加热过程;(2)可逆 定温加热过程和可逆绝热膨胀过程。
2、将满足空气下列要求的多变过程表示在p-v图和T-s 图上:1)空气升压、升温,又放热;2)空气膨胀、 升温,又吸热;3)n=1.6的膨胀过程,并判断q、 w、△u的正负;4) n=1.3的压缩过程,并判断q、 w、△u的正负;
W
mw
2
pdV
1
1 n 1
(
p1V1
p2V2
)
8.58kJ
④ U mcv (T2 T1) 5.36kJ
H mcp (T2 T1) 7.51kJ
S
m(cvIn
T2 T1
Rg In
v2 v1
)
0.0087kJ/K
9
v2n
T1v1n1
T2v2n1
T1 T2
v n 1 2
vn1 1
1
v n 1 2
v1n1,已知v2
v1
0 n1
5
3)n=1.6的膨胀过程,并判断q、w、△u的正负
此过程为放热,对外做功,内能减少
6
4) n=1.3的压缩过程,并判断q、w、△u的正负;
此过程为放热,外界对空气做功,内能增加。
3、初态为p1=0.1MPa,t1=40℃的空气, V1=0.052立方米,在气缸中被可逆多变地压缩到 p2=0.565MPa,V2=0.013立方米,试求该多变 过程的多变指数n,压缩后的温度t2,过程中空气和 外界交换的功量和热量,压缩过程中气体热力学能、1
1、在p-v图和T-s图上画出定比热容理想气体的可 逆定容加热过程、可逆定压加热过程、可逆定温加 热过程和可逆绝热膨胀过程。 1)可逆定容加热过程、可逆定压加热过程
定容过程
定压过程
2
2)可逆定温加热过程、可逆绝热膨胀过程
3
2、1)空气升压、升温,又放热
q
n
n 1
cV
T2
T1
0, 且T2
T1
所以: 1 n k
4
2)空气膨胀、升温,又吸热
q
n
n 1
cV
T2
T1
0, 且T2
T1
n
n 1
0
n
1或者n
p1v1n
p2v2n
RgT1 v1
v1n
Hale Waihona Puke RgT2 v2p2v2n
n
In( p2 / p1) In(v1 / v2 )
1.25
②
(1)T2
(2)m
Tp11(v1vv12)n0.10584k4g2=Kp2v2
RgT1
RgT2
T2
p2v2 Rg m
0.565106 0.013 287 0.058
441.25K
8
③
n
Q mq m n 1 cv (T2 T1) 3.21kJ
7
3、初态为p1=0.1MPa,t1=40℃的空气, V1=0.052m3,在气缸中被可逆多变地压缩到 p2=0.565MPa,V2=0.013m3,试求该多变过程 的多变指数n,压缩后的温度t2,过程中空气和外界 交换的功量和热量,压缩过程中气体热力学能、焓
和熵可的逆多变边化压。缩过程
①
p1v1n
