(INITIAL SINK SOURCE)),
实验室用水的种类和区别

水是实验室内一个常常被忽视但至关重要的试剂。
实验室用水有那些种类?能达到什么级别?不同实验对水的要求有那些?实验室常见的水的种类:1、蒸馏水(Distilled Water ):实验室最常用的一种纯水,虽设备便宜,但极其耗能和费水且速度慢,应用会逐渐减少。
蒸馏水能去除自来水内大部分的污染物,但挥发性的杂质无法去除,如二氧化碳、氨、二氧化硅以及一些有机物。
新鲜的蒸馏水是无菌的,但储存后细菌易繁殖;此外,储存的容器也很讲究,若是非惰性的物质,离子和容器的塑形物质会析出造成二次污染。
2、去离子水(Deionized Water ):应用离子交换树脂去除水中的阴离子和阳离子,但水中仍然存在可溶性的有机物,可以污染离子交换柱从而降低其功效,去离子水存放后也容易引起细菌的繁殖。
3、反渗水(Reverse osmosis Water):其生成的原理是水分子在压力的作用下,通过反渗透膜成为纯水,水中的杂质被反渗透膜截留排出。
反渗水克服了蒸馏水和去离子水的许多缺点,利用反渗透技术可以有效的去除水中的溶解盐、胶体,细菌、病毒、细菌内毒素和大部分有机物等杂质,但不同厂家生产的反渗透膜对反渗水的质量影响很大。
4、超纯水(Ultra-pure grade water):其标准是水电阻率为18.2MΩ-cm。
但超纯水在TOC、细菌、内毒素等指标方面并不相同,要根据实验的要求来确定,如细胞培养则对细菌和内毒素有要求,而HPLC则要求TOC低。
评价水质的常用指标:1、电阻率(electrical resistivity):衡量实验室用水导电性能的指标,单位为MΩ-cm,随着水内无机离子的减少电阻加大则数值逐渐变大,实验室超纯水的标准:电阻率为18.2MΩ-cm。
2、总有机碳(Total Organic Carbon ,TOC):水中碳的的浓度,反映水中氧化的有机化合物的含量,单位为ppm 或 ppb。
3、内毒素(Endotoxin):革兰氏阴性细菌的脂多糖细胞壁碎片,又称之为“热原”,单位cuf/ml。
流体力学:第5章 势流理论-上

z x iy
dW u2 v2 v V dz
5.2.1 复势与复速度(复平面)
3)复速度的环路积分与速度环量和流量的关系:
l
dw dz dw d id l iQl l l dz
dw l Re l dz
y x
V0
m
2 a
均匀流和源叠加可模拟绕弹形物体的流动。调整源强m和速度V0, 改变流线的形状。
5.4.1 均匀流和点源的叠加 流场中压力分布
p ( p0 1 2 1 v0 ) V 2 2 2
压力系数
V 2 p p0 cp 1 v2 1 2 0 v0 2
y
V V0e
i
u V0 cos , v V0 sin
o
平板
V0
u d x v d y V0 x cos V0 y sin
v d x u d y V0 x sin V0 y cos
x
W ( z) V0 z cos iV0 z sin V0 ze i
( R )
v
p
F
奇点叠加法;保角变换法(平面流)。 数值解:复杂边界问题。
CFD — Computational Fluid Dynamics
5.2 复势(complex potential )
借助复变函数数学工具解平面势流问题。
平面势流:φ和ψ都是调和函数, 2 0, 2 0,且满足
5-4
W ( z ) (1 i ) z
补充题:已知复势为:
z 1) w ( z ) (1 i ) ln z4
信号与系统》专业术语中英文对照表

《信号与系统》专业术语中英文对照表第 1 章绪论信号(signal)系统(system)电压(voltage)电流(current)信息(information)电路(circuit)网络(network)确定性信号(determinate signal)随机信号(random signal)一维信号(one –dimensional signal)多维信号(multi–dimensional signal)连续时间信号(continuous time signal)离散时间信号(discrete time signal)取样信号(sampling signal)数字信号(digital signal)周期信号(periodic signal)非周期信号(nonperiodic(aperiodic)signal)能量(energy)功率(power)能量信号(energy signal)功率信号(power signal)平均功率(average power)平均能量(average energy)指数信号(exponential signal)时间常数(time constant)正弦信号(sine signal)余弦信号(cosine signal)振幅(amplitude)角频率(angular frequency)初相位(initial phase)周期(period)频率(frequency)欧拉公式(Euler’s formula)复指数信号(complex exponential signal)复频率(complex frequency)实部(real part)虚部(imaginary part)抽样函数Sa(t)(sampling(Sa)function)偶函数(even function)奇异函数(singularity function)奇异信号(singularity signal)单位斜变信号(unit ramp signal)斜率(slope)单位阶跃信号(unit step signal)符号函数(signum function)单位冲激信号(unit impulse signal)广义函数(generalized function)取样特性(sampling property)冲激偶信号(impulse doublet signal)奇函数(odd function)偶分量(even component)奇分量(odd component)正交函数(orthogonal function)正交函数集(set of orthogonal function)数学模型(mathematics model)电压源(voltage source)基尔霍夫电压定律(Kirchhoff’s voltage law(KVL))电流源(current source)连续时间系统(continuous time system)离散时间系统(discrete time system)微分方程(differential function)差分方程(difference function)线性系统(linear system)非线性系统(nonlinear system)时变系统(time–varying system)时不变系统(time–invariant system)集总参数系统(lumped–parameter system)分布参数系统(distributed–parameter system)偏微分方程(partial differential function)因果系统(causal system)非因果系统(noncausal system)因果信号(causal signal)叠加性(superposition property)均匀性(homogeneity)积分(integral)输入–输出描述法(input–output analysis)状态变量描述法(state variable analysis)单输入单输出系统(single–input and single–output system)状态方程(state equation)输出方程(output equation)多输入多输出系统(multi–input and multi–output system)时域分析法(time domain method)变换域分析法(transform domain method)卷积(convolution)傅里叶变换(Fourier transform)拉普拉斯变换(Laplace transform)第 2 章连续时间系统的时域分析齐次解(homogeneous solution)特解(particular solution)特征方程(characteristic function)特征根(characteristic root)固有(自由)解(natural solution)强迫解(forced solution)起始条件(original condition)初始条件(initial condition)自由响应(natural response)强迫响应(forced response)零输入响应(zero-input response)零状态响应(zero-state response)冲激响应(impulse response)阶跃响应(step response)卷积积分(convolution integral)交换律(exchange law)分配律(distribute law)结合律(combine law)第3 章傅里叶变换频谱(frequency spectrum)频域(frequency domain)三角形式的傅里叶级数(trigonomitric Fourier series)指数形式的傅里叶级数(exponential Fourier series)傅里叶系数(Fourier coefficient)直流分量(direct composition)基波分量(fundamental composition)n 次谐波分量(nth harmonic component)复振幅(complex amplitude)频谱图(spectrum plot(diagram))幅度谱(amplitude spectrum)相位谱(phase spectrum)包络(envelop)离散性(discrete property)谐波性(harmonic property)收敛性(convergence property)奇谐函数(odd harmonic function)吉伯斯现象(Gibbs phenomenon)周期矩形脉冲信号(periodic rectangular pulse signal)周期锯齿脉冲信号(periodic sawtooth pulse signal)周期三角脉冲信号(periodic triangular pulse signal)周期半波余弦信号(periodic half–cosine signal)周期全波余弦信号(periodic full–cosine signal)傅里叶逆变换(inverse Fourier transform)频谱密度函数(spectrum density function)单边指数信号(single–sided exponential signal)双边指数信号(two–sided exponential signal)对称矩形脉冲信号(symmetry rectangular pulse signal)线性(linearity)对称性(symmetry)对偶性(duality)位移特性(shifting)时移特性(time–shifting)频移特性(frequency–shifting)调制定理(modulation theorem)调制(modulation)解调(demodulation)变频(frequency conversion)尺度变换特性(scaling)微分与积分特性(differentiation and integration)时域微分特性(differentiation in the time domain)时域积分特性(integration in the time domain)频域微分特性(differentiation in the frequency domain)频域积分特性(integration in the frequency domain)卷积定理(convolution theorem)时域卷积定理(convolution theorem in the time domain)频域卷积定理(convolution theorem in the frequency domain)取样信号(sampling signal)矩形脉冲取样(rectangular pulse sampling)自然取样(nature sampling)冲激取样(impulse sampling)理想取样(ideal sampling)取样定理(sampling theorem)调制信号(modulation signal)载波信号(carrier signal)已调制信号(modulated signal)模拟调制(analog modulation)数字调制(digital modulation)连续波调制(continuous wave modulation)脉冲调制(pulse modulation)幅度调制(amplitude modulation)频率调制(frequency modulation)相位调制(phase modulation)角度调制(angle modulation)频分多路复用(frequency–division multiplex(FDM))时分多路复用(time –division multiplex(TDM))相干(同步)解调(synchronous detection)本地载波(local carrier)系统函数(system function)网络函数(network function)频响特性(frequency response)幅频特性(amplitude frequency response)相频特性(phase frequency response)无失真传输(distortionless transmission)理想低通滤波器(ideal low–pass filter)截止频率(cutoff frequency)正弦积分(sine integral)上升时间(rise time)窗函数(window function)理想带通滤波器(ideal band–pass filter)第 4 章拉普拉斯变换代数方程(algebraic equation)双边拉普拉斯变换(two-sided Laplace transform)双边拉普拉斯逆变换(inverse two-sided Laplace transform)单边拉普拉斯变换(single-sided Laplace transform)拉普拉斯逆变换(inverse Laplace transform)收敛域(region of convergence(ROC))延时特性(time delay)s 域平移特性(shifting in the s-domain)s 域微分特性(differentiation in the s-domain)s 域积分特性(integration in the s-domain)初值定理(initial-value theorem)终值定理(expiration-value)复频域卷积定理(convolution theorem in the complex frequency domain)部分分式展开法(partial fraction expansion)留数法(residue method)第 5 章策动点函数(driving function)转移函数(transfer function)极点(pole)零点(zero)零极点图(zero-pole plot)暂态响应(transient response)稳态响应(stable response)稳定系统(stable system)一阶系统(first order system)高通滤波网络(high-low filter)低通滤波网络(low-pass filter)二阶系统(second system)最小相移系统(minimum-phase system)维纳滤波器(Winner filter)卡尔曼滤波器(Kalman filter)低通(low-pass)高通(high-pass)带通(band-pass)带阻(band-stop)有源(active)无源(passive)模拟(analog)数字(digital)通带(pass-band)阻带(stop-band)佩利-维纳准则(Paley-Winner criterion)最佳逼近(optimum approximation)过渡带(transition-band)通带公差带(tolerance band)巴特沃兹滤波器(Butterworth filter)切比雪夫滤波器(Chebyshew filter)方框图(block diagram)信号流图(signal flow graph)节点(node)支路(branch)输入节点(source node)输出节点(sink node)混合节点(mix node)通路(path)开通路(open path)闭通路(close path)环路(loop)自环路(self-loop)环路增益(loop gain)不接触环路(disconnect loop)前向通路(forward path)前向通路增益(forward path gain)梅森公式(Mason formula)劳斯准则(Routh criterion)第 6 章数字系统(digital system)数字信号处理(digital signal processing)差分方程(difference equation)单位样值响应(unit sample response)卷积和(convolution sum)Z 变换(Z transform)序列(sequence)样值(sample)单位样值信号(unit sample signal)单位阶跃序列(unit step sequence)矩形序列(rectangular sequence)单边实指数序列(single sided real exponential sequence)单边正弦序列(single sided exponential sequence)斜边序列(ramp sequence)复指数序列(complex exponential sequence)线性时不变离散系统(linear time-invariant discrete-time system)常系数线性差分方程(linear constant-coefficient difference equation)后向差分方程(backward difference equation)前向差分方程(forward difference equation)海诺塔(Tower of Hanoi)菲波纳西(Fibonacci)冲激函数串(impulse train)第7 章数字滤波器(digital filter)单边Z 变换(single-sided Z transform)双边Z 变换(two-sided (bilateral) Z transform) 幂级数(power series)收敛(convergence)有界序列(limitary-amplitude sequence)正项级数(positive series)有限长序列(limitary-duration sequence)右边序列(right-sided sequence)左边序列(left-sided sequence)双边序列(two-sided sequence)Z 逆变换(inverse Z transform)围线积分法(contour integral method)幂级数展开法(power series expansion)z 域微分(differentiation in the z-domain)序列指数加权(multiplication by an exponential sequence)z 域卷积定理(z-domain convolution theorem)帕斯瓦尔定理(Parseval theorem)传输函数(transfer function)序列的傅里叶变换(discrete-time Fourier transform:DTFT)序列的傅里叶逆变换(inverse discrete-time Fourier transform:IDTFT)幅度响应(magnitude response)相位响应(phase response)量化(quantization)编码(coding)模数变换(A/D 变换:analog-to-digital conversion)数模变换(D/A 变换:digital-to- analog conversion)第8 章端口分析法(port analysis)状态变量(state variable)无记忆系统(memoryless system)有记忆系统(memory system)矢量矩阵(vector-matrix )常量矩阵(constant matrix )输入矢量(input vector)输出矢量(output vector)直接法(direct method)间接法(indirect method)状态转移矩阵(state transition matrix)系统函数矩阵(system function matrix)冲激响应矩阵(impulse response matrix)朱里准则(July criterion)。
计算机IT 英语专业词汇

数据结构基本英语词汇Recursion 递归pivot ['pivət] 轴数据抽象data abstraction数据元素data element数据对象data object数据项data item数据类型data type抽象数据类型abstract data type逻辑结构logical structure物理结构phyical structure线性结构linear structure非线性结构nonlinear structure基本数据类型atomic data type固定聚合数据类型fixed-aggregate data type可变聚合数据类型variable-aggregate data type线性表linear list栈stack队列queue串string数组array树tree图gragh查找,线索searching更新updating排序(分类) sorting插入insertion删除deletion前趋predecessor后继successor直接前趋immediate predecessor直接后继immediate successor双端列表deque(double-ended queue) 循环队列cirular queue指针pointer先进先出表(队列)first-in first-out list 后进先出表(队列)last-in first-out list 栈底bottom栈定top压入push弹出pop队头front队尾rear上溢overflow下溢underflow数组array矩阵matrix多维数组multi-dimentional array以行为主的顺序分配row major order 以列为主的顺序分配column major order三角矩阵truangular matrix对称矩阵symmetric matrix稀疏矩阵sparse matrix转置矩阵transposed matrix链表linked list线性链表linear linked list单链表single linked list多重链表multilinked list循环链表circular linked list双向链表doubly linked list十字链表orthogonal list广义表generalized list链link指针域pointer field链域link field头结点head node头指针head pointer尾指针tail pointer串string空白(空格)串blank string空串(零串)null string子串substring树tree子树subtree森林forest根root叶子leaf结点node深度depth层次level双亲parents孩子children兄弟brother祖先ancestor子孙descentdant二叉树binary tree平衡二叉树banlanced binary tree 满二叉树full binary tree完全二叉树complete binary tree遍历二叉树traversing binary tree 二叉排序树binary sort tree二叉查找树binary search tree线索二叉树threaded binary tree哈夫曼树Huffman tree有序数ordered tree无序数unordered tree判定树decision tree双链树doubly linked tree数字查找树digital search tree树的遍历traversal of tree先序遍历preorder traversal中序遍历inorder traversal后序遍历postorder traversal图graph子图subgraph有向图digraph(directed graph)无向图undigraph(undirected graph) 完全图complete graph连通图connected graph非连通图unconnected graph强连通图strongly connected graph 弱连通图weakly connected graph 加权图weighted graph有向无环图directed acyclic graph 稀疏图spares graph 稠密图dense graph重连通图biconnected graph二部图bipartite graph边edge顶点vertex弧arc路径path回路(环)cycle弧头head弧尾tail源点source终点destination汇点sink权weight连接点articulation point初始结点initial node终端结点terminal node相邻边adjacent edge相邻顶点adjacent vertex关联边incident edge入度indegree出度outdegree最短路径shortest path有序对ordered pair无序对unordered pair简单路径simple path简单回路simple cycle连通分量connected component邻接矩阵adjacency matrix邻接表adjacency list邻接多重表adjacency multilist遍历图traversing graph生成树spanning tree最小(代价)生成树minimum(cost)spanning tree生成森林spanning forest拓扑排序topological sort偏序partical order拓扑有序topological orderAOV网activity on vertex network AOE网activity on edge network关键路径critical path匹配matching最大匹配maximum matching增广路径augmenting path增广路径图augmenting path graph查找searching线性查找(顺序查找)linear search (sequential search)二分查找binary search分块查找block search散列查找hash search平均查找长度average search length电脑专业术语散列表hash table散列函数hash funticion直接定址法immediately allocating method数字分析法digital analysis method平方取中法mid-square method折叠法folding method除法division method随机数法random number method排序sort内部排序internal sort外部排序external sort插入排序insertion sort随小增量排序diminishing increment sort选择排序selection sort堆排序heap sort快速排序quick sort归并排序merge sort基数排序radix sort外部排序external sort平衡归并排序balance merging sort二路平衡归并排序balance two-way merging sort多步归并排序ployphase merging sort 置换选择排序replacement selection sort 文件file主文件master file顺序文件sequential file索引文件indexed file索引顺序文件indexed sequential file 索引非顺序文件indexed non-sequential file直接存取文件direct access file多重链表文件multilist file倒排文件inverted file目录结构directory structure树型索引tree indexJava基础常见英语词汇(共70个)Compile:编绎Run:运行Class:类Object:对象System:系统out:输出print:打印line:行variable:变量type:类型operation:操作,运算array:数组parameter:参数method:方法function:函数member-variable:成员变量member-function:成员函数get:得到set:设置public:公有的private:私有的protected:受保护的default:默认access:访问package:包import:导入static:静态的void:无(返回类型) extends:继承parent class:父类base class:基类super class:超类child class:子类derived class:派生类override:重写,覆盖overload:重载final:最终的,不能改变的abstract:抽象interface:接口implements:实现exception:异常Runtime:运行时ArithmeticException:算术异常ArrayIndexOutOfBoundsException:数组下标越界异常NullPointerException:空引用异常ClassNotFoundException:类没有发现异常NumberFormatException:数字格式异常(字符串不能转化为数字)Try:尝试Catch:捕捉Finally:最后Throw:抛出Throws: (投掷)表示强制异常处理Throwable:(可抛出的)表示所有异常类的祖先类Lang:language,语言Util:工具Display:显示Random:随机Collection:集合ArrayList:(数组列表)表示动态数组HashMap: 散列表,哈希表Swing:轻巧的Awt:abstract window toolkit:抽象窗口工具包Vertical:垂直Horizonatal:水平Label:标签TextField:文本框TextArea:文本域Button:按钮Checkbox:复选框Radiobutton:单选按钮Combobox:复选框Event:事件Mouse:鼠标Key:键Focus:焦点Listener:监听Tree:树Node:节点Jdbc:java database connectivity,java数据库连接DriverManager:驱动管理器Connection:连接Statement:表示执行对象Preparedstatement:表示预执行对象Resultset:结果集Next:下一个Close:关闭executeQuery:执行查询JSP中常用英文URL: Universal Resource Location:统一资源定位符IE: Internet Explorer 因特网浏览器JSP:java server page.java服务器页面Model:模型View:视图C:controller:控制器Tomcat:一种jsp的web服务器WebModule:web模块Servlet:小服务程序Request:请求Response:响应Init: initialize,初始化Service:服务Destroy:销毁Startup:启动Mapping:映射pattern:模式Getparameter:获取参数Session:会话Application:应用程序Context:上下文redirect:重定向dispatch:分发forward:转交setattribute:设置属性getattribute:获取属性page:页面contentType:内容类型charset:字符集include:包含tag:标签taglib:标签库EL:expression language,表达式语言Scope:作用域Empty:空JSTL:java standard tag library,java标准标签库TLD:taglib description,标签库描述符Core:核心Test:测试Foreach:表示循环Var:variable,变量Status:状态Items:项目集合Fmt:format,格式化Filter:过滤器。
《信号与系统》专业术语中英文对照表(20200705175237)

《信号与系统》专业术语中英文对照表第 1 章绪论信号(signal)系统(system)电压(voltage)电流(current)信息(information)电路(circuit)网络(network)确定性信号(determinate signal)随机信号(random signal)一维信号(one–dimensional signal)多维信号(multi–dimensional signal)连续时间信号(continuous time signal)离散时间信号(discrete time signal)取样信号(sampling signal)数字信号(digital signal)周期信号(periodic signal)非周期信号(nonperiodic(aperiodic) signal)能量(energy)功率(power)能量信号(energy signal)功率信号(power signal)平均功率(average power)平均能量(average energy)指数信号(exponential signal)时间常数(time constant)正弦信号(sine signal)余弦信号(cosine signal)振幅(amplitude)角频率(angular frequency)初相位(initial phase)周期(period)频率(frequency)欧拉公式(Euler’s formula)复指数信号(complex exponential signal)复频率(complex frequency)实部(real part)虚部(imaginary part)抽样函数 Sa(t)(sampling(Sa) function)偶函数(even function)奇异函数(singularity function)奇异信号(singularity signal)单位斜变信号(unit ramp signal)斜率(slope)单位阶跃信号(unit step signal)符号函数(signum function)单位冲激信号(unit impulse signal)广义函数(generalized function)取样特性(sampling property)冲激偶信号(impulse doublet signal)奇函数(odd function)偶分量(even component)奇分量(odd component)正交函数(orthogonal function)正交函数集(set of orthogonal function)数学模型(mathematics model)电压源(voltage source)基尔霍夫电压定律(Kirchhoff’s voltage law(KVL))电流源(current source)连续时间系统(continuous time system)离散时间系统(discrete time system)微分方程(differential function)差分方程(difference function)线性系统(linear system)非线性系统(nonlinear system)时变系统(time–varying system)时不变系统(time–invariant system)集总参数系统(lumped–parameter system)分布参数系统(distributed–parameter system)偏微分方程(partial differential function)因果系统(causal system)非因果系统(noncausal system)因果信号(causal signal)叠加性(superposition property)均匀性(homogeneity)积分(integral)输入–输出描述法(input–output analysis)状态变量描述法(state variable analysis)单输入单输出系统(single–input and single–output system)状态方程(state equation)输出方程(output equation)多输入多输出系统(multi–input and multi–output system)时域分析法(time domain method)变换域分析法(transform domain method)卷积(convolution)傅里叶变换(Fourier transform)拉普拉斯变换(Laplace transform)第 2 章连续时间系统的时域分析齐次解(homogeneous solution)特解(particular solution)特征方程(characteristic function)特征根(characteristic root)固有(自由)解(natural solution)强迫解(forced solution)起始条件(original condition)初始条件(initial condition)自由响应(natural response)强迫响应(forced response)零输入响应(zero-input response)零状态响应(zero-state response)冲激响应(impulse response)阶跃响应(step response)卷积积分(convolution integral)交换律(exchange law)分配律(distribute law)结合律(combine law)第3 章傅里叶变换频谱(frequency spectrum)频域(frequency domain)三角形式的傅里叶级数(trigonomitric Fourier series)指数形式的傅里叶级数(exponential Fourier series)傅里叶系数(Fourier coefficient)直流分量(direct composition)基波分量(fundamental composition) n 次谐波分量(nth harmonic component)复振幅(complex amplitude)频谱图(spectrum plot(diagram))幅度谱(amplitude spectrum)相位谱(phase spectrum)包络(envelop)离散性(discrete property)谐波性(harmonic property)收敛性(convergence property)奇谐函数(odd harmonic function)吉伯斯现象(Gibbs phenomenon)周期矩形脉冲信号(periodic rectangular pulse signal)周期锯齿脉冲信号(periodic sawtooth pulse signal)周期三角脉冲信号(periodic triangular pulse signal)周期半波余弦信号(periodic half–cosine signal)周期全波余弦信号(periodic full–cosine signal)傅里叶逆变换(inverse Fourier transform)频谱密度函数(spectrum density function)单边指数信号(single–sided exponential signal)双边指数信号(two–sided exponential signal)对称矩形脉冲信号(symmetry rectangular pulse signal)线性(linearity)对称性(symmetry)对偶性(duality)位移特性(shifting)时移特性(time–shifting)频移特性(frequency–shifting)调制定理(modulation theorem)调制(modulation)解调(demodulation)变频(frequency conversion)尺度变换特性(scaling)微分与积分特性(differentiation and integration)时域微分特性(differentiation in the time domain)时域积分特性(integration in the time domain)频域微分特性(differentiation in the frequency domain)频域积分特性(integration in the frequency domain)卷积定理(convolution theorem)时域卷积定理(convolution theorem in the time domain)频域卷积定理(convolution theorem in the frequency domain)取样信号(sampling signal)矩形脉冲取样(rectangular pulse sampling)自然取样(nature sampling)冲激取样(impulse sampling)理想取样(ideal sampling)取样定理(sampling theorem)调制信号(modulation signal)载波信号(carrier signal)已调制信号(modulated signal)模拟调制(analog modulation)数字调制(digital modulation)连续波调制(continuous wave modulation)脉冲调制(pulse modulation)幅度调制(amplitude modulation)频率调制(frequency modulation)相位调制(phase modulation)角度调制(angle modulation)频分多路复用(frequency–division multiplex(FDM))时分多路复用(time–division multiplex (TDM))相干(同步)解调(synchronous detection)本地载波(local carrier)系统函数(system function)网络函数(network function)频响特性(frequency response)幅频特性(amplitude frequency response)相频特性(phase frequency response)无失真传输(distortionless transmission)理想低通滤波器(ideal low–pass filter)截止频率(cutoff frequency)正弦积分(sine integral)上升时间(rise time)窗函数(window function)理想带通滤波器(ideal band–pass filter)第 4 章拉普拉斯变换代数方程(algebraic equation)双边拉普拉斯变换(two-sided Laplace transform)双边拉普拉斯逆变换(inverse two-sided Laplace transform)单边拉普拉斯变换(single-sided Laplace transform)拉普拉斯逆变换(inverse Laplace transform)收敛域(region of convergence(ROC))延时特性(time delay)s 域平移特性(shifting in the s-domain)s 域微分特性(differentiation in the s-domain) s 域积分特性(integration in the s-domain)初值定理(initial-value theorem)终值定理(expiration-value)复频域卷积定理(convolution theorem in the complex frequency domain)部分分式展开法(partial fraction expansion)留数法(residue method)第 5 章策动点函数(driving function)转移函数(transfer function)极点(pole)零点(zero)零极点图(zero-pole plot)暂态响应(transient response)稳态响应(stable response)稳定系统(stable system)一阶系统(first order system)高通滤波网络(high-low filter)低通滤波网络(low-pass filter)二阶系统(second system)最小相移系统(minimum-phase system)维纳滤波器(Winner filter)卡尔曼滤波器(Kalman filter)低通(low-pass)高通(high-pass)带通(band-pass)带阻(band-stop)有源(active)无源(passive)模拟(analog)数字(digital)通带(pass-band)阻带(stop-band)佩利-维纳准则(Paley-Winner criterion)最佳逼近(optimum approximation)过渡带(transition-band)通带公差带(tolerance band)巴特沃兹滤波器(Butterworth filter)切比雪夫滤波器(Chebyshew filter)方框图(block diagram)信号流图(signal flow graph)节点(node)支路(branch)输入节点(source node)输出节点(sink node)混合节点(mix node)通路(path)开通路(open path)闭通路(close path)环路(loop)自环路(self-loop)环路增益(loop gain)不接触环路(disconnect loop)前向通路(forward path)前向通路增益(forward path gain)梅森公式(Mason formula)劳斯准则(Routh criterion)第 6 章数字系统(digital system)数字信号处理(digital signal processing)差分方程(difference equation)单位样值响应(unit sample response)卷积和(convolution sum)Z 变换(Z transform)序列(sequence)样值(sample)单位样值信号(unit sample signal)单位阶跃序列(unit step sequence)矩形序列 (rectangular sequence)单边实指数序列(single sided real exponential sequence)单边正弦序列(single sided exponential sequence)斜边序列(ramp sequence)复指数序列(complex exponential sequence)线性时不变离散系统(linear time-invariant discrete-time system)常系数线性差分方程(linear constant-coefficient difference equation)后向差分方程(backward difference equation)前向差分方程(forward difference equation)海诺塔(Tower of Hanoi)菲波纳西(Fibonacci)冲激函数串(impulse train)第 7 章数字滤波器(digital filter)单边 Z 变换(single-sided Z transform)双边 Z 变换(two-sided (bilateral) Z transform) 幂级数(power series)收敛(convergence)有界序列(limitary-amplitude sequence)正项级数(positive series)有限长序列(limitary-duration sequence)右边序列(right-sided sequence)左边序列(left-sided sequence)双边序列(two-sided sequence) Z 逆变换(inverse Z transform)围线积分法(contour integral method)幂级数展开法(power series expansion) z 域微分(differentiation in the z-domain)序列指数加权(multiplication by an exponential sequence) z 域卷积定理(z-domain convolution theorem)帕斯瓦尔定理(Parseval theorem)传输函数(transfer function)序列的傅里叶变换(discrete-time Fourier transform:DTFT)序列的傅里叶逆变换(inverse discrete-time Fourier transform:IDTFT)幅度响应(magnitude response)相位响应(phase response)量化(quantization)编码(coding)模数变换(A/D 变换:analog-to-digital conversion)数模变换(D/A 变换:digital-to- analog conversion)第 8 章端口分析法(port analysis)状态变量(state variable)无记忆系统(memoryless system)有记忆系统(memory system)矢量矩阵(vector-matrix )常量矩阵(constant matrix )输入矢量(input vector)输出矢量(output vector)直接法(direct method)间接法(indirect method)状态转移矩阵(state transition matrix)系统函数矩阵(system function matrix)冲激响应矩阵(impulse response matrix)朱里准则(July criterion)。
莫加ioLogik E1200系列以太网远程输入输出(I O)及两口以太网交换机特点和优势说明书

ioLogik E1200SeriesEthernet remote I/O with2-port Ethernet switchFeatures and Benefits•User-definable Modbus TCP Slave addressing•Supports EtherNet/IP Adapter mode1•Supports RESTful API for IIoT applications•2-port Ethernet switch for daisy-chain topologies•Saves time and wiring costs with peer-to-peer communications•Active communication with MX-AOPC UA Server•Supports SNMP v1/v2c•Easy mass deployment and configuration with ioSearch utility•Friendly configuration via web browser•Simplifies I/O management with MXIO library for Windows or Linux•Class I Division2,ATEX Zone2certification2•Wide operating temperature models available for-40to75°C(-40to167°F)environmentsCertificationsIntroductionThe ioLogik E1200Series supports the most often-used protocols for retrieving I/O data,making it capable of handling a wide variety of applications.Most IT engineers use SNMP or RESTful API protocols,but OT engineers are more familiar with OT-based protocols,such as Modbus and EtherNet/IP.Moxa's Smart I/O makes it possible for both IT and OT engineers to conveniently retrieve data from the same I/O device.The ioLogik E1200Series speaks six different protocols,including Modbus TCP,EtherNet/IP,and Moxa AOPC for OT engineers,as well as SNMP, RESTful API,and Moxa MXIO library for IT engineers.The ioLogik E1200retrieves I/O data and converts the data to any of these protocols at the same time,allowing you to get your applications connected easily and effortlessly.Daisy-Chained Ethernet I/O ConnectionThis industrial Ethernet remote I/O comes with two switched Ethernet ports to allow for the free flow of information downstream to another local Ethernet device,or upstream to a control server via expandable daisy-chained Ethernet I/O arrays.Applications such as factory automation, security and surveillance systems,and tunneled connections can make use of daisy-chained Ethernet for building multidrop I/O networks over standard Ethernet cables.Many industrial automation users are familiar with multidrop as the configuration most typically used in fieldbus solutions.The daisy-chain capabilities supported by ioLogik Ethernet remote I/O units not only increase the expandability and installation possibilities for your remote I/O applications,but also lower overall costs by reducing the need for separate Ethernet switches.Daisy-chaining devices in this way will also reduce overall labor and cabling expenses.1.Requires online registration(available free of charge)2.Class I Division2and ATEX currently do not apply to the E1213/E1213-T models.Save Time and Wiring Costs with Peer-to-Peer CommunicationsIn remote automation applications,the control room and sensors areoften far removed,making wiring over long distances a constantchallenge.With peer-to-peer networking,users may now map a pairof ioLogik Series modules so that input values will be directlytransferred to output channels,greatly simplifying the wiring processand reducing wiring costs.User-Definable Modbus TCP Addressing for Painless Upgrading of Existing SystemsFor Modbus devices that are controlled and detected by fixedaddresses,users need to spend a vast amount of time researchingand verifying initial ers need to locate each device’snetworking details,such as I/O channels or vendor-definedaddresses,to enable the initial or start address of a SCADA system orPLC.Devices that support user-definable Modbus TCP addressingoffer greater flexibility and easier setup.Instead of worrying aboutindividual devices,users simply configure the function and addressmap to fit their needs.Push Technology for EventsWhen used with MX-AOPC UA Server,devices can use active pushcommunications when communicating changes in state and/orevents to a SCADA system.Unlike a polling system,when using apush architecture for communications with a SCADA system,messages will only be delivered when changes in state or configuredevents occur,resulting in higher accuracy and lower amounts of datathat need to be transferred.SpecificationsInput/Output InterfaceAnalog Input Channels ioLogik E1240models:8ioLogik E1242models:4Analog Output Channels ioLogik E1241models:4Configurable DIO Channels(by jumper)ioLogik E1212models:8ioLogik E1213/E1242models:4Digital Input Channels ioLogik E1210models:16ioLogik E1212/E1213models:8ioLogik E1214models:6ioLogik E1242models:4Digital Output Channels ioLogik E1211models:16ioLogik E1213models:4Isolation3k VDC or2k VrmsRelay Channels ioLogik E1214models:6RTD Channels ioLogik E1260models:6Thermocouple Channels ioLogik E1262models:8Buttons Reset buttonDigital InputsConnector Screw-fastened Euroblock terminalCounter Frequency250HzDigital Filtering Time Interval Software configurableDry Contact On:short to GNDOff:openI/O Mode DI or event counterPoints per COM ioLogik E1210/E1212models:8channelsioLogik E1213models:12channelsioLogik E1214models:6channelsioLogik E1242models:4channelsSensor Type Dry contactWet Contact(NPN or PNP)Wet Contact(DI to COM)On:10to30VDCOff:0to3VDCDigital OutputsConnector Screw-fastened Euroblock terminalCurrent Rating ioLogik E1211/E1212/E1242models:200mA per channelioLogik E1213models:500mA per channelI/O Mode DO or pulse outputI/O Type ioLogik E1211/E1212/E1242models:SinkioLogik E1213models:SourceOver-Current Protection ioLogik E1211/E1212/E1242models:2.6A per channel@25°CioLogik E1213models:1.5A per channel@25°COver-Temperature Shutdown175°C(typical),150°C(min.)Over-Voltage Protection35VDCPulse Output Frequency500Hz(max.)RelaysBreakdown Voltage500VACConnector Screw-fastened Euroblock terminalContact Current Rating Resistive load:5A@30VDC,250VAC,110VACContact Resistance100milli-ohms(max.)Electrical Endurance100,000operations@5A resistive loadInitial Insulation Resistance1,000mega-ohms(min.)@500VDCMechanical Endurance5,000,000operationsPulse Output Frequency0.3Hz at rated load(max.)Type Form A(N.O.)power relayNote Ambient humidity must be non-condensing and remain between5and95%.The relaysmay malfunction when operating in high condensation environments below0°C. Analog InputsAccuracy ioLogik E1240/E1242:±0.1%FSR@25°C±0.3%FSR@-10to60°CioLogik E1240-T/E1242-T:±0.1%FSR@25°C±0.3%FSR@-10to60°C±0.5%FSR@-40to75°CBuilt-in Resistor for Current Input120ohmsConnector Screw-fastened Euroblock terminalI/O Mode Voltage/CurrentI/O Type DifferentialInput Impedance10mega-ohms(min.)Input Range0to10VDC0to20mA4to20mA4to20mA(with burn-out detection)Resolution16bitsSampling Rate All channels:12samples/secPer channel:1.5samples/secAnalog OutputsAccuracy ioLogik E1241:±0.1%FSR@25°C±0.3%FSR@-10to60°CioLogik E1241-T:±0.1%FSR@25°C±0.3%FSR@-40to75°CConnector Screw-fastened Euroblock terminalVoltage Output Short-Circuit Protection10mAInternal Resistor400ohmsNote:24V of external power required when loading exceeds1000ohmsOutput Range0to10VDC4to20mAResolution12-bitRTDsAccuracy ioLogik E1260:±0.1%FSR@25°C±0.3%FSR@-10to60°CioLogik E1260-T:±0.1%FSR@25°C±0.3%FSR@-40to75°CConnector Screw-fastened Euroblock terminalInput Connection2-or3-wireInput Impedance625kilo-ohms(min.)Sensor Type PT1000(-200to350°C)PT50,PT100,PT200,PT500(-200to850°C)Resistance Type310,620,1250,and2200ohmsResolution0.1°C or0.1ohmsSampling Rate All channels:12samples/secPer channel:2samples/secThermocouplesMillivolt Accuracy ioLogik E1262:±0.1%FSR@25°C±0.3%FSR@-10to60°CioLogik E1262-T:±0.1%FSR@25°C±0.3%FSR@-40to75°CConnector Screw-fastened Euroblock terminalTC Accuracy Types J,T,E,S,B:±5°CTypes K,R,N:±8°CCJC Accuracy±0.5°C@25°C±1.5°C@-40to75°CInput Impedance10mega-ohms(min.)Millivolt Type±19.532mV±39.062mV±78.126mVFault and over-voltage protection:-35to+35VDC(power off);-25to+30VDC(poweron)Resolution16bitsSampling Rate All channels:12samples/secPer channel:1.5samples/secSensor Type J,K,T,E,R,S,B,NEthernet Interface10/100BaseT(X)Ports(RJ45connector)2,1MAC address(Ethernet bypass)Magnetic Isolation Protection 1.5kV(built-in)Ethernet Software FeaturesConfiguration Options Web Console(HTTP),Windows Utility(ioSearch)Industrial Protocols EtherNet/IP Adapter(Slave),Modbus TCP Server(Slave),Moxa AOPC(Active Tag),MXIO LibraryManagement BOOTP,RESTful API,DHCP Client,HTTP,IPv4,TCP/IP,UDP,SNMPv1Trap,SNMPv1/v2cMIB Device Settings MIBSecurity Access control listLED InterfaceLED Indicators Power,Ready,Port1,Port2Modbus TCPFunctions Supported1,2,3,4,5,6,15,16,23Mode ServerMax.No.of Client Connections10EtherNet/IPMode AdapterMax.No.of Scanner Connections9(for read-only),1(for read/write)Power ParametersPower Connector Screw-fastened Euroblock terminalNo.of Power Inputs1Input Voltage12to36VDCPower Consumption ioLogik E1210Series:110mA@24VDCioLogik E1211Series:200mA@24VDCioLogik E1212Series:155mA@24VDCioLogik E1213Series:130mA@24VDCioLogik E1214Series:188mA@24VDCioLogik E1240Series:121mA@24VDCioLogik E1241Series:194mA@24VDCioLogik E1242Series:139mA@24VDCioLogik E1260Series:110mA@24VDCioLogik E1262Series:118mA@24VDCPhysical CharacteristicsHousing PlasticDimensions27.8x124x84mm(1.09x4.88x3.31in)Weight200g(0.44lb)Installation DIN-rail mounting,Wall mountingWiring I/O cable,16to26AWGPower cable,12to24AWGEnvironmental LimitsOperating Temperature Standard Models:-10to60°C(14to140°F)Wide Temp.Models:-40to75°C(-40to167°F)Storage Temperature(package included)-40to85°C(-40to185°F)Ambient Relative Humidity5to95%(non-condensing)Altitude2000m3Standards and CertificationsEMC EN55032/24,EN61000-6-2/-6-4EMI CISPR32,FCC Part15B Class AEMS IEC61000-4-2ESD:Contact:4kV;Air:8kVIEC61000-4-3RS:80MHz to1GHz:10V/mIEC61000-4-4EFT:Power:2kV;Signal:1kVIEC61000-4-5Surge:Power:2kV;Signal:1kVIEC61000-4-6CS:10VIEC61000-4-8PFMFHazardous Locations ATEX,Class I Division24Safety UL508Shock IEC60068-2-27Freefall IEC60068-2-32Vibration IEC60068-2-6DeclarationGreen Product RoHS,CRoHS,WEEEMTBFTime ioLogik E1210Series:671,345hrsioLogik E1211Series:923,027hrsioLogik E1212Series:561,930hrsioLogik E1213Series:715,256hrsioLogik E1214Series:808,744hrsioLogik E1240Series:474,053hrsioLogik E1241Series:888,656hrsioLogik E1242Series:502,210hrsioLogik E1260Series:660,260hrsioLogik E1262Series:631,418hrsStandards Telcordia SR332WarrantyWarranty Period ioLogik E1214:2years5ioLogik E1210/E1211/E1212/E1213/E1240/E1241/E1242/E1260/E1262:5years Details See /warrantyPackage ContentsDevice1x ioLogik E1200Series remote I/OInstallation Kit1x terminal block,8-pin,3.81mm1x terminal block,12-pin,3.81mm1x terminal block,3-pin,5.00mmDocumentation1x quick installation guide1x warranty card3.Please contact Moxa if you require products guaranteed to function properly at higher altitudes.4.ATEX and Class I Division2currently do not apply to the ioLogik E1213/E1213-T models.5.Because of the limited lifetime of power relays,products that use this component are covered by a2-year warranty.DimensionsOrdering InformationModel Name Input/Output Interface Digital Output Type Operating Temp. ioLogik E121016x DI–-10to60°C ioLogik E1210-T16x DI–-40to75°C ioLogik E121116x DO Sink-10to60°C ioLogik E1211-T16x DO Sink-40to75°C ioLogik E12128x DI,8x DIO Sink-10to60°C ioLogik E1212-T8x DI,8x DIO Sink-40to75°C ioLogik E12138x DI,4x DO,4x DIO Source-10to60°C ioLogik E1213-T8x DI,4x DO,4x DIO Source-40to75°C ioLogik E12146x DI,6x Relay–-10to60°C ioLogik E1214-T6x DI,6x Relay–-40to75°C ioLogik E12408x AI–-10to60°C ioLogik E1240-T8x AI–-40to75°C ioLogik E12414x AO–-10to60°C ioLogik E1241-T4x AO–-40to75°C ioLogik E12424DI,4x DIO,4x AI Sink-10to60°C ioLogik E1242-T4DI,4x DIO,4x AI Sink-40to75°C ioLogik E12606x RTD–-10to60°C ioLogik E1260-T6x RTD–-40to75°C ioLogik E12628x TC–-10to60°C ioLogik E1262-T8x TC–-40to75°CAccessories(sold separately)SoftwareMX-AOPC UA Server OPC UA Server software for converting fieldbus to the OPC UA standard©Moxa Inc.All rights reserved.Updated Aug01,2019.This document and any portion thereof may not be reproduced or used in any manner whatsoever without the express written permission of Moxa Inc.Product specifications subject to change without notice.Visit our website for the most up-to-date product information.。
Source_初始化代码流程图_ADK_2.5.1
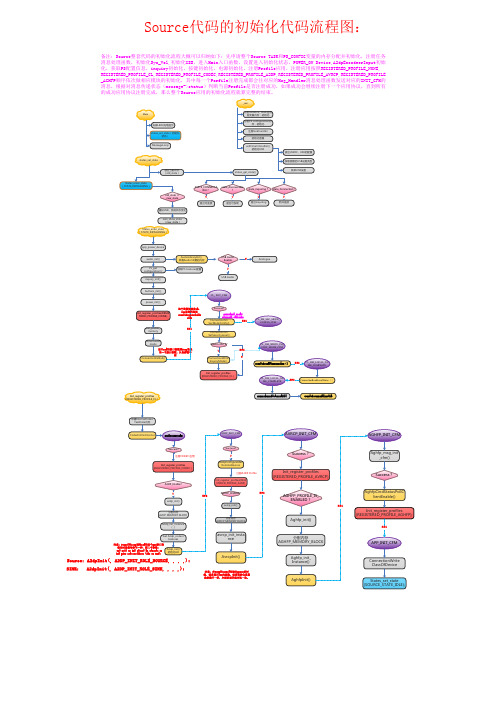
注意:Source :SINK :备注:Source 整套代码的初始化流程大概可以归纳如下:先申请整个Source TASK 和PS_CONFIG 变量的内存分配并初始化,注册任务消息处理函数,初始化Sys_Vol,初始化USB ,进入Main 入口函数,设置进入初始化状态,POWER_ON Device,A2dpEncodeerInput 初始化,获取PS 配置信息,inquiry 初始化,按键初始化,电源初始化,注册Profile 应用,注册应用按照REGISTERED_PROFILE_NONE, REGISTERED_PROFILE_CL,REGISTERED_PROFILE_CODEC,REGISTERED_PROFILE_A2DP,REGISTERED_PROFILE_AVRCP,REGISTERED_PROFILE _AGHFP 顺序依次做相应模块的初始化,其中每一个Porfile 注册完成都会往对应的Msg_Handler 消息处理函数发送对应的INIT_CFM 的消息,根据对消息传递状态(message->status )判断当前Profile 是否注册成功,如果成功会继续注册下一个应用协议,直到所有的成功应用协议注册完成,那么整个Source 应用的初始化流程就算完整的结束。
Source 代码的初始化代码流程图:。
地下水溶质运移软件介绍

2、MT3DMS
一、MT3DMS的开发历史
1990年代以前,虽然已经有很多有关地下水中污染物运移的研究,但是,还很少 见到一个完全公开的用于地下水中污染物运移的模拟软件。而地下水中污染物的运移 过程要比地下水流本身的运动要复杂得多,再加上数值模拟污染物运移过程中存在的 数值弥散和人工振荡,因此,开发一套能够有效应用于实际区域地下水中污染物运移 的模块化软件成为一种必需。正是为了适应这一要求,C. Zheng(郑春苗)在S. S. Papadopulos & Associates公司工作期间,由美国环境保护署(U.S. Environmental Protection Agency,USEPA)资助开发并于1990年发布了一个用于地下水中污染物运 移的一个实际应用模拟软件——MT3D。MT3D软件一经发布,其源代码即由USEPA完 全公开。
12
三、MT3DMS的特点
1、程序结构的模块化 2、程序代码的公开化 3、离散方法的简单化 4、求解方法的多样化
13
四、MT3DMS软件的应用现状
运用MT3DMS软件不但能模拟地下水中污染物的对流、弥散,而且能够同时模拟 多种污染物组分在地下水中的运移过程以及它们各自的变化反应过程(不包括各种组 分之间的化学反应),包括平衡控制的等温吸附过程、非平衡吸附过程、放射性衰变 或简单生物降解过程。
解的精度。
在程序中包含了多种对流-弥散方程的求解方法使得MT3D程序能够使用于 不同的地下水流场条件,这是MT3D的一个最主要的特色,同时也是它被广泛 认可的一个很重要的原因。
6
图1中是对一个均匀流场中连续点 源问题的模拟结果(Zheng,1990), 其中地下水渗透流速为0.33m/d,纵 向弥散度为10m,横向弥散度为3m, 孔隙度为0.3,连续点源的注人流量为 1m/d,注入浓度为1000×10-6。对流 弥散方程的求解采用HMOC方法。图1 是模拟时间为365d时地下水中污染物 浓度的等值线与解析解的对比。可以 看出,MT3D的模拟结果与解析解十 分吻合。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
VERIFICATION OF THE STENNING PROTOCOLBenedetto L. DiVitoTechnical Report 26 August 1982Institute for Computing ScienceThe University of Texas at AustinAustin, Texas 78712This report contains the transcript of a mechanical verification of the Stenning protocol [3]. A description of this protocol, as well as complete documentation on the methods used, can be found in a separate report [2]. Reference to this report is necessary, since the following material is not self-contained. The transcripts themselves were produced by the Boyer-Moore theorem prover [1].VC Proof Log 27-Jun-82 09:54:20 ++++++++++++++++++++++++++++++++++++++++Proof of VC ’TRANSPORT#1’(IMPLIES (AND (SENDER.EXT SOURCE ACK.IN PKT.OUT)(RECEIVER.EXT PKT.IN SINK ACK.OUT)(FOLLOWS PKT.IN PKT.OUT)(FOLLOWS ACK.IN ACK.OUT))(INITIAL SINK SOURCE))This formula can be simplified, using the abbreviations SENDER.EXT, AND, and IMPLIES, to:(IMPLIES(AND (CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(EQUAL SOURCE(FAPPLY (QUOTE MSSG)(RANGE (LATEST (QUOTE SEQNO) PKT.OUT)))) (RECEIVER.EXT PKT.IN SINK ACK.OUT)(FOLLOWS PKT.IN PKT.OUT)(FOLLOWS ACK.IN ACK.OUT))(INITIAL SINK SOURCE)),which we simplify, applying CONSISTENT.FOLLOWS, INITIAL.FAPPLY, INITIAL.CONSEC.FOLLOWS, NUMBERP.SEQNO, TEST.CONSISTENT, TEST, INITIAL.RANGE, and INITIAL.TRANS, and opening up RECEIVER.EXT and INITIAL, to:T.Q.E.D.13069 conses9.963 seconds0.0 seconds, garbage collection time----------------------------------------VC Proof Log 27-Jun-82 09:55:11 ++++++++++++++++++++++++++++++++++++++++Proof of VC ’SENDER#1’(SENDER.INT (NULL)(NULL)(NULL)(QUOTE IDLE)0 0(NULL)0)This formula can be simplified, using the abbreviation SENDER.INT,to the following six new conjectures:Case 6. (PMAPP (QUOTE (1QUOTE NULL))),which simplifies, opening up PMAPP, to:T.Case 5. (NUMBERP 0).This simplifies, clearly, to:T.Case 4. (FOLLOWS (RANGE (QUOTE (1QUOTE NULL)))(QUOTE (1QUOTE NULL))),which simplifies, opening up the definitions of RANGE and FOLLOWS, to:T.Case 3. (CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)(QUOTE (1QUOTE NULL))),which we simplify, opening up SEQP and CONSISTENT, to:T.Case 2. (EQUAL (QUOTE (1QUOTE NULL))(FAPPLY (QUOTE MSSG)(RANGE (LATEST (QUOTE SEQNO)(QUOTE (1QUOTE NULL)))))).This simplifies, opening up the definitions of SEQP, LATEST,RANGE, FAPPLY, and EQUAL, to:T.Case 1. (IF(EQUAL 0 0)(IF (EQUAL (QUOTE (1QUOTE NULL))(QUOTE (1QUOTE NULL)))(EQUAL (QUOTE (1QUOTE NULL))(QUOTE (1QUOTE NULL)))F)(IF (SEQP (QUOTE (1QUOTE NULL)))(IF (EQUAL (DOM (LST (LATEST (QUOTE SEQNO)(QUOTE (1QUOTE NULL)))))(SUB1 0))(IF (EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO)(QUOTE (1QUOTE NULL))))(SUB1 0))(IF (SEQP (QUOTE (1QUOTE NULL)))(EQUAL (DOM (LST (QUOTE (1QUOTE NULL))))(SUB1 0))T)F)F)F)).This simplifies, opening up the function EQUAL, to:T.Q.E.D.1052 conses2.57 seconds0.0 seconds, garbage collection time----------------------------------------++++++++++++++++++++++++++++++++++++++++Proof of VC ’SENDER#2’(IMPLIES (SENDER.INT SOURCE ACK.IN PKT.OUT STATE UNACK NEXTQUEUE TOT)(SENDER.EXT SOURCE ACK.IN PKT.OUT))This conjecture can be simplified, using the abbreviationsSENDER.INT and IMPLIES, to:$ (IMPLIES(AND(PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(EQUAL SOURCE(FAPPLY (QUOTE MSSG)(RANGE (LATEST (QUOTE SEQNO) PKT.OUT)))) (IF(EQUAL NEXT 0)(IF (EQUAL PKT.OUT (QUOTE (1QUOTE NULL)))(EQUAL QUEUE (QUOTE (1QUOTE NULL)))F)(IF (SEQP PKT.OUT)(IF (EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))(SUB1 NEXT))(IF (EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))(SUB1 NEXT))(IF (SEQP QUEUE)(EQUAL (DOM (LST QUEUE)) (SUB1 NEXT))T)F)F)F)))(SENDER.EXT SOURCE ACK.IN PKT.OUT)),which simplifies, opening up SENDER.EXT, LATEST, RANGE, SEQP, FAPPLY, EQUAL, and CONSISTENT, to:T.Q.E.D.15990 conses13.576 seconds3.261 seconds, garbage collection time----------------------------------------++++++++++++++++++++++++++++++++++++++++Proof of VC ’SENDER#3’(IMPLIES (AND (SENDER.INT SOURCE ACK.IN PKT.OUT STATE UNACKNEXT QUEUE TOT)(NUMBERP ACK)(LESSP UNACK ACK))(SENDER.INT SOURCE(APR ACK.IN ACK)PKT.OUT STATE UNACK NEXT(UPPER QUEUE ACK)TOT))This conjecture can be simplified, using the abbreviationsSENDER.INT, AND, and IMPLIES, to:(IMPLIES(AND(PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(EQUAL SOURCE(FAPPLY (QUOTE MSSG)(RANGE (LATEST (QUOTE SEQNO) PKT.OUT)))) (IF(EQUAL NEXT 0)(IF (EQUAL PKT.OUT (QUOTE (1QUOTE NULL)))(EQUAL QUEUE (QUOTE (1QUOTE NULL)))F)(IF (SEQP PKT.OUT)(IF (EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))(SUB1 NEXT))(IF (EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))(SUB1 NEXT))(IF (SEQP QUEUE)(EQUAL (DOM (LST QUEUE)) (SUB1 NEXT))T)F)F)F))(NUMBERP ACK)(LESSP UNACK ACK))(SENDER.INT SOURCE(APR ACK.IN ACK)PKT.OUT STATE UNACK NEXT(UPPER QUEUE ACK)TOT)),which simplifies, rewriting with the lemmas LST.UPPER,FOLLOWS.RANGE.UPPER, and PMAPP.UPPER, and expanding the functions UPPER, FOLLOWS, SEQP, RANGE, PMAPP, SENDER.INT, LATEST, FAPPLY, EQUAL, and CONSISTENT, to:T.Q.E.D.24249 conses20.704 seconds0.0 seconds, garbage collection time----------------------------------------++++++++++++++++++++++++++++++++++++++++Proof of VC ’SENDER#4’(IMPLIES (AND (SENDER.INT SOURCE ACK.IN PKT.OUT STATE UNACKNEXT QUEUE TOT)(NUMBERP ACK)(EQUAL ACK NEXT))(SENDER.INT SOURCE(APR ACK.IN ACK)PKT.OUT(QUOTE IDLE)ACK NEXT(NULL)TOT))This conjecture can be simplified, using the abbreviationsSENDER.INT, AND, and IMPLIES, to:$(IMPLIES(AND(PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(EQUAL SOURCE(FAPPLY (QUOTE MSSG)(RANGE (LATEST (QUOTE SEQNO) PKT.OUT)))) (IF(EQUAL NEXT 0)(IF (EQUAL PKT.OUT (QUOTE (1QUOTE NULL)))(EQUAL QUEUE (QUOTE (1QUOTE NULL)))F)(IF (SEQP PKT.OUT)(IF (EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))(SUB1 NEXT))(IF (EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))(SUB1 NEXT))(IF (SEQP QUEUE)(EQUAL (DOM (LST QUEUE)) (SUB1 NEXT))T)F)F)F))(NUMBERP ACK)(EQUAL ACK NEXT))(SENDER.INT SOURCE(APR ACK.IN ACK)PKT.OUT(QUOTE IDLE)ACK NEXT(QUOTE (1QUOTE NULL))TOT)),which simplifies, opening up FOLLOWS, SEQP, RANGE, PMAPP,SENDER.INT, LATEST, FAPPLY, EQUAL, and CONSISTENT, to:T.Q.E.D.21684 conses18.532 seconds3.342 seconds, garbage collection time----------------------------------------++++++++++++++++++++++++++++++++++++++++Proof of VC ’SENDER#5’(IMPLIES (SENDER.INT SOURCE ACK.IN PKT.OUT STATE UNACK NEXTQUEUE TOT)(SENDER.INT SOURCE ACK.IN(JOIN PKT.OUT (RANGE QUEUE))STATE UNACK NEXT QUEUE TOT))This conjecture can be simplified, using the abbreviationsSENDER.INT and IMPLIES, to:$(IMPLIES(AND(PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(EQUAL SOURCE(FAPPLY (QUOTE MSSG)(RANGE (LATEST (QUOTE SEQNO) PKT.OUT)))) (IF(EQUAL NEXT 0)(IF (EQUAL PKT.OUT (QUOTE (1QUOTE NULL)))(EQUAL QUEUE (QUOTE (1QUOTE NULL)))F)(IF (SEQP PKT.OUT)(IF (EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))(SUB1 NEXT))(IF (EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))(SUB1 NEXT))(IF (SEQP QUEUE)(EQUAL (DOM (LST QUEUE)) (SUB1 NEXT))T)F)F)F)))(SENDER.INT SOURCE ACK.IN(JOIN PKT.OUT (RANGE QUEUE))STATE UNACK NEXT QUEUE TOT)),which simplifies, rewriting with the lemmas HIGHEST.JOIN.FOLLOWS, PISEQP.FAPPLY, FOLLOWS.FAPPLY, FAPPLY.JOIN, LATEST.JOIN.FOLLOWS, NUMBERP.SEQNO, CONSISTENT.JOIN.FOLLOWS, FOLLOWS.JOIN.2, andPMAPP.NLST, and expanding the functions RANGE, SEQP, JOIN, FOLLOWS, PMAPP, SENDER.INT, LATEST, FAPPLY, EQUAL, and CONSISTENT, to sixnew conjectures:Case 6. (IMPLIES(AND (PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(NOT (EQUAL NEXT 0))(SEQP PKT.OUT)(EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))(SUB1 NEXT))(EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))(SUB1 NEXT))(NOT (SEQP QUEUE)))(EQUAL QUEUE (QUOTE (1QUOTE NULL)))),which again simplifies, opening up the definition of PMAPP, to: T.Case 5. (IMPLIES(AND (PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(NOT (EQUAL NEXT 0))(SEQP PKT.OUT)(EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))(SUB1 NEXT))(EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))(SUB1 NEXT))(EQUAL (DOM (LST QUEUE)) (SUB1 NEXT))(NOT (SEQP QUEUE)))(EQUAL QUEUE (QUOTE (1QUOTE NULL)))),which we again simplify, opening up PMAPP, to:T.Case 4. (IMPLIES(AND (PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(NOT (EQUAL NEXT 0))(SEQP PKT.OUT)(EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))(SUB1 NEXT))(EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))(SUB1 NEXT))(EQUAL (DOM (LST QUEUE)) (SUB1 NEXT))(SEQP QUEUE)(SEQP (NLST QUEUE)))(MPAIRP (LST (NLST QUEUE)))).However this simplifies again, expanding PMAPP, to:T.Case 3. (IMPLIES(AND (PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(NOT (EQUAL NEXT 0))(SEQP PKT.OUT)(EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))(SUB1 NEXT))(EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))(SUB1 NEXT))(EQUAL (DOM (LST QUEUE)) (SUB1 NEXT))(SEQP QUEUE)(SEQP (NLST QUEUE)))(LESSP (DOM (LST (NLST QUEUE)))(DOM (LST QUEUE)))).But this simplifies again, unfolding the definition of PMAPP, to: T.Case 2. (IMPLIES(AND (PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(NOT (EQUAL NEXT 0))(SEQP PKT.OUT)(EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))(SUB1 NEXT))(EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))(SUB1 NEXT))(EQUAL (DOM (LST QUEUE)) (SUB1 NEXT))(SEQP QUEUE)(NOT (SEQP (NLST QUEUE))))(EQUAL (NLST QUEUE)(QUOTE (1QUOTE NULL)))).This simplifies again, unfolding the function PMAPP, to:T.Case 1. (IMPLIES(AND (PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(NOT (EQUAL NEXT 0))(SEQP PKT.OUT)(EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))(SUB1 NEXT))(EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))(SUB1 NEXT))(EQUAL (DOM (LST QUEUE)) (SUB1 NEXT))(SEQP QUEUE))(MPAIRP (LST QUEUE))).However this simplifies again, unfolding the function PMAPP, to: T.Q.E.D.26435 conses24.43 seconds3.375 seconds, garbage collection time----------------------------------------++++++++++++++++++++++++++++++++++++++++Proof of VC ’SENDER#6’(IMPLIES (SENDER.INT SOURCE ACK.IN PKT.OUT STATE UNACK NEXTQUEUE TOT)(SENDER.INT (APR SOURCE MESS)ACK.IN(APR PKT.OUT (PACKET MESS NEXT))(QUOTE BUSY)UNACK(ADD1 NEXT)(WITHE QUEUE NEXT (PACKET MESS NEXT))(PLUS TOT DELTA)))This conjecture can be simplified, using the abbreviations SENDER.INT and IMPLIES, to:$(IMPLIES(AND(PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(EQUAL SOURCE(FAPPLY (QUOTE MSSG)(RANGE (LATEST (QUOTE SEQNO) PKT.OUT)))) (IF(EQUAL NEXT 0)(IF (EQUAL PKT.OUT (QUOTE (1QUOTE NULL)))(EQUAL QUEUE (QUOTE (1QUOTE NULL)))F)(IF (SEQP PKT.OUT)(IF (EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))(SUB1 NEXT))(IF (EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))(SUB1 NEXT))(IF (SEQP QUEUE)(EQUAL (DOM (LST QUEUE)) (SUB1 NEXT))T)F)F)F)))(SENDER.INT (APR SOURCE MESS)ACK.IN(APR PKT.OUT (PACKET MESS NEXT))(QUOTE BUSY)UNACK(ADD1 NEXT)(WITHE QUEUE NEXT (PACKET MESS NEXT))(PLUS TOT DELTA))).This simplifies, applying the lemmas LST.NSEQP, WITHE.LESSP.DOM.LST, DOM.MPAIR, SUB1.ADD1, LST.WITHE, TEST, APPLY2.EQUAL, SEQNO.PACKET, APPLY1.SEQNO, FOLLOWS.APR.IN, FOLLOWS.APR,FOLLOWS.SAME, FOLLOWS.TRANS, RNG.MPAIR, LST.APR, NLST.APR,PMAPP.WITHE, WITHE.EQUAL.DOM.LST, NLST.NSEQP, andCONSISTENT.APR.NOT.IN, and opening up LESSP, EQUAL, DOM, HIGHEST, MAX, FAPPLY, LATEST, CONSISTENT, CONSISTENT2, IN, RANGE, PMAPP, SENDER.INT, SEQP, and FOLLOWS, to the following 23 new goals:Case 23.(IMPLIES(AND (PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(NOT (EQUAL NEXT 0))(SEQP PKT.OUT)(EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))(SUB1 NEXT))(EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))(SUB1 NEXT))(NOT (SEQP QUEUE)))(EQUAL QUEUE (QUOTE (1QUOTE NULL)))),which we again simplify, expanding the definition of PMAPP, to: T.Case 22.(IMPLIES(AND (PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(NOT (EQUAL NEXT 0))(SEQP PKT.OUT)(EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))(SUB1 NEXT))(EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))(SUB1 NEXT))(NOT (SEQP QUEUE)))(CONSISTENT2 (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT(PACKET MESS NEXT))),which again simplifies, using linear arithmetic, applyingSEQNO.PACKET, APPLY1.SEQNO, NUMBERP.SEQNO, andCONSISTENT2.LESSP.HIGHEST, and opening up the functions PMAPP, RANGE, SEQP, and FOLLOWS, to:T.$Case 21.(IMPLIES(AND (PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(NOT (EQUAL NEXT 0))(SEQP PKT.OUT)(EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))(SUB1 NEXT))(EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))(SUB1 NEXT))(NOT (SEQP QUEUE)))(EQUAL (APR (FAPPLY (QUOTE MSSG)(RANGE (LATEST (QUOTE SEQNO) PKT.OUT)))MESS)(FAPPLY (QUOTE MSSG)(RANGE (WITHE (LATEST (QUOTE SEQNO) PKT.OUT)NEXT(PACKET MESS NEXT)))))).This again simplifies, using linear arithmetic, applying thelemmas TEST, WITHE.LESSP.DOM.LST, RNG.MPAIR, LST.APR,NLST.APR, MSSG.PACKET, and APPLY1.MSSG, and unfolding PMAPP,RANGE, SEQP, FOLLOWS, and FAPPLY, to:T.Case 20.(IMPLIES(AND(PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(NOT (EQUAL NEXT 0))(SEQP PKT.OUT)(EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))(SUB1 NEXT))(EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))(SUB1 NEXT))(NOT (SEQP QUEUE))(NOT (LESSP NEXT(DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))))) (EQUAL (DOM (MPAIR NEXT (PACKET MESS NEXT)))NEXT)),which we again simplify, rewriting with DOM.MPAIR, and expanding the definitions of PMAPP, RANGE, SEQP, and FOLLOWS, to:T.Case 19.(IMPLIES(AND (PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(NOT (EQUAL NEXT 0))(SEQP PKT.OUT)(EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))(SUB1 NEXT))(EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))(SUB1 NEXT))(NOT (SEQP QUEUE))(LESSP NEXT(DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT))))) (EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))NEXT)).But this again simplifies, using linear arithmetic, to:T.Case 18.(IMPLIES(AND (PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(NOT (EQUAL NEXT 0))(SEQP PKT.OUT)(EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))(SUB1 NEXT))(EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))(SUB1 NEXT))(NOT (SEQP QUEUE))(LESSP (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))NEXT))(EQUAL NEXT NEXT)),which again simplifies, using linear arithmetic, to:T.Case 17.(IMPLIES(AND (PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(NOT (EQUAL NEXT 0))(SEQP PKT.OUT)(EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))(SUB1 NEXT))(EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))(SUB1 NEXT))(NOT (SEQP QUEUE))(NOT (SEQP (FAPPLY (QUOTE SEQNO) PKT.OUT))))(EQUAL NEXT NEXT)).This again simplifies, using linear arithmetic, to:T.Case 16.(IMPLIES(AND (PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(NOT (EQUAL NEXT 0))(SEQP PKT.OUT)(EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))(SUB1 NEXT))(EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))(SUB1 NEXT))(NOT (SEQP QUEUE))(SEQP (FAPPLY (QUOTE SEQNO) PKT.OUT))(NOT (LESSP (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))NEXT)))(EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))NEXT)),which we again simplify, using linear arithmetic, to:T.Case 15.(IMPLIES(AND (PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(NOT (EQUAL NEXT 0))(SEQP PKT.OUT)(EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))(SUB1 NEXT))(EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))(SUB1 NEXT))(EQUAL (DOM (LST QUEUE)) (SUB1 NEXT)))(FOLLOWS (RANGE (WITHE QUEUE NEXT (PACKET MESS NEXT)))(APR PKT.OUT (PACKET MESS NEXT)))), which again simplifies, using linear arithmetic, applyingWITHE.LESSP.DOM.LST, RNG.MPAIR, LST.APR, NLST.APR, FOLLOWS.TRANS, FOLLOWS.SAME, FOLLOWS.APR, and FOLLOWS.APR.IN, and expandingRANGE and IN, to:T.Case 14.(IMPLIES(AND (PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(NOT (EQUAL NEXT 0))(SEQP PKT.OUT)(EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))(SUB1 NEXT))(EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))(SUB1 NEXT))(EQUAL (DOM (LST QUEUE)) (SUB1 NEXT)))(CONSISTENT2 (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT(PACKET MESS NEXT))).This again simplifies, using linear arithmetic and applyingSEQNO.PACKET, APPLY1.SEQNO, NUMBERP.SEQNO, andCONSISTENT2.LESSP.HIGHEST, to:T.$Case 13.(IMPLIES(AND (PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(NOT (EQUAL NEXT 0))(SEQP PKT.OUT)(EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))(SUB1 NEXT))(EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))(SUB1 NEXT))(EQUAL (DOM (LST QUEUE)) (SUB1 NEXT)))(EQUAL (APR (FAPPLY (QUOTE MSSG)(RANGE (LATEST (QUOTE SEQNO) PKT.OUT)))MESS)(FAPPLY (QUOTE MSSG)(RANGE (WITHE (LATEST (QUOTE SEQNO) PKT.OUT)NEXT(PACKET MESS NEXT)))))).However this simplifies again, using linear arithmetic, applying TEST, WITHE.LESSP.DOM.LST, RNG.MPAIR, LST.APR, NLST.APR, MSSG.PACKET, and APPLY1.MSSG, and expanding the functions RANGE and FAPPLY, to:T.Case 12.(IMPLIES(AND(PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(NOT (EQUAL NEXT 0))(SEQP PKT.OUT)(EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))(SUB1 NEXT))(EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))(SUB1 NEXT))(EQUAL (DOM (LST QUEUE)) (SUB1 NEXT))(NOT (LESSP NEXT(DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))))) (EQUAL (DOM (MPAIR NEXT (PACKET MESS NEXT)))NEXT)).This simplifies again, rewriting with DOM.MPAIR, to:T.Case 11.(IMPLIES(AND (PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(NOT (EQUAL NEXT 0))(SEQP PKT.OUT)(EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))(SUB1 NEXT))(EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))(SUB1 NEXT))(EQUAL (DOM (LST QUEUE)) (SUB1 NEXT))(NOT (LESSP NEXT (DOM (LST QUEUE)))))(EQUAL (DOM (MPAIR NEXT (PACKET MESS NEXT)))NEXT)).This simplifies again, applying DOM.MPAIR, to:T.Case 10.(IMPLIES(AND (PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(NOT (EQUAL NEXT 0))(SEQP PKT.OUT)(EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))(SUB1 NEXT))(EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))(SUB1 NEXT))(EQUAL (DOM (LST QUEUE)) (SUB1 NEXT))(LESSP NEXT(DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT))))) (EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))NEXT)),which again simplifies, using linear arithmetic, to:T.Case 9. (IMPLIES(AND (PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(NOT (EQUAL NEXT 0))(SEQP PKT.OUT)(EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))(SUB1 NEXT))(EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))(SUB1 NEXT))(EQUAL (DOM (LST QUEUE)) (SUB1 NEXT))(LESSP (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))NEXT))(EQUAL NEXT NEXT)),which again simplifies, using linear arithmetic, to:T.Case 8. (IMPLIES(AND (PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(NOT (EQUAL NEXT 0))(SEQP PKT.OUT)(EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))(SUB1 NEXT))(EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))(SUB1 NEXT))(EQUAL (DOM (LST QUEUE)) (SUB1 NEXT))(NOT (SEQP (FAPPLY (QUOTE SEQNO) PKT.OUT))))(EQUAL NEXT NEXT)).This again simplifies, using linear arithmetic, to:T.Case 7. (IMPLIES(AND (PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(NOT (EQUAL NEXT 0))(SEQP PKT.OUT)(EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))(SUB1 NEXT))(EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))(SUB1 NEXT))(EQUAL (DOM (LST QUEUE)) (SUB1 NEXT))(SEQP (FAPPLY (QUOTE SEQNO) PKT.OUT))(NOT (LESSP (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))NEXT)))(EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))NEXT)),which again simplifies, using linear arithmetic, to:T.Case 6. (IMPLIES(AND (PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(NOT (EQUAL NEXT 0))(SEQP PKT.OUT)(EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))(SUB1 NEXT))(EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))(SUB1 NEXT))(EQUAL (DOM (LST QUEUE)) (SUB1 NEXT))(LESSP NEXT (DOM (LST QUEUE))))(EQUAL (DOM (LST QUEUE)) NEXT)),which again simplifies, using linear arithmetic, to:T.Case 5. (IMPLIES(AND (PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(EQUAL NEXT 0)(EQUAL PKT.OUT (QUOTE (1QUOTE NULL)))(EQUAL QUEUE (QUOTE (1QUOTE NULL))))(EQUAL (APR (QUOTE (1QUOTE NULL)) MESS)(FAPPLY (QUOTE MSSG)(RANGE (WITHE (LATEST (QUOTE SEQNO) PKT.OUT)NEXT(PACKET MESS NEXT)))))).But this again simplifies, rewriting with WITHE.ZERO.2, RNG.MPAIR, LST.APR, NLST.APR, MSSG.PACKET, APPLY1.MSSG, and APR.EQUAL, and opening up the definitions of PMAPP, NUMBERP, RANGE, FOLLOWS,SEQP, CONSISTENT, LATEST, DOMAIN, IN, JOIN, and FAPPLY, to: (EQUAL (QUOTE (1QUOTE NULL))(FAPPLY (QUOTE MSSG)(QUOTE (1QUOTE NULL)))).This again simplifies, opening up the definitions of SEQP, FAPPLY, and EQUAL, to:T.Case 4. (IMPLIES(AND (PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(EQUAL NEXT 0)(EQUAL PKT.OUT (QUOTE (1QUOTE NULL)))(EQUAL QUEUE (QUOTE (1QUOTE NULL)))(NOT (EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))0)))(EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))NEXT)).But this again simplifies, expanding the definitions of PMAPP, NUMBERP, RANGE, FOLLOWS, SEQP, CONSISTENT, LATEST, LST, DOM, and EQUAL, to:T.Case 3. (IMPLIES(AND (PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(EQUAL NEXT 0)(EQUAL PKT.OUT (QUOTE (1QUOTE NULL)))(EQUAL QUEUE (QUOTE (1QUOTE NULL)))(EQUAL (DOM (LST (LATEST (QUOTE SEQNO) PKT.OUT)))0))(EQUAL (DOM (MPAIR NEXT (PACKET MESS NEXT)))NEXT)).But this simplifies again, applying DOM.MPAIR, and expanding the functions PMAPP, NUMBERP, RANGE, FOLLOWS, SEQP, CONSISTENT,LATEST, LST, DOM, and EQUAL, to:T.Case 2. (IMPLIES (AND (PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(EQUAL NEXT 0)(EQUAL PKT.OUT (QUOTE (1QUOTE NULL)))(EQUAL QUEUE (QUOTE (1QUOTE NULL)))(NOT (SEQP (FAPPLY (QUOTE SEQNO) PKT.OUT))))(EQUAL NEXT NEXT)),which again simplifies, using linear arithmetic, to:T.Case 1. (IMPLIES (AND (PMAPP QUEUE)(NUMBERP NEXT)(FOLLOWS (RANGE QUEUE) PKT.OUT)(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)PKT.OUT)(EQUAL NEXT 0)(EQUAL PKT.OUT (QUOTE (1QUOTE NULL)))(EQUAL QUEUE (QUOTE (1QUOTE NULL)))(SEQP (FAPPLY (QUOTE SEQNO) PKT.OUT)))(EQUAL (HIGHEST (FAPPLY (QUOTE SEQNO) PKT.OUT))NEXT)),which again simplifies, expanding PMAPP, NUMBERP, RANGE, FOLLOWS, SEQP, CONSISTENT, and FAPPLY, to:T.Q.E.D.101452 conses94.17 seconds10.246 seconds, garbage collection time----------------------------------------VC Proof Log 27-Jun-82 10:06:29 ++++++++++++++++++++++++++++++++++++++++Proof of VC ’RECEIVER#1’(RECEIVER.INT (NULL)(NULL)(NULL)(NULL))This conjecture can be simplified, using the abbreviation RECEIVER.INT, to three new conjectures:Case 3. (PMAPP (QUOTE (1QUOTE NULL))),which simplifies, expanding the definition of PMAPP, to:T.Case 2. (NUMBERP 0),which we simplify, clearly, to:T.Case 1. (IMPLIES(CONSISTENT (QUOTE SEQNO)(QUOTE EQUAL)(QUOTE (1QUOTE NULL)))(IF(FOLLOWS (QUOTE (1QUOTE NULL))(UPPER (LATEST (QUOTE SEQNO)(QUOTE (1QUOTE NULL)))1))(IF(LESSP (REACH (LATEST (QUOTE SEQNO)(QUOTE (1QUOTE NULL))))0)F(IF(IN 0(DOMAIN (LATEST (QUOTE SEQNO)(QUOTE (1QUOTE NULL)))))(IF(LESSP 0 0)(EQUAL(QUOTE (1QUOTE NULL))(FAPPLY (QUOTE MSSG)(RANGE (LOWER (LATEST (QUOTE SEQNO)(QUOTE (1QUOTE NULL)))(SUB1 0)))))F)(IF (EQUAL 0 0)(EQUAL (QUOTE (1QUOTE NULL))(QUOTE (1QUOTE NULL)))F)))F)),which simplifies, expanding the functions SEQP, CONSISTENT,LATEST, UPPER, FOLLOWS, REACH, LESSP, DOMAIN, IN, and EQUAL, to: T.。
