2013年全国高考理科数学试题分类汇编7:立体几何 Word版含答案
2013-2017高考数学全国卷--立体几何汇编(完整资料).doc
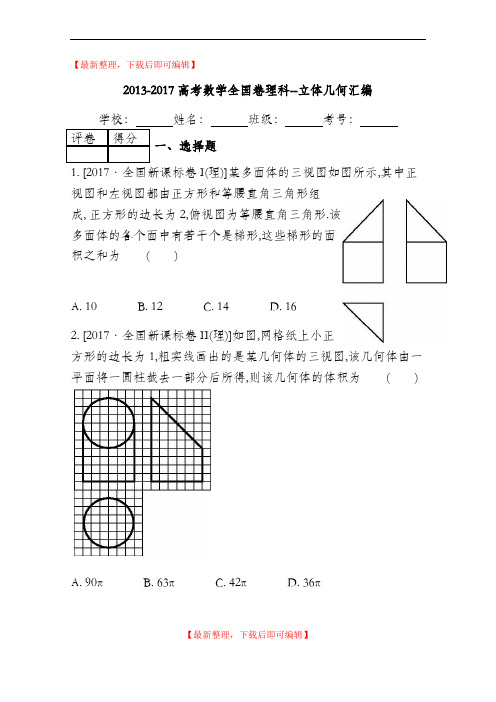
【最新整理,下载后即可编辑】2013-2017高考数学全国卷理科--立体几何汇编学校:姓名:班级:考号:评卷得分一、选择题I(理)]某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成, 正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为()A. 10B. 12C. 14D. 162. [2017·全国新课标卷II(理)]如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为()A. 90πB. 63πC. 42πD. 36π【最新整理,下载后即可编辑】【最新整理,下载后即可编辑】 3. [2017·全国新课标卷II(理)]已知直三棱柱ABC-A 1B 1C 1中,∠ABC=120°,AB=2,BC=CC 1=1,则异面直线AB 1与BC 1所成角的余弦值为 ( )A. √32B. √155C. √105D. √33 4. [2017·全国新课标卷III(理)]已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A. πB. 3π4C. π2D. .π4 5. [2016·高考全国新课标卷Ⅰ,6]如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是28π3,则它的表面积是 ( )A. 17πB. 18πC. 20πD. 28π6. [2016·高考全国新课标卷Ⅰ,11]平面α过正方体ABCD -A 1B 1C 1D 1的顶点A ,α∥平面CB 1D 1,α∩平面ABCD =m ,α∩平面ABB 1A 1=n ,则m ,n 所成角的正弦值为 ( )A. √32B. √22C. √33D. 13【最新整理,下载后即可编辑】7. [2016·高考全国新课标卷Ⅱ,6]如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为 ( )A. 20πB. 24πC. 28πD. 32π8. [2016·高考全国新课标卷Ⅲ,9]如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为( )A. 18+36√5B. 54+18√5C. 90D. 819. [2016·高考全国新课标卷Ⅲ,10]在封闭的直三棱柱ABC -A 1B 1C 1内有一个体积为V 的球.若AB ⊥BC ,AB =6,BC =8,AA 1=3,则V 的最大值是 ( )A. 4πB. 9π2C. 6πD. 32π310. [2015·高考全国新课标卷Ⅰ,6]《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米【最新整理,下载后即可编辑】 (如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )A. 14斛B. 22斛C. 36斛D. 66斛11. [2015·高考全国新课标卷Ⅰ,11]圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体三视图中的正视图和俯视图如图所示,若该几何体的表面积为16+20π,则r=( )正视图 俯视图A. 1B. 2C. 4D. 812. [2015·高考全国新课标卷Ⅱ,6]一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则截去部分体积与剩余部分体积的比值为( )A. 18B. 17C. 16D. 15【最新整理,下载后即可编辑】 13. [2015·高考全国新课标卷Ⅱ,9]已知A ,B 是球O 的球面上两点,∠AOB=90°,C 为该球面上的动点.若三棱锥O-ABC 体积的最大值为36,则球O 的表面积为( )A. 36πB. 64πC. 144πD. 256π14. [2014·高考全国新课标卷Ⅰ,12]如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )A. 6√2B. 6C. 4√2D. 4 15. [2014·全国新课标卷Ⅱ,6]如图,网格纸上正方形小格的边长为1(表示1 cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3 cm,高为6 cm 的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )A. 1727 B. 59 C. 1027 D. 13【最新整理,下载后即可编辑】 16. [2014·全国新课标卷Ⅱ,11]直三棱柱ABC A 1B 1C 1中,∠BCA =90°,M ,N 分别是A 1B 1,A 1C 1的中点,BC =CA =CC 1,则BM 与AN 所成角的余弦值为( ) A. 110 B. 25 C. √3010 D. √22 17. [2013·高考全国新课标卷Ⅰ,6]如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm ,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm ,如果不计容器的厚度,则球的体积为( )A. 500π3 cm 3B. 866π3 cm 3C. 1372π3 cm 3D.2048π3 cm 318. [2013·高考全国新课标卷Ⅰ,8]某几何体的三视图如图所示,则该几何体的体积为( )A. 16+8πB. 8+8πC. 16+16π D. 8+16π19. [2013·高考全国新课标卷Ⅱ,4]已知m ,n 为异面直线,m ⊥平面α,n ⊥平面β.直线l 满足l ⊥m ,l ⊥n ,l ⊄α,l ⊄β,则( )A. α∥β且l ∥αB. α⊥β且l ⊥βC. α与β相交,且交线垂直于lD. α与β相交,且交线平行l20. [2013·高考全国新课标卷Ⅱ,7]一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx平面为投影面,则得到的正视图可以为( )A. B. C. D.评卷得分二、填空题I(理)]如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O.D,E,F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D,E,F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为.22. [2017·全国新课标卷III(理)]a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:①当直线AB与a成60°角时,AB与b成30°角;【最新整理,下载后即可编辑】【最新整理,下载后即可编辑】 ②当直线AB 与a 成60°角时,AB 与b 成60°角;③直线AB 与a 所成角的最小值为45°;④直线AB 与a 所成角的最大值为60°.其中正确的是 .(填写所有正确结论的编号)23. [2016·高考全国新课标卷Ⅱ,14]α,β是两个平面,m ,n 是两条直线,有下列四个命题:①如果m ⊥n ,m ⊥α,n ∥β,那么α⊥β.②如果m ⊥α,n ∥α,那么m ⊥n .③如果α∥β,m ⊂α,那么m ∥β.④如果m ∥n ,α∥β,那么m 与α所成的角和n 与β所成的角相等. 其中正确的命题有 .(填写所有正确命题的编号)三、解答题 I(理)] (本小题满分12分)如图,在四棱锥P-ABCD 中,AB ∥CD ,且∠BAP=∠CDP=90°.(1)证明:平面PAB⊥平面PAD ; (2)若PA=PD=AB=DC ,∠APD=90°,求二面角A-PB-C 的余弦值.25. [2017·全国新课标卷II(理)] (本小题满分12分)如图,四棱锥P-ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD,AB=BC=12AD,∠BAD=∠ABC=90°,E是PD的中点.(1)证明:直线CE∥平面PAB;(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M-AB-D的余弦值.26. [2017·全国新课标卷III(理)] (本小题满分12分)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.(1)证明:平面ACD⊥平面ABC;(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D-AE-C的余弦值.【最新整理,下载后即可编辑】【最新整理,下载后即可编辑】27. [2016·高考全国新课标卷Ⅰ,18] (本小题满分12分)如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,面ABEF 为正方形,AF =2FD ,∠AFD =90°,且二面角D -AF -E 与二面角C -BE -F 都是60°.(1)证明:平面ABEF ⊥平面EFDC ;(2)求二面角E -BC -A 的余弦值.28. [2016·高考全国新课标卷Ⅱ,19] (本小题满分12分)如图,菱形ABCD 的对角线AC 与BD 交于点O ,AB =5,AC =6,点E ,F 分别在AD ,CD 上,AE =CF =54,EF 交BD 于点H .将△DEF 沿EF 折到△D'EF 的位置,OD'=√10.(1)证明:D'H⊥平面ABCD;(2)求二面角B-D'A-C的正弦值.29. [2016·高考全国新课标卷Ⅲ,19] (本小题满分12分) 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.(1)证明MN∥平面PAB;(2)求直线AN与平面PMN所成角的正弦值.【最新整理,下载后即可编辑】【最新整理,下载后即可编辑】30. [2015·高考全国新课标卷Ⅰ,18](本小题满分12分)如图,四边形ABCD 为菱形,∠ABC=120°,E ,F 是平面ABCD 同一侧的两点,BE ⊥平面ABCD ,DF ⊥平面ABCD ,BE=2DF ,AE ⊥EC.(1)证明:平面AEC ⊥平面AFC ; (2)求直线AE 与直线CF 所成角的余弦值.31. [2015·高考全国新课标卷Ⅱ,19](本小题满分12分)如图,长方体ABCD-A 1B 1C 1D 1中,AB=16,BC=10,AA 1=8,点E ,F 分别在A 1B 1,D 1C 1上,A 1E=D 1F= 4.过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法和理由);(2)求直线AF 与平面α所成角的正弦值.【最新整理,下载后即可编辑】32. [2014·高考全国新课标卷Ⅰ,19] (本小题满分12分) 如图,三棱柱ABC A 1B 1C 1中,侧面BB 1C 1C 为菱形,AB ⊥B 1C .(1)证明:AC =AB 1;(2)若AC ⊥AB 1,∠CBB 1=60°,AB =BC ,求二面角A A 1B 1C 1的余弦值.33. [2014·全国新课标卷Ⅱ,18] (本小题满分12分) 如图,四棱锥P ABCD 中,底面ABCD 为矩形,PA ⊥平面ABCD ,E 为PD 的中点.(1)证明:PB ∥平面AEC ;(2)设二面角D AE C 为60°,AP =1,AD =√3,求三棱锥E ACD 的体积.【最新整理,下载后即可编辑】34. [2013·高考全国新课标卷Ⅰ,18](本小题满分12分) 如图,三棱柱ABC -A 1B 1C 1中,CA =CB ,AB =AA 1,∠BAA 1=60°. (1)证明:AB ⊥A 1C ;(2)若平面ABC ⊥平面AA 1B 1B ,AB =CB ,求直线A 1C 与平面BB 1C 1C 所成角的正弦值.35. [2013·高考全国新课标卷Ⅱ,18](本小题满分12分)如图,直三棱柱ABC -A 1B 1C 1中,D ,E 分别是AB ,BB 1的中点,AA 1=AC =CB =√22AB .(1)证明:BC 1∥平面A 1CD ;C-E的正弦值.(2)求二面角D-A1【最新整理,下载后即可编辑】。
2013年高考真题解析分类汇编(文科数学)7:立体几何 )

2013年高考解析分类汇编7:立体几何一、选择题1 .(2013年高考重庆卷(文8))某几何体的三视图如题(8)所示,则该几何体的表面积为()A.180B.200C.220D.240【答案】D【解析】本题考查三视图以及空间几何体的表面积公式。
由三视图可知该几何体是个四棱柱。
棱柱的底面为等腰梯形,高为10.等腰梯形的上底为2,下底为8,高为4,腰长为5。
所以梯形的面积为284202+⨯=,梯形的周长为282520++⨯=。
所以四棱柱的表面积为2022010240⨯+⨯=,选D.2 .(2013年高考课标Ⅱ卷(文9))一个四面体的顶点在空间直角坐标系O xyz-中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到正视图可以为()(A) (B) (C) (D)【答案】A【解析】在空间直角坐标系中,先画出四面体O ABC-的直观图,以zOx平面为投影面,则得到正视图(坐标系中红色部分),所以选A.3 .(2013年高考课标Ⅰ卷(文11))某几何函数的三视图如图所示,则该几何的体积为( )A .168π+B .88π+C .1616π+D .816π+ 【答案】A【解析】由三视图可知,该几何体的下部分是平放的半个圆柱,圆柱的底面半径为2,圆柱的高为4。
上部分是个长方体,长方体的棱长分别为2,2,4.所以半圆柱的体积为212482ππ⨯⨯⨯=,正方体的体积为22416⨯⨯=,所以该几何体的体积为168π+,选A.4 .(2013年高考大纲卷(文11))已知正四棱锥1111112,ABCD A B C D AA AB CD BDC -=中,则与平面所成角的正弦值等于( )A .23B.3C.3D .13【答案】A【解析】如图,因为BD ⊥平面ACC 1A 1,所以平面ACC 1A 1⊥平面BDC 1,在Rt △CC 1O 中,过C 作CH ⊥C 1O 于H ,连结DH ,则∠CDH 即为所求,令a AB =,显然2223a CH a ⨯===,所以223sin 3a CDH a ∠==,故选A.5 .(2013年高考四川卷(文2))一个几何体的三视图如图所示,则该几何体可以是 ( )A .棱柱B .棱台C .圆柱D .圆台【答案】D【解析】由三视图可知,该几何体为圆台. 6 .(2013年高考浙江卷(文5))已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )A .108cm 3B .100 cm 3C .92cm 3D .84cm 3【答案】B【解析】此图的直观图是一个底面边长为6和3,高为6的长方体截去一个角,对应三棱锥的的三条侧棱上分别为3,4,4.如图。
2013年高考理科数学试卷及答案---全国卷(新课标版)word版

2013年全国卷新课标数学(理)一、选择题:本大题共12小题,在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 已知集合}5,4,3,2,1{=A ,},,|),{(A y x A y A x y x B ∈-∈∈=,则B 中所含元素的个数为A. 3B. 6C. 8D. 102. 将2名教师,4名学生分成两个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由一名教师和2名学生组成,不同的安排方案共有 A. 12种 B. 10种 C. 9种 D. 8种3. 下面是关于复数iz +-=12的四个命题: :1P 2||=z:2P i z 22= :3P z 的共轭复数为i +1:4P z 的虚部为1-其中的真命题为A. 2P ,3PB. 1P ,2PC. 2P ,4PD. 3P ,4P4. 设21,F F 是椭圆:E 12222=+by a x )0(>>b a 的左右焦点,P 为直线23a x =上的一点,12PF F △是底角为︒30的等腰三角形,则E 的离心率为A.21B.32 C.43 D.54 5. 已知}{n a 为等比数列,274=+a a ,865-=a a ,则=+101a aA.7B. 5C.5-D. 7-6. 如果执行右边的程序框图,输入正整数N )2(≥N 和 实数N a a a ,,,21 ,输出A ,B ,则A. B A +为N a a a ,,,21 的和B.2BA +为N a a a ,,,21 的算术平均数 C. A 和B 分别是N a a a ,,,21 中最大的数和最小的数D. A 和B 分别是N a a a ,,,21 中最小的数和最大的数7. 如图,网格纸上小正方形的边长为1,粗线画出的 是某几何体的三视图,则此几何体的体积为 A. 6 B. 9 C. 12 D. 188. 等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线x y 162=的准线交于A ,B ,两点,34||=AB ,则的实轴长为A.2B. 22C. 4D. 89. 已知0>ω,函数)4sin()(πω+=x x f 在),2(ππ单调递减,则ω的取值范围是A. ]45,21[B. ]43,21[C. ]21,0(D. ]2,0(10. 已知函数xx x f -+=)1ln(1)(,则)(x f y =的图像大致为11. 已知三棱锥ABC S -的所有顶点都在球O 的球面上,ABC △是边长为1的正三角形,SC 为球O 的直径,且2=SC ,则此棱锥的体积为A.62 B.63 C.32 D.22 12. 设点P 在曲线xe y 21=上,点Q 在曲线)2ln(x y =上,则||PQ 的最小值为A. 2ln 1-B.)2ln 1(2- C. 2ln 1+D.)2ln 1(2+二、填空题.本大题共4小题,每小题5分.13.已知向量a ,b 夹角为︒45,且1=||a ,102=-||b a ,则=||b .14. 设y x ,满足约束条件⎪⎪⎩⎪⎪⎨⎧≥≥≤+-≥-0031y x y x y x 则y x Z 2-=的取值范围为 .15. 某一部件由三个电子元件按下图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作.设三个电子元件的使用寿命(单位:小时)服从正态分布)50,1000(2N ,且各元件能否正常工作互相独立,那么该部件的使用寿命超过1000小时的概率为 .16. 数列}{n a 满足12)1(1-=-++n a a n n n ,则}{n a项和为 . 三、解答题:解答题应写出文字说明,证明过程或演算步骤. 17. (本小题满分12分) 已知a ,b ,c 分别为ABC △三个内角A ,B ,C 的对边,0sin 3cos =--+c b C a C a . (Ⅰ) 求A ;(Ⅱ) 若2=a ,ABC △的面积为3,求b ,c .18. (本小题满分12分) 某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花做垃圾处理.(Ⅰ) 若花店某天购进16枝玫瑰花,求当天的利润y (单位:元)关于当天需求量n (单位:枝,N n ∈)的函数解析式;(Ⅱ) 花店记录了100以100天记录的各需求量的频率作为各需求量发生的概率. (ⅰ)若花店一天购进16枝玫瑰花,X 表示当天的利润(单位:元),求X 的分布列、数学期望及方差; (ⅱ)若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?请说明理由.19. (本小题满分12分)如图,直三棱柱111C B AABC -中,121AA BC AC ==,D 是棱1AA 的中点,BD DC ⊥1 (Ⅰ) 证明:BC DC ⊥1(Ⅱ) 求二面角11C BD A --的大小.20. (本小题满分12分)设抛物线:C py x 22=)0(>p 的焦点为F ,准线为l ,A 为C 上一点,已知以F 为圆心,FA 为半径的圆F 交l 于B 、D 两点(Ⅰ) 若90BFD ∠=︒,ABD △面积为24,求p 的值及圆F 的方程;(Ⅱ)若A 、B 、F 三点在同一直线m 上,直线n 与m 平行,且n 与C 只有一个公共点,求坐标原点到m ,n 的距离的比值.21. (本小题满分12分) 已知函数121()(1)(0)2x f x f ef x x -'=-+. (Ⅰ) 求)(x f 的解析式及单调区间;(Ⅱ) 若b ax x x f ++≥221)(,求b a )1(+的最大值请考生在第22、23、24题中任选一题作答,如果多做,则按所做第一题记分,作答时请写清题号. 22. (本小题满分10分)选修4—1:几何证明选讲 如图,D ,E 分别为ABC △边AB ,AC 的中点,直线DE 交ABC △的 外接圆于F ,G 两点.若AB CF //,证明: (Ⅰ) BC CD =;(Ⅱ) GBD BCD ∽△△.23. (本小题满分10分)选修4—4:坐标系与参数方程已知曲线1C 的参数方程是2cos 3sin x y ϕϕ=⎧⎨=⎩(ϕ为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线2C 的极坐标方程是2=ρ.正方形ABCD 的顶点都在2C 上,且A ,B ,C ,D 依逆时针次序排列,点A 的极坐标为)3,2(π.(Ⅰ)点A ,B ,C ,D 的直角坐标;(Ⅱ) 设P 为1C 上任意一点,求2222||||||||PD PC PB PA +++的取值范围.24. (本小题满分10分)选修4—5:不等式选讲 已知函数|2|||)(-++=x a x x f .(Ⅰ) 当3a =-时,求不等式3)(≥x f 的解集;(Ⅱ) |4|)(-≤x x f 的解集包含]2,1[,求a 的取值范围.参考答案1-12:DACCD CBCAB AB 13、 14、[]3,3-. 15、3816、1830. 17、解:(Ⅰ)由cos sin 0a C C b c --=及正弦定理可得sin cos sin sin sin 0A C A C B C --=,()sin cos sin sin sin 0A C A C A C C +-+-=,sin cos sin sin 0A C A C C --=,sin 0C >,cos 10A A --=,2sin 106A π⎛⎫∴--= ⎪⎝⎭,1sin 62A π⎛⎫-= ⎪⎝⎭,0A π<< ,5666A πππ∴-<-<,66A ππ∴-=3A π∴=(Ⅱ)ABC S = △1sin 2bc A ∴==4bc ∴=, 2,3a A π==,222222cos 4a b c bc A b c bc ∴=+-=+-=, 228b c ∴+=. 解得2b c ==.18、解:(Ⅰ) ()()1080,1580,16 n n y n -≤⎧⎪=⎨≥⎪⎩(n N ∈); (Ⅱ) (ⅰ)若花店一天购进16枝玫瑰花,X 的分布列为X 的数学期望()E X =60×0.1+70×0.2+80×0.7=76,X 的方差()D X =(60-762)×0.1+(70-762)×0.2+(80-762)×0.7=44.(ⅱ)若花店计划一天购进17枝玫瑰花,XX 的数学期望()E X =55×0.1+65×0.2+75×0.16+85×0.54=76.4,因为76.4>76,所以应购进17枝玫瑰花. 19、(Ⅰ) 证明:设112AC BC AA a ===, 直三棱柱111C B A ABC -, 1DC DC ∴==, 12CC a =,22211DC DC CC ∴+=,1DC DC ∴⊥. 又1DC BD ⊥ ,1DC DC D =,1DC ∴⊥平面BDC .BC⊂ 平面BDC ,1DC BC ∴⊥.(Ⅱ)由 (Ⅰ)知,1DC =,1BC =,又已知BD DC ⊥1,BD ∴=. 在Rt ABD △中,,,90BD AD a DAB =∠= , AB ∴=.222AC BC AB ∴+=,AC BC ∴⊥.取11A B 的中点E ,则易证1C E ⊥平面1BDA ,连结DE ,则1C E ⊥BD , 已知BD DC ⊥1,BD ∴⊥平面1DC E ,BD ∴⊥DE ,1C DE ∴∠是二面角11C BD A --平面角.在1Rt C DE △中,1111sin 2C EC DE C D∠===,130C DE ∴∠= .即二面角11C BD A --的大小为30.20、解: (Ⅰ)由对称性可知,BFD △为等腰直角三角形,斜边上的高为p ,斜边长2BD p =.点A 到准线l的距离d FB FD ===.由ABD S =△,11222BD d p ⨯⨯=⨯=2p ∴=.圆F 的方程为()2218x y +-=.(Ⅱ)由对称性,不妨设点(),A A A x y 在第一象限,由已知得线段AB 是圆F 的在直径,90o ADB ∠=,2BD p ∴=,32A y p ∴=,代入抛物线:C py x 22=得A x . 直线m的斜率为3AF k ==.直线m的方程为0x =. 由py x 22= 得22x y p=,x y p '=.由3x y p '==, 3x p =.故直线n 与抛物线C的切点坐标为6p ⎫⎪⎪⎝⎭, 直线n的方程为06x -=. 所以坐标原点到m ,n3=. 21、解: (Ⅰ) 1()(1)(0)x f x f ef x -''=-+,令1x =得,(0)1f =, 再由121()(1)(0)2x f x f e f x x -'=-+,令0x =得()1f e '=. 所以)(x f 的解析式为21()2x f x e x x =-+. ()1x f x e x '=-+,易知()1x f x e x '=-+是R 上的增函数,且(0)0f '=.所以()00,()00,f x x f x x ''>⇔><⇔<所以函数)(x f 的增区间为()0,+∞,减区间为(),0-∞.(Ⅱ) 若b ax x x f ++≥221)(恒成立,即()()21()102x h x f x x ax b e a x b =---=-+-≥恒成立, ()()1x h x e a '=-+ ,(1)当10a +<时,()0h x '>恒成立, ()h x 为R 上的增函数,且当x →-∞时, ()h x →-∞,不合题意;(2)当10a +=时,()0h x >恒成立, 则0b ≤,(1)0a b +=;(3)当10a +>时, ()()1xh x e a '=-+为增函数,由()0h x '=得()ln 1x a =+, 故()()()0ln 1,()0ln 1,f x x a f x x a ''>⇔>+<⇔<+当()ln 1x a =+时, ()h x 取最小值()()()()ln 111ln 1h a a a a b +=+-++-.依题意有()()()()ln 111ln 10h a a a a b +=+-++-≥,即()()11ln 1b a a a ≤+-++, 10a +> ,()()()()22111ln 1a b a a a ∴+≤+-++,令()()22ln 0 u x x x x x =->,则()()22ln 12ln u x x x x x x x '=--=-, ()00()0u x x u x x ''>⇔<<⇔,所以当x =, ()u x取最大值2e u =.故当12a b+==时, ()1a b+取最大值2e.综上, 若baxxxf++≥221)(,则ba)1(+的最大值为2e.22、证明:(Ⅰ) ∵D,E分别为ABC△边AB,AC的中点,∴//DE BC.//CF AB,//DF BC,CF BD∴ 且=CF BD,又∵D为AB的中点,CF AD∴ 且=CF AD,CD AF∴=.//CF AB,BC AF∴=.CD BC∴=.(Ⅱ)由(Ⅰ)知,BC GF,GB CF BD∴==,BGD BDG DBC BDC∠=∠=∠=∠BCD GBD∴△∽△.23、解:(Ⅰ)依题意,点A,B,C,D的极坐标分别为.所以点A,B,C,D的直角坐标分别为、(、(1,-、1)-;(Ⅱ) 设()2cos,3sinPϕϕ,则2222||||||||PDPCPBPA+++())2212cos3sinϕϕ=-+()()222cos13sinϕϕ++-()()2212cos3sinϕϕ+--+)()222cos13sinϕϕ++--2216cos36sin16ϕϕ=++[]23220sin32,52ϕ=+∈.所以2222||||||||PD PC PB PA +++的取值范围为[]32,52.24、解:(Ⅰ) 当3a =-时,不等式3)(≥x f ⇔ |3||2|3x x -+-≥⇔ ()()2323x x x ≤⎧⎪⎨----≥⎪⎩或()()23323x x x <<⎧⎪⎨-++-≥⎪⎩或()()3323x x x ≥⎧⎪⎨-+-≥⎪⎩⇔或4x ≥.所以当3a =-时,不等式3)(≥x f 的解集为{1x x ≤或}4x ≥. (Ⅱ) ()|4|f x x ≤-的解集包含]2,1[,即|||2||4|x a x x ++-≤-对[]1,2x ∈恒成立,即||2x a +≤对[]1,2x ∈恒成立,即22a x a --≤≤-对[]1,2x ∈恒成立, 所以2122a a --≤⎧⎨-≥⎩,即30a -≤≤.所以a 的取值范围为[]3,0-.。
2013年高考数学(全国卷)理科及答案

2013年普通高等学校招生全国统一考试(新课标Ⅱ卷)数学(理科)注意事项:1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前考生将自己的姓名\准考证号填写在本试卷和答题卡相应位置。
2. 回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号标黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3. 答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。
4. 考试结束,将试题卷和答题卡一并交回。
第Ⅰ卷(选择题共50分)一、选择题:本大题共10小题。
每小题5分,共50分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
(1)已知集合M={x|(x+1)2 < 4,x∈R},N={-1,0,1,2,3},则M∩N=()(A){0,1,2}(B){-1,0,1,2}(C){-1,0,2,3} (D){0,1,2,3}(2)设复数z满足(1-i)z=2 i,则z= ()(A)-1+i (B)-1-i (C)1+i (D)1-i(3)等比数列{a n}的前n项和为S n,已知S3 = a2 +10a1 ,a5 = 9,则a1= ()(A)(B)-(C)(D)-(4)已知m,n为异面直线,m⊥平面α,n⊥平面β。
直线l满足l ⊥m,l ⊥n,l β,则()(A)α∥β且l ∥α(B)α⊥β且l⊥β(C)α与β相交,且交线垂直于l (D)α与β相交,且交线平行于l(5)已知(1+ɑx)(1+x)5的展开式中x2的系数为5,则ɑ=(A)-4 (B)-3 (C)-2 (D)-1(6)执行右面的程序框图,如果输入的N=10,那么输出的s=(A)1+ + +…+(B )1++ +…+(C )1+ + +…+(D )1++ +…+(7)一个四面体的顶点在空间直角坐标系O-xyz 中的坐标分别是(1,0,1),(1,1,0),(1,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为搞影面,则得到正视图可以为(A) (B) (C) (D)(8)设ɑ=log 36,b=log 510,c=log 714,则(A )c >b >a (B )b >c >a(C )a >c >b (D)a >b >c(9)已知a >0,x ,y 满足约束条件 ,若z=2x+y 的最小值为1,则a=(A)(B) (C)1 (D)2(10)已知函数f(x)=x2+αx2+bx+,下列结论中错误的是(A )∑x α∈R f(x α)=0(B )函数y=f(x)的图像是中心对称图形(C )若x α是f(x)的极小值点,则f(x)在区间(-∞,x α)单调递减(D )若xn 是f (x )的极值点,则f 1(x α)=0(11)设抛物线y2=3px(p ≥0)的焦点为F ,点M 在C 上,|MF|=5若以MF 为直径的园过点(0,3),则C 的方程为(A )y2=4x 或y2=8x (B )y2=2x 或y2=8x(C )y2=4x 或y2=16x (D )y2=2x 或y2=16x(12)已知点A (-1,0);B (1,0);C (0,1),直线y=ax+b(a>0)将△ABC 分割为面积相等的两部分,则b 的取值范围是x ≥1, x+y ≤3, y ≥a(x-3). {(A)(0,1)(B)(1-,1/2)( C)(1-,1/3)(D)[ 1/3, 1/2)第Ⅱ卷本卷包括必考题和选考题,每个试题考生都必修作答。
2013年高考数学(理)真题分类解析汇编7.立体几何

2013年高考数学〔理〕真题分类解析汇编7:立体几何一、选择题1 .〔2013年高考新课标1〔理〕〕如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为〔〕 A .35003cm π B .38663cm π C .313723cm πD .320483cm π【答案】A【天利解析】设正方体上底面所在平面截球得小圆M , 则圆心M 为正方体上底面正方形的中心.如图.设球的半径为R ,根据题意得球心到上底面的距离等于〔R ﹣2〕cm ,而圆M 的半径为4,由球的截面圆性质,得R 2=〔R ﹣2〕2+42, 解出R=5,所以根据球的体积公式,该球的体积V===.故选A .2 .〔2013年普通高等学校招生统一考试广东省数学〔理〕卷〔纯WORD 版〕〕设,m n 是两条不同的直线,,αβ是两个不同的平面,以下命题中正确的选项是 〔 〕A .假设αβ⊥,m α⊂,n β⊂,则m n ⊥B .假设//αβ,m α⊂,n β⊂,则//m nC .假设m n ⊥,m α⊂,n β⊂,则αβ⊥D .假设m α⊥,//m n ,//n β,则αβ⊥ 【答案】D【天利解析】ABC 是典型错误命题,选D .3 .〔2013年普通高等学校招生统一考试大纲版数学〔理〕WORD 版含答案〔已校对〕〕已知正四棱柱1111ABCD A B C D -中12AA AB =,则CD 与平面1BDC 所成角的正弦值等于〔〕 A .23B .33C .23D .13【答案】A【天利解析】设AB=1,则AA 1=2,分别以的方向为x 轴、y 轴、z 轴的正方向建立空间直角坐标系, 如以下图所示:则D 〔0,0,2〕,C 1〔0,1,0〕,B 〔1,1,2〕,C 〔0,1,2〕, =〔1,1,0〕,=〔0,1,﹣2〕,=〔0,1,0〕,设=〔x ,y ,z 〕为平面BDC 1的一个法向量,则,即,取=〔﹣2,2,1〕,设CD 与平面BDC 1所成角为θ,则sin θ=||=,故选A .4 .〔2013年高考新课标1〔理〕〕某几何体的三视图如下图,则该几何体的体积为〔〕A .168π+B .88π+C .1616π+D .816π+ 【答案】A【天利解析】三视图复原的几何体是一个长方体与半个圆柱的组合体,如图,其中长方体长、宽、高分别是:4,2,2,半个圆柱的底面半径为2,母线长为4. 所以长方体的体积=4×2×2=16, 半个圆柱的体积=×22×π×4=8π 所以这个几何体的体积是16+8π; 故选A .5 .〔2013年高考湖北卷〔理〕〕一个几何体的三视图如下图,该几何体从上到下由四个简单几何体组成,其体积分别记为1V ,2V ,3V ,4V ,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则有〔 〕 A .1243V V V V <<< B .1324V V V V <<<C .2134V V V V <<<D .2314V V V V <<<【答案】C【天利解析】此题考查三视图以及空间几何体的体积。
(2014年高考必备)2013年全国各地高考理科数学立体几何

2013年全国高考理科数学试题分类汇编7:立体几何一、选择题1 .(2013年高考新课标1(理))如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为( )A .35003cm πB .38663cm πC .313723cm πD .320483cm π【答案】A2 .(2013年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))设,m n 是两条不同的直线,,αβ是两个不同的平面,下列命题中正确的是( )A .若αβ⊥,m α⊂,n β⊂,则m n ⊥B .若//αβ,m α⊂,n β⊂,则//m nC .若m n ⊥,m α⊂,n β⊂,则αβ⊥D .若m α⊥,//m n ,//n β,则αβ⊥【答案】D3 .(2013年上海市春季高考数学试卷(含答案))若两个球的表面积之比为1:4,则这两个球的体积之比为( )A .1:2B .1:4C .1:8D .1:16【答案】C4 .(2013年普通高等学校招生统一考试大纲版数学(理)WORD 版含答案(已校对))已知正四棱柱1111ABCD A B C D -中12AA AB =,则CD 与平面1BDC 所成角的正弦值等于( )A .23B C D .13【答案】A5 .(2013年高考新课标1(理))某几何体的三视图如图所示,则该几何体的体积为( )A .168π+B .88π+C .1616π+D .816π+【答案】A6 .(2013年高考湖北卷(理))一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为1V ,2V ,3V ,4V ,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则有( )A .1243V V V V <<< B.1324V V V V <<<C .2134V V V V <<<D .2314V V V V <<<【答案】C7 .(2013年高考湖南卷(理))已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能...等于 ( )A .1B C D 【答案】C8 .(2013年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))某四棱台的三视图如图所示,则该四棱台的体积是( )A .4B .143C .163D .6【答案】B9 .(2013年普通高等学校招生统一考试新课标Ⅱ卷数学(理)(纯WORD 版含答案))已知n m ,为异面直线,⊥m 平面α,⊥n 平面β.直线l 满足,,,l m l n l l αβ⊥⊥⊄⊄,则 ( )A .βα//,且α//lB .βα⊥,且β⊥lC .α与β相交,且交线垂直于lD .α与β相交,且交线平行于l【答案】D10.(2013年普通高等学校招生统一考试山东数学(理)试题(含答案))已知三棱柱111ABC A B C -的侧棱与底面垂直,体积为94,.若P 为底面111A B C 的中心,则PA 与平面ABC所成角的大小为( )A .512πB .3πC .4πD .6π【答案】B11.(2013年普通高等学校招生统一考试重庆数学(理)试题(含答案))某几何体的三视图如题()5图所示,则该几何体的体积为 ( )A .5603B .5803C .200D .240正视图俯视图侧视图第5题图【答案】C12.(2013年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))已知三棱柱111ABC A B C -的6个顶点都在球O 的球面上,若34AB AC ==,,AB AC ⊥,112AA =,则球O 的半径为( )A B .C .132D .【答案】C13.(2013年高考江西卷(理))如图,正方体的底面与正四面体的底面在同一平面α上,且AB CD ,正方体的六个面所在的平面与直线CE,EF 相交的平面个数分别记为,m n ,那么m n +=( )A .8B .9C .10D .11【答案】A14.(2013年普通高等学校招生统一考试新课标Ⅱ卷数学(理)(纯WORD 版含答案))一个四面体的顶点在空间直角坐标系O xyz -中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到正视图可以为( )A .B .C .D .【答案】A15.(2013年普通高等学校招生统一考试安徽数学(理)试题(纯WORD 版))在下列命题中,不是公理..的是 ( )A .平行于同一个平面的两个平面相互平行B .过不在同一条直线上的三点,有且只有一个平面C .如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内D .如果两个不重合的平面有一个公共点, 那么他们有且只有一条过该点的公共直线 【答案】A 16.(2013年普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))在空间中,过点A 作平面π的垂线,垂足为B ,记)(A f B π=.设βα,是两个不同的平面,对空间任意一点P ,)]([)],([21P f f Q P f f Q βααβ==,恒有21PQ PQ =,则( )A .平面α与平面β垂直B .平面α与平面β所成的(锐)二面角为045C .平面α与平面β平行D .平面α与平面β所成的(锐)二面角为060【答案】A 17.(2013年高考四川卷(理))一个几何体的三视图如图所示,则该几何体的直观图可以是【答案】D 二、填空题18.(2013年高考上海卷(理))在xOy 平面上,将两个半圆弧22(1)1(1)x y x -+=≥和22(3)1(3)x y x -+=≥、两条直线1y = 和1y =-围成的封闭图形记为D,如图中阴影部分.记D 绕y轴旋转一周而成的几何体为Ω,过(0,)(||1)y y ≤作Ω的水平截面,所得截面面积为48ππ,试利用祖暅原理、一个平放的圆柱和一个长方体,得出Ω的体积值为__________【答案】2216ππ+.19.(2013年高考陕西卷(理))某几何体的三视图如图所示, 则其体积为___3π_____.【答案】3π 20.(2013年普通高等学校招生统一考试大纲版数学(理)WORD 版含答案(已校对))已知圆O 和圆K 是球O的大圆和小圆,其公共弦长等于球O 的半径,32OK =,且圆O 与圆K 所在的平面所成的一个二面角为60 ,则球O 的表面积等于______.【答案】16π21.(2013年高考北京卷(理))如图,在棱长为2的正方体ABCD -A1B 1C 1D 1中,E 为BC 的中点,点P 在线段D 1E上,点P 到直线CC 1的距离的最小值为__________.【答案】 22.(2013年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))如图,在三棱柱ABC C B A -111中,F E D ,,分别是1AA AC AB ,,的中点,设三棱锥ADE F -的体积为1V ,三棱柱ABC C B A -111的体积为2V ,则=21:V V ____________.【答案】1:2423.(2013年普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))若某几何体的三视图(单位:cm)如图所示,则此几何体的体积等于________2cm .【答案】2424.(2013年普通高等学校招生统一考试安徽数学(理)试题(纯WORD 版))如图,正方体1111ABCD A BC D -的棱长为1,P 为BC 的中点,Q 为线段1CC 上的动点,过点A,P,Q 的平面截该正方体所得的截面记为S.则下列命题正确的是__①②③⑤___(写出所有正确命题的编号).①当102CQ <<时,S 为四边形;②当12CQ =时,S 为等腰梯形;③当34CQ =时,S 与11C D 的交点R 满足1113C R =;④当314CQ <<时,S 为六边形;⑤当1CQ =时,S的面积为2【答案】①②③⑤25.(2013年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))某几何体的三视图如图所示,则该几何体的体积是____________.A BCADEF BC【答案】1616π-26.(2013年普通高等学校招生统一考试福建数学(理)试题(纯WORD 版))已知某一多面体内接于一个简单组合体,如果该组合体的正视图.测试图.俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是_______________【答案】12π27.(2013年上海市春季高考数学试卷(含答案))在如图所示的正方体1111ABCD A BC D -中,异面直线1A B 与1B C 所成角的大小为_______【答案】3π三、解答题28.(2013年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))如图,AB 是圆的直径,PA 垂直圆所在的平面,C 是圆上的点.(I)求证:PAC PBC ⊥平面平面;(II)2.AB AC PA C PB A ===--若,1,1,求证:二面角的余弦值D 1 C 1 B 1A 1D C AB【答案】29.(2013年普通高等学校招生统一考试重庆数学(理)试题(含答案))如图,四棱锥P ABCD-中,PA ABCD ⊥底面,2,4,3BC CD AC ACB ACD π===∠=∠=,F 为PC 的中点,AF PB ⊥.(1)求PA 的长; (2)求二面角B AF D --的正弦值.【答案】1.(2013年普通高等学校招生统一考试安徽数学(理)试题(纯WORD版))如图,圆锥顶点为p.底面圆心为o,其母线与底面所成的角为22.5°.AB和CD是底面圆O上的两条平行的弦,轴OP与平面PCD所成的角为60°.(Ⅰ)证明:平面PAB 与平面PCD 的交线平行于底面; (Ⅱ)求cos COD ∠.【答案】解: (Ⅰ) PAB P D ,////C m AB CD CD PCD AB PCD ⋂=⊂⇒ 设面面直线且面面//AB m ⇒直线 ABCD m ABCD AB 面直线面//⇒⊂ . 所以,ABCD D P PAB的公共交线平行底面与面面C . (Ⅱ) rPOOPF F CD r =︒︒=∠5.22tan .60,由题知,则的中点为线段设底面半径为. ︒-︒=︒∠==︒⋅︒⇒=︒5.22tan 15.22tan 245tan ,2cos 5.22tan 60tan 60tan ,2COD r OF PO OF . )223(3)],1-2(3[21cos ,1-25.22tan 12cos 2cos 22-==+∠=︒⇒-∠=∠COD COD COD 212-17cos .212-17cos =∠=∠COD COD 所以.法二:1.(2013年普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))如图,在四面体BCD A -中,⊥AD 平面BCD ,22,2,==⊥BD AD CD BC .M 是AD 的中点,P 是BM 的中点,点Q 在线段AC 上,且QC AQ 3=.(1)证明://PQ 平面BCD ;(2)若二面角D BM C --的大小为060,求BDC ∠的大小.【答案】解:证明(Ⅰ)方法一:如图6,取MD 的中点F ,且M 是AD 中点,所以3AF FD =.因为P 是BM 中点,所以//PF BD ;又因为(Ⅰ)3AQ QC =且3AF FD =,所以//QF BD ,所以面//PQF 面BDC ,且PQ ⊂面BDC ,所以//PQ 面BDC ;ABCDPQM(第20题图)方法二:如图7所示,取BD 中点O ,且P 是BM 中点,所以1//2PO MD ;取CD 的三等分点H ,使3DH CH =,且3AQ QC =,所以11////42QH AD MD ,所以////P O Q H P Q O H∴,且OH BCD ⊂,所以//PQ 面BDC ;(Ⅱ)如图8所示,由已知得到面ADB ⊥面BDC ,过C 作CG BD ⊥于G ,所以CG BMD ⊥,过G 作GH BM ⊥于H ,连接CH ,所以C H G ∠就是C B M D --的二面角;由已知得到3BM ==,设BDC α∠=,所以cos ,sin ,sin ,,CD CG CBCD CG BC BD CD BDαααααα===⇒===, 在RT BCG ∆中,2sin BGBCG BG BCααα∠=∴=∴=,所以在R T B H G ∆中, 13HG =∴=,所以在RT CHG ∆中tan tan 60CG CHG HG ∠====tan (0,90)6060BDC ααα∴=∈∴=∴∠= ;2.(2013年上海市春季高考数学试卷(含答案))如图,在正三棱锥111ABC A B C -中,16AA =,异面直线1BC与1AA 所成角的大小为6π,求该三棱柱的体积.【答案】[解]因为1CC 1AA .所以1BC C ∠为异面直线1BC 与1AA .所成的角,即1BC C ∠=6π. 在Rt 1BC C ∆中,11tan 6BC CC BC C =⋅∠==,从而24ABC S BC ∆==因此该三棱柱的体积为16ABC V S AA ∆=⋅==3.(2013年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))本小题满分14分.如图,在三棱锥ABC S -中,平面⊥SAB 平面SBC ,BC AB ⊥,AB AS =,过A 作SB AF ⊥,垂足为F ,点G E ,分别是棱SC SA ,的中点.求证:(1)平面//EFG 平面ABC ; (2)SA BC ⊥.【答案】证明:(1)∵AB AS =,SB AF ⊥∴F 分别是SB 的中点∵E.F 分别是SA.SB 的中点 ∴EF∥AB又∵EF ⊄平面ABC, AB ⊆平面ABC ∴EF∥平面ABC 同理:FG∥平面ABC又∵EF FG=F, EF.FG ⊆平面ABC∴平面//EFG 平面ABC (2)∵平面⊥SAB 平面SBC 平面SAB 平面SBC =BC AF ⊆平面SABAF⊥SB∴AF⊥平面SBC 又∵BC ⊆平面SBC ∴AF⊥BC又∵BC AB ⊥, AB AF=A, AB.AF ⊆平面SAB ∴BC⊥平面SAB 又∵SA ⊆平面SAB∴BC⊥SA4.(2013年高考上海卷(理))如图,在长方体ABCD-A 1B 1C 1D 1中,AB=2,AD=1,A 1A=1,证明直线BC 1平行于平面ABCS GFEB 1A 1C 1ACBDA 1C,并求直线BC 1到平面D 1AC 的距离.C 11【答案】因为ABCD-A 1B 1C 1D 1为长方体,故1111//,AB C D AB C D =,故ABC 1D 1为平行四边形,故11//BC AD ,显然B 不在平面D 1AC 上,于是直线BC 1平行于平面DA 1C; 直线BC 1到平面D 1AC 的距离即为点B 到平面D 1AC 的距离设为h考虑三棱锥ABCD 1的体积,以ABC 为底面,可得111(12)1323V =⨯⨯⨯⨯= 而1ADC ∆中,11AC DC AD ===故132AD C S ∆= 所以,13123233V h h =⨯⨯=⇒=,即直线BC 1到平面D 1AC 的距离为23.5.(2013年高考湖北卷(理))如图,AB 是圆O 的直径,点C 是圆O 上异于,A B 的点,直线PC ⊥平面ABC ,E ,F 分别是PA ,PC 的中点.(I)记平面BEF 与平面ABC 的交线为l ,试判断直线l 与平面PAC 的位置关系,并加以证明;(II)设(I)中的直线l 与圆O 的另一个交点为D ,且点Q 满足12DQ CP =.记直线PQ 与平面ABC所成的角为θ,异面直线PQ 与EF 所成的角为α,二面角E l C --的大小为β,求证:sin sin sin θαβ=.【答案】解:(I)EFAC ,AC ABC ⊆平面,EF ABC ⊆平面EF ABC ∴ 平面又EF BEF ⊆平面EF l ∴第19题图平面l PAC(II)连接DF,用几何方法很快就可以得到求证.(这一题用几何方法较快,向量的方法很麻烦,特别是用向量不能方便的表示角的正弦.个人认为此题与新课程中对立体几何的处理方向有很大的偏差.)6.(2013年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))如图1,在等腰直角三角形ABC中,90A ∠=︒,6BC =,,D E 分别是,AC AB 上的点,CD BE =,O 为BC 的中点.将ADE ∆沿DE 折起,得到如图2所示的四棱锥A BCDE '-,其中A O '=(Ⅰ) 证明:A O '⊥平面BCDE ; (Ⅱ) 求二面角A CD B '--的平面角的余弦值.【答案】(Ⅰ) 在图1中,易得3,OC AC AD ===.CO BDEA CDOBE'A图1图2连结,OD OE ,在OCD ∆中,由余弦定理可得OD==由翻折不变性可知A D '=所以222A O OD A D ''+=,所以A O OD '⊥,理可证A O OE '⊥, 又OD OE O = ,所以A O '⊥平面BCDE . (Ⅱ) 传统法:过O 作OH CD ⊥交CD 的延长线于H ,连结A H ', 因为A O '⊥平面BCDE ,所以A H CD '⊥, 所以A HO '∠为二面角A CD B '--的平面角. 结合图1可知,H 为AC 中点,故OH =,从而AH '==所以cos OH A HO A H '∠=='所以二面角A CD B '--向量法:以O 点为原点,建立空间直角坐标系O xyz -则(A ',()0,3,0C -,()1,2,0D -所以(CA '= ,(1,DA '=-设(),,n x y z =为平面A CD '的法向量,则00n CA n DA ⎧'⋅=⎪⎨'⋅=⎪⎩,即3020y x y ⎧+=⎪⎨-++=⎪⎩,解得y x z =-⎧⎪⎨=⎪⎩,令1x =,得(1,n =- 由(Ⅰ) 知,(OA '=为平面CDB 的一个法向量,所以cos ,n OA n OA n OA '⋅'===',即二面角A CD B '--.7.(2013年普通高等学校招生统一考试天津数学(理)试题(含答案))如图, 四棱柱ABCD -A 1B 1C 1D 1中, 侧棱A 1A ⊥底面ABCD , AB //DC , AB ⊥AD , AD = CD = 1, AA 1 = AB = 2,E 为棱AA 1的中点.(Ⅰ) 证明B 1C 1⊥CE ;(Ⅱ) 求二面角B 1-CE -C 1的正弦值.C D OBE'AH(Ⅲ) 设点M在线段C1E上, 且直线AM与平面ADD1A1, 求线段AM的长.【答案】8.(2013年高考新课标1(理))如图,三棱柱ABC-A1B1C1中,CA=CB,AB=A A1,∠BA A1=60°.(Ⅰ)证明AB⊥A1C;(Ⅱ)若平面ABC⊥平面AA1B1B,AB=CB=2,求直线A1C 与平面BB1C1C所成角的正弦值.【答案】(Ⅰ)取AB 中点E,连结CE,1A B ,1A E,∵AB=1AA ,1BAA ∠=060,∴1BAA ∆是正三角形,∴1A E ⊥AB, ∵CA=CB, ∴CE⊥AB, ∵1CE A E ⋂=E,∴AB⊥面1CEA,∴AB⊥1AC ;(Ⅱ)由(Ⅰ)知EC⊥AB,1EA ⊥AB,又∵面ABC⊥面11ABB A ,面ABC∩面11ABB A =AB,∴EC⊥面11ABB A ,∴EC⊥1EA ,∴EA,EC,1EA 两两相互垂直,以E 为坐标原点,EA 的方向为x 轴正方向,|EA|为单位长度,建立如图所示空间直角坐标系O xyz -, 有题设知A(1,0,0),1A(0,,0),C(0,0,),B(-1,0,0),则BC1BB =1AA),1AC),设n =(,,)x y z 是平面11CBB C 的法向量,则100BC BB ⎧∙=⎪⎨∙=⎪⎩n n ,即0x x ⎧+=⎪⎨+=⎪⎩,可取n,1,-1), ∴1cos ,A C n =11|A C A C ∙n |n||∴直线A 1C 与平面BB 1C 1C9.(2013年高考陕西卷(理))如图, 四棱柱ABCD -A 1B 1C 1D 1的底面ABCD 是正方形, O 为底面中心, A 1O ⊥平面ABCD, 1AB AA =(Ⅰ) 证明: A 1C ⊥平面BB 1D 1D ;(Ⅱ) 求平面OCB 1与平面BB 1D 1D 的夹角θ的大小.1A【答案】解:(Ⅰ) BD O A ABCD BD ABCD O A ⊥∴⊂⊥11,,面且面 ;又因为,在正方形AB CD中,BD C A AC A C A AC A BD A AC O A BD AC ⊥⊂⊥=⋂⊥11111,,故面且面所以;且. 在正方形AB CD 中,AO = 1 . .111=∆O A OA A RT 中,在O E C A OCE A E D B 1111111⊥为正方形,所以,则四边形的中点为设. [来源:学_科_网],所以由以上三点得且,面面又O O BD D D BB O D D BB BD =⋂⊂⊂111111E .E ,D D BB C A 111面⊥.(证毕)(Ⅱ) 建立直角坐标系统,使用向量解题.以O 为原点,以OC 为X 轴正方向,以OB 为Y 轴正方向.则)1,0,1()1,1,1(),100(),001(,0,1,0111-=⇒A B A C B ,,,,)(.由(Ⅰ)知, 平面BB 1D 1D 的一个法向量.0,0,1),1,1,1(),1,0,1(111)(==-==OC OB C A n 设平面OCB 1的法向量为,则0,0,2122=⋅=⋅n OB n n ).1-,1,0(法向量2=n 为解得其中一个21221|||||,cos |cos 212111=⋅=⋅=><=n n n n θ. 所以,平面OCB 1与平面BB 1D 1D 的夹角θ为3π 10.(2013年高考江西卷(理))如图,四棱锥P A B-中,PA ,ABCD E BD ⊥平面为的中点,G PD 为的中点,1A3,12DAB DCB EA EB AB PA ∆≅∆====,,连接CE 并延长交AD 于F . (1) 求证:AD CFG ⊥平面;(2) 求平面BCP 与平面DCP 的夹角的余弦值.【答案】解:(1)在ABD ∆中,因为E 是BD 的中点,所以1EA EB ED AB ====,故,23BAD ABE AEB ππ∠=∠=∠=,因为DAB DCB ∆≅∆,所以EAB ECB ∆≅∆, 从而有FED FEA ∠=∠,故,EF AD AF FD ⊥=,又因为,PG GD =所以FG ∥PA . 又PA ⊥平面ABCD ,所以,GF AD ⊥故AD ⊥平面CFG .(3) 以点A 为坐标原点建立如图所示的坐标系,则3(0,0,0),(1,0,0),(,22A B C D , (4)3(0,0,)2P ,故1333(0),(),(2222BC CP CD ==-=-设平面BCP 的法向量111(1,,)n y z = ,则111102233022y y z ⎧+=⎪⎪⎨⎪-+=⎪⎩ ,解得1123y z ⎧=⎪⎪⎨⎪=⎪⎩,即12(1,)33n =- .设平面DCP 的法向量222(1,,)n y z = ,则22232233022y y z ⎧-+=⎪⎪⎨⎪-+=⎪⎩,解得222y z ⎧=⎪⎨=⎪⎩,即2(1n = .从而平面BCP 与平面DCP的夹角的余弦值为12124cos 4n n n n θ⋅=== . 11.(2013年高考四川卷(理))如图,在三棱柱11ABC A B C -中,侧棱1AA ⊥底面ABC ,12AB AC AA ==,120BAC ∠= ,1,D D 分别是线段11,BC B C 的中点,P 是线段AD 的中点.(Ⅰ)在平面ABC 内,试作出过点P 与平面1A BC 平行的直线l ,说明理由,并证明直线l ⊥平面11ADD A ;(Ⅱ)设(Ⅰ)中的直线l 交AB 于点M ,交AC 于点N ,求二面角1A A M N --的余弦值.1C【答案】解:()I 如图,在平面ABC 内,过点P 做直线l //BC ,因为l 在平面1ABC 外,BC 在平面1ABC 内,由直线与平面平行的判定定理可知, l //平面1ABC . 由已知,AB AC =,D 是BC 的中点,所以,BC AD ⊥,则直线l AD ⊥.因为1AA ⊥平面ABC ,所以1AA ⊥直线l .又因为1,AD AA 在平面11ADDA 内,且AD 与1AA 相交,所以直线平面11ADD A()II 解法一:连接1A P ,过A 作1AE A P ⊥于E ,过E 作1EF AM ⊥于F ,连接AF . 由()I 知,MN ⊥平面1AEA ,所以平面1AEA ⊥平面1A MN . 所以AE ⊥平面1A MN ,则1AM AE ⊥. 所以1A M ⊥平面AEF ,则1A M ⊥AF .故AFE ∠为二面角1A AM N --的平面角(设为θ). 设11AA =,则由12AB AC AA ==,120BAC ∠=,有60BAD ∠=,2,1AB AD ==. 又P 为AD 的中点,所以M 为AB 的中点,且1,12AP AM ==, 在1Rt AAP 中, 1AP =在1Rt A AM 中, 1AM =从而,11AA AP AE A P ∙==11AA AM AF A M ∙==所以sin AE AF θ==.所以cos θ===. 故二面角1A AM N --解法二:设11AA =.如图,过1A 作1A E 平行于11B C ,以1A 为坐标原点,分别以111,AE AD ,1AA的方向为x轴,y 轴,z 轴的正方向,建立空间直角坐标系Oxyz (点O 与点1A 重合).则()10,0,0A ,()0,0,1A .因为P 为AD 的中点,所以,M N 分别为,AB AC 的中点,故11,1,,122M N ⎫⎛⎫⎪ ⎪⎪ ⎪⎝⎭⎝⎭,所以11,12A M ⎫=⎪⎪⎝⎭,()10,0,1A A =,)NM =.设平面1AA M 的一个法向量为()1111,,n x y z =,则1111,,n A M n A A ⎧⊥⎪⎨⊥⎪⎩ 即11110,0,n A M n A A ⎧∙=⎪⎨∙=⎪⎩故有 ()()()1111111,,,10,2,,0,0,10,x y z x y z ⎧⎫∙=⎪⎪⎪⎨⎝⎭⎪∙=⎩从而111110,220.x y z z ++=⎪⎨⎪=⎩取11x =,则1y =,所以()11,n =. 设平面1A MN 的一个法向量为()2222,,n x y z =,则212,,n A M n NM ⎧⊥⎪⎨⊥⎪⎩ 即2120,0,n A M n NM ⎧∙=⎪⎨∙=⎪⎩故有()())2222221,,,10,22,,0,x y z x y z ⎧⎛⎫∙=⎪ ⎪ ⎪⎪⎝⎭⎨⎪∙=⎪⎩从而222210,20.y z ++=⎨⎪=⎩取22y =,则21z =-,所以()20,2,1n =-.设二面角1A AM N --的平面角为θ,又θ为锐角, 则1212cos n n n n θ∙===∙.故二面角1A AM N --的余弦值为512.(2013年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))本小题满分10分.如图,在直三棱柱111A B C ABC -中,AC AB ⊥,2==AC AB ,41=AA ,点D 是BC 的中点 (1)求异面直线B A 1与D C1所成角的余弦值 (2)求平面1ADC 与1ABA 所成二面角的正弦值.【答案】本题主要考察异面直线.二面角.空间向量等基础知识以及基本运算,考察运用空间向量解决问题的能力.解:(1)以{}1,,AA AC AB 为为单位正交基底建立空间直角坐标系xyz A -,则)0,0,0(A )0,0,2(B ,)0,2,0(C ,)4,0,0(1A ,)0,1,1(D ,)4,2,0(1C ∴)4,0,2(1-=B A ,)4,1,1(1--=B A∴10103182018,cos 11==∙>=<D C B A C A∴异面直线B A 1与D C 1所成角的余弦值为10103 (2))0,2,0(=AC 是平面1ABA 的的一个法向量设平面1ADC 的法向量为),,(z y x m =,∵)0,1,1(=AD ,)4,2,0(1=AC 由1,AC ⊥⊥ ∴⎩⎨⎧=+=+0420z y y x 取1=z ,得2,2=-=x y ,∴平面1ADC 的法向量为)1,2,2(-=设平面1ADC 与1ABA 所成二面角为θ∴32324,cos cos =⨯-==><=m AC θ, 得35sin =θ ∴平面1ADC 与1ABA 所成二面角的正弦值为3513.(2013年普通高等学校招生统一考试大纲版数学(理)WORD 版含答案(已校对))如图,四棱锥P ABCD-中,902,ABC BAD BC AD PAB ∠=∠==∆ ,与PAD ∆都是等边三角形. (I)证明:;PB CD ⊥ (II)求二面角A PD C --的大小.【答案】14.(2013年普通高等学校招生统一考试山东数学(理)试题(含答案))如图所示,在三棱锥P ABQ -中,PB ⊥平面ABQ ,BA BP BQ ==,,,,D C E F 分别是,,,AQ BQ AP BP 的中点,2AQ BD =,PD 与EQ 交于点G ,PC 与FQ 交于点H ,连接GH .(Ⅰ)求证:AB GH ; (Ⅱ)求二面角D GH E --的余弦值.【答案】解:(Ⅰ)证明:因为,,,D C E F 分别是,,,AQ BQ AP BP 的中点,所以EF ∥AB ,DC ∥AB ,所以EF ∥DC ,又EF ⊂平面PCD ,DC ⊂平面PCD ,所以EF ∥平面PCD ,又EF ⊂平面EFQ ,平面EFQ 平面PCD GH =,所以EF ∥GH ,又EF ∥AB ,所以AB ∥GH .(Ⅱ)解法一:在△ABQ 中, 2AQ BD =,AD DQ =,所以=90ABQ ∠ ,即AB BQ ⊥,因为PB ⊥平面ABQ ,所以AB PB ⊥,又BP BQ B = ,所以AB ⊥平面PBQ ,由(Ⅰ)知AB ∥GH ,所以GH ⊥平面PBQ ,又FH ⊂平面PBQ ,所以GH FH ⊥,同理可得GH HC ⊥,所以FHC ∠为二面角D GH E --的平面角,设2BA BQ BP ===,连接PC ,在t R △FBC 中,由勾股定理得,FC =在t R △PBC 中,由勾股定理得,PC =,又H 为△PBQ 的重心,所以13HC PC == 同理FH =,在△FHC 中,由余弦定理得552499cos 5529FHC +-∠==-⨯,即二面角D GH E --的余弦值为45-. 解法二:在△ABQ 中,2AQ BD =,AD DQ =,所以90ABQ ∠=,又PB ⊥平面ABQ ,所以,,BA BQ BP 两两垂直,以B 为坐标原点,分别以,,BA BQ BP 所在直线为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系,设2BA BQ BP ===,则(1,0,1)E ,(0,0,1)F ,(0,2,0)Q ,(1,1,0)D ,(0,1,0)C (0,0,2)P ,,所以(1,2,1)EQ =-- ,(0,2,1)FQ =- ,(1,1,2)DP =-- ,(0,1,2)CP =- ,设平面EFQ 的一个法向量为111(,,)m x y z = , 由0m EQ ⋅= ,0m FQ ⋅=,得111112020x y z y z -+-=⎧⎨-=⎩取11y =,得(0,1,2)m = . 设平面PDC 的一个法向量为222(,,)n x y z = 由0n DP ⋅= ,0n CP ⋅=,得222222020x y z y z --+=⎧⎨-+=⎩取21z =,得(0,2,1)n = .所以4cos ,5m n m n m n ⋅==因为二面角D GH E --为钝角,所以二面角D GH E --的余弦值为45-. 15.(2013年高考湖南卷(理))如图5,在直棱柱1111//ABCD A BC D AD BC -中,,90,,1BAD AC BD BC ∠=⊥= ,13AD AA ==.(I)证明:1AC B D ⊥; (II)求直线111B C ACD 与平面所成角的正弦值.【答案】解: (Ⅰ) AC BB ABCD BD ABCD BB D C B A ABCD ⊥⇒⊂⊥∴-111111,面且面是直棱柱D B AC BDB D B BDB AC B BB BD BD AC 11111,,⊥∴⊂⊥∴=⋂⊥,面。
2013年高考数学分类试题汇编:立体几何(理科(高考必看典藏版))

12012年高考真题理科数学解析汇编:立体几何一、选择题 1 .(2012年高考(新课标理))已知三棱锥S ABC -的所有顶点都在球O 的求面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =;则此棱锥的体积为 ( )A.BCD2 .(2012年高考(新课标理))如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为A .6B .9C .12D .18 3 .(2012年高考(浙江理))已知矩形ABCD ,AB =1,BC将∆ABD 沿矩形的对角线BD 所在的直线进行翻着,在翻着过程中,A .存在某个位置,使得直线AC 与直线BD 垂直B .存在某个位置,使得直线AB 与直线CD 垂直C .存在某个位置,使得直线AD 与直线BC 垂直D .对任意位置,三直线“AC 与BD ”,“AB 与CD ”,“AD 与BC ”均不垂直4 .(2012年高考(重庆理))设四面体的六条棱的长分别为a ,且长为a 的棱与长,则a 的取值范围是 ( )A .B .C .D .5 .(2012年高考(四川理))如图,半径为R 的半球O 的底面圆O 在平面α内,过点O 作平面α的垂线交半球面于点A ,过圆O 的直径CD 作平面α成45角的平面与半球面相交,所得交线上到平面α的距离最大的点为B ,该交线上的一点P 满足60BOP ∠= ,则A 、P 两点间的球面距离为 ( ) A .arccos4R B .4R πC .arccos3R D .3R π6 .(2012年高考(四川理))下列命题正确的是 ( )A .若两条直线和同一个平面所成的角相等,则这两条直线平行B .若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C .若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D .若两个平面都垂直于第三个平面,则这两个平面平行 7 .(2012年高考(上海春))已知空间三条直线.l m n 、、若l 与m 异面,且l 与n 异面,则2( ) A .m 与n 异面. B .m 与n 相交. C .m 与n 平行. D .m 与n 异面、相交、平行均有可能. 8 .(2012年高考(陕西理))如图,在空间直角坐标系中有直三棱柱111ABC A B C -,12CA CC CB ==,则直线1BC 与直线1AB 夹角的余弦值为 ( )A.BCD .359 .(2012年高考(江西理))如图,已知正四棱锥S-ABCD 所有棱长都为1,点E 是侧棱SC 上一动点,过点E 垂直于SC 的截面将正四棱锥分成上、下两部分.记SE=x(0<x<1),截面下面部分的体积为V(x),则函数y=V(x)的图像大致为10.(2012年高考(湖南理))某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是11.(2012年高考(湖北理))我国古代数学名著《九章算术》中“开立圆术”曰:置积尺数,以十六乘之,九而一,所得开立方除之,即立圆径. “开立圆术”相当于给出了已知球的体积V ,求其直径d的一个近似公式d ≈. 人们还用过一些类似的近似公式. 根据π =3.14159 判断,下列近似公式中最精确的一个是( )A.d ≈ B.d C.d ≈D(一)必考题(11—14题) 12.(2012年高考(湖北理)何体的体积为 A 图1 B C D侧视图正视图 俯视图3A .8π3B .3πC .10π3D .6π13.(2012年高考(广东理))(立体几何)某几何体的三视图如图1所示,它的体积为 ( )A .12πB .45πC .57πD .81π14.(2012年高考(福建理))一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是 ( ) A .球 B .三棱柱 C .正方形 D .圆柱 15.(2012年高考(大纲理))已知正四棱柱1111ABCD A BC D -中,12,AB CC E ==为1CC 的中点,则直线1AC 与平面BED 的距离为 ( )A .2 BC.D .116.(2012年高考(北京理))某三棱锥的三视图如图所示,该三棱锥的表面积是( )A.28+ B.30+C.56+D.60+17.(2012年高考(安徽理))设平面α与平面β相交于直线m ,直线a 在平面α内,直线b 在平面β内,且b m ⊥,则“αβ⊥”是“a b ⊥”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .即不充分不必要条件 二、填空题 18.(2012年高考(天津理))―个几何体的三视图如图所示(单位:m ),则该几何体的体积为______3m .419.(2012年高考(浙江理))已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的体积等于___________cm 3.20.(2012年高考(四川理))如图,在正方体1111ABCD A BC D -中,M 、N 分别是CD 、1CC 的中点,则异面直线1A M 与DN 所成角的大小是____________.21.(2012年高考(上海理))如图,AD 与BC 是四面体ABCD 中互相垂直的棱,BC=2。
全国高考理科数学试题分类汇编7:立体几何 Word版含答案

2013年全国高考理科数学试题分类汇编7:立体几何一、选择题1 .(2013年高考新课标1(理))如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为( )A .35003cm π B .38663cm π C .313723cm πD .320483cm π【答案】A2 .(2013年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))设,m n 是两条不同的直线,,αβ是两个不同的平面,下列命题中正确的是( )A .若αβ⊥,m α⊂,n β⊂,则m n ⊥B .若//αβ,m α⊂,n β⊂,则//m nC .若m n ⊥,m α⊂,n β⊂,则αβ⊥D .若m α⊥,//m n ,//n β,则αβ⊥【答案】D3 .(2013年上海市春季高考数学试卷(含答案))若两个球的表面积之比为1:4,则这两个球的体积之比为( )A .1:2B .1:4C .1:8D .1:16【答案】C4 .(2013年普通高等学校招生统一考试大纲版数学(理)WORD 版含答案(已校对))已知正四棱柱1111ABCD A B C D -中12AA AB =,则CD 与平面1BDC 所成角的正弦值等于( )A .23B C .3D .13【答案】A5 .(2013年高考新课标1(理))某几何体的三视图如图所示,则该几何体的体积为( )A .168π+B .88π+C .1616π+D .816π+【答案】A6 .(2013年高考湖北卷(理))一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为1V ,2V ,3V ,4V ,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则有 ( )A .1243V V V V <<<B .1324V V V V <<<C .213V V V <<<【答案】C7 .(2013年高考湖南卷(理))已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能...等于 ( )A .1BC .2D .2【答案】C8 .(2013年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))某四棱台的三视图如图所示,则该四棱台的体积是( )A .4B .143C .163D .6【答案】B 9 .(2013年普通高等学校招生统一考试新课标Ⅱ卷数学(理)(纯WORD 版含答案))已知nm ,为异面直线,⊥m 平面α,⊥n 平面β.直线l 满足,,,l m l n l l αβ⊥⊥⊄⊄,则 ( )A .βα//,且α//lB .βα⊥,且β⊥lC .α与β相交,且交线垂直于lD .α与β相交,且交线平行于l【答案】D10.(2013年普通高等学校招生统一考试山东数学(理)试题(含答案))已知三棱柱111ABC A B C -的侧棱与底面垂直,体积为94,的正三角形.若P 为底面111A B C 的中心,则PA 与平面ABC 所成角的大小为( )A .512πB .3πC .4πD .6π【答案】B11.(2013年普通高等学校招生统一考试重庆数学(理)试题(含答案))某几何体的三视图如题()5图所示,则该几何体的体积为 ( )A .5603B .5803C .200D .240正视图俯视图侧视图第5题图【答案】C12.(2013年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))已知三棱柱111ABC A B C -的6个顶点都在球O的球面上,若34AB AC ==,,AB AC ⊥,112AA =,则球O 的半径为( )A .2B .C .132D .【答案】C13.(2013年高考江西卷(理))如图,正方体的底面与正四面体的底面在同一平面α上,且AB CD ,正方体的六个面所在的平面与直线CE,EF 相交的平面个数分别记为,m n ,那么m n +=( )A .8B .9C .10D .11【答案】A14.(2013年普通高等学校招生统一考试新课标Ⅱ卷数学(理)(纯WORD 版含答案))一个四面体的顶点在空间直角坐标系O xyz -中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到正视图可以为( )A .B .C .D .【答案】A15.(2013年普通高等学校招生统一考试安徽数学(理)试题(纯WORD 版))在下列命题中,不是公理..的是 ( )A .平行于同一个平面的两个平面相互平行B .过不在同一条直线上的三点,有且只有一个平面C .如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内D .如果两个不重合的平面有一个公共点, 那么他们有且只有一条过该点的公共直线 【答案】A 16.(2013年普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))在空间中,过点A作平面π的垂线,垂足为B ,记)(A f B π=.设βα,是两个不同的平面,对空间任意一点P ,)]([)],([21P f f Q P f f Q βααβ==,恒有21PQ PQ =,则( )A .平面α与平面β垂直B .平面α与平面β所成的(锐)二面角为045C .平面α与平面β平行D .平面α与平面β所成的(锐)二面角为060【答案】A 17.(2013年高考四川卷(理))一个几何体的三视图如图所示,则该几何体的直观图可以是【答案】D 二、填空题18.(2013年高考上海卷(理))在xOy 平面上,将两个半圆弧22(1)1(1)x y x -+=≥和22(3)1(3)x y x -+=≥、两条直线1y = 和1y =-围成的封闭图形记为D,如图中阴影部分.记D 绕y 轴旋转一周而成的几何体为Ω,过(0,)(||1)y y ≤作Ω的水平截面,所得截面面积为48π,试利用祖暅原理、一个平放的圆柱和一个长方体,得出Ω的体积值为__________【答案】2216ππ+.19.(2013年高考陕西卷(理))某几何体的三视图如图所示, 则其体积为___3π_____.【答案】3π 20.(2013年普通高等学校招生统一考试大纲版数学(理)WORD 版含答案(已校对))已知圆O和圆K 是球O 的大圆和小圆,其公共弦长等于球O 的半径,32OK =,且圆O 与圆K 所在的平面所成的一个二面角为60,则球O 的表面积等于______.【答案】16π21.(2013年高考北京卷(理))如图,在棱长为2的正方体ABCD -A 1B 1C 1D 1中,E 为BC 的中点,点P 在线段D 1E 上,点P 到直线CC 1的距离的最小值为__________.【答案】51B22.(2013年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))如图,在三棱柱ABC C B A -111中,F E D ,,分别是1AA AC AB ,,的中点,设三棱锥ADE F -的体积为1V ,三棱柱ABC C B A -111的体积为2V ,则=21:V V ____________.【答案】1:2423.(2013年普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))若某几何体的三视图(单位:cm)如图所示,则此几何体的体积等于________2cm .【答案】2424.(2013年普通高等学校招生统一考试安徽数学(理)试题(纯WORD 版))如图,正方体1111ABCD A B C D -的棱长为1,P 为BC 的中点,Q 为线段1CC 上的动点,过点A,P,Q 的平面截该正方体所得的截面记为S.则下列命题正确的是__①②③⑤___(写出所有正确命题的编号).①当102CQ <<时,S 为四边形;②当12CQ =时,S 为等腰梯形;③当34CQ =时,S 与A BCADEF BC11C D 的交点R 满足1113C R =;④当314CQ <<时,S 为六边形;⑤当1CQ =时,S 的面积【答案】①②③⑤25.(2013年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))某几何体的三视图如图所示,则该几何体的体积是____________.【答案】1616π-26.(2013年普通高等学校招生统一考试福建数学(理)试题(纯WORD 版))已知某一多面体内接于一个简单组合体,如果该组合体的正视图.测试图.俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是_______________【答案】12π27.(2013年上海市春季高考数学试卷(含答案))在如图所示的正方体1111ABCD A B C D -中,异面直线1A B 与1B C 所成角的大小为_______【答案】3πD 1 C 1 B 1A 1D C AB三、解答题28.(2013年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))如图,AB 是圆的直径,PA垂直圆所在的平面,C 是圆上的点. (I)求证:PAC PBC ⊥平面平面;(II)2.AB AC PA C PB A ===--若,1,1,求证:二面角的余弦值【答案】29.(2013年普通高等学校招生统一考试重庆数学(理)试题(含答案))如图,四棱锥P ABCD-中,PA ABCD ⊥底面,2,4,3BC CD AC ACB ACD π===∠=∠=,F 为PC 的中点,AF PB ⊥.(1)求PA 的长; (2)求二面角B AF D --的正弦值.【答案】1.(2013年普通高等学校招生统一考试安徽数学(理)试题(纯WORD版))如图,圆锥顶点为p.底面圆心为o ,其母线与底面所成的角为22.5°.AB 和CD 是底面圆O 上的两条平行的弦,轴OP 与平面PCD 所成的角为60°.(Ⅰ)证明:平面PAB 与平面PCD 的交线平行于底面; (Ⅱ)求cos COD ∠. 【答案】解:(Ⅰ)PAB P D ,////C m AB CD CD PCD AB PCD ⋂=⊂⇒设面面直线且面面//AB m ⇒直线 ABCD m ABCD AB 面直线面//⇒⊂ . 所以,ABCD D P PAB 的公共交线平行底面与面面C . (Ⅱ)rPOOPF F CD r =︒︒=∠5.22tan .60,由题知,则的中点为线段设底面半径为. ︒-︒=︒∠==︒⋅︒⇒=︒5.22tan 15.22tan 245tan ,2cos 5.22tan 60tan 60tan ,2COD r OF PO OF . )223(3)],1-2(3[21cos ,1-25.22tan 12cos 2cos 22-==+∠=︒⇒-∠=∠COD COD COD 212-17cos .212-17cos =∠=∠COD COD 所以.法二:1.(2013年普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))如图,在四面体BCD A -中,⊥AD 平面BCD ,22,2,==⊥BD AD CD BC .M 是AD 的中点,P是BM 的中点,点Q 在线段AC 上,且QC AQ 3=.(1)证明://PQ 平面BCD ;(2)若二面角D BM C --的大小为060,求BDC ∠的大小.【答案】解:证明(Ⅰ)方法一:如图6,取MD 的中点F ,且M 是AD 中点,所以3AF FD =.因为P 是BM 中点,所以//PF BD ;又因为(Ⅰ)3AQ QC =且ABCDPQM(第20题图)3AF FD =,所以//QF BD ,所以面//PQF 面BDC ,且PQ ⊂面BDC ,所以//PQ 面BDC ;方法二:如图7所示,取BD 中点O ,且P 是BM 中点,所以1//2PO MD ;取CD 的三等分点H ,使3DH CH =,且3AQ QC =,所以11////42QH AD MD ,所以////P O Q H P Q O H ∴,且OH BCD ⊂,所以//PQ 面BDC ;(Ⅱ)如图8所示,由已知得到面ADB ⊥面BDC ,过C 作CG BD ⊥于G ,所以CG BMD⊥,过G 作GH BM ⊥于H ,连接CH ,所以CHG ∠就是C BM D --的二面角;由已知得到3BM ==,设BDC α∠=,所以cos ,sin ,sin ,,CD CG CBCD CG BC BD CD BDαααααα===⇒===,在RT BCG ∆中,2sin BGBCG BG BCααα∠=∴=∴=,所以在RT BHG ∆中2133HG α=∴=,所以在RT CHG ∆中tan tan 603CG CHGHG ∠==== tan (0,90)6060BDC ααα∴=∈∴=∴∠=;2.(2013年上海市春季高考数学试卷(含答案))如图,在正三棱锥111ABC A B C -中,16AA =,异面直线1BC 与1AA 所成角的大小为6π,求该三棱柱的体积.【答案】[解]因为1CC 1AA .所以1BC C ∠为异面直线1BC 与1AA .所成的角,即1BC C ∠=6π. 在Rt 1BC C ∆中,11tan 63BC CC BC C =⋅∠=⨯=从而24ABCS BC ∆==, 因此该三棱柱的体积为16ABC V S AA ∆=⋅==3.(2013年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))本小题满分14分.如图,在三棱锥ABC S -中,平面⊥SAB 平面SBC ,BC AB ⊥,AB AS =,过A 作SB AF ⊥,垂足为F ,点G E ,分别是棱SC SA ,的中点. 求证:(1)平面//EFG 平面ABC ; (2)SA BC ⊥.【答案】证明:(1)∵AB AS =,SB AF ⊥∴F 分别是SB 的中点∵E.F 分别是SA.SB 的中点 ∴EF∥ABB 1A 1C 1ACBABCSGFE又∵EF ⊄平面ABC, AB ⊆平面ABC ∴EF∥平面ABC 同理:FG∥平面ABC又∵EF FG=F, EF.FG ⊆平面ABC∴平面//EFG 平面ABC (2)∵平面⊥SAB 平面SBC 平面SAB 平面SBC =BC AF ⊆平面SABAF⊥SB∴AF⊥平面SBC 又∵BC ⊆平面SBC ∴AF⊥BC又∵BC AB ⊥, AB AF=A, AB.AF ⊆平面SAB ∴BC⊥平面SAB 又∵SA ⊆平面SAB∴BC⊥SA4.(2013年高考上海卷(理))如图,在长方体ABCD-A 1B 1C 1D 1中,AB=2,AD=1,A 1A=1,证明直线BC 1平行于平面DA 1C,并求直线BC 1到平面D 1AC 的距离.C 11A【答案】因为ABCD-A 1B 1C 1D 1为长方体,故1111//,AB C D AB C D =,故ABC 1D 1为平行四边形,故11//BC AD ,显然B 不在平面D 1AC 上,于是直线BC 1平行于平面DA 1C;直线BC 1到平面D 1AC 的距离即为点B 到平面D 1AC 的距离设为h考虑三棱锥ABCD 1的体积,以ABC 为底面,可得111(12)1323V =⨯⨯⨯⨯= 而1AD C ∆中,11AC DC AD ===故132AD C S ∆= 所以,13123233V h h =⨯⨯=⇒=,即直线BC 1到平面D 1AC 的距离为23.5.(2013年高考湖北卷(理))如图,AB 是圆O 的直径,点C 是圆O 上异于,A B 的点,直线PC ⊥平面ABC ,E ,F 分别是PA ,PC 的中点.(I)记平面BEF 与平面ABC 的交线为l ,试判断直线l 与平面PAC 的位置关系,并加以证明;(II)设(I)中的直线l 与圆O 的另一个交点为D ,且点Q 满足12DQ CP =.记直线PQ 与平面ABC 所成的角为θ,异面直线PQ 与EF 所成的角为α,二面角E l C --的大小为β,求证:sin sin sin θαβ=.【答案】解:(I)EF AC ,AC ABC ⊆平面,EF ABC ⊆平面EF ABC ∴平面又EF BEF ⊆平面EF l ∴ l PAC ∴平面(II)连接DF,用几何方法很快就可以得到求证.(这一题用几何方法较快,向量的方法很麻烦,特别是用向量不能方便的表示角的正弦.个人认为此题与新课程中对立体几何的处理方向有很大的偏差.)第19题图6.(2013年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))如图1,在等腰直角三角形ABC 中,90A ∠=︒,6BC =,,D E 分别是,AC AB 上的点,CD BE =O 为BC 的中点.将ADE ∆沿DE 折起,得到如图2所示的四棱锥A BCDE '-,其中A O '=(Ⅰ) 证明:A O '⊥平面BCDE ; (Ⅱ) 求二面角A CDB '--的平面角的余弦值.【答案】(Ⅰ) 在图1中,易得3,OC AC AD ===.CO BDEA CDOBE'A图1图2连结,OD OE,在OCD ∆中,由余弦定理可得OD ==由翻折不变性可知A D '=,所以222A O OD A D ''+=,所以A O OD '⊥, 理可证A O OE '⊥, 又ODOE O =,所以A O '⊥平面BCDE .(Ⅱ) 传统法:过O 作OH CD ⊥交CD 的延长线于H ,连结A H ', 因为A O '⊥平面BCDE ,所以A H CD '⊥, 所以A HO '∠为二面角A CD B '--的平面角.结合图1可知,H 为AC 中点,故OH =,从而A H '== 所以cos 5OH A HO A H '∠==',所以二面角A CD '--向量法:以O 点为原点,建立空间直角坐标系O xyz -则(A ',()0,3,0C -,()1,2,0D -所以(CA '=,(1,DA '=- 设(),,n x y z =为平面A CD '的法向量,则00n CA n DA ⎧'⋅=⎪⎨'⋅=⎪⎩,即3020y x y ⎧=⎪⎨-++=⎪⎩,解得y x z =-⎧⎪⎨=⎪⎩,令1x =,得(1,n =- 由(Ⅰ) 知,(OA '=为平面CDB 的一个法向量,所以cos ,53n OA n OA n OA '⋅'===',即二面角A CD B '--的平面角的余弦C D OBE'AH.(2013年普通高等学校招生统一考试天津数学(理)试题(含答案))如图, 四棱柱ABCD-A1B1C1D1 7.中, 侧棱A1A⊥底面ABCD, AB//DC, AB⊥AD, AD = CD = 1, AA1 = AB = 2, E为棱AA1的中点.(Ⅰ) 证明B1C1⊥CE;(Ⅱ) 求二面角B1-CE-C1的正弦值.(Ⅲ) 设点M在线段C1E上, 且直线AM与平面ADD1A1, 求线段AM 的长.【答案】8.(2013年高考新课标1(理))如图,三棱柱ABC-A1B1C1中,CA=CB,AB=A A1,∠BA A1=60°.(Ⅰ)证明AB⊥A1C;(Ⅱ)若平面ABC⊥平面AA1B1B,AB=CB=2,求直线A1C 与平面BB1C1C所成角的正弦值.【答案】(Ⅰ)取AB 中点E,连结CE,1A B ,1A E,∵AB=1AA ,1BAA ∠=060,∴1BAA ∆是正三角形,∴1A E ⊥AB, ∵CA=CB, ∴CE⊥AB, ∵1CE A E ⋂=E,∴AB⊥面1CEA,∴AB⊥1AC ;(Ⅱ)由(Ⅰ)知EC⊥AB,1EA ⊥AB,又∵面ABC⊥面11ABB A ,面ABC∩面11ABB A =AB,∴EC⊥面11ABB A ,∴EC⊥1EA , ∴EA,EC,1EA 两两相互垂直,以E 为坐标原点,EA 的方向为x 轴正方向,|EA |为单位长度,建立如图所示空间直角坐标系O xyz -, 有题设知A(1,0,0),1A(0,,0),C(0,0,),B(-1,0,0),则BC),1BB =1AA1A C),设n =(,,)x y z 是平面11CBB C 的法向量,则100BC BB ⎧∙=⎪⎨∙=⎪⎩n n ,即0x x ⎧=⎪⎨=⎪⎩,可取n,1,-1), ∴1cos ,A C n =11|A C A C∙n |n ||∴直线A 1C 与平面BB 1C 1C9.(2013年高考陕西卷(理))如图, 四棱柱ABCD -A 1B 1C 1D 1的底面ABCD 是正方形, O 为底面中心, A 1O ⊥平面ABCD, 1AB AA ==(Ⅰ) 证明: A 1C ⊥平面BB 1D 1D ;(Ⅱ) 求平面OCB 1与平面BB 1D 1D 的夹角θ的大小.1A【答案】解:(Ⅰ) BD O A ABCD BD ABCD O A ⊥∴⊂⊥11,,面且面 ;又因为,在正方形ABCD 中,BDC A AC A C A AC A BD A AC O A BD AC ⊥⊂⊥=⋂⊥11111,,故面且面所以;且.在正方形AB CD 中,AO = 1 . .111=∆O A OA A RT 中,在O E C A OCE A E D B 1111111⊥为正方形,所以,则四边形的中点为设.,所以由以上三点得且,面面又O O BD D D BB O D D BB BD =⋂⊂⊂111111E .E ,D D BB C A 111面⊥.(证毕)(Ⅱ) 建立直角坐标系统,使用向量解题.以O 为原点,以OC 为X 轴正方向,以OB 为Y 轴正方向.则)1,0,1()1,1,1(),100(),001(,0,1,0111-=⇒C A B A C B ,,,,)(.由(Ⅰ)知, 平面BB 1D 1D 的一个法向量.0,0,1),1,1,1(),1,0,1(111)(==-==OB A n 设平面OCB 1的法向量为,则0,0,2122=⋅=⋅OC n OB n n ).1-,1,0(法向量2=n 为解得其中一个21221|||||,cos |cos 212111=⋅=⋅=><=n n n n θ.1A所以,平面OCB 1与平面BB 1D 1D 的夹角θ为3π 10.(2013年高考江西卷(理))如图,四棱锥P A B C-中,PA ,ABCD E BD ⊥平面为的中点,G PD 为的中点,3,12DAB DCB EA EB AB PA ∆≅∆====,,连接CE 并延长交AD 于F . (1) 求证:AD CFG ⊥平面;(2) 求平面BCP 与平面DCP 的夹角的余弦值.【答案】解:(1)在ABD ∆中,因为E 是BD 的中点,所以1EA EB ED AB ====,故,23BAD ABE AEB ππ∠=∠=∠=,因为DAB DCB ∆≅∆,所以EAB ECB ∆≅∆, 从而有FED FEA ∠=∠,故,EF AD AF FD ⊥=,又因为,PG GD =所以FG ∥PA . 又PA ⊥平面ABCD ,所以,GF AD ⊥故AD ⊥平面CFG . (3) 以点A 为坐标原点建立如图所示的坐标系,则3(0,0,0),(1,0,0),(,22A B C D ,(4)3(0,0,)2P ,故133333(0),(,),(,2222222BC CP CD ==--=-,,,设平面BCP 的法向量111(1,,)n y z =,则1111022330222y y z ⎧+=⎪⎪⎨⎪--+=⎪⎩ ,解得1123y z ⎧=⎪⎪⎨⎪=⎪⎩,即12(1,)3n =. 设平面DCP 的法向量222(1,,)n y z =,则222322330222y y z ⎧-+=⎪⎪⎨⎪--+=⎪⎩,解得222y z ⎧=⎪⎨=⎪⎩,即2n =.从而平面B C P 与平面D C P 的夹角的余弦值为12124cos 416n n n n θ⋅===. 11.(2013年高考四川卷(理))如图,在三棱柱11ABC A B C -中,侧棱1AA ⊥底面ABC ,12AB AC AA ==,120BAC ∠=,1,D D 分别是线段11,BC B C 的中点,P 是线段AD 的中点.(Ⅰ)在平面ABC 内,试作出过点P 与平面1A BC 平行的直线l ,说明理由,并证明直线l ⊥平面11ADD A ;(Ⅱ)设(Ⅰ)中的直线l 交AB 于点M ,交AC 于点N ,求二面角1A A M N --的余弦值.1C【答案】解:()I 如图,在平面ABC 内,过点P 做直线l //BC ,因为l 在平面1A BC 外,BC 在平面1A BC 内,由直线与平面平行的判定定理可知, l //平面1A BC .由已知,AB AC =,D 是BC 的中点,所以,BC AD ⊥,则直线l AD ⊥.因为1AA ⊥平面ABC ,所以1AA ⊥直线l .又因为1,AD AA 在平面11ADD A 内,且AD 与1AA 相交,所以直线平面11ADD A()II 解法一:连接1A P ,过A 作1AE A P ⊥于E ,过E 作1EF A M ⊥于F ,连接AF . 由()I 知,MN ⊥平面1AEA ,所以平面1AEA ⊥平面1A MN . 所以AE ⊥平面1A MN ,则1A M AE ⊥. 所以1A M ⊥平面AEF ,则1A M ⊥AF .故AFE ∠为二面角1A A M N --的平面角(设为θ). 设11AA =,则由12A B AC A A ==,120BAC ∠=,有60BAD ∠=,2,1AB AD ==.又P 为AD 的中点,所以M 为AB 的中点,且1,12AP AM ==,在1Rt AA P 中, 1A P =;在1Rt A AM 中, 1AM =从而,11AA AP AE A P ∙==,11AA AM AF A M ∙==所以sin AE AF θ==.所以cos θ===. 故二面角1A A M N --解法二:设11AA =.如图,过1A 作1A E 平行于11B C ,以1A 为坐标原点,分别以111,A E A D ,1AA 的方向为x 轴,y 轴,z 轴的正方向,建立空间直角坐标系Oxyz (点O 与点1A 重合).则()10,0,0A ,()0,0,1A .因为P 为AD 的中点,所以,M N 分别为,AB AC 的中点,故11,1,,12222M N ⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,所以131,122A M ⎛⎫= ⎪⎪⎝⎭,()10,0,1A A =,()3,0,0NM =.设平面1AA M 的一个法向量为()1111,,n x y z =,则1111,,n A M n A A ⎧⊥⎪⎨⊥⎪⎩即11110,0,n A M n A A ⎧∙=⎪⎨∙=⎪⎩故有()()()1111111,,,10,2,,0,0,10,x y z x y z ⎧⎫∙=⎪⎪⎪⎨⎝⎭⎪∙=⎩从而111110,20.x y z z ++=⎪=⎩取11x =,则1y =所以()11,n =. 设平面1A MN 的一个法向量为()2222,,n x y z =,则212,,n A M n NM ⎧⊥⎪⎨⊥⎪⎩即2120,0,n A M n NM ⎧∙=⎪⎨∙=⎪⎩故有()())2222221,,,10,22,,0,x y z x y z ⎧⎛⎫∙=⎪⎪ ⎪⎪⎝⎭⎨⎪∙=⎪⎩从而222210,20.x y z ++=⎨⎪=⎩取22y =,则21z =-,所以()20,2,1n =-. 设二面角1A A M N --的平面角为θ,又θ为锐角,则1212cos n n n n θ∙===∙.故二面角1A A M N --的余弦值为512.(2013年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))本小题满分10分.如图,在直三棱柱111A B C ABC -中,AC AB ⊥,2==AC AB ,41=AA ,点D 是BC 的中点(1)求异面直线B A 1与D C 1所成角的余弦值 (2)求平面1ADC 与1ABA 所成二面角的正弦值.【答案】本题主要考察异面直线.二面角.空间向量等基础知识以及基本运算,考察运用空间向量解决问题的能力.解:(1)以{}1,,AA 为为单位正交基底建立空间直角坐标系xyz A -,则)0,0,0(A )0,0,2(B ,)0,2,0(C ,)4,0,0(1A ,)0,1,1(D ,)4,2,0(1C ∴)4,0,2(1-=A ,)4,1,1(1--=A∴10103182018,cos 11==>=<C A ∴异面直线B A 1与D C 1所成角的余弦值为10103 (2))0,2,0(= 是平面1ABA 的的一个法向量设平面1ADC 的法向量为),,(z y x =,∵)0,1,1(=,)4,2,0(1=AC 由1,AC ⊥⊥ ∴⎩⎨⎧=+=+0420z y y x 取1=z ,得2,2=-=x y ,∴平面1ADC 的法向量为)1,2,2(-=m设平面1ADC 与1ABA 所成二面角为θ∴32324,cos cos =⨯-==><=m AC θ, 得35sin =θ ∴平面1ADC 与1ABA 所成二面角的正弦值为3513.(2013年普通高等学校招生统一考试大纲版数学(理)WORD 版含答案(已校对))如图,四棱锥P ABCD -中,902,ABC BAD BC AD PAB ∠=∠==∆,与PAD ∆都是等边三角形.(I)证明:;PB CD ⊥ (II)求二面角A PD C --的大小.【答案】14.(2013年普通高等学校招生统一考试山东数学(理)试题(含答案))如图所示,在三棱锥P ABQ -中,PB ⊥平面ABQ ,BA BP BQ ==,,,,D C E F 分别是,,,A Q B Q A P B P 的中点, 2AQ BD =,PD 与EQ 交于点G ,PC 与FQ 交于点H ,连接GH .(Ⅰ)求证:AB GH ; (Ⅱ)求二面角D GH E --的余弦值.【答案】解:(Ⅰ)证明:因为,,,D C E F 分别是,,,AQ BQ AP BP 的中点,所以EF ∥AB ,DC ∥AB ,所以EF ∥DC , 又EF ⊂平面PCD ,DC ⊂平面PCD , 所以EF ∥平面PCD , 又EF ⊂平面EFQ ,平面EFQ 平面PCD GH =,所以EF ∥GH , 又EF ∥AB , 所以AB ∥GH .(Ⅱ)解法一:在△ABQ 中, 2AQ BD =,AD DQ =,所以=90ABQ ∠,即AB BQ ⊥,因为PB ⊥平面ABQ ,所以AB PB ⊥, 又BPBQ B =,所以AB ⊥平面PBQ ,由(Ⅰ)知AB ∥GH ,所以GH ⊥平面PBQ ,又FH ⊂平面PBQ ,所以GH FH ⊥,同理可得GH HC ⊥, 所以FHC ∠为二面角D GH E --的平面角,设2BA BQ BP ===,连接PC , 在t R △FBC 中,由勾股定理得,FC =在t R △PBC 中,由勾股定理得,PC =,又H 为△PBQ 的重心,所以13HC PC ==同理FH =,在△FHC 中,由余弦定理得552499cos 5529FHC +-∠==-⨯,即二面角D GH E --的余弦值为45-.解法二:在△ABQ 中,2AQ BD =,AD DQ =,所以90ABQ ∠=,又PB ⊥平面ABQ ,所以,,BA BQ BP 两两垂直,以B 为坐标原点,分别以,,BA BQ BP 所在直线为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系,设2BA BQ BP ===,则(1,0,1)E ,(0,0,1)F ,(0,2,0)Q ,(1,1,0)D ,(0,1,0)C (0,0,2)P ,,所以(1,2,EQ =--,(0,2,1)FQ =-,(1,1,2)DP =--,(0,1,2)CP =-,设平面EFQ 的一个法向量为111(,,)m x y z =,由0m EQ ⋅=,0m FQ ⋅=,得111112020x y z y z -+-=⎧⎨-=⎩取11y =,得(0,1,2)m =.设平面PDC 的一个法向量为222(,,)n x y z =由0n DP ⋅=,0n CP ⋅=,得222222020x y z y z --+=⎧⎨-+=⎩取21z =,得(0,2,1)n =.所以4cos ,5m n m n m n⋅==因为二面角D GH E --为钝角,所以二面角D GH E --的余弦值为45-.15.(2013年高考湖南卷(理))如图5,在直棱柱1111//ABCD A B C D AD BC -中,,90,,1BAD AC BD BC ∠=⊥=,13AD AA ==.(I)证明:1AC B D ⊥; (II)求直线111B C ACD 与平面所成角的正弦值.【答案】解: (Ⅰ)AC BB ABCD BD ABCD BB D C B A ABCD ⊥⇒⊂⊥∴-111111,面且面是直棱柱 D B AC BDB D B BDB AC B BB BD BD AC 11111,,⊥∴⊂⊥∴=⋂⊥,面。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013年全国高考理科数学试题分类汇编7:立体几何一、选择题1 .(2013年高考新课标1(理))如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为( )A .35003cm π B .38663cm π C .313723cm πD .320483cm π【答案】A2 .(2013年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))设,m n 是两条不同的直线,,αβ是两个不同的平面,下列命题中正确的是( )A .若αβ⊥,m α⊂,n β⊂,则m n ⊥B .若//αβ,m α⊂,n β⊂,则//m nC .若m n ⊥,m α⊂,n β⊂,则αβ⊥D .若m α⊥,//m n ,//n β,则αβ⊥【答案】D3 .(2013年上海市春季高考数学试卷(含答案))若两个球的表面积之比为1:4,则这两个球的体积之比为( )A .1:2B .1:4C .1:8D .1:16【答案】C4 .(2013年普通高等学校招生统一考试大纲版数学(理)WORD 版含答案(已校对))已知正四棱柱1111ABCD A B C D -中12AA AB =,则CD 与平面1BDC 所成角的正弦值等于( )A .23B C .3D .13【答案】A5 .(2013年高考新课标1(理))某几何体的三视图如图所示,则该几何体的体积为( )A .168π+B .88π+C .1616π+D .816π+【答案】A6 .(2013年高考湖北卷(理))一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为1V ,2V ,3V ,4V ,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则有 ( )A .1243V V V V <<<B .1324V V V V <<<C .213V V V <<<【答案】C7 .(2013年高考湖南卷(理))已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能...等于 ( )A .1BC .2D .2【答案】C8 .(2013年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))某四棱台的三视图如图所示,则该四棱台的体积是( )A .4B .143C .163D .6【答案】B9 .(2013年普通高等学校招生统一考试新课标Ⅱ卷数学(理)(纯WORD 版含答案))已知nm ,为异面直线,⊥m 平面α,⊥n 平面β.直线l 满足,,,l m l n l l αβ⊥⊥⊄⊄,则 ( )A .βα//,且α//lB .βα⊥,且β⊥lC .α与β相交,且交线垂直于lD .α与β相交,且交线平行于l【答案】D10.(2013年普通高等学校招生统一考试山东数学(理)试题(含答案))已知三棱柱111ABC A B C -的侧棱与底面垂直,体积为94,的正三角形.若P 为底面111A B C 的中心,则PA 与平面ABC 所成角的大小为( )A .512πB .3πC .4πD .6π【答案】B11.(2013年普通高等学校招生统一考试重庆数学(理)试题(含答案))某几何体的三视图如题()5图所示,则该几何体的体积为 ( )A .5603B .5803C .200D .240正视图俯视图侧视图第5题图【答案】C12.(2013年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))已知三棱柱111ABC A B C -的6个顶点都在球O的球面上,若34AB AC ==,,AB AC ⊥,112AA =,则球O 的半径为( )A B .C .132D .【答案】C13.(2013年高考江西卷(理))如图,正方体的底面与正四面体的底面在同一平面α上,且AB CD ,正方体的六个面所在的平面与直线CE,EF 相交的平面个数分别记为,m n ,那么m n +=( )A .8B .9C .10D .11【答案】A14.(2013年普通高等学校招生统一考试新课标Ⅱ卷数学(理)(纯WORD 版含答案))一个四面体的顶点在空间直角坐标系O xyz -中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到正视图可以为( )A .B .C .D .【答案】A15.(2013年普通高等学校招生统一考试安徽数学(理)试题(纯WORD 版))在下列命题中,不是公理..的是 ( )A .平行于同一个平面的两个平面相互平行B .过不在同一条直线上的三点,有且只有一个平面C .如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内D .如果两个不重合的平面有一个公共点, 那么他们有且只有一条过该点的公共直线 【答案】A16.(2013年普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))在空间中,过点A 作平面π的垂线,垂足为B ,记)(A f B π=.设βα,是两个不同的平面,对空间任意一点P ,)]([)],([21P f f Q P f f Q βααβ==,恒有21PQ PQ =,则 ( )A .平面α与平面β垂直B .平面α与平面β所成的(锐)二面角为045C .平面α与平面β平行D .平面α与平面β所成的(锐)二面角为060【答案】A17.(2013年高考四川卷(理))一个几何体的三视图如图所示,则该几何体的直观图可以是【答案】D二、填空题18.(2013年高考上海卷(理))在xOy 平面上,将两个半圆弧22(1)1(1)x y x -+=≥和22(3)1(3)x y x -+=≥、两条直线1y = 和1y =-围成的封闭图形记为D,如图中阴影部分.记D 绕y 轴旋转一周而成的几何体为Ω,过(0,)(||1)y y ≤作Ω的水平截面,所得截面面积为48π,试利用祖暅原理、一个平放的圆柱和一个长方体,得出Ω的体积值为__________【答案】2216ππ+.19.(2013年高考陕西卷(理))某几何体的三视图如图所示, 则其体积为___3π_____.【答案】3π 20.(2013年普通高等学校招生统一考试大纲版数学(理)WORD 版含答案(已校对))已知圆O 和圆K 是球O 的大圆和小圆,其公共弦长等于球O 的半径,32OK =,且圆O 与圆K 所在的平面所成的一个二面角为60,则球O 的表面积等于______.【答案】16π21.(2013年高考北京卷(理))如图,在棱长为2的正方体ABCD -A 1B 1C 1D 1中,E 为BC 的中点,点P 在线段D 1E 上,点P 到直线CC 1的距离的最小值为__________.【答案】 22.(2013年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))如图,在三棱柱ABC C B A -111中,F E D ,,分别是1AA AC AB ,,的中点,设三棱锥A D E F -的体积为1V ,三棱柱A B C C B A -111的体积为2V ,则=21:V V ____________.【答案】1:2423.(2013年普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))若某几何体的三视图(单位:cm)如图所示,则此几何体的体积等于________2cm .【答案】2424.(2013年普通高等学校招生统一考试安徽数学(理)试题(纯WORD 版))如图,正方体A BCADEF BC 1B1111ABCD A B C D -的棱长为1,P 为BC 的中点,Q 为线段1CC 上的动点,过点A,P,Q 的平面截该正方体所得的截面记为S.则下列命题正确的是__①②③⑤___(写出所有正确命题的编号).①当102CQ <<时,S 为四边形;②当12CQ =时,S 为等腰梯形;③当34CQ =时,S 与11C D 的交点R 满足1113C R =;④当314CQ <<时,S 为六边形;⑤当1CQ =时,S 的面积为2【答案】①②③⑤25.(2013年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))某几何体的三视图如图所示,则该几何体的体积是____________.【答案】1616π-26.(2013年普通高等学校招生统一考试福建数学(理)试题(纯WORD 版))已知某一多面体内接于一个简单组合体,如果该组合体的正视图.测试图.俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是_______________【答案】12π27.(2013年上海市春季高考数学试卷(含答案))在如图所示的正方体1111ABCD A B C D -中,异面直线1A B 与1B C 所成角的大小为_______【答案】3π三、解答题28.(2013年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))如图,AB 是圆的直径,PA 垂直圆所在的平面,C 是圆上的点. (I)求证:PAC PBC ⊥平面平面;(II)2.AB AC PA C PB A ===--若,1,1,求证:二面角的余弦值【答案】D 1 C 1 B 1A 1D C AB29.(2013年普通高等学校招生统一考试重庆数学(理)试题(含答案))如图,四棱锥P ABCD-中,PA ABCD ⊥底面,2,4,3BC CD AC ACB ACD π===∠=∠=,F 为PC 的中点,AF PB ⊥.(1)求PA 的长; (2)求二面角B AF D --的正弦值.【答案】1.(2013年普通高等学校招生统一考试安徽数学(理)试题(纯WORD版))如图,圆锥顶点为p .底面圆心为o ,其母线与底面所成的角为22.5°.AB 和CD 是底面圆O 上的两条平行的弦,轴OP 与平面PCD 所成的角为60°.(Ⅰ)证明:平面PAB 与平面PCD 的交线平行于底面; (Ⅱ)求cos COD ∠. 【答案】解:(Ⅰ)PAB P D ,////C m AB CD CD PCD AB PCD ⋂=⊂⇒设面面直线且面面//AB m ⇒直线 ABCD m ABCD AB 面直线面//⇒⊂ . 所以,ABCD D P PAB 的公共交线平行底面与面面C . (Ⅱ)rPOOPF F CD r =︒︒=∠5.22tan .60,由题知,则的中点为线段设底面半径为. ︒-︒=︒∠==︒⋅︒⇒=︒5.22tan 15.22tan 245tan ,2cos 5.22tan 60tan 60tan ,2COD r OF PO OF . )223(3)],1-2(3[21cos ,1-25.22tan 12cos 2cos 22-==+∠=︒⇒-∠=∠COD COD COD 212-17cos .212-17cos =∠=∠COD COD 所以.法二:1.(2013年普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))如图,在四面体BCD A -中,⊥AD 平面BCD ,22,2,==⊥BD AD CD BC .M 是AD 的中点,P是BM 的中点,点Q 在线段AC 上,且QC AQ 3=.(1)证明://PQ 平面BCD ;(2)若二面角D BM C --的大小为060,求BDC ∠的大小.【答案】解:证明(Ⅰ)方法一:如图6,取MD 的中点F ,且M 是AD 中点,所以3AF FD =.因为P 是BM 中点,所以//PF BD ;又因为(Ⅰ)3AQ QC =且ABCDPQM(第20题图)3AF FD =,所以//QF BD ,所以面//PQF 面BDC ,且PQ ⊂面BDC ,所以//PQ 面BDC ;方法二:如图7所示,取BD 中点O ,且P 是BM 中点,所以1//2PO MD ;取CD 的三等分点H ,使3DH CH =,且3AQ QC =,所以11////42QH AD MD ,所以////P O Q H P Q O H ∴,且OH BCD ⊂,所以//PQ 面BDC ;(Ⅱ)如图8所示,由已知得到面ADB ⊥面BDC ,过C 作CG BD ⊥于G ,所以CG BMD⊥,过G 作GH BM ⊥于H ,连接CH ,所以CHG ∠就是C BM D --的二面角;由已知得到3BM ==,设BDC α∠=,所以cos ,sin ,sin ,,CD CG CBCD CG BC BD CD BDαααααα===⇒===,在RT BCG ∆中,2sin BGBCG BG BCααα∠=∴=∴=,所以在RT BHG ∆中2133HG α=∴=,所以在RT CHG ∆中tan tan 603CG CHGHG ∠==== tan (0,90)6060BDC ααα∴=∈∴=∴∠=;2.(2013年上海市春季高考数学试卷(含答案))如图,在正三棱锥111ABC A B C -中,16AA =,异面直线1BC 与1AA 所成角的大小为6π,求该三棱柱的体积.【答案】[解]因为1CC 1AA .所以1BC C ∠为异面直线1BC 与1AA .所成的角,即1BC C ∠=6π. 在Rt1BC C ∆中,11tan 63BC CC BC C =⋅∠=⨯=从而24ABCS BC ∆==, 因此该三棱柱的体积为16ABC V S AA ∆=⋅==.3.(2013年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))本小题满分14分.如图,在三棱锥ABC S -中,平面⊥SAB 平面SBC ,BC AB ⊥,AB AS =,过A 作SB AF ⊥,垂足为F ,点G E ,分别是棱SC SA ,的中点. 求证:(1)平面//EFG 平面ABC ; (2)SA BC ⊥.【答案】证明:(1)∵AB AS =,SB AF ⊥∴F 分别是SB 的中点ABCSGFEB 1A 1C 1ACB∵E.F 分别是SA.SB 的中点 ∴EF∥AB又∵EF ⊄平面ABC, AB ⊆平面ABC ∴EF∥平面ABC 同理:FG∥平面ABC又∵EF FG=F, EF.FG ⊆平面ABC∴平面//EFG 平面ABC (2)∵平面⊥SAB 平面SBC 平面SAB 平面SBC =BC AF ⊆平面SABAF⊥SB∴AF⊥平面SBC 又∵BC ⊆平面SBC ∴AF⊥BC又∵BC AB ⊥, AB AF=A, AB.AF ⊆平面SAB ∴BC⊥平面SAB 又∵SA ⊆平面SAB∴BC⊥SA4.(2013年高考上海卷(理))如图,在长方体ABCD-A 1B 1C 1D 1中,AB=2,AD=1,A 1A=1,证明直线BC 1平行于平面DA 1C,并求直线BC 1到平面D 1AC 的距离.C 11A【答案】因为ABCD-A 1B 1C 1D 1为长方体,故1111//,AB C D AB C D =,故ABC 1D 1为平行四边形,故11//BC AD ,显然B 不在平面D 1AC 上,于是直线BC 1平行于平面DA 1C;直线BC 1到平面D 1AC 的距离即为点B 到平面D 1AC 的距离设为h考虑三棱锥ABCD 1的体积,以ABC 为底面,可得111(12)1323V =⨯⨯⨯⨯= 而1AD C ∆中,11AC DC AD ==,故132AD C S ∆= 所以,13123233V h h =⨯⨯=⇒=,即直线BC 1到平面D 1AC 的距离为23.5.(2013年高考湖北卷(理))如图,AB 是圆O 的直径,点C 是圆O 上异于,A B 的点,直线PC ⊥平面ABC ,E ,F 分别是PA ,PC 的中点.(I)记平面BEF 与平面ABC 的交线为l ,试判断直线l 与平面PAC 的位置关系,并加以证明;(II)设(I)中的直线l 与圆O 的另一个交点为D ,且点Q 满足12DQ CP =.记直线PQ 与平面ABC 所成的角为θ,异面直线PQ 与EF 所成的角为α,二面角E l C --的大小为β,求证:sin sin sin θαβ=.【答案】解:(I)EF AC ,AC ABC ⊆平面,EF ABC ⊆平面EF ABC ∴平面又EF BEF ⊆平面EF l ∴ l PAC ∴平面(II)连接DF,用几何方法很快就可以得到求证.(这一题用几何方法较快,向量的方法很麻烦,特别是用向量不能方便的表示角的正弦.个人认为此题与新课程中对立体几何的处理方向有很大的偏差.)第19题图6.(2013年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))如图1,在等腰直角三角形ABC 中,90A ∠=︒,6BC =,,D E 分别是,A C A B 上的点,CD BE ==O 为BC 的中点.将ADE ∆沿DE 折起,得到如图2所示的四棱锥A BCDE '-,其中A O '=(Ⅰ) 证明:A O '⊥平面BCDE ; (Ⅱ) 求二面角A CD B '--的平面角的余弦值.【答案】(Ⅰ) 在图1中,易得3,OC AC AD ===.CO BDEA CDOBE'A图1图2连结,OD OE ,在OCD ∆中,由余弦定理可得OD==由翻折不变性可知A D '=,所以222A O OD A D ''+=,所以A O OD '⊥, 理可证A O OE '⊥, 又ODOE O =,所以A O '⊥平面BCDE .(Ⅱ) 传统法:过O 作OH CD ⊥交CD 的延长线于H ,连结A H ', 因为A O '⊥平面BCDE ,所以A H CD '⊥, 所以A HO '∠为二面角A CD B '--的平面角.结合图1可知,H 为AC 中点,故OH =,从而A H '== 所以cos OH A HO A H '∠==',所以二面角A CD '--向量法:以O 点为原点,建立空间直角坐标系O xyz -则(A ',()0,3,0C -,()1,2,0D -所以(CA '=,(1,DA '=- 设(),,n x y z =为平面A CD '的法向量,则00n CA n DA ⎧'⋅=⎪⎨'⋅=⎪⎩,即3020y x y⎧+=⎪⎨-++=⎪⎩,解得y x z =-⎧⎪⎨=⎪⎩,令1x =,得(1,n =- 由(Ⅰ) 知,(OA '=为平面CDB 的一个法向量,所以cos ,3n OA n OA n OA '⋅'===',即二面角A CD B '--的平面角的余弦. C D OBE'AH7.(2013年普通高等学校招生统一考试天津数学(理)试题(含答案))如图, 四棱柱ABCD-A1B1C1D1中, 侧棱A1A⊥底面ABCD, AB//DC, AB⊥AD, AD = CD = 1, AA1 = AB = 2, E为棱AA1的中点.(Ⅰ) 证明B1C1⊥CE;(Ⅱ) 求二面角B1-CE-C1的正弦值., 求线段AM (Ⅲ) 设点M在线段C1E上, 且直线AM与平面ADD1A1所成角的正弦值为6的长.【答案】8.(2013年高考新课标1(理))如图,三棱柱ABC-A1B1C1中,CA=CB,AB=A A1,∠BA A1=60°.(Ⅰ)证明AB⊥A1C;(Ⅱ)若平面ABC⊥平面AA1B1B,AB=CB=2,求直线A1C 与平面BB1C1C所成角的正弦值.【答案】(Ⅰ)取AB 中点E,连结CE,1A B ,1A E,∵AB=1AA ,1BAA ∠=060,∴1BAA ∆是正三角形,∴1A E ⊥AB, ∵CA=CB, ∴CE⊥AB, ∵1CE A E ⋂=E,∴AB⊥面1CEA,∴AB⊥1AC ;(Ⅱ)由(Ⅰ)知EC⊥AB,1EA ⊥AB,又∵面ABC⊥面11ABB A ,面ABC∩面11ABB A =AB,∴EC⊥面11ABB A ,∴EC⊥1EA , ∴EA,EC,1EA 两两相互垂直,以E 为坐标原点,EA 的方向为x 轴正方向,|EA |为单位长度,建立如图所示空间直角坐标系O xyz -, 有题设知A(1,0,0),1A(0,,0),C(0,0,),B(-1,0,0),则BC),1BB =1AA1A C),设n =(,,)x y z 是平面11CBB C 的法向量,则100BC BB ⎧∙=⎪⎨∙=⎪⎩n n ,即0x x ⎧=⎪⎨=⎪⎩,可取n,1,-1), ∴1cos ,A C n =11|A C A C∙n |n ||∴直线A 1C 与平面BB 1C 1C9.(2013年高考陕西卷(理))如图, 四棱柱ABCD -A 1B 1C 1D 1的底面ABCD 是正方形, O 为底面中心, A 1O ⊥平面ABCD, 1AB AA ==(Ⅰ) 证明: A 1C ⊥平面BB 1D 1D ;(Ⅱ) 求平面OCB 1与平面BB 1D 1D 的夹角θ的大小.1A【答案】解:(Ⅰ) BD O A ABCD BD ABCD O A ⊥∴⊂⊥11,,面且面 ;又因为,在正方形ABCD 中,BDC A AC A C A AC A BD A AC O A BD AC ⊥⊂⊥=⋂⊥11111,,故面且面所以;且.在正方形AB CD 中,AO = 1 . .111=∆O A OA A RT 中,在O E C A OCE A E D B 1111111⊥为正方形,所以,则四边形的中点为设.,所以由以上三点得且,面面又O O BD D D BB O D D BB BD =⋂⊂⊂111111E .E ,D D BB C A 111面⊥.(证毕)(Ⅱ) 建立直角坐标系统,使用向量解题.以O 为原点,以OC 为X 轴正方向,以OB 为Y 轴正方向.则)1,0,1()1,1,1(),100(),001(,0,1,0111-=⇒A B A C B ,,,,)(.由(Ⅰ)知, 平面BB 1D 1D 的一个法向量.0,0,1),1,1,1(),1,0,1(111)(==-==OB A n 设平面OCB 1的法向量为,则0,0,2122=⋅=⋅n OB n n ).1-,1,0(法向量2=n 为解得其中一个1A21221|||||,cos |cos 212111=⋅=⋅⋅=><=n n n n θ. 所以,平面OCB 1与平面BB 1D 1D 的夹角θ为3π 10.(2013年高考江西卷(理))如图,四棱锥P ABCD-中,PA ,ABCD E BD ⊥平面为的中点,G PD 为的中点,3,12DAB DCB EA EB AB PA ∆≅∆====,,连接CE 并延长交AD 于F . (1) 求证:AD CFG ⊥平面;(2) 求平面BCP 与平面DCP 的夹角的余弦值.【答案】解:(1)在ABD ∆中,因为E 是BD 的中点,所以1EA EB ED AB ====,故,23BAD ABE AEB ππ∠=∠=∠=,因为DAB DCB ∆≅∆,所以EAB ECB ∆≅∆, 从而有FED FEA ∠=∠,故,EF AD AF FD ⊥=,又因为,PG GD =所以FG ∥PA . 又PA ⊥平面ABCD ,所以,GF AD ⊥故AD ⊥平面CFG . (3) 以点A 为坐标原点建立如图所示的坐标系,则3(0,0,0),(1,0,0),(2A B C D ,(4)3(0,0,)2P ,故133333(0),(,),(,2222222BC CP CD ==--=-,,, 设平面BCP 的法向量111(1,,)n y z =,则1111022330222y y z ⎧+=⎪⎪⎨⎪--+=⎪⎩ ,解得1123y z ⎧=⎪⎪⎨⎪=⎪⎩,即12(1,)3n =. 设平面DCP 的法向量222(1,,)n y z =,则222322330222y y z ⎧-+=⎪⎪⎨⎪--+=⎪⎩,解得222y z ⎧=⎪⎨=⎪⎩,即2n =.从而平面BCP 与平面D C P 的夹角的余弦值为12124cos 416n n n n θ⋅===. 11.(2013年高考四川卷(理))如图,在三棱柱11ABC A B C -中,侧棱1AA ⊥底面ABC ,12AB AC AA ==,120BAC ∠=,1,D D 分别是线段11,BC B C 的中点,P 是线段AD 的中点.(Ⅰ)在平面ABC 内,试作出过点P 与平面1A BC 平行的直线l ,说明理由,并证明直线l ⊥平面11ADD A ;(Ⅱ)设(Ⅰ)中的直线l 交AB 于点M ,交AC 于点N ,求二面角1A A M N --的余弦值.1C【答案】解:()I如图,在平面ABC 内,过点P 做直线l //BC ,因为l 在平面1A BC 外,BC 在平面1A BC 内,由直线与平面平行的判定定理可知, l //平面1A BC .由已知,AB AC =,D 是BC 的中点,所以,BC AD ⊥,则直线l AD ⊥.因为1AA ⊥平面ABC ,所以1AA ⊥直线l .又因为1,AD AA 在平面11ADD A 内,且AD 与1AA 相交,所以直线平面11ADD A()II 解法一:连接1A P ,过A 作1AE A P ⊥于E ,过E 作1EF A M ⊥于F ,连接AF . 由()I 知,MN ⊥平面1AEA ,所以平面1AEA ⊥平面1A MN . 所以AE ⊥平面1A MN ,则1A M AE ⊥. 所以1A M ⊥平面AEF ,则1A M ⊥AF .故AFE ∠为二面角1A A M N --的平面角(设为θ). 设11AA =,则由12A B AC A A ==,120BAC ∠=,有60BAD ∠=,2,1AB AD ==.又P 为AD 的中点,所以M 为AB 的中点,且1,12AP AM ==,在1Rt AA P 中, 1A P =;在1Rt A AM 中, 1AM =从而,11AA AP AE A P ∙==11AA AM AF A M ∙==所以sin AE AF θ==.所以cos θ===. 故二面角1A A M N --解法二:设11AA =.如图,过1A 作1A E 平行于11B C ,以1A 为坐标原点,分别以111,AE AD ,1AA 的方向为x 轴,y 轴,z 轴的正方向,建立空间直角坐标系Oxyz (点O 与点1A 重合).则()10,0,0A ,()0,0,1A .因为P 为AD 的中点,所以,M N 分别为,AB AC 的中点,故11,1,,12222M N ⎛⎫⎛⎫-⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭, 所以131,122A M ⎛⎫= ⎪⎪⎝⎭,()10,0,1A A =,()3,0,0NM =.设平面1AA M 的一个法向量为()1111,,n x y z =,则1111,,n A M n A A ⎧⊥⎪⎨⊥⎪⎩即11110,0,n A M n A A ⎧∙=⎪⎨∙=⎪⎩故有()()()1111111,,,10,2,,0,0,10,x y z x y z ⎧⎫∙=⎪⎪⎪⎨⎝⎭⎪∙=⎩从而111110,20.x y z z ++=⎪=⎩取11x =,则1y =,所以()11,n =. 设平面1A MN 的一个法向量为()2222,,n x y z =,则212,,n A M n NM ⎧⊥⎪⎨⊥⎪⎩即2120,0,n A M n NM ⎧∙=⎪⎨∙=⎪⎩故有()())2222221,,,10,22,,0,x y z x y z ⎧⎛⎫∙=⎪⎪ ⎪⎪⎝⎭⎨⎪∙=⎪⎩从而222210,20.x y z ++=⎨⎪=⎩取22y =,则21z =-,所以()20,2,1n =-. 设二面角1A A M N --的平面角为θ,又θ为锐角,则1212cos n n n n θ∙===∙.故二面角1A A M N --的余弦值为512.(2013年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))本小题满分10分.如图,在直三棱柱111A B C ABC -中,AC AB ⊥,2==AC AB ,41=AA ,点D 是BC 的中点(1)求异面直线B A 1与D C 1所成角的余弦值 (2)求平面1ADC 与1ABA 所成二面角的正弦值.【答案】本题主要考察异面直线.二面角.空间向量等基础知识以及基本运算,考察运用空间向量解决问题的能力.解:(1)以{}1,,AA 为为单位正交基底建立空间直角坐标系xyz A -,则)0,0,0(A )0,0,2(B ,)0,2,0(C ,)4,0,0(1A ,)0,1,1(D ,)4,2,0(1C ∴)4,0,2(1-=A ,)4,1,1(1--=A∴10103182018,cos 11==>=<C A ∴异面直线B A 1与D C 1所成角的余弦值为10103 (2))0,2,0(= 是平面1ABA 的的一个法向量设平面1ADC 的法向量为),,(z y x =,∵)0,1,1(=,)4,2,0(1=AC 由1,AC ⊥⊥ ∴⎩⎨⎧=+=+0420z y y x 取1=z ,得2,2=-=x y ,∴平面1ADC 的法向量为)1,2,2(-=m设平面1ADC 与1ABA 所成二面角为θ∴32324,cos cos =⨯-==><=θ, 得35sin =θ ∴平面1ADC 与1ABA 所成二面角的正弦值为3513.(2013年普通高等学校招生统一考试大纲版数学(理)WORD 版含答案(已校对))如图,四棱锥P ABCD -中,902,ABC BAD BC AD PAB ∠=∠==∆,与PAD ∆都是等边三角形.(I)证明:;PB CD ⊥ (II)求二面角A PD C --的大小.【答案】14.(2013年普通高等学校招生统一考试山东数学(理)试题(含答案))如图所示,在三棱锥P ABQ -中,PB ⊥平面ABQ ,BA BP BQ ==,,,,D C E F 分别是,,,A Q B Q A P B P 的中点, 2AQ BD =,PD 与EQ 交于点G ,PC 与FQ 交于点H ,连接GH .(Ⅰ)求证:AB GH ; (Ⅱ)求二面角D GH E --的余弦值.【答案】解:(Ⅰ)证明:因为,,,D C E F 分别是,,,AQ BQ AP BP 的中点,所以EF ∥AB ,DC ∥AB ,所以EF ∥DC , 又EF ⊂平面PCD ,DC ⊂平面PCD , 所以EF ∥平面PCD , 又EF ⊂平面EFQ ,平面EFQ 平面PCD GH =,所以EF ∥GH , 又EF ∥AB , 所以AB ∥GH .(Ⅱ)解法一:在△ABQ 中, 2AQ BD =,AD DQ =,所以=90ABQ ∠,即AB BQ ⊥,因为PB ⊥平面ABQ ,所以AB PB ⊥, 又BPBQ B =,所以AB ⊥平面PBQ ,由(Ⅰ)知AB ∥GH ,所以GH ⊥平面PBQ ,又FH ⊂平面PBQ ,所以GH FH ⊥,同理可得GH HC ⊥, 所以FHC ∠为二面角D GH E --的平面角,设2BA BQ BP ===,连接PC , 在t R △FBC 中,由勾股定理得,FC =在t R △PBC 中,由勾股定理得,PC =,又H 为△PBQ 的重心,所以13HC PC ==同理FH =,在△FHC 中,由余弦定理得552499cos 5529FHC +-∠==-⨯,即二面角D GH E --的余弦值为45-.解法二:在△ABQ 中,2AQ BD =,AD DQ =,所以90ABQ ∠=,又PB ⊥平面ABQ ,所以,,BA BQ BP 两两垂直,以B 为坐标原点,分别以,,BA BQ BP 所在直线为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系,设2BA BQ BP ===,则(1,0,1)E ,(0,0,1)F ,(0,2,0)Q ,(1,1,0)D ,(0,1,0)C (0,0,2)P ,,所以(1,2,EQ =--,(0,2,1)FQ =-,(1,1,2)DP =--,(0,1,2)CP =-,设平面EFQ 的一个法向量为111(,,)m x y z =,由0m EQ ⋅=,0m FQ ⋅=,得111112020x y z y z -+-=⎧⎨-=⎩取11y =,得(0,1,2)m =.设平面PDC 的一个法向量为222(,,)n x y z =由0n DP ⋅=,0n CP ⋅=,得222222020x y z y z --+=⎧⎨-+=⎩取21z =,得(0,2,1)n =.所以4cos ,5m n m n m n⋅==因为二面角D GH E --为钝角,所以二面角D GH E --的余弦值为45-.15.(2013年高考湖南卷(理))如图5,在直棱柱1111//ABCD A B C D AD BC -中,,90,,1BAD AC BD BC ∠=⊥=,13AD AA ==.(I)证明:1AC B D ⊥; (II)求直线111B C ACD 与平面所成角的正弦值.【答案】解: (Ⅰ)AC BB ABCD BD ABCD BB D C B A ABCD ⊥⇒⊂⊥∴-111111,面且面是直棱柱 D B AC BDB D B BDB AC B BB BD BD AC 11111,,⊥∴⊂⊥∴=⋂⊥,面。
