几何证明题集-R5
(完整版)初中几何证明题五大经典(含答案)
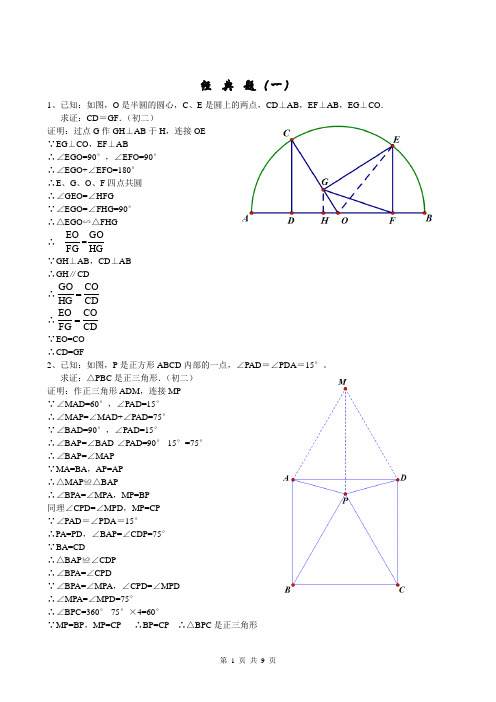
经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)证明:过点G 作GH ⊥AB 于H ,连接OE ∵EG ⊥CO ,EF ⊥AB∴∠EGO=90°,∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG ∴FG EO =HGGO∵GH ⊥AB ,CD ⊥AB ∴GH ∥CD∴CD COHG GO =∴CDCO FG EO = ∵EO=CO ∴CD=GF2、已知:如图,P 是正方形ABCD 内部的一点,∠PAD =∠PDA =15°。
求证:△PBC 是正三角形.(初二) 证明:作正三角形ADM ,连接MP ∵∠MAD=60°,∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°,∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ,AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ,MP=BP 同理∠CPD=∠MPD ,MP=CP ∵∠PAD =∠PDA =15°∴PA=PD ,∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ,∠CPD=∠MPD ∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ,MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN于E 、F .求证:∠DEN =∠F .证明:连接AC ,取AC 的中点G ,连接NG 、MG ∵CN=DN ,CG=DG ∴GN ∥AD ,GN=21AD ∴∠DEN=∠GNM ∵AM=BM ,AG=CG ∴GM ∥BC ,GM=21BC ∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二) 证明:(1)延长AD 交圆于F ,连接BF ,过点O 作OG ⊥AD 于G ∵OG ⊥AF ∴AG=FG ∵AB⌒ =AB ⌒ ∴∠F=∠ACB又AD ⊥BC ,BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2(GH+DH )=2GD 又AD ⊥BC ,OM ⊥BC ,OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM (2)连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC ,OM ⊥BC ∴∠BOM=21∠BOC=60°∴∠OBM=30° ∴BO=2OM由(1)知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线,过O 作OA ⊥MN 于A ,自A 引圆的两条割线交圆O 于B 、C 及D 、E ,连接CD 并延长交MN 于Q ,连接EB 并延长交MN 于P. 求证:AP =AQ .证明:作点E 关于AG 的对称点F ,连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ,PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF ∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP3、设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)证明:作OF ⊥CD 于F ,OG ⊥BE 于G ,连接OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ,∠E=∠C ∴△ABE ∽△ADC ∴DFBGFD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN , ∴OA ⊥MN 又OG ⊥BE ,∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°,OA=OA ∴△OAQ ≌△OAP ∴AP=AQ 在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQ4、如图,分别以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE ,点O 是DF 的中点,OP ⊥BC求证:BC=2OP (初二)证明:分别过F 、A 、D 作直线BC 的垂线,垂足分别是L 、M 、N ∵OF=OD ,DN ∥OP ∥FL ∴PN=PL∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB ∴△BFL ≌△ABM ∴FL=BM同理△AMC ≌△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)证明:连接BD 交AC 于O 。
高中数学立体几何证明题汇总

高中数学立体几何证明题汇总立体几何常考证明题1.已知四边形ABCD是空间四边形,E,F,G,H分别是边AB,BC,CD,DA的中点。
1)证明EFGH是平行四边形。
2)已知BD=23,AC=2,EG=2,求异面直线AC、BD所成的角和EG、BD所成的角。
2.如图,已知空间四边形ABCD中,BC=AC,AD=BD,E 是AB的中点。
1)证明AB垂直于平面CDE。
2)证明平面CDE垂直于平面ABC。
3.如图,在正方体ABCD-A1B1C1D1中,E是AA1的中点。
证明A1C平行于平面BDE。
4.已知三角形ABC中∠ACB=90,SA垂直于面ABC,AD垂直于SC。
证明AD垂直于面SBC。
5.已知正方体ABCD-A1B1C1D1,O是底面ABCD对角线的交点。
1)证明C1O平行于面AB1D1.2)证明AC1垂直于面AB1D1.6.正方体ABCD-A1B1C1D1中。
1)证明AC垂直于平面B1D1D。
2)证明BD1垂直于平面ACB1.7.正方体ABCD-A1B1C1D1中。
1)证明平面A1BD平行于平面B1DC。
2)已知E、F分别是AA1、CC1的中点,证明平面EB1D1平行于平面FBD。
8.四面体ABCD中,AC=BD,E、F分别为AD、BC的中点,且EF=AC/2,∠XXX。
证明BD垂直于平面ACD。
9.如图P是△ABC所在平面外一点,PA=PB,CB垂直于平面PAB,M是PC的中点,N是AB上的点,AN=3NB。
1)证明XXX垂直于AB。
2)当∠APB=90,AB=2BC=4时,求MN的长度。
10.如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AB、AD、C1D1的中点。
证明平面D1EF平行于平面BDG。
11.如图,在正方体ABCD-A1B1C1D1中,E是AA1的中点。
1)证明A1C平行于平面BDE。
2)证明平面A1AC垂直于平面BDE。
12、已知矩形ABCD,PA垂直于平面ABCD,AB=2,PA=AD=4,E为BC的中点。
七年级数学典型几何证明50题

七年级数学典型几何证明50题初一典型几何证明题1、已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 解:延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE ∠BDE=∠ADC BD=DC∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+2 1<AD <3 ∴AD=22、已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴△BCF ≌△EDF (S.A.S)A BC DEF 21 ADBC∴ BF=EF,∠CBF=∠DEF 连接BE在△BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在△ABF 和△AEF 中 AB=AE,BF=EF, ∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴△ABF ≌△AEF 。
∴ ∠BAF=∠EAF (∠1=∠2)。
3、已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG∥EF 交AD 的延长线于点G CG∥EF,可得,∠EFD=CGD DE =DC∠FDE=∠GDC(对顶角)∴△EFD≌△CGD EF =CG ∠CGD=∠EFD又,EF∥AB ∴,∠EFD=∠1 ∠1=∠2 ∴∠CGD=∠2∴△AGC 为等腰三角形, AC =CG 又 EF =CG ∴EF =AC4、已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CBA CDF2 1 EA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C5、已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB ≌△CEF ∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180° ∴∠D =∠CFA ∵AC 平分∠BAD ∴∠DAC =∠FAC ∵AC =AC∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE6、如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
立体几何证明题精选

立体几何证明题精选1.在多面体中,矩形ABB1A1和ACC1A1,AC垂直于BC。
证明BC垂直于平面ACC1A1,同时在线XXX上存在一点M,使得DE与平面A1MC平行。
2.在三棱锥P-ABC中,D,E,F分别是棱PC,AC,AB 的中点。
已知PA垂直于AC,PA=6,BC=8,DF=5.证明PA 平行于平面DEF,同时平面BDE垂直于平面ABC。
3.在四棱锥P-ABCD中,AP垂直于平面PCD,AD平行于BC,AB和BC分别为线段AD和PC的中点。
证明AP平行于平面BEF,同时BE垂直于平面PAC。
4.在四棱锥P-ABCD中,底面ABCD是平行四边形,BA=BD=BC=1,AD=2,PA=PD=√5,E和F分别是棱AD和PC的中点。
证明EF平行于平面PAB,同时平面PBC垂直于平面ABCD。
5.在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB垂直于BC,AA1=AC=2,BC=1,E和F分别是A1C1和BC的中点。
证明平面ABE垂直于平面B1BCC1,C1F平行于平面ABE,同时求三棱锥E-ABC的体积。
6.在四棱锥P-ABCD中,底面ABCD为矩形,PA垂直于平面ABCD,E为PD的中点。
证明PB平行于平面AEC,同时若AP=1,AD=3,则三棱锥P-ABD的体积为2/3,求A到平面PBC的距离。
7.在四棱锥中,平面ACD和平面ABD的交线为直线L,平面ABC和平面ACD的交线为直线M,平面ABC和平面ABD的交线为直线N,P为直线L上一点,Q为直线M上一点,R为直线N上一点,且PQR平行于平面ABCD,证明PR 平行于直线BD,同时求四面体PQRD的体积。
8.在长方体ABCD-A1B1C1D1中,底面A1B1C1D1为正方形,O为BD的中点,E为棱AA1上任意一点。
证明BD垂直于EC1,同时若AB=2,AE=2,OE垂直于EC1,则AA1的长度为2√2.。
立体几何证明练习册必刷题练习册

立体几何证明练习册必刷题练习册立体几何是数学中的一个重要分支,它涉及到空间中物体的形状、大小和位置关系。
以下是一些立体几何证明的练习题,旨在帮助学生加深对立体几何概念的理解和应用。
练习一:证明长方体的对角线问题:在长方体ABCD-A'B'C'D'中,证明对角线AC'的长度等于\(\sqrt{AB^2 + BC^2 + AA'^2}\)。
证明:首先,我们设长方体的边长为AB=a, BC=b, AA'=c。
根据勾股定理,我们可以得到对角线AC的长度为\(\sqrt{a^2 + b^2}\),对角线AA'的长度为c。
由于AC'是AC和AA'的合成线,我们可以应用勾股定理,得出AC'的长度为\(\sqrt{(\sqrt{a^2 + b^2})^2 + c^2} =\sqrt{a^2 + b^2 + c^2}\)。
练习二:证明正四面体的体积问题:在正四面体ABCD中,已知边长为a,求四面体的体积。
证明:正四面体的底面是一个等边三角形,设其边长为a。
底面的高为\(h = \frac{\sqrt{3}}{2}a\)。
四面体的高是垂直于底面的线段,设其为h'。
由于正四面体的对称性,我们可以得出h' = h。
四面体的体积公式为V = \(\frac{1}{3} \times \text{底面积} \times\text{高}\)。
代入数值,得到V = \(\frac{1}{3} \times\frac{\sqrt{3}}{4}a^2 \times \frac{\sqrt{3}}{2}a =\frac{\sqrt{3}}{12}a^3\)。
练习三:证明球体的表面积和体积问题:给定一个半径为r的球体,证明其表面积为\(4\pi r^2\),体积为\(\frac{4}{3}\pi r^3\)。
证明:球体的表面积可以通过将球体切割成无数个微小的三角形面元来计算。
初中数学几何证明题经典例题(超全)
完整版ppt
9
• 已知:如图正方形ABCD,P、Q分别是BC、 DC上的点,若∠1=∠2 求证:PB+QD=PA
完整版ppt
10
• 已知:如图正方形ABCD,AC、BD交于点 O,E、F分别是BC、OD的中点 求证: AF⊥EF
完整版ppt
11
• 已知:如图,,AB=BC,D、E分别是AB、 BC上一点,DM⊥AE交AC于M, BN⊥AE 交AC于N,若BD=BE求证:MN=NC。
完整版ppt
20
• 如图,在四边形ABCD中,AB=DC,E、F 分别是AD、BC的中点,G、H分别是BD、 AC的中点,猜一猜EF与GH的位置关系, 并证明你的结论.
完整版ppt
21
• 如图,分别以△ABC的三边为边长,在BC 的同侧作等边三角形ABD,等边三角形 BCE,等边三角形ACF,连接DE,EF。求 证:四边形ADE 2,AB=3AC,BE⊥AD,
求证:AD=DE
完整版ppt
15
• 已知:如图,AB//CD, D=90 o, BE=EC=DC,求证: AEC=3 BAE
完整版ppt
16
• 已知如图,AB=DC,AE=DE,BF=FC,
FE交BA、CD的延长线于G、H,求证:1= 2。
完整版ppt
17
• 已知:如图,正方形ABCD中,E是DC上一 点,DF⊥AE交BC于F 求证:OE⊥OF
完整版ppt
18
• 已知:如图,AB//CD, ADC=90o , BE=EC,求证: AED=2 EDC
完整版ppt
19
• 已知:如图,正方形ABCD中,E是DC上一 点,DF⊥AE交BC于F 求证:OE⊥OF
(完整版)八年级几何证明题集锦及解答值得收藏

(完整版)八年级几何证明题集锦及解答值得收藏八年级几何全等证明题归纳1.如图,梯形ABCD中,AD∥BC,∠DCB=45°,BD⊥CD.过点C作CE⊥AB 于E,交对角线BD于F,点G为BC中点,连接EG、AF.求证:CF=AB+AF.证明:在线段CF上截取CH=BA,连接DH,∵BD⊥CD,BE⊥CE,∴∠EBF+∠EFB=90°,∠DFC+∠DCF=90°,∵∠EFB=∠DFC,∴∠EBF=∠DCF,∵DB=CD,BA=CH,∴△ABD≌△HCD,∴AD=DH,∠ADB=∠HDC,∵AD∥BC,∴∠ADB=∠DBC=45°,∴∠HDC=45°,∴∠HDB=∠BDC—∠HDC=45°,∴∠ADB=∠HDB,∵AD=HD,DF=DF,∴△ADF≌△HDF,∴AF=HF,∴CF=CH+HF=AB+AF,∴CF=AB+AF.2.如图,ABCD为正方形,E为BC边上一点,且AE=DE,AE与对角线BD交于点F,连接CF,交ED于点G.判断CF与ED的位置关系,并说明理由.解:垂直.理由:∵四边形ABCD为正方形,∴∠ABD=∠CBD,AB=BC,∵BF=BF,∴△ABF≌△CBF,∴∠BAF=∠BCF,∵在RT△ABE和△DCE中,AE=DE,AB=DC,∴RT△ABE≌△DCE,∴∠BAE=∠CDE,∴∠BCF=∠CDE,∵∠CDE+∠DEC=90°,∴∠BCF+∠DEC=90°,∴DE⊥CF.3.如图,在直角梯形ABCD中,AD∥BC,∠A=90o,AB=AD,DE⊥CD交AB于E,DF平分∠CDE交BC于F,连接EF.证DA明:CF=EF解:EB F C过D作DG⊥BC于G.由已知可得四边形ABGD为正方形,∵DE⊥DC∴∠ADE+∠EDG=90°=∠GDC+∠EDG,∴∠ADE=∠GDC.又∵∠A=∠DGC且AD=GD,∴△ADE≌△GDC,∴DE=DC且AE=GC.在△EDF和△CDF中∠EDF=∠CDF,DE=DC,DF为公共边,∴△EDF ≌△CDF,∴EF=CF4.已知:在⊿ABC中,∠A=900,AB=AC,D是AC的中点,AE⊥BD,AE延长线交BC于F,求证:∠ADB=∠FDC。
八年级几何证明专题训练(50题)
(2) 当取何值时, 与 全等.
38. 如图,在Rt△ABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在边AC上,与点 重合,AE为折痕,求 的长度
39. 如图,已知ΔABC是等腰直角三角形,∠C=90°.
(1)操作并观察,如图,将三角板的45°角的顶点与点C重合,使这个角落在∠ACB的内部,两边分别与斜边AB交于E、F两点,然后将这个角绕着点C在∠ACB的内部旋转,观察在点E、F的位置发生变化时,AE、EF、FB中最长线段是否始终是EF写出观察结果.
源户卷件材源载丰讯网wwwzxxkcom源户卷件材源载丰讯网wwwzxxkcom源户卷件材源载丰讯网wwwzxxkcom源户卷件材源载丰讯网wwwzxxkcom源户卷件材源载丰讯网wwwzxxkcom源户卷件材源载丰讯网wwwzxxkcom源户卷件材源载丰讯网wwwzxxkcom源户卷件材源载丰讯网wwwzxxkcom源户卷件材源载丰讯网wwwzxxkcom源户卷件材源载丰讯
(3)试探索CF、GF和BG之间的等量关系,并证明你的结论.
28. 如图,在在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一单,点E在BC上,且AE=CF。
(1)求证:
(2)若∠CAE=30°,求∠ACF的度数
29. 如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交DC于F,BD分别交CE,AE于点G、H. 试猜测线段AE和BD数量关系,并说明理由.
(2)求证:CF=EF.
36.在 中, 平分 ,点 为直线 上一动点, 于点 .
(1)如图1 ,当 , ,点 与点 重合时,求 的度数;
(2)如图2,当点 在 延长线时, 求证: ;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
因此n []122()n E K K K K =-++++,故有:2n K =。
2.50 证明有七条棱的多面体不存在。
证明:首先可证,每一面只能是三角形。
若有一面是四边形或更多的多边形,则剩下至多三条棱,这剩下的至多三条棱无法与四顶点或更多的顶点相连而得到一多面体。
因此可得,假若存在有七条棱的多面体V ,设V 的面数为F ,棱数为E ,则23E F =。
∵7E =,∴143F =(非整数),与假设没有矛盾(由假设知F 必为正整数)。
故不存在有七条棱的多面体。
2.51 证明正四面体一双对棱中点的连线垂直于这两棱。
题设:在正四面体ABCD 中,E F 、是AB CD 、中点。
题断:EF AB ⊥,EF CD ⊥。
证明:连AF BF DE CE 、、、。
ABCD 是正四面体,∴FA FB =。
又EA EB =,∴FE AB ⊥。
同理得:EF CD ⊥。
2.52 正四面体以一顶点所引高的中点到其他三顶点连线,证明它们是一个三直三面角的三棱。
题设:在正四面体ABCD 中,'AA ⊥平面BCD 于且'A ,O 为'AA 的中点。
题断:O BCD -是三直三面角。
证明:设正四面体ABCD 的棱长为a 。
我们不难知道:'A 为正△BCD 的中心,因此'BA ''CA DA == 33a =。
22226''33a AA AB BA a a ∴=-=-=。
'6'26AA OA a ==, 2222362''()()362OB BA A O a a a ∴=+=+=。
同样得22OC a =,22OD a =。
22222222()()22OB OC a a a BC ∴+=+==。
题图 2-51题图 2-52因而知:BOC ∠=90︒。
同理可证:COD ∠=90︒,DOB ∠=90︒。
故O BCD -是三直三面角。
2.53 证明正四面体一双对棱互相垂直。
题设:AB CD 、是正四面体ABCD 的一双对棱。
题断:AB CD ⊥。
证明:取AB 的中点E ,连CE DE 、。
∵CE AB ⊥,DE AB ⊥, ∴AB ⊥平面DCE CD ⊃。
故AB ⊥CD 。
2.54 求作一平面使截正四面体的截面成矩形。
题设:正四面体ABCD 。
求作:一平面π截此四面体,使截面PQRS 为矩形。
分析:由已解决的2.28题知,首先π必平行于一双对棱(这是由于矩形⊂平行四边形)。
在这里,不妨假设π已作成,π是平行于一双对棱AC 、BD 的。
P Q R S 、、、在AB 、BC 、CD 、DA 上,我们不难知道PQ ∥AC ,QR ∥BD 。
由上题得:AC BD ⊥。
∴PQ ⊥QR ,因而PQRS 为矩形。
由此可见:平行于一双对棱的任一平面合条件。
因而本题有无限多解。
作图:从略。
2.55 求作一平面使截正四面体的截面成正方形。
题设:正四面体ABCD 。
题作:平面α截此体,使得截面PQRS 为正方形。
分析:假定图已作成,由上题知:当PQRS 为矩形,是可作出的。
若:PQRS 为正方形,则PQ QR =,即BQ QCAC BD BC BC=⋅⋅。
AC BD =,BQ QC ∴=。
因此Q 为BC 中点。
从而可知P R S 、、分别是AB CD DA 、、的中点。
作图极易,故从略。
讨论:本题永有三解。
题图 2-53题图 2-55题图 2-542.56 计算正四面体和正八面体的二面角,从而证明二者互补。
题设:α、β分别为正四面体和正八面体的二面角。
题断:2d αβ+=证明:取23A A 中点N ,连1A N 、4A N (图2-56-1), 则1A N ⊥23A A ,4A N ⊥23A A ,14A NA α∴∠=。
因此cos α=2221414142NA NA A A NA NA +-⋅。
令正四面体1234A A A A 的棱长为一个单, ∴cos α=222233()()1122332()2+-=。
因面α=arc cos 1()3。
取'BC 中点D ,连AD 、'A D , 则'AD BC ⊥,''A D BC ⊥。
'ADA β∴∠=。
设正八面体的棱长为一个单位,则3','2AD A D AA ===2。
22222233()()(2)''22cos 2'332()()22DA DA AA DA DA β+-+-==⋅13=-。
因而β=arc cos 1()3-。
故a β+=arc cos 1()3+arc cos 1()23d -=。
2.57 三等线段'AA 、'BB 、'CC 的中点重合且两两互垂,证明:A 、B 、C 、'A 、'B 、'C 决定一个正八面体。
证明:设O 点是'AA 、'BB 、'CC 的公共中点。
'AA 、'BB 、'CC 相等且垂直平分于O 。
,'O ABC O BCA ∴- -……是互为相等的正直棱锥。
因此得:八面体的各面△ABC 、△'BCA ……是全等的正三角形且任相邻的二面角是相等的。
(例如:'A BC A C ∠=∠⋅⋅⋅'AB C ⋅,这是A BC O ∠=⋅⋅题图 2-56-2题图 2-56-1题图 2-57O BC A '=∠=⋅⋅C BA O O BA C '∠=∠⋅⋅⋅⋅,A BC O ∴∠+⋅⋅'O BC A ∠⋅⋅C BA O =∠+⋅⋅'O BA C ∠⋅⋅,即'A BC A ∠⋅⋅'C BA C =∠⋅⋅)。
故得A 、B 、C 、'A 、'B 、'C 决定一个正八面体。
2.58 证明正四面体各棱中点是正八面体的顶点。
题设:正四面体1111A B C D 中,A 、'A 、B 、'B 、C 、'C 分别是三双对棱11A B 、11CD ,11A D 、11B C ,11A C 、11B D 的中点。
题断:A 、'A 、B 、'B 、C 、'C 是正八面体的顶点。
证明:由2.55题结论可知:''ABA B 、''ACA C 、''BCB C 各为正方形,'AA ∴⊥'BB 且中点重合;'AA ⊥'CC 且中点重合;'BB ⊥'CC 且中点重合。
因此:'AA 、'BB 、'CC 是三等长线段且它们中点重合,两两垂直。
故A 、'A 、B 、'B 、C 、'C 是正八面体的顶点(由上题知)。
2.59 证明正八面体可以用一个平面截得一正六边形。
题设:正八面体'''ABCA B C 中题断:可以用一个平面截得一正六边形123456A A A A A A 。
证明:取AC 、CB 、'BA 、''A C 、''C B 、'B A 的中点126A A A ,连12A A …6A 得六边形123456A A A A A A 。
12A A ∥AB ⊂平面'ABC ,23A A ∥'CA ∥'AC ⊂平面'ABC ,……61A A ∥'CB ∥'BC ⊂平面'ABC ,1A ∴、2A 、3A …6A 共平面π,且π∥平面'ABC 。
(1) 我们很易得六边形123456A A A A A A 各边长均为正八面体的棱长d 的12。
(2)又∵△OAC 是等腰直角三角形,∴11122OA AC a ==。
同理得23612OA OA OA a ====。
题图 2-59题图 2-58因此1A 、2A 、3A …6A 到正八面体中心O 距离相等,且等于12A A 。
(3)故由(1)、(2)、(3)得:123456A A A A A A 是正六边形,题断成立。
2.60 证明以平行于正八面体一面的任一平面截此体,截面的周界有定长。
题设:在正八面体'''ABCA B C 中,一平面π∥平面ABC 截之,得截面为123456A A A A A A (题图2-60)。
题断:122361A A A A A A +++,S S =为定长。
证明:设正八面体棱长为a 。
平面π∥平面ABC ,平面ABC ∥平面'''A B C , ∴平面π∥平面'''A B C 。
又AB =平面'ABC ∩平面ABC ,12A A =平面'ABC ∩平面π,∴12A A ∥AB (由1.11节节问题一)。
同理得:23A A ∥34''C A A A ,∥45BC A A ,∥56''A B A A ,∥61AC A A ,∥''B C 。
由此可设:356124123456''''''BA CA AA AA BA A Ck AC A C A A A A A B A A ======。
112'1'1C A A A AB a C A k ∴==+⋅⋅; 2231'''1BA A A C A a BC k ==+⋅⋅; 434'1'1A A A A BC a CA k ==+⋅⋅; 5451'''1CA A A A B a CB k ==+⋅⋅; 656'1'1A B A A CA a AB k ==+⋅⋅; 1611'''1AA A A C B a AC k ==+⋅⋅; 故122334455661A A A A A A A A A A A A +++++11131k k ka a k+++++==+⋅(定长)。
2.61 计算五种正多面体各有多少对角线。
解:(1)正四面体 ∵任一顶点与其它顶点都各在一个面角内,∴没有对角线。
(2)正六面体 ∵任一顶点与其它7顶点中只有一顶点不在同一面角内,∴过一顶点只有一条对角线。
题图 2-60又∵一对角线过两顶点,∴正六面体共有8142⨯=条对角线。
(3)正八面体 ∵任一顶点与其它五顶点中只有一顶点不在同一面角内,∴过每一顶点只有一条对角线。
