2019年全国中考真题分类汇编(图形操作题)
2019年全国各地中考数学试题分类汇编(第二期) 专题28 解直角三角形(含解析)

解直角三角形一.选择题1. (2019•广东省广州市•3分)如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是∠BAC,若tan∠BAC=,则此斜坡的水平距离AC为()A.75m B.50m C.30m D.12m【分析】根据题目中的条件和图形,利用锐角三角函数即可求得AC的长,本题得以解决.【解答】解:∵∠BCA=90°,tan∠BAC=,BC=30m,∴tan∠BAC=,解得,AC=75,故选:A.【点评】本题考查解直角三角形的应用﹣坡度坡角问题,解答本题的关键是明确题意,利用数形结合的思想解答.2. (2019•广西北部湾经济区•3分)小菁同学在数学实践活动课中测量路灯的高度.如图,已知她的目高AB为1.5米,她先站在A处看路灯顶端O的仰角为35°,再往前走3米站在C处,看路灯顶端O的仰角为65°,则路灯顶端O到地面的距离约为(已知sin35°≈0.6,cos35°≈0.8,tan35°≈0.7,sin65°≈0.9,cos65°≈0.4,tan65°≈2.1)()A. 米B. 米C. 米D. 米【答案】C【解析】解:过点O作OE⊥AC于点F,延长BD交OE于点F,设DF=x,∵tan65°=,∴OF=xtan65°,∴BD=3+x,∵tan35°=,∴OF=(3+x)tan35°,∴2.1x=0.7(3+x),∴x=1.5,∴OF=1.5×2.1=3.15,∴OE=3.15+1.5=4.65,故选:C.过点O作OE⊥AC于点F,延长BD交OE于点F,设DF=x,根据锐角三角函数的定义表示OF的长度,然后列出方程求出x的值即可求出答案.本题考查解直角三角形,解题的关键是熟练运用锐角三角函数的定义,本题属于中等题型.二.填空题1. (2019•江苏宿迁•3分)如图,∠MAN=60°,若△ABC的顶点B在射线AM上,且AB=2,点C在射线AN上运动,当△ABC是锐角三角形时,BC的取值范围是<BC <.【分析】当点C在射线AN上运动,△ABC的形状由钝角三角形到直角三角形再到钝角三角形,画出相应的图形,根据运动三角形的变化,构造特殊情况下,即直角三角形时的BC的值.【解答】解:如图,过点B作BC1⊥AN,垂足为C1,BC2⊥AM,交AN于点C2在Rt△ABC1中,AB=2,∠A=60°∴∠ABC1=30°∴AC1=AB=1,由勾股定理得:BC1=,在Rt△ABC2中,AB=2,∠A=60°∴∠AC2B=30°∴AC2=4,由勾股定理得:BC2=2,当△ABC是锐角三角形时,点C在C1C2上移动,此时<BC<2.故答案为:<BC<2.【点评】本题考查解直角三角形,构造直角三角形,利用特殊直角三角形的边角关系或利用勾股定理求解.考察直角三角形中30°的角所对的直角边等于斜边的一半,勾股定理等知识点.2. (2 019·江苏盐城·3分)如图,在△ABC 中,BC =26+,∠C =45°,AB =2AC ,则AC 的长为________.【答案】2【解析】过A 作AD ⊥BC 于D 点,设AC =x 2,则AB =x 2,因为∠C =45°,所以AD =AC =x ,则由勾股定理得BD =x AD AB 322=-,因为AB =26+,所以AB =263+=+x x ,则x =2.则AC =2.3. (2 019·江苏盐城·3分)如图,在平面直角坐标系中,一次函数y =2x -1的图像分别交x 、y 轴于点A 、B ,将直线AB 绕点B 按顺时针方向旋转45°,交x 轴于点C ,则直线BC 的函数表达式是__________.【答案】131-=x y 【解析】因为一次函数y =2x -1的图像分别交x 、y 轴于点A 、B ,则A (21,0),B (0,-1),则AB =25. 过A 作AD ⊥BC 于点D ,因为∠ABC =45°,所以由勾股定理得AD =410,设BC =x ,则AC =OC -OA =2112--x ,根据等面积可得:AC ×OB =BC ×AD ,即2112--x =410x ,解得x =10.则AC =3,即C (3,0),所以直线BC 的函数表达式是131-=x y .4. (2019•浙江湖州•4分)有一种落地晾衣架如图1所示,其原理是通过改变两根支撑杆夹角的度数来调整晾衣杆的高度.图2是支撑杆的平面示意图,AB 和CD 分别是两根不同长度的支撑杆,夹角∠BOD =α.若AO =85cm ,BO =DO =65cm .问:当α=74°时,较长支撑杆的端点A 离地面的高度h 约为 120 cm .(参考数据:sin 37°≈0.6,cos 37°≈0.8,sin 53°≈0.8,cos 53°≈0.6.)【分析】过O 作OE ⊥BD ,过A 作AF ⊥BD ,可得OE ∥AF ,利用等腰三角形的三线合一得到OE 为角平分线,进而求出同位角的度数,在直角三角形AFB 中,利用锐角三角函数定义求出h 即可.【解答】解:过O 作OE ⊥BD ,过A 作AF ⊥BD ,可得OE ∥AF , ∵BO =DO , ∴OE 平分∠BOD ,∴∠BOE =∠BOD =×74°=37°, ∴∠F AB =∠BOE =37°,在Rt △ABF 中,AB =85+65=150cm , ∴h =AF =AB •cos ∠F AB =150×0.8=120cm , 故答案为:120【点评】此题考查了解直角三角形的应用,弄清题中的数据是解本题的关键.三.解答题1. (2019•江苏宿迁•10分)宿迁市政府为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面上的实物图,图②是其示意图,其中AB、CD都与地面l平行,车轮半径为32cm,∠BCD=64°,BC=60cm,坐垫E与点B的距离BE为15cm.(1)求坐垫E到地面的距离;(2)根据经验,当坐垫E到CD的距离调整为人体腿长的0.8时,坐骑比较舒适.小明的腿长约为80cm,现将坐垫E调整至坐骑舒适高度位置E',求EE′的长.(结果精确到0.1cm,参考数据:sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)【分析】(1)作EM⊥CD于点M,由EM=ECsin∠BCM=75sin46°可得答案;(2)作E′H⊥CD于点H,先根据E′C=求得E′C的长度,再根据EE′=CE﹣CE′可得答案【解答】解:(1)如图1,过点E作EM⊥CD于点M,由题意知∠BCM=64°、EC=BC+BE=60+15=75cm,∴EM=ECsin∠BCM=75sin64°≈67.5(cm),则单车车座E到地面的高度为67.5+32≈99.5(cm);(2)如图2所示,过点E′作E′H⊥CD于点H,由题意知E′H=80×0.8=64,则E′C==≈71,1,∴EE′=CE﹣CE′=75﹣71.1=3.9(cm).【点评】本题考查解直角三角形的应用,解题的关键是明确题意,利用锐角三角函数进行解答.2. (2019•江西•8分)图1是一台实物投影仪,图2是它的示意图,折线B-A-O表示固定支架,AO垂直水平桌面OE于点O,点B为旋转点,BC可转动,当BC绕点B顺时针旋转时,投影探头CD始终垂直于水平桌面OE,经测量:AO=6.8cm,CD=8cm,AB=30cm,BC=35cm.(结果精确到0.1)(1)如图2,∠ABC=70°,BC∥OE。
2019年全国各地中考数学试题分类汇编(第二期) 专题35 尺规作图(含解析)

尺规作图一.选择题1.(2019•贵阳•3分)如图,在△ABC中,AB=AC,以点C为圆心,CB长为半径画弧,交AB于点B和点D,再分别以点B,D为圆心,大于BD长为半径画弧,两弧相交于点M,作射线CM交AB于点E.若AE=2,BE=1,则EC的长度是()A.2 B.3 C.D.【分析】利用基本作图得到CE⊥AB,再根据等腰三角形的性质得到AC=3,然后利用勾股定理计算CE的长.【解答】解:由作法得CE⊥AB,则∠AEC=90°,AC=AB=BE+AE=2+1=3,在Rt△ACE中,CE==.故选:D.【点评】本题考查了作图﹣基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).2. (2019•河北•3分)根据圆规作图的痕迹,可用直尺成功找到三角形外心的是()A.B.C.D.【解答】解:三角形外心为三边的垂直平分线的交点,由基本作图得到C选项作了两边的垂直平分线,从而可用直尺成功找到三角形外心.故选:C.3. (2019•河南•3分)如图,在四边形ABCD中,AD∥BC,∠D=90°,AD=4,BC=3.分别以点A,C为圆心,大于AC长为半径作弧,两弧交于点E,作射线BE交AD于点F,交AC于点O.若点O是AC的中点,则CD的长为()A.2B.4 C.3 D.【分析】连接FC,根据基本作图,可得OE垂直平分AC,由垂直平分线的性质得出AF =FC.再根据ASA证明△FOA≌△BOC,那么AF=BC=3,等量代换得到FC=AF=3,利用线段的和差关系求出FD=AD﹣AF=1.然后在直角△FDC中利用勾股定理求出CD 的长.【解答】解:如图,连接FC,则AF=FC.∵AD∥BC,∴∠F AO=∠BCO.在△FOA与△BOC中,,∴△FOA≌△BOC(ASA),∴AF=BC=3,∴FC=AF=3,FD=AD﹣AF=4﹣3=1.在△FDC中,∵∠D=90°,∴CD2+DF2=FC2,∴CD2+12=32,∴CD=2.故选:A.【点评】本题考查了作图﹣基本作图,勾股定理,线段垂直平分线的判定与性质,全等三角形的判定与性质,难度适中.求出CF与DF是解题的关键.二.填空题1.2.3.4.三.解答题1. (2019•江苏无锡•10分)按要求作图,不要求写作法,但要保留作图痕迹.(1)如图1,A为⊙O上一点,请用直尺(不带刻度)和圆规作出⊙O的内接正方形;(2)我们知道,三角形具有性质:三边的垂直平分线相交于同一点,三条角平分线相交于一点,三条中线相交于一点,事实上,三角形还具有性质:三条高所在直线相交于一点.请运用上述性质,只用直尺(不带刻度)作图.①如图2,在▱ABCD中,E为CD的中点,作BC的中点F.②如图3,在由小正方形组成的4×3的网格中,△ABC的顶点都在小正方形的顶点上,作△ABC的高AH.【分析】(1)连结AE并延长交圆E于点C,作AC的中垂线交圆于点B,D,四边形ABCD 即为所求.(2)①连结AC,BD交于点O,连结EB交AC于点G,连结DG并延长交CB于点F,点F即为所求;②结合网格特点和三角形高的概念作图可得.【解答】解:(1)如图1,连结AO并延长交圆O于点C,作AC的中垂线交圆于点B,D,四边形ABCD即为所求.(2)①如图2,连结AC,BD交于点O,连结EB交AC于点G,连结DG并延长交CB 于点F,F即为所求②如图3所示,AH即为所求.【点评】本题主要考查作图﹣应用与设计作图,解题的关键是掌握圆的有关性质和平行四边形的性质及三角形垂心的性质.2. (2019•江苏宿迁•10分)在Rt△ABC中,∠C=90°.(1)如图①,点O在斜边AB上,以点O为圆心,OB长为半径的圆交AB于点D,交BC于点E,与边AC相切于点F.求证:∠1=∠2;(2)在图②中作⊙M,使它满足以下条件:①圆心在边AB上;②经过点B;③与边AC相切.(尺规作图,只保留作图痕迹,不要求写出作法)【分析】(1)连接OF,可证得OF∥BC,结合平行线的性质和圆的特性可求得∠1=∠OFB =∠2,可得出结论;(2)由(1)可知切点是∠ABC的角平分线和AC的交点,圆心在BF的垂直平分线上,由此即可作出⊙M.【解答】解:(1)证明:如图①,连接OF,∵AC是⊙O的切线,∴OE⊥AC,∵∠C=90°,∴OE∥BC,∴∠1=∠OFB,∵OF=OB,∴∠OFB=∠2,∴∠1=∠2.(2)如图②所示⊙M为所求.①①作∠ABC平分线交AC于F点,②作BF的垂直平分线交AB于M,以MB为半径作圆,即⊙M为所求.证明:∵M在BF的垂直平分线上,∴MF=MB,∴∠MBF=∠MFB,又∵BF平分∠ABC,∴∠MBF=∠CBF,∴∠CBF=∠MFB,∴MF∥BC,∵∠C=90°,∴FM⊥AC,∴⊙M与边AC相切.【点评】本题主要考查圆和切线的性质和基本作图的综合应用.掌握连接圆心和切点的半径与切线垂直是解题的关键,3. (2019•江西•6分)在△ABC中,AB=AC,点A在以BC为直径的半圆内.请仅用无刻度的直尺分别按下列要求画图(保留作图痕迹).(1)在图1中作弦EF,使EF//BC;(2)在图2中以BC为边作一个45°的圆周角.F(1)EF就是所求作的弦;(2)角BCQ或角CBQ就是所求作的角。
2019年全国中考数学真题分类汇编:尺规作图(含答案)

2019 年全国中考数学真题分类汇编:尺规作图、选择题1. (2019 年北京市)已知锐角∠ AOB 如图,(1)在射线OA 上取一点C,以点O 为圆心,OC长为半径作弧PQ,交射线OB 于点D,连接CD;2)分别以点C,D 为圆心,CD 长为半径作弧,交弧PQ 于点M,N;3)连接OM,MN .根据以上作图过程及所作图形,下列结论中错误的是()A.∠COM= ∠CODB.若 OM=MN ,则∠ AOB=20°C.MN ∥CDD.MN=3CD【考点 】尺规作图【解答 】连接 ON ,由作图可知 △COM ≌△ DON.A. 由△COM ≌△DON.,可得∠ COM= ∠COD ,故 A正确.B. 若 OM=MN ,则 △OMN 为等边三角形,由全等可知∠ COM= ∠COD= ∠DON=2°0 ,故 B 正确180 CODC.由题意, OC=OD ,∴∠ OCD= .设 OC2 180 与 OD 与MN 分别交于 R ,S ,易证△ MOR ≌△ NOS ,则OR=OS ,∴∠ ORS= 2∴∠ OCD= ∠ORS.∴MN ∥CD ,故 C 正确.D.由题意,易证 MC=CD=DN ,∴ MC+CD+DN=3CD. ∵两点之间线段最短 .∴MN < MC+CD+DN=3CD ,故选 D2. (2019 年河南省)如图,在四边形 ABCD 中, AD ∥ BC ,∠D =90°,AD =4,BC =3.分 别以点 A , C 为圆心,大于 C 长为半径作弧,两弧交于点 交 AC 于点 O .若点 O 是 AC 的中点,则 CD 的长为( )A .2B .4C . 3D .【考点 】尺规作图、 线段垂直平分线的判定与性质、 勾股定理、 全等三角形的判定与性质【解答 】解:如图,连接 FC ,则 AF =FC .∵AD ∥ BC ,∴∠ FAO =∠ BCO .在 △FOA 与 △BOC 中,COD ,E ,作射线 BE 交 AD 于点F ,A .正方形B .矩形C .梯形D .菱形考点 】尺规作图、菱形的判定解答 】解:由作图可知: AC = AD =BC = BD ,∴四边形ACBD 是菱形,故选: D.通过如下尺规作图,能确定点 D是BC 边中点的是(,∴△ FOA ≌△ BOC ( ASA ),∴AF =BC =3,∴FC = AF =3,FD =AD ﹣AF =4﹣3=1. 在△FDC 中,∵∠ D =90°, ∴CD 2+DF 2=FC 2,∴CD 2+12=32,∴CD =2 .故选: A .3. ( 2019年湖北省襄阳市)如图,分别以线段 AB 的两个端点为圆心,大于 AB 的一半的长为半径画弧,两弧分别交于 C ,D 两点,连接 AC ,BC ,AD ,BD ,则四边形 ADBC 一定 是( )4. (2019 年湖北省宜昌市) C . D .考点】尺规作图解答】解:作线段BC 的垂直平分线可得线段BC 的中点.由此可知:选项 A 符合条件,故选: A .5. (2019年内蒙古包头市)如图,在Rt△ABC 中,∠ B=90°,以点A为圆心,适当长为半径画弧,分别交AB、AC 于点D,E,再分别以点D、E为圆心,大于DE 为半径画弧,两弧交于点F,作射线AF 交边BC 于点G,若BG=1,AC=4,则△ACG 的面积是()A .BP 是∠ ABC 的平分线B.AD =BDC .S△CBD:S△ ABD=1: 3 D.CD=BD考点】尺规作图-角的平分线A .1 B.C. 2考点】尺规作图-角的平分线解答】解:由作法得AG 平分∠ BAC,∴G点到AC的距离等于BG 的长,即G 点到AC 的距离为1,所以△ACG 的面积=×4×1=2.故选: C .D.6. (2019 年新疆)如图,在△ ABC 中,∠ C=90°,∠ A=30°,以点 B 为圆心,适当长为半径画弧,分别交BA,BC于点M,N;再分别以点M,N 为圆心,大于MN 的长为半径画弧,两弧交于点P,作射线BP 交AC 于点D.则下列说法中不正确的是()解答】解:由作法得BD 平分∠ ABC,所以 A 选项的结论正确;∵∠ C=90°,∠ A=30∴∠ ABC=60°,∴∠ ABD=30°=∠ A,∴AD=BD,所以 B 选项的结论正确;∵∠ CBD=∠ ABC=30°,∴BD=2CD,所以 D 选项的结论正确;∴AD=2CD,∴ S△ABD=2S△CBD,所以 C 选项的结论错误.故选: C .二、填空题1. (2019 年辽宁省本溪市)如图,BD 是矩形ABCD 的对角线,在BA 和BD 上分别截取BE,BF,使BE=BF;分别以E,F为圆心,以大于EF的长为半径作弧,两弧在∠ ABD 内交于点G,作射线BG 交AD 于点P,若AP=3,则点P到BD 的距离为.考点】尺规作图解答】解:结合作图的过程知:BP平分∠ ABD,∵∠ A=90°,AP=3,∴点P到BD 的距离等于AP的长,为3,故答案为:3.1. (2019 年山东省菏泽市)如图,四边形ABCD 是矩形.(1)用尺规作线段AC的垂直平分线,交AB于点E,交CD于点F(不写作法,保留作图痕迹);(2)若BC =4,∠ BAC=30°,求BE 的长.考点】尺规作图、垂直平分线解答】解:(1)如图所示:(2)∵四边形ABCD 是矩形,EF 是线段AC 的垂直平分线,∴ AE=EC ,∠ CAB =∠ ACE=30°,∴∠ ECB=60°,∴∠ ECB=30°,∵BC=4,∴ BE=.2. (2019年山东省济宁市)如图,点M 和点N在∠ AOB 内部.(1)请你作出点P,使点P到点M和点N的距离相等,且到∠ AOB 两边的距离也相等(保留作图痕迹,不写作法);(2)请说明作图理由.考点】作角平分线、作线段垂直平分线解答】解:(1)如图,点P到点M和点N的距离相等,且到∠ AOB两边的距离也相等;(2)理由:角的平分线上的点到角的两边的距离相等、直平分线上的点到线段两端点的3. (2019 年山东省青岛市)请用直尺、圆规作图,不写作法,但要保留作图痕迹.已知:∠α,直线l 及l 上两点A,B.考点】尺规作图解答】解:如图,△ ABC 为所作.4. (2019 年山东省枣庄市)如图,BD 是菱形ABCD 的对角线,∠ CBD=75°,(1)请用尺规作图法,作AB的垂直平分线EF ,垂足为E,交AD 于F;(不要求写作法,保留作图痕迹)(2)在(1)条件下,连接BF,求∠ DBF 的度数.考点】尺规作图-线段的垂直平分线、菱形的性质解答】解:(1)如图所示,直线EF 即为所求;(2)∵四边形ABCD 是菱形,∴∠ ABD=∠ DBC=∠ABC=75°,DC∥AB,∠ A=∠C.∴∠ ABC=150°,∠ ABC+∠C=180°,∴∠ C=∠ A=30°,∵ EF 垂直平分线段AB,∴AF=FB,∴∠ A=∠ FBA =30°,∴∠ DBF =∠ ABD﹣∠ FBE=455. (2019 年四川省达州市)如图,在Rt△ABC 中,∠ ACB=90°,AC=2,BC=3.1)尺规作图:不写作法,保留作图痕迹.① 作∠ ACB 的平分线,交斜边AB 于点 D ;② 过点 D 作BC 的垂线,垂足为点 E .(2)在(1)作出的图形中,求DE 的长.考点】尺规作图-角的平分线、相似三角形解答】解:(1)如图,DE 为所作;(2)∵CD 平分∠ ACB,∴∠ BCD=∠ ACB=45°,∵DE⊥ BC,∴△CDE 为等腰直角三角形,∴DE=CE,∵DE∥ AC,∴△ BDE ∽△ BAC ,=,即=.6. (2019 年广西贵港市)尺规作图(只保留作图痕迹,不要求写出作法):如图,已知△ABC,请根据“SAS”基本事实作出△DEF ,使△DEF≌△ABC.△ABC 中,∠ C=900,AC=4, BC=8,(1)用直尺和圆规作AB 的垂直平分线;(保留作图痕迹,不要求写作法)(2)若(1)中所作的垂直平分线交BC 于点D,求BD 的长.解答】解:(1)略;2)由作图可知AD =BD,设BD= x,∵∠ C=900,AC=4, BC=8,则CD=(8- x),∴由勾股定理可得:AC 2+CD 2=AD 2;∴42+x2=(8-x)2;考点】尺规作图-线段的垂直平分线、勾股定理∴DE=7. (2019 年江苏省泰州市)如图,、全等三角形的判定解得:x= 5.∴ BD = 5.8. (2019年陕西省)如图,在△ABC中,AB=AC,AD是BC边上的高,请用尺规作图法,求作△ ABC 的外接圆.(保留作图痕迹,不写作法)得点M 到AB 和AC 两边的距离相等,并且到点B和点P 的距离相等.(不写作法,保留考点】尺规作图-角平分线解答】解:如图,点M 即为所求,10. (2019 年甘肃省武威市)已知:在△ ABC 中,AB=AC.(1)求作:△ ABC 的外接圆.(要求:尺规作图,保留作图痕迹,不写作法)(2)若△ ABC的外接圆的圆心O到BC边的距离为4,BC=6,则S⊙O=考点】尺规作图-线段的垂直平分线解答】9. 2019 年甘肃省)如图,在△ ABC 中,点P 是AC 上一点,连接BP,求作一点M ,使作图痕迹)考点】尺规作图-角平分线、等腰三角形的性质、三角形的外接圆与外心解答】解:(1)如图⊙O 即为所求.(2)设线段BC 的垂直平分线交BC 于点E.由题意OE=4,BE=EC=3,在Rt△ OBE 中,OB ==5,2∴S 圆O=π?5 =25π.故答案为25π.11. (2019 年内蒙古赤峰市)已知:AC 是? ABCD 的对角线.(1)用直尺和圆规作出线段AC 的垂直平分线,与AD 相交于点E,连接CE.(保留作图痕迹,不写作法);(2)在(1)的条件下,若AB=3,BC=5,求△ DCE的周长.考点】尺规作图-垂直平分线、平行四边形的性质解答】解:(1)如图,CE 为所作;(2)∵四边形ABCD 为平行四边形,∴AD=BC=5,CD=AB=3,∵点E在线段AC 的垂直平分线上,∴EA=EC,∴△ DCE 的周长=CE+DE+CD=EA+DE+CD=AD+CD =5+3=8.。
2019全国中招物理作图题汇总(带答案)
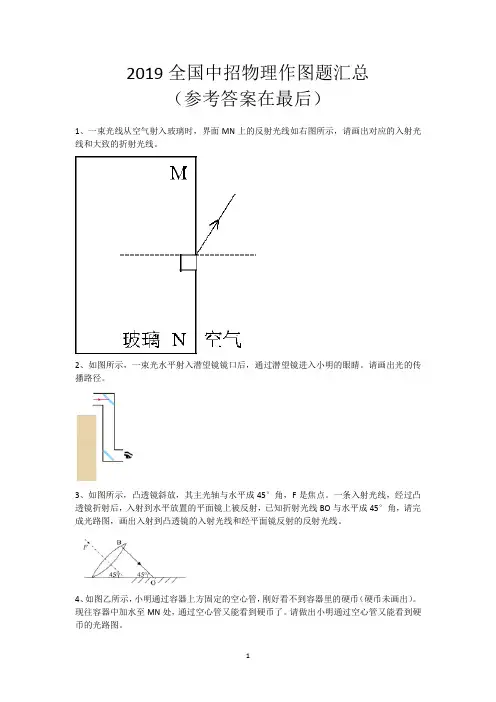
2019全国中招物理作图题汇总(参考答案在最后)1、一束光线从空气射入玻璃时,界面MN上的反射光线如右图所示,请画出对应的入射光线和大致的折射光线。
2、如图所示,一束光水平射入潜望镜镜口后,通过潜望镜进入小明的眼睛。
请画出光的传播路径。
3、如图所示,凸透镜斜放,其主光轴与水平成45°角,F是焦点。
一条入射光线,经过凸透镜折射后,入射到水平放置的平面镜上被反射,已知折射光线BO与水平成45°角,请完成光路图,画出入射到凸透镜的入射光线和经平面镜反射的反射光线。
4、如图乙所示,小明通过容器上方固定的空心管,刚好看不到容器里的硬币(硬币未画出)。
现往容器中加水至MN处,通过空心管又能看到硬币了。
请做出小明通过空心管又能看到硬币的光路图。
5、(1)从焦点射向凸透饶的一朿光如图甲所示,请画出通过透镜后的光线6、如图所示,ab是经平面镜反射后的一条光线。
请在图中画出ab的入射光线和ab经凹透镜折射后的光线。
7、“坐井观天,所见甚小”,青蛙在枯井和有水的井中“观天”的范围大小是不同的。
如图所示,一只青蛙在井底(井中有水)中央,请用光路图作出井底之蛙“观天”的最大范围。
8、如图所示,ab是光源S发出经平面镜反射后射向凸透镜焦点F的一条光线,S′是光源S 在平面镜中的像。
请画出:(1)光源S的位置;(2)光线ab经凸透镜后折射光线的大致位置。
9、如图乙所示,请画出两条光线经过凹透镜后的折射光线。
10、有一点光源S,它在平面镜中的像与凸透镜的焦点F重合,S发出的一条光线经平面镜反射后,反射光线为a,如图所示。
请在图中画出:凸透镜的焦点F;点光源S的位置;光线a经过凸透镜后的折射光线。
11、质量均匀的小球a从地面冲上弧形轨道,如图乙所示,是小球a向上运动的某一状态,请画出此时小球所受重力及小球对弧形轨道压力的示意图。
12、(1)如图所示,小车A与B一起向右做匀速直线运动,当小车A与正前方的墙碰撞时,请画出物体B受到的重力和摩擦力的示意图(两力均画在重心上)13、请在图中画出足球所受重力的示意图。
2019年中考物理真题分类汇编 作图题(含解析)

作图题分类汇编1(2018日照)如图所示,在探究“凸透镜成像规律”的实验中,将蜡烛放在位置A时,观测到在位置C成倒立、缩小的实像。
若把蜡烛移到位置B,试作图找出蜡烛通过透镜的成像位置。
解析:从物体A的顶端做平行于主光轴的光线,过凸透镜后经过焦点而会聚到像点。
由A的顶端发出过光心的光线,传播方向不变。
从物体B的顶端做平行主光轴的光线,折射后过焦点,再从B的顶端做过光心的光线,这两条折射光线的反向延长线的交点就是像的位置,如图所示:2.(2018•青岛)物体A、B一起在水平面上向右做匀速直线运动,请画出A的受力示意图解:物体A随B一起做匀速直线运动,处于平衡状态,A受到竖直向下的重力G和竖直向上的支持力F,G 与F是一对平衡力,它们大小相等、方向相反,且作用在同一直线上,作用点在物体A的重心;由于A与B处于相对静止状态,故A与B之间无摩擦力,则A在水平方向上不受力的作用;重力从重心竖直向下画,符号为G;支持力从重心竖直向上画,符号为F,注意两条线段的长度相同,如图所示:3.(2018德州)如图所示,光S发出的一束光经墙上的平面镜反射后,射入游泳池中。
请画出它经平面镜发生反射及进入水中发生折射的光路图。
___________【答案】【解析】过入射点作法线,根据光的反射定律反射角等于入射角,作出反射光线;再根据当光从空气斜射入水中时,折射角小于入射角,作出其折射光线,如图所示:4.(2018日照)某学习小组在老师的指导下,探究电流通过导体时产生热量的多少跟什么因素有关。
他们用的实验器材如图所示,两个透明容器中密封着等量空气,U形管中液面最初相平,两个密闭容器中都有一段电阻丝。
(1)请你用笔画线代替导线,把图甲两个容器的电阻丝接到电路中。
(2)实验中通过观察液面高度的变化比较电流通过导体产生热量的多少,这种方法叫转换法。
(3)接好电路,闭合开关,通电一段时间后,右(填“左”或“右”)侧U形管中液面高度变化大,此实验现象表明,在电流和通电时间均相同的情况下,电阻越大,所产生的热量越多。
2019年中考真题化学真题分类汇编专题27坐标图像题(第01期)(解析版)

2019年中考真题化学真题分类汇编专题27坐标图像题(第01期)(解析版)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN专题27 坐标图像题1.【2019年甘肃省兰州市】实验室使用一定质量的高锰酸钾加热分解制氧气,各物理量随加热时间变化的图像正确的是A.B.C.D.【答案】D【解析】A、高锰酸钾受热分解,开始的一段时间不会生成氧气,氧气的质量逐渐增大,然后不变,故A错误;B、高锰酸钾受热分解,固体质量逐渐减少,钾元素的质量分数逐渐增大,然后不变,故B错误;C、二氧化锰的质量从零开始逐渐增大,然后不变,故C错误;D、固体中锰,钾元素的质量比不变,故D正确。
故选D。
2.【2019年河南省】下列图像分别与选项中的操作相对应,其中合理的是A.向pH为13的氢氧化钠溶液中加水B.向一定质量二氧化锰固体中加一定质量过氧化氢溶液C.温度不变,向一定质量饱和氢氧化钙溶液中加入氧化钙D.向一定质量硫酸和硫酸铜的混合溶液中加入氢氧化钠溶液【答案】D【解析】A、向pH为13的氢氧化钠溶液中加水,pH减小,但是不能减小到7,更不能小于7,该选项对应关系不正确;B、过氧化氢在二氧化锰催化作用下分解生成水和氧气,过程中固体质量始终不变,该选项对应关系不正确;C、温度不变,向一定质量饱和氢氧化钙溶液中加入氧化钙,氧化钙和水反应生成氢氧化钙,水减少导致部分氢氧化钙析出,溶液质量减小,该选项对应关系不正确;D、向一定质量硫酸和硫酸铜的混合溶液中加入氢氧化钠溶液,氢氧化钠先和硫酸反应生成硫酸钠和水,后和硫酸铜反应生成氢氧化铜沉淀和硫酸钠,该选项对应关系正确。
故选D。
3.【2019年湖北省宜昌市】对一定量氯酸钾和二氧化锰的混合物加热,下列图像能正确表示对应变化关系的是A.B.C.D.【答案】C【解析】A、氯酸钾在二氧化锰催化作用下受热分解生成氯化钾和氧气,随着反应进行,氧气质量增大,完全反应后氧气质量不再变化,该选项对应关系不正确;B、随着反应进行,固体质量减小,剩余固体中锰元素质量分数增大,该选项对应关系不正确;C、随着反应进行,不断生成氧气,剩余固体中氧元素质量减小,完全反应后氧元素质量不再变化,该选项对应关系正确;D、反应前氯化钾质量是0,该选项对应关系不正确。
2019年全国中考数学真题分类汇编:全等三角形(有答案)
2019年全国中考数学真题分类汇编:全等三角形一、选择题1. (2019年山东省滨州市)如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:①AC=BD;②∠AMB =40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的个数为()A.4 B.3 C.2 D.1【考点】全等三角形的判定与性质、三角形的外角性质、角平分线的判定【解答】解:∵∠AOB=∠COD=40°,∴∠AOB+∠AOD=∠COD+∠AOD,即∠AOC=∠BOD,在△AOC和△BOD中,,∴△AOC≌△BOD(SAS),∴∠OCA=∠ODB,AC=BD,①正确;∴∠OAC=∠OBD,由三角形的外角性质得:∠AMB+∠OAC=∠AOB+∠OBD,∴∠AMB=∠AOB=40°,②正确;作OG⊥MC于G,OH⊥MB于H,如图所示:则∠OGC=∠OHD=90°,在△OCG和△ODH中,,∴△OCG≌△ODH(AAS),∴OG=OH,∴MO平分∠BMC,④正确;正确的个数有3个;故选:B.2. (2019年山东省青岛市)如图,BD是△ABC的角平分线,AE⊥BD,垂足为F.若∠ABC=35°,∠C=50°,则∠CDE的度数为()A.35°B.40°C.45°D.50°【考点】三角形的内角和、全等三角形的判定和性质、三角形的外角的性质【解答】解:∵BD是△ABC的角平分线,AE⊥BD,∴∠ABD=∠EBD,∠AFB=∠EFB,∵BF=BF,∴△ABF∽△EBF(ASA),∴AF=EF,AB=BE,∴AD=DE,∵∠ABC=35°,∠C=50°,∴∠BAC=180°﹣∠ABC﹣∠C=95°,在△DAB与△DEB中,∴△ABD≌△EAD(SSS),∴∠BED=∠BAD=95°,∴∠ADE=360°﹣95°﹣95°﹣35°=145°,∴∠CDE=180°﹣∠ADE=35°,故选:A.二、填空题1. (2019年湖北省襄阳市)如图,已知∠ABC=∠DCB,添加下列条件中的一个:①∠A=∠D,②AC=DB,③AB=DC,其中不能确定△ABC≌△DCB的是(只填序号).【考点】全等三角形的判定【解答】解:∵已知∠ABC=∠DCB,且BC=CB∴若添加①∠A =∠D ,则可由AAS 判定△ABC ≌△DCB ;若添加②AC =DB ,则属于边边角的顺序,不能判定△ABC ≌△DCB ; 若添加③AB =DC ,则属于边角边的顺序,可以判定△ABC ≌△DCB . 故答案为:②. 三、解答题1.(2019年乐山市)如图10,线段AC 、BD 相交于点E ,DE AE = ,CE BE =.求证:C B ∠=∠.【考点】全等三角形的判定和性质 【解答】证明:在AEB ∆和DEC ∆中,DE AE = ,CE BE =,DEC AEB ∠=∠AEB ∆∴≌DEC ∆,故C B ∠=∠,得证.2. (2019年重庆市)如图,在平行四边形ABCD 中,点E 在边BC 上,连结AE ,EM ⊥AE ,垂足为E ,交CD 于点M ,AF ⊥BC ,垂足为F ,BH ⊥AE ,垂足为H ,交AF 于点N ,点P 是AD 上一点,连接CP . (1)若DP =2AP =4,CP =,CD =5,求△ACD 的面积.(2)若AE =BN ,AN =CE ,求证:AD =CM +2CE .【考点】平行四边形的性质、全等三角形的判定和性质、勾股定理 【解答】(1)解:作CG ⊥AD 于G ,如图1所示: 设PG =x ,则DG =4﹣x ,在Rt △PGC 中,GC 2=CP 2﹣PG 2=17﹣x ,在Rt △DGC 中,GC 2=CD 2﹣GD 2=52﹣(4﹣x )2=9+8x ﹣x 2, ∴17﹣x 2=9+8x ﹣x 2, 解得:x =1,即PG =1, ∴GC =4, ∵DP =2AP =4,CE 图10∴S△ACD=×AD×CG=×6×4=12;(2)证明:连接NE,如图2所示:∵AH⊥AE,AF⊥BC,AE⊥EM,∴∠AEB+∠NBF=∠AEB+∠EAF=∠AEB+∠MEC=90°,∴∠NBF=∠EAF=∠MEC,在△NBF和△EAF中,,∴△NBF≌△EAF(AAS),∴BF=AF,NF=EF,∴∠ABC=45°,∠ENF=45°,FC=AF=BF,∴∠ANE=∠BCD=135°,AD=BC=2AF,在△ANE和△ECM中,,∴△ANE≌△ECM(ASA),∴CM=NE,又∵NF=NE=MC,∴AF=MC+EC,∴AD=MC+2EC.3. (2019年山东省枣庄市)在△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D.(1)如图1,点M,N分别在AD,AB上,且∠BMN=90°,当∠AMN=30°,AB=2时,求线段AM的长;(2)如图2,点E,F分别在AB,AC上,且∠EDF=90°,求证:BE=AF;(3)如图3,点M在AD的延长线上,点N在AC上,且∠BMN=90°,求证:AB+AN【考点】等腰直角三角形的性质、全等三角形的判定和性质、勾股定理【解答】(1)解:∵∠BAC=90°,AB=AC,AD⊥BC,∴AD=BD=DC,∠ABC=∠ACB=45°,∠BAD=∠CAD=45°,∵AB=2,∴AD=BD=DC=,∵∠AMN=30°,∴∠BMD=180°﹣90°﹣30°=60°,∴∠MBD=30°,∴BM=2DM,由勾股定理得,BM2﹣DM2=BD2,即(2DM)2﹣DM2=()2,解得,DM=,∴AM=AD﹣DM=﹣;(2)证明:∵AD⊥BC,∠EDF=90°,∴∠BDE=∠ADF,在△BDE和△ADF中,,∴△BDE≌△ADF(ASA)∴BE=AF;(3)证明:过点M作ME∥BC交AB的延长线于E,∴∠AME=90°,则AE=AM,∠E=45°,∴ME=MA,∵∠AME=90°,∠BMN=90°,∴∠BME=∠AMN,在△BME和△AMN中,,∴△BME ≌△AMN (ASA ), ∴BE =AN ,∴AB +AN =AB +BE =AE =AM .4. (2019年云南省)如图,AB =AD ,CB =CD. 求证:∠B =∠D.【考点】全等三角形的判定和性质【解答】证明:在△ABC 和△ADC 中,⎪⎩⎪⎨⎧===AC AC DC BC AD AB ∴△ABC ≌ADC (SSS ) ∴∠B =∠D5.(2019年广西贺州市)如图,在矩形ABCD 中,E ,F 分别是BC ,AD 边上的点,且AE =CF .(1)求证:△ABE ≌△CDF ;(2)当AC ⊥EF 时,四边形AECF 是菱形吗?请说明理由.【考点】矩形的性质、全等三角形的判定与性质、菱形的判定、平行四边形的判定 【解答】(1)证明:∵四边形ABCD 是矩形, ∴∠B =∠D =90°,AB =CD ,AD =BC ,AD ∥BC , 在Rt △ABE 和Rt △CDF 中,,∴Rt △ABE ≌Rt △CDF (HL );(2)解:当AC ⊥EF 时,四边形AECF 是菱形,理由如下: ∵△ABE ≌△CDF , ∴BE =DF , ∵BC =AD , ∴CE =AF , ∵CE ∥AF ,∴四边形AECF 是平行四边形, 又∵AC ⊥EF ,∴四边形AECF 是菱形.6. (2019年江苏省苏州市)如图,ABC △中,点E 在BC 边上,AE AB =,将线段AC 绕点A 旋转到AF 的位置,使得CAF BAE ∠=∠,连接EF ,EF 与AC 交于点G (1)求证:EF BC =;(2)若65ABC ∠=︒,28ACB ∠=︒,求FGC ∠的度数.BAC EAF ∴∠=∠AE AB AC AF==又, ()BAC EAF SAS ∴△≌△EF BC ∴=(2)65AB AE ABC =∠=︒, 18065250BAE ∴∠=︒-︒⨯=︒ 50FAG ∴∠=︒ BAC EAF 又△≌△ 28F C ∴∠=∠=︒502878FGC ∴∠=︒+︒=︒7.(2019年江苏省泰州市)如图,线段AB =8,射线BG ⊥AB ,P 为射线BG 上一点,以AP 为边作正方形APCD ,且点C 、D 与点B 在AP 两侧,在线段DP 上取一点E ,使∠EAP=∠BAP .直线CE 与线段AB 相交于点F (点F 与点A 、B 不重合).(1)求证:△AEP ≌△CEP;(2)判断CF 与AB 的位置关系,并说明理由; (3)求△AEF 的周长.【考点】全等三角形、正方形的性质【解答】(1)证明:∵四边形APCD 正方形,∴DP 平分∠APC , PC =PA,OBED∴∠APD =∠CPD =45°, ∴△AEP ≌△CEP.(2) CF ⊥AB .理由如下: ∵△AEP ≌△CEP,∴∠EAP =∠ECP , ∵∠EAP=∠BAP . ∴∠BAP =∠FCP ,∵∠FCP +∠CMP =90°,∠AMF =∠CMP , ∴∠AMF +∠PAB =90°, ∴∠AFM =90°, ∴CF ⊥AB .(3)过点 C 作CN ⊥PB .可证得△PCN ≌△APB,∴ CN =PB =BF, PN =AB,∵△AEP ≌△CEP, ∴AE =CE, ∴AE+EF+AF=CE+EF+AF =BN+AF =PN+PB+AF =AB+CN+AF =AB+BF+AF =2 AB =16.8.(2019年江苏省无锡市)如图,在△ABC 中,AB =AC ,点D 、E 分别在AB 、AC 上,BD =CE ,BE 、CD 相交于点O .(1)求证:△DBC ≌△ECB ; (2)求证:OB =OC .【考点】全等三角形、等腰三角形的判定 【解答】(1)证明:∵AB=AC ,∴∠ECB=∠DBC 在中与ECB DBC ∆∆ECB CB BC DBC CE BD ∠⎪⎩⎪⎨⎧==∠=∴ ECB DBC ∆≅∆(2)证明:由(1)知ECB DBC ∆≅∆ ∴∠DCB=∠EBC ∴OB=OC9. (2019年陕西省)如图,点A 、E 、F 、B 在直线l 上,AE =BF ,AC ∥BD ,且AC =BD .求证:CF =DE . 【考点】全等三角形 【解答】证明:∵AE =BF ,∴AF =BE ∵AC ∥BD ,∴∠CAF =∠DBE 又AC =BD , ∴△ACF ≌△BDE ∴CF =DE10.(2019年浙江省衢州市)已知:如图,在菱形ABCD 中,点E ,F 分别在边BC ,CD 上,且BE=DF ,连结AE ,AF.求证:AE=AF.【考点】菱形的性质【解答】 证明:∵四边形ABCD 是菱形, ∴AB=AD ,∠B=∠D , ∵BE=DF∴△ABE ≌△ADF . ∴AE=CF11. (2019年浙江省温州市)如图,在△ABC中,AD是BC边上的中线,E是AB边上一点,过点C作CF∥AB交ED的延长线于点F.(1)求证:△BDE≌△CDF.(2)当AD⊥BC,AE=1,CF=2时,求AC的长.【考点】全等三角形的判定和性质,平行线的性质【解答】(1)证明:∵CF∥AB,∴∠B=∠FCD,∠BED=∠F,∵AD是BC边上的中线,∴BD=CD,∴△BDE≌△CDF(AAS);(2)解:∵△BDE≌△CDF,∴BE=CF=2,∴AB=AE+BE=1+2=3,∵AD⊥BC,BD=CD,∴AC=AB=3.12.(2019年甘肃省)如图,在正方形ABCD中,点E是BC的中点,连接DE,过点A作AG⊥ED交DE于点F,交CD于点G.(1)证明:△ADG≌△DCE;(2)连接BF,证明:AB=FB.【考点】正方形的性质、全等三角形的判定和性质【解答】解:(1)∵四边形ABCD是正方形,∴∠ADG=∠C=90°,AD=DC,又∵AG⊥DE,∴∠DAG+∠ADF=90°=∠CDE+∠ADF,∴∠DAG=∠CDE,∴△ADG≌△DCE(ASA);(2)如图所示,延长DE交AB的延长线于H,∵E是BC的中点,∴BE=CE,又∵∠C=∠HBE=90°,∠DEC=∠HEB,∴△DCE≌△HBE(ASA),∴BH=DC=AB,即B是AH的中点,又∵∠AFH=90°,∴Rt△AFH中,BF=AH=AB.13. (2019年湖北省宜昌市)如图,在△ABC中,D是BC边上的一点,AB=DB,BE平分∠ABC,交AC边于点E,连接DE.(1)求证:△ABE≌△DBE;(2)若∠A=100°,∠C=50°,求∠AEB的度数.【考点】全等三角形的判定与性质、角平分线的定义、三角形内角和定理【解答】(1)证明:∵BE平分∠ABC,∴∠ABE=∠DBE,在△ABE和△DBE中,,∴△ABE≌△DBE(SAS);(2)解:∵∠A=100°,∠C=50°,∴∠ABC=30°,∵BE平分∠ABC,∴∠ABE=∠DBE=∠ABC=15°,在△ABE中,∠AEB=180°﹣∠A﹣∠ABE=180°﹣100°﹣15°=65°.14. (2019年甘肃省武威市)阅读下面的例题及点拨,并解决问题:例题:如图①,在等边△ABC中,M是BC边上一点(不含端点B,C),N是△ABC的外角∠ACH的平分线上一点,且AM=MN.求证:∠AMN=60°.点拨:如图②,作∠CBE=60°,BE与NC的延长线相交于点E,得等边△BEC,连接EM.易证:△ABM≌△EBM(SAS),可得AM=EM,∠1=∠2;又AM=MN,则EM=MN,可得∠3=∠4;由∠3+∠1=∠4+∠5=60°,进一步可得∠1=∠2=∠5,又因为∠2+∠6=120°,所以∠5+∠6=120°,即:∠AMN=60°.问题:如图③,在正方形A1B1C1D1中,M1是B1C1边上一点(不含端点B1,C1),N1是正方形A1B1C1D1的外角∠D1C1H1的平分线上一点,且A1M1=M1N1.求证:∠A1M1N1=90°.【考点】全等三角形的判定与性质、正方形的性质、等腰直角三角形的判定与性质、等腰三角形的判定与性质、三角形的外角性质【解答】解:延长A1B1至E,使EB1=A1B1,连接EM1C、EC1,如图所示:则EB1=B1C1,∠EB1M1中=90°=∠A1B1M1,∴△EB1C1是等腰直角三角形,∴∠B1EC1=∠B1C1E=45°,∵N1是正方形A1B1C1D1的外角∠D1C1H1的平分线上一点,∴∠M1C1N1=90°+45°=135°,∴∠B1C1E+∠M1C1N1=180°,∴E、C1、N1,三点共线,在△A1B1M1和△EB1M1中,,∴△A1B1M1≌△EB1M1(SAS),∴A1M1=EM1,∠1=∠2,∵A1M1=M1N1,∴EM1=M1N1,∴∠3=∠4,∵∠2+∠3=45°,∠4+∠5=45°,∴∠1=∠2=∠5,∵∠1+∠6=90°,∴∠5+∠6=90°,∴∠A1M1N1=180°﹣90°=90°.15. (2019年辽宁省本溪市)在Rt△ABC中,∠BCA=90°,∠A<∠ABC,D是AC边上一点,且DA=DB,O是AB的中点,CE是△BCD的中线.(1)如图a,连接OC,请直接写出∠OCE和∠OAC的数量关系:;(2)点M是射线EC上的一个动点,将射线OM绕点O逆时针旋转得射线ON,使∠MON =∠ADB,ON与射线CA交于点N.①如图b,猜想并证明线段OM和线段ON之间的数量关系;②若∠BAC=30°,BC=m,当∠AON=15°时,请直接写出线段ME的长度(用含m的代数式表示).【考点】全等三角形的判定和性质、三角形的有关性质、分类讨论思想【解答】解:(1)结论:∠ECO=∠OAC.理由:如图1中,连接OE.∵∠BCD=90°,BE=ED,BO=OA,∵CE=ED=EB=BD,CO=OA=OB,∴∠OCA=∠A,∵BE=ED,BO=OA,∴OE∥AD,OE=AD,∴CE=EO.∴∠EOC=∠OCA=∠ECO,∴∠ECO=∠OAC.故答案为:∠OCE=∠OAC.(2)如图2中,∵OC=OA,DA=DB,∴∠A=∠OCA=∠ABD,∴∠COA=∠ADB,∵∠MON=∠ADB,∴∠AOC=∠MON,∴∠COM=∠AON,∵∠ECO=∠OAC,∴∠MCO=∠NAO,∵OC=OA,∴△COM≌△AON(ASA),∴OM=ON.②如图3﹣1中,当点N在CA的延长线上时,∵∠CAB=30°=∠OAN+∠ANO,∠AON=15°,∴∠AON=∠ANO=15°,∴OA=AN=m,∵△OCM≌△OAN,∴CM=AN=m,在Rt△BCD中,∵BC=m,∠CDB=60°,∴BD=m,∵BE=ED,∴CE=BD=m,∴EM=CM+CE=m+m.如图3﹣2中,当点N在线段AC上时,作OH⊥AC于H.∵∠AON=15°,∠CAB=30°,∴∠ONH=15°+30°=45°,∴OH=HN=m,∵AH=m,∴CM=AN=m﹣m,∵EC=m,∴EM=EC﹣CM=m﹣(m﹣m)=m﹣m,综上所述,满足条件的EM的值为m+m或m﹣m.16. (2019年辽宁省大连市)如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C,求证:AF=DE.【考点】全等三角形的判定和性质【解答】证明:∵BE=CF,∴BE+EF=CF+EF,即BF=CE,在△ABF和△DCE中,,∴△ABF≌△DCE(SAS)∴AF=DE.17. (2019年贵州安顺市)(1)如图①,在四边形ABCD中,AB∥CD,点E是BC的中点,若AE是∠BAD的平分线,试判断AB、AD、DC之间的等量关系.解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC得到AB =FC ,从而把AB,AD,DC 转化在一个三角形中即可判断AB 、AD 、DC 之间的等量关系________________________;(2)问题探究:如图②,在四边形ABCD 中,AB ∥CD ,AF 与DC 的延长线交于点F ,点E 是BC 的中点,若AE 是∠BAF 的平分线,试探究AB,AF,CF 之间的等量关系,并证明你的结论.【考点】全等三角形的判定和性质【解答】(1) AD =AB+DC(2) AB =AF+CF证明:如图②,延长AE 交DF 的延长线于点G∵E 是BC 的中点,∴CE =BE ,∵AB ∥DC ,∴∠BAE =∠G.在△AEB 和△GEC 中⎪⎩⎪⎨⎧=∠=∠∠=∠CE BE GEC AEB G BAE∴△AEB ≌△GEC ∴AB =GC.∵AE 是∠BAF 的平分线 ∴∠BAG =∠FAG ,∵∠BAG ∠G , ∴∠FAG =∠G , ∴FA =FG,∵CG =CF + FG,∴AB =AF+CF18.(2019年西藏)如图,点E 、C 在线段BF 上,BE =CF ,AB =DE ,AC =DF .求证:∠ABC =∠DEF .【考点】全等三角形的判定【解答】解:∵BE =CF ,∴BE +EC =CF +EC ,∴BC =EF ,在△ABC 与△DEF 中,∴△ABC≌△DEF(SSS)∴∠ABC=∠DEF。
2019年全国中考试题解析版分类汇编-尺规作图
2019年全国中考试题解析版分类汇编-尺规作图注意事项:认真阅读理解,结合历年的真题,总结经验,查找不足!重在审题,多思考,多理解!【一】选择题1.〔2017•台湾33,4分〕如图,AB为圆O的直径,在圆O上取异于A、B的一点C,并连接BC、AC、假设想在AB上取一点P,使得P与直线BC的距离等于AP长,判断以下四个作法何者正确?〔〕A、作的中垂线,交于P点B、作∠ACB的角平分线,交于P点C、作∠ABC的角平分线,交于D点,过D作直线BC平行线,交于P点D、过A作圆O的切线,交直线BC于D点,作∠ADC的角平分线,交于P点考点:切线的性质;角平分线的性质。
分析:A圆内弦中垂线过原点;角平分线上点到到两边距离相等;角平分线上点到两边距离相等;D角平分线上点到两边距离相等,与切线与过切点的直径垂直、从而判断出来、解答:解:A、圆内弦的中垂线过原点,有圆内弦性质可知,所以交AB于圆点O,故本选项错误;B、作∠ACB的角平分线,那么点P到BC的距离等于点P到AC的距离,而不等于AP,故本选项错误;C、假设过点D作直线BC的平行线交AB于点P,那么点P的距离,等于DP也不等于AP,故本选项错误;D、角平分线DP交直径AB与点P,根据角平分线定理,由PA⊥AD,得到点P到BC的距离等于AP,故正确、点评:此题考查了切线的性质,A考查了圆内弦中垂线过原点;B考查了角平分线上点到到两边距离相等;C考查了角平分线上点到两边距离相等;D考查了角平分线上点到两边距离相等,与切线与过切点的直径垂直、2.〔2017湖北荆州,15,3分〕请将含60°顶角的菱形分割成至少含一个等腰梯形且面积相等的六部分,用实线画出分割后的图形、答案不唯一、考点:作图—应用与设计作图、专题:作图题、分析:整个图形含有36个小菱形,分为面积相等的六部分,那么每一个部分含6个小菱形,由此设计分割方案、解答:解:分割后的图形如下图、此题答案不唯一、点评:此题考查了应用与设计作图、关键是理解题意,根据图形设计分割方案、3.〔2017•西宁〕用直尺和圆规作一个菱形,如图,能得到四边形ABCD是菱形的依据是〔〕A、一组临边相等的四边形是菱形B、四边相等的四边形是菱形C、对角线互相垂直的平行四边形是菱形D、每条对角线平分一组对角的平行四边形是菱形考点:菱形的判定;作图—复杂作图。
2019年全国中考真题分类汇编(图形的平移、位似与旋转)
(分类)第26讲 图形的平移、对称、旋转与位似第2课时 图形的平移、位似与旋转知识点1 图形的平移 知识点2 图形的位似 知识点3 图形的旋转 知识点4 网格作图知识点1 图形的平移(2019乐山)下列四个图形中,可以由图1通过平移得到的是(D )()A ()B ()C ()D(2019苏州)如图,菱形ABCD 的对角线AC, BD 交于点0, AC=4,BD=16,将△ABO 沿点A 到点C 的方向平移,得到△O B A '''.当点A '与点C 重合时,点A 与点B '之间的距离为( C )A.6B.8C.10D.12知识点2 图形的位似 (2019滨州)(2019邵阳)(2019烟台)(2019陇南)知识点3 图形的旋转(2019黄石)如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB边的中点是坐标原点O,将正方形绕点C按逆时针方向旋转90°后,点B的对应点'B的坐标是CA.(-1,2)B.(1,4)C.(3,2)D.(-1,0)(2019荆门)A(孝感)(2019宜昌)如图,平面直角坐标系中,点B 在第一象限,点A 在x 轴的正半轴上,∠AOB=∠B=30°,OA=2,将△AOB 绕点O 逆时针旋转90°,点B 的对应点B '的坐标是( B ) A.)32,1(+- B.)3,3(- C.)32,3(+- D.)3,3(-(2019随州)(2019广州)一副三角板如图5放置,将三角板ADE 绕点A 逆时针旋转)900(<<αα,使得三角板ADE 的一边所在的直线与BC 垂直,则α的度数为________.(2019天津)答案:D(2019邵阳)(2019广元)(2019益阳)(2019淄博)(2019建设兵团)(2019绵阳)如图,△ABC、△BDE都是等腰直角三角形,BA=BC,BD=BE,AC=4,DE=2.将△BDE绕点B逆时针方向旋转后得△BD′E′,当点E′恰好落在线段AD′上时,则CE′=.(2019哈尔滨)如图将△ABC绕点C逆时针旋转得到△A′B′C,其中点A′与A是对应点,点B′与B是对应点,点B′落在边AC上,连接A′B,若∠ACB=45°,AC=3,BC=2,则A′B的长为____。
2019年全国中考数学试题分类解析汇编(159套63专题)3
2019年全国中考数学试题分类解析汇编(159套63专题)专题19:反比例函数的应用一、选择题1. (2019福建福州4分)如图,过点C(1,2)分别作x 轴、y 轴的平行线,交直线y =-x+6于A 、B两点,若反比例函数y =kx(x >0)的图像与△ABC 有公共点,则k 的取值范围是【 】A .2≤k≤9 B.2≤k≤8 C.2≤k≤5 D.5≤k≤8 【答案】A 。
【考点】反比例函数综合题,曲线上点的坐标与方程的关系,二次函数的性质。
【分析】∵ 点C(1,2),BC∥y 轴,AC∥x 轴,∴ 当x =1时,y =-1+6=5;当y =2时,-x +6=2,解得x =4。
∴ 点A 、B 的坐标分别为A(4,2),B(1,5)。
根据反比例函数系数的几何意义,当反比例函数与点C 相交时,k =1×2=2最小。
设与线段AB 相交于点(x ,-x +6)时k 值最大, 则k =x(-x +6)=-x 2+6x =-(x -3)2+9。
∵ 1≤x≤4,∴ 当x =3时,k 值最大,此时交点坐标为(3,3)。
因此,k 的取值范围是2≤k≤9。
故选A 。
2. (2019湖北黄石3分)如图所示,已知A 11(,y )2,B 2(2,y )为反比例函数1y x=图像上的两点,动点P (x,0)在x 正半轴上运动,当线段AP 与线段BP 之差达到最大时,点P 的坐标是【 】A. 1(,0)2B. (1,0)C. 3(,0)2D. 5(,0)2【答案】D 。
【考点】反比例函数综合题,待定系数法,曲线上点的坐标与方程的关系,三角形三边关系。
【分析】∵把A 11(,y )2,B 2(2,y )分别代入反比例函数1y x =得:y 1=2,y 2=12, ∴A(12 ,2),B (2,12)。
∵在△ABP 中,由三角形的三边关系定理得:|AP -BP|<AB ,∴延长AB 交x 轴于P′,当P 在P′点时,PA -PB=AB , 即此时线段AP 与线段BP 之差达到最大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(分类)专题复习(三)图形操作题
类型1 折叠与翻折 类型2 分割与剪接
类型1 折叠与翻折 (2019资阳)
(2019深圳)
(2019天水)如图,在矩形ABCD 中,AB=3,AD=5,点E 在DC 上,将矩形ABCD 沿AE 折叠,点D 恰好落在BC 边上的点F 处,那么sin ∠EFC 的值为
.
(2019乐山)如图4,在边长为3的菱形ABCD 中,︒=∠30B ,过点A 作BC AE ⊥于点E ,现将△ABE 沿直线AE 翻折至△AFE 的位置,AF 与CD 交于点G .则CG 等于(A ) ()
A 13- ()
B 1 ()
C 2
1
()D 23
(2019淮安)
(2019杭州)如图,把某矩形纸片ABCD 沿EF 、GH 折叠(点E 、H 在AD 边,点E,G 在BC 边上),使点B 和点C 落在AD 边上同一点P 处,A 点的对称点为A '点,D 点的对称点为D '点,若∠FPG=90°,△A 'EP 的面积为4,△PH D '的面积为1,则矩形ABCD
的面积等于
.
(2019天津)答案:
(2019潍坊)
(2019青岛)如图,在正方形纸片 ABCD
中, E 是 CD 的中点,将正方形纸片折叠,点 B 落在线段 AE 上的点 G 处,折痕为 AF .若 AD =4 cm ,则 CF 的长为(6-.
图4
(2019泰安)
(2019南充)如图,正方形MNCB 在宽为2的矩形纸片一端,对折正方形MNCB 得到折痕AE ,再翻折纸片,使AB 与AD 重合.以下结论错误的是( D ) A.52102
+=AH B.
215-=BC CD C.EH CD BC ⋅=2 D.5
1
5sin +=∠AHD
(2019重庆B 卷)如图,在△ABC 中,∠ABC=45°,AB=3,AD ⊥BC 于点D ,BE ⊥AC 于点E ,AE=1,连接DE ,将△AED 沿直线沿直线AE 翻折至△ABC 所在的平面内,得到△AEF ,连接DF ,过点D 作DG ⊥DE 交BE 于点G.则四边形DFEG 的周长为( D ) A 、8
B 、24
C 、422+
D 、223+.
(2019重庆A 卷)如图,在△ABC 中,D 是AC 边上的中点,连结BD ,把△BDC ′沿BD 翻折,得到△BDC',DC 与AB 交于点E ,连结AC',若AD =AC =2,BD =3则点D 到BC 的距离为( B )
A .
2
3
3 B .
7
21
3 C .7 D .13
(2019金华)答案:A
12题图
类型2 分割与剪接
(2019资阳)
(2019烟台)
(2019广东)如题16-1图所示的图形是一个轴对称图形,且每个角都是直角,
长度如图所示,小明按题16-2图所示方法玩拼图游戏,两两相扣,
相互间不留空隙,那么小明用9个这样的图形(题16-1图)拼出米的
图形的总长度是a+8b(结果用含a,b代数式表示).
(2019江西)
(2019湖州)在数学拓展课上,小明发现:若一条直线经过平行四边形对角线的交点,则这条直线平分该平行四边形的面积,如图是由5个边长为1的小正方形拼成的图形,P是其中4个小正方形的公共顶点,小强在小明的启发下,将该图形沿着过点P的某条直线剪一刀,把它剪成了面积相等的两部分,则剪痕的长度是( D )
A.22
B.5
C.
2
5
3 D.10
(2019绍兴)把边长为2的正方形纸片ABCD 分割成如图的四块,其中点O 为正方形的中心,点E,F 分别是AB,AD 的中点,用这四块纸片拼成与此正方形不全等的四边形MNPQ (要求这四块纸片不重叠无缝隙),则四边形MNPQ 的周长是
.。
