高等数学I(本科类)第1阶段考试试题及答案
高数一真题及答案解析

高数一真题及答案解析高等数学(一)是大多数理工科学生在大学期间必须修习的一门课程。
它作为数学的一门重要基础科目,不仅在理论上具有重要意义,更在实际应用中广泛发挥作用。
因此,掌握高等数学(一)的知识点和解题技巧对每位理工科学生都是至关重要的。
为了帮助同学们更好地复习和准备高等数学(一)的考试,下面将提供一些高数一真题及其答案的解析。
1.【题目】已知函数f(x)=x^2+2x,求f(-1)的值。
【解析】根据题目给出的函数f(x),我们需要求解f(-1)的值。
解题的关键在于将x替换为-1,然后计算f(-1)。
将x替换为-1,得到:f(-1) = (-1)^2 + 2(-1)化简得:f(-1) = 1 - 2f(-1) = -1所以,f(-1)的值为-1。
2.【题目】已知等差数列的首项为a,公差为d,前n项和为Sn,求Sn的表达式。
【解析】根据等差数列的定义,我们知道等差数列的第n项的表达式为an = a + (n-1)d。
要求解等差数列前n项和Sn的表达式,我们可以将Sn拆分为每一项an的和。
Sn = a + (a + d) + (a + 2d) + ... + [a + (n-1)d]通过观察,我们可以发现这个等差数列中的每一项an都包含一个公共的项a,并且公差d会依次增加。
所以,Sn可以写成公共项a与公差d的函数。
Sn = a + (a + d) + (a + 2d) + ... + [a + (n-1)d]Sn = n * a + (1 + 2 + ... + (n-1)) * d在这里,我们可以利用等差数列前n项和的公式来化简上式。
Sn = n * a + (n(n-1)/2) * d所以,Sn的表达式为Sn = n * a + (n(n-1)/2) * d。
通过解析以上两道题目,我们可以看到高等数学(一)题目的求解方法并不是单一的,需要根据具体问题的不同选择相应的解题技巧和数学公式。
因此,在复习高等数学(一)的过程中,我们需要掌握不同的解题方法,并且灵活应用于实际题目中。
2019年成人高考专升本考试高等数学(一)真题与标准答案解析

2019年成人高考专升本考试高等数学(一)真题(总分:150.00,做题时间:150分钟)一、选择题(总题数:10,分数:40.00)1.当x→0时,x+x2+x3+x4为x的________。
(分数:4.00)A.等价无穷小√B.2阶无穷小C.3阶无穷小D.4阶无穷小解析:2.________。
(分数:4.00)A.-e2B.-eC.eD.e2√解析:3.设函数y=cos2x,则y'= ________。
(分数:4.00)A.2sin2xB.-2sin2x √C.sin2xD.-sin2x解析:y'= (cos2x)'=-sin2x·(2x)'=-2sin2x。
4.设函数f(x)在[a,b]上连续,在(a,b)可导,f(x)>0,f(a)f(b)<0, 则f(x)在(a,b)零点的个数为________。
(分数:4.00)A.3B.2C.1 √D.0解析:由零点存在定理可知,f(x)在(a,b),上必有零点.且函数是单调函数,故其在(a,b) 上只有一个零点。
5.设2x为f(x)的一个原函数,则f(x)=________。
(分数:4.00)A.0B.2 √C.x2D.x2+C解析:由题可知∫f(x)dx=2x+C,故f(x)=(∫f(x)dx)=(2x+C)'=2。
6.设函数f(x)=arctanx,则∫f'(x)dx=________。
(分数:4.00)A.-arctanx+CB.C.arctanx+C √D.解析:∫f'(x)dx= f(x)+C=arctanx+C。
7.则________。
(分数:4.00)A.l1> l2> I3√B.l2> I3> I1C.I3> I2> I1D.l1> I3> I2解析:在区间(0,1)内,有x2>x3>x4由积分的性质可知8.设函数z=x2e y,则________。
高等数学I本科类第阶段测试题

江南大学现代远程教育 第一阶段测试卷 考试科目:《高等数学》专升本 第一章至第三章(总分100分) 时间:90分钟__________学习中心(教学点) 批次: 层次: 专业: 学号: 身份证号: 姓名: 得分:一、选择题 (每题4分,共20分)1. 函数y = 的定义域是 ( A ). (a) (2,6)- (b) (2,6] (c)[2,6) (d)[2,6]- 2. 10lim(13)xx x →+ ( C) (a) e (b) 1 (c) 3e (d) ∞ 3.要使函数()f x x=在0x =处连续, 应给(0)f 补充定义的数值是( D ). (a) 1 (b)2(c)(d) 5 4. 设 sin 3x y -=, 则 y ' 等于 ( B ). (a)sin 3(ln 3)cos x x - (b) sin 3(ln 3)cos x x -- (c) sin 3cos x x -- (d) sin 3(ln 3)sin x x --5. 设函数 ()f x 在点 0x 处可导, 则 000(3)()lim h f x h f x h→+-等于 ( B ). (a) 03()f x '- (b) 03()f x ' (c) 02()f x '- (d) 02()f x '二.填空题(每题4分,共28分)6. 设 2(1)3f x x x -=++, 则 ()f x =__ x 2+3x+5 __.7. 2sin(2)lim 2x x x →-++=__1__. 8. 设 1,0,()5,0,1,0x x f x x x x -<⎧⎪==⎨⎪+>⎩, 则 0lim ()x f x +→=___1__.9. 设 ,0(),2,0x e x f x a x x -⎧≤=⎨+>⎩ 在点 0x = 处连续, 则常数 a =__0.5__ 10. 曲线 54y x -= 在点 (1,1) 处的法线方程为___y=(4/5)x+1/5__ 11. 由方程 2250xyx y e -+=确定隐函数 ()y y x =, 则 y '=__2xy 22e y +2y -2xy x ()___ 12. 设函数 2()ln(2)f x x x =, 则 (1)f ''=__3+2ln 2___三. 解答题(满分52分)13. 求 45lim()46x x x x →∞--. 答:14. 求01lim sin 3x x→. 答:15. 确定A 的值, 使函数 62cos ,0(),tan ,0sin 2x e x x f x Ax x x -⎧-≤⎪=⎨>⎪⎩在点 0x = 处连续。
课程:高等数学Ⅰ(专升本)试题和答案

课程:高等数学Ⅰ(专升本)--习题和答案1. (单选题) 若函数区间上连续,则在区间上函数一定存在最大值和最小值的是( )(本题3.5分)A、B、C、D、学生答案:未答题标准答案:B解析:得分:2. (单选题) 函数在区间(-1,1)内( )(本题3.5分)A、递减B、递增C、不增不减D、有增有减学生答案:未答题标准答案:D解析:得分:3. (单选题) 下列各对函数中表示同一函数的是( )(本题3.5分)A、与B、与C、与D、与学生答案:未答题标准答案:C解析:得分:4. (单选题) 当时,是( )(本题3.5分)A、无穷大B、无穷小C、有界函数D、无界函数学生答案:未答题标准答案:C解析:得分:5. (单选题) 下列定积分其值为零的是( )(本题3.5分)A、B、C、D、学生答案:未答题标准答案:A解析:得分:6. (单选题) 当时,和都是无穷小,下列变量中,当时,可能不是无穷小的是( )(本题3.5分)A、B、C、D、学生答案:未答题标准答案:D解析:得分:7. (单选题) 函数( )(本题3.5分)A、充分条件B、充分必要条件C、必要条件D、既非充分也非必要条件学生答案:未答题标准答案:C解析:得分:8. (单选题) 如果函数( )(本题3.5分)A、B、C、D、学生答案:未答题标准答案:C解析:得分:9. (单选题) 已知( )(本题3.5分)A、B、C、D、标准答案:B解析:得分:10. (单选题) 设函数,则当且时,( )(本题3.5分)A、B、C、D、学生答案:未答题标准答案:C解析:得分:11. (单选题) 下列函数在定义域内既是奇函数,又是无界函数的是( )。
(本题3.5分)A、B、C、D、标准答案:C解析:无.得分:12. (单选题) 当时,下列函数为无穷小量的是( )。
(本题3.5分)A、B、C、D、学生答案:未答题标准答案:B解析:无.得分:13. (单选题) 函数的间断点是( )。
专升本考试:2022高等数学一真题及答案(1)

专升本考试:2022高等数学一真题及答案(1)1、方程x 2+y 2-2z=0表示的二次曲面是()(单选题)A. 柱面B. 球面C. 旋转抛物面D. 椭球面试题答案:C2、国际标准化委员会(1SO)、国际电工委员会(1Ec)等制定的针对产品和服务的质量及技术要求的标准是()(单选题)A. 国家标准B. 国际公约C. 国际惯例D. 国际标准试题答案:D3、封口机按照封口方式的不同,额分为()封口机。
(多选题)A. 手压式B. 脚踏式C. 热压式D. 熔焊式E. 液压式试题答案:C,D,E4、()是入库商品堆存的操作及其方式、方法的总称。
(单选题)B. 翻垛C. 倒堆D. 堆码试题答案:D5、组织对人力资源的开发过程主要包括()等环节。
(多选题)A. 招聘B. 专业定向C. 岗位培训D. 脱产培训试题答案:B,C,D6、在计算机中,bit含义是()。
(单选题)A. 字B. 字长C. 字节D. 二进制位试题答案:D7、()(单选题)A.B. ƒ(2x)+CC. 2ƒ(2x)+CD.试题答案:A8、GIS系统定位的精度取决于对信号传播()的测定。
(单选题)B. 范围C. 频率D. 时间试题答案:D9、选择合作伙伴的评价指标体系设置原则有()。
(多选题)A. 系统全面性B. 简明科学性C. 稳定可比性D. 灵活可操作性E. 距离相近性试题答案:A,B,C,D10、若y=1+cosx,则dy= ()(单选题)A. (1+sinx)dxB. (1-sinx)dxC. sinxdxD. -sinxdx试题答案:D11、在下拉菜单里的各个操作命令项中有一类命令项的右面标有省略号(…)这类命令项的执行特点是()。
(单选题)A. 被选中执行时会要求用户加以确认B. 被选中执行时会弹出菜单C. 被选中执行时会弹出对话框D. 当前情况下不能执行试题答案:C12、()的四个阶段首尾相接,不断循环,每一次循环都会有新的内容和要求,他把计划的编制、执行与控制有机地结合在一起,有利于提高计划管理的水平。
自考高数(一)试题及答案

自考高数(一)试题及答案自考高等数学(一)试题及答案一、选择题(每题3分,共30分)1. 下列函数中,哪个不是基本初等函数?A. 正弦函数B. 常数函数C. 指数函数D. 绝对值函数答案:D2. 函数f(x) = x^2 + 3x + 2在区间(-∞,-2)上的单调性是:A. 单调递增B. 单调递减C. 不确定D. 非单调答案:B3. 微积分基本定理指出:A. 定积分可以转化为不定积分求解B. 不定积分是定积分的基础C. 定积分的值等于其原函数的不定积分的差值D. 所有连续函数都有原函数答案:C4. 曲线y = x^3在点(1,1)处的切线斜率是:A. 0B. 1C. 3D. 2答案:C5. 以下哪个级数是发散的?A. 1 + 1/2 + 1/3 + ...B. (1/2) + (1/4) + (1/8) + ...C. 1 - 1/2 + 1/3 - 1/4 + ...D. 1 - 1/2^2 + 1/3^2 - 1/4^2 + ...答案:A6. 微分方程dy/dx = x^2 - y^2的解的形式是:A. y = x^2B. y = C/xC. y = x + CD. y = Cx^2答案:B7. 函数f(x) = e^x在x=0处的泰勒展开式的前两项是:A. 1 + xB. 1 - xC. 1 + x^2D. 1 + x + x^2答案:A8. 以下哪个选项是二元函数f(x, y) = x^2 + y^2的极值点?A. (0, 0)B. (1, 1)C. (-1, -1)D. (2, -2)答案:A9. 曲线积分∮(x^2 + y^2) ds 在圆周x^2 + y^2 = 1上的值是:A. 0B. 1C. 2πD. 4π答案:D10. 以下哪个选项是函数f(x) = sin(x)的傅里叶变换?A. 1/2B. 1/2δ(x - π)C. 1/2δ(x)D. δ(x - π)答案:C二、填空题(每题4分,共20分)11. 极限lim (x→0) (sin(x)/x) 的值是 _______。
专升本(高等数学一)-试卷106
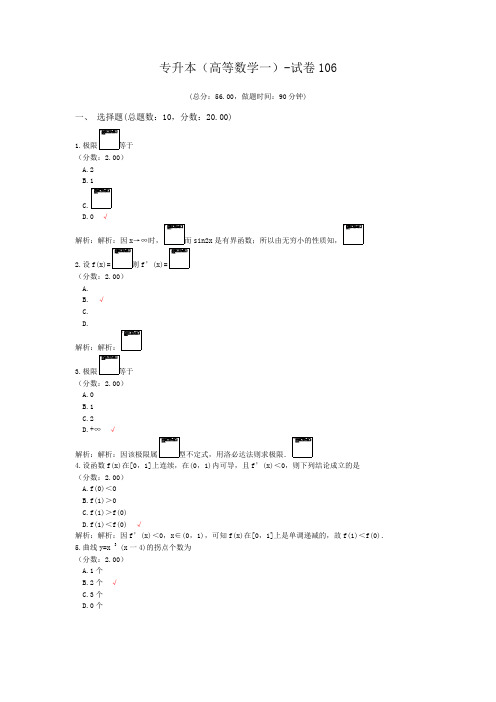
专升本(高等数学一)-试卷106(总分:56.00,做题时间:90分钟)一、选择题(总题数:10,分数:20.00)1.(分数:2.00)A.2B.1D.0 √解析:解析:因x→∞时,而sin2x2.设f(x)=则(分数:2.00)A.B. √C.D.3.(分数:2.00)A.0B.1C.2D.+∞√解析:解析:因该极限属型不定式,用洛必达法则求极限.4.设函数f(x)在[0,1]上连续,在(0,1)内可导,且f’(x)<0,则下列结论成立的是(分数:2.00)A.f(0)<OB.f(1)>0C.f(1)>f(0)D.f(1)<f(0) √解析:解析:因f’(x)<0,x∈(0,1),可知f(x)在[0,1]上是单调递减的,故f(1)<f(0).5.曲线y=x 3 (x一4)的拐点个数为(分数:2.00)A.1个B.2个√C.3个D.0个解析:解析:因y=x 4一4x 3,于是y’=4x 3一12x 2,y"=12x 2一24x=12x(x一2),令y"=0,得x=0,x=2;具有下表:由表知,函数曲线有两个拐点为(0,0),(2,一16).6.设F(x)是f(x)的一个原函数,则∫cosxf(sinx)dx等于(分数:2.00)A.F(cosx)+CB.F(sinx)+C √C.一F(cosx)+CD.一F(sinx)+C解析:7.(分数:2.00)A. √B.C.D.解析:解析:对于A选项,xsin 2x为奇函数,由积分性质知,=0;对于B选项,∫ -11|x|dx=2∫01 xdx=x 2 |1 =1;对于C选项,对于D选项,.故选A.8.(分数:2.00)A.过原点且与y轴垂直√B.不过原点但与y轴垂直C.过原点且与y轴平行D.不过原点但与y轴平行解析:解析:若直线方程为令比例系数为t,则直线可化为x 0 =y 0 =z 0 =0说明直线过原点。
又β=0.则y=0,即此直线在xOz内,即垂直于y轴,所以选A.9.设函数f(x,y)=xy+(x一 f y (1,0)等于(分数:2.00)A.0B.1 √C.2D.不存在解析:解析:因f(1.y)=y,故f y (1,0)=f’(1,y)| y=0 =1.10.(分数:2.00)A.B.C. √D.解析:二、填空题(总题数:10,分数:20.00)11.当x=1时,f(x)=x 3 +3px+q取到极值(其中q为任意常数),则p= 1(分数:2.00)填空项1:__________________ (正确答案:正确答案:一1)解析:解析:f'(x)=3x 2 +3p,f'(1)=3+3p=0,所以p=-1.12.设f(x)=∫ 0x |t|dt则f'(x)= 1.(分数:2.00)填空项1:__________________ (正确答案:正确答案:|x|)解析:解析:当x>0时,当x<0时,当x=0f'(0)=0,所以f'(0)=0,故f'(x)=|x|.13.设f’(x 2f(x)= 1(分数:2.00)填空项1:__________________ (正确答案:正确答案:[*])解析:解析:令x 2 =t,则因此14.设f(x)是连续的奇函数,且∫ 01 f(x)dx=1,则∫ -10 f(x)dx= 1(分数:2.00)填空项1:__________________ (正确答案:正确答案:—1)解析:解析:f(x)是奇函数,则∫ -11 f(x)dx=0,因此∫ -10 f(x)dx=一∫ 01 f(x)dx=一1.15.设z=x y,则dz= 1.(分数:2.00)填空项1:__________________ (正确答案:正确答案:yx y-1 dx+x y lnxdy)解析:解析:z=x y,则dz=yx y-1 dx+x y lnxdy.16.,y)dx交换积分次序,则有I= 1(分数:2.00)填空项1:__________________ (正确答案:正确答案:[*])17.当p 1(分数:2.00)填空项1:__________________ (正确答案:正确答案:<0)解析:解析:收敛,必有p<0,因如果p≥0,则当x>118. 1(分数:2.00)填空项1:__________________ (正确答案:正确答案:发散)19.ylnxdx+xlnydy=0的通解是 1.(分数:2.00)填空项1:__________________ (正确答案:正确答案:(lnx) 2 +(lny) 2 =C)解析:解析:分离变量得积分得 (lnx) 2 +(lny) 2 =C.20.y"一2y’一3y=0的通解是 1.(分数:2.00)填空项1:__________________ (正确答案:正确答案:y=C 1 e -x +C 2 e 3x)解析:解析:由y"一2y’一3y=0的特征方程为r 2—2r一3=0.得特征根为r 1 =3,r 2 =一1,所以方程的通解为 y=C 1 e -x +C 2 e 3x.三、解答题(总题数:8,分数:16.00)21.设y=y(x)是由方程2y-x=(x—y)ln(x—y)确定的隐函数,求dy.(分数:2.00)__________________________________________________________________________________________正确答案:(正确答案:方程两边对x求导有(注意y是x的函数))解析:22.已知曲线y=ax 4 +bx 3 +x 2 +3在点(1,6)处与直线y=11x-5相切,求a,b.(分数:2.00)__________________________________________________________________________________________ 正确答案:(正确答案:曲线过点(1,6),即点(1,6)满足曲线方程,所以6=a+b+4,(1) 再y’=4ax 3+3bx 2 +2x,且曲线在点(1,6)处与y=11x一5相切,所以y'|x=1 =4a+3b+2=11, (2) 联立(1)(2)解得a=3,b=一1.)解析:23.(分数:2.00)__________________________________________________________________________________________正确答案:(正确答案:原式两边对x)解析:(分数:2.00)__________________________________________________________________________________________正确答案:()解析:25.求方程y’=e 3x-2y满足初始条件y| x=0 =0的特解.(分数:2.00)__________________________________________________________________________________________正确答案:()解析:26.dz.(分数:2.00)__________________________________________________________________________________________正确答案:()解析:27.求2一y 2 )dxdy,其中D是由y=x,y=0,x 2 +y 2 =1在第一象限内所围的区域.(分数:2.00)__________________________________________________________________________________________ 正确答案:(正确答案:积分区域D如图所示,据被积函数特点(含x 2+y 2),及积分区域的特点(扇形),该积分易用极坐标计算.)解析:28.一艘轮船以20海里/小时的速度向东行驶,同一时间另一艘轮船在其正北82海里处以16海里/小时的速度向南行驶,问经过多少时间后,两船相距最近?(分数:2.00)__________________________________________________________________________________________正确答案:(正确答案:设经过t小时两船相距S海里,则即S 2=(82—16t) 2+(20t) 2,所以(S 2)’=2.(82—16t).(一16)+2×20t.20,令(S 2)’=0,得驻点t=2,即经过两小时后两船相距最近.) 解析:。
大学高等数学第一册考试试题答案详解

大学高等数学第一册考试试题答案详解【大学高等数学第一册考试试题答案详解】一、选择题:1. 答:B解析:首先应用导数求解微分方程,得到特解y=e^x。
再将y=e^x 代入$x^2y''+xy'-y=0$式中,可以得到等式左边为0,故选项B正确。
2. 答:D解析:根据导数的定义得出,当x=1时,函数f(x)的导数为0,由此可推知f(x)在x=1处取极值。
又根据极值点的判定条件,当导数变号时,极值达到。
从而得出答案为选项D。
3. 答:C解析:由公式算得h(t)=1−0.2t,比较上下限得到兴趣区间为(0,5],同时根据积分的定义算得兴趣总量为1.2。
4. 答:A解析:利用二重积分计算可以得出此立体体积为选项A中的数字。
5. 答:D解析:根据函数与其导函数的关系,对f(-3)进行积分,可以得到选项D的答案。
二、填空题:1. 答:$-1/4$解析:利用分部积分法计算,并带入上下限,得到此结果。
2. 答:2解析:根据积分的性质计算得到积分结果为2。
3. 答:27解析:由多重积分公式计算得积分结果为27。
4. 答:0.5解析:利用积分求解二次方程得出结果为0.5。
5. 答:$\arcsin(2/3)+C$解析:通过求导验证可得到该结果。
三、解答题:1. 答:解释二重积分与定积分的关系。
解析:二重积分是定积分的推广,用于计算平面区域上的面积,其中积分的上下限分别为该区域的y轴边界函数和x轴边界函数。
定积分则是对一个区间上的函数进行求和,其中积分的上下限为该区间的起点和终点。
2. 答:证明洛必达法则在极限存在的条件下成立。
解析:洛必达法则用于解决极限存在但无法直接求解的情况。
在证明洛必达法则成立时,可以通过应用导数定义以及泰勒级数展开等方法进行推导,最终得到洛必达法则的条件以及成立的证明过程。
四、应用题:1. 答:$\frac{1}{6}\pi^3$解析:根据旋转体体积的计算公式,可以得到此结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江南大学现代远程教育 第一阶段测试卷
考试科目:《高等数学》专升本 第一章至第三章(总分100分)
时间:90分钟
__________学习中心(教学点) 批次: 层次: 专业: 学号: 身份证号: 姓名: 得分: 一、 选择题 (每题4分,共20分)
1. 函数
y = 的定义域是 ( A ). (a) (2,6)- (b) (2,6] (c) [2,6) (d)[2,6]- 2. 110lim(1)x x x +→+ A
(a) e (b) 1 (c) 3e (d) ∞
3. 要使函数sin 3()x f x x
=
在 0x = 处连续, 应给(0)f 补充定义的数值是 ( C ). (a) 1 (b) 2 (c) 3 (d) 4 4. 设 23(21)y x =+, 则 y ' 等于 ( B ).
(a) 2212(21)x x -+ (b) 2212(21)x x + (c) 222(21)x x + (d) 226(21)x x +
5. 设函数 ()f x 在点 0x 处可导, 则 000()(3)lim h f x f x h h
→-+ 等于 ( A ). (a) 03()f x '- (b) 03()f x ' (c) 02()f x '- (d) 02()f x '
二.填空题(每题4分,共28分)
6. 设 (4)3f x x =+, 则 ()f x =___
________.
7. 2sin[2(2)]lim 2
x x x →-++=__2___. 8. 设 12,0,()5,0,34,0x x f x x x x -<⎧⎪==⎨⎪+>⎩
, 则 0lim ()x f x +→=___3____. 9. 设 2,0(),4,0
x e x f x a x x -⎧≤=⎨+>⎩ 在点 0x = 处极限存在, 则常数 a =___
___ 10. 曲线 1y x -= 在点 (1,1) 处的法线方程为__
11. 由方程 250y xy e -+=确定隐函数 ()y y x =, 则 y '=___
_____
12. 设函数 ()ln cos f x x =, 则 (0)f ''=___-1_____
三. 解答题(满分52分)
13. 求 78lim()79
x x x x →∞--
.
14. 求 301lim sin 3x x e x
→-
.
15. 确定A 的值, 使函数 5cos ,0(),sin ,02x e x x f x Ax x x -⎧-≤⎪=⎨>⎪⎩
在点 0x = 处极限存在。
16. 设 cos x y x =, 求 dy 。
17. 已知曲线方程为 2(0)y x x =>, 求它与直线 y x = 交点处的切线方程。
18. 曲线 1(0)y x x
=>, 有平行于直线 10y x ++= 的切线, 求此切线方程。
19. 若()f x 是奇函数, 且(0)f '存在, 求 0(9)lim x f x x
→。
