中国数学会2020年学术年会报告摘要10-10
全国通用2020-2022年三年高考数学真题分项汇编专题10解三角形

10 解三角形1.【2022年全国甲卷】沈括的《梦溪笔谈》是中国古代科技史上的杰作,其中收录了计算圆弧长度的“会圆术”,如图,AB是以O为圆心,OA为半径的圆弧,C是的AB中点,D在AB 上,CD⊥AB.“会圆术”给出AB的弧长的近似值s的计算公式:s=AB+CD2OA.当OA=2,∠AOB=60°时,s=()A.11−3√32B.11−4√32C.9−3√32D.9−4√32【答案】B【解析】【分析】连接OC,分别求出AB,OC,CD,再根据题中公式即可得出答案. 【详解】解:如图,连接OC,因为C是AB的中点,所以OC⊥AB,又CD⊥AB,所以O,C,D三点共线,即OD=OA=OB=2,又∠AOB=60°,所以AB=OA=OB=2,则OC=√3,故CD=2−√3,所以s=AB+CD2OA =2+(2−√3)22=11−4√32.故选:B.2.【2021年甲卷文科】在ABC 中,已知120B =︒,AC 2AB =,则BC =( )A .1 BC D .3【答案】D 【解析】 【分析】利用余弦定理得到关于BC 长度的方程,解方程即可求得边长. 【详解】设,,AB c AC b BC a ===,结合余弦定理:2222cos b a c ac B =+-可得:21942cos120a a c =+-⨯⨯⨯, 即:22150a a +-=,解得:3a =(5a =-舍去), 故3BC =. 故选:D. 【点睛】利用余弦定理及其推论解三角形的类型: (1)已知三角形的三条边求三个角;(2)已知三角形的两边及其夹角求第三边及两角; (3)已知三角形的两边与其中一边的对角,解三角形.3.【2021年乙卷理科】魏晋时刘徽撰写的《海岛算经》是有关测量的数学著作,其中第一题是测海岛的高.如图,点E ,H ,G 在水平线AC 上,DE 和FG 是两个垂直于水平面且等高的测量标杆的高度,称为“表高”,EG 称为“表距”,GC 和EH 都称为“表目距”,GC 与EH 的差称为“表目距的差”则海岛的高AB =( )A .⨯+表高表距表目距的差表高B .⨯-表高表距表目距的差表高C .⨯+表高表距表目距的差表距D .⨯表高表距-表目距的差表距【答案】A 【解析】 【分析】利用平面相似的有关知识以及合分比性质即可解出. 【详解】 如图所示:由平面相似可知,,DE EH FG CGAB AH AB AC==,而 DE FG =,所以 DE EH CG CG EH CG EHAB AH AC AC AH CH--====-,而 CH CE EH CG EH EG =-=-+, 即CG EH EG EG DE AB DE DE CG EH CG EH-+⨯=⨯=+--=+⨯表高表距表高表目距的差. 故选:A. 【点睛】本题解题关键是通过相似建立比例式,围绕所求目标进行转化即可解出.4.【2020年新课标3卷理科】在△ABC 中,cos C =23,AC =4,BC =3,则cos B =( ) A .19B .13C .12D .23【答案】A 【解析】 【分析】根据已知条件结合余弦定理求得AB ,再根据222cos 2AB BC AC B AB BC +-=⋅,即可求得答案.【详解】在ABC 中,2cos 3C =,4AC =,3BC = 根据余弦定理:2222cos AB AC BC AC BC C =+-⋅⋅ 2224322433AB =+-⨯⨯⨯可得29AB = ,即3AB = 由22299161cos22339AB BC AC B AB BC +-+-===⋅⨯⨯故1cos 9B =. 故选:A. 【点睛】本题主要考查了余弦定理解三角形,考查了分析能力和计算能力,属于基础题.5.【2022年全国甲卷】已知△ABC 中,点D 在边BC 上,∠ADB =120°,AD =2,CD =2BD .当AC AB取得最小值时,BD =________.【答案】√3−1−1+√3 【解析】 【分析】设CD =2BD =2m >0,利用余弦定理表示出AC 2AB 2后,结合基本不等式即可得解.【详解】设CD =2BD =2m >0,则在△ABD 中,AB 2=BD 2+AD 2−2BD ⋅ADcos ∠ADB =m 2+4+2m , 在△ACD 中,AC 2=CD 2+AD 2−2CD ⋅ADcos ∠ADC =4m 2+4−4m , 所以AC 2AB 2=4m 2+4−4m m 2+4+2m =4(m 2+4+2m)−12(1+m)m 2+4+2m=4−12(m+1)+3m+1≥42√(m+1)⋅3m+1=4−2√3,当且仅当m +1=3m+1即m =√3−1时,等号成立, 所以当ACAB 取最小值时,m =√3−1. 故答案为:√3−1.6.【2021年乙卷文科】记ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,60B =︒,223a c ac +=,则b =________.【答案】【解析】 【分析】由三角形面积公式可得4ac =,再结合余弦定理即可得解. 【详解】由题意,1sin 2ABCSac B === 所以224,12ac a c =+=,所以22212cos 122482b ac ac B =+-=-⨯⨯=,解得b =(负值舍去).故答案为:7.【2020年新课标1卷理科】如图,在三棱锥P –ABC 的平面展开图中,AC =1,AB AD ==AB ⊥AC ,AB ⊥AD ,∠CAE =30°,则cos ∠FCB =______________.【答案】14-【解析】 【分析】在ACE 中,利用余弦定理可求得CE ,可得出CF ,利用勾股定理计算出BC 、BD ,可得出BF ,然后在BCF △中利用余弦定理可求得cos FCB ∠的值. 【详解】AB AC ⊥,AB =1AC =,由勾股定理得2BC =,同理得BD BF BD ∴==在ACE 中,1AC =,AE AD ==30CAE ∠=,由余弦定理得2222cos3013211CE AC AE AC AE =+-⋅=+-⨯=, 1CF CE ∴==,在BCF △中,2BC =,BF =1CF =,由余弦定理得2221461cos 22124CF BC BF FCB CF BC +-+-∠===-⋅⨯⨯.故答案为:14-.【点睛】本题考查利用余弦定理解三角形,考查计算能力,属于中等题.8.【2022年全国乙卷】记△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ﹐已知sinCsin (A −B )=sinBsin (C −A ). (1)若A =2B ,求C ; (2)证明:2a 2=b 2+c 2 【答案】(1)5π8;(2)证明见解析. 【解析】 【分析】(1)根据题意可得,sinC =sin (C −A ),再结合三角形内角和定理即可解出; (2)由题意利用两角差的正弦公式展开得sinC (sinAcosB −cosAsinB )=sinB (sinCcosA −cosCsinA ),再根据正弦定理,余弦定理化简即可证出. (1)由A =2B ,sinCsin (A −B )=sinBsin (C −A )可得,sinCsinB =sinBsin (C −A ),而0<B <π2,所以sinB ∈(0,1),即有sinC =sin (C −A )>0,而0<C <π,0<C −A <π,显然C ≠C −A ,所以,C +C −A =π,而A =2B ,A +B +C =π,所以C =5π8.(2)由sinCsin (A −B )=sinBsin (C −A )可得,sinC (sinAcosB −cosAsinB )=sinB (sinCcosA −cosCsinA ),再由正弦定理可得, accosB −bccosA =bccosA −abcosC ,然后根据余弦定理可知,12(a 2+c 2−b 2)−12(b 2+c 2−a 2)=12(b 2+c 2−a 2)−12(a 2+b 2−c 2),化简得:2a 2=b 2+c 2,故原等式成立.9.【2022年全国乙卷】记△ABC 的内角A,B,C 的对边分别为a,b,c ,已知sinCsin(A −B)=sinBsin(C −A).(1)证明:2a2=b2+c2;(2)若a=5,cosA=2531,求△ABC的周长.【答案】(1)见解析(2)14【解析】【分析】(1)利用两角差的正弦公式化简,再根据正弦定理和余弦定理化角为边,从而即可得证;(2)根据(1)的结论结合余弦定理求出bc,从而可求得b+c,即可得解.(1)证明:因为sinCsin(A−B)=sinBsin(C−A),所以sinCsinAcosB−sinCsinBcosA=sinBsinCcosA−sinBsinAcosC,所以ac⋅a2+c2−b22ac −2bc⋅b2+c2−a22bc=−ab⋅a2+b2−c22ab,即a2+c2−b22−(b2+c2−a2)=−a2+b2−c22,所以2a2=b2+c2;(2)解:因为a=5,cosA=2531,由(1)得b2+c2=50,由余弦定理可得a2=b2+c2−2bccosA,则50−5031bc=25,所以bc=312,故(b+c)2=b2+c2+2bc=50+31=81,所以b+c=9,所以△ABC的周长为a+b+c=14.10.【2022年新高考1卷】记△ABC的内角A,B,C的对边分别为a,b,c,已知cosA1+sinA =sin2B1+cos2B.(1)若C=2π3,求B;(2)求a2+b2c2的最小值.【答案】(1)π6;(2)4√2−5.【解析】【分析】(1)根据二倍角公式以及两角差的余弦公式可将cosA1+sinA =sin2B1+cos2B化成cos(A+B)=sinB,再结合0<B <π2,即可求出;(2)由(1)知,C =π2+B ,A =π2−2B ,再利用正弦定理以及二倍角公式将a 2+b 2c 2化成4cos 2B +2cos 2B−5,然后利用基本不等式即可解出.(1)因为cosA1+sinA =sin2B1+cos2B =2sinBcosB 2cos 2B=sinBcosB ,即sinB =cosAcosB −sinAsinB =cos (A +B )=−cosC =12,而0<B <π2,所以B =π6;(2)由(1)知,sinB =−cosC >0,所以π2<C <π,0<B <π2,而sinB =−cosC =sin (C −π2),所以C =π2+B ,即有A =π2−2B .所以a 2+b 2c 2=sin 2A+sin 2Bsin 2C=cos 22B+1−cos 2Bcos 2B=(2cos 2B−1)2+1−cos 2Bcos 2B=4cos 2B +2cos 2B−5≥2√8−5=4√2−5.当且仅当cos 2B =√22时取等号,所以a 2+b 2c 2的最小值为4√2−5.11.【2022年新高考2卷】记△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,分别以a ,b ,c 为边长的三个正三角形的面积依次为S 1,S 2,S 3,已知S 1−S 2+S 3=√32,sinB =13.(1)求△ABC 的面积; (2)若sinAsinC =√23,求b .【答案】(1)√28(2)12 【解析】 【分析】(1)先表示出S 1,S 2,S 3,再由S 1−S 2+S 3=√32求得a 2+c 2−b 2=2,结合余弦定理及平方关系求得ac ,再由面积公式求解即可; (2)由正弦定理得b 2sin 2B=acsinAsinC ,即可求解. (1)由题意得S 1=12⋅a 2⋅√32=√34a 2,S 2=√34b 2,S 3=√34c 2,则S 1−S 2+S 3=√34a 2−√34b 2+√34c 2=√32,即a 2+c 2−b 2=2,由余弦定理得cosB =a 2+c 2−b 22ac,整理得accosB =1,则cosB >0,又sinB =13,则cosB =√1−(13)2=2√23,ac =1cosB =3√24,则S △ABC =12acsinB =√28; (2)由正弦定理得:b sinB =a sinA =csinC ,则b 2sin 2B =a sinA ⋅c sinC =acsinAsinC =3√24√23=94,则b sinB =32,b =32sinB =12. 12.【2021年新高考1卷】记ABC 是内角A ,B ,C 的对边分别为a ,b ,c .已知2b ac =,点D 在边AC 上,sin sin BD ABC a C ∠=. (1)证明:BD b =;(2)若2AD DC =,求cos ABC ∠. 【答案】(1)证明见解析;(2)7cos 12ABC ∠=. 【解析】 【分析】(1)根据正弦定理的边角关系有acBD b=,结合已知即可证结论. (2)方法一:两次应用余弦定理,求得边a 与c 的关系,然后利用余弦定理即可求得cos ABC ∠的值.【详解】(1)设ABC 的外接圆半径为R ,由正弦定理, 得sin sin ,22b c R ABC C R==∠, 因为sin sin BD ABC a C ∠=,所以22b cBD a R R⋅=⋅,即BD b ac ⋅=. 又因为2b ac =,所以BD b =.(2)[方法一]【最优解】:两次应用余弦定理因为2AD DC =,如图,在ABC 中,222cos 2a b c C ab+-=,①在BCD △中,222()3cos 23ba b b a C +-=⋅.② 由①②得2222223()3b a b c a b ⎡⎤+-=+-⎢⎥⎣⎦,整理得22211203a b c -+=.又因为2b ac =,所以2261130a ac c -+=,解得3c a =或32ca =, 当22,33c c ab ac ===时,222()733cos =622c c c ABC c c ∠⋅+-=⋅(舍去).当2233,22c c a b ac ===时,22233()722cos 31222c c ABC c c c +⋅-==⋅∠. 所以7cos 12ABC ∠=. [方法二]:等面积法和三角形相似 如图,已知2AD DC =,则23ABD ABC S S =△△, 即21221sin sin 2332b ac AD A B BC ⨯=⨯⨯∠∠,而2b ac =,即sin sin ADB ABC ∠=∠, 故有ADB ABC ∠=∠,从而ABD C ∠=∠. 由2b ac =,即b ca b =,即CA BA CB BD=,即ACB ABD ∽, 故AD ABAB AC=,即23bc c b =,又2b ac =,所以23c a =, 则2227cos 212c a b ABC ac +-==∠. [方法三]:正弦定理、余弦定理相结合由(1)知BD b AC ==,再由2AD DC =得21,33AD b CD b ==.在ADB △中,由正弦定理得sin sin AD BDABD A=∠.又ABD C ∠=∠,所以s 3sin n 2i C b A b=,化简得2sin sin 3C A =. 在ABC 中,由正弦定理知23c a =,又由2b ac =,所以2223b a =. 在ABC 中,由余弦定理,得222222242793cos 221223a a a a c b ABC ac a +--⨯∠+===. 故7cos 12ABC ∠=. [方法四]:构造辅助线利用相似的性质如图,作DE AB ∥,交BC 于点E ,则DEC ABC △∽△.由2AD DC =,得2,,333c a aDE EC BE ===.在BED 中,2222()()33cos 2323BED a c b a c -=⋅∠+⋅.在ABC 中222cos 2a a BC c A b c +-=∠.因为cos cos ABC BED ∠=-∠, 所以2222222()()3322233a c ba cb ac ac +-+-=-⋅⋅,整理得22261130a b c -+=.又因为2b ac =,所以2261130a ac c -+=, 即3c a =或32a c =.下同解法1.[方法五]:平面向量基本定理 因为2AD DC =,所以2AD DC =. 以向量,BA BC 为基底,有2133BD BC BA =+. 所以222441999BD BC BA BC BA =+⋅+, 即222441cos 999b ac c ABC a ∠=++, 又因为2b ac =,所以22944cos ac a ac ABC c ⋅∠=++.③ 由余弦定理得2222cos b a c ac ABC =+-∠, 所以222cos ac a c ac ABC =+-∠④ 联立③④,得2261130a ac c -+=.所以32a c =或13a c =.下同解法1. [方法六]:建系求解以D 为坐标原点,AC 所在直线为x 轴,过点D 垂直于AC 的直线为y 轴,DC 长为单位长度建立直角坐标系,如图所示,则()()()0,0,2,0,1,0D A C -.由(1)知,3BD b AC ===,所以点B 在以D 为圆心,3为半径的圆上运动. 设()(),33B x y x -<<,则229x y +=.⑤ 由2b ac =知,2BA BC AC ⋅=,9=.⑥联立⑤⑥解得74x =-或732x =≥(舍去),29516y =,代入⑥式得||||3a BC c BA b =====,由余弦定理得2227cos 212a c b ABC ac +-∠==.【整体点评】(2)方法一:两次应用余弦定理是一种典型的方法,充分利用了三角形的性质和正余弦定理的性质解题;方法二:等面积法是一种常用的方法,很多数学问题利用等面积法使得问题转化为更为简单的问题,相似是三角形中的常用思路;方法三:正弦定理和余弦定理相结合是解三角形问题的常用思路;方法四:构造辅助线作出相似三角形,结合余弦定理和相似三角形是一种确定边长比例关系的不错选择;方法五:平面向量是解决几何问题的一种重要方法,充分利用平面向量基本定理和向量的运算法则可以将其与余弦定理充分结合到一起;方法六:建立平面直角坐标系是解析几何的思路,利用此方法数形结合充分挖掘几何性质使得问题更加直观化.13.【2021年新高考2卷】在ABC 中,角A 、B 、C 所对的边长分别为a 、b 、c ,1b a =+,2c a =+..(1)若2sin 3sin C A =,求ABC 的面积;(2)是否存在正整数a ,使得ABC 为钝角三角形?若存在,求出a 的值;若不存在,说明理由.【答案】(1(2)存在,且2a =. 【解析】 【分析】(1)由正弦定理可得出23c a =,结合已知条件求出a 的值,进一步可求得b 、c 的值,利用余弦定理以及同角三角函数的基本关系求出sin B ,再利用三角形的面积公式可求得结果; (2)分析可知,角C 为钝角,由cos 0C <结合三角形三边关系可求得整数a 的值. 【详解】(1)因为2sin 3sin C A =,则()2223c a a =+=,则4a =,故5b =,6c =,2221cos 28a b c Cab,所以,C 为锐角,则sin C ==因此,11sin 4522ABC S ab C ==⨯⨯△ (2)显然c b a >>,若ABC 为钝角三角形,则C 为钝角,由余弦定理可得()()()()22222221223cos 022121a a a a b c a a C ab a a a a ++-++---===<++,解得13a -<<,则0<<3a ,由三角形三边关系可得12a a a ++>+,可得1a >,a Z ∈,故2a =.14.【2020年新课标1卷文科】ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知B =150°.(1)若a ,b ,求ABC 的面积;(2)若sin AC C . 【答案】(1(2)15︒. 【解析】 【分析】(1)已知角B 和b 边,结合,a c 关系,由余弦定理建立c 的方程,求解得出,a c ,利用面积公式,即可得出结论;(2)方法一 :将30A C =︒-代入已知等式,由两角差的正弦和辅助角公式,化简得出有关C 角的三角函数值,结合C 的范围,即可求解.【详解】(1)由余弦定理可得2222282cos1507b a c ac c ==+-⋅︒=,2,c a ABC ∴==∴△的面积1sin 2S ac B =(2)[方法一]:多角换一角 30A C +=︒,sin sin(30)A C C C ∴=︒-1cos sin(30)2C C C =+=+︒=, 030,303060C C ︒<<︒∴︒<+︒<︒, 3045,15C C ∴+︒=︒∴=︒.[方法二]:正弦角化边 由正弦定理及150B =︒得22sin sin sin ====a c b R b A C B .故sin ,sin 22==a cA C b b.由sin A C +=a .又由余弦定理得22222cos =+-⋅=+b a c ac B a 2+c ,所以()222()2=++a a c ,解得a c =. 所以15=︒C . 【整体点评】本题考查余弦定理、三角恒等变换解三角形,熟记公式是解题的关键,考查计算求解能力,属于基础题.其中第二问法一主要考查三角恒等变换解三角形,法二则是通过余弦定理找到三边的关系,进而求角.15.【2020年新课标2卷理科】ABC 中,sin 2A -sin 2B -sin 2C =sin B sin C .(1)求A ;(2)若BC =3,求ABC 周长的最大值.【答案】(1)23π;(2)3+【解析】 【分析】(1)利用正弦定理角化边,配凑出cos A 的形式,进而求得A ;(2)方法一:利用余弦定理可得到()29AC AB AC AB +-⋅=,利用基本不等式可求得AC AB +的最大值,进而得到结果.【详解】(1)由正弦定理可得:222BC AC AB AC AB --=⋅,2221cos 22AC AB BC A AC AB +-∴==-⋅,()0,A π∈,23A π∴=. (2)[方法一]【最优解】:余弦+不等式由余弦定理得:2222cos BC AC AB AC AB A =+-⋅229AC AB AC AB =++⋅=, 即()29AC AB AC AB +-⋅=.22AC AB AC AB +⎛⎫⋅≤ ⎪⎝⎭(当且仅当AC AB =时取等号), ()()()22223924AC AB AC AB AC AB AC AB AC AB +⎛⎫∴=+-⋅≥+-=+ ⎪⎝⎭,解得:AC AB +≤(当且仅当AC AB =时取等号),ABC ∴周长3L AC AB BC =++≤+ABC ∴周长的最大值为3+[方法二]:正弦化角(通性通法)设,66ππαα=+=-B C ,则66ππα-<<,根据正弦定理可知sin sin sin a b cA B C===以sin )b c B C +=+sin sin 66ππαα⎤⎛⎫⎛⎫=++- ⎪ ⎪⎥⎝⎭⎝⎭⎦α=≤0α=,即6B C π==时,等号成立.此时ABC 周长的最大值为3+[方法三]:余弦与三角换元结合在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .由余弦定理得229b c bc =++,即2213924⎛⎫++= ⎪⎝⎭b c c.令13sin ,20,2b c c θπθθ⎧+=⎪⎛⎫∈⎨ ⎪⎝⎭⎪=⎩,得3sin b c θθ+=6πθ⎛⎫+≤ ⎪⎝⎭6C π=时,max ()b c +=所以ABC周长的最大值为3+ 【整体点评】本题考查解三角形的相关知识,涉及到正弦定理角化边的应用、余弦定理的应用、三角形周长最大值的求解问题;方法一:求解周长最大值的关键是能够在余弦定理构造的等式中,结合基本不等式构造不等关系求得最值.方法二采用正弦定理边化角,利用三角函数的范围进行求解最值,如果三角形是锐角三角形或有限制条件的,则采用此法解决.方法三巧妙利用三角换元,实现边化角,进而转化为正弦函数求最值问题. 16.【2020年新课标2卷文科】△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知25cos ()cos 24A A π++=.(1)求A ; (2)若b c -=,证明:△ABC 是直角三角形. 【答案】(1)3A π=;(2)证明见解析【解析】 【分析】(1)根据诱导公式和同角三角函数平方关系,25cos cos 24A A π⎛⎫++= ⎪⎝⎭可化为251cos cos 4A A -+=,即可解出; (2)根据余弦定理可得222b c a bc +-=,将b c -=代入可找到,,a b c 关系, 再根据勾股定理或正弦定理即可证出. 【详解】(1)因为25cos cos 24A A π⎛⎫++= ⎪⎝⎭,所以25sin cos 4A A +=,即251cos cos 4A A -+=,解得1cos 2A =,又0A π<<, 所以3A π=;(2)因为3A π=,所以2221cos 22b c a A bc +-==, 即222b c a bc +-=①,又b c -=②, 将②代入①得,()2223b c b c bc +--=, 即222250b c bc +-=,而b c >,解得2b c =,所以a =, 故222b a c =+, 即ABC 是直角三角形. 【点睛】本题主要考查诱导公式和平方关系的应用,利用勾股定理或正弦定理,余弦定理判断三角形的形状,属于基础题.17.【2020年新高考1卷(山东卷)】在①ac sin 3c A =,③=c 这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求c 的值;若问题中的三角形不存在,说明理由.问题:是否存在ABC ,它的内角,,A B C 的对边分别为,,a b c ,且sin 3sin A B ,6C π=,________?注:如果选择多个条件分别解答,按第一个解答计分. 【答案】详见解析 【解析】 【分析】方法一:由题意结合所给的条件,利用正弦定理角化边,得到a ,b 的比例关系,根据比例关系,设出长度长度,由余弦定理得到c 的长度,根据选择的条件进行分析判断和求解. 【详解】[方法一]【最优解】:余弦定理由sin 3sin AB 可得:ab=(),0a b m m =>,则:2222222cos 32c a b ab C m m m m =+-=+-⨯=,即c m =. 若选择条件①:据此可得:2ac m =⨯==1m ∴=,此时1c m ==.若选择条件②:据此可得:222222231cos 222b c a m m m A bc m +-+-===-,则:sin A ==sin 3c A m ==,则:c m ==若选择条件③: 可得1c mb m==,c b =,与条件=c 矛盾,则问题中的三角形不存在. [方法二]:正弦定理 由,6C A B C ππ=++=,得56A B π=-. 由sin 3sin A B,得5sin 6B B π⎛⎫-= ⎪⎝⎭,即1cos 2B B B =,得tan B =.由于0B π<<,得6B π=.所以2,3b c A π==.若选择条件①:由sin sin a c A C=,得2sin sin 36a cππ=,得a =.解得1,c b a ===.所以,选条件①时问题中的三角形存在,此时1c =. 若选择条件②: 由sin 3c A =,得2sin33c π=,解得c =,则b c == 由sin sin a c A C=,得2sin sin 36a cππ=,得6a ==.所以,选条件②时问题中的三角形存在,此时c =. 若选择条件③:由于=c 与b c =矛盾,所以,问题中的三角形不存在. 【整体点评】方法一:根据正弦定理以及余弦定理可得,,a b c 的关系,再根据选择的条件即可解出,是本题的通性通法,也是最优解;方法二:利用内角和定理以及两角差的正弦公式,消去角A ,可求出角B ,从而可得2,,36b c A B C ππ====,再根据选择条件即可解出.。
青霉素废水的生化处理研究

日 期:
学位论文版权使用授权书
本学位论文作者和指导教师完全了解东北大学有关保留、使用学位 论文的规定:即学校有权保留并向国家有关部门或机构送交论文的复印 件和磁盘,允许论文被查阅和借阅。本人同意东北大学可以将学位论文 的全部或部分内容编入有关数据库进行检索、交流。
作者和导师同意stern University July 2009
独创性声明
本人声明,所呈交的学位论文是在导师的指导下完成的。论文中取 得的研究成果除加以标注和致谢的地方外,不包含其他人己经发表或撰 写过的研究成果,也不包括本人为获得其他学位而使用过的材料。与我 一同工作的同志对本研究所做的任何贡献均己在论文中作了明确的说 明并表示谢意。
评阅人:
林国梁 副教授 袁俊斌 高级工程师
东北大学 2009 年 7 月
A Dissertation in Environmental Engineering
Research on the biochemical treatment of penicillin wastewater
by Feng Lizhong Supervisor: Professor Xu Xinyang
Key words: antibiotic wastewater; bacterial domesticated; penicillin; drug-fast performance
VI
东北大学硕士学位论文
目录
目录
独创性声明................................................................................................................................... I
中国工业与应用数学学会年会手册

我国工业与应用数学学会年会手册我国工业与应用数学学会(简称"学会")是我国工业与应用数学领域的权威学术机构,每年都会举办一次学术盛会——我国工业与应用数学学会年会。
年会手册作为年会的重要组成部分,记录着学术研究的最新成果和学术交流的精华内容,对于促进学术交流、推动学科发展具有重要意义。
1. 学会年会手册的编排我国工业与应用数学学会年会手册包括以下内容:年会的主题和议程、学术委员会和组织委员会名单、学术报告摘要、论文摘要集、会议日程安排、参会人员名单等。
年会手册的编排严谨、内容丰富,旨在为与会者提供一份全面且有条理的参考资料。
2. 年会手册的意义和作用年会手册对于学术交流和学科发展起着重要的推动作用。
年会手册为与会者提供了解年会主题和议程、参会人员情况的便捷途径,有助于参会者充分了解学术交流的重点和关注点。
年会手册记录了学术报告的摘要和论文的摘要集,这些内容集中展示了学术研究的前沿成果和学术热点,为与会者提供了广泛而深入的学术视野。
另外,年会手册中还包括了会议日程安排和参会人员名单,这些内容有助于与会者更好地安排自己的学术交流时间、寻找合作伙伴和拓展人脉。
3. 个人观点和理解作为高质量的学术交流评台,我国工业与应用数学学会年会手册在促进学术交流、推动学科发展方面发挥着不可替代的作用。
年会手册所记录的学术成果和学术交流内容,不仅是学术研究者了解前沿成果和学术热点的重要参考,也是推动学科发展、促进学术合作的有效工具。
学会年会手册也为学术界提供了一个重要的互动评台,促进了学术交流、合作与创新。
总结回顾我国工业与应用数学学会年会手册作为学会年会的重要组成部分,记录了学术交流的重要内容和学术研究的最新成果,对于促进学术交流、推动学科发展具有重要意义。
年会手册的编排严谨、内容丰富,旨在为与会者提供一份全面且有条理的参考资料。
年会手册对于学术交流和学科发展起着重要的推动作用,为与会者提供了解学术热点、寻找合作伙伴、拓展学术视野的重要途径。
pku北大学子毕业生去向
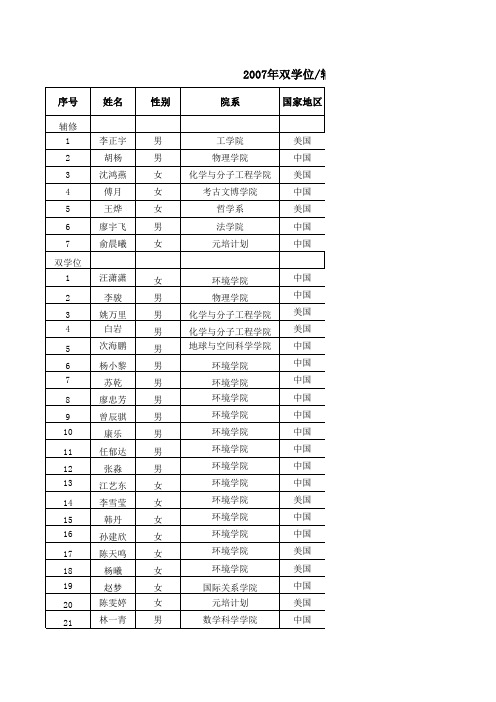
环境学院 心理学系 心理学系 心理学系 心理学系 心理学系 心理学系 新闻与传播学院 新闻与传播学院 新闻与传播学院 新闻与传播学院 新闻与传播学院 新闻与传播学院 新闻与传播学院 新闻与传播学院 新闻与传播学院 新闻与传播学院 新闻与传播学院 新闻与传播学院 新闻与传播学院 新闻与传播学院 新闻与传播学院 新闻与传播学院 新闻与传播学院 新闻与传播学院 新闻与传播学院 新闻与传播学院 新闻与传播学院 新闻与传播学院 新闻与传播学院 新闻与传播学院 新闻与传播学院 新闻与传播学院
美国 中国 中国 美国 中国 中国 美国 美国 香港 中国 中国 美国 美国 中国 美国 美国 美国 中国 美国 美国 中国 中国 美国 美国 中国 美国 中国 英国 美国 中国 中国 美国 中国
55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87
化学与分子工程学院 化学与分子工程学院 化学与分子工程学院 化学与分子工程学院 化学与分子工程学院 化学与分子工程学院 化学与分子工程学院 化学与分子工程学院 化学与分子工程学院 化学与分子工程学院 化学与分子工程学院 化学与分子工程学院 化学与分子工程学院 生命科学学院 生命科学学院 生命科学学院 生命科学学院 生命科学学院 生命科学学院 生命科学学院 生命科学学院 生命科学学院 生命科学学院 生命科学学院 生命科学学院 生命科学学院 生命科学学院 生命科学学院 生命科学学院 地球与空间科学学院 地球与空间科学学院 地球与空间科学学院 地球与空间科学学院
姓名
性别
院系
国家地区
22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54
中国数学会召开第十次全国代表大会

开 幕式上 同时颁 发 了第八 届 华 罗庚数学 奖 、 第十一 届 陈省身数学奖和 第八 届 钟 家庆数学奖。 复 旦 大学李 大潜 院
士和 中国科学 院数学与 系统科学研 究院严 加安 院士 共 同摘取 了 第八 届 “ 华 罗庚数学奖 ” 的桂 冠 , 北 京大学 数学科学 学 院 宗传 明 教 授 和 中国 科学 院数学 与 系统科学研 究院吉 敏研 究员 荣 膺第十一 届 陈省 身数学 奖 , 8 位优 秀青年学者 获
第八 届 钟 家庆数学 奖 。 据悉 , 本次会议是 中国数学 会历 史上 规模最 大 的一 次全 国 代 表 大 会 , 议 程 包 括 听 取 文 兰 理 事 长 题 为 《团 结 广 大
数 学 工 作 者 开 创 我 国 数 学 事 业 的 新 局 面 》的 工 作 报告 , 审议 《中 国 数 学 会 章 程 ( 修 改 草 案 )》, 选 举 产 生 新 一 届 理 事 会和 常务理 事会 。 学会 2 0 0 7 学术年会也 于 同期举 行 , 为期三 天 的大会邀请 5 0 多位近 年来在数学各 个领域取 得 出色 成绩的优秀数学家作 四 十五 分钟邀请报告 , 同时还 安排若 干场十五 分钟报告 。
冯 长根 强调 , 胡 锦涛总 书记 在党 的十七 大报告 中强调 , 科学 发展 观 , 第一 要 义 是 发展 , 核心 是 以人 为本。 这也 为今 后 的学会工 作在新的层 面 上 提 出 了 要 求。 建设 创 新型 国 家 , 构建和谐社会, 关键在人 。 学会是群众性学术团体, 是科技 工 作者 之 家, 是推动社会和谐发展 的重 要 力量 : 学会 的第一 功 能是 作 为桥梁和 纽 带组 织科技工 作者 , 通 过科学 交流、 学 术交流 、 科学 家与科学 家之 间的交流来推动学科发展 。
1982-2020中等数学

1982-2020中等数学
《中等数学》是由天津师范大学、天津市数学学会、中国数学会普及工作委员会合办的期刊,创刊于1982年11月。
它是中国国内唯一一份以报道数学竞赛为主要内容的刊物。
多年来,《中等数学》及时报道国内外的重大赛事,反映国内外数学竞赛的进展和最新信息和成果,刊文有较强的现实性和针对性,并能结合初、高中不同读者对象的年龄和知识结构特点,向读者提供科学、详实的资料。
然而,对于1982年至2020年期间《中等数学》的具体内容、影响力、读者反馈等方面的详细历史回顾和评价,可能需要查阅该期刊的历年档案、相关的学术评价报告或读者调查数据等。
这些信息可能对于了解该期刊在这一时期内的发展和变化具有重要意义。
此外,需要注意的是,数学教育和数学竞赛本身也在这段时间内经历了许多变化和发展,例如数学竞赛的参赛人数、赛事规模、赛题难度等方面可能都有所变化。
因此,对于《中等数学》在这一时期内的表现和影响,也需要结合当时的社会背景和学术环境进行综合考虑。
总之,对于1982年至2020年期间《中等数学》的详细历史回顾和评价,需要查阅更多的相关资料和数据,并结合当时的社会背景和学术环境进行综合分析。
中国教育学会中学数学教学专业委员会第十五届学术年会简讯
要求还有一定 的距离. 与我们的实践水平 比较 ,理论概括水 平尚 有很大的提高空间. 我们还需在 以下方面继续努力 :( ) 1 教科研 是一项严 肃认 真 的事业 ;( ) 意积累教 学研究论 文的写作 经 2 注
验 ;( ) 自己的亲身实践 中寻找研究课题 ; 4) 3从 ( 提高研究水平 , 解决实际问题 ;( ) 5 提倡有系统 、持续的研究 . 我会 副理 事 长 关 成 志先 生 对本 届 学 术 年 会进 行 了总 结 .本 届 ( E D j年一 度的 2 0 OC ) 三 0 9年 国际学 生评估 项 目 (IA) PS .首次 年会 :( ) 1 主题 鲜明 ,内容丰 富;( ) 2 大会学术报告 和参评 论文 参加 PS IA的 中国上海 1 5岁学生 ,在数学 素养 、科学 素养 以及 有高度 、有广度 、有深度 ;( ) 3 开眼界 、学经验 、有提升 ,引发 阅读能力i项评价 中均排在第一位. 如此优异的表现 ,引起 了国 了许多新 的思考和追求.教而不研则浅 ,研 而不教则空.我会将
指标定理在中国的萌芽:纪念陈省身先生
D 的分析 指 标 = D 的拓扑 指标 . = =
编 者 按: 此文原载于 2 0 0 6年 的《 中国数学会通讯 》原题 为《 , 指标定
理在 中国的萌芽: 纪念 陈 省 身 先 生 9 5诞 辰 》 今 征 得 作 者 . 同意 , 补 充 中英 文摘 要 等信 息 后 , 本 刊 正 式 发 表 , 纪 并 在 以 念 陈省 身先 生 百年 诞 辰 .
中 图 分 类 号 O 1 ; l 9 N1 文 献 标 识 码 E 文 章 编 号 1 0 — 3 9 2 1 ) 50 0 — 3 0 819 (0 1 0 —010
1 O月 2 8日, 陈省 身先 生 诞 辰 纪念 日. 是 长久 以 来 一 直想 写些 什 么作 为 纪 念 , 苦 于 找 不 到适 当 的 但 题 目. 然 与一位 多 日不 见 的朋友 聊 天 , 起 陈先 生 偶 谈
陈示 性 类 的提 出 和发 展 , 开 了微 分 几 何 的新 掀
篇章 . 面提 到过 的 大 数 学 家霍 普 夫 评 论 到 : 微 分 上 “
2 中国 数 学 家 的先 驱 性 贡 献
中 国数学 家对 阿 蒂亚 一 格指 标 定 理 的形 成做 辛 出 了先 驱性 的贡献 . 中最 突 出的 就 是 陈 省身 先 生 其 于上世 纪 4 0年 代 中期 的一 系列开 创性 工作 , 别是 特 上面 已经 提到 的高 斯 一 内特 一 博 陈省 身定 理 , 有就 还 是 陈省 身示 性类 的提 出和研 究. 陈先生 自己说 过 , 他
一
个 在任 意 维 数都 成 立 的指 标 定 理 的 一
个 特 例 , 指标 定理 的先 驱 ; 是
事 实 上 , 省 身先 生 的工 作可 以追 朔 到 著名 的 陈 古 希腊 欧几 里得 ( u l ) 几何 原 本 》 E c d 的《 i 中的一 个基
郭友中-李国平院士对数学和数理科学的贡献
李国平院士对数学、数理科学和系统科学的贡献郭友中(中国科学院数学计算技术研究所,武汉430071)—纪念李国平院士诞辰100周年—摘要缅怀著名数学和数理科学家,我国函数论、数学物理和系统工程奠基人之一,纪念他的百岁诞生,回顾他在数学和数理科学的若干重要领域的开创性和奠基性工作,包括半(亚)纯函数与整函数理论、准解析函数与函数逼近理论、微分方程解析理论与Minkowski-Denjoy函数理论、广义Reimann几何与混合量分析学、微分差分方程与算子函数论、纤维丛积分与相对性量子场论、电磁风暴说与数理地震学、外微分形式与场论、各向异性能带理论与统计岩体力学、数学模型与自动控制、学科规划与人才培养等方面的巨大贡献,诗词书画与音乐艺术等方面的天赋与造诣;缅怀他严谨的治学态度和一贯的创新精神。
关键词李国平、数学、数理科学、系统科学、贡献引言李国平(1910-1996),幼名海、海清,字慕陶,1910年11月15日(庚戍年10月14日)出生于广东省丰顺黄花村;1996年2月8日(丙子年12月20日)于武汉逝世, 享寿86岁。
1933年,毕业于中山大学数学天文系;1934年至1936年在东京帝国大学数学研究所作竹内端三教授指导下读研究生;1937年任中华教育文化基金会研究员,远赴法国巴黎大学Poincare研究所工作。
1939年抗日军兴,民族危亡,他毅然回国。
历任四川大学数学系教授(1939-1940),武汉大学数学系教授(1940-1996)、系主任、副校长、校务委员会副主任、数学研究所所长,中国科学院数学计算技术研究所(709研究所)、中国科学院武汉数学物理研究所所长,国家科委中南计算中心主任,湖北省科协副主席、顾问,国家科委数学学科组成员,中国数学会理事,中国系统工程学会副理事长兼学术委员会主任,中国数学会名誉理事,湖北省暨武汉市数学会名誉理事长,中国科学院武汉数学物理研究所名誉所长,《数学物理学报》主编,《数学年刊》副主编,《数学杂志》及《系统工程与决策》名誉主编。
中国现代数学史
• 中国科学社
• 1914年6月10日,在美国康乃尔大学留学的 胡明复、赵元任、任鸿隽、周仁、杨杏佛 等人聚集一起谈论世界及中国风云时,有 人提出:中国缺乏的莫过于科学,我们为 什么不能刊行一种杂志向中国介绍科学? 并决定成立组织科学社。
• Probability当时译为“决疑数”
• 洋务派的工作
• 1862年,成立同文馆, 是清代最早培养译员 的洋务学堂和从事翻 译出版的机构。
• 在同文馆设立天文算 学馆,主要工作是科 技翻译和科技人才的 培养。
• 1865年,由曾国藩、李鸿章在上海设立江 南机器局,1868年,在江南机器局设立翻 译馆,翻译西方科技著作。
• 李善兰的翻译工作
• 1847年,英国传教士伟烈亚力来到上海经 营由英国麦都思所设立的墨海书馆。
• 1852年,李善兰来到上海与伟烈亚力相识, 开始了西方科学著作的翻译工作。
• 1857年,李善兰与伟烈亚力合作完成了 《原本》后九卷。
• 1859年,李善兰与伟烈亚力合作完成了中 国引入第一部微积分著作《代微积拾级》。
• 1866年,曾国藩资助李善兰出版《则古昔 斋算学》,代表当时中国传统数学的最高 成就。
• 中国数学家数学创作成就
• 其一,由于清朝政府的腐败,使一部分开 明的知识分子以研究数学来消遣。
• 其二,追随洋务派研究数学使中国数学图 强。
• 以函数的幂级数展开式为例,1845年- 1865年,出现了戴煦、李善兰、徐有壬、 顾观光、邹伯奇、夏鸾翔等数学家的数学 研究成果。其中李善兰恒等式受到了国际 关注。
• 背景
• 中国现代数学基本上是另起炉灶,是从西 方移植过来的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中国数学会2020年学术年会会议报告摘要目录大会邀请报告 (1)TM A 代数与数论 (3)TM B 几何与拓扑 (9)TM C1 常微动力统 (15)TM C2 偏微分方程 (19)TM C3 实分析和复分析 (27)TM D 计算数学 (32)TM E 概率和统计 (48)TM F 运筹与控制 (53)TM G 组合与计算数学 (57)TM H 数学教育 (62)大会邀请报告机器学习的数学理论鄂维南北京大学现代机器学习的核心问题是怎样有效地逼近一个高维空间的函数。
传统的逼近论方法会导致维数灾难,这是对许多领域来说困惑了我们多年的问题。
在这个演讲里,我们将介绍以下几方面的内容。
1.怎样建立起一个数学理论?这里的问题本身跟传统的数值分析基本一样。
不同的是机器学习需要处理的核心问题是维数灾难。
所以我们需要建立起一个高维数值分析理论,包括逼近论,先验和后验误差估计,优化理论等。
这个理论会帮助我们理解什么样的模型和算法没有维数灾难。
2.怎样formulate一个好的机器学习的数学模型?正确的方法是首先在连续的层面formulate好的机器学习的模型,然后采用数值分析的想法,对这些连续模型作离散化而得到所需要的机器学习算法。
我们发现许多神经网络模型,包括残差网络模型,都可以通过这种途径得到。
因为有一个好的连续模型作为背景,这样得到的机器学习模型和算法自然就有比较好的性质。
3.实际应用中有一些比较奇怪的现象,比方说double descent。
怎样解释这些现象?实际应用中人们也没有按照前面所说的套路来做,那为什么其效果也还很好呢?4.哪些问题还有待解决?数学机械化新进展高小山中国科学院数学与系统科学研究院数学机械化主要研究如何借助计算机进行定理自动证明与发现,是我国数学家吴文俊教授创立的的重要研究方向。
本报告将简要介绍数学机械化的基本想法与若干新进展:微分Chow坐标与稀疏微分结式。
1Weierstrass 型函数图像的分形性质沈维孝复旦大学Weierstrass 处处不可微连续函数的图像是分形几何的经典研究对象之一.我们将回顾这些函数图像的研究历史,并介绍近期如下二分性定理(与任浩杰合作)的证明:假设b 是大于1的整数,f 是周期的解析函数,0<t <1.那么要么函数W (x )=∑︀∞n =0b−nt f (b n x )是解析函数,要么其图像的Hausdorff 维数等于2−t .2分组报告TM A代数与数论Some results about finite p-groups安立坚山西师范大学In Shanxi Normal University,there is a team of theorists who are interested in finite p-groups mainly.This team began from2003.It has8members now.In this talk,we present some results and progresses about finite p-groups obtained by this team.This talk contains four aspects:commutativity,normality,anzahl and lattice of subgroups.On the aspects of commutativity and normality,we classified some finite p-groups with“stronger”commutativity or normality.On the aspect of anzahl,we investigate a conjecture proposed by Chinese late mathematicians Loo-Keng Hua and Hsin-Fu Tuan.On the aspect of lattice of subgroups,we concentrate on Chermak-Delgado lattice.Twisted quantum affinizations陈福林厦门大学In this talk,I will introduce a notion of twisted quantum affinization of an arbitrary quantum Kac-Moody algebra and discuss some of its algebraic properties,including the triangular decomposition,the(topological)Hopf algebra structure,the specialization and etc.Constructions and applications of recollements of derivedmodule categories陈红星首都师范大学3In1982Beilinson,Bernstein and Deligne introduced recollements of triangulated categories in contexts of the derived categories of perverse sheaves over singular spaces, which provide a derived version of Grothendieck’s six functors on abelian categories. Since then,they have been used in algebraic geometry and topology and recently in representation theory.For instance,Happel used recollements of bounded derived mod-ule categories to establish reduction techniques for homological conjectures.To produce recollements of triangulated categories,there are many methods available.For instance, one may take stable categories of Frobenius categories or quotient categories by smash-ing subcategories.But,to construct recollements of derived module categories of rings seems to be a difficult question and little was known about it before2010.A known ex-ample is the Cline-Parshall-Scott construction from hereditary ideals,or more generally stratifying ideals of rings.In this talk,I will report two general methods to construct recollements of derived module categories of rings from infinitely generated tilting modules and homological exact contexts,based on a series of joint work with Changchang Xi.These recollements have many applications in algebraic representation theory and algebraic K-theory.For example,they were applied to establish estimation inequalities of finitistic dimensions of rings and also infinite Mayer-Vietoris sequences of higher algebraic K-groups of rings.Gorenstein flat representations of left rooted quivers狄振兴西北师范大学We study Gorenstein flat objects in the category Rep(Q,R)of representations of a left rooted quiver Q with values in Mod(R),the category of all left R-modules,where R is an arbitrary associative ring.We show that a representation X in Rep(Q,R)is Goren-stein flat if and only if for each vertex i the canonical homomorphismϕXi :⊕a:j→i X(j)→X(i)is injective,and the left R-modules X(i)and CokerϕXi are Gorenstein flat.As anapplication of this result,we show that there is a hereditary abelian model structure on Rep(Q,R)whose cofibrant objects are precisely the Gorenstein flat representations, fibrant objects are precisely the cotorsion representations,and trivial objects are pre-cisely the representations with values in the right orthogonal category of all projectively coresolved Gorenstein flat left R-modules.The integral form of U(̂︀gl n)and U(gl n[t])4付强同济大学In the seminal work,Beilinson–Lusztig–MacPherson gave a beautiful realization for quantum gl n via a geometric setting of quantum Schur algebras.In particular they give a geometric construction of canonical bases for the integral form of modified quantum gl n.We will investigate the integral form of U(̂︀gl n)and U(gl n[t]).In particular we will construct canonical bases for the integral form of modified quantum̂︀gl n and modifiedquantum gl n[t].Basepoint-freeness of primitive line bundles on abelian varieties江智上海数学中心/复旦大学Given an ample line bundle L on abelian varieties,it is well-known that L⊗2is basepoint free and L⊗3is very ample.In general,it is difficult to tell when L is basepoint free.In this talk we will present some recent progress on this topic.V-topologies and beyondWill Johnson复旦大学A V-topology is a field topology induced by a valuation ring or an absolute value. V-topologies play an important role in number theory and algebra.A more general class of“finite weight”field topologies naturally arises from problems in mathematical logic. Weight-1topologies are equivalent to V-topologies.The picture in higher weights is unexpectedly complicated,but a classification may be possible.On the algebraic side, there is a class of“weight n”integral domains generalizing valuation rings.We will discuss the basic theory,examples,and open problems.Geometry of moduli space of hyper-K¨a hler varieties李志远上海数学中心/复旦大学5The study of moduli space of hyper-K¨a hler varieties have received a lot of attentions from different aspects in the past decades.In this talk,I will survey the recent progress in this area,especially for K3surfaces.I will explain an important interaction between the geometry of such moduli spaces and arithmetic properties of automorphic forms.There are a lot of useful consequences and I will focus on some fundamental problems,such as Noether-Lefchetz conjectures,Tautological conjectures and Effective cone problems.Cells in affine q-Schur algebra罗栗华东师范大学We introduced the notion of affine q-Schur algebras of arbitrary type and devel-oped their algebraic and geometrical approaches toward canonical bases.The cells and asymptotic forms for these q-Schur algebras are studied.These results are generaliza-tions of those for affine Hecke algebras due to Lusztig.It is joint work with Weideng Cui and Weiqiang Wang.丢番图逼近中上极限集的分形维数王保伟华中科技大学由一列球或矩形确定的上极限集是丢番图逼近中两类基本的集合,一个源自于Dirichlet定理另一个源自于Minkowski定理.由球确定的上极限集的度量理论已经非常丰富/完备,然而由矩形确定的上极限集的研究却非常滞后,甚至一些基本问题都尚未完全解决.在此报告中,通过引入矩形的无处不在性/满测性,我们确定了由矩形生成的上极限集的Hausdorff理论的一般原理.函数域上的一个Siegel-Weil公式熊玮湖南大学6Siegel-Weil公式是一个等式,它说的是在很多情况下Eisenstein级数和Theta函数的积分是相等的.在这个报告中,我们将介绍函数域上的一个Siegel-Weil公式.这个公式是A.Weil在1964年建立的数域上的Siegel-Weil公式在函数域上的一个类比.我们将首先介绍下Siegel-Weil公式的雏形及一些例子,然后介绍下C.L.Siegel的经典结果,再介绍下Weil用表示论及Adele的语言对Siegel工作的推广,最后介绍下函数域上的结果.Periods,global packets,and L-functions许宾四川大学The central values of L-functions play an important role in the study of automorphic representations.For example,it is closely related to the periods of automorphic forms via the Gan-Gross-Prasad conjectures,and is crucial for the non-vanishing of global theta lifts.In this talk,we will recall some relations among global Arthur(Vogan)packets, automorphic periods,and automorphic L-functions.Then we introduce a new approach to show that,for a cuspidal representation of PGL2having a quadratic twist with root number+1,there exist infinitely many quadratic twists with non-zero central L-values.The new approach is based on concrete constructions of automorphic representa-tions.A bound of permutation resolutions of modules for some blocks徐行忠湖北大学Recently,Balmer and Benson introduce a kind of resolution whose objects are permutation modules,and those resolutions are finite.In this talk,we recall these resolutions and try to give a bound of these permutation resolutions for some module in some given blocks.This is a jointed work with H.Liu and J.Zhang.Free idempotent generated semigroups:maximal subgroups, general structures and word problems杨丹丹西安电子科技大学7The set of idempotents of any semigroup carries the structure of a biordered set, which contains a great deal of information concerning the idempotent generated subsemi-group of the semigroup in question.This leads to the construction of a free idempotent generated semigroup IG(E)–the‘free-est’semigroup with a given biordered set E of idempotents.It was thought from the1970s that all maximal subgroups of IG(E)would be free,but this conjecture was false.In this talk,I will present my joint work with my collaborators on this topic,including maximal subgroups,general structures and word problems of IG(E).Construction of Gelfand-Tsetlin modules for gl n张健华中师范大学A classical paper of Gelfand and Tsetlin describes a basis of irreducible finite di-mensional modules over the Lie algebra gl n.This is one of the most remarkable results of the representation theory of Lie algebras which initiated a development of the theory of Gelfand-Tsetlin modules.The Gelfand-Tsetlin modules form the largest subcategory of gl n-modules where there is some understanding of irreducible modules.The main remaining problem is how to construct explicitly these modules.We propose a new effective method of constructing explicitly Gelfand-Tsetlin modules for gl n and obtain a large family of irreducible modules that have a basis consisting of Gelfand-Tsetlin tableaux and the action of the Lie algebra is given by the Gelfand-Tsetlin formulas.As an application of our construction we prove necessary and sufficient condition for the Gelfand and Graev’s continuation construction to define a module which was conjec-tured by Lemire and Patera.The talk is based on joint results with Vyacheslav Futorny and Luis Enrique Ramirez.8TM B几何与拓扑Regularity for Dirac-harmonic maps into Lorentzian manifolds艾万君西南大学Dirac-harmonic maps are motivated by the supersymmetric nonlinear sigma model in quantum field theory,which generalize the classical harmonic maps and harmonic spinors.In recent decades,the existence,regularity and blow-up analysis of Dirac-harmonic maps from a Riemann surface to another compact Riemannian manifold have been extensively studied.In this presentation,we will start from classical regularity results of spherical harmonic maps and Lorentz spherical harmonic maps,and then show some generalizations of these results for general target manifolds,both in Riemannian and Lorentzian cases.Finally,we present a new result about the regularity of Dirac-harmonic maps from a Riemann surfaces into a stationary Lorentzian manifolds.It turns out the regularity of weakly Dirac-harmonic maps depends on a general regularity theorem of critical elliptic systems without an L2-antisymmetric structure.Our results generalize the corresponding regularity results of H´e lein,Rivi`e re and Rivi`e re–Struwe for harmonic maps.This is joint work with Zhu,Miaomiao.Shifted derived Poisson manifolds associated with Lie pairs陈酌清华大学I will talk about the shifted analogue of the“Lie-Poisson”construction between L∞algebroids and shifted derived Poisson manifolds via the example of a Lie algebroid pair(L,A).We show that the pullback of the normal bundle L/A over the dg manifold (A[1],d A)is an L∞algebroid,thus the space totΩA(∧L/A)admits a canonical degree (+1)derived Poisson algebra structure with the wedge product as associative multi-plication and the Chevalley-Eilenberg differential d BottA as the unary L∞bracket.As aconsequence,its Chevalley-Eilenberg hypercohomology admits a canonical Gerstenhaber algebra structure.If time were permitted,I will explain that this degree(+1)derived Poisson algebra structure can also be recovered from Fedosov dg Lie algebroid of this Lie pair and from the Dirac deformation of the associated Courant algebroid,respectively. This is a joint work with R.Bandiera,M.Sti´e non,and P.Xu.Recent progress in symplectic birational geometry杜承勇四川师范大学In this talk,we first introduce the backgrounds of and basic notions in symplectic birational geometry,and then we review some recent progresses of the symplectic bira-tional invariance of symplectic uniruledness and some results on symplectically rational connectedness.Part of the results are based on joint work with Bohui Chen,Jianxun Hu and Rui Wang.Maxwell-Einstein度量关庄丹河南大学In every K¨a hler class of a compact almost homogeneous manifold with two ends we found an unique Calabi extremal metric earlier.Moreover,we found an unique extremal metric in a given K¨a hler class on certain C P1bundle if certain function there is positive. We realized later on that this is equivalent to the geodesic stability of the K¨a hler class. In this talk,we shall prove that for these kind of manifolds,there is another natural K¨a hler metric in the given K¨a hler class,which is called the Maxwell-Einstein metrics. This kind of metrics came from physics and in the efforts of finding Hermitian-Einstein metrics.Recently,it became a hot topic in the K¨a hler geometry.It is worked by several famous mathematicians as Le Brun and Futaki.Our solution gave an answer to a central problem people tried to obtain in series of many papers.曲率有下界球面区域的刚性来米加上海交通大学在本报告中,我将汇报两个有关球面区域的几何刚性定理:一个是在里奇曲率有下界时,由Clifford环面界定的球面区域的刚性;另一个是在Q曲率有下界时半球面的刚性.后者是和上海数学中心韦韡合作的.Recent progress on eta invariants and eta forms刘博华东师范大学In1975,Atiyah-Patodi-Singer developed an index theory for the Dirac operator on compact manifolds with boundary.Their index formula involves a contribution of the boundary,called the eta invariant.In1989,Bismut-Cheeger extended the eta invariant to the family case,called eta form,which is the boundary contribution of the family index theorem with boundary.In this talk,we will discuss the recent progress on eta invariants and eta forms.Some results in this talk are based on works jointed with Xiaonan Ma.凸几何中的赋值理论马丹上海师范大学在1872年德国著名数学家Klein提出了Erlangen纲领之后,研究和刻画在变换群作用下不变的几何量一直是几何学研究的核心.赋值则是几何量通常满足的另一性质.经典的赋值Z是定义在K n(n维欧氏空间中的凸体空间)上取值于阿贝尔半群的一类满足以下性质的映射Z(K)+Z(L)=Z(K∪L)+Z(K∩L),其中,K,L,K∪L∈K n.凸几何中的赋值理论在积分几何、泛函分析、微分几何、随机几何、信息论、体视学、图像分析和物理学中均有广泛的应用.本报告将介绍一些列凸几何中的赋值刻画结果,包括Sobolev空间上的L p范数,凸体空间上的Laplace 变换,凸多胞形空间上的矩向量、矩矩阵和LYZ矩阵.Projective embedding of pairs and K-stability孙京洲汕头大学Given a smooth polarized Riemann surface(X;L)endowed with a hyperbolic metric with cusp singularities along a divisor D,we show the L2projective embedding of(X;D) defined by L k is asymptotically almost balanced in a weighted sense.We also show its generalization to the higher dimensional case of projective completion of a positive line bundle over a smooth projective manifold.Topological data analysis and topological approaches to drugdesign and discovery吴杰河北师范大学In this talk,we will report our current research on topological data analysis.The talk will consist of three sections.In the first section,we give a brief introduction to topological data analysis.Then,in the second section,we will give a report on the current progress of topological approach to drug design and discovery in the world.In the last section,we give a report on our works.度量黎曼几何近年来的新发展胥世成首都师范大学从上世纪七、八十年代以来,几何分析与度量黎曼几何得到了蓬勃的发展。
