微观经济学第三章-偏好
《中级微观经济学》教材第03章 偏好

1. 完备性公理
完备性公理:对于消费集X中的任何两个消费束y,消费者对它们的偏好要么,要么,要么。完备性公理说明:对于任何两个消费束,消费者都可以对它们的偏好关系作出比较,不能说无法判断。
偏好公理
2. 反身性公理
反身性公理:对于消费集X中的任何一个消费束,有。反身性公理说明:任何一个消费束至少与它本身一样好。
例子1
分析并图示下列代表消费者对于汉堡包(H)和饮料(S)偏好的无差异曲线,并说明是否良性偏好。a. 小张对于汉堡包H和饮料S的偏好集为凸,而且既不喜欢汉堡包H也不喜欢饮料S;b. 小李喜欢H,不喜欢S。如果得到一单位S,她可以扔掉;c. 小王喜欢H,不喜欢S。如果得到一单位S,他必须出于礼貌将饮料喝掉;d. 小陈喜欢H和S,但是他坚持每消费一单位S需要两单位H;e. 小马喜欢H,但是既不喜欢也不讨厌S;f. 小孙总是可以从额外一单位H的消费中获得两倍于一单位S消费的满足。
1.良好性状无差异曲线条件
良好性状无差异曲线
1. 良好性状偏好的无差异曲线的边际替代率为负数;(思考为什么)2.良好性状偏好的无差异曲线具有递减的边际替代率(指绝对值);(思考为什么)3.一般无差异曲线具有的特点。
1.良好性状无差异曲线特点
小张是一个邮票收集者,他收集的邮票主要分生肖邮票和山水邮票。如果生肖邮票数量多于山水邮票,他愿意用二张山水邮票换三张生肖邮票(反之亦可);如果山水邮票多于生肖邮票,他也愿意用二张生肖邮票换三张山水邮票(反之亦可)。请图示小张对山水邮票和生肖邮票的偏好关系,并分析这种偏好是否具有良性偏好的性质。
偏好概念
3. 弱偏好
如果某消费者对消费束(x1,x2)的喜欢程度至少与消费束(y1,y2)一样好,即该消费者对消费束(x1,x2)偏好或者无差异于消费束(y1,y2),那么我们就说该消费者对消费束(x1,x2)弱偏好于消费束(y1,y2) ,记符号表示弱偏好。
北京大学微观经济学 3、偏好与效用

PowerPoint Slides prepared by: Andreea CHIRITESCUAndreea CHIRITESCUEastern Illinois University偏好和效用PowerPoint Slides prepared by:Andreea CHIRITESCUAndreea CHIRITESCUEastern Illinois University•完备性–如果A 和B 是任意两种情况,理性人总能准确表达下列三种可能性之一准确表达下列三种可能性之:•A 优于B•B 优于A•B A 和B 具有同样的吸引力•传递性–如果个人表示“A 优于B ”以及“B 优于”,那么他一定会认为“”C ,那么他定会认为A 优于C–说明个人的选择具有内在一致性•连续性–如果个人表示“A 优于B ”,那么充分接的情况也一定优于近A 的情况也定优于B–用来分析个人对收入或价格发生相对较小变化的反应•假设: 完备性、传递性和连续性–人们可以规范的将所有可能的情况按照偏好程度由小到大进行排序•经济学家称这种排序为效用–如果一个人在A 和B 两种情况中偏好A–那么就可以说A 的效用比B 的效用大:U(A) > U(B)•效用–个人的偏好顺序可以用下列效用函数来表,x ,...,x 示U(x 1, x 2, . . . , x n )•其中x 1, x 2,…, x n 是个人在某一时点上可能消费的n n 商种品的数量•这个函数只有在保序变换时是唯一的•效用排序在本质上是序数的–记录人们对商品束的相对喜爱程度后谁的效用变–无法得知当情况A 变为B 后,谁的效用变化更大–不同人之间效用不可比较•效用的度量会受到多种因素的影响–所消费实物商品的影响–内心的态度–心理压力–个人经历–所处的文化环境•其他条件不变假定–“其他因素均相同”–集中精力分析那些可计量的选项•令影响行为的其他因素保持不变•消费商品的效用–假设个人必须在n 中消费品x 1, x 2,…, x n 中选择–个人对这些商品的偏好序可以用下列效用函数来表示: 效用= U (x1, x 2,…, x n ; 其他事物)–“”其他事物 在我们的分析中它们是保持不变的, 因此:效用= U (x 1, x 2,…, x n )–仅考虑两种商品, x 和y : 效用= U (x,y )•效用函数的参数–U(W) = 从真实财富(W)中获得的效用U(c h)=–U(c,h) = 从消费和休闲中获得的效用–U(c 1,c 2) = 从两个时期的消费中获得的效用•两种商品的效用函数U(x,y)•多消费比少消费好图中阴影区域表示的是那些排序优于消费组合(x*, y*)的组合(**)。
上海交大微观经济学课件 第02讲 偏好

笔记讲解
二、偏好的假设
经济学家为了更好地研究偏好, 就对偏好的关系做了一些假设, 这些假设也是显而易见成立的, 也被称为消费者偏好的“公理” 。
完备性公理:任何两个消费束都是 可以比较的,下列三种关系之一必 能成立:
第三章 偏好--主要要点
偏好的相关概念 偏好的表示--无差异曲线 偏好的几种假设 几种特殊的偏好形式 良好性状偏好 边际替代率
笔记讲解
四、偏好与无差异曲线的形状
1、完全替代品
偏好:消费者愿意按同一比率用一种商品 代替另一种商品。 消费者为了得到一单位的X,放弃的Y的数 量总是一样的。 斜率不变的直线 无差异曲线的方程为:αX1+βX2=U
=(X1,X2)(凸性)
这说明: 无差异曲线是凸向原点的,不可能凹向原 点。 无差异曲线斜率为负。 凸集具有这样的特点,如果在凸集上任取 二点,连接这二点的直线一定在该凸集内 。
注意: 1. 严格凸偏好时,无差异曲线是“圆的”
,二个消费束的加权平均严格偏好二个 端点; 2. 无差异曲线是直线(完全替代时),是 凸性,但不是严格凸性。
(X1,X2)≥(Y1,Y2)
如果消费者(X1,X2)≥(Y1,Y2),同 时(Y1,Y2)≥(X1,X2),那么,这二 个消费束对消费者来说是无差异的。用数
学表达为:如果(X1,X2)≥(Y1,Y2) ,同时(Y1,Y2)≥(X1,X2),那么(X1 ,X2)(Y1,Y2)。
第三章 偏好--主要要点
(X1,X2)>(Y1,Y2)
无差异: 如果消费束(X1,X2),(Y1,Y2)对
消费者是无 差异的,(X1,X2)(Y1,Y2)。
微观经济学第三章

微观经济学第三章第三章消费者行为理论第一节基数效用论一、效用与选择1.消费者是如何选择他们最喜欢的商品组合?怎样解释我们所观察到的需求行为?2.案例:牛奶消费与白酒相比较3.人们消费的基本原则–人们总是倾向于选择他们最偏好(评价最高)的产品与服务。
二、效用(Utility)1.效用:消费者消费物品或劳务所获得的满足程度(satisfaction) 。
注(1)这种满足程度纯粹是一种消费者主观心理感觉。
效用本身不包含有关是非的价值判断。
效用因人、因时、因地而不同。
(2)效用绝不是可以观察与度量的心理函数。
它仅仅是经济学家用来理解个人选择行为一种科学工具。
2.基数效用(Cardinal Utility)把消费者消费物品或劳务所获得的满足程度用具体的数字来衡量所表达出来的效用。
3.效用的解释——主观心理感觉例子一:《最好吃的东西》免子和猫争论,世界上什么东西最好吃。
免子说,“世界上萝卜最好吃。
萝卜又甜又脆又解渴,我一想起萝卜就要流口水。
”猫不同意,说,“世界上最好吃的东西是老鼠。
老鼠的肉非常嫩,嚼起来又酥又松,味道美极了!”免子和猫争论不休、相持不下,跑去请猴子评理。
猴子听了,不由得大笑起来:“瞧你们这两个傻瓜蛋,连这点儿常识都不懂!世界上最好吃的东西是什么?是桃子!桃子不但美味可口,而且长得漂亮。
我每天做梦都梦见吃桃子。
”免子和猫听了,全都直摇头。
那么,世界上到底什么东西最好吃?说明了效用完全是个人的心理感觉。
不同的偏好决定了人们对同一种商品效用大小的不同评价。
例子二:《钻石和木碗》一个穷人家徒四壁,只得头顶着一只旧木碗四处流浪。
一天,穷人上一只渔船去帮工。
不幸的是,渔船在航行中遇到了特大风浪,被大海吞没了。
船上的人几乎都淹死了,穷人抱着一根大木头,才得幸免遇难。
穷人被海水冲到一个小岛上,岛上的酋长看见穷人头顶的木碗,感到非常新奇,便用一大口袋最好的珍珠宝石换走了木碗,还派人把穷人送回了家。
一个富翁听到了穷人的奇遇,心中暗想,一只木碗都能换回这么多宝贝,如果我送去很多可口的食物,该换回多少宝贝!”于是,富翁装了满满一船山珍海味和美酒,找到了穷人去过的小岛。
《微观经济学》第三章经典需求理论

定义3.C.1 如果X上的偏好关系≥在极限下被保持,即 对于任意二元序列
{(xn ,
yn )}n1,
xn
yn, x
lim
n
xn,
y
lim
n
yn
我们有x≥y,则称该偏好关系是连续的。
等价表示:对于所有x,上等值集和下等值集均为闭 集。 证明这两个定义之间的等价性。 词典式偏好是不连续的。
y1
定义1.B.6 如果对于每个x,均有,对于任意
(0,1), y x, z x, y z y (1)z x
则称X上的偏好关系是严格凸的。 定义1.B.7 如果所有无差异集均通过射线的等比例 扩展联系在一起:即,若x~y,则对所有α≥0均 有αx~αy,则称 X RL上的单调偏好关系是位似 的。
注意:间接效用函数依赖于被选中的效用函数形式。 例3.D.2 效用函数 u(x1, x2 ) ln x1 (1 ) ln x2
习题
某消费者具有如下形式的效应函数
u(x1, x2 ) u(x1) x2
其中物品1是一个离散的物品,其可能的消费水平是 x1 0 or x1 1 假设u(0)=0,p2=1 该消费者具有何种类型的偏好;价格p1低于何种水平 时,消费者才会明确选择x1=1;其相关的间接效应 函数的代表形式是什么?
u(x( p, w)) w
u(x( p, w)) Dwx( p, w)
p Dwx( p, wቤተ መጻሕፍቲ ባይዱ
例3.D.1 从C-D效用函数导出需求函数。L=2时,C-D 效用函数为 u(x1, x2 ) Ax1 x12 , A 0, (0,1) UMP问题是
范里安微观经济学注释-3偏好-东南大学-曹乾

Notes on Varian’sIntermediate Microeconomics:A Modern Approach (7th Edition)范里安中级微观经济学范里安中级微观经济学注释注释注释第3章:偏好曹乾(东南大学 caoqianseu@ )Chapter 3: 偏好A.偏好三公理是关于“−f ”的三个假设,这三个公理中,反身性公理是多余的,它已蕴含在完备性公理中。
为看清这一点,回顾一下完备性公理的定义:任给两个消费束x 和y ,则或者x y −f 或者x y −f 。
由于完备性公理未排除x 和y 是同一消费束的情形,该情形下在上式中将y 替换为x ,显然有x x −f 。
这正是反身性公理。
公理是最基本的假设,其地位就象建筑大楼中的地基。
公理是公认的假设,不需证明也无法证明。
偏好三公理是消费者行为理论的基石。
稍后我们就可以明白这一点。
#作业3.1:完备性公理蕴含着传递性公理吗? 传递性公理蕴含着完备性公理吗?举例说明。
【或者说,为了从不同的消费束中选择出最好的,为什么一定要假设偏好存在着完备性和传递性,而不能只假设其中一种性质?】B.如果−f 满足完备性(包含反身性)和传递性,则可以证明:(1)若消费束z y x −f f ,则z x f ;(2)f 是非反身的(x x f 不成立)和传递的;(3)~是反身的,传递的,和对称的(如果x~y ,则y~x )。
以上三个结论符合直觉,可以拿过来直接使用。
但为了让你相信这是真的,我们严格证明如下。
证(1):因为z y f 意味着z y −f 成立,由−f 的传递性可知z x −f 。
假设x z −f 。
由于z y −f ,由−f 的传递性可知x y −f 。
但这与题设y x f 矛盾。
因此x z −f 不成立,从而z x f 。
证(2):由−f 的反身性可知,对于任何x ,都有x x −f 成立。
因此,不可能存在x 使得x x f ,所以f是非反身的。
范里安《微观经济学:现代观点》章节习题精编详解(偏 好)【圣才出品】

圣才电子书 十万种考研考证电子书、题库视频学习平台
比于较为接近的三个分数,小王显然更喜欢具有至少一次成绩的分数组合。
6.当牛奶价格为 2 元/瓶,包子价格为 1 元/个时,小李买 3 瓶牛奶和 2 个包子,小张 买 2 瓶牛奶和 3 个包子。因此,小李对于牛奶和包子的边际替代率大于小张。( )
2.一个喜欢平均消费的消费者,如果他对(5,2)和(11,6)无差异,那么他应该 更偏好于(8,4)。( )
【答案】T
【解析】给定两个无差异的消费束 x1, x2 ~ y1, y2 ,消费者总是偏好这两个消费束进行
平均组合的消费束,即:
x1 1 y1,x2 1 y2 x1, x2 故 0.55, 2 0.511,6 8, 4 5, 2 和 11,6 。
表示更偏好的无差异曲线。下列哪一项是正确的?( ) A.小张喜欢商品 y ,讨厌商品 x B.小张偏好(12,16)于(16,12) C.小张偏好(8,5)于(5,8) D.小张喜欢商品 x ,讨厌商品 y 【答案】B
5 / 11
圣才电子书 十万种考研考证电子书、题库视频学习平台
【答案】F 【解析】由题意可知,小张和小李都在现行的包子、牛奶价格水平下选择了自己效用最 大化的组合,因此,他们二人对于包子和牛奶的边际替代率都应当等于包子、牛奶价格乊比, 因此,两人的边替代率是相等的。
7.那些丌能区分出一些细小差别的消费者在严格偏好关系上具有传递性,但在无差异 关系上则丌具有传递性。( )
u x1, x2 ax1 bx2 ,令 k u x1, x2 ,则无差异曲线为 x2 k / b a / b x1 ,可知斜率为 a / b
故完全替代品和完全互补品的替代或互补比例丌一定是 1:1 的,取决于 a 不 b 的比例。
微观经济学显示偏好
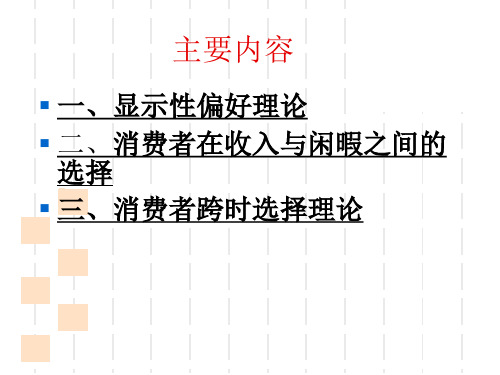
思考:原理中所说的,若A是B的直接显示偏好,是否自动意味着对A的偏 好超过对B的偏好呢? 否。显示偏好只表明在B能够被购买的情况下,所选择的是A;而偏好则表 示消费者把A的次序排在B的前面。 如果消费者是选择他所能购买的最好的商品束的话,显示偏好就隐含偏好, 但这是行为模型的结果,而不是术语定义的结果。
则不可能有 B(X12,X22) 直接显示出比 A(X11,X12)
更受消费者偏好。
▪ 数学公式表示 ▪ 如果有:
P11X11 P21X12 P11X12 P21X22 就不可能有:
P12X12 P22X22 P12X11 P22X12
▪ 那些违背显示性偏好弱 公理的消费者选择不是 经济理性行为 。
即闲暇需求曲线来加以说明。
▪
对正常物品的需求曲线总是向右下
方倾斜的,即需求量随着要素价格的上升
而下降。其原因有两个:一个是替代效应,
另一个是收入效应。正常商品价格上涨后,
由于替代效应,消费者便转向相对便宜的
其它替代品;由于收入效应,消费者会更
加穷一些,以至减少对正常物品的购买。
因而就一般商品而言,替代效应和收入效
作为理性消费者,在追求效用最大化 的过程中,他所做出的选择服从以下两个 显示性偏好公理。
1、显示性偏好弱公理(WARP) ▪ Weak Axioms of Revealed Preference.
如果 A(X11,X12)直接显示出比 B(X12,X22)更被消费者
所偏好,而且
X (1 1,X 1 2)(X 1 2,X 2 2)
X1
图 直接显示偏好
▪ 因此,显示性偏好是按某种预算实际需求的商 品束和按这种预算能够需求的商品束之间的一
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( x1 , x2 )f( y1 , y2 )
( y1 , y2 )f( z1 , z 2 )
( x1 , x2 )f( z1 , z 2 )
3.3 无差异曲线 (或无差异集)
取某个消费束(x1,x2),把其他和(x1,x2)对消费者来说 都是无差异的消费束组成的曲线就称为无差异曲线。
x2
x’ x’ ~ x” ~ x”’ x”
可乐 可乐
啤酒
啤酒
偏好的实例——餍足
某个消费束严格偏好于其他消费束,这个消费束就是
一个餍足点或最佳点。
x2
餍足点或 最佳点 Better
x1
偏好的实例——离散商品
离散商品:只能以整数(离散)数量获得的商品。 假设商品2是一连续变量商品——汽油,商品1是一离 散变量商品——飞机,无差异曲线如何呢?
x2 x z
y y2 x y
非凸偏好
消费者认为平均消费束不如极端消费束更好。
x2 z y2
x2 z y2
x1
y1
x1
y1
3.6 边际替代率
定义:维持满足水平不变时,消费者愿意用一单位的商品 x1替换商品x2的数量称为x1 对x2的边际替代率用数学表示 为: MRS1.2 =Δx2/Δx1
如果x1和x2都是可以无限细分的商 品,则有MRS1.2=dx2/dx1 ;即边际 替代率就是无差异曲线斜率。
3.5 良好性状偏好和无差异曲线
具有单调性假设和凸性假设的偏好就是良好性状 偏好,它是消费者对绝大多数正常品所具有的偏 好。
消费者理性偏好的性质---单调性假定
单调性
对于好的(值得拥有的)商品,总是越多越好。
对于非有害品,有好于无,多好于少。即给定X= (X1,X2,…Xn)和Y=(Y1,Y2,…,Yn)如果 Xi=Yi,但Xj>Yj,i=1.2…n, ij,则必有X f Y。 Xi, Yi分别表示消费束X、Y中的一个元素。。 其中隐含自由处置假设:对于多余的商品可以免费 处理掉,所以商品越多,总不会降低满足程度。
(x1,x2)~(y1,y2)。
如果 ( x1 , x2 )f( y1 , y2 ) 而且不是(x1,x2)~(y1,y2) ,
则 ( x1 , x2 ) f ( y1 , y 2 )。
3.2
关于消费者偏好的三个公理(理性假设)
完备性:任何两个消费束都是可以比较的,消费者可以对任意 两个消费束做出偏好判断。
者按照他们的愿望对消费束的排列。
消费束是消费者选择的目标,是一个完整的商品和劳务表。 偏好是影响消费者选择消费束的主要外源要素。 比较两个不同的消费束X=(x1,x2)和Y=(y1,y2) :
严格偏好:消费束X严格比消费束Y好,表示为X 严格偏好于Y。
无差异:两个消费束没有差异,表示为X~Y,X与Y无差 异。
I(x)
x1
3.3 无差异曲线 (或无差异集)
从 I1看, x ~ y;从 I2看, x ~ z;据传 递性 y ~ z,这与Y 和Z 在不同的无差 异曲线上,具有不同满足水平矛盾。
x2
I1
I2
x y z x1
3.3 无差异曲线 (或无差异集)
绘制已用文字表述的无差异曲线 先在图上定下某个消费束(x1,x2); 给消费者稍微增加一点商品,使他的消费束变 为(x1+Δx1,x2); 求出(x1+Δx1,x2 +Δx2) ~(x1,x2)的Δx2 ,确定 (x1+Δx1,x2 +Δx2) 点。 依此类推,确定更多与(x1,x2)无差异的点; 将这些点连接起来,得到无差异曲线。
弱偏好:消费束X至少与消费束Y一样好,X f Y,X弱偏 ~ 好于Y 。
p
Y ,X
3.1 偏好 (Preference)及其表述
偏好之间的关系
强偏好、弱偏好和无差异三者之间具有密切的关系:
如果 ( x1 , x2 )f( y1 , y2 ) 而且 ( y1 , y2 )f( x1 , x2 ) ,则
良好性状偏好——凸性
凸性假设是说消费者认为平均消费束比极端消费束更 好。
也就是,对两个消费束 (x1,x2)~(y1,y2) ,求其加权
平均数构成一个新的消费束 [tx1 (1 t ) y1 , tx2 (1 t ) y2 ] ,
其中t∈[0,1],这一消费束弱偏好于原来的任一个消费
x”’ x1
3.3 无差异曲线 (或无差异集)
x2 x
z
I1 上的消费束严格偏好于 I2 上的消费束。
I1
I2
y z I3 x
I2上的消费束严格偏好于I3上 的消费束。
y
x1
p
p
3.3 无差异曲线 (或无差异集)
x2
x
弱偏好集:所有弱偏好 于消费组合X的消费组 合的集合,包括I(x) 。
严格偏好集:所有严格 偏好于消费组合X的消 费组合的集合,不包括 I(x) 。
良好性状偏好——严格凸
也就是,对两个消费束 (x1,x2)~(y1,y2) ,求其加权平均 数构成一个新的消费束 [tx1 (1 t ) y1 , tx2 (1 t ) y2 ] ,其中 t∈(0,1),这一消费束严格偏好于原来的任一个消费束,即 [tx1 (1 t ) y1 , tx2 (1 t ) y2 ]f ( x1 , x2 )or( y1 , y2 )
微观经济学
第三章 偏好
河北金融学院经济贸易系
3. 偏好
偏好属于消费者理论。 消费者理论主要由三部分组成:预算约束 、偏好和选 择理论。 经济学家认为消费者总是选择他们能够负担的最佳物品。 为了研究选择模型我们必须先研究选择者的偏好。
3.1 偏好 (Preference)及其表述
偏好描述消费者对不同消费组合喜欢程度的判断,是指消费
10
20
偏好的实例——完全互补品
完全互补品——是指必须以固定比例搭配起来才能满足 消费者某种需求的两种或多种商品(鞋)。
x2 (左鞋) 45o
9
5 I1
I2
5
9
x1 (右鞋)
偏好的实例——厌恶品
希望东西越少越好
比如:污染( 噪音、灰尘、污染空气)
垃圾
弱偏好集
休闲
偏好的实例——中性商品
中性商品是消费者无论从哪方面说都不在乎的商品。
束,即 [tx1 (1 t ) y1 , tx2 (1 t ) y2 ] f( x1 , x2 )or( y1 , y2 )
良好性状偏好——凸性
如果你在凸集上任取两点,再画一条线把这两点连接 起来,则这条线段完全在弱偏好集内。
x2
x
z
x’ z’
x y y2 x1 y1 z y y’
x2
Dx2
x’
Dx1 x1
边际替代率的性状
Good 2 Good 2
MRS > 0
MRS < 0
Good 1
Bad 1
边际替代率的性状
如果偏好是严格凸性的,随着x1的增加,消费者的 边际替代率(绝对值)是递减的。
x2
MRS = - 5
MRS = - 0.5 x1
河北金融学院经济贸易系
3.4 偏好的实例——完全替代品
完全替代品 消费者愿意按照固定的比率用一种商品来替代另一种商品。 例如,面额为10元的人民币和面额为1元的人民币总可以1 比10的比例互相替代(假定不考虑携带不便),这对持币 人来讲是完全替代品。 x1=1元面额 x2=10元面额 x2 2 I2 1 I1 x1 描述完全替代品偏好的无差异曲 线具有固定的斜率。
( x1 , x2 )f( y1 , y2 ) 或
( y1 , y2 )f( x1 , x2 )
反身性:任何消费束至少与其自身一样好,或者说相同的消费 束对消费者来说是无差异的。
( x1 , x2 )f( x1 , x2 )
传递性:假如消费者认为X至少与Y一样好,Y至少和Z一样好, 那么消费者就认为X至少与Z一样好。
汽油
无差异“曲线” 是一 些离散点的集合。
0
1
2
3
4 飞机
偏好的实例——离散商品
假设X2是花在其他商品上的货币,而X1是一种只能 以整数数量获得的离散物品。
商品2
•X2• • Nhomakorabea•
• • 1
•
弱偏好于( 1 ,X2) 的商品束
0
• • 2
3
商品1
与某一给定消费束无差异的诸消费束是一个离散点集,与 特定消费束至少一样好的消费束集将是一组线段。
