北京市西城区2013届高三上学期期中考试(数学理)无答案
北京2013西城高三数学一模理科试题及答案

北京市西城区2013年高三一模试卷高三数学(理科) 2013.4第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. 1.已知全集U=R ,集合{|02}A x x =<<,2{|10}B x x =->,那么U A B = ð(A ){|01}x x << (B ){|01}x x <≤ (C ){|12}x x << (D ){|1x2.若复数i2ia +的实部与虚部相等,则实数a = (A )1- (B )1 (C )2- (D )23.执行如图所示的程序框图.若输出y ==θ(A )π6 (B )π6- (C )π3 (D )π3-4.从甲、乙等5名志愿者中选出4名,分别从事A ,B ,C ,D 四项不同的工作,每人承担一项.若甲、乙二人均不能从事A 工作,则不同的工作分配方案共有(A )60种 (B )72种 (C )84种 (D )96种 5.某正三棱柱的三视图如图所示,其中正(主)视 图是边长为2的正方形,该正三棱柱的表面积是(A )6 (B )12(C )12+ (D )24+6.等比数列{}n a 中,10a >,则“13a a <”是“36a a <”的(A )充分而不必要条件(B )必要而不充分条件(C )充分必要条件(D )既不充分也不必要条件 7.已知函数22()log 2log ()f x x x c =-+,其中0c >.若对于任意的(0,)x ∈+∞,都有()1f x ≤,则c 的取值范围是(A )1(0,]4 (B )1[,)4+∞ (C )1(0,]8 (D )1[,)8+∞ 8.如图,正方体1111ABCD ABC D -中,P 为底面ABCD上的动点,1PE AC ⊥于E ,且PA PE =,则点P 的轨迹是(A )线段 (B )圆弧 (C )椭圆的一部分 (D )抛物线的一部分第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.9.已知曲线C 的参数方程为2cos 12sin x y =⎧⎨=+⎩αα(α为参数),则曲线C 的直角坐标方程为 .10.设等差数列{}n a 的公差不为0,其前n 项和是n S .若23S S =,0k S =,则k =______.11.如图,正六边形ABCDEF 的边长为1,则AC DB ⋅=______.12.如图,已知AB 是圆O 的直径,P 在AB 的延长线上,PC切圆O 于点C ,CD OP ⊥于D .若6CD =,10CP =, 则圆O 的半径长为______;BP =______.13.在直角坐标系xOy 中,点B 与点(1,0)A -关于原点O 对称. 点00(,)P x y 在抛物线24y x =上,且直线AP 与BP 的斜率之积等于2,则0x =______.14.记实数12,,,n x x x 中的最大数为12max{,,,}n x x x ,最小数为12min{,,,}n x x x .设△ABC 的三边边长分别为,,a b c ,且a b c ≤≤,定义△ABC 的倾斜度为max{,,}min{,a b c a t b c a b =⋅,}b c c a.(ⅰ)若△ABC 为等腰三角形,则t=______;(ⅱ)设1a =,则t 的取值范围是______.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤. 15.(本小题满分13分)已知函数()sin cos f x x a x =-的一个零点是π4.(Ⅰ)求实数a 的值;(Ⅱ)设()()()cos g x f x f x x x =⋅-+,求()g x 的单调递增区间.16.(本小题满分13分)某班有甲、乙两个学习小组,两组的人数如下:现采用分层抽样的方法(层内采用简单随机抽样)从甲、乙两组中共抽取3名同学进行学业检测. (Ⅰ)求从甲组抽取的同学中恰有1名女同学的概率;(Ⅱ)记X 为抽取的3名同学中男同学的人数,求随机变量X 的分布列和数学期望.17.(本小题满分14分)在如图所示的几何体中,面CDEF 为正方形,面ABCD 为等腰梯形,AB //CD ,BC AB 2=,60ABC ︒∠=,AC FB ⊥.(Ⅰ)求证:⊥AC 平面FBC ;(Ⅱ)求BC 与平面EAC 所成角的正弦值;(Ⅲ)线段ED 上是否存在点Q ,使平面EAC ⊥平面QBC ? 证明你的结论. 18.(本小题满分13分)已知函数()ln f x ax x =-,()e 3ax g x x =+,其中a ∈R .(Ⅰ)求)(x f 的极值;(Ⅱ)若存在区间M ,使)(x f 和()g x 在区间M 上具有相同的单调性,求a 的取值范围.19.(本小题满分14分)如图,椭圆22221(0)x y a b a b+=>>的左焦点为F ,过点F 的直线交椭圆于A ,B 两点.当直线AB 经过椭圆的一个顶点时,其倾斜角恰为60︒. (Ⅰ)求该椭圆的离心率;(Ⅱ)设线段AB 的中点为G ,AB 的中垂线与x 轴和y 轴分别 交于,D E 两点.记△GFD 的面积为1S ,△OED (O 为原点) 的面积为2S ,求12S S 的取值范围. 20.(本小题满分13分)已知集合*12{|(,,,),,1,2,,}(2)nn i S X X x x x x i n n ==∈=≥N .对于12(,,,)n A a a a = ,12(,,,)n n B b b b S =∈ ,定义1122(,,,)n n AB b a b a b a =---; 1212(,,,)(,,,)()n n a a a a a a =∈R λλλλλ;A 与B 之间的距离为1(,)||ni i i d A B a b ==-∑.(Ⅰ)当5n =时,设5(1,2,1,2,)A a =,(2,4,2,1,3)B =.若(,)7d A B =,求5a ;(Ⅱ)(ⅰ)证明:若,,n A B C S ∈,且0∃>λ,使AB BC λ= ,则(,)(,)(,)d A B d B C d A C +=;(ⅱ)设,,n A B C S ∈,且(,)(,)(,)d A B d B C d A C +=.是否一定0∃>λ,使AB BC λ=?说明理由; (Ⅲ)记(1,1,,1)n IS =∈ .若A ,n B S ∈,且(,)(,)d I A d I B p ==,求(,)d A B 的最大值.北京市西城区2013年高三一模试卷高三数学(理科)参考答案及评分标准2013.4一、选择题:本大题共8小题,每小题5分,共40分.1. B ; 2.A ; 3.D ; 4.B ; 5.C ; 6.B ; 7.D ; 8.A . 二、填空题:本大题共6小题,每小题5分,共30分.9.22230x y y +--=; 10.5; 11.32-12.152,5; 13.1 14.1,1[1,2. 注:12、14题第一问2分,第二问3分.三、解答题:本大题共6小题,共80分.若考生的解法与本解答不同,正确者可参照评分标准给分. 15.(本小题满分13分) (Ⅰ)解:依题意,得π()04f =, ………………1分 即ππsincos 04422a -=-=, ………………3分 解得 1a =. ………………5分 (Ⅱ)解:由(Ⅰ)得()sin cos f x x x =-. ………………6分()()()cos g x f x f x x x =⋅-+(sin cos )(sin cos )x x x x x =--- ………………7分22(cossin )x x x =- ………………8分cos2x x = ………………9分 π2sin(2)6x =+. ………………10分由 πππ2π22π262k x k -≤+≤+,得 ππππ36k x k -≤≤+,k ∈Z . ………………12分所以 ()g x 的单调递增区间为ππ[π,π]36k k -+,k ∈Z . ………………13分16.(本小题满分13分)(Ⅰ)解:依题意,甲、乙两组的学生人数之比为 (35):(22)2:1++=, ……………1分所以,从甲组抽取的学生人数为2323⨯=;从乙组抽取的学生人数为1313⨯=.………2分 设“从甲组抽取的同学中恰有1名女同学”为事件A , ………………3分则 113528C C 15()C 28P A ⋅==,故从甲组抽取的同学中恰有1名女同学的概率为1528.………5分 (Ⅱ)解:随机变量X 的所有取值为0,1,2,3. ………………6分21522184C C 5(0)C C 28P X ⋅===⋅, 111213525221218484C C C C C 25(1)C C C C 56P X ⋅⋅⋅==+=⋅⋅, 211113235221218484C C C C C 9(2)C C C C 28P X ⋅⋅⋅==+=⋅⋅, 21322184C C 3(3)C C 56P X ⋅===⋅.……………10分 所以,随机变量X 的分布列为:………………11分5259350123285628564EX =⨯+⨯+⨯+⨯=. ………………13分 17.(本小题满分14分)(Ⅰ)证明:因为BC AB 2=,60ABC ︒∠=,在△ABC 中,由余弦定理可得 BC AC 3=,所以 BC AC ⊥. ………………2分 又因为AC FB ⊥,所以⊥AC 平面FBC . ………………4分 (Ⅱ)解:因为⊥AC 平面FBC ,所以FC AC ⊥.因为FC CD ⊥,所以⊥FC 平面ABCD . ………………5分 所以,,CA CF CB 两两互相垂直,如图建立的空间直角坐标系xyz C -. ………………6分 在等腰梯形ABCD 中,可得 CB CD =. 设1BC =,所以11(0,0,0),(0,1,0),(,,0),(,,1)2222C A BDE --. 所以)1,21,23(-=CE ,)0,0,3(=CA ,)0,1,0(=CB . 设平面EAC 的法向量为=()x,y,z n ,则有0,0.CE CA ⎧⋅=⎪⎨⋅=⎪⎩n n 所以 10,20.x y z -+== 取1z =,得=n (0,2,1). ………………8分设BC 与平面EAC 所成的角为θ,则||sin |cos ,|||||CB CB CB ⋅=〈〉==θn n n 所以 BC 与平面EAC 所成角的正弦值为552. ………………9分 (Ⅲ)解:线段ED 上不存在点Q ,使平面EAC ⊥平面QBC .证明如下: ………………10分假设线段ED 上存在点Q ,设 ),21,23(t Q - )10(≤≤t ,所以),21,23(t CQ -=. 设平面QBC 的法向量为=m ),,(c b a ,则有0,0.CB CQ ⎧⋅=⎪⎨⋅=⎪⎩m m 所以0,10.2b b tc =⎧-+= 取 1=c ,得=m )1,0,32(t -. ………………12分 要使平面EAC ⊥平面QBC ,只需0=⋅n m , ………………13分 即002110⨯+⨯+⨯=, 此方程无解. 所以线段ED 上不存在点Q ,使平面EAC ⊥平面QBC . ………………14分 18.(本小题满分13分) (Ⅰ)解:()f x 的定义域为(0,)+∞, ………………1分且11()ax f x a x x-'=-=. ………………2分① 当0a ≤时,()0f x '<,故()f x 在(0,)+∞上单调递减.从而)(x f 没有极大值,也没有极小值. ………………3分② 当0a >时,令()0f x '=,得1x a=.()f x 和()f x '的情况如下:故()f x 的单调减区间为(0,)a ;单调增区间为(,)a +∞.从而)(x f 的极小值为1()1ln f a a=+;没有极大值. ………………5分(Ⅱ)解:()g x 的定义域为R ,且 ()e 3ax g x a '=+. ………………6分③ 当0a >时,显然 ()0g x '>,从而()g x 在R 上单调递增. 由(Ⅰ)得,此时()f x 在1(,)a+∞上单调递增,符合题意. ………………8分④ 当0a =时,()g x 在R 上单调递增,()f x 在(0,)+∞上单调递减,不合题意.……9分⑤ 当0a <时,令()0g x '=,得013ln()x a a=-. ()g x 和()g x '的情况如下表:当30a -≤<时,00x ≤,此时()g x 在0(,)x +∞上单调递增,由于()f x 在(0,)+∞上单调递减,不合题意. ………………11分当3a <-时,00x >,此时()g x 在0(,)x -∞上单调递减,由于()f x 在(0,)+∞上单调递减,符合题意.综上,a 的取值范围是(,3)(0,)-∞-+∞ . ………………13分 19.(本小题满分14分)(Ⅰ)解:依题意,当直线AB 经过椭圆的顶点(0,)b 时,其倾斜角为60︒. ………………1分设 (,0)F c -,则tan60bc︒=.………………2分将 b 代入 222a b c =+,解得 2a c =.………………3分 所以椭圆的离心率为 12c e a ==. ………………4分 (Ⅱ)解:由(Ⅰ),椭圆的方程可设为2222143x y c c+=. ………………5分设11(,)A x y ,22(,)B x y .依题意,直线AB 不能与,x y 轴垂直,故设直线AB 的方程为()y k x c =+,将其代入2223412x y c +=,整理得 222222(43)84120k x ck x k c c +++-=. ………………7分则 2122843ck x x k -+=+,121226(2)43cky y k x x c k +=++=+,22243(,)4343ck ck G k k -++. ………………8分因为 GD AB ⊥,所以 2223431443Dck k k ck x k +⨯=---+,2243D ck x k -=+. ………………9分 因为 △GFD ∽△OED ,所以 2222222212222243()()||434343||()43ck ck ck S GD k k k ck S OD k ---++++==-+ ………………11分 222242222242(3)(3)99999()ck ck c k c k ck c k k++===+>. ………………13分 所以12S S 的取值范围是(9,)+∞. ………………14分 20.(本小题满分13分)(Ⅰ)解:当5n =时,由51(,)||7iii d A B a b ==-=∑,得 5|12||24||12||21||3|7a -+-+-+-+-=,即 5|3|2a -=. 由 *5a ∈N ,得 51a =,或55a =. ………………3分(Ⅱ)(ⅰ)证明:设12(,,,)n A a a a = ,12(,,,)n B b b b = ,12(,,,)n C c c c = .因为 0∃>λ,使 AB BC λ=,所以 0∃>λ,使得 11221122(,,)((,,)n n n n b a b a b a c b c b c b ---=--- λ,,, 即 0∃>λ,使得 ()i i i i b a c b λ-=-,其中1,2,,i n = .所以 ii b a -与(1,2,,)i i c b i n -= 同为非负数或同为负数. ………………5分所以 11(,)(,)||||n n iiiii i d A B d B C a b b c ==+=-+-∑∑1(||||)niiiii b a c b ==-+-∑1||(,)ni i i c a d A C ==-=∑. ………………6分(ⅱ)解:设,,n A B C S ∈,且(,)(,)(,)d A B d B C d A C +=,此时不一定0∃>λ,使得AB BC λ=. ………………7分反例如下:取(1,1,1,,1)A = ,(1,2,1,1,,1)B = ,(2,2,2,1,1,,1)C ,则 (,)1d A B =,(,)2d B C =,(,)3d A C =,显然(,)(,)(,)d A B d B C d A C +=.因为(0,1,0,0,,0)AB = ,(1,0,1,0,0,,0)BC =,所以不存在>0λ,使得AB BC λ=. ………………8分(Ⅲ)解法一:因为 1(,)||niii d A B b a ==-∑,设(1,2,,)ii b a i n -= 中有()m m n ≤项为非负数,n m -项为负数.不妨设1,2,,i m = 时0i i b a -≥;1,2,,i m m n =++ 时,0i i b a -<.所以 1(,)||niii d A B b a ==-∑12121212[()()][()()]m m m m n m m n b b b a a a a a a b b b ++++=+++-+++++++-+++因为 (,)(,)d I A d I B p ==,所以11(1)(1)nniii i a b ==-=-∑∑, 整理得 11nn iii i a b ===∑∑.所以 12121(,)||2[()]niimm i d A B b a b b ba a a ==-=+++-+++∑ .……………10分因为 121212()()m n m m n b b b b b b b b b +++++=+++-+++ ()()1p n n m p m ≤+--⨯=+;又 121ma a a m m +++≥⨯= ,所以 1212(,)2[()]m m d A B b b b a a a =+++-+++ 2[()]2p m m p ≤+-=.即 (,)2d A B p ≤.…12分 对于 (1,1,,1,1)A p =+ ,(1,1,1,,1)B p =+ ,有 A ,n B S ∈,且(,)(,)d I A d I B p ==,(,)2d A B p =.综上,(,)d A B 的最大值为2p . ……………13分 解法二:首先证明如下引理:设,x y ∈R ,则有 ||||||x y x y +≤+. 证明:因为 ||||x x x -≤≤,||||y y y -≤≤,所以 (||||)||||x y x y x y -+≤+≤+,即 ||||||x y x y +≤+. 所以 11(,)|||(1)(1)|n niiiii i d A B b a b a ===-=-+-∑∑1(|1||1|)niii b a =≤-+-∑11|1||1|2nni i i i a b p ===-+-=∑∑. ……………11分上式等号成立的条件为1i a =,或1i b =,所以 (,)2d A B p ≤. ……………12分对于 (1,1,,1,1)A p =+ ,(1,1,1,,1)B p =+ ,有 A ,n B S ∈,且(,)(,)d I A d I B p ==,(,)2d A B p =.综上,(,)d A B 的最大值为2p . ……………13分。
北京市西城区2013—2014学年度高三年级第一学期期末数学理科
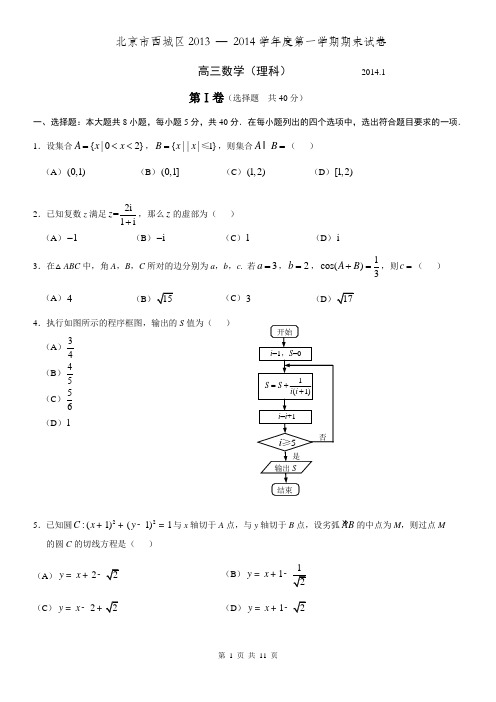
北京市西城区2013 — 2014学年度第一学期期末试卷高三数学(理科)2014.1第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. 1.设集合{|02}A x x =<<,1{|||}B x x =≤,则集合A B = ( ) (A )(0,1)(B )(0,1](C )(1,2)(D )[1,2)3.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c . 若3a =,2b =,1cos()3A B +=,则c =( ) (A )4(B(C )3(D4.执行如图所示的程序框图,输出的S 值为( ) (A )34 (B )45(C )56(D )12.已知复数z 满足2i=1iz +,那么z 的虚部为( ) (A )1-(B )i -(C )1(D )i5.已知圆22:(1)(1)1C x y ++-=与x 轴切于A 点,与y 轴切于B 点,设劣弧»AB 的中点为M ,则过点M 的圆C 的切线方程是( ) (A)2y x =+-(B)1y x =+-(C)2y x =-+(D)1y x =+-6. 若曲线221ax by +=为焦点在x 轴上的椭圆,则实数a ,b 满足( ) (A )22a b > (B )11a b< (C )0a b <<(D )0b a <<7.定义域为R 的函数()f x 满足(1)2()f x f x +=,且当(0,1]x ∈时,2()f x x x =-,则当[2,1]x ∈--时,()f x 的最小值为( ) (A )116-(B ) 18-(C ) 14-(D ) 08. 如图,正方体1111ABCD A B C D -的棱长为P 在对角线1BD 上,过点P 作垂直于1BD 的平面α,记这样得到的截面多边形(含三角形)的周长为y ,设BP =x , 则当[1,5]x ∈时,函数()y f x =的值域为( )(A) (B) (C) (D)第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.9. 在平面直角坐标系xOy 中,点(1,3)A ,(2,)B k -,若向量OA AB ⊥,则实数k = ____. 10.若等差数列{}n a 满足112a =,465a a +=,则公差d =______;24620a a a a ++++= ______.11.已知一个正三棱柱的所有棱长均相等,其侧(左)视图如图所示,那么此三棱柱正(主)视图的面积为______.12.甲、乙两名大学生从4个公司中各选2个作为实习单位,则两人所选的实习单位中恰有1个相同的选法种数是______. (用数字作答)13. 如图,,B C 为圆O 上的两个点,P 为CB 延长线上一点,PA 为圆O 的切线,A 为切点. 若2PA =,3BC =,则PB =______;ACAB=______.1侧(左)视图14.在平面直角坐标系xOy 中,记不等式组220,0,2x y x y x y +⎧⎪-⎨⎪+⎩≥≤≤所表示的平面区域为D .在映射,:u x y T v x y =+⎧⎨=-⎩的作用下,区域D 内的点(,)x y 对应的象为点(,)u v . (1)在映射T 的作用下,点(2,0)的原象是 ; (2)由点(,)u v 所形成的平面区域的面积为______.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤. 15.(本小题满分13分)已知函数()f x x ω=,π()sin()(0)3g x x ωω=->,且()g x 的最小正周期为π.(Ⅰ)若()2f α=[π,π]α∈-,求α的值; (Ⅱ)求函数()()y f x g x =+的单调增区间.16.(本小题满分13分)以下茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩.乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以a 表示.(Ⅰ)若甲、乙两个小组的数学平均成绩相同,求a 的值; (Ⅱ)求乙组平均成绩超过甲组平均成绩的概率;(Ⅲ)当2a =时,分别从甲、乙两组中各随机选取一名同学,记这两名同学数学成绩之差的绝对值为X ,求随机变量X 的分布列和数学期望.17.(本小题满分14分)如图,在多面体ABCDEF 中,底面ABCD 是边长为2的菱形, 60=∠BAD ,四边形BDEF 是矩形,平面BDEF ⊥平面ABCD ,BF =3, H 是CF 的中点.(Ⅰ)求证:AC ⊥平面BDEF ;(Ⅱ)求直线DH 与平面BDEF 所成角的正弦值; (Ⅲ)求二面角H BD C --的大小.甲组 乙组 891 a822 F CEHD18.(本小题满分13分)已知函数()()e xf x x a =+,其中e 是自然对数的底数,a ∈R . (Ⅰ)求函数)(x f 的单调区间;(Ⅱ)当1a <时,试确定函数2()()g x f x a x =--的零点个数,并说明理由.19.(本小题满分14分)已知,A B 是抛物线2:W y x =上的两个点,点A 的坐标为(1,1),直线AB 的斜率为k , O 为坐标原点. (Ⅰ)若抛物线W 的焦点在直线AB 的下方,求k 的取值范围;(Ⅱ)设C 为W 上一点,且AB AC ⊥,过,B C 两点分别作W 的切线,记两切线的交点为D ,求OD 的最小值.20.(本小题满分13分)设无穷等比数列{}n a 的公比为q ,且*0()n a n >∈N ,[]n a 表示不超过实数n a 的最大整数(如[2.5]2=),记[]n n b a =,数列{}n a 的前n 项和为n S ,数列{}n b 的前n 项和为n T . (Ⅰ)若114,2a q ==,求n T ; (Ⅱ)若对于任意不超过2014的正整数n ,都有21n T n =+,证明:120122()13q <<. (Ⅲ)证明:n n S T =(1,2,3,n =L )的充分必要条件为1,a q N N **挝.北京市西城区2013 — 2014学年度第一学期期末高三数学(理科)参考答案及评分标准2014.1一、选择题:本大题共8小题,每小题5分,共40分.1.B 2.C 3.D 4.B 5.A 6.C 7.A 8.D 二、填空题:本大题共6小题,每小题5分,共30分. 9.4 10.125511. 12.24 13.1 214.(1,1) π注:第10、13、14题第一问2分,第二问3分.三、解答题:本大题共6小题,共80分. 其他正确解答过程,请参照评分标准给分. 15.(本小题满分13分)(Ⅰ)解:因为π()sin()(0)3g x x ωω=->的最小正周期为π, 所以2||ωπ=π,解得2ω=. ……………… 3分由 ()2f α=22α=, 即 cos 22α=, ……… 4分 所以 π22π4k α=±,k ∈Z . 因为 [π,π]α∈-, 所以7πππ7π{,,,}8888α∈--. ……………… 6分(Ⅱ)解:函数 π()()2sin(2)3y f x g x x x =+=+-ππ2sin 2cos cos 2sin 33x x x =+- ……………… 8分1sin 222x x =πsin(2)3x =+, ……………10分 由 2πππ2π2π232k k x -++≤≤, ………………11分 解得 5ππππ1212k k x -+≤≤. ………………12分所以函数()()y f x g x =+的单调增区间为5ππ[ππ]()1212k k k -+∈Z ,.…………13分16.(本小题满分13分)(Ⅰ)解:依题意,得 11(889292)[9091(90)]33a ++=+++, ……………… 2分解得 1a =. ……………… 3分 (Ⅱ)解:设“乙组平均成绩超过甲组平均成绩”为事件A , ……………… 4分依题意 0,1,2,,9a = ,共有10种可能. ……………… 5分 由(Ⅰ)可知,当1a =时甲、乙两个小组的数学平均成绩相同,所以当2,3,4,,9a = 时,乙组平均成绩超过甲组平均成绩,共有8种可能.… 6分 所以乙组平均成绩超过甲组平均成绩的概率84()105P A ==. ……………… 7分 (Ⅲ)解:当2a =时,分别从甲、乙两组同学中各随机选取一名同学,所有可能的成绩结果有339⨯=种, 它们是:(88,90),(88,91),(88,92),(92,90),(92,91),(92,92),(92,90),(92,91),(92,92), ……………… 9分则这两名同学成绩之差的绝对值X 的所有取值为0,1,2,3,4. ……………… 10分 因此2(0)9P X ==,2(1)9P X ==,1(2)3P X ==,1(3)9P X ==,1(4)9P X ==. ……………… 11分所以随机变量X 的分布列为:………………12分所以X 的数学期望221115()01234993993E X =⨯+⨯+⨯+⨯+⨯=.……………13分 17.(本小题满分14分)(Ⅰ)证明:因为四边形ABCD 是菱形,所以 AC BD ⊥. ……… 1分因为平面BDEF ⊥平面ABCD ,且四边形BDEF 是矩形,所以 ED ⊥平面ABCD , ……………… 2分 又因为 AC ⊂平面ABCD ,所以 ED AC ⊥. …………… 3分 因为 ED BD D = ,所以 AC ⊥平面BDEF . …………… 4分 (Ⅱ)解:设AC BD O = ,取EF 的中点N ,连接ON ,因为四边形BDEF 是矩形,,O N 分别为,BD EF 的中点,所以 //ON ED ,又因为 ED ⊥平面ABCD ,所以 ON ⊥平面ABCD ,由AC BD ⊥,得,,OB OC ON 两两垂直.所以以O 为原点,,,OB OC ON 所在直线分别为x 轴,y 轴,z 轴,如图建立空间直角坐标系. ……… 5分 因为底面ABCD 是边长为2的菱形,60BAD ∠= ,3BF =, 所以(0,A ,(1,0,0)B ,(1,0,0)D -,(1,0,3)E -,(1,0,3)F,C,13()22H . ………………6分因为 AC ⊥平面BDEF ,所以平面BDEF的法向量AC =. …………7分设直线DH 与平面BDEF 所成角为α,由33(,)222DH = , 得sin |cos ,|DH AC DH AC DH ACα⋅=<>=== ,所以直线DH 与平面BDEF. ………………9分 (Ⅲ)解:由(Ⅱ),得13()222BH =- ,(2,0,0)DB = .设平面BDH 的法向量为111(,,)x y z =n ,所以0,0,BH DB ⎧⋅=⎪⎨⋅=⎪⎩ n n ………………10分即111130,20,x z x ⎧-++=⎪⎨=⎪⎩ 令11z =,得(0,=n . ………………11分由ED ⊥平面ABCD ,得平面BCD 的法向量为(0,0,3)ED =-,则00(01(3)1cos ,232ED ED ED⋅⨯+⨯+⨯-<>===-⨯n n n . ………………13分 由图可知二面角H BD C --为锐角,所以二面角H BD C --的大小为60 . ………………14分18.(本小题满分13分)(Ⅰ)解:因为()()e xf x x a =+,x ∈R ,所以()(1)e x f x x a '=++. ……………… 2分 令()0f x '=,得1x a =--. ……………… 3分 当x 变化时,()f x 和()f x '的变化情况如下:……………… 5分故()f x 的单调减区间为(,1)a -∞--;单调增区间为(1,)a --+∞.………… 6分 (Ⅱ)解:结论:函数()g x 有且仅有一个零点. ……………… 7分理由如下:由2()()0g x f x a x =--=,得方程2e x ax x -=,显然0x =为此方程的一个实数解.所以0x =是函数()g x 的一个零点. ……………… 9分 当0x ≠时,方程可化简为e x ax -=.设函数()ex aF x x -=-,则()e 1x a F x -'=-,令()0F x '=,得x a =.当x 变化时,()F x 和()F x '的变化情况如下:即()F x 的单调增区间为(,)a +∞;单调减区间为(,)a -∞.所以()F x 的最小值min ()()1F x F a a ==-. ………………11分 因为 1a <,所以min ()()10F x F a a ==->, 所以对于任意x ∈R ,()0F x >, 因此方程e x a x -=无实数解.所以当0x ≠时,函数()g x 不存在零点.综上,函数()g x 有且仅有一个零点. ………………13分19.(本小题满分14分)(Ⅰ)解:抛物线2y x =的焦点为1(0,)4. ……………… 1分由题意,得直线AB 的方程为1(1)y k x -=-, ……………… 2分 令 0x =,得1y k =-,即直线AB 与y 轴相交于点(0,1)k -. ……………… 3分 因为抛物线W 的焦点在直线AB 的下方, 所以 114k ->, 解得 34k <. ……………… 5分 (Ⅱ)解:由题意,设211(,)B x x ,222(,)C x x ,33(,)D x y ,联立方程21(1),,y k x y x -=-⎧⎨=⎩ 消去y ,得210x kx k -+-=,由韦达定理,得11x k +=,所以 11x k =-. ……………… 7分 同理,得AC 的方程为11(1)y x k-=--,211x k =--. ……………… 8分对函数2y x =求导,得2y x '=,所以抛物线2y x =在点B 处的切线斜率为12x ,所以切线BD 的方程为21112()y x x x x -=-, 即2112y x x x =-. ……………… 9分 同理,抛物线2y x =在点C 处的切线CD 的方程为2222y x x x =-.………………10分联立两条切线的方程2112222,2,y x x x y x x x ⎧=-⎪⎨=-⎪⎩ 解得12311(2)22x x x k k +==--,3121y x x k k==-,所以点D 的坐标为111((2),)2k k k k---. ………………11分 因此点D 在定直线220x y ++=上. ………………12分因为点O 到直线220x y ++=的距离d ==所以5OD ≥,当且仅当点42(,)55D --时等号成立. ………………13分 由3125y k k =-=-,得k =.所以当k =OD………………14分20.(本小题满分13分)(Ⅰ)解:由等比数列{}n a 的14a =,12q =, 得14a =,22a =,31a =,且当3n >时,01n a <<. ……………… 1分所以14b =,22b =,31b =,且当3n >时,[]0n n b a ==. ……………… 2分即 ,6, 2,4, 17, 3.n n n T n ==⎧⎪=⎨⎪⎩≥ ……………… 3分(Ⅱ)证明:因为 201421()n T n n =+≤,所以 113b T ==,120142(2)n n n b T T n -=-=≤≤. ……………… 4分 因为 []n n b a =,所以 1[3,4)a ∈,2014[2,3)(2)n a n ∈≤≤. ……………… 5分 由 21a q a =,得 1q <. ……………… 6分 因为 201220142[2,3)a a q =∈,所以 20122223qa >≥,第 11 页 共 11 页 所以 2012213q <<,即 120122()13q <<. ……………… 8分 (Ⅲ)证明:(充分性)因为 1a N *Î,q N *Î, 所以 11n n a a q N -*= ,所以 []n n n b a a == 对一切正整数n 都成立.因为 12n n S a a a =+++L ,12n n T b b b =+++L ,所以 n n S T =. ……………… 9分 (必要性)因为对于任意的n N *Î,n n S T =,当1n =时,由1111,a S b T ==,得11a b =;当2n ≥时,由1n n n a S S -=-,1n n n b T T -=-,得n n a b =.所以对一切正整数n 都有n n a b =.由 n b Z Î,0n a >,得对一切正整数n 都有n a N *Î, ………………10分 所以公比21a q a =为正有理数. ………………11分 假设 q N *Ï,令p q r=,其中,,1p r r N *?,且p 与r 的最大公约数为1. 因为1a 是一个有限整数,所以必然存在一个整数()k k N Î,使得1a 能被k r 整除,而不能被1k r+整除. 又因为111211k k k k a p a a q r++++==,且p 与r 的最大公约数为1. 所以2k a Z +Ï,这与n a N *Î(n N *Î)矛盾.所以q *∈N .因此1a N *Î,q *∈N . ……………13分。
【Word版解析】北京四中2013届高三上学期期中测验数学(理)试题

北京四中2012-2013年度第一学期高三年级期中数学测试(理)试卷满分为150分,考试时间为120分钟。
考生务必将答案写在答题纸上,在试卷上作答无效。
第一部分(选择题,共40分)一、选择题:本大题共8小题,每小题5分,共计40分.请把答案填写在答题卡的相应位置上. 1. 已知集合,,则( )A .B .C .D .【答案】B【解析】{(3)0}{03}P x xx x x =-<=<<,={2}{22}Q x x x x <=-<<,所以{02}(0,2)P Q x x =<<= , 选B.2. 函数的定义域为( )A .B .C .D .【答案】D【解析】要使函数有意义,则有23400x x x ⎧--+≥⎨≠⎩,即2+3400x x x ⎧-≤⎨≠⎩,解得41x -≤≤且0x ≠,选D.3.下列命题中是假命题的是( ) A .都不是偶函数B .有零点C .D .上递减【答案】A 【解析】当=2πϕ时,()=sin(2)=cos 22f x x x π+为偶函数,所以A 错误,选A. 4.边长为的三角形的最大角与最小角的和是( )A .B .C .D .【答案】B【解析】边7对角为θ,则由余弦定理可知2225871cos ==2582θ+-⨯⨯,所以=60θ ,所以最大角与最小角的和为120 ,选B. 5. 已知数列,若利用如图所示的程序框图计算该数列的第10项,则判断框内的条件是( )A .B .C .D .【答案】B【解析】通过分析,本程序框图为“当型“循环结构.判断框内为满足循环的条件 第1次循环,s=1+1=2 n=1+1=2;第2次循环,s=2+2=4 n=2+1=3;当执行第10项时,11n =, n 的值为执行之后加1的值,所以,判断条件应为进入之前的值。
故答案为:9n ≤或10n <,选B. 6.已知函数的图象如图所示则函数的图象是( )【答案】A【解析】由函数的两个根为.x a x b ==,图象可知01,1a b <<<-。
北京市西城区2013届高三上学期期末考试数学理科试题

北京市西城区2013届高三上学期期末考试数学理科试题一、选择题(共8小题;共40分)1. 已知集合,,则 ______A. B.C. D.2. 在复平面内,复数的对应点位于______A. 第一象限B. 第二象限C. 第三象限D. 第四象限3. 在极坐标系中,已知点,则过点且平行于极轴的直线的方程是______A. B. C. D.4. 执行如图所示的程序框图.若输出,则框图中①处可以填入______A. B. C. D.5. 已知函数,其中为常数.那么“ ”是“ 为奇函数”的______A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件6. 已知,是非负数,且满足.那么的取值范围是______A. B. C. D.7. 某四面体的三视图如图所示.该四面体的六条棱的长度中,最大的是______A. B. C. D.8. 将正整数,,,,,,随机分成两组,使得每组至少有一个数,则两组中各数之和相等的概率是______A. B. C. D.二、填空题(共6小题;共30分)9. 已知向量,,那么 ______.10. 如图,中,,,.以为直径的圆交于点,则______; ______.11. 设等比数列的各项均为正数,其前项和为.若,,,则______.12. 已知椭圆的两个焦点是,,点在该椭圆上.若,则的面积是______.13. 已知函数,其中.当时,的值域是______;若的值域是,则的取值范围是______.14. 已知函数的定义域为.若常数,对,有,则称函数具有性质.给定下列三个函数:①;②;③.其中,具有性质的函数的序号是______.三、解答题(共6小题;共78分)15. 在中,已知.(1)求角的值;(2)若,,求的面积.16. 如图,四棱锥中,底面为正方形,,平面,为棱的中点.(1)求证: 平面;(2)求证:平面平面;(3)求二面角的余弦值.17. 生产,两种元件,其质量按测试指标划分为:指标大于或等于为正品,小于为次品.现随机抽取这两种元件各件进行检测,检测结果统计如下:测试指标元件元件(1)试分别估计元件,元件为正品的概率;(2)生产一件元件,若是正品可盈利元,若是次品则亏损元;生产一件元件,若是正品可盈利元,若是次品则亏损元.在(1)的前提下,(i)记为生产件元件和件元件所得的总利润,求随机变量的分布列和数学期望;(ii)求生产件元件所获得的利润不少于元的概率.18. 已知函数,其中.(1)求的单调区间;(2)设.若,使,求的取值范围.19. 如图,已知抛物线的焦点为.过点的直线交抛物线于,两点,直线,分别与抛物线交于点,.(1)求的值;(2)记直线的斜率为,直线的斜率为.证明:为定值.20. 如图,设是由个实数组成的行列的数表,其中表示位于第行第列的实数,且.记为所有这样的数表构成的集合.对于,记为的第行各数之积,为的第列各数之积.令.(1)请写出一个,使得;(2)是否存在,使得 ?说明理由;(3)给定正整数,对于所有的,求的取值集合.答案第一部分1. D2. B3. A4. C5. C6. B7. C8. B第二部分9.10. ;11.12.13. ;14. ①③第三部分15. (1)解法一:因为,所以.因为,所以,从而,所以.解法二:依题意得,所以,即.因为,所以,所以,所以.(2)解法一:因为,,根据正弦定理得,所以.因为,所以,所以的面积.解法二:因为,,根据正弦定理得,所以.根据余弦定理得,化简为,解得.所以的面积为.16. (1)如图,连接,与相交于点,连接.为正方形,所以为中点.因为为棱中点.所以.因为平面,平面,所以直线 平面.(2)因为平面,所以.因为四边形为正方形,所以,而,所以平面.又因为平面,所以平面平面.(3)解法一:如图,在平面内过作直线.因为平面平面,所以平面.由两两垂直,建立如图所示的空间直角坐标系.,则,,,,.所以,.设平面的法向量为,则有所以取,得.易知平面的法向量为.所以,,由图可知二面角的平面角是钝角,所以二面角的余弦值为.解法二:如图,取中点,中点,连接,.为正方形,所以.由(2)可得平面.因为,所以.由,,两两垂直,建立如图所示的空间直角坐标系.设,则,,,,,.所以,.设平面的法向量为,则有所以取,得.易知平面的法向量为.所以,,由图可知二面角的平面角是钝角,所以二面角的余弦值为.17. (1)元件为正品的概率约为.元件为正品的概率约为.(2)(i)随机变量的所有取值为,,,.;;;.所以,随机变量的分布列为:.(ii)设生产的件元件中正品有件,则次品有件.依题意,得,解得.所以,或.设“生产件元件所获得的利润不少于元”为事件,则.18. (1)(i)当时,.故的单调减区间为,;无单调增区间.(ii)当时,.令,得,.和的情况如下:极小值极大值故的单调减区间为,;单调增区间为.(iii)当时,的定义域为.因为在上恒成立,故的单调减区间为,,;无单调增区间.(2)因为,,所以等价于,其中.设,在区间上的最大值为.则“ ,使得”等价于.所以,的取值范围是.19. (1)依题意,设直线的方程为.将其代入,消去,整理得.从而.(2)设,.则.设直线的方程为,将其代入,消去,整理得.所以.同理可得.故.由(1)得,为定值.20. (1)答案不唯一,如图所示数表符合要求.(2)不存在,使得.证明如下:假设存在,使得.因为,,所以,,,,,,,这个数中有个,个.令.一方面,由于这个数中有个,个,从而另一方面,表示数表中所有元素之积(记这个实数之积为),也表示,从而相矛盾,从而不存在,使得.(3)记这个实数之积为.一方面,从“行”的角度看,有;另一方面,从“列”的角度看,有.从而有注意到.下面考虑,,,,,,,中的个数:由知,上述个实数中,的个数一定为偶数,该偶数记为;则的个数为,所以.对数表:,显然.将数表中的由变为,得到数表,显然.将数表中的由变为,得到数表,显然.依此类推,将数表中的由变为,得到数表.即数表满足:,其余.所以,.所以.由的任意性知,的取值集合为.。
北京市西城区2013届高考一模数学理试题(WORD解析版)

北京市西城区2013届高三下学期(4月)一模数学(理)试卷2013.4第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.已知全集U =R ,集合{|02}A x x =<<,2{|10}B x x =->,那么U A B = ð (A ){|01}x x << (B ){|01}x x <≤(C ){|12}x x <<(D ){|12}x x ≤<【答案】B【解析】2{|10}={11}B x x x x x =->><-或,所以{|11U B x x =-≤≤ð,所以{01}U A B x x =<≤ ð,选B.2.若复数i2ia +的实部与虚部相等,则实数a = (A )1- (B )1(C )2-(D )2【答案】A 【解析】i ()112i 2222a a i i ai a i ++-===---,因为i 2i a +的实部与虚部相等,所以122a=-,即1a =-,选A.3.执行如图所示的程序框图.若输出3y =-,则输入角=θ (A )π6 (B )π6-(C )π3(D )π3-【答案】D【解析】由题意知sin ,4tan ,42y πθθππθθ⎧<⎪⎪=⎨⎪≤≤⎪⎩。
因为31y =-<-,所以只有tan 3θ=-,因为42ππθ≤≤,所以3πθ=-,选D.4.从甲、乙等5名志愿者中选出4名,分别从事A ,B ,C ,D 四项不同的工作,每人承担一项.若甲、乙二人均不能从事A 工作,则不同的工作分配方案共有 (A )60种 (B )72种 (C )84种 (D )96种【答案】B【解析】若选甲不选乙,则有133318C A =种。
若选乙不选甲,则有133318C A =种。
若选甲,乙都选,则有21332336C C A =种,所以共有72种,选B.5.某正三棱柱的三视图如图所示,其中正(主)视 图是边长为2的正方形,该正三棱柱的表面积是 (A )63+ (B )123+ (C )1223+ (D )2423+ 【答案】C【解析】由三视图可知,正三棱柱的高为2,底面边长为2,所以底面积为213222322⨯⨯⨯=,侧面积为32212⨯⨯=,所以正三棱柱的表面积是1223+,选C.6.等比数列{}n a 中,10a >,则“13a a <”是“36a a <”的 (A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件【答案】B【解析】由13a a <得211a a q <,且30a >,解得21q >,即1q >或1q <-。
无锡新领航教育 一对一 北京市西城区2013届高三上学期期末考试 数学理科试题

- 1 -
北京市西城区2012 — 2013学年度第一学期期末试卷
高三数学(理科) 2013.1
第Ⅰ卷(选择题 共40分)
一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符
合题目要求的一项.
1.已知集合{|01}A x x =∈<<R ,{|(21)(1)0}B x x x =∈-+>R ,则A B = ( )
(A )1(0,)2(B )(1,1)-(C )1
(,1)(,)2-∞-+∞ (D )(,1)(0,)-∞-+∞ 【答案】D
【解析】1
{|(21)(1)0}{
2B x x x x x x =-+>=><-或,所以{0
1}A B x x x =><- 或,即(,1)(0,)-∞-+∞ ,选D. 2.在复平面内,复数5i
2i -的对应点位于( )
(A )第一象限(B )第二象限(C )第三象限(D )第四象限
【答案】B 【解析】55(2)5(2)122(2)(2)5i
i i i i i i i i ++===-+-+-,,对应的点的坐标为(1,2)-,所以在第二象限,选B.
3.在极坐标系中,已知点(2,)6P π
,则过点P 且平行于极轴的直线的方程是( )
(A )sin 1=ρθ(B
)sin =
ρθ(C )cos 1=ρθ(D
)cos =ρθ
【答案】A 【解析】先将极坐标化成直角坐标表示,(2,)6P π
转化为
点cos 2cos sin 2sin 166x y π
π
ρθρθ======,
即),
过点且平行于。
北京2013届西城高三二模数学理科试题及答案

北京市西城区2013年高三二模试卷高三数学(理科) 2013.5第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. 1.已知全集{0,1,2,3,4}U =,集合{0,1,2,3}A =,{2,3,4}B =,那么()U A B = ð (A ){0,1} (B ){2,3} (C ){0,1,4} (D ){0,1,2,3,4}2.在复平面内,复数1z 的对应点是1(1,1)Z ,2z 的对应点是2(1,1)Z -,则12z z ⋅= (A )1 (B )2 (C )i - (D )i3.在极坐标系中,圆心为(1,)2π,且过极点的圆的方程是(A )2sin =ρθ (B )2sin =-ρθ (C )2cos =ρθ (D )2cos =-ρθ4.如图所示的程序框图表示求算式“235917⨯⨯⨯⨯” 之值, 则判断框内可以填入 (A )10k ≤ (B )16k ≤ (C )22k ≤ (D )34k ≤5.设122a =,133b =,3log 2c =,则(A )b a c << (B )a b c << (C )c b a << (D )c a b << 6.对于直线m ,n 和平面α,β,使m ⊥α成立的一个充分条件是 (A )m n ⊥,n ∥α (B )m ∥β,⊥βα (C )m ⊥β,n ⊥β,n ⊥α (D )m n ⊥,n ⊥β,⊥βα7.已知正六边形A B C D E F 的边长是2,一条抛物线恰好经过该六边形的四个顶点,则抛物线的焦点到准线的距离是(A 4(B 2(C (D )8.已知函数()[]f x x x =-,其中[]x 表示不超过实数x 的最大整数.若关于x 的方程()f x kx k =+有三个不同的实根,则实数k 的取值范围是(A )111[1,)(,]243-- (B )111(1,][,)243-- (C )111[,)(,1]342-- (D )111(,][,1)342-- 第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.9.右图是甲,乙两组各6名同学身高(单位:cm )数据 的茎叶图.记甲,乙两组数据的平均数依次为x 甲和x 乙, 则 x 甲______x 乙. (填入:“>”,“=”,或“<”) 10.5(21)x -的展开式中3x 项的系数是______.(用数字作答)11.在△A B C 中,2B C =,A C =,3B π=,则A B =______;△A B C 的面积是______.12.如图,A B 是半圆O 的直径,P 在A B 的延长线上,P D 与半圆O 相切于点C ,A D P D ⊥.若4P C =,2P B =,则C D =______.13.在等差数列{}n a 中,25a =,1412a a +=,则n a =______;设*21()1n n b n a =∈-N ,则数列{}n b 的前n项和n S =______.14.已知正数,,a b c 满足a b ab +=,a b c abc ++=,则c 的取值范围是______.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤. 15.(本小题满分13分)如图,在直角坐标系xO y 中,角α的顶点是原点,始边与x 轴正半轴重合,终边交单位圆于点A ,且,)62ππ∈(α.将角α的终边按逆时针方向旋转3π,交单位圆于点B .记),(),,(2211y x B y x A .(Ⅰ)若311=x ,求2x ;(Ⅱ)分别过,A B 作x 轴的垂线,垂足依次为,C D .记△A O C 的面积为1S ,△B O D 的面积为2S .若122S S =,求角α的值.16.(本小题满分13分)某超市在节日期间进行有奖促销,凡在该超市购物满300元的顾客,将获得一次摸奖机会,规则如下:奖盒中放有除颜色外完全相同的1个红球,1个黄球,1个白球和1个黑球.顾客不放回的每次摸出1个球,若摸到黑球则停止摸奖,否则就要将奖盒中的球全部摸出才停止.规定摸到红球奖励10元,摸到白球或黄球奖励5元,摸到黑球不奖励.(Ⅰ)求1名顾客摸球3次停止摸奖的概率;(Ⅱ)记X 为1名顾客摸奖获得的奖金数额,求随机变量X 的分布列和数学期望. 17.(本小题满分14分)如图1,四棱锥ABCD P -中,⊥PD 底面ABCD ,面ABCD 是直角梯形,M 为侧棱PD 上一点.该四棱锥的俯视图和侧(左)视图如图2所示. (Ⅰ)证明:⊥BC 平面PBD ; (Ⅱ)证明:A M ∥平面PBC ;(Ⅲ)线段CD 上是否存在点N ,使AM 与BN 所成角的余弦值为43?若存在,找到所有符合要求的点N ,并求C N 的长;若不存在,说明理由.18.(本小题满分13分)如图,椭圆22:1(01)yC x m m+=<<的左顶点为A ,M 是椭圆C 上异于点A 的任意一点,点P 与点A 关于点M 对称.(Ⅰ)若点P 的坐标为9(,55,求m 的值;(Ⅱ)若椭圆C 上存在点M ,使得O P O M ⊥,求m 19.(本小题满分14分)已知函数322()2(2)13f x x x a x =-+-+,其中a ∈R .(Ⅰ)若2a =,求曲线()y f x =在点(1,(1))f 处的切线方程; (Ⅱ)求()f x 在区间[2,3]上的最大值和最小值.20.(本小题满分13分)已知集合1212{(,,,)|,,,n n n S x x x x x x = 是正整数1,2,3,,n 的一个排列}(2)n ≥,函数1,0,()1,0.x g x x >⎧=⎨-<⎩对于12(,,)n n a a a S ∈…,定义:121()()(),{2,3,,}i i i i i b g a a g a a g a a i n -=-+-++-∈ ,10b =,称i b 为i a 的满意指数.排列12,,,n b b b 为排列12,,,n a a a 的生成列;排列12,,,n a a a 为排列12,,,n b b b 的母列.(Ⅰ)当6n =时,写出排列3,5,1,4,6,2的生成列及排列0,1,2,3,4,3--的母列;(Ⅱ)证明:若12,,,n a a a 和12,,,n a a a ''' 为n S 中两个不同排列,则它们的生成列也不同; (Ⅲ)对于n S 中的排列12,,,n a a a ,定义变换τ:将排列12,,,n a a a 从左至右第一个满意指数为负数的项调至首项,其它各项顺序不变,得到一个新的排列.证明:一定可以经过有限次变换τ将排列12,,,n a a a 变换为各项满意指数均为非负数的排列.北京市西城区2013年高三二模试卷高三数学(理科)2013.5参考答案一、选择题:本大题共8小题,每小题5分,共40分.1.C ; 2.B ; 3.A ; 4.C ; 5.D ; 6.C ; 7.B ; 8.B . 二、填空题:本大题共6小题,每小题5分,共30分.9. >; 10.80; 11.3,2; 12.125; 13. 21n +,4(1)n n +; 14. 4(1,]3.注:11、13题第一空2分,第二空3分.三、解答题:本大题共6小题,共80分.若考生的解法与本解答不同,正确者可参照评分标准给分. 15.(本小题满分13分)(Ⅰ)解:由三角函数定义,得 1co s x =α,2co s()3x π=+α.因为 ,)62ππ∈(α,1co s 3=α,所以 sin 3==α. ………………3分所以 21co s()co s 3226x π=+==αα-α.(Ⅱ)解:依题意得 1sin y =α,2sin ()3y π=+α.所以 111111co s sin sin 2224S x y ==⋅=ααα, ………………7分 2221112||[co s()]sin ()sin (2)223343S x y πππ==-+⋅+=-+ααα. ……………9分依题意得 2sin 22sin (2)3π=-+αα,整理得 cos 20=α. ………………11分 因为62ππ<<α, 所以23π<<πα,所以 22π=α, 即 4π=α. ………………13分16.(本小题满分13分)(Ⅰ)解:设“1名顾客摸球3次停止摸奖”为事件A , ………………1分则 2334A 1()A 4P A ==,故1名顾客摸球3次停止摸奖的概率为14. ………………4分(Ⅱ)解:随机变量X 的所有取值为0,5,10,15,20. ………………5分1(0)4P X ==, 2224A 1(5)A 6P X ===,222344A 11(10)A A 6P X ==+=, 122234C A 1(15)A 6P X ⋅===,3344A 1(20)A 4P X ===. ………………10分所以,随机变量X 的分布列为:………………11分11111051015201046664E X =⨯+⨯+⨯+⨯+⨯=. ………………13分17.(本小题满分14分) 【方法一】(Ⅰ)证明:由俯视图可得,222B D BC CD +=,所以 BD BC ⊥. ………………1分 又因为 ⊥PD 平面ABCD ,所以 PD BC ⊥, ………………3分所以 ⊥BC 平面PBD . ………………4分 (Ⅱ)证明:取PC 上一点Q ,使:1:4P Q P C =,连结M Q ,B Q . ………………5分由左视图知 4:1:=PD PM ,所以 M Q ∥C D ,14M Q C D =. ………………6分在△B C D 中,易得60C D B ︒∠=,所以 30A D B ︒∠=.又 2=BD , 所以1A B =, A D =又因为 A B ∥C D ,CD AB 41=,所以 A B ∥M Q ,A B M Q =.所以四边形A B Q M 为平行四边形,所以 A M ∥B Q . ………………8分 因为 ⊄AM 平面PBC ,B Q ⊂平面PBC ,所以 直线A M ∥平面PBC . ………………9分 (Ⅲ)解:线段C D 上存在点N ,使AM 与BN 所成角的余弦值为43.证明如下:………10分因为 ⊥PD 平面ABCD ,DC DA ⊥,建立如图所示的空间直角坐标系xyz D -. 所以 )3,0,0(),0,4,0(),0,1,3(),0,0,3(),0,0,0(M C B A D .设 )0,,0(t N ,其中40≤≤t . ………………11分 所以)3,0,3(-=AM ,)0,1,3(--=t BN .要使AM 与BN 所成角的余弦值为43,则有 ||4||||A MB N A M B N ⋅= , ………………12分所以43)1(332|3|2=-+⋅t ,解得 0=t 或2,均适合40≤≤t . ………………13分故点N 位于D 点处,此时4C N =;或CD 中点处,此时2C N =, 有AM 与BN 所成角的余弦值为43.………………14分【方法二】(Ⅰ)证明:因为⊥PD 平面ABCD ,DC DA ⊥,建立如图所示 的空间直角坐标系xyz D -.在△B C D 中,易得60C D B ︒∠=,所以 30A D B ︒∠=,因为 2=BD , 所以1A B =, A D =由俯视图和左视图可得:,0,0(),3,0,0(),0,4,0(),0,1,3(),0,0,3(),0,0,0(P M C B A D所以 )0,3,3(-=BC ,)0,1,3(=DB .因为 0001333=⋅+⋅+⋅-=⋅DB BC ,所以BD BC ⊥. ………………2分 又因为 ⊥PD 平面ABCD ,所以 PD BC ⊥, ………………3分 所以 ⊥BC 平面PBD . ………………4分(Ⅱ)证明:设平面PBC 的法向量为=()x,y,z n ,则有 0,0.P C B C ⎧⋅=⎪⎨⋅=⎪⎩ n n因为 )0,3,3(-=BC ,)4,4,0(-=PC ,所以440,30.y z y -=⎧⎪⎨+=⎪⎩取1=y ,得=n )1,1,3(. ………………6分因为 )3,0,3(-=AM ,所以 ⋅AM =n 03101)3(3=⋅+⋅+-⋅. ………………8分因为 ⊄AM 平面PBC , 所以 直线A M ∥平面PBC . ………………9分 (Ⅲ)解:线段C D 上存在点N ,使AM 与BN 所成角的余弦值为43.证明如下:………10分设 )0,,0(t N ,其中40≤≤t . ………………11分 所以 )3,0,3(-=AM ,)0,1,3(--=t BN .要使AM 与BN 所成角的余弦值为43,则有43=, ………………12分所以43)1(332|3|2=-+⋅t ,解得0=t 或2,均适合40≤≤t . ………………13分故点N 位于D 点处,此时4C N =;或CD 中点处,此时2C N =, 有AM 与BN 所成角的余弦值为43. ………………14分18.(本小题满分13分)(Ⅰ)解:依题意,M 是线段A P 的中点,因为(1,0)A -,9(55P , 所以 点M的坐标为2(55.………………2分由点M 在椭圆C 上,所以41212525m+=, ………………4分解得 47m =. ………………5分(Ⅱ)解:设00(,)M x y ,则 22001y x m+=,且011x -<<.① ………………6分因为 M 是线段A P 的中点,所以 00(21,2)P x y +. ………………7分 因为 O P O M ⊥,所以 2000(21)20x x y ++=.② ………………8分由 ①,② 消去0y ,整理得 20020222x x m x +=-. ………………10分所以001116242(2)82m x x =+≤-++-+, ………………12分当且仅当02x =-+时,上式等号成立.所以 m的取值范围是1(0,24-. ………………13分19.(本小题满分14分)(Ⅰ)解:()f x 的定义域为R , 且 2()242f x x x a '=-+-. ………………2分当2a =时,1(1)3f =-,(1)2f '=-,所以曲线()y f x =在点(1,(1))f 处的切线方程为 12(1)3y x +=--,即 6350x y +-=. ………………4分 (Ⅱ)解:方程()0f x '=的判别式为8a =∆.(ⅰ)当0a ≤时,()0f x '≥,所以()f x 在区间(2,3)上单调递增,所以()f x 在区间[2,3] 上的最小值是7(2)23f a =-;最大值是(3)73f a =-. ………………6分(ⅱ)当0a >时,令()0f x '=,得112x =-,或212x =+.()f x 和()f x '的情况如下:故()f x 的单调增区间为(,12-∞-,(1)2++∞;单调减区间为(122-+.………………8分① 当02a <≤时,22x ≤,此时()f x 在区间(2,3)上单调递增,所以()f x 在区间[2,3] 上的最小值是7(2)23f a =-;最大值是(3)73f a =-. ………………10分② 当28a <<时,1223x x <<<,此时()f x 在区间2(2,)x 上单调递减,在区间2(,3)x 上单调递增,所以()f x 在区间[2,3]上的最小值是 25()33f x a =--. ………………11分因为 14(3)(2)3f f a -=-,所以 当1423a <≤时,()f x 在区间[2,3]上的最大值是(3)73f a =-;当1483a <<时,()f x 在区间[2,3]上的最大值是7(2)23f a =-. ………………12分③ 当8a ≥时,1223x x <<≤,此时()f x 在区间(2,3)上单调递减, 所以()f x 在区间[2,3]上的最小值是(3)73f a =-;最大值是7(2)23f a =-.………………14分综上,当2a ≤时,()f x 在区间[2,3]上的最小值是723a -,最大值是73a -;当1423a <≤时,()f x 在区间[2,3]上的最小值是533a --,最大值是73a -;当1483a <<时,()f x 在区间[2,3]上的最小值是533a --723a -;当8a ≥时,()f x 在区间[2,3]上的最小值是73a -,最大值是723a -.20.(本小题满分13分)(Ⅰ)解:当6n =时,排列3,5,1,4,6,2的生成列为0,1,2,1,4,3--; ………………2分排列0,1,2,3,4,3--的母列为3,2,4,1,6,5. ………………3分(Ⅱ)证明:设12,,,n a a a 的生成列是12,,,n b b b ;12,,,n a a a ''' 的生成列是与12,,,n b b b ''' .从右往左数,设排列12,,,n a a a 与12,,,n a a a ''' 第一个不同的项为k a 与k a ',即:n n a a '=,11n n a a --'=, ,11k ka a ++'=,k k a a '≠. 显然 n nb b '=,11n n b b --'=, ,11k k b b ++'=,下面证明:k k b b '≠. ………………5分 由满意指数的定义知,i a 的满意指数为排列12,,,n a a a 中前1i -项中比i a 小的项的个数减去比i a 大的项的个数.由于排列12,,,n a a a 的前k 项各不相同,设这k 项中有l 项比k a 小,则有1k l --项比k a 大,从而(1)21k b l k l l k =---=-+.同理,设排列12,,,n a a a ''' 中有l '项比k a '小,则有1k l '--项比k a '大,从而21k b l k ''=-+. 因为 12,,,k a a a 与12,,,k a a a ''' 是k 个不同数的两个不同排列,且k k a a '≠, 所以 l l '≠, 从而 k k b b '≠.所以排列12,,,n a a a 和12,,,n a a a ''' 的生成列也不同. ………………8分 (Ⅲ)证明:设排列12,,,n a a a 的生成列为12,,,n b b b ,且k a 为12,,,n a a a 中从左至右第一个满意指数为负数的项,所以 1210,0,,0,1k k b b b b -≥≥≥≤- . ………………9分进行一次变换τ后,排列12,,,n a a a 变换为1211,,,,,,k k k n a a a a a a -+,设该排列的生成列为12,,,n b b b ''' . 所以 1212()()n n b b b b b b '''+++-+++ 121121[()()()][()()()]k k k k k k k k g a a g a a g a a g a a g a a g a a --=-+-++---+-++-1212[()()()]k k k k g a a g a a g a a -=--+-++-22k b =-≥. ………………11分因此,经过一次变换τ后,整个排列的各项满意指数之和将至少增加2. 因为i a 的满意指数1i b i ≤-,其中1,2,3,,i n = ,所以,整个排列的各项满意指数之和不超过(1)123(1)2n nn -++++-= ,即整个排列的各项满意指数之和为有限数,所以经过有限次变换τ后,一定会使各项的满意指数均为非负数. ………………13分。
北京市西城区2013届高考一模数学理试题(WORD解析版)

北京市西城区2013届高三下学期(4月)一模数学(理)试卷2013.4第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.已知全集U =R ,集合{|02}A x x =<<,2{|10}B x x =->,那么U A B = ð (A ){|01}x x << (B ){|01}x x <≤(C ){|12}x x <<(D ){|12}x x ≤<【答案】B【解析】2{|10}={11}B x x x x x =->><-或,所以{|11U B x x =-≤≤ð,所以{01}U A B x x =<≤ ð,选B.2.若复数i2ia +的实部与虚部相等,则实数a = (A )1- (B )1(C )2-(D )2【答案】A 【解析】i ()112i 2222a a i i ai ai ++-===---,因为i 2i a +的实部与虚部相等,所以122a =-,即1a =-,选A.3.执行如图所示的程序框图.若输出3y =-,则输入角=θ (A )π6 (B )π6-(C )π3(D )π3-【答案】D【解析】由题意知sin ,4tan ,42y πθθππθθ⎧<⎪⎪=⎨⎪≤≤⎪⎩。
因为31y =-<-,所以只有tan 3θ=-,因为42ππθ≤≤,所以3πθ=-,选D.4.从甲、乙等5名志愿者中选出4名,分别从事A ,B ,C ,D 四项不同的工作,每人承担一项.若甲、乙二人均不能从事A 工作,则不同的工作分配方案共有 (A )60种 (B )72种 (C )84种 (D )96种【答案】B【解析】若选甲不选乙,则有133318C A =种。
若选乙不选甲,则有133318C A =种。
若选甲,乙都选,则有21332336C C A =种,所以共有72种,选B.5.某正三棱柱的三视图如图所示,其中正(主)视 图是边长为2的正方形,该正三棱柱的表面积是 (A )63+ (B )123+ (C )1223+ (D )2423+ 【答案】C【解析】由三视图可知,正三棱柱的高为2,底面边长为2,所以底面积为213222322⨯⨯⨯=,侧面积为32212⨯⨯=,所以正三棱柱的表面积是1223+,选C.6.等比数列{}n a 中,10a >,则“13a a<”是“36a a <”的 (A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件【答案】B【解析】由13a a <得211a a q <,且30a >,解得21q>,即1q >或1q <-。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012-2013学年度理科数学高三(上)期中试题2012.11
(试卷满分:150分,考试时间:120分钟)
一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1.若全集U =R ,集合{10}A x x =+<,{30}B x x =-<,则集合()U C A ∩B =
( )
A .{3}x x >
B .{13}x x -<<
C .{1}x x <-
D .{13}x x -≤< 2.“2()6k k π
απ=
+∈Z ”是“1
cos 22
α=
”的 ( )
A .充分而不必要条件
B .必要而不充分条件
C .充分必要条件
D .既不充分也不必要条件
3.函数y = )
4.设323log ,log log a b c π===,则 ( ) A. b c a >>
B. a c b >>
C. b a c >>
D. a b c >>
5.将函数sin 2y x =的图象向左平移4
π
个单位, 再向上平移1个单位,所得图象的函数解析式是 ( )
A.cos 2y x =
B.22cos y x =
C.)4
2sin(1π
+
+=x y D.22sin y x =
6.已知、a b 均为单位向量,它们的夹角为60 ,那么||-a b 等于( )
A. 1
B.
C.
D. 2
7.若偶函数()x f ()x ∈R 满足()()x f x f =+2且[]1,0∈x 时,(),x x f =则方程
()x x f 3lo g =的根的个数是( )
A. 2个
B. 4个
C. 3个
D. 多于4个 8.对于函数
()f x ,若存在区间[,],(M a b a b =<,使得
{|(),y y
f x x M M =∈=,则称区间M 为函数()f x 的一个“稳定区间”.给出下
列4个函数:①()e x f x =;②3()f x x =;③()cos 2
f x x π
=;④()ln 1f x x =+.
其中存在稳定区间的函数有( )
A.①②
B.①③
C.②③
D.②④ 二、填空题共6小题,每小题5分,共30分。
9.5
0(24)x dx -⎰=__________.
10.若向量(12)=,a 与向量(1)λ=-,b 共线,则实数=λ___________ . 11.若角α的终边经过点(12)P -,,
则tan 2α=___________ .
12.函数()sin()f x A x ωϕ=+ (0,0,A ω>>
0)ϕπ<<的图象如图所示,则()f x 的
解析式为 .
13.等比数列{}n a 的前n 项和为n S ,且41a ,22a ,3a 成等差数列. 若1a =1,则
4S = .
14.已知数列{}n a 的各项均为正整数,对于⋅⋅⋅=,3,2,1n ,有
1135,2n n n n
n n k
k a a a a a a +++⎧⎪=⎨⎪⎩为奇数为偶数.其中为使为奇数的正整数,,
当111a =时,100a =______;若存在*m ∈N ,当n m >且n a 为奇数时, n a 恒为常数p ,则p 的值为______.
三、解答题共6小题,共80分。
解答应写出文字说明,演算步骤或证明过程。
15.(本小题满分13分)
已知:等差数列{n a }中,4a =14,前10项和18510=S .
(Ⅰ)求n a ;
(Ⅱ)将{n a }中的第2项,第4项,…,第n 2项按原来的顺序排成一个新数列,求此数列的前n 项和n G .
16.(本小题满分13分)
在锐角ABC ∆中,a ,b ,c 分别为内角A ,B ,C 所对的边,且满
足
2s i n 0b A -=.
(Ⅰ)求角B 的大小;
(Ⅱ)若5a c +=,且a c >,b =,求AB AC →
→
⋅的值.
17.(本小题满分14分)
已知a 为实数,()()()24f x x x a =--. (I )求导数()f x ';
(II )若()10f '-=,求()f x 在[]2,2-上的最大值和最小值; (III )若()f x 在(],2-∞-和[)2,+∞上都是递增的,求a 的取值范围.
18.(本小题满分13分)
已知函数222π()2sin cos )4f x x x x ⎛⎫=++- ⎪⎝⎭,ππ42x ⎡⎤
∈⎢⎥⎣⎦
,.
(I )求5π12f ⎛⎫
⎪⎝⎭
的值;
(Ⅱ)求()f x 的单调区间;
(III )若不等式()2f x m -<恒成立,求实数m 的取值范围.
19. (本小题满分13分)
设数列}{n a 的前n 项和为n S ,且11a =,*2(1)()n n S na n n n =--∈N . (Ⅰ)求数列}{n a 的通项公式; (Ⅱ)证明:
1223111114
n n a a a a a a -++⋅⋅⋅+<.
20.(本小题满分14分)
已知函数2221
()1
ax a f x x +-=+,其中a ∈R .
(Ⅰ)当1a =时,求曲线()y f x =在原点处的切线方程; (Ⅱ)求)(x f 的单调区间;
(Ⅲ)若)(x f 在[0,) 上存在最大值和最小值,求a 的取值范围.。
