《集合、简易逻辑、函数》经典常考题2011定[1].doc

合集下载

集合函数试题及答案

集合函数试题及答案1. 集合A={1,2,3}，集合B={3,4,5}，求A∩B。

答案：A∩B={3}。

2. 集合C={x|x^2-5x+6=0}，求C的元素。

答案：C={2,3}。

3. 如果集合D={x|x>0}，集合E={x|x<0}，求D∪E。

答案：D∪E=R（实数集）。

4. 集合F={x|x^2-4x+3=0}，求F的补集。

答案：F的补集是{x|x≠1且x≠3}。

5. 集合G={x|x^2-x-2=0}，求G的元素。

答案：G={-1,2}。

6. 集合H={1,2,3}，集合I={2,3,4}，求H∩I。

答案：H∩I={2,3}。

7. 集合J={x|x^2-6x+8=0}，求J的元素。

答案：J={2,4}。

8. 如果集合K={x|x>0}，集合L={x|x<0}，求K∩L。

答案：K∩L=∅（空集）。

9. 集合M={x|x^2-9=0}，求M的补集。

答案：M的补集是{x|x≠3且x≠-3}。

答案：N={2,4}。

11. 集合O={x|x^2-2x-3=0}，求O的元素。

答案：O={-1,3}。

12. 集合P={x|x^2-5x+6=0}，求P的补集。

答案：P的补集是{x|x≠2且x≠3}。

13. 集合Q={x|x^2+x-6=0}，求Q的元素。

答案：Q={2,-3}。

14. 集合R={x|x^2-4x+4=0}，求R的补集。

答案：R的补集是{x|x≠2}。

15. 集合S={x|x^2-x-6=0}，求S的元素。

答案：S={3,-2}。

16. 集合T={x|x^2-7x+10=0}，求T的补集。

答案：T的补集是{x|x≠2且x≠5}。

17. 集合U={x|x^2-8x+16=0}，求U的元素。

答案：U={4}。

18. 集合V={x|x^2-9=0}，求V的补集。

答案：V的补集是{x|x≠3且x≠-3}。

19. 集合W={x|x^2-4x+4=0}，求W的元素。

答案：W={2}。

专题1.1 集合与简易逻辑(测试卷)(原卷版)

专题一集合与简易逻辑测试卷一．填空题(14*5=70分)1．【温州二外2016届上学期高三10月阶段性测试1】已知}22{≤≤-=x x M ，}1{x y x N -==，那么=N M ．2．【江苏省泰州中学2015--2016学年度第一学期高三第二次月考】命题“02016,10200>-+->∃x x x ”的否定是．3．【哈尔滨市第六中学2016届上学期期中考试】已知集合}1,1{-=M ，},4221|{1Z ∈<<=+x x N x ，则=⋂N M __________．4．【山东师范大学附属中学2016届高三上学期第二次模拟】已知集合{}cos0,sin 270A =，{}20B x x x =+=，则A B ⋂为．5．【重庆市巴蜀中学2016级高三学期期中考试】已知命题1p ：函数22x x y -=-在R 上为增函数，2p ：函数22x x y -=+在R 上为减函数，在下列四个命题112:q p p ∨；212:q p p ∧；()312:q p p ⌝∨和()412:q p p ∧⌝中，真命题是．6．【江苏省泰州中学2015--2016学年度第一学期高三第二次月考】已知命题1211:≤+-x p ，命题)0(012:22><-+-m m x x q ，若p 是q 的充分不必要条件，则实数m 的范围是．7．【河北省衡水中学2016届高三二调】设全集{}1,3,5,6,8U =，集合{}1,6A =，集合{}5,6,8B =，则()U A B ⋂= ．8．【江苏省清江中学2016届高三上学期周练】若函数()f x 是定义在R 上的函数，则“()00f =”是“函数()f x 为奇函数”的条件(“充分不必要” “必要不充分” “充要” “既不充分也不必要”中选一个)．9．【哈尔滨市第六中学2016届上学期期中】定义在R 上的函数)(x f y =满足5522f x f x ⎛⎫⎛⎫+=- ⎪ ⎪⎝⎭⎝⎭，5()02x f x ⎛⎫'-> ⎪⎝⎭，则对任意的21x x <，都有)()(21x f x f >是521<+x x 的条件．10．【泰州市2015届高三第三次调研测试】给出下列三个命题：①“a ＞b ”是“3a ＞3b”的充分不必要条件； ②“α＞β”是“cos α＜co s β”的必要不充分条件；③“0a =”是“函数()()32f x x ax x =+∈R 为奇函数”的充要条件．其中正确命题的序号为．11．【黑龙江省牡丹江市一高2016届高三10月】已知, a b 是两个非零向量，给定命题:p ⋅=a b a b ，命题:q t ∃∈R ，使得t =a b ，则p 是q 的________条件．12．【吉林省长春外国语学校2016届上学期高三第一次质量检测】设集合}log ,3{2a P =，{}b a Q ,=，若}0{=Q P ，则=Q P ________．13．【2016届河北省邯郸市馆陶县一中高三7月调研考试】下列说法中，正确的是________．①任取x >0，均有3x >2x ；②当a >0，且a ≠1时，有a 3>a 2； ③y ＝(3)－x 是增函数；④y ＝2|x |的最小值为1； ⑤在同一坐标系中，y ＝2x 与y ＝2－x的图象关于y 轴对称． 14．【2016届湖北省部分重点中学高三上学期起点考试】以A 表示值域为R 的函数组成的集合，B 表示具有如下性质的函数()x ϕ组成的集合：对于函数()x ϕ，存在一个正数M ，使得函数()x ϕ的值域包含于区间[,]MM -．例如，当31()x x ϕ=，2()s i n x x ϕ=时，1()x A ϕ∈，2()x B ϕ∈．现有如下命题： ①设函数()f x 的定义域为D ，则“()f x A ∈”的充要条件是“b ∀∈R ，a D ∃∈，()f a b =”；②函数()f x B∈的充要条件是()f x 有最大值和最小值； ③若函数()f x ，()g x 的定义域相同，且()f x A ∈，()g x B ∈，则()()f x g x B+∉； ④若函数2()ln(2)1x f x a x x =+++(2x >-，a ∈R )有最大值，则()f x B ∈．其中的真命题有__________________．(写出所有真命题的序号)二．解答题(6*12=72分)15．【湖北宜昌一中、龙泉中学2016届高三十月联考】已知函数()(2)()f x x x m =-+-(其中2m >-)，()22x g x =-﹒(1)若命题“2log ()1g x ≤”是真命题，求x 的取值范围；(2)设命题p ：(1,)x ∀∈+∞，()0f x <或()0g x <，若p ⌝是假命题，求m 的取值范围﹒16．【江西临川一中2016届上学期高三期中】已知集合{}015A x ax =∈<+≤R ，()1202B x x a ⎧⎫=∈-<≤≠⎨⎬⎩⎭R ． ⑴若B A =，求出实数a 的值；⑵若命题,:A x p ∈命题B x q ∈:且p 是q 的充分不必要条件，求实数a 的取值范围．17．【山东省潍坊第一中学2016届高三10月月考16】已知集合{}2log 8A x x =<，204x B x x ⎧⎫+=<⎨⎬-⎩⎭，{}|1C x a x a =<<+．(1)求集合A B ⋂； (2)若B C B ⋃=，求实数a 的取值范围．18．【山东省潍坊第一中学2016届高三10月月考】设命题p ：函数1y kx =+在R 上是增函数，命题q ：x ∃∈R ，2(23)10x k x +-+=，如果p q ∧是假命题，p q ∨是真命题，求k 的取值范围．19．【辽宁省葫芦岛市一高2016届上学期期中考试】已知命题p ：函数()log 21a y x =+在定义域上单调递增；命题q ：不等式2(2)2(2)40a x a x -+--<对任意实数x 恒成立，若p 且q ⌝为真命题，求实数a 的取值范围．20．【江苏省阜宁中学2016届高三年级第一次调研考试】已知命题p ：指数函数()()26xf x a =-在R 上是单调减函数；命题q ：关于x 的方程223210x ax a -++=的两根均大于3，若p 或q 为真，p 且q 为假，求实数a 的范围．。

高中数学《集合与简易逻辑》知识点与考试试题

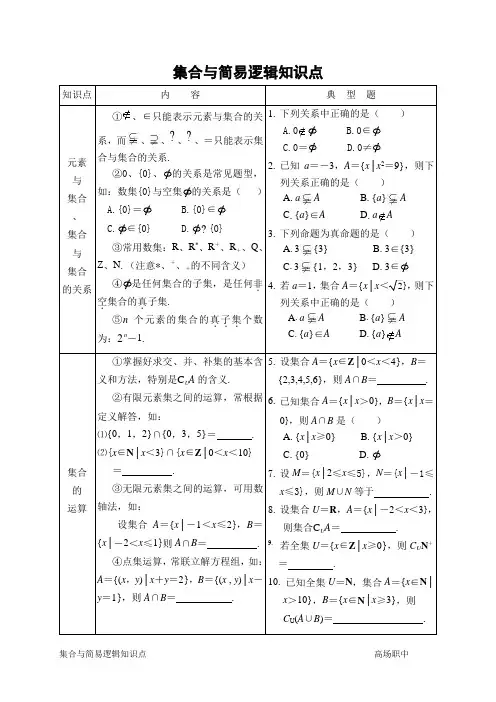
集合与简易逻辑知识点系，而、、的关系是（B.{0}∈{0} D.B.0≠}A{3}{1A Ap一个实数一个实数(p∧q)＝p∨q(q)))第一章集合与简易逻辑测试题一、选择题1.集合A={x|x≤}，a=3，则 ( )A.a AB.a AC.{a}∈AD.{a} A2.集合M={x|x=3k-2，k∈Z}，Q={y|y=3l+1，l∈Z}，S={z|z=6m+1，m∈Z}之间的关系是 ( )A.S Q MB.S=Q MC.S Q=MD.S Q=M3.若A={1，3，x}，B={x2，1}，且A∪B=A，则这样x的不同取值有 ( )A.1个B.2个C.3个D.4个4.符合条件{a}P{a，b，c}的集合P的个数是 ( )A.2B.3C.4D.55.若A={x|x2-4x+3＜0}，B={x|x2-6x+8＜0}，C={x|2x2-9x+a＜0}，(A∩B)C，则a的取值范围是 ( )A.a≤10B.a≥9C.a≤9D.9≤a≤106.若a＞0，使不等式|x-4|+|3-x|＜a在R上的解非空，则a的值必为 ( )A.0＜a＜1B.0＜a≤1C.a＞1D.a≥17.集合A={x|x2-5x+4≤0}，B={x|x2-5x+6≥0}，则A∩B= ( )A.{x|1≤x≤2，或3≤x≤4}B.{x|1≤x≤2，且3≤x≤4}C.{1，2，3，4}D.{x|1≤x≤4或2≤x≤3}8.如果方程x2+(m-3)x+m的两根都是正数，则m的取值范围是 ( )A.0＜m≤3B.m≥9或m≤1C.0＜m≤1D.m＞99.由下列各组命题构成“P或Q”，“P且Q”，“非P”形式的复合命题中，“P或Q”为真命题，“P且Q”为假命题，“非P”为真命题的是 ( )A.P：3是偶数；q：4是奇数B.P：3+2=6；q：3＞2C.P：a∈{a，b}；q：{a}{a，b}D.p：Q R；q：N=N+10.对于实数x、y，条件A：|x|≤1且|y|≤1；条件B：|x|+|y|≤1；条件C：x2+ y2≤1.则正确的是 ( )A.B是C的充分不必要条件；A是C的必要不充分条件B.B是C的必要不充分条件；A是C的充分不必要条件C.C是A的必要不充分条件；C是B的充分不必要条件D.C是A的充要条件；B是A的既不充分也不必要条件11.若a、b为实数，则ab(a-b)＜0成立的一个充要条件是 ( )A.0＜＜B.0＜＜C.＜D.＜12.给出以下四个命题：p：若x2-3x+2=0，则x=1或x=2；q：若2≤x＜3，则(x-2) (x-3)≤0；r：若x=y=0，则x2+y2=0；s：若x、y∈N，x+y是奇数，则x、y中一个是奇数一个是偶数，那么 ( )A.p的逆命题为真B.q的否命题为真C.r的否命题为假D.s的逆命题为假二、填空题13.已知集合M={x|x∈N+，且8-x∈N+}，则M中只含有两个元素的子集的个数有__ __个.14.已知集合A={x|x2-x-2≤0}，B={x|a＜x＜a+3}，满足A B=，则实数a的取值范围是____.15.“若a+b是偶数，则a、b必定同为奇数或偶数”的逆否命题为____.16.已知集合M{0，1，2，3，4}，且M{0，2，4，8}，则集合M中最多有____个元素.三、解答题：本大题共6小题，共74分.解答应写出文字说明，证明过程或演算步骤.17.已知三元素集合A={x，xy，x-y}，B={0，|x|，y}，且A=B，求x与y的值.18设集合A={|a+1|，3，5}，集合B={2a+1，a2+2a，a2+2a-1}，当A∩B={2，3}时，求A∪B.19.设A={x|-2＜x＜-1，或x＞1}，B={x|x2+ax+b≤0}，已知A∪B={x|x＞-2}，A ∩B={x|1＜x≤3}，试求a，b的值.20.已知不等式ax2+bx+c＞0的解集为{x|0＜m＜x＜n}，求关于x的不等式cx2-bx +a＜0的解.21.已知集合A={x|1＜|x-2|＜2}，B={x|(x-a)(x-1)＜0，a≠1}，且A∩B≠，试确定a的取值范围.22关于实数x的不等式与x2-3(a+1)x+2(3a+1)≤0的解集依次为A、B(1)求集合A、B(2)若A B，求此时a的取值范围.参考答案一、选择题1-12：DCCBC CACBB DA二、填空题13.21个14.a≥2或a≤-415.“若a、b不同为奇数且不同为偶数则a+b不是偶数”16.3个三、解答题17.解：∵0∈B，A=B，∴0∈A∵集合A为三元素集，∴x≠xy，∴x≠0，y≠1又∵0∈B，y∈B，∴y≠0从而，x-y=0，x=y这时，A={x，x2，0}，B={0，|x|，x}∴x2=|x|，x=0(舍去)或x=1(舍去)，或x=-1经验证x=-1，y=-1是本题的解.18.解：∵|a+1|=2，∴a=1或a=-3当a=1时，集合B的元素a2+2a=3，2a+1=3，由集合的元素的互异性可知，a≠1当a=-3时，集合B={-5，3，2}∴A∪B={-5，2，3，5}19.解：由A∪B={x|x＞-2}，A∩B={x|1＜x≤3}得B={x|-1≤x≤3}，根据二次不等式与二次方程的关系，可知-1与3是方程x2+ax+b=0的两根.∴a=-(-1+3)=-2，b=(-1)×3=-320.解：m＜x＜n(x-m)(x-n)＜0x2-(m+n)x+mn＜0，对照-ax2-bx-c＜0，∴，∴a=-k，b=k(m+n)，c=-kmn，代入cx2-bx+a＜0，∴-kmnx2-k(m+n)x-k＜0，mnx2+(m+n)x+1＞0，∵0＜m＜n，∴∴所求不等式的解集为21.解：A={x|1＜|x-2|＜2}={x|0＜x＜1，或3＜x＜4}(1)当a＞1时，B={x|1＜x＜a}∵A∩B≠∴a＞3(2)当a＜1时，B={x|a＜x＜1}∵A∩B≠∴a＜1综合(1)、(2)可知，a的取值范围是a＜1，或a＞322.解：(1)A==={x|2a≤x≤a2+1}B={x|x2-3(a+1)x+2(3a+1)≤0}={x|(x-2)(x-3a-1)≤0}当a≤时，B={x|3a+1≤x≤2}当a＞时，B={x|2≤x≤3a+1}(2)当a≤时，若，则2a≥3a+1且a2+1≤2得a=-1当a＞时，若，则2a≥2且a2+1≤3a+1得1≤a≤3∴a的取值范围是：a=-1，或1≤a≤3。

高考数学试题分类汇编集合简易逻辑word

1.已知集合{|320},{|(1)(3)0}A x R x B x R x x =∈+>=∈+->，则A B ⋂=( )A ．（﹣∞，﹣1） B.｛﹣1，-23｝ C. ﹙﹣23，3﹚ D.（3，＋∝） 2. 设集合U={1,2,3,4,5,6}， M={1,2,4 } 则CuM=A .UB {1,3,5}C {3,5,6}D {2,4,6}3.设集合M={-1,0,1}，N={x|x 2≤x}，则M ∩N=A.{0}B.{0,1}C.{-1,1}D.{-1,0,0}4.命题“若α=4π，则tan α=1”的逆否命题是 A.若α≠4π，则tan α≠1 B. 若α=4π，则tan α≠1 C. 若tan α≠1，则α≠4π D. 若tan α≠1，则α=4π 5.已知集合A={x ∈R|3x+2＞0} B={x ∈R|（x+1）(x-3)＞0} 则A ∩B=A （-∞，-1）B （-1，-23）C （-23,3）D (3,+∞) 6.下列命题中，真命题是（）A ．0,00≤∈∃x e R xB ．22,x R x x >∈∀C ．0=+b a 的充要条件是1-=ba D ．1,1>>b a 是1>ab 的充分条件 7. 命题“∃x 0∈C R Q ， 30x ∈Q ”的否定是A ∃x 0∉C R Q ，30x ∈QB ∃x 0∈C R Q ，30x ∉QC ∀x 0∉C R Q ， 30x ∈QD ∀x 0∈C R Q ，30x ∉Q 8.已知命题p ：∀x 1，x 2∈R ，(f (x 2)-f (x 1))(x 2-x 1)≥0，则⌝p 是(A) ∃x 1，x 2∈R ，(f (x 2)-f (x 1))(x 2-x 1)≤0(B) ∀x 1，x 2∈R ，(f (x 2)-f (x 1))(x 2-x 1)≤0(C) ∃x 1，x 2∈R ，(f (x 2)-f (x 1))(x 2-x 1)<0(D) ∀x 1，x 2∈R ，(f (x 2)-f (x 1))(x 2-x 1)<09. 已知全集={0,1,2,3,4}，集合A={1,2,3,}，B={2,4} ，则（CuA ）B 为A {1,2,4}B {2,3,4}C {0,2,4}D {0,2,3,4} 10. 设a ＞0 a ≠1 ，则“函数f(x)= a x 在R 上是减函数 ”，是“函数g(x)=(2-a) 3x 在R 上是增函数”的A 充分不必要条件B 必要不充分条件C 充分必要条件D 既不充分也不必要条件11.集合{|lg 0}M x x =>，2{|4}N x x =≤，则M N =（）（A ） (1,2) （B ） [1,2) （C ） (1,2] （D ） [1,2]12.若集合}012|{>+=x x A ，}2|1||{<-=x x B ，则=B A 。

全国高考数学试题分类汇编——集合与简易逻辑

2011年集合与简易逻辑(必修一第一章、选修2-1第一章)安徽1、理(7)命题“所有能被2整除的数都是偶数”的否定．．是（A ）所有不能被2整除的数都是偶数（B ）所有能被2整除的数都不是偶数（C ）存在一个不能被2整除的数是偶数（D ）存在一个能被2整除的数不是偶数【命题意图】本题考查全称命题的否定.属容易题.【解析】把全称量词改为存在量词，并把结果否定. D2、理（8）设集合{}1,2,3,4,5,6,A ={}4,5,6,7,B =则满足S A ⊆且S B φ≠的集合S 的个数为（A ）57 （B ）56 （C ）49 （D ）8【命题意图】本题考查集合间的基本关系，考查集合的基本运算，考查子集问题，考查组合知识.属中等难度题.【解析】集合A 的所有子集共有6264=个，其中不含4,5,6,7的子集有328=个，所以集合S 共有56个.故选B.3、文（2）集合}{,,,,,U =123456，}{,,S =145,}{,,T =234,则()U S C T I 等于（A ）}{,,,1456 (B) }{,15 (C) }{4 (D) }{,,,,12345【命题意图】本题考查集合的补集与交集运算.属简答题.【解析】{}1,5,6U T =ð，所以(){}1,6U S T =ð.故选B. 北京1、理（1）已知集合P=｛x ︱x 2≤1｝,M=｛a ｝.若P ∪M=P,则a 的取值范围是（A ）(-∞, -1] （B ）[1, +∞）（C ）[-1，1] （D ）（-∞，-1] ∪[1，+∞）【解析】：2{|1}{|11}P x x x x =≤=-≤≤，[1,1]P M P a =⇒∈-，选C 。

2、文（1）已知全集U=R,集合P=｛x ︱x 2≤1｝,那么A ．(-∞, -1]B ．[1, +∞）C ．[-1，1]D ．（-∞，-1] ∪[1，+∞） 3、文（4）若p 是真命题，q 是假命题，则A ．p ∧q 是真命题B ．p ∨q 是假命题C ．﹁p 是真命题D ．﹁q 是真命题福建1、理（1）i 是虚数单位，若集合S=}{1.0.1-，则A.i S ∈B.2i S ∈C. 3i S ∈D.2S i∈ 2、理（2）若a ∈R ，则a=2是（a-1）（a-2）=0的A.充分而不必要条件 B 必要而不充分条件C.充要条件 C.既不充分又不必要条件3、文1. 若集合M=｛-1，0，1｝，N=｛0，1，2｝，则M ∩N 等于A.｛0，1｝B.｛-1，0，1｝C.｛0，1，2｝D.｛-1，0，1，2｝4、文3. 若a ∈R ，则“a=1”是“|a|=1”的A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分又不必要条件广东 1、理2．已知集合{(,)|,A x y x y =为实数，且221}x y +=，{(,)|,B x y x y =为实数，且}y x =，则A B ⋂的元素个数为A ．0B ．1C ．2D ．3解析：A B ⋂的元素个数等价于圆221x y +=与直线y x =的交点个数，显然有2个交点2、理8．设S 是整数集Z 的非空子集，如果,a b S ∀∈，有ab S ∈，则称S 关于数的乘法是封闭的．若,T V 是Z 的两个不相交的非空子集，T V Z ⋃=，且,,a b c T ∀∈，有abc T ∈；,,x y z V ∀∈，有xyz V ∈，则下列结论恒成立的是A ．,T V 中至少有一个关于乘法是封闭的B ．,T V 中至多有一个关于乘法是封闭的C ．,T V 中有且只有一个关于乘法是封闭的D ．,T V 中每一个关于乘法都是封闭的解析：若T 为奇数集，V 为偶数集，满足题意，此时T 与V 关于乘法都是封闭的，排除B 、C若T 为负整数集，V 为非负整数集，也满足题意，此时只有V 关于乘法是封闭的，排除D3、文（2）.已知集合A=(,),x y x y 为实数，B=(,),x y x y 为实数，且1x y +=则A ⋂B 的元素个数为A.4B.3C.2D.14、文（5）不等式2x 2-x-1>0的解集是 A.1(,1)2-B.（1， +∞）C.（-∞，1）∪（2，+∞）D.1(,)(1,)2-∞-⋃+∞ 湖北1、理2.已知{}1,log 2>==x x y y U ，⎭⎬⎫⎩⎨⎧>==2,1x x y y P ，则=P C U A. ⎪⎭⎫⎢⎣⎡+∞,21 B.⎪⎭⎫ ⎝⎛21,0 C.()+∞,0 D. ()⎪⎭⎫⎢⎣⎡+∞∞-,210, 解析：由已知()+∞=,0U .⎪⎭⎫ ⎝⎛=21,0P ，所以⎪⎭⎫⎢⎣⎡+∞=,21P C U ,故选A .2、理9.若实数b a ,满足0,0≥≥b a ，且0=ab ，则称a 与b 互补，记()b a b a b a --+=22,ϕ，那么()0,=b a ϕ是a 与b 互补A. 必要而不充分条件 B . 充分而不必要条件C. 充要条件D. 既不充分也不必要的条件解析：若实数b a ,满足0,0≥≥b a ，且0=ab ，则a 与b 至少有一个为0，不妨设0=b ，则()0,2=-=-=a a a a b a ϕ；反之，若()0,22=--+=b a b a b a ϕ，022≥+=+b a b a 两边平方得ab b a b a 22222++=+0=⇔ab ，则a 与b 互补，故选C.湖南1、理2.设{1,2}M =，2{}N a =，则“1a =”是“N M ⊆”则（）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分又不必要条件解析：因“1a =”，即{1}N =，满足“N M ⊆”，反之“N M ⊆”，则2{}={1}N a =，或2{}={2}N a =，不一定有“1a =”。

集合与简易逻辑知识点总结及基础训练题

第一讲集合、简易逻辑、不等式知识梳理：1、集合：某些指定的对象集在一起就构成一个集合。

集合中的每一个对象称为该集合的元素。

元素与集合的关系：A a ∈或A a ∉集合的常用表示法：列举法、描述法。

集合元素的特征：确定性、互异性、无序性。

常用一些数集及其代号：非负整数集或自然数集N ；正整数集*N ，整数集Z ；有理数集Q ；实数集R2、子集：如果集合A 的任意一个元素都是集合B 的元素，那么集合A 称为集合B 的子集，记为A ⊆B3、真子集：如果A ⊆B ，并且B A ≠，那么集合A 成为集合B 的真子集，记为A ⊄B ，读作“A 真包含于B 或B 真包含A ”，如：}{}{b a a ,⊆。

注：空集是任何集合的子集。

是非空集合的真子集结论：设集合A 中有n 个元素，则A 的子集个数为n 2个，真子集个数为12-n 个4、补集：设A ⊆S ，由S 中不属于A 的所有元素组成的集合称为S 的子集A 的补集，记为A C s ，读作“A 在S 中的补集”，即A C s =}{A x S x x ∉∈且,|。

5、全集：如果集合S 包含我们所要研究的各个集合，这时S 可以看作一个全集。

通常全集记作U 。

6、交集：一般地，由所有属于集合A 且属于B 的元素构成的集合，称为A 与B 的交集，记作B A ⋂即：B A ⋂=}{B x A x x ∈∈且,|。

7、并集：一般地，由所有属于集合A 或属于B 的元素构成的集合，称为A 与B 的并集，记作B A ⋃即：B A ⋂=}{B x A x x ∈∈或,|。

记住两个常见的结论：B A A B A ⊆⇔=⋂；A B A B A ⊆⇔=⋃；9、命题：可以判断真假的语句叫做命题。

（全称命题特称命题）⑴全称量词——“所有的”、“任意一个”等，用“∀”表示；全称命题p ：)(,x p M x ∈∀；全称命题p 的否定⌝p ：)(,x p M x ⌝∈∃。

完整版)集合与常用逻辑用语测试题及详解

完整版)集合与常用逻辑用语测试题及详解本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分，考试时间为120分钟。

第Ⅰ卷（选择题共60分）一、选择题（本大题共12个小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项符合题目要求。

）1.（文）（2011·巢湖市质检）设U={1,2,3,4,5}，A={1,2,3}，B={2,3,4}，则下列结论中正确的是（）。

A。

A⊆BB。

A∩B={2}C。

A∪B={1,2,3,4,5}D。

A∩(∁U B)={1}答案：C解析：由集合的定义可知，XXX表示A是B的子集，即A中的每个元素都在B中出现。

显然，A不是B的子集，排除A选项。

XXX表示A和B的交集，即A和B中都出现的元素构成的集合。

根据A和B的定义可知，它们的交集为{2,3}，因此排除B选项。

A∪B表示A和B的并集，即A和B中所有元素构成的集合。

根据A和B的定义可知，它们的并集为{1,2,3,4,5}，因此选C。

A∩(∁U B)表示A和B的补集的交集，即除去B中所有元素后，A中剩余的元素构成的集合。

根据A和B的定义可知，它们的补集分别为{4,5}和{1}，因此A∩(∁U B)={1}，排除D选项。

2.（2011·安徽百校联考）已知集合M={-1,0,1}，N={x|x=ab，a，b∈M且a≠b}，则集合M与集合N的关系是（）。

A。

M=NB。

MNC。

NMD。

M∩N=∅答案：C解析：根据集合N的定义可知，N中的元素是由M中的元素相乘得到的，其中a≠b。

因此，当a=-1时，b为0或1，x 为-1或0；当a=0时，x为0；当a=1时，b为-1或0，x为-1或0.综上所述，N={-1,0}，因此M和N的关系是NM。

3.（2011·福州期末）已知p：|x|<2；q：x^2-x-2<0，则綈p是綈q的（）。

A。

充分不必要条件B。

必要不充分条件C。

充要条件D。

集合与简易逻辑、函数与导数测试题(含答案)

集合与简易逻辑、函数与导数测试题1．若集合{}8,7,6,5,4,3,2,1=U ，{}8,5,2=A ，{}7,5,3,1=B ，那么(A U)B 等于（）A.{}5 B . {}7,3,1 C .{}8,2 D. {}8,7,6,5,4,3,12．函数()2()log 6f x x =-的定义域是（）A ．{}|6x x >B ．{}|36x x -<<C ．{}|3x x >-D ．{}|36x x -<≤ 3．已知23:,522:≥=+q p ,则下列判断中，错误的是（）A ．p 或q 为真，非q 为假B ． p 或q 为真，非p 为真C ．p 且q 为假，非p 为假D ． p 且q 为假，p 或q 为真 4．下列函数中,既是偶函数又在)0,(-∞上单调递增的是 ( ) A ．3y x = B ．y cos x = C ．y ln x = D ．21y x = 5．对命题”“042,0200≤+-∈∃x x R x 的否定正确的是（） A ．042,0200>+-∈∃x x R x B ．042,2≤+-∈∀x x R x C ．042,2>+-∈∀x x R x D ．042,2≥+-∈∀x x R x6．为了得到函数x y )31(3⨯=的图象，可以把函数x y )31(=的图象A ．向左平移3个单位长度B ．向右平移3个单位长度C ．向左平移1个单位长度D ．向右平移1个单位长度 7．如图是函数)(x f y =的导函数)(x f '的图象，则下面判断正确的是A ．在区间（－2,1）上)(x f 是增函数B ．在（1,3）上)(x f 是减函数C ．在（4,5）上)(x f 是增函数 8. 若函数))(12()(a x x xx f -+=为奇函数，则a 的值为（）A ．21B ．32C ．43D ．19.已知定义域为R 的函数f (x )在区间(4,+∞)上为减函数，且函数y =f (x +4)为偶函数，则（）A ．f (2)>f (3)B ．f (3)>f (6)C ．f (3)>f (5)D ． f (2)>f (5) 10.已知a >0且a ≠1，若函数f （x ）= log a （ax 2 –x ）在[3，4]是增函数，则a 的取值范围是（）A ．（1，+∞）B ．11[,)(1,)64+∞C ．11[,)(1,)84+∞D ．11[,)6411. 用},,min{c b a 表示c b a ,,三个数中的最小值，}102,2min{)(x x x f x -+=，, (x ≥0) , 则)(x f 的最大值为（）A ．4B ．5C ．6D ．712. 若函数f (x )=⎩⎨⎧>+≤0)( 1)ln(0)( x x x x ,若f (2-x 2)>f (x )，则实数x 的取值范围是A ．（-∞，-1）∪（2，+∞）B ．（-2,1）C ．（-∞，-2）∪（1，+∞）D ．（-1,2）13．设全集U 是实数集R ，{}24M x |x >＝，{}|13N x x =<<，则图中阴影部分所表示的集合是___________。

高考数学试题分类(集合、简易逻辑、函数)

集合与简易逻辑考点一：集合一、选择题1.（2003北京春，理1）若集合M ={y |y =2x -}，P ={y |y =1-x }，则M ∩P 等于（）A.{y |y >1}B.{y |y ≥1}C.{y |y >0}D.{y |y ≥0}2.（2002北京，1）满足条件M ∪{1}={1，2，3}的集合M 的个数是（） A.4 B.3 C.2 D.13.（2002全国文6，理5）设集合M ={x |x =412+k ，k ∈Z }，N ={x |x =214+k ，k ∈Z }，则（）A.M =NB.M NC.M ND.M ∩N =∅4.（2000北京春，2）设全集I ={a ，b ，c ，d ，e }，集合M ={a ，b ，c }，N ={b ，d ，e }，那么I M ∩I N是（）A.∅B.{d }C.{a ，c }D.{b ，e } 5.（2000全国文，1）设集合A ＝｛x ｜x ∈Z 且－10≤x ≤－1｝，B ＝｛x ｜x ∈B 且｜x ｜≤5｝，则A ∪B 中元素的个数是（）A.11B.10C.16D.156.（2000广东，1）已知集合A ={1，2，3，4}，那么A 的真子集的个数是（） A.15 B.16 C.3 D.47.（1999全国，1）如图，I 是全集，M 、P 、S 是I 的3个子集，则阴影部分所表示的集合是（）A.（M ∩P ）∩SB.（M ∩P ）∪SC.（M ∩P ）∩I SD.（M ∩P ）∪I S8.（1998上海，15）设全集为R ，A ＝｛x ｜x 2－5x －6＞0｝，B ＝｛x ｜|x －5｜＜a ｝（a 为常数），且11∈B ，则（）A.R A ∪B ＝RB.A ∪R B ＝RC.R A ∪R B ＝RD.A ∪B ＝R9.（1997全国，1）设集合M =｛x ｜0≤x ＜2｝，集合N ＝｛x ｜x 2－2x －3＜0｝，集合M ∩Ｎ等于（）A.｛x ｜0≤x ＜1}B.｛x ｜0≤x ＜2}C.｛x ｜0≤x ≤1｝D.｛x ｜0≤x ≤2｝10.（1997上海，1）设全集是实数集R ，M ＝｛x ｜x ≤1＋2，x ∈R ｝，N ＝｛1，2，3，4｝，则R M ∩N等于（） A.｛4｝B.｛3，4｝C.｛2，3，4｝D.｛1，2，3，4｝11.（1996上海，1）已知集合M＝｛（x，ｙ）｜x＋ｙ＝2｝，N＝｛（x，ｙ）｜x－ｙ＝4｝，那么集合M∩N为（）A.x=3，y=－1B.（3，－1）C.{3，－1}D.{（3，－1）}12.（1996全国文，1）设全集I＝｛1，2，3，4，5，6，7｝，集合A＝｛1，3，5，7｝，B＝｛3，5｝，则（）A.I＝A∪BB.I＝I A∪BC.I＝A∪I BD.I＝I A∪I B13.（2000上海，15）若集合S＝｛y｜y＝3x，x∈R｝，T＝｛y｜y＝x2－1，x∈R｝，则S ∩T是（）A.SB.TC.∅D.有限集14.（1996全国理，1）已知全集I＝N*，集合A＝｛x｜x＝2n，n∈N*｝，B＝｛x｜x＝4n，n∈N｝，则（）A.I＝A∪BB.I＝I A∪BC.I＝A∪I BD.I＝I A∪I B15.（1995上海，2）如果P＝｛x｜（x－1）（2x－5）＜0}，Q＝｛x｜0＜x＜10｝，那么（）A.P∩Q＝∅B.P QC.P QD.P∪Q＝R16.（1995全国文，1）已知全集I＝｛0，－1，－2，－3，－4｝，集合M＝｛0，－1，－2｝，N＝｛0，－3，－4｝，则I M∩N等于（）A.｛0｝B.｛－3，－4｝C.｛－1，－2｝D.∅17.（1995全国理，1）已知I为全集，集合M、N I，若M∩N＝N，则（）A.I M⊇I NB.M I NC. I M I ND.M⊇I N18.（1994全国，1）设全集I＝｛0，1，2，3，4｝，集合A＝｛0，1，2，3｝，集合B＝｛2，3，4｝，则I A∪I B等于（）A.｛0｝B.｛0，1｝C.｛0，1，4｝D.｛0，1，2，3，4｝19.（1994上海，15）设I是全集，集合P、Q满足P Q，则下面的结论中错误的是（）A.P∪I Q=∅B.I P∪Q=IC.P∩I Q=∅D.I P∩I Q=I P二、填空题20.（2003上海春，5）已知集合A ={x ||x |≤2，x ∈R }，B ={x |x ≥a }，且A B ，则实数a 的取值范围是_____.21.（2002上海春，3）若全集I =R ，f （x ）、g （x ）均为x 的二次函数，P ={x |f （x ）＜0}，Q ={x |g （x ）≥0}，则不等式组⎩⎨⎧<<0)(0)(x g x f 的解集可用P 、Q 表示为_____.22.（2000上海春，12）设I 是全集，非空集合P 、Q 满足P Q I .若含P 、Q 的一个集合运算表达式，使运算结果为空集∅，则这个运算表达式可以是（只要写出一个表达式）.考点二：简易逻辑一、选择题1.（2002河南、广西、广东7）函数f （x ）=x |x +a |+b 是奇函数的充要条件是（） A.ab =0 B.a +b =0 C.a =b D.a 2+b 2=02.（2001上海，3）a =3是直线ax +2y +3a =0和直线3x +（a －1）y =a －7平行且不重合的（）A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分也非必要条件 3.（2000上海春，15）“a =1”是“函数y =cos 2ax －sin 2ax 的最小正周期为π”的（） A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既非充分条件也非必要条件4.（1996上海文，6）若y =f （x ）是定义在R 上的函数，则y =f （x ）为奇函数的一个充要条件为（）A.f （x ）=0B.对任意x ∈R ，f （x ）=0都成立C.存在某x 0∈R ，使得f （x 0）+f （－x 0）=0D.对任意的x ∈R ，f （x ）+f （－x ）=0都成立 5.（1995上海，9）“ab <0”是“方程ax 2+by 2=c 表示双曲线”的（） A.必要条件但不是充分条件 B.充分条件但不是必要条件 C.充分必要条件 D.既不是充分条件又不是必要条件二、填空题6.（2001天津理，15）在空间中①若四点不共面，则这四点中任何三点都不共线； ②若两条直线没有公共点，则这两条直线是异面直线. 以上两个命题中，逆命题为真命题的是_____.7.（1999全国，18）α、β是两个不同的平面，m 、n 是平面α及β之外的两条不同直线，给出四个论断:①m ⊥n ②α⊥β ③n ⊥β ④m ⊥α 以其中三个论断作为条件，余下一个论断作为结论，写出你认为正确的一个．．命题：_____.函数考点一：函数的概念与性质一、选择题1.（2003北京春，文3，理2）若f （x ）=xx 1-，则方程f （4x ）=x 的根是（） A.－2 B.2C.－21 D. 21 2.（2003北京春，文8）函数f （x ）=|x |和g （x ）=x （2－x ）的递增区间依次是（） A.（－∞，0]，（－∞，1] B.（－∞，0]，［1，+∞) C.［0，+∞)，（－∞，1]D.［0，+∞），［1，+∞）3.（2001北京春，理4）函数y =－x -1（x ≤1）的反函数是（）A.y =x 2－1（－1≤x ≤0）B.ｙ＝x 2－1（0≤x ≤1）Ｃ.ｙ＝1－x 2（x ≤0） D.ｙ＝1－x 2（0≤x ≤1） 4.（2001全国，10）设f （x ）、g （x ）都是单调函数，有如下四个命题： ①若f （x ）单调递增，g （x ）单调递增，则f （x ）－g （x ）单调递增； ②若f （x ）单调递增，g （x ）单调递减，则f （x ）－g （x ）单调递增； ③若f （x ）单调递减，g （x ）单调递增，则f （x ）－g （x ）单调递减； ④若f （x ）单调递减，g （x ）单调递减，则f （x ）－g （x ）单调递减. 其中，正确的命题是（） A.①② B.①④ C.②③ D.②④5.（2000全国理，1）设集合A 和B 都是自然数集合N ，映射f ：A →B 把集合A 中的元素n 映射到集合B 中的元素2n ＋n ，则在映射f 下，象20的原象是（）A.2B.3C.4D.56.（1999全国，2）已知映射f ：A →B ，其中，集合A ＝｛－3，－2，－1，1，2，3，4｝，集合B 中的元素都是A 中元素在映射f 下的象，且对任意的a ∈A ，在B 中和它对应的元素是｜a ｜，则集合B 中元素的个数是（）A.4B.5C.6D.7 7.（1999全国，3）若函数y ＝f （x ）的反函数是y ＝g （x ），f （a ）＝b ，ab ≠0，则 g （b ）等于（）A.aB.a －1C.bD.b －18.（1998全国，5）函数f （x ）=x1（x ≠0）的反函数f －1（x ）等于（） A.x （x ≠0） B.x 1（x ≠0） C.－x （x ≠0） D.－x1（x ≠0） 9.（1997全国，13）定义在区间（－∞，＋∞）的奇函数f （x ）为增函数，偶函数 g （x ）在区间［0，＋∞）的图象与f （x ）的图象重合，设a ＞b ＞0，给出下列不等式，其中成立的是（）①f （b ）－f （－a ）＞g （a ）－g （－b ） ②f （b ）－f （－a ）＜g （a ）－g （－b ） ③f （a ）－f （－b ）＞g （b ）－g （－a ） ④f （a ）－f （－b ）＜g （b ）－g （－a ） A.①与④ B.②与③ C.①与③ D.②与④ 10.（1996全国，15）设f （x ）是（－∞，＋∞）上的奇函数，f （x +2）=－f （x ），当 0≤x ≤1时，f （x ）=x ，则f （7.5）等于（）A.0.5B.－0.5C.1.5D.－1.511.（1994全国，15）定义在（－∞，＋∞）上的任意函数f （x ）都可以表示成一个奇函数g （x ）和一个偶函数h （x ）之和，如果f （x ）=lg （10x ＋1），x ∈（－∞，＋∞），那么（）A.g （x ）=x ，h （x ）=lg （10x ＋10－x ＋2）B.g （x ）=21lg ［（10x ＋1）＋x ］，h （x ）＝21lg ［（10x ＋1）－x ］ C.g （x ）＝2x ，h （x ）＝lg （10x ＋1）－2x D.g （x ）＝－2x ，h （x ）＝lg （10x ＋1）＋2x二、填空题12.（2003北京春，理16）若存在常数p >0，使得函数f （x ）满足f （px ）=f （px －2p）（x ∈R ），则f （x ）的一个正周期为_____.13.（2002上海春，1）函数y =2231xx --的定义域为_____.14.（2002全国文，14）函数y =xx+12（x ∈（－1，+∞））图象与其反函数图象的交点坐标为_____.15.（2002全国理，16）已知函数f （x ）=221x x +，那么f （1）+f （2）+f （21）+f （3）+f （31）+f （4）+f （41）=_____. 16. (2002天津文.16)设函数f （x ）在（－∞，+∞）内有定义,下列函数:①y =－|f （x ）| ②y =xf （x 2） ③y =－f （－x ） ④y =f （x ）－f （－x ）中必为奇函数的有_____.（要求填写正确答案的序号）17.（2002上海，12）已知函数y =f （x ）（定义域为D ，值域为A ）有反函数y =f －1（x ），则方程f （x ）=0有解x =a ，且f （x ）＞x （x ∈D ）的充要条件是y =f －1（x ）满足_____.18.（2001上海春，1）函数f （x ）=x 2+1（x ≤0）的反函数f －1（x ）=_____.19.（2001上海春，10）若记号“*”表示求实数a 与b 的算术平均数的运算，即a *b =2ba +，则两边均含有运算符号“*”和“+”，且对于任意3个实数a 、b 、c 都能成立的一个等式可以是_____.20.（2000上海春，2）若函数f （x ）=2+x x ，则f －1（31）=_____.21.（2000上海，2）函数y ＝log 2xx --312的定义域为 . 22.（2000上海，5）已知f （x ）＝2x ＋b 的反函数为f －1（x ），若 y ＝f －1（x ）的图象经过点Q （5，2），则b ＝ .23.（2000上海，8）设函数y ＝f （x ）是最小正周期为2的偶函数，它在区间［0，1］上的图象为如图所示的线段AB ，则在区间［1，2］上f （x ）＝ .24.（1998上海，4）函数f （x ）=（x －1）31＋2的反函数是f －1（x ）＝ .25.（1998上海，8）函数y ＝⎪⎩⎪⎨⎧>+-≤<+≤+1,510,30,32x x x x x x 的最大值是 .26.（1996上海，10）函数y ＝)2(log 121x -的定义域是 .27.（1995上海文，15）函数y =3x 2＋1（x ≤0）的反函数是y = . 28.（1995上海文，16）函数y ＝lg 210-x 的定义域是 .29.（1994上海，6）函数y ＝12-x （x ≤－1）的反函数是 .三、解答题30.（2002京、皖春，18）已知f （x ）是偶函数，而且在（0，+∞）上是减函数，判断f （x ）在（－∞，0）上是增函数还是减函数，并加以证明.31.（2002北京文，22）已知f （x ）是定义在R 上的不恒为零的函数，且对于任意的a ，b ∈R 都满足：f （a ·b ）=af （b ）+bf （a ）.（1）求f （0），f （1）的值；（2）判断f （x ）的奇偶性，并证明你的结论；（3）若f （2）=2，u n =f （2n ）（n ∈N ），求证：u n +1＞u n （n ∈N ）.32.（2001全国文，22）设f （x ）是定义在R 上的偶函数，其图象关于直线x ＝1对称，对任意x 1，x 2∈［0，21］，都有f （x 1＋x 2）＝f （x 1）·f （x 2）.（1）设f （1）＝2，求f （21），f （41）；（2）证明f （x ）是周期函数.33.（2001春季北京、安徽，12）设函数f （x ）＝bx ax ++（a ＞b ＞0），求f （x ）的单调区间，并证明f （x ）在其单调区间上的单调性.考点二：函数的图象一、选择题1.（2002全国理，10）函数y =1－11-x 的图象是（）2.（2002北京文，12）如图所示，f 1（x ），f 2（x ），f 3（x ），f 4（x ）是定义在［0，1］上的四个函数，其中满足性质：“对［0，1］中任意的x 1和x 2，f （221x x +）≤21［f （x 1）+f （x 2）］恒成立”的只有（）3.（2002北京理，12）如图所示，f i （x ）（i =1，2，3，4）是定义在［0，1］上的四个函数，其中满足性质：“对［0，1］中任意的x 1和x 2，任意λ∈［0，1］，f ［λx 1+（1－λ）x 2］≤λf （x 1）+（1－λ）f （x 2）恒成立”的只有（）A.f 1（x ），f 3（x ）B.f 2（x ）C.f 2（x ），f 3（x ）D.f 4（x ）4.（2000春季北京、安徽，14）已知函数f （x ）＝ax 3＋bx 2＋cx ＋d 的图象如图，则（）A.b ∈（－∞，0）B.b ∈（0，1）C.b ∈（1，2）D.b ∈（2，＋∞）5.（1995全国，文2）函数y=11+x 的图象是（）6.（1997全国，文7）设函数y =f （x ）定义在实数集上，则函数y =f （x －1）与y = f （1－x ）的图象关于（）A.直线y =0对称B.直线x =0对称C.直线y =1对称D.直线x =1对称二、解答题7.（2000上海春，17）设f （x ）为定义在R 上的偶函数，当 x ≤－1时，y ＝f （x ）的图象是经过点（－2，0），斜率为1的射线，又在y ＝f （x ）的图象中有一部分是顶点在（0，2），且过点（－1，1）的一段抛物线.试写出函数f （x ）的表达式，并作出其图象.考点三：二次函数一、选择题1.（2003北京春，理4）函数f （x ）=)1(11x x --的最大值是（）A.54 B.45C.43D.34 2.（2002全国文10，理9）函数y =x 2+bx +c （x ∈［0，+∞））是单调函数的充要条件是（）A.b ≥0B.b ≤0C.b ＞0D.b ＜0二、填空题3.（2003上海春，11）若函数y =x 2+（a +2）x +3，x ∈［a ，b ］的图象关于直线x =1对称，则b =_____.三、解答题4.（2002京、皖春，22）对于函数f （x ），若存在x 0∈R ，使f （x 0）=x 0成立，则称x 0为f （x ）的不动点.已知函数f （x ）=ax 2+（b +1）x +（b －1）（a ≠0）. （1）当a =1，b =－2时，求函数f （x ）的不动点；（2）若对任意实数b ，函数f （x ）恒有两个相异的不动点，求a 的取值范围；（3）在（2）的条件下，若y =f （x ）图象上A 、B 两点的横坐标是函数f （x ）的不动点，且A 、B 两点关于直线y =kx +1212+a 对称，求b 的最小值.5.（2002全国文，20）设函数f （x ）=x 2+|x －2|－1，x ∈R . （1）判断函数f （x ）的奇偶性；（2）求函数f （x ）的最小值.6.（2002全国理，21）设a 为实数，函数f （x ）=x 2+|x －a |+1，x ∈R . （1）讨论f （x ）的奇偶性；（2）求f （x ）的最小值.7.（2002上海文，19）已知函数f （x ）=x 2+2ax +2，x ∈［－5，5］（1）当a =－1时，求函数f （x ）的最大值和最小值；（2）求实数a 的取值范围，使y =f （x ）在区间［－5，5］上是单调函数. 8.（2002河南、广东、广西，22）已知a >0，函数f （x ）=ax －bx 2. （1）当b >0时，若对任意x ∈R 都有f （x ）≤1，证明a ≤2b ；（2）当b >1时，证明：对任意x ∈［0，1］，|f （x ）|≤1的充要条件是b －1≤a ≤2b ；（3）当0<b ≤1时，讨论：对任意x ∈［0，1］，|f （x ）|≤1的充要条件.9.（2000上海，19）已知函数f （x ）＝xax x ++22，x ∈［1，＋∞)．（1）当a ＝21时，求函数f （x ）的最小值；（2）若对任意x ∈［1，＋∞)，f （x ）＞0恒成立，试求实数a 的取值范围.10.（1996上海，20）在如图所示的直角坐标系中，一运动物体经过点A （0，9），其轨迹方程为y =ax 2＋c （a ＜0），D =（6，7）为x 轴上的给定区间.（1）为使物体落在D 内，求a 的取值范围；（2）若物体运动时又经过点P （2，8.1），问它能否落在D 内?并说明理由.考点四：指数函数与对数函数一、选择题1.（2002上海春，5）设a ＞0，a ≠1，函数y =lo g a x 的反函数和y =lo g ax1的反函数的图象关于（）A.x 轴对称B.y 轴对称C.y =x 对称D.原点对称2.（2002全国文4，理13）函数y =a x 在［0，1］上的最大值与最小值的和为3，则a 等于（）A.21 B.2 C.4 D.41 3.（2002全国文，9）已知0＜x ＜y ＜a ＜1，则有（） A.lo g a （xy ）＜0 B.0＜lo g a （xy ）＜1 C.1＜lo g a （xy ）＜2 D.lo g a （xy ）＞24.（2001北京春，理7）已知f （x 6）＝log 2x ，那么f （8）等于（） A.34 B.8 C.18 D.21 5.（2001北京春，2）函数f （x ）=a x （a >0，且a ≠1）对于任意的实数x 、y 都有（） A.f （xy ）=f （x ）·f （y ） B.f （xy ）=f （x ）+f （y ） C.f （x +y ）=f （x ）·f （y ） D.f （x +y ）=f （x ）+f （y ）6.（2001全国，4）若定义在区间（－1，0）内的函数f （x ）=log 2a （x ＋1）满足f （x ）＞0，则a 的取值范围是（）A.（0，21） B.（0，21] C.（21，＋∞） D.（0，＋∞）7.（2001全国文，6）函数y =2x -＋1（x ＞0）的反函数是（） A.y =log 211-x ，x ∈（1，2） B.y ＝－1og 211-x ，x ∈（1，2） C.y =log 211-x ，x ∈（1，2]D.y ＝－1og 211-x ，x ∈（1，2] 8.（2000春季北京、安徽，7）函数y ＝ｌg ｜x ｜（） A.是偶函数，在区间（－∞，0）上单调递增 B.是偶函数，在区间（－∞，0）上单调递减 C.是奇函数，在区间（0，＋∞）上单调递增 D.是奇函数，在区间（0，＋∞）上单调递减9.（2000上海春，16）若0＜a ＜1，b ＜－1，则函数f （x ）＝a x ＋b 的图象不经过（） A.第一象限 B.第二象限 C.第三象限 D.第四象限10.（1998上海，文、理13）若0<a <1，则函数y =lo g a （x +5）的图象不经过（） A.第一象限 B.第二象限 C.第三象限 D.第四象限 11.（1998全国，2）函数y ＝a |x |（a ＞1）的图象是（）12.（1997上海，2）三个数60．7，0．76，log 0．76的大小顺序是（）A.0．76＜log 0．76＜60．7B.0．76＜60．7＜log 0．76C.log 0．76＜60．7＜0．76D.log 0．76＜0．76＜60．713.（1997全国，理7）将y =2x 的图象_____，再作关于直线y =x 对称的图象，可得到y =lo g 2（x +1）的图象（）A.先向左平行移动1个单位B.先向右平行移动1个单位C.先向上平行移动1个单位D.先向下平行移动1个单位14.（1996上海，3）如果log a 3＞log b 3＞0，那么a 、b 间的关系是（）A.0＜a ＜b ＜1B.1＜a ＜bC.0＜b ＜a ＜1D.1＜b ＜a15.（1996全国，2）当a ＞1时，在同一坐标系中，函数y =a －x 与y ＝log a x 的图象是（）16.（1996上海，文、理8）在下列图象中，二次函数y =ax 2+bx 与指数函数y =（a b ）x 的图象只可能是（）17.（1995上海，7）当0＜a ＜b ＜1时，下列不等式中正确的是（）A.（1－a ）b 1＞（1－a ）bB.（1＋a ）a ＞（1＋b ）bC.（1－a ）b ＞（1－a ）b 2D.（1－a ）a ＞（1－b ）b18.（1995上海，6）当a ≠0时，函数y =ax +b 和y =b ax 的图象只可能是（）19.（1995全国文，11）已知y =log a （2－x ）是x 的增函数，则a 的取值范围是（）A.（0，2）B.（0，1）C.（1，2）D.（2，+∞）20.（1995全国理，11）已知y ＝log a （2－ax ）在［0，1］上是x 的减函数，则a 的取值范围是（）A.（0，1）B.（1，2）C.（0，2）D.［2，＋∞）21.（1994上海）如果0<a <1，那么下列不等式中正确的是（）A.（1－a ）31>（1－a ）21 B.lo g 1－a （1+a ）>0C.（1－a ）3>（1+a ）2D.（1－a ）1+a >122.（1994上海，11）当a ＞1时，函数y ＝log a x 和y =（1－a ）x 的图象只能是（）二、填空题23.（2002上海春，4）设f （x ）是定义在R 上的奇函数，若当x ≥0时，f （x ）=lo g 3（1+x ），则f （－2）=_____.24.（2002上海，3）方程lo g 3（1－2·3x ）=2x +1的解x =_____.25.（2001上海春，3）方程lo g 4（3x －1）=lo g 4（x －1）+lo g 4（3+x ）的解是_____.26.（2001上海文，1）设函数f （x ）=log 9x ，则满足f （x ）＝21的x 值为． 27.（2001上海理，1）设函数f （x ）＝⎩⎨⎧+∞∈-∞∈-),1(,log ]1,(,281x x x ，则满足f （x ）=41的x 值为．28.（1999上海，文9）64log 2log 273=_____. 29.（1999上海，2）函数f （x ）=lo g 2x +1（x ≥4）的反函数f －1（x ）的定义域是_____.30.（1998上海，1）lg20＋log 10025＝ .31.（1998上海，11）函数f （x ）=a x （a ＞0，a ≠1）在［1，2］中的最大值比最小值大2a ，则a 的值为 . 32.（1997上海，7）方程l g （1－3x ）=l g （3－x ）+l g （7+x ）的解是_____.33.（1996上海，9）方程log 2（9x －5）＝log 2（3x －2）＋2的解是 .34.（1996上海，12）函数y ＝2x -（x ＜0)的反函数是 .35.（1995全国文，16）方程log 2（x ＋1）2＋log 4（x ＋1）＝5的解是 .36.（1994上海，4）方程log 3（x －1）＝log 9（x ＋5）的解是 .三、解答题37.（2003上海春，20）已知函数5)(,5)(31313131--+=-=xx x g xx x f .（1）证明f （x ）是奇函数；并求f （x ）的单调区间.（2）分别计算f （4）－5f （2）g （2）和f （9）－5f （3）g （3）的值，由此概括出涉及函数f （x ）和g （x ）的对所有不等于零的实数x 都成立的一个等式，并加以证明.38.（2002上海春，20）已知函数f （x ）=a x +12+-x x （a ＞1）. （1）证明：函数f （x ）在（－1，+∞）上为增函数；（2）用反证法证明方程f （x ）=0没有负数根.39.（2001天津，19）设a ＞0，f （x ）＝x x ea a e +是R 上的偶函数. （1）求a 的值；（2）证明f （x ）在（0，＋∞）上是增函数．40.（2000春季北京、安徽文，19）已知二次函数f （x ）＝（lg a ）x 2＋2x ＋4lg a 的最大值为3，求a 的值.41.（2000春季北京安徽理，21）设函数f （x ）＝|lg x |，若0＜a ＜b ，且f （a ）＞f （b ），证明：ab ＜1．42.（1999全国文，19）解方程2lg 3-x －3l gx +4=0.43.（1995全国文，21）解方程3x +2－32－x =80.考点五：函数的应用一、选择题1.（2002上海文，理16）一般地，家庭用电量（千瓦时）与气温（℃）有一定的关系，如图所示，图（1）表示某年12个月中每月的平均气温.图（2）表示某家庭在这年12个月中每个月的用电量.根据这些信息，以下关于该家庭用电量与其气温间关系的叙述中，正确的是（）A.气温最高时，用电量最多B.气温最低时，用电量最少C.当气温大于某一值时，用电量随气温增高而增加D.当气温小于某一值时，用电量随气温渐低而增加2.（2002全国理，12）据2002年3月5日九届人大五次会议《政府工作报告》：“2001年国内生产总值达到95933亿元，比上年增长7.3%.”如果“十·五”期间（2001年～2005年）每年的国内生产总值都按此年增长率增长，那么到“十·五”末我国国内年生产总值约为（）A.115000亿元B.120000亿元C.127000亿元D.135000亿元3.（2001全国，12）如图2—2，小圆圈表示网络的结点，结点之间的连线表示它们有网线相联.连线标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息，信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为（）A.26B.24C.20D.194.（1998全国文11，理10）向高为H的水瓶中注水，注满为止.如果注水量V与水深h的函数关系的图象如图2—4所示，那么水瓶的形状是（）二、填空题5.（2002全国，文13）据新华社2002年3月12日电，1985年到2000年间，我国农村人均居住面积如图所示，其中从_____年到_____年的五年间增长最快.6．（2001上海，12）根据报道，我国目前已成为世界上受荒漠化危害最严重的国家之一．图中（1）表示我国土地沙化总面积在上个世纪五六十年代、七八十年代、九十年代的变化情况．由图中的相关信息，可将上述有关年代中，我国年平均土地沙化面积在图2—6中（2）中图示为：7.（1998上海，文6）某工程的工序流程图如图（工时单位：天），则工程总时数为_____天.8.（1994全国，20）在测量某物理量的过程中，因仪器和观察的误差，使得n次测量分别得到a1，a2，……，a n，共n个数据.我们规定所测量物理量的“最佳近似值”a是这样一个量：与其他近似值比较，a与各数据的差的平方和最小.依此规定，从a1，a2，……，a n推出的a = .三、解答题9.（2003北京春，理、文21）某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时，可全部租出.当每辆车的月租金每增加50元时，未租出的车将会增加一辆.租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元.（1）当每辆车的月租金定为3600元时，能租出多少辆车？（2）当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益是多少？10.（2001全国文，21）设计一幅宣传画，要求画面面积为4840 cm 2，画面的宽与高的比为λ（λ＜1)，画面的上、下各留8 cm 空白，左、右各留5 cm 空白.怎样确定画面的高与宽尺寸，能使宣传画所用纸张面积最小?11.（2001上海，文、理21）用水清洗一堆蔬菜上残留的农药．对用一定量的水清洗一．．．次．的效果作如下假定：用1个单位量的水可洗掉蔬菜上残留农药量的21，用水越多洗掉的农药量也越多，但总还有农药残留在蔬菜上．设用x 单位量的水清洗一次．．．．以后，蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数f （x ）.（1）试规定f （0）的值，并解释其实际意义；（2）试根据假定写出函数f （x ）应该满足的条件和具有的性质；（3）设f （x ）=211x ，现有a （a ＞0）单位量的水，可以清洗一次，也可以把水平均分成2份后清洗两次，试问用哪种方案清洗后蔬菜上残留的农药量比较少?说明理由．12.（2000全国，21）某蔬菜基地种植西红柿，由历年市场行情得知，从二月一日起的300天内，西红柿市场售价与上市时间的关系用图中（1）的一条折线表示；西红柿的种植成本与上市时间的关系用图中（2）的抛物线表示.（1）写出图中（1）表示的市场售价与时间的函数关系式P ＝f （t ）；写出图中（2）表示的种植成本与时间的函数关系式Q ＝g （t ）；（2）认定市场售价减去种植成本为纯收益，问何时上市的西红柿纯收益最大?（注：市场售价和种植成本的单位：元／102 ，ｋg ，时间单位：天）。

集合与简易逻辑练习题与答案

一、选择题(每小题5分，共25分)1．(2011·北京)已知集合P ＝{x |x 2≤1}，M ＝{a }．若P ∪M ＝P ，则a 的取值范围是( )．A ．(－∞，－1]B ．[1，＋∞)C ．[－1,1]D ．(－∞，－1]∪[1，＋∞)析由题设P ∪M ＝P ，可得M ⊆P ，∴a 2≤1，解得－1≤a ≤1.故选 C2．(2011·陕西)设集合M ＝{y |y ＝|cos 2x －sin 2x |，x ∈R }，N ＝⎩⎨⎧⎭⎬⎫x ⎪⎪⎪⎪⎪⎪x －1i <2，i 为虚数单位，x ∈R ，则M ∩N 为( )． A ．(0,1) B ．(0,1] C ．[0,1) D ．[0,1]解析由题意得M ＝{y |y ＝|cos 2x |}＝[0,1]，N ＝{x ||x ＋i|<2}＝{x |x 2＋1<2}＝(－1,1)，∴M ∩N ＝[0,1)．故选 C3．(2011·山东)对于函数y ＝f (x )，x ∈R ，“y ＝|f (x )|的图象关于y 轴对称”是“y ＝f (x )是奇函数”的( )．A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件解析若y ＝f (x )是奇函数，则f (－x )＝－f (x )，∴|f (－x )|＝|－f (x )|＝|f (x )|，∴y ＝|f (x )|的图象关于y 轴对称，但若y ＝|f (x )|的图象关于y 轴对称，如y ＝f (x )＝x 2，而它不是奇函数．故选 B4．已知命题“函数f (x )、g (x )定义在R 上，h (x )＝f (x )·g (x )，若f (x )、g (x )均为奇函数，则h (x )为偶函数”的原命题、逆命题、否命题、逆否命题中正确命题的个数是( )．A ．0B ．1C ．2D ．3解析由f (x )、g (x )均为奇函数，可得h (x )＝f (x )·g (x )为偶函数，反之则不成立，如h (x )＝x 2是偶函数，但函数f (x )＝x 2e x ，g (x )＝e x 都不是奇函数，故逆命题不正确，故其否命题也不正确，即只有原命题和逆否命题正确．故选C.故选 C5．下列命题错误的是( )．A ．命题“若m >0，则方程x 2＋x －m ＝0有实根”的逆否命题为：“若方程x 2＋x －m ＝0无实根，则m ≤0”B ．“x ＝1”是“x 2－3x ＋2＝0”的充分不必要条件C ．命题“若xy ＝0，则x ，y 中至少有一个为零”的否定是：“若xy ≠0，则x ，y 都不为零”D ．对于命题p ：∃x ∈R ，使得x 2＋x ＋1<0；则綈p ：∀x ∈R ，均有x 2＋x ＋1≥0解析对C 选项中命题的否定是“若xy ＝0，则x ，y 都不为零”，C 错．命题：“若p 则q ”的否命题是：“若綈p ，则綈q ”，命题的否定是：“若p 则綈q ”．故选 C二、填空题(每小题5分，共15分)6．(2010·重庆)设U ＝{0,1,2,3}，A ＝{x ∈U |x 2＋mx ＝0}，若∁U A ＝{1,2}，则实数m ＝________. 解析 ∵U ＝{0,1,2,3}，∁U A ＝{1,2}，∴A ＝{0,3}，即方程x 2＋mx ＝0的两根为0和3，∴m ＝－3.故填－37．设p ：方程x 2＋2mx ＋1＝0有两个不相等的正根；q ：方程x 2＋2(m －2)x －3m ＋10＝0无实根，则使p 或q 为真，p 且q 为假的实数m 的取值范围是________．解析令f (x )＝x 2＋2mx ＋1.则由f (0)>0，且－b 2a>0，且Δ>0，求得m <－1，∴p ：m ∈(－∞，－1)．q ：Δ＝4(m －2)2－4(－3m ＋10)<0⇒－2<m <3. 由p 或q 为真，p 且q 为假知，p 、q 一真一假．①当p 真q 假时，⎩⎪⎨⎪⎧ m <－1，m ≤－2或m ≥3，即m ≤－2； ②当p 假q 真时，⎩⎪⎨⎪⎧m ≥－1，－2<m <3，即－1≤m <3. ∴m 的取值范围是m ≤－2或－1≤m <3.故填 (－∞，－2]∪[－1,3)8．已知命题p ：∃x ∈R ，使sin x ＝52；命题q ：∀x ∈R ，都有x 2＋x ＋1＞0，给出下列结论： ①命题“p ∧q ”是真命题；②命题“綈p ∨綈q ”是假命题；③命题“綈p ∨綈q ”是真命题；④命题“p ∧q ”是假命题．其中正确的是________．解析命题p 是假命题，命题q 是真命题，故结论③④正确．故填 ③④三、解答题(每小题10分，共20分)9．设a ∈R ，二次函数f (x )＝ax 2－2x －2a .设不等式f (x )>0的解集为A ，又知集合B ＝{x |1<x <3}，A ∩B ≠∅，求a 的取值范围．解: 由f (x )为二次函数知，a ≠0.令f (x )＝0，解得其两根为x 1＝1a－ 2＋1a2， x 2＝1a ＋ 2＋1a 2. 由此可知x 1<0，x 2>0.(1)当a >0时，A ＝{x |x <x 1或x >x 2}．A ∩B ≠∅的充要条件是x 2<3，即1a ＋ 2＋1a 2<3.∴a >67. (2)当a <0时，A ＝{x |x 1<x <x 2}．A ∩B ≠∅的充要条件是x 2>1，即1a＋ 2＋1a 2>1，解得a <－2. 综上，使A ∩B ≠∅成立的a 的取值范围是(－∞，－2)∪⎝⎛⎭⎫67，＋∞.10．已知集合A ＝{y |y 2－(a 2＋a ＋1)y ＋a (a 2＋1)>0}，B ＝⎩⎨⎧⎭⎬⎫y |y ＝12x 2－x ＋52，0≤x ≤3. (1)若A ∩B ＝∅，求a 的取值范围；(2)当a 取使不等式x 2＋1≥ax 恒成立的a 的最小值时，求(∁R A )∩B .解:A ＝{y |y <a 或y >a 2＋1}，B ＝{y |2≤y ≤4}．(1)当A ∩B ＝∅时，⎩⎪⎨⎪⎧a 2＋1≥4，a ≤2， ∴3≤a ≤2或a ≤－ 3. ∴a 的取值范围是(－∞，－3]∪[3，2]．(2)由x 2＋1≥ax ，得x 2－ax ＋1≥0，依题意Δ＝a 2－4≤0，∴－2≤a ≤2.∴a的最小值为－2.当a＝－2时，A＝{y|y<－2或y>5}．∴∁R A＝{y|－2≤y≤5}．∴(∁R A)∩B＝{y|2≤y≤4}．。

集合常用逻辑用语不等式测试

质量检测测试内容：集合、常用逻辑用语不等式(时间：120分钟满分：150分)一、选择题(本大题共12小题，每小题5分，共60分)1．(2011年北京西城期末)设集合A ＝{1,2,3,4}，B ＝{3,4,5}，全集U ＝A ∪B ，则集合∁U (A ∩B )的元素个数为( )A ．1个B ．2个C ．3个D ．4个解析：由已知条件可得U ＝A ∪B ＝{1,2,3,4,5}，A ∩B ＝{3,4}，∴∁U (A ∩B )＝{1,2,5}，即集合∁U (A ∩B )的元素个数有3个，故应选C.本题考查了集合的交集、并集与补集的运算，属于基础运算题．答案：C2．若b <a <0，则下列不等式中正确的是( )A.1a >1bB ．|a |>|b | C.b a ＋a b >2 D ．a ＋b >ab解析：∵1a －1b ＝b －a ab <0，故A 错；b <a <0⇒－b >－a >0⇒|b |>|a |，故B 错；b a ＋a b ＝|b a |＋|a b |≥2，又b a ≠a b，所以等号不成立，故C 正确；a ＋b <0，而ab >0，故D 错，因此，选C. 答案：C3．(2011年合肥第一次质检)集合A ＝{－1,0,4}，集合B ＝{x |x 2－2x －3≤0，x ∈N }，全集为U ，则图中阴影部分表示的集合是( )A ．{4}B ．{4,1}C ．{4,5}D ．{－1,0}解析：本题主要考查集合的运算与韦恩图．由图可知阴影部分表示的集合为(∁U B )∩A ，因为B ＝{x |－1≤x ≤3，x ∈N }＝{0,1,2,3}，因此(∁U B )∩A ＝{4，－1}，选B.本题为容易题．答案：B4．(2011年天津河西区高三质量调查)已知命题p ：任意有理数都是实数，命题q ：正数的对数都是负数，则以下命题中为真命题的是( )A ．p ∧qB ．(¬p )∨q C(¬p )∧(¬q ) D ．(¬p )∨(¬q )解析：∵命题p ：任意有理数都是实数是真命题；命题q ：正数的对数是负数是假命题，则p ∧q 是假命题；(¬p )∨q 是假命题；(¬p )∧(¬q )是假命题；(¬p )∨(¬q )是真命题，故应选D.答案：D5．(2011年福建莆田四中第一次月考)已知条件p ：x ≤1，条件q ：1x<1，则¬p 是q 的( ) A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既非充分也非必要条件解析：¬p ：x >1，x >1⇒1x<1，反之不成立，故¬p 是q 的充分不必要条件．答案：A6．已知命题p ：“∀x ∈[1,2]，x 2－a ≥0”，命题q ：“∃x ∈R ，x 2＋2ax ＋2－a ＝0”，若命题“p ∧q ”是真命题，则实数a 的取值范围是( )A ．(－∞，－2]∪{1}B ．(－∞，－2]∪[1,2]C ．[1，＋∞)D ．[－2,1]解析：由命题“p ∧q ”是真命题可知，命题p 与命题q 都是真命题，由命题p ：“∀x ∈[1,2]，x 2－a ≥0”为真命题，即a ≤x 2，x ∈[1,2]，则a ≤1；由命题q 为真命题可得Δ＝(2a )2－4(2－a )≥0，即a ≤－2，或a ≥1成立．综上可得实数a 的取值范围是(－∞，－2]∪{1}．答案：A7．若a <b <0，则下列不等式中不一定成立的是( )A.1a >1bB.1a －b >1bC.－a >－bD ．|a |>－b解析：∵1a －1b ＝b －a ab>0， ∴A 一定成立；∵a <b <0，∴－a >－b >0， ∴－a >－b ，即C 一定成立； |a |＝－a ；∴|a |>－b ⇔－a >－b ，成立，∴D 成立；当a ＝－2，b ＝－1时，1a －b ＝1－2＋1＝－1＝1b ，所以B 不一定成立，故选B. 答案：B8．(2011年青岛高三质检)若a >0，b >0，且a ＋b ＝4，则下列不等式恒成立的是( ) A.1ab >12 B.1a ＋1b≤1C.ab ≥2 D ．a 2＋b 2≥8解析：a ＋b ＝4≥2ab ，ab ≤2，ab ≤4∴1ab ≥14，故C 错，A 错． 1a ＋1b ＝a ＋b ab ＝4ab≥1，故B 错． (a ＋b )2＝a 2＋b 2＋2ab ≤2(a 2＋b 2)∴a 2＋b 2≥8，故选D.答案：D9．若不等式(a －2)x 2＋2(a －2)x －4<0对于x ∈R 恒成立，则a 的取值范围是( )A ．(－2,2)B ．[－2,2]C ．(－2,2]D ．[－2,2)解析：当a ＝2时，不等式－4<0恒成立；当a ≠2时，由⎩⎪⎨⎪⎧a －2<0Δ＝4(a －2)2＋4×4(a －2)<0，解得－2<a <2，∴符合要求的a 的取值范围是(－2,2]，故选C.答案：C10．(2011年辽宁名校一轮综合测试)若关于x 的不等式ax －b >0的解集是(1，＋∞)，则关于x 的不等式ax ＋b x －2>0的解集是( ) A ．(－∞，－1)∪(2，＋∞)B ．(－1,2)C ．(－1,2]D ．(－∞，1)∪(2，＋∞) 解析：因为不等式ax －b >0的解集是(1，＋∞)，所以a ＝b >0，所以ax ＋b x －2>0等价于(x ＋1)(x －2)>0，所以x <－1，或x >2.答案：A11．(2011年山西四校联考)下列命题①命题“若x ≠1，则x 2－3x ＋2≠0”的逆否命题是“若x 2－3x ＋2＝0，则x ＝1”． ②命题p ：∀x ∈R ，x 2＋x ＋1≠0，则綈p ：∃x 0∈R ，x 20＋x 0＋1＝0.③若p ∨q 为真命题，则p 、q 均为真命题．④“x >2”是“x 2－3x ＋2>0”的充分不必要条件．其中真命题的个数有( )A ．1个B ．2个C ．3个D ．4个解析：①②④正确，③错：p ∨q 一真则真．答案：C12．若不等式组⎩⎪⎨⎪⎧x 2－2x －3≤0，x 2＋4x －(1＋a )≤0的解集不是空集，则实数a 的取值范围是( ) A ．(－∞，－4]B ．[－4，＋∞)C ．[－4,20]D ．[－40,20)解析：由x 2－2x －3≤0得－1≤x ≤3；若不等式组的解集不是空集，则需不等式x 2＋4x －(1＋a )≤0在[－1,3]上有解，即a ≥x 2＋4x －1在[－1,3]上有解；令h (x )＝x 2＋4x －1，h (x )在[－1,3]上单调递增，所以h (x )min ＝h (－1)＝－4，h (x )max ＝h (3)＝20，则a ≥－4.答案：B二、填空题(本大题共4小题，每小题5分，共20分)13．命题p ：∀x ∈R ，f (x )≥m ，则命题p 的否定¬p 是________．答案：∃x ∈R ，f (x )<m14．设f (x )＝⎩⎪⎨⎪⎧ 1x (x >0)x 2(x ≤0)，则不等式f (x )>1的解集为________．解析：由⎩⎪⎨⎪⎧ 1x >1x >0⇔0<x <1；由⎩⎪⎨⎪⎧x 2>1x ≤0⇔x <－1 ∴不等式的解集为(－∞，－1)∪(0,1)．答案：(－∞，－1)∪(0,1)15．已知条件p ：|x ＋1|>2，条件q ：5x －6>x 2，则非p 是非q 的________条件．解析：∵p ：x <－3或x >1，∴¬p ：－3≤x ≤1.∵q ：2<x <3，∴¬q ：x ≤2或x ≥3，则¬p ⇒¬q .答案：充分不必要16．给出下列四个命题：①若a <b ，则a 2<b 2；②若a ≥b >－1，则a 1＋a ≥b 1＋b；③若正整数m 和n 满足：m <n ，则m (n －m )≤n 2；④若x >0，且x ≠1，则ln x ＋1ln x≥2. 其中真命题的序号是________．(请把真命题的序号都填上)解析：对于①，a ＝－2<b ＝－1，a 2>b 2，故①错．对于④，ln x 不一定为正数，0<x <1时，ln x ＋1ln x≤－2. x >1时，ln x ＋1ln x≥2，故④错．答案：②③三、解答题(本大题共6小题，共70分，17题10分，18～22题，每题12分．解答应写出文字说明，证明过程或演算步骤．)17．判断下列命题是否是全称命题或特称命题，若是，用符号表示，并判断其真假．(1)有一个实数α，sin2α＋cos2α≠1；(2)任何一条直线都存在斜率；(3)所有的实数a，b，方程ax＋b＝0恰有惟一解；(4)存在实数x0，使得1x20－x0＋1＝2.解：(1)是一个特称命题，用符号表示为：∃α∈R，sin2α＋cos2α≠1，是一个假命题．(2)是一个全称命题，用符号表示为：∀直线l，l存在斜率，是一个假命题．(3)是一个全称命题，用符号表示为：∀a，b∈R，方程ax＋b＝0恰有惟一解，是一个假命题．18．已知集合A＝{x|x2－5x＋6＝0}，B＝{x|mx＋1＝0}，且A∪B＝A，求由实数m的值组成的集合．解：A＝{x|x2－5x＋6＝0}＝{2,3}，∵A∪B＝A，∴B⊆A.①m＝0时，B＝Ø，B⊆A；②m≠0时，由mx＋1＝0，得x＝－1m.∵B⊆A，∴－1m∈A.∴－1m＝2，或－1m＝3，得m＝－12，或m＝－13.∴满足题意的m的集合为{0，－12，－13}．19．已知集合A＝{x|2－a≤x≤2＋a}，B＝{x|x2－5x＋4≥0}，(1)当a＝3时，求A∩B，A∪(∁U B)；(2)若A∩B＝Ø，求实数a的取值范围．解：(1)当a＝3时，A＝{x|－1≤x≤5}，B＝{x|x2－5x＋4≥0}＝{x|x≤1或x≥4}．∁U B＝{x|1<x<4}，A∩B＝{x|－1≤x≤1或4≤x≤5}，A∪(∁U B)＝{x|－1≤x≤5}．(2)当a<0时，A＝Ø，显然A∩B＝Ø，当a≥0时，A≠Ø，A＝{x|2－a≤x≤2＋a}，B＝{x|x2－5x＋4≥0}＝{x|x≤1或x≥4}．由A ∩B ＝Ø，得⎩⎪⎨⎪⎧2－a >12＋a <4，解得0≤a <1.故实数a 的取值范围是(－∞，1)．20．已知p ：x －5x －3≥2，q ：x 2－ax ≤x －a ，若¬p 是¬q 的充分条件，求实数a 的取值范围．解：由x －5x －3≥2，得x －1x －3≤0，∴1≤x <3. 由x 2－ax ≤x －a ，得(x －a )(x －1)≤0.(1)当a <1时，a ≤x ≤1；(2)当a ＝1时，x ＝1；(3)当a >1时，1≤x ≤a .∵¬p 是¬q 的充分条件，∴q 是p 的充分条件．设p 对应集合A ，q 对应集合B ，则A ＝{x |1≤x <3}且B ⊆A .当a <1时，B ＝{x |a ≤x ≤1}，B A ，不符合题意；当a ＝1时，B ＝{x |x ＝1}，B ⊆A ，符合题意；当a >1时，B ＝{x |1≤x ≤a }，若B ⊆A ，需1<a <3.综上，得1≤a <3.∴实数a 的取值范围是[1,3)．21．已知关于x 的不等式ax －5x 2－a<0的解集为M . (1)当a ＝4时，求集合M ；(2)若3∈M 且5∉M ，求实数a 的取值范围．解：(1)a ＝4时，不等式化为4x －5x 2－4<0，解得M ＝(－∞，－2)∪(54，2)． (2)a ≠25时，由⎩⎪⎨⎪⎧ 3∈M ，5∉M ，得⎩⎪⎨⎪⎧ 3a －59－a <0，5a －525－a ≥0∴a ∈[1，53]∪(9,25)；当a ＝25时，不等式为25x －5x 2－25<0⇒M ＝(－∞，－5)∪(15，5)．满足3∈M 且5∉M ，∴a ＝25满足条件．综上所述，得a 的取值范围是[1，53)∪(9,25]． 22．已知二次函数f (x )＝ax 2＋x ，若对任意x 1、x 2∈R ，恒有2f (x 1＋x 22)≤f (x 1)＋f (x 2)成立，不等式f (x )<0的解集为A .(1)求集合A ；(2)设集合B ＝{x ||x ＋4|<a }，若集合B 是集合A 的子集，求a 的取值范围．解：(1)对任意x 1、x 2∈R ，由f (x 1)＋f (x 2)－2f (x 1＋x 22) ＝12a (x 1－x 2)2≥0成立，要使上式恒成立，所以a ≥0.由f (x )＝ax 2＋x 是二次函数知a ≠0，故a >0.所以f (x )＝ax 2＋x ＝ax (x ＋1a)<0. 解得A ＝(－1a，0)． (2)B ＝{x ||x ＋4|<a }＝(－a －4，a －4)，因为集合B 是集合A 的子集，所以a －4≤0，且－a －4≥－1a. 解得－2－5≤a ≤－2＋ 5.又a >0，∴a 的取值范围为0<a ≤－2＋ 5.。

集合及简易逻辑解答题-含答案

-第II 卷〔非选择题〕1．:21p x -≤；()()2:30q x x m +-≤, 假设p 是q 的充分非必要条件，数m 的取值围。

【答案】m m ≤≥【解析】试题分析：解：根据题意，由于:21p x -≤；()()2:30q x x m +-≤则可知2:13,:3P x q x m ≤≤-≤≤，又因为p 是q 的充分非必要条件，则2,3p q m m m ⊂∴≥∴≤≥考点：集合的关系点评：主要是考察了集合的思想来判定充分条件的运用，属于根底题。

2．命题p ：函数2()24f x x ax =++有零点；命题q ：函数()(32)x f x a =-是增函数，假设命题p q ∧是真命题，数a 的取值围．【答案】2a ≤-【解析】试题分析：根据题意，由于命题p ：函数2()24f x x ax =++有零点；则可知判别式241602,2a a a ∆=-≥∴≥≤-或，对于命题q ：函数()(32)x f x a =-是增函数，则可知3-2a>1，a<1,由于命题p q ∧是真命题，则说明p,q 都是真命题，则可知参数a 的围是2a ≤-考点：复合命题的真值点评：主要是考察了方程的解以及函数单调性的运用，属于根底题。

3．集合{}2|230A x x x =--≥，{}|||1B x x a =-<,U R =．〔1〕当3a =时，求A B ；〔2〕假设U A C B ⊆，数a 的取值围．【答案】〔1〕{}|34AB x x =≤<。

〔2〕02a ≤≤。

【解析】试题分析：由题意得，{}|31A x x x =≥≤-或，{}|11B x a x a =-<<+。

4分〔1〕3a =时，{}|24B x x =<<， ∴{}|34A B x x =≤<。

8分〔2〕因为U A C B ⊆，所以1311a a +≤-≥-且，解之得02a ≤≤，所以实数a 的取值围是02a ≤≤。

集合与简易逻试题.docx

集合与简易逻辑2、设集合 A= {3, 5, 6, 8),集合 B= {4, 5, 7, 8},则等于()6、若集合 M={”一2VxVl}, B={X \0<X <2}9 则集合 AC\B=( )A. {”一lVxVl} B ・{”一2<xVl} C ・{”一2VxV2} D. {”0<xVl}7、集合 /1={”一1W A <2}, 〃={”A <1},贝Ij/in 〃=……() A. U|A -<1} B. {”一1W X W2} C. {”一1W X W1} D. {”一1W A<1} 8、设 P={x\x<l}9 (Z={x|z<4},则 P^Q=( )B. {x|-3<A <-1}C. {X |1<A <4)D. {X \ ~2<X <1}A. (0,2)B. [0,2] C ・{0,2} D ・{0,1,2} 13、集合 8{X £Z|0W A <3}, J/={xGR HW9},则 PCM 等于( )A. {1,2}B. {0,1,2}C. {”0WxV3}D. {”0WxW3}14. “自>0” 是 “|引>0” 的( )A. {34 5,6,7,8}B. {3,6} C ・{4,7} D. {5, 8}3.设全集 ^{xGbf|x<6},集合 J={1,3), 8= {3, 5), 则[BC4UQ 等于(A. (1,4)C. {2,4} B. (1,5)D. {2,5} 5、设集合A={x x —a <1, A ^R} , {x\ 1<-¥<5, •若 AQB= 则实数自的取值范圉是（A. {日I0&W6}B. Q|aW2,或 &4}C. {引 &W0,或 Q6}D. {a|2WaW4}IK 已知集合？1={”|”W2,, B= ,x^Z},则 AC\B=(A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件15、已知全集〃 =R,集合,0{”#-4WO},贝I] 等于（）A. U|-2<A <2）B. {”一2W/W2}C. {A |A <-2 或 X >2}D. {A |A ^-2 或17、对于数列{&}, “如>&|S=1,2,…）”是“⑹为递增数列”的（）A •必要不充分条件 B.充分不必要条件 C.充要条件 D.既不充分也不必要条件18、若集合 A={x\ |%|^L xWR}, 〃={y|y=也 ,贝 ij AC\B=( )A. {x|—lWxWl}B. [x\x^O]C. {x|OW 牙Wl}22.设 /^={X \X <4}9 片{”#V4},贝lj( )23.若集合 A= {0,1,2, 3}, )7= {1,2, 4},则集合 AUB=……( )A. {0, 1,2,3,4} B ・{1,2,3,4} C ・{1,2} D ・{0}24、设集合妇{1,2,4,8}, A'= {x\ x 是 2 的倍数}, MO -4/A ；V=()A. {2,4}B. {1,2,4}C. {2,4,8}D. {1,2,4,8)26、若 M={”x+l>0}, B={x\x~,3<0},贝 )A. (-1, +8) B ・(一8, 3) C ・(一1,3) D ・(1,3)在集合3, b, c,団上定义两种运算回n 如F ：2k 设全集 6= {1,2, 3,4,5},集合 H}, A-{1,3, 5}, 则；vnA. {1,3)B. {1,5)C. {3, 5) 0. {4,5} c.D.27.那么d 回3回』） = （）集合/={”一 1W/W2}, B=(x\x<\},则/n a =(已知集合"={1,3,5, 7, 9},力={1,5,7}, 则亚)对于实数弘b, c, u a ＞b n 是“曲〉b£”的（）D ：函数尸2”一2"在R 上为增函数,A ：函数y=2”+2"在R 上为减函数,A. B. b C. c D. d29. 设集合 A= (x| | x —a\ <1, xGR}, B= {”| x—b\ >2, xGR}. 若力则实数⑦0必满足（）A. |a+引 W3B. |a+》|M3C. |a —》|W3D. | a — b\ ^330.A. U|A >1)B. C ・{”1V X W2} D. {”1W X W2}31.A. {1,3}B. {3,7,9} C ・{3,5,9} D. {3,9}32、已知集合 A={x\ |%|^2, xGR}, B= {x\ SJ^4,用Z}, 则〃n 〃=（）A. (0, 2)B. L0, 2] C- {0, 2} D. {0, 1,2}33、 A.充分不必要条件氏必要不充分条件 C.充要条件 D.既不充分也不必要条件34、若集合 A ={X \ l^l^l}, B={X \X ^0}9 则 AQB 等于…(A. {”一1W/W1}B. [x\x^O} C ・{”OW/W1}35. 设｛/｝是等比数列，则“&＜氐＜5”是“数列｛加是递增数列”的（）A. 充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件 36.己知命题:则在命题 G ： PiVpj, P\f\p“ <73：（C^pi ） \Jpi 和 4： Q /\ （匚哥0 中，真命题是（）A ・ g ， SB ・ G ， S C- g ， q\ D. q“ g38、己知全集〃=R,集合3仁{”"一1丨冬2},则）A. U|-1<A <3）B. {H-1W/W3}C. {A |A <一1 或 />3}D. 1 或 ^3} 41、设非空集合S={x\m^^ 1}满足：当用S 时，有ZGS.给出如下三个命题：其中正确命题的个数是（）42.若集合 S={”1W/W3}, B={X \X >2}9 则月0〃等于( )已知日>0,则乂满足关于x 的方程ax=b 的充要条件是（）4仁集合 P= {^EZ|0^%<3}, Jf= {^GZ A. (1,2) B ・{0,1,2} C ・{1,2,3} □ ①若刃=1,则S= {1}；②若刃=——,E]则 W1W 1 ； A. 0B. 1C. 2D. 3A. {”2VxW3}B. {x|x$l} C ・{”2WxV3} D. {x\ x>2} 43. A. /ER, — a^~bx^ zBu. B ・C. A ^R,□ 一加一方D. {0, 1,2, 3}45.设集合 /1={U, K ) a] _ + _ = 1}, B=Ux, y ）|y=3Al ，则的子集的个数是（ Ea* — bxW充分非必要条件 B.必要非充分条件 C.非充分非必要条件 D.充要条件48己知力，〃均为集合片{1,3, 5, 7, 9}的子集，且m 吐⑶， QA= {9),则/=(49.已知集合 J/^{1,2,3}, A={2,3,4},则( )A. •“星yB.C. 〃nAJ{2,3}D. MUAJ{1,4}二、填空题(本大题共12题，共计55分)1、命题“对任何朋R, |x —2| + |x —4|>3”的否定是 __________________ ・2、若规定E=- {fii, az,…，$】o}的了集{$厶，al 2t …，也}为疋的第&个了集，其中&=2厶—1+2N —1 +…+ 2人一1,贝I 」(1) U,須是F 的第 _____________ 个子集；(2) 疋的第211个子集是 __________ .3、已知集合力={1,3,的，4 {3, 4},力U 4 {1,2, 3, 4}则刃= _________________ .4、命题“存在xER,使得H+2X +5 = 0”的否定是 ___________________ .5、设力={”北+1>0}, 4 {”/VO},贝lj AQB= ____________________ .6、设片{0,1,2,3},力={胆〃 |"+财=0},若I 」1力={1,2},则实数刃A ・4B ・3 C. 246.D ・1 “A>0” 是“ Ho ”成立的()A. 47. 下列命题中的假命题是()A.E^jrGR, 2x_1>0 B.逼]YUN 。