第05章习题解答
高等数学第05章 定积分及其应用习题详解

0
x 1 sin tdt 0dt 1 , 2
b a
f ( x)dx 在 几 何 上 表 示 由 曲 线 y f ( x) , 直 线
x a, x b 及 x 轴所围成平面图形的面积. 若 x a, b时,f ( x) 0, 则 b f ( x)dx 在几何 a
上表示由曲线 y f ( x) ,直线 x a, x b 及 x 轴所围平面图形面积的负值. (1)由下图(1)所示, 1 xdx ( A1 ) A1 0 .
n
2
i
i 1
n
2
1 1 1 1 1 n(n 1)(2n 1) = (1 )(2 ) 3 n 6 6 n n 1 1 2 当 0时 (即 n 时 ) ,由定积分的定义得: x d x = . 0 3
= 5. 利用定积分的估值公式,估计定积分
4 3
1 1
(4 x 4 2 x 3 5) dx 的值.
上任取一点 i 作乘积 f ( i ) xi 的和式:
n
f ( i ) xi c ( xi xi1 ) c(b a) ,
i 1 i 1
n
n
记 max{xi } , 则
1i n
b a
cdx lim f ( i ) xi lim c(b a) c(b a) .
x
0
(t 1)dt ,求 y 的极小值
解: 当 y x 1 0 ,得驻点 x 1 , y '' 1 0. x 1 为极小值点, 极小值 y (1)
( x 1)dx - 2
第05章习题解答
证明:因为单色点光源通过会聚透镜成像(或会聚)在光轴的 S 位置,所以根据会聚球面波的 性质,在 S 之前距离为 d 的物体之间的光场分布就近似为:
U 0 ( x, y )
a0 ikd i 2kd ( x02 y02 ) e e d
式中:a0 是与振幅有关的常数。假设物体的复振幅透过率函数为 t ( x0 , y0 ) ,则物体的透射光场 为:
sin
yf
f
则任意两个空间频率在后焦面上的间隔为:
3
y f f
由题意, 0.6μm ,最小空间频率 min 20mm 1 ,最大空间频率 max 200mm 1 ,当要 求它们之间对应的间隔为 y f 50mm ,则透镜焦距为:
f y f 50 103 mm 463mm 0.6 180
习题 5 参考解答
5.1
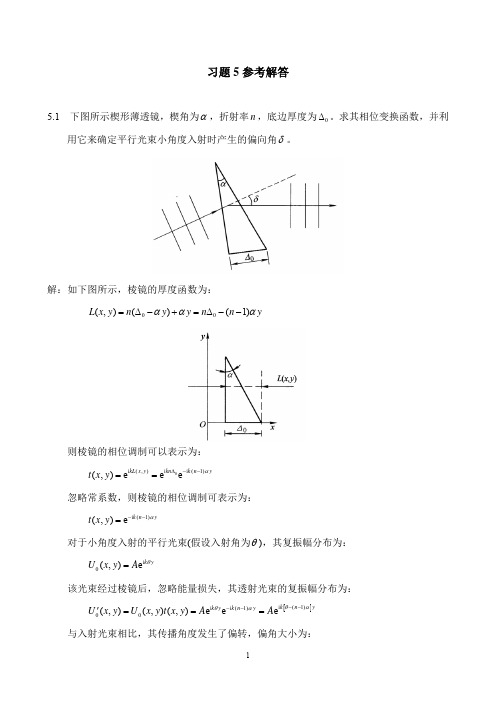
下图所示楔形薄透镜,楔角为 ,折射率 n ,底边厚度为 0 。求其相位变换函数,并利 用它来确定平行光束小角度入射时产生的偏向角 。
解:如下图所示,棱镜的厚度函数为: L( x, y ) n( 0 y ) y n 0 (n 1) y
Af , T 2 i d d d
i k ( 2 2 ) 2d
时,二次相位因子消除 。上式中, e
是一个焦距为 f d 的凸透镜的相位调制因子。
因此,只要在输出平面之前放置一个焦距为 f d 的凸/透镜,则输出光场的相位弯曲就可以 消除。
单色点光源 S 通过一个会聚透镜在光轴上 S ' 位置。 物体(透明片)位于透镜后方, 5.5 参看下图, 相距 S 的距离为 d ,被完全照明。求证物体的频谱出现在点光源的像平面上。
练习题答案05

第五章 概率、概率分布与临床决策练 习 题一、最佳选择题1.若事件A 和事件B 互不相容,则一定有( )。
A. P (A +B )=P (A )+P (B )B. P (A +B )=P (AB )C. P (AB )= P (A ) P (B )D. P (A │B )= P (A )E. P (B │A )= P (B )2.若人群中某疾病发生的阳性数X 服从二项分布,则从该人群随机抽取n 个人,阳性数X 不小于k 人的概率为( )。
A. P (k )+ P (k +1)+…+ P (n )B. P (k +1)+ P (k +2)+…+ P (n )C. P (0)+ P (1)+…+ P (k )D. P (0)+ P (1)+…+ P (k -1)E. P (1)+ P (2)+…+ P (k -1)3.Poisson 分布的标准差σ和平均数λ的关系是( )。
A.λ=σ B. λ<σ C. λ=σ2 D. λ= E. λ>σ4.当n 很大,二项分布在下列条件下可用Poisson 分布近似( )。
A. λπ≈nB. λ≈n X /C. λππ≈-)1(nD. λππ≈-)1(E. λππ≈-n /)1(5.对于任何两个随机变量X1和X2,一定有( )。
A. E (X 1+X 2)=E (X 1)+E (X 2)B. V (X 1+X 2)=V (X 1)+ V (X 2)C. E (X 1+X 2)=E (X 1)·E (X 2)D. V (X 1+X 2)=V (X 1)·V (X 2)E. E (X 1+X 2)=E (X 1X 2)二、问答题1.简述概率的统计定义。
2.举例说明医学观察结果中的离散型随机变量和连续型随机变量。
3.举例说明医学现象中的先验概率和后验概率。
4.简述二项分布的应用条件。
5.简述Poisson 分布的性质特征。
6.简述概率和概率分布在临床决策中的运用。
05工程力学(静力学和材料力学)第2版课后习题答案_范钦珊主编_第5章_轴向拉伸与压缩

eBook工程力学(静力学与材料力学)习题详细解答(教师用书)(第5章)范钦珊 唐静静2006-12-18第5章轴向拉伸与压缩5-1试用截面法计算图示杆件各段的轴力,并画轴力图。
解:(a)题(b)题(c)题(d)题习题5-1图F NxF N(kN)x-3F Nx A5-2 图示之等截面直杆由钢杆ABC 与铜杆CD 在C 处粘接而成。
直杆各部分的直径均为d =36 mm ,受力如图所示。
若不考虑杆的自重,试求AC 段和AD 段杆的轴向变形量AC l Δ和AD l Δ解:()()N N 22ssππ44BCAB BC AB ACF l F l l d dE E Δ=+33321501020001001030004294720010π36.××+××=×=××mm ()3N 232c100102500429475286mm π10510π364..CDCD AD AC F l l l d E ΔΔ×××=+=+=×××5-3 长度l =1.2 m 、横截面面积为1.10×l0-3 m 2的铝制圆筒放置在固定的刚性块上;-10F N x习题5-2图刚性板固定刚性板A E mkN习题5-4解图直径d =15.0mm 的钢杆BC 悬挂在铝筒顶端的刚性板上;铝制圆筒的轴线与钢杆的轴线重合。
若在钢杆的C 端施加轴向拉力F P ,且已知钢和铝的弹性模量分别为E s =200GPa ,E a =70GPa ;轴向载荷F P =60kN ,试求钢杆C 端向下移动的距离。
解: a a P A E l F u u ABB A −=−(其中u A = 0)∴ 935.0101010.11070102.1106063333=×××××××=−B u mm钢杆C 端的位移为33P 32s s601021100935450mm π20010154...BC C B F l u u E A ×××=+=+=×××5-4 螺旋压紧装置如图所示。
现代心理与教育统计学第05章习题解答

1. 解释相关系数时应注意什么?相关系数的值表示两个变量之间的关联程度,但只说明其大概的趋势,不存在精确的数值关系。
相关系数的数值大小,表示两个变量关联的强弱。
相关系数即使是1,也不能推出因果关系的结论。
要能区分虚假相关,不能仅依据相关系数的大小确定变量的相关。
在纯理论研究中,即使有很小的相关,如果在统计上有显著性,也能说明心理规律。
2. 假设两变量为线性关系,计算下列各种相关应用什么方法? (1)积差相关(2)斯皮尔曼等级相关(3)二列相关(4)多列相关(5)点二列相关(6)等级相关(斯皮尔曼或肯德尔和谐系数) 3.如何区别点二列和二列相关?主要看是人为的划分还是自然划分,而为为二列相关,自然为点二列相关 4.品质相关有几种?各种品质相关的条件? 主要有四分相关、φ相关、列联表相关 四分相关:当两个变量都是连续变量,且每一个变量的变化都被人为地分为两种类型时, 求两个变量之间的相关。
Φ相关:当两变量是真正(自然)的二分变量时,求两变量之间的相关。
列联相关:当两个变量都是计数数据时,求它们的相关。
5.用肯德尔和谐系数6.将数据带入公式计算得: 解7.此题的数据为非正态的等距数据,故用斯皮尔曼等级相关求相关系数8.解此题符合点二列相关的条件85=男X 91=女X 8.3=X S成绩与性别有关,即男女生的成绩存在显著差异 9.此题该用二列相关求解2.88=奇X 8.87=偶X 8.3=X S)(()819.02222=∑∑∑∑∑∑∑---=Y Y N X X N YX XY N r ()()794.011413=++⎥⎥⎦⎤⎢⎢⎣⎡-∙-=∑n n n R R n r y x R ()()972.011413=++⎥⎥⎦⎤⎢⎢⎣⎡-∙-=∑n n n R R n r y x R 789.04/1*8.38591=-=-=pq S X X r x q P pb在某题上及格或不及格对总分的影响不大,亦即该题几乎没有区分度。
大学物理基础教程答案第05章习题分析与解答

5-1 若理想气体的体积为V ,压强为p ,温度为T ,一个分子的质量为m ,k 为玻尔兹曼常数,R 为摩尔气体常数,则该理想气体的分子数为( )。
(A )PV m (B )PV kT (C )PV RT (D ) PVmT解:由N p nkT kT V ==得,pVN kT=,故选B 5-2 两个体积相同的容器,分别储有氢气和氧气(视为刚性气体),以1E 和2E 分别表示氢气和氧气的内能,若它们的压强相同,则( )。
(A )12E E = (B )12E E > (C )12E E < (D ) 无法确定 解:pV RT ν=,式中ν为摩尔数,由于两种气体的压强和体积相同,则T ν相同。
又刚性双原子气体的内能52RT ν,所以氢气和氧气的内能相等,故选A 5-3 两瓶不同种类的气体,分子平均平动动能相同,但气体分子数密度不同,则下列说法正确的是( )。
(A )温度和压强都相同 (B )温度相同,压强不同 (C )温度和压强都不同(D )温度相同,内能也一定相等解:所有气体分子的平均平动动能均为32kT ,平均平动动能相同则温度相同,又由p nkT =可知,温度相同,分子数密度不同,则压强不同,故选B5-4 两个容器中分别装有氦气和水蒸气,它们的温度相同,则下列各量中相同的量是( )。
(A )分子平均动能 (B )分子平均速率 (C )分子平均平动动能 (D )最概然速率解:分子的平均速率和最概然速率均与温度的平方根成正比,与气体摩尔质量的平方根成反比,两种气体温度相同,摩尔质量不同的气体,所以B 和D 不正确。
分子的平均动能2i kT ε=,两种气体温度相同,自由度不同,平均动能则不同,故A 也不正确。
而所有分子的平均平动动能均为k 32kT ε=,只要温度相同,平均平动动能就相同,如选C 5-5 理想气体的压强公式 ,从气体动理论的观点看,气体对器壁所作用的压强是大量气体分子对器壁不断碰撞的结果。
05《工程测量》第五章测量误差的基本知识作业与习题答案

dZ =
∂f ∂f ∂f dx1 + dx2 + L + dxn ∂x1 ∂x2 ∂xn
因 dZ、dx1、dx2、…都是微小的变量,可看成是相应的真误差ΔZ、Δx1、Δx2、…,因此上式 就相当于真误差关系式,系数
∂f 均为常数。 ∂xi
(3)求出中误差关系式。只要把真误差换成中误差的平方,系数也平方,即可直接写出中误差 关系式:
(
三、简答题
1.研究测量误差的目的和任务是什么? 由于在测量的结果中含有误差是不可避免的,因此,研究误差理论的目的不是为了去消灭误差, 而是要对误差的来源、性质及其产生和传播的规律进行研究,以便解决测量工作中遇到的一些实际 问题。例如:在一系列的观测值中,如何确定观测量的最可靠值;如何来评定测量的精度;以及如 何确定误差的限度等。所有这些问题,运用测量误差理论均可得到解决。 2.应用误差理论可以解决测量中的哪些问题? 在一系列的观测值中,如何确定观测量的最可靠值;如何来评定测量的精度;以及如何确定误 差的限度等。所有这些问题,运用测量误差理论均可得到解决。 3.系统误差和偶然误差有什么不同?在测量工作中对这二种误差应如何处理? 在相同的观测条件下,对某一未知量进行一系列观测,若误差的大小和符号保持不变,或按照 一定的规律变化,这种误差称为系统误差。例如水准仪的视准轴与水准管轴不平行而引起的读数误 差,与视线的长度成正比且符号不变;经纬仪因视准轴与横轴不垂直而引起的方向误差,随视线竖 直角的大小而变化且符号不变;距离测量尺长不准产生的误差随尺段数成比例增加且符号不变。这 些误差都属于系统误差。 系统误差主要来源于仪器工具上的某些缺陷;来源于观测者的某些习惯的影响,例如有些人习 惯地把读数估读得偏大或偏小;也有来源于外界环境的影响,如风力、温度及大气折光等的影响。 系统误差的特点是具有累积性,对测量结果影响较大,因此,应尽量设法消除或减弱它对测量 成果的影响。方法有两种:一是在观测方法和观测程序上采取一定的措施来消除或减弱系统误差的 影响。例如在水准测量中,保持前视和后视距离相等,来消除视准轴与水准管轴不平行所产生的误 差;在测水平角时,采取盘左和盘右观测取其平均值,以消除视准轴与横轴不垂直所引起的误差。 另一种是找出系统误差产生的原因和规律,对测量结果加以改正。例如在钢尺量距中,可对测量结 果加尺长改正和温度改正,以消除钢尺长度的影响。 在相同的观测条件下,对某一未知量进行一系列观测,如果观测误差的大小和符号没有明显的 规律性,即从表面上看,误差的大小和符号均呈现偶然性,这种误差称为偶然误差。例如在水平角 测量中照准目标时,可能稍偏左也可能稍偏右,偏差的大小也不一样;又如在水准测量或钢尺量距 中估读毫米数时,可能偏大也可能偏小,其大小也不一样,这些都属于偶然误差。 产生偶然误差的原因很多,主要是由于仪器或人的感觉器官能力的限制,如观测者的估读误差、 照准误差等,以及环境中不能控制的因素如不断变化着的温度、风力等外界环境所造成。 偶然误差在测量过程中是不可避免的,从单个误差来看,其大小和符号没有一定的规律性,但 对大量的偶然误差进行统计分析,就能发现在观测值内部却隐藏着一种必然的规律,这给偶然误差 的处理提供了可能性。 4.偶然误差有哪些特性? 在相同的观测条件下,对某一未知量进行一系列观测,如果观测误差的大小和符号没有明显的 规律性,即从表面上看,误差的大小和符号均呈现偶然性,这种误差称为偶然误差。 偶然误差具有如下四个特性:
力学答案——漆安慎,05章

5.1.3
一个具有单位质量的质点在力场
ˆ + (12t − 6) ˆ F = (3t 2 − 4t )i j 中运动,其中 t 是时间。该质点在 t=0
时位于原点,且速度为零。求 t=2 时该质点所受的对原点的力矩。 解:据质点动量定理的微分形式, Fdt = d (mv ) = dv ( m = 1)
2
(2)'
解此方程组,求得:v0 ≈1.3 m/s
v ≈0.33 m/s
ˆ + b sin ω tˆ ˆ + bω cos ω tˆ L = r × mv = (a cos ω ti j ) × m(−aω sin ω ti j) ˆ ˆ×i ˆ= ˆ ˆ× ˆ ˆ) = k ∵i j× ˆ j = 0, i j= ˆ j × (−i ˆ + mabω sin 2 ω tk ˆ = mabω k ˆ ∴ L = mabω cos 2 ω tk
∵ τ = r × F = r × m a = r × m(−ω r ) = −mω r × r = 0 ,∴该质点 角动量守恒。 5.1.9 质量为 200g 的小球 v0 B 以弹性绳在光滑水平面上与固 A B 30º 定点 A 相连。弹性绳的劲度系数 为 8 N/m,其自由伸展长度为 600mm.最初小球的位置及速度 v0 如图所示。 当小球的速率变为 v 时,
5.1.8
一个质量为 m 的质点在 o-xy 平面内运动, 其位置矢量为
ˆ + b sin ω t ˆ r = a cos ω t i j ,其中 a、b 和ω是正常数,试以运动学
和动力学观点证明该质点对于坐标原点角动量守恒。 证明:
另外,在此过程中,只有保守内力(绳的弹力)做功,因而能量守恒,
