第05章习题解答
高等数学第05章 定积分及其应用习题详解

0
x 1 sin tdt 0dt 1 , 2
b a
f ( x)dx 在 几 何 上 表 示 由 曲 线 y f ( x) , 直 线
x a, x b 及 x 轴所围成平面图形的面积. 若 x a, b时,f ( x) 0, 则 b f ( x)dx 在几何 a
上表示由曲线 y f ( x) ,直线 x a, x b 及 x 轴所围平面图形面积的负值. (1)由下图(1)所示, 1 xdx ( A1 ) A1 0 .
n
2
i
i 1
n
2
1 1 1 1 1 n(n 1)(2n 1) = (1 )(2 ) 3 n 6 6 n n 1 1 2 当 0时 (即 n 时 ) ,由定积分的定义得: x d x = . 0 3
= 5. 利用定积分的估值公式,估计定积分
4 3
1 1
(4 x 4 2 x 3 5) dx 的值.
上任取一点 i 作乘积 f ( i ) xi 的和式:
n
f ( i ) xi c ( xi xi1 ) c(b a) ,
i 1 i 1
n
n
记 max{xi } , 则
1i n
b a
cdx lim f ( i ) xi lim c(b a) c(b a) .
x
0
(t 1)dt ,求 y 的极小值
解: 当 y x 1 0 ,得驻点 x 1 , y '' 1 0. x 1 为极小值点, 极小值 y (1)
( x 1)dx - 2
《管理学》习题与答案——第05章 管理伦理

第五章管理伦理一、教学要点1、伦理的功利观的基本观点。
2、伦理的权利观的基本观点。
3、公平理论伦理观的基本观点。
4、综合社会契约理论观的基本观点。
5、伦理管理的特征。
6、影响管理伦理的因素。
7、道德发展所经历的三层次和六阶段的基本内容。
8、改善伦理行为的途径。
9、伦理行为的具体体现。
10、关键名词:伦理的功利观、伦理的权利观、公平理论伦理观、综合社会契约理论观、道德发展阶段、个人特征、自我强度、控制中心、组织文化、伦理守则、决策规则二、习题(一)填充题1. 有关伦理的观点包括_________,__________,_____________,_____________。
2.伦理的功利观认为决策要完全依据其___________或__________做出。
3.功利主义的目标是为尽可能多的人提高尽可能多的___________。
4.伦理的权力观认为决策要在尊重和保护_______________的前提下作出。
5.合乎伦理的管理不仅从组织自身角度更从_____________角度看问题。
6.合乎伦理的管理不仅把人看成___________,更把人看作___________。
7.合乎伦理的管理以_______________为行为导向。
8.道德发展要经历________,___________,_______________三个层次。
9.人们发现有两个个性变量影响个人行为,这两个变量是_________,____________。
10.综合社会契约理论观主张把__________和__________两种方法并入商业伦理中。
11. 企业的伦理行为可以体现在__________,__________,___________,__________,_____________,____________等方面。
12.合乎伦理的管理以组织的______________为行为导向。
13.正式的规章制度可以降低模糊程度,从而__________伦理行为的产生。
练习题答案05

第五章 概率、概率分布与临床决策练 习 题一、最佳选择题1.若事件A 和事件B 互不相容,则一定有( )。
A. P (A +B )=P (A )+P (B )B. P (A +B )=P (AB )C. P (AB )= P (A ) P (B )D. P (A │B )= P (A )E. P (B │A )= P (B )2.若人群中某疾病发生的阳性数X 服从二项分布,则从该人群随机抽取n 个人,阳性数X 不小于k 人的概率为( )。
A. P (k )+ P (k +1)+…+ P (n )B. P (k +1)+ P (k +2)+…+ P (n )C. P (0)+ P (1)+…+ P (k )D. P (0)+ P (1)+…+ P (k -1)E. P (1)+ P (2)+…+ P (k -1)3.Poisson 分布的标准差σ和平均数λ的关系是( )。
A.λ=σ B. λ<σ C. λ=σ2 D. λ= E. λ>σ4.当n 很大,二项分布在下列条件下可用Poisson 分布近似( )。
A. λπ≈nB. λ≈n X /C. λππ≈-)1(nD. λππ≈-)1(E. λππ≈-n /)1(5.对于任何两个随机变量X1和X2,一定有( )。
A. E (X 1+X 2)=E (X 1)+E (X 2)B. V (X 1+X 2)=V (X 1)+ V (X 2)C. E (X 1+X 2)=E (X 1)·E (X 2)D. V (X 1+X 2)=V (X 1)·V (X 2)E. E (X 1+X 2)=E (X 1X 2)二、问答题1.简述概率的统计定义。
2.举例说明医学观察结果中的离散型随机变量和连续型随机变量。
3.举例说明医学现象中的先验概率和后验概率。
4.简述二项分布的应用条件。
5.简述Poisson 分布的性质特征。
6.简述概率和概率分布在临床决策中的运用。
现代心理与教育统计学第05章习题解答

1. 解释相关系数时应注意什么?相关系数的值表示两个变量之间的关联程度,但只说明其大概的趋势,不存在精确的数值关系。
相关系数的数值大小,表示两个变量关联的强弱。
相关系数即使是1,也不能推出因果关系的结论。
要能区分虚假相关,不能仅依据相关系数的大小确定变量的相关。
在纯理论研究中,即使有很小的相关,如果在统计上有显著性,也能说明心理规律。
2. 假设两变量为线性关系,计算下列各种相关应用什么方法? (1)积差相关(2)斯皮尔曼等级相关(3)二列相关(4)多列相关(5)点二列相关(6)等级相关(斯皮尔曼或肯德尔和谐系数) 3.如何区别点二列和二列相关?主要看是人为的划分还是自然划分,而为为二列相关,自然为点二列相关 4.品质相关有几种?各种品质相关的条件? 主要有四分相关、φ相关、列联表相关 四分相关:当两个变量都是连续变量,且每一个变量的变化都被人为地分为两种类型时, 求两个变量之间的相关。
Φ相关:当两变量是真正(自然)的二分变量时,求两变量之间的相关。
列联相关:当两个变量都是计数数据时,求它们的相关。
5.用肯德尔和谐系数6.将数据带入公式计算得: 解7.此题的数据为非正态的等距数据,故用斯皮尔曼等级相关求相关系数8.解此题符合点二列相关的条件85=男X 91=女X 8.3=X S成绩与性别有关,即男女生的成绩存在显著差异 9.此题该用二列相关求解2.88=奇X 8.87=偶X 8.3=X S)(()819.02222=∑∑∑∑∑∑∑---=Y Y N X X N YX XY N r ()()794.011413=++⎥⎥⎦⎤⎢⎢⎣⎡-∙-=∑n n n R R n r y x R ()()972.011413=++⎥⎥⎦⎤⎢⎢⎣⎡-∙-=∑n n n R R n r y x R 789.04/1*8.38591=-=-=pq S X X r x q P pb在某题上及格或不及格对总分的影响不大,亦即该题几乎没有区分度。
大学物理基础教程答案第05章习题分析与解答

5-1 若理想气体的体积为V ,压强为p ,温度为T ,一个分子的质量为m ,k 为玻尔兹曼常数,R 为摩尔气体常数,则该理想气体的分子数为( )。
(A )PV m (B )PV kT (C )PV RT (D ) PVmT解:由N p nkT kT V ==得,pVN kT=,故选B 5-2 两个体积相同的容器,分别储有氢气和氧气(视为刚性气体),以1E 和2E 分别表示氢气和氧气的内能,若它们的压强相同,则( )。
(A )12E E = (B )12E E > (C )12E E < (D ) 无法确定 解:pV RT ν=,式中ν为摩尔数,由于两种气体的压强和体积相同,则T ν相同。
又刚性双原子气体的内能52RT ν,所以氢气和氧气的内能相等,故选A 5-3 两瓶不同种类的气体,分子平均平动动能相同,但气体分子数密度不同,则下列说法正确的是( )。
(A )温度和压强都相同 (B )温度相同,压强不同 (C )温度和压强都不同(D )温度相同,内能也一定相等解:所有气体分子的平均平动动能均为32kT ,平均平动动能相同则温度相同,又由p nkT =可知,温度相同,分子数密度不同,则压强不同,故选B5-4 两个容器中分别装有氦气和水蒸气,它们的温度相同,则下列各量中相同的量是( )。
(A )分子平均动能 (B )分子平均速率 (C )分子平均平动动能 (D )最概然速率解:分子的平均速率和最概然速率均与温度的平方根成正比,与气体摩尔质量的平方根成反比,两种气体温度相同,摩尔质量不同的气体,所以B 和D 不正确。
分子的平均动能2i kT ε=,两种气体温度相同,自由度不同,平均动能则不同,故A 也不正确。
而所有分子的平均平动动能均为k 32kT ε=,只要温度相同,平均平动动能就相同,如选C 5-5 理想气体的压强公式 ,从气体动理论的观点看,气体对器壁所作用的压强是大量气体分子对器壁不断碰撞的结果。
运营管理第6版习题与参考答案_第05章

习题与参考答案第05章一、名词解释1、选址规划答案:定工厂或服务设施的位置,涉及两个层面:第一个是选位,即选择一定的区域,如国家、地区、省市等;第二个层面是定址,即选择工厂或服务设施的具体地址。
答案解析:略。
难易程度:易。
知识点:选址规划。
2、因素评分法答案:对影响决策问题的主要因素进行评分,并根据其影响决策问题的重要性,对备选方案进行综合评分,在此基础上选择最佳决策方案。
答案解析:略。
难易程度:中。
知识点:因素评分法。
3、重心法答案:根据重心在物理上的这种含义,借助重心来辅助选择经济中心(如物流配送中心、仓储中心、销售中心、社区医院等)的地理位置,使从该经济中心到各个配送目的地的总的配送成本最低。
答案解析:略。
难易程度:中。
知识点:重心法。
二、单选题1、在用重心法进行社区医院选址时,计算重心位置时所用的权重应该是()。
A. 距离B. 人口C. 物资量D. 成本答案:B。
答案解析:略。
难易程度:中。
知识点:重心法。
三、多选题无。
四、判断题1、运输模型中物资配送方案的“唯一性”是指理论上只有一个配送方案是最优的。
答案:错。
答案解析:这里的“唯一性”是指最低费用是唯一的。
难易程度:难。
知识点:物资配送方案的“唯一性”。
2、为了科学选址,会引入定量方法。
要选择的位置一定是定量方法所计算出来的最优解。
答案:错。
答案解析:实际中不可能把所有的因素都纳入到定量模型中,用定量方法所计算出来的最优解往往是不可行的。
难易程度:难。
知识点:因素评分法、重心法、运输模型。
五、填空题1、需要选址的情况有三种,即:()、()、()。
答案:新建、增加、搬迁。
答案解析:略。
难易程度:中。
知识点:选址规划的可能性。
六、简答题1、简述需要进行选址的情况。
答案:(1)完全新建。
(2)保留现址并增加新址。
(3)放弃现址而迁至新址。
答案解析:略。
难易程度:易。
知识点:企业选址的可能性。
2、简述选址规划的重要性。
答案:(1)影响企业的竞争力。
力学答案——漆安慎,05章

5.1.3
一个具有单位质量的质点在力场
ˆ + (12t − 6) ˆ F = (3t 2 − 4t )i j 中运动,其中 t 是时间。该质点在 t=0
时位于原点,且速度为零。求 t=2 时该质点所受的对原点的力矩。 解:据质点动量定理的微分形式, Fdt = d (mv ) = dv ( m = 1)
2
(2)'
解此方程组,求得:v0 ≈1.3 m/s
v ≈0.33 m/s
ˆ + b sin ω tˆ ˆ + bω cos ω tˆ L = r × mv = (a cos ω ti j ) × m(−aω sin ω ti j) ˆ ˆ×i ˆ= ˆ ˆ× ˆ ˆ) = k ∵i j× ˆ j = 0, i j= ˆ j × (−i ˆ + mabω sin 2 ω tk ˆ = mabω k ˆ ∴ L = mabω cos 2 ω tk
∵ τ = r × F = r × m a = r × m(−ω r ) = −mω r × r = 0 ,∴该质点 角动量守恒。 5.1.9 质量为 200g 的小球 v0 B 以弹性绳在光滑水平面上与固 A B 30º 定点 A 相连。弹性绳的劲度系数 为 8 N/m,其自由伸展长度为 600mm.最初小球的位置及速度 v0 如图所示。 当小球的速率变为 v 时,
5.1.8
一个质量为 m 的质点在 o-xy 平面内运动, 其位置矢量为
ˆ + b sin ω t ˆ r = a cos ω t i j ,其中 a、b 和ω是正常数,试以运动学
和动力学观点证明该质点对于坐标原点角动量守恒。 证明:
另外,在此过程中,只有保守内力(绳的弹力)做功,因而能量守恒,
05第五章扭转习题解析
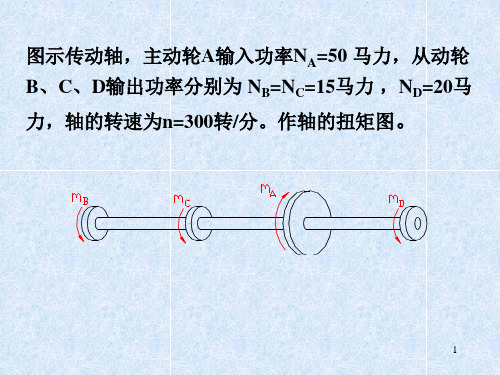
力,轴的转速为n=300转/分。作轴的扭矩图。
1
解:
NA 50 m A 7024 7024 1170 N m n 300
NB 15 mB mC 7024 7024 351 N m n 300 NC 20 mD 7024 7024 468 N m n 300
d 63.3mm
10
m
得 D 791 . mm
已知直径d=50mm的钢制圆轴在扭转角为 6°时,轴
内最大剪应力等于90MPa,G=80GPa。求该轴长度。
Tl GIp
T Wt
解:
(1)
max
( 2)
(1) 得: ( 2)
G Ip l max Wt
2.33 m
6
15
解:外管与内轴承受的扭矩相等,设为T
m
ml Tl Tl G I p内 G I p内 G I p外
16
例:两端固定的圆截面等直杆AB,在截面
C受外力偶矩m作用,试求杆两端的支座反力
偶矩。
17
解:
静力平衡方程为: m A mB m 变形协调条件为: AB AC CB 0
12
解:由
d l 2
2 2 300 40
2 得 l d
30
max G 2.7 2
m max Wt
180
0.09425 MPa
0.09425 106
0.04 3
16
118 . Nm
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
证明:因为单色点光源通过会聚透镜成像(或会聚)在光轴的 S 位置,所以根据会聚球面波的 性质,在 S 之前距离为 d 的物体之间的光场分布就近似为:
U 0 ( x, y )
a0 ikd i 2kd ( x02 y02 ) e e d
式中:a0 是与振幅有关的常数。假设物体的复振幅透过率函数为 t ( x0 , y0 ) ,则物体的透射光场 为:
sin
yf
f
则任意两个空间频率在后焦面上的间隔为:
3
y f f
由题意, 0.6μm ,最小空间频率 min 20mm 1 ,最大空间频率 max 200mm 1 ,当要 求它们之间对应的间隔为 y f 50mm ,则透镜焦距为:
f y f 50 103 mm 463mm 0.6 180
习题 5 参考解答
5.1
下图所示楔形薄透镜,楔角为 ,折射率 n ,底边厚度为 0 。求其相位变换函数,并利 用它来确定平行光束小角度入射时产生的偏向角 。
解:如下图所示,棱镜的厚度函数为: L( x, y ) n( 0 y ) y n 0 (n 1) y
Af , T 2 i d d d
i k ( 2 2 ) 2d
时,二次相位因子消除 。上式中, e
是一个焦距为 f d 的凸透镜的相位调制因子。
因此,只要在输出平面之前放置一个焦距为 f d 的凸/透镜,则输出光场的相位弯曲就可以 消除。
单色点光源 S 通过一个会聚透镜在光轴上 S ' 位置。 物体(透明片)位于透镜后方, 5.5 参看下图, 相距 S 的距离为 d ,被完全照明。求证物体的频谱出现在点光源的像平面上。
测量透镜后焦面上的强度分布。假定 D d 。
(1) 写出所测强度准确代表物体功率谱的最大空间频率的表达式,并计算 D 6 cm ,
d 2.5 cm,焦距 f 50 cm 以及 0.6μm 时,这个频率的数值(单位:/mm)
(2) 在多大的频率以上测得的频谱为零?尽管物体可以在更高的频率上有不为零的频率
a0 ikd i 2kd ( x02 y02 ) ( x0 , y0 ) U 0 ( x0 , y0 )t ( x0 , y0 ) e e U0 t ( x0 , y0 ) d
根据傅里叶变换形式的菲涅耳衍射公式,可计算出 S 位置处的场分布为
U ( x, y )
k 2 2 y0 ) i ( x0 eikd i 2kd ( x2 y 2 ) ( x0 , y0 )e 2 d F U 0 e i d
x y , 2 a 2 a
由傅里叶变换的性质,可知:
x y F T1 2 , 2 2a 2a F t2 ( x2 , y2 )
t ( x, y )
x y , 2 a 2 a
x y , 2 a 2 a
2
y2 )
eik y
上式应用在傍轴近似下,有 tan 。
由 5.1 题的分析可知,对于楔角为 、折射率为 n 的棱镜,共相位变换函数为:
2
t ( x, y ) e ik ( n 1) y
则透射光波的复振幅分布为:
i (x z0 i a ( x, y ) U 0 ( x, y )t ( x, y ) 0 eikz0 e 2 z0 e 2 z0 U0 z0 i (x z0 i a 0 eikz0 e 2 z0 e 2 z0 z0 k
则棱镜的相位调制可以表示为: t ( x, y ) eikL ( x , y ) eikn0 e ik ( n 1) y 忽略常系数,则棱镜的相位调制可表示为: t ( x, y ) e ik ( n 1) y 对于小角度入射的平行光束(假设入射角为 ),其复振幅分布为:
2
ห้องสมุดไป่ตู้
k
2
k
2
y2 )
eik y e ik ( n 1) y
k 2 2 i 2 z [( x ( y z0 ) ] 0
k
2
y2 )
e
ik ( n 1) y
1 a ikz0 0e z0
2 2
2
e
式中: (n 1) 。 因此,透射光波还是一个球面波,其虚像的位置为 S (0, z0 , z0 ) 。
1
(n 1)
5.2 见下图,点光源 S 与楔形薄透镜距离为 z0 ,它发出倾角为 的傍轴球面波照射棱镜,棱镜
楔角为 ,折射率 n 。求透射光波的特征和 S 点虚像的位置。
解:如下图所示,假设点光源 S 位于 y z 平面内。 S 点的坐标为 (0, z0 tan , z0 ) ,则从点光 源 S 发出的倾角为 的球面波在 x y 平面上的复振幅分布可近似表示为:
y x , T2 2a 2a
略去常系数及积分号前的相位因子,则最终在观察屏上衍射图样的复振幅分布正比于 t1 和 t2 变换式的卷积
y x U ( x, y ) t ( x, y ) * T2 , 2a 2a
6
5.7 一个被直径为 d 的圆形孔径的物函数 U 0 , 把它放在直径为 D 的圆形会聚透镜的前焦面上,
U 0 ( x, y ) Aeik y
该光束经过棱镜后,忽略能量损失,其透射光束的复振幅分布为:
( x, y ) U 0 ( x, y )t ( x, y ) Aeik y e ik ( n 1) y Ae U0
ik ( n 1) y
与入射光束相比,其传播角度发生了偏转,偏角大小为:
t1 ( x1 , y1 ) 的傅里叶变换。因此,在透明 t2 ( x2 , y2 ) 之前光场分布为
5
2 2 1 i 2 f1 ( x2 y2 ) x2 y2 U 2 ( x2 , y2 ) e T1 , i f1 f1 f1
k
x y 式中: T1 2 , 2 F{t1 ( x1 , y1 )} x2 y2 。经过透明片 t2 ( x2 , y2 ) 和透镜 L2 后的透射光场为: , f1 f1 f1 f1
( x2 , y2 ) U 2 ( x2 , y2 )t2 ( x2 , y2 )e U2
k k i k 2 2 ( x2 y2 ) 2 f2
2 2 2 2 1 i 2 f1 ( x2 y2 ) i 2 f 2 ( x2 y2 ) x2 y2 e e T1 , t2 ( x2 , y2 ) i f1 f1 f1
eikf1 i 2 f1 ( x e U ( x, y ) i f1 1 i 2 f1 ( x e ( f1 ) 2
k
2
k
2
y2 )
k 2 2 i ( x2 ) y2 2 f1 ( x2 , y2 )e F U 2
x
f1
,
将 f1 2a, f 2 a 的关系代入上式,上式就可简化为:
( x2 , y2 ) U2
2 2 1 i 2 f1 ( x2 y2 ) x2 y2 e T1 , t2 ( x2 , y2 ) i f1 f1 f1
k
利用傅里叶变换形式的菲涅耳衍射方程, 则得到距 L2 后 2a f1 处观察屏上菲涅耳衍射图 样的复振幅分布为:
测得频谱为零。 如下图所示,当传播方面倾角超过 M 时,该平面波分量正是这种情况。在小角度的情况 下,
D d Dd M 2 2 , 2f f
( D f , d f )
7
相应的空间频率为:
M
sin M
i [x a U 0 ( x, y ) 0 eikz0 e 2 z0 z0 k
2
( y z0 tan ) 2 ]
i [x a 0 eikz0 e 2 z0 z0
k
2
( y z0 )2 ]
a0 ikz0 i 2 z0 z0 i 2 z0 ( x e e e z0
k
2
k
分量。 解:(1) 透镜有限孔径对于物面空间频率成分传播的限制称为渐晕。仅当某一方向上的平面 波分量不受拦阻地通过透镜时,在后焦面上相应会聚点测得的强度才准确代表物相应空间频 率的傅里叶谱的模的平方。 如下图所示,在小角度情况下,满足这一要求的平面波分量的传播方向 角最大为:
D d 2 2 Dd , 0 2f f
5.4 对于下图所示的变换光路,为了消除在物体频谱上附加的相位弯曲,可在紧靠输出平面
之前放置一个透镜。问这个透镜的类型以及焦距如何选取?
解:如题图所示,在忽略透镜孔径的影响下,输出平面上得到的光场分布为:
Af i 2kd ( 2 2 ) e , U ( , ) T i d 2 d d
x
d
,
y
d
a0 i 2kd ( x2 y 2 ) a0 i 2kd ( x2 y 2 ) x y F t ( x0 , y0 ) x , y T e e , i d 2 i d 2 d d d d
可见在点光源的像面上的复振幅分布正比于物体的傅里叶变换, 但是变换式之前存在二次 相位因子,这使物体频谱产生了相位弯曲。
5.6 如下图所示,透明片 t1 ( x1 , y1 ) 和 t2 ( x2 , y2 ) 分别紧贴在焦距为 f1 2a, f 2 a 的两个透镜之
前。透镜 L1 , L2 和观察屏三者间隔相等,都等于 2a 。如果用单位振幅单色平面波垂直照 明,求观察零上的复振幅分布。
