4.4.2正方形
47013 2新国际讲解(射线检测) 第二部分

增加了有效评定区搭接的技术要求,修 改了定位标记和识别标记的放置原则
5.5.5 有效评定区搭接 5.5.5.1 焊缝进行全部射线检测时,采取的曝光次数和有效评定 区的重叠应能保证检测到被检测区的整个体积范围。 5.5.5.2 如果采用暗盒直接搭接透照的方式,也应保证整个有效 评定区的底片黑度满足5.16.1的要求。 5.13.3……检测区标记采取的方式能够清晰标识检测区范围即可。 5.13.6 定位标记应放在工件上,其摆放应符合附录J的规定。 由于结构原因,定位标记需要放置于胶片侧时,检测记录和报告 应标注实际的评定范围.
修改和增加了部分规范性引用文件
增加了射线检测专用术语和定义的内容
• 透照厚度比K :一次透照长度范围内射线束穿过母材的最大 厚度和最小厚度之比。
• 一次透照长度 :符合标准规定的单次曝光有效检测长度。 • 底片评定范围:本部分规定底片上必须观察和评定的范围。 • 缺陷评定区 :在质量分级评定时,为评价缺陷数量和密集程
射线,如:Ir192、Co60等。 • 3、滤光板作用:减少康普顿效应的散射线,降低散
射比。(暗盒中的铅箔厚度一般比较薄,能够阻挡 光电效应的低能散射线,但对阻挡康普顿效应的中 等能量散射线不够有力,滤光板厚度0.5-2mm,对 阻挡康普顿效应的散射线比较有力)。
加滤光板的射线检测灵敏度试验
新标准关于滤光板使用的规定
老标准无此规定。
增加了内偏心透照时透照次数计算公式
一次透照长度: a) 一次透照长度应以透照厚度比K进行控制。……通 过K值确定整条环向对接焊接接头所需的透照次数可参 照附录F的曲线图确定。
正方形的知识总结(两篇)

引言概述:正方形是一种几何形状,具有许多独特的属性和特征。
本文将深入探讨正方形的知识总结,从正方形的定义和性质,到相关的数学公式和应用,并给出一些实际生活中与正方形相关的例子。
通过本文的阐述,读者将能更深入地理解和运用正方形的概念。
正文内容:1.正方形的定义和性质1.1正方形的定义:介绍正方形是一种四边相等、四个角都是直角的特殊四边形。
1.2正方形的性质:阐述正方形具有对称性、对角线相等、对角线垂直等性质,并给出证明。
2.正方形的周长和面积公式2.1周长公式的推导:详细介绍如何推导正方形的周长公式。
2.2面积公式的推导:详细介绍如何推导正方形的面积公式。
2.3周长和面积公式的比较:比较周长和面积公式之间的关系和特点,解释为什么周长公式是面积公式的一半。
3.正方形的应用3.1图形的分类:介绍几何图形的分类,重点讲述正方形在图形分类中的作用。
3.2建筑和设计中的应用:介绍正方形在建筑和设计中的应用,比如正方形的房间布局,正方形的花园设计等。
3.3数学问题的解决:解释如何使用正方形的性质和公式来解决一些数学问题,例如寻找最大正方形的面积等。
4.正方形的实际应用举例4.1城市规划:举例说明正方形在城市规划中的应用,如正方形的街区设计,正方形的公园规划等。
4.2网格和排版设计:介绍正方形在网格和排版设计中的应用,如正方形的网格布局,正方形的页面排版等。
4.3绘画和艺术:探讨正方形在绘画和艺术中的应用,如正方形的画框设计,正方形的艺术装饰等。
4.4数字图像处理:介绍正方形在数字图像处理中的应用,如正方形的像素处理,正方形的图像编码等。
4.5生活中的实际应用:举例说明正方形在日常生活中的实际应用,如正方形的餐桌布置,正方形的画框选择等。
5.结论通过本文的详细阐述,我们可以总结出正方形的定义和性质,掌握正方形的周长和面积公式,并了解了正方形在实际应用中的重要性。
正方形作为一种几何形状,在数学、建筑、设计、绘画等领域都具有广泛的应用,为我们的生活带来了便利和美感。
华师大版数学七年级上册《4.4平面图形》说课稿

华师大版数学七年级上册《4.4 平面图形》说课稿一. 教材分析华师大版数学七年级上册《4.4 平面图形》这一节的内容,主要围绕着平面图形的性质和判定进行展开。
本节课的内容是学生学习了平面几何的基础知识之后,进一步深入研究平面图形的特点和规律。
通过本节课的学习,学生能够掌握平面图形的性质和判定方法,提高解决几何问题的能力。
教材从简单的图形入手,逐步引出平面图形的性质和判定定理。
例如,通过观察和操作,学生可以发现平行四边形的性质,掌握平行四边形的判定方法。
接着,教材又引导学生探究矩形、菱形、正方形的性质和判定,使学生能够灵活运用这些性质和判定方法解决实际问题。
此外,教材还通过丰富的例题和练习题,帮助学生巩固所学知识,提高解题能力。
学生在学习过程中,可以通过自主探究、合作交流的方式,深入理解平面图形的性质和判定,培养逻辑思维能力和创新意识。
二. 学情分析七年级的学生已经具备了一定的几何基础,对于一些基本的平面图形有一定的了解。
但是,他们对平面图形的性质和判定方法的认识还比较模糊,需要通过具体的学习和实践来进一步掌握。
此外,学生在学习过程中可能存在对几何图形直观感知不足、逻辑思维能力有待提高等问题。
针对学生的实际情况,教师在教学过程中要注重启发引导,让学生通过观察、操作、思考、交流等方式,自主探索平面图形的性质和判定方法。
同时,要关注学生的个体差异,给予不同程度的学生个性化的指导,使他们在原有基础上得到提高。
三. 说教学目标1.知识与技能目标:使学生掌握平行四边形、矩形、菱形、正方形的性质和判定方法,能够灵活运用这些性质和判定方法解决实际问题。
2.过程与方法目标:通过观察、操作、思考、交流等过程,培养学生的逻辑思维能力和创新意识。
3.情感态度与价值观目标:激发学生学习几何的兴趣,培养他们克服困难、解决问题的信心和勇气。
四. 说教学重难点1.教学重点:平行四边形、矩形、菱形、正方形的性质和判定方法。
2.教学难点:对平面图形性质和判定方法的理解和运用。
学而思-第四讲-长方体和正方体
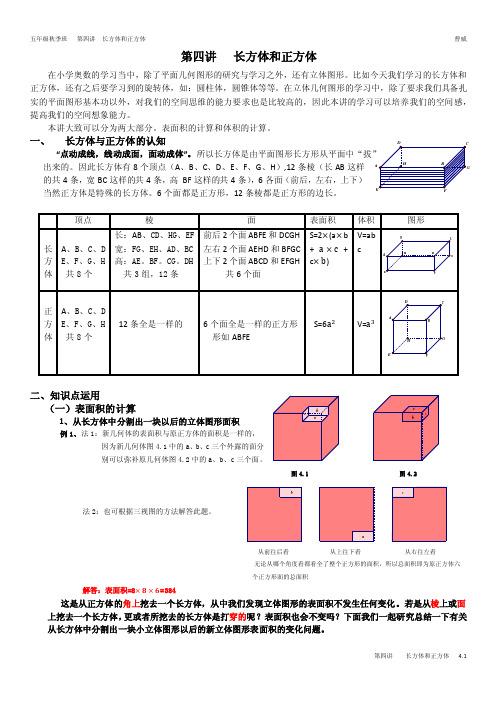
小的长方体 60块 ,那么这 60块长方体表面积的总和是 多少平方米?答案: 96平方米
(2)三个小正方体拼成如图右所示,表面积比原来少了 100平方厘米,求这个图形的体积?
答案:375立 方厘米
3、堆积体的 表面积问题 对于 由若干个小正方体堆积而成的不规则 立体图形的表面积,只要掌握“三视 图”的这个法宝即可 。
比原来正方体的总面积多两个 AEFB 的面积。
解答:表面积=8
+(2 ) =396
(2)如图 4.4 从棱长为 8 的正方体的面上挖去一个 2
的长方体形成一个新的几何体, 求该几何体的表面积?
分析:由图 4.4 可知,挖去后新几何体中的 BFHC 面可弥补原正方体的 AEGD 面。此时已经构成了原正方体的 6 个
2 个 AEFB 面,上下面则没有发生变化,( EHGF 面可弥补 ABCD 面)。因此,新几何体的表面积总体来说比
原来正方体的总面积少了 2 个 AEHD 面而多了 2 个 AEFB 面。
解答:表面积=8
-(2 ) +(2 ) =400
(5)如图 4.7 从棱长为 8 的正方体的面上挖去一个 2
的长方体形成一个新的 几何体,求该几何体的表面积?
分析:由图 4.7 可知,新几何体的前后两个面比原来的正方体前后面也是共少了 2 个 AEHD 面,而左右面共多了
2 个 AEFB 面,上下面也多了 2 个 EHGF 面。因此,新几何体的表面积总体来说比原来正方体的总面积少了
2 个 AEHD 面而多了 4 个内壁面积(2 个 AEFB+2 个 EHGF)。
体有几个。答案:8块 (此题为1层的长方体)
第四讲 长方体和正方体 4.4
五年级秋季班 第四讲 长方体和正方体
北师大版二年级下册数学第6单元 认识图形 测试卷(二)附答案

第六单元测试卷(二)时间:60分钟满分:100分分数:一、填空题。
(14分)1. 一个角有( )个顶点,( )条边。
2. 三角板上的最大的角是( )角,比这个角小的是( )角,比这个角大的是( )角。
3. 三角板上有( )个直角,( )个锐角,( )个钝角。
4. 长方形的对边( ),四个角都是( );正方形的四条边都( ),四个角都是( )。
5. 平行四边形,两组对边( ),易( )。
二、下图中是角的在括号里画“√”。
(16分)( ) ( ) ( )( ) ( ) ( ) ( ) ( )三、把下列图形归类。
(14分)长方形:( ) 正方形:( ) 平行四边形:( )四、数出下列图形中角的个数。
(12分)( )个( )个( )个五、写出下列各角是什么角。
(12分)( )角( )角( )角( )角六、解决问题。
(32分)1. 用一张长12厘米、宽9厘米的长方形纸,剪一个最大的正方形。
正方形的边长是几厘米?剩下的纸至少还可以剪几个最大的小正方形?(7分)2. 在下面的方格纸上画一个正方形、一个长方形和一个平行四边形。
(8分)3. 看图填空。
(9分)三角形有( )个,平行四边形有( )个,长方形有( )个。
4. 在下面的图形中你能找出几个锐角?几个直角和几个钝角?(8分)参考答案一、1. 122. 直锐钝3. 1204. 相等直角相等直角5.相等变形二、(√)( )(√)(√)(√)(√)(√)( )三、④⑦①⑥②③四、657五、钝直锐锐六、1. 9厘米3个 2. 略 3. 183 34. 4个锐角,3个直角,2个钝角。
第六单元过关检测卷一、我会填。
(每空1分,共10分)1.《典中点》的封面有( )个角,这些角都是( )角。
2.钟面上( )时整和( )时整,时针和分针成直角。
3.红领巾有1个( )角,2个( )角。
4.在长10厘米、宽8厘米的长方形中剪一个最大的正方形,正方形的边长是( )厘米。
5.是( )形,有( )个钝角,( )个锐角。
五年级数学下册教案-4.4.1 用最大公因数解决铺砖实际问题25-人教版
数学
年级/册
五年级(下)
教材版本
人教版
课题名称
第四章 用最大公因数解决铺地砖的实际问题
教学目标
理解用公因数和最大公因数的知识来解决相关的实际问题。
重难点分析
重点分析
1.全面读取问题信息、有效分析读取的信息,如对“整块、正好铺满”含义的理解并能转化为数学语言具有一定的难度。
2.结合实际情境,运用公因数、最大公因数,将生活实际问题转化为数学问题,并形成解决此类问题的方法与策略难度较大。
用边长 6dm 的方砖,短边满足,长边不满足,不可以铺满。
课堂练习
(难点巩固)
巩固练习1:小明家厨房的地面是长3m、宽2.4m的长方形,要给它铺上整块正方形地砖,需要边长是多少分米的方砖,最大是多少分米?
解: 3m=30dm 2.4m=24dm
30和24的公因数,其中最大的公因数是6
答:可以选边长是1dm,2dm,3dm,6dm的方砖,边长最大是6dm。
解决问题:16 的因数: 1, 2, 4, 8, 16
12 的因数: 1, 2, 3, 4, 6, 12
16和12的公因数:1,2,4; 最大公因数是4。
所以,可以选边长是 1dm,2dm,4dm的正方形地砖,边长最大是4dm。
用长方形长和宽的公因数作为正方形地砖的边长,一定能满足小明家的要求吗?验证一下。
巩固练习2:有三根长12cm,16cm,44cm的小棒,要把它们截成同样长的小棒,不能有剩余,每根小棒最长是多少厘米?
分析:把它们截成同样长的小棒,
所截得的小棒必须能被12、16、
44整除,也就是要找出这三4的最大公因数:2×2=4
因为,12,16和44的最大公因数为:2×2=4。所以,每根小棒最长4厘米。
人教版小学数学二年级上册观察物体(一)第二课时

人教版小学数学二年级上册观察物体(一)第二课时学校:___________姓名:___________班级:___________考号:___________一、填空题1.下面各图分别是谁看到的?()()()()2.仔细思考,下面这些立体图形依次从正面、侧面、上面观察,分别是什么形状,请把相应序号填到下面的括号里.①②③④⑤⑥(1)从正面看,看到的是长方形的有(),看到的是正方形的有(),看到的是圆的有();(2)从侧面看,看到的是长方形的有(),看到的是正方形的有(),看到的是圆的有();(3)从上面看,看到的是长方形的有(),看到的是正方形的有(),看到的是圆的有().3.(1)从正面看,是图(A)的有( ).(2)从正面看,是图(B)的有( ).(3)从侧面看,是图(B)的有( ).(4)从上面看,是图(B)的有( ).4.下面每堆中有多少个小正方体?()个()个()个()个二、解答题5.看到立体图形的一个面是正方形,这个立体图形可能是什么?6.一个立体图形,从上、下、前、后、左、右看到的图形都完全相同,这个立体图形是我们学过的,这个图形可能是什么立体图形?(至少说出两种)7.思考题如图是一个标有1、2、3、4、5、6的正方体三种不同的摆法,请你说出与数字1、2、3相对的面的数字分别是多少?参考答案1.小明,小亮,小红,小刚【解析】从不同方位观察到的物体的形状不同.考点:观察物体.总结:本题主要考查观察物体,熟练掌握从不同方向看到的物体形状不同是关键.2.(1)①④,②,⑥;(2)①④,②,⑥;(3)①④,②,③⑤⑥【解析】从正面看,即是从我们现在对着的面看,根据各物体的形状判定即可;从侧面看,发挥自己的空间想象力,判断;从上面,也是通过想象,根据各物体的形状来判定.考点:从不同方向观察物体和几何体.总结:本题主要考查观察物体,由于各几何体的形状不同,故而从不同的方向看到的形状也不一样.3.(1)①;(2)③④;(3)③④;(4)②【解析】从正面看,即是从我们现在对着的面看,根据各物体的形状判定即可;从侧面看,发挥自己的空间想象力,根据各物体的形状来判定.考点:从不同方向看几何体.总结:本题主要考查观察物体,主要是由几个几何体组成的图形,解题的关键是能够从几何体各自所在的方位,通过空间想象来判断.4.4,4,4,11【解析】此题可以分层计数,观察图形可知,第一个图形1层都是4个小正方体;第二个图形有2层,每层都是2个小正方体;第三个图形是2层:下面1层都是3个小正方体,上层1个是一个;第四个图形是3层:下面两层都是3+2=5个小正方体,上层1个小正方体,据此即可解答.考点:立体图形的认识.总结:此题考查小正方体的计数方法,要注意分层计数,做到不重不漏.5.这个立体图形可能是长方体和正方体.【解析】根据长方体的特征,长方体的6个面都是正方形,6个面的面积都相等.据此解答.考点:立体图形的认识.总结:此题考查的目的是理解掌握长方体、正方体的特征.6.正方体或球.【解析】常见的从物体正面、左面和上面看得到的图形全等的几何体有:球体、正三棱柱、正方体.考点:立体图形的认识.总结:本题考查三视图的有关知识,注意三视图都相同的常见的几何体有球、正方体、正三棱锥.7.与数字1、2、3相对的面的数字分别是6、5、4.【解析】由图一和图三可看出看出5的相对面是2;再由图二和图三可看出看出6的相对面是1,即可求出3的相对面是4.考点:立体图形的认识.总结:本题考查灵活运用正方体的相对面解答问题,立意新颖,是一道不错的题.。
小学二年级数学试卷题及答案(精选题)

小学二年级数学试卷题及答案(精选题)(考试时间:90分钟,满分:100分)一、选择题(每题2分,共30分)1.3+4=?A.7B.8C.9答案:A2.85=?A.3B.4C.5答案:A3.2×4=?A.6B.8C.10答案:B4.9÷3=?A.2B.3C.4答案:B5.5+6=?A.10B.11C.12答案:B6.104=?A.5B.6C.7答案:B7.7×2=?A.12B.14C.16答案:B8.12÷4=?A.2B.3C.4答案:C9.4+7=?A.10B.11C.12答案:C10.156=?A.8B.9C.10答案:C二、判断题(每题1分,共20分)1.6+3=9()答案:√2.86=2()答案:√3.5×4=20()答案:√4.18÷3=6()答案:√5.9+5=14()答案:×6.127=5()答案:×7.3×6=18()答案:√8.21÷7=3()答案:√9.7+8=15()答案:×10.169=7()答案:×三、填空题(每空1分,共10分)1.4+5=____答案:92.104=____答案:63.3×7=____答案:214.20÷5=____答案:45.6+9=____答案:15四、简答题(每题10分,共10分)1.请计算8+7的结果。
答案:152.请计算149的结果。
答案:5五、综合题(1和2两题7分,3和4两题8分,共30分)1.小明有5个苹果,他又买了3个苹果,请问他现在有多少个苹果?答案:8个苹果。
2.小红有10个糖果,她吃掉了4个糖果,请问她现在还剩几个糖果?答案:6个糖果。
3.请计算6×8的结果。
答案:484.请计算30÷5的结果。
答案:6五、综合题(1和2两题7分,3和4两题8分,共30分)3.小华有12个橘子,他想把它们平均分给4个朋友,每个朋友能分到几个橘子?答案:每个朋友可以分到3个橘子。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D
B
C
B
C
正方形
矩形
⒉怎样将菱形木框变成正方形的木框?
90
菱形
正方形
正方形、矩形、菱形以及平行四边形四者之间的关系:
(3)
有一组邻边相等且有一个角是直角 (1) (4)
平行四边形
(2)
矩形
正 方 形 菱形
正方形的性质=
正方形性质: 边: 对边平行,四边相等 角 :四个角都是直角 对角线:互相垂直平分且相等, 练习: 每条对角线平分一组对角。
2002年世界数学大会会标
课 件 编 制 : 周 效 世
教学目标: 1.探索正方形有关性质和判别条件; 2.经历探索过程培养合情推理能力 探究习惯; 3.感受正方形的美,特殊 的之间联系和辩证观点。 教学重点:正方形的定义. 教学难点:正方形的性质与判定的应用.
操
A
作
D
⒈如何将矩形木框变成正方形木框?
2. 如图点A’、B’、C’、D’分别是
A A/
D/
D
正方形ABCD的四条边上的点,
并且AA'=BB‘=CC'=DD‘. 请说明:四边形A'B'C'D'是正方形
C/ B B/ C
3.给一张长方形纸片,如何裁出正方形纸片? 你能判断你剪出的纸片是正方形吗? 4.如图ABCD和AKLM都是正方形,请说明:MD=KB。
2.如何用一根长为40cm的绳子围成一个面积最大是直角且一组邻边相等
既是中心对 称图形又是 轴对称图形
1.如图,正方形ABCD中,
一条对角线把它分成 个全等的 三角形; 两条对角线把它分成 个全等的 三角形; 此时图中一共有 个等腰直角三角形。 2.正方形的一条对角线长为4cm,面积为 。
3. 如图,在正方形ABCD中, 求∠ABD、∠DAC、∠DOC的度数。
例1.如图,在正方形ABCD中,E在BC的延长线上, 且CE=AC,AE交CD于F,则求∠AFC的度数。 例2.如图在正方形ABCD中,F为CD延长线上一点, CE⊥AF于E,交AD于M,求证:∠MFD=45° 例3.如图正方形ABCD中,AC、BD相交于O, MN∥AB且MN分别交OA、OB于M、N, 求证:BM=CN。
5.如图,已知正方形ABCD中,E、F分别为BC和 DC上的点,且BE=DF。 试说明:1)EF∥BD 2)FE⊥AC
A A D
B E C F
D
F
B
E
C
1.在一块正方形的花坛上,欲修建两条直的小路, 使得两条直的小路将花坛平均分成面积相等的四 部分(不考虑道路的宽度),你有几种方法? (至少说出三种)
5.如图,点E、F在正方形ABCD的边BC、CD上, BE=CF.AE与BF相等吗?为什么?
6.矩形ABCD中,CE⊥BD于E,∠DCE:∠ECB=3:1, 求∠ACE的度数。
A D
D
O E
C
F G B E C A
B
4.已知菱形ABCD中,E、F是BC、CD边上的点, 且AE=EF=AF=AB,求:∠C的度数。
练习:1.判断下列命题是否正确,不是正方形的补充什么 条件能让它成为正方形? (1).四个角都相等的四边形是正方形; (×) (2).四条边都相等的四边形是正方形; ( ) × √ ) (3).对角线相等的菱形是正方形; ( √ ) (4).对角线互相垂直的矩形是正方形; ( (5).对角线垂直且相等的四边形是正方形; × ) ( (6).四边相等,有一个角是直角的四边形是正方形. ( ) √
A D F
B
C
E
讨
论
具备什么条件的矩形是正方形? 具备什么条件的菱形是正方形? 可从边,角,对角线上考虑
正方形的判定 有一组邻边相等的矩形是正方形。 1 定义法:
有一个角是直角的菱形是正方形。 2、 对角线法: 两条对角线互相垂直的矩形是正方形 两条对角线相等的菱形是正方形
3、矩形菱形法:
既是矩形又是菱形的四边形是正方形。
