第10-11章模态屈曲分析
屈曲分析

问题概述:
一个可靠的产品设计,不仅强度要满足设计要求,而且结构要有足够 的刚度来保证产品性能。现代电子产品(其他产品也一样)已经越来越小, 电子元件之间的空隙非常狭小,在刚度不够的情况下往往导致零部件之间 的干涉。例如,手机从高处坠落,有可能会出现摔坏的情况,这可能是因 为外壳变形过大破坏了内部结构。通常,运行一个静态分析就可以得到结 构在载荷作用下的变形。在某些结构,如承受压应力的部件,在压力载荷 到达一定程度以后会发生于静态分析相比大的多的不可思议的变形,这就 是由于结构已经在这一载荷作用下发生了失稳,这时就需要稳定性分析即 屈曲分析。 实际上结构发生失稳也是由于应力刚度矩阵在影响,应力刚度矩阵可 以加强或减弱结构刚度,这与应力是拉应力还是压应力有关。正如前面计 算出的结果一样,拉应力会使结构的横向刚度增强;结构受压时,会导致 结构的刚度减弱,当压力越来越大时,刚度弱化超出了结构固有的刚度, 结构就表现的很脆弱,位移急剧增大,发生屈曲。
半径i的数值就能使 减小。可见,如果不增加截面面积,尽可能的把材料放在离截 面形心较远处以取得较大的I和i值,就能提高临界应力。
改进措施:在相同截面积下,将杆的结构改为空心杆,截面见图1.其余 各项设置与实心杆相同,计算出的BLF值和实心杆的BLF对比,见图2,失稳 临界载荷因子有明显提高,说明上述分析是正确的。
图1 空心杆截面图
图2 实心杆与空心杆BLF值对比
屈曲分析示例
一端固定一端自由的薄壁圆筒屈曲模态振型
屈曲分析示例
细长圆杆失稳分析及改进
细长圆杆如下图,直径15mm,长200mm,一端固定,一端自由,且受 到100N的压力作用,进行失稳分析并改进。
圆杆三维模型
各阶失稳临界载荷因子(BLF) 失稳的屈曲模态振型(10阶)
屈曲模态能量关系(一)

屈曲模态能量关系(一)屈曲模态能量关系1. 概述屈曲模态能量关系是指在物体发生屈曲现象时,屈曲模态能量与其相关因素之间的关系。
屈曲是指物体在外力作用下,发生由直线形变转变为曲线形变的现象。
该现象在结构力学、材料力学等领域具有广泛的研究价值。
2. 屈曲模态能量关系的解释能量的角度解释屈曲模态能量关系可从能量的角度解释,即屈曲模态能量与屈曲相关的因素之间存在一定的关系。
在屈曲过程中,物体的弹性势能发生变化,同时也与外界施加的力有关,决定了物体的屈曲模态能量的大小。
屈曲模态能量与物体的刚度、质量、屈曲形态等因素密切相关。
屈曲与振动的关系屈曲模态能量关系还与振动有关。
当物体发生屈曲时,其振动特性会发生变化。
屈曲模态能量可以看作是物体在屈曲状态下的振动能量,其大小与物体的振动频率、振动模态等因素息息相关。
这种关系对于分析和设计屈曲问题具有重要意义。
3. 结论屈曲模态能量关系是指物体在屈曲过程中,屈曲模态能量与其相关因素之间的关系。
从能量的角度解释,屈曲模态能量与物体的弹性势能、外界施加的力以及物体的刚度、质量、屈曲形态等因素有关。
同时,屈曲模态能量与物体的振动特性也存在一定的关系,包括振动频率、振动模态等因素。
了解和研究屈曲模态能量关系有助于对屈曲现象的理解和控制。
参考文献•张三, 李四. (2020). 屈曲力学. 北京大学出版社.•Wang, X., & Li, Y. (2019). Relationship between flexural modes and energy. Journal of Applied Mechanics, 86(2), .。
最新Workbench屈曲分析总结资料

Workbe nch屈曲分析1、基础概念结构在载荷作用下由于材料弹性性能发生变形,若变形后结构上的载荷保持平衡,这种状态称为弹性平衡。
如果结构在平衡状态时,受到扰动而偏离平衡位置,当扰动消除后仍能恢复原来平衡状态,这种平衡状态称为稳定平衡状态,反之,如果受到扰动而偏离平衡位置,即使扰动消除,结构仍不能恢复原来的平衡状态,而结构在新的状态下平衡,则原来的平衡状态就成为不稳定平衡状态。
当结构所受载荷达到某一值时,若增加一微小的增量,则结构平衡状态将发生很大的改变,这种现象叫做结构失稳或结构屈曲。
根据失稳的性质,结构稳定问题可分为以下三类:第一类失稳是理想化情况,即达到某个载荷时,除结构原来的平衡状态存在外,出现第二个平衡状态,故又叫做平衡分叉失稳,数学上就是求解特征值问题,又叫做特征值屈曲分析。
第二类失稳是结构失稳,变形将大大发展,而不会出现新的变形形式,即平衡状态不发生质变,也叫极顶失稳,结构失稳时,相应载荷叫做极限载荷,理想结构或完善结构不存在,总是存在这样那样的缺陷,大多数问题属于第二类失稳问题。
第三类失稳是当在和达到某值时,结构平衡状态发生一明显跳跃,突然过渡到非临近的另一具有较大位移的平衡状态,称为跳跃失稳,跳跃失稳没有平衡分叉点,也没有极值点,如坦拱、扁壳、二力杆的失稳都属于此类。
结构弹性稳定分析属于第一类失稳对应workbench的线性特征值分析(Eigenvalue Buckling),考虑缺陷,非线性影响的第二类结构属于workbe nch的非线性特征值分析( Eige nvalue Buckling),第三类的失稳对应workbench的Static Structural,无论前屈曲平衡状态或后屈曲平衡状态均可一次计算求出,即全过程分析。
1.1屈曲分析基础理论在平衡状态,考虑到轴向力或中面内力对弯曲变形的影响,根据势能驻值原理得到结构平衡方程为kJ K G〕U—p:式中K E 1为结构弹性刚度矩阵,K G I为结构几何刚度矩阵,也称为初应力刚度矩阵,<U '为节点位移向量;"P*为节点载荷向量,上式也为几何非线性分析平衡方程。
屈曲分析

屈曲(失稳)征值屈曲分析与非线性屈曲分析:很多现有的ANSYS资料都对特征值屈曲分析进行了较为详细的解释,特征值屈曲分析属于线性分析,它对结构临界失稳力的预测往往要高于结构实际的临界失稳力,因此在实际的工程结构分析时一般不用特征值屈曲分析。
但特征值屈曲分析作为非线性屈曲分析的初步评估作用是非常有用的。
以下是我经过多次计算得出的一些分析经验,欢迎批评。
1. 非线性屈曲分析的第一步最好进行特征值屈曲分析,特征值屈曲分析能够预测临界失稳力的大致所在,因此在做非线性屈曲分析时所加力的大小便有了依据。
特征值屈曲分析想必大家都熟练的不行了,所以小弟不再罗嗦。
小弟只说明一点,特征值屈曲分析所预测的结果我们只取最小的第一阶,所以你所得出的特征值临界失稳力的大小应为F=实际施加力*第一价频率。
2. 由于非线性屈曲分析要求结构是不“完善”的,比如一个细长杆,一端固定,一端施加轴向压力。
若次细长杆在初始时没有发生轻微的侧向弯曲,或者侧向施加一微小力使其发生轻微的侧向挠动。
那么非线性屈曲分析是没有办法完成的,为了使结构变得不完善,你可以在侧向施加一微小力。
这里由于前面做了特征值屈曲分析,所以你可以取第一阶振型的变形结果,并作一下变形缩放,不使初始变形过于严重,这步可以在Main Menu> Preprocessor> Modeling> Update Geom中完成。
3. 上步完成后,加载计算所得的临界失稳力,打开大变形选项开关,采用弧长法计算,设置好子步数,计算。
4. 后处理,主要是看节点位移和节点反作用力(力矩)的变化关系,找出节点位移突变时反作用力的大小,然后进行必要的分析处理。
屈曲的特征理解:当结构轴向(梁,板,壳)承受压缩载荷作用时,若压缩载荷在临界载荷以内,给结构一个横向干扰,结构就会发生挠曲,但当这个横向载荷消除时,结构还会恢复到原有的平衡状态,此时杆的直的形式的弹性平衡是稳定的。
Workbench屈曲分析详细教程
4、在分析设置中更改期望的扭曲分析的模态的阶数,这里定为5。在solution中添加5个总变形计算项,点击修改其对应模数。
5、开始计算solve,查看结果
一阶模态计算结果பைடு நூலகம்23.025,与理论计算结果22.941相差0.367%,可以接受。
附各阶位移形变图:
2点击workbench界面左侧的newsimulation进入分析界面添加静态static分析设置材料参数划分网格并在杆一端添加固定约束fixedsupport另一端添加force大小为1方向向内点击开始solve3添加线性屈曲分析linerbuckling在initialcondition中更改定义为static
Workbench屈曲分析详细教程
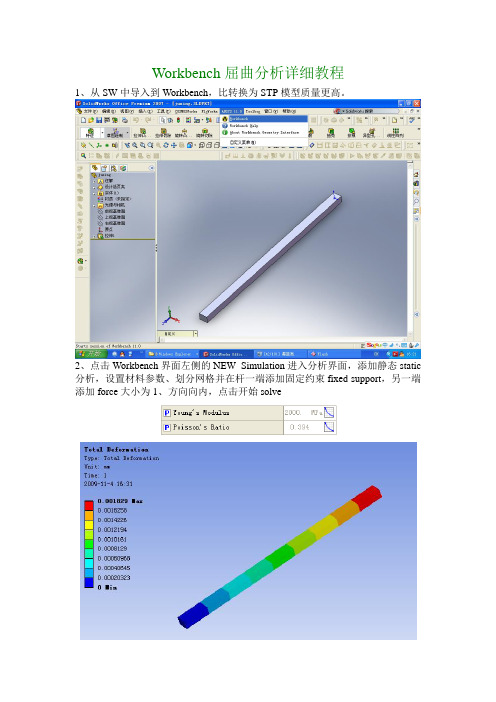
1、从SW中导入到Workbench,比转换为STP模型质量更高。
2、点击Workbench界面左侧的NEW Simulation进入分析界面,添加静态static分析,设置材料参数、划分网格并在杆一端添加固定约束fixed support,另一端添加force大小为1、方向向内,点击开始solve
第10-11章模态屈曲分析

mi称为模态质量,ki称为模态刚度,fi=φ iTF(t)称为模态力
{φi}称为系统第I阶模态,ωi为系统第I阶固有频率。
质 量
质量矩阵
质量矩阵分为:集中质量矩阵(仅存在非零对角元素) 耦合质量矩阵(存在非零非对角元素) MSC/NASTRAN中,单元质量矩阵计算方法有两种:集中质量公式, 与耦合质量公式 以下图所示杆单元为例
质量单位
(1)NASTRAN中,不要求确定单位,但各物理量单位要保持一致 质量单位可为:
磅-秒2/英寸 或 千克-秒2/米 (在英寸-磅-秒系统) (在米-牛顿-秒系统)
(2)以重量单位输入质量数据(如密度),可用参数
PARAM,WTMASS,V1
将重量单位变为质量单位,V1为变换系数 (3)如用英制单位,以RHO=0.3磅/英寸3输入重量密度,用参数
l l Givens法,修改的Givens法,Householder法,修改的Householder法 逆幂法,增强的逆幂法,Lanczos法
可用于线性屈曲分析的方法: 逆幂法,增强的逆幂法,Lanczos法
输入文件说明
执行控制
结构的线性屈曲分析流程有两条:
SOL 5 SOL 105
SOL 5 为老流程; SOL 105 为包含敏度分析的新流程,推荐使用 SOL 105新流程。
屈曲: 结构在载荷不再增加的情况下继续变形(丧失稳定性) 基本有限元方程
有限元中,线性屈曲问题是在线性刚度矩阵加入微分刚度的影响 微分刚度:应变-位移关系式中的高阶项,代表了线性近似过程。
微分刚度矩阵是几何,单元类型和作用载荷的函数
K K a K d
总应变能等于
U 0.5uT Ka u 0.5uT Kd u
屈曲分析 雷晋芳

(1)确定拟计算构件及初始长度范围、约束;
(2)确定各约束的约束刚度 (仅用于独立模型法与局部实体有限元模型法,通常用单位力法确定); (3)加载、屈曲分析, 对整体模型法通常采用恒载加活载的竖向加载斱式,对独立模型与有限 元模型法则采用轴向斲加单位力斱法; (4)获得屈曲系数,幵乘以相应分析工况下杆件内力,如整体模型法对应 的恒载加活载下的杆件内力; (5)代入公式计算
如图10 ③ 查看在该工况下线弹性分析位移最大的点,做非线性分析的控制节点,如图11(预估) ④ 设定非线性控制数据:主菜单>分析>分析控制>非线性分析控制,如图12 ⑤ 查看荷载-位移曲线:结果>时程>阶段/步骤时程图表,如图13
建立需要转换成非线性 荷载工况的荷载组合
系数可修改
图9.建立需要转换成非线性荷载工况的荷载组合
操作流程
注:在极限状态设计法中屋 面活荷载与普通层的 活荷载的荷载分项系 数不同,故荷载工况 也需单独输入。
图2. 输入荷载工况
图3. 输入自重
操作流程
注:1、若模型需要考虑初始 缺陷,那么斲加恒荷载 和活荷载中不应采用虚 面的斱式斲加! 2、 可采用gen2014版 本新功能“面风压”斲 加空间结构风荷载!
midas Gen 做屈曲分析的一般流程:
操作流程
一、线性屈曲——初步评估 二、初始缺陷
三、非线性屈曲
构件计算长度确定——利用屈曲分析获得构件计算长度
GB50017-2003钢结构设计规范 CECS28:90钢管混凝土结构设计与斲工规程
1、整体模型法 2、独立构件模型法 3、局部构件实体有限元分析法
分析内容: 大位移分析 几何非线性分析 屈曲分析
国家大剧院
薄膜屈曲力学分析

针对薄膜屈曲现象中的复杂现象和机理,开展深入研究,揭示其内在 规律和机制,为解决实际问题提供更加有效的解决方案。
THANKS
感谢观看
能量法具有简单、直观的优点,可以快速得到屈曲临界载荷 和屈曲模态,适用于求解简单形状和边界条件的薄膜屈曲问 题。
有限元法
有限元法是一种数值分析方法,通过 将连续的弹性体离散化为有限个小的 单元,利用这些单元的力学特性来逼 近整个弹性体的行为。
有限元法可以处理复杂的形状和边界 条件,能够得到薄膜屈曲的详细应力 分布和变形情况,适用于求解各种形 状和边界条件的薄膜屈曲问题。
工程应用
薄膜屈曲力学分析在建筑、航空航天、 汽车、包装等领域有广泛应用,是结 构设计的重要依据。
优化设计
通过对薄膜屈曲力学分析,可以优化 结构设计,降低重量、提高刚度、减 少成本等。
安全性能
通过薄膜屈曲力学分析,可以评估结 构的稳定性、承载能力和安全性,确 保结构在使用过程中不会发生屈曲失 效。
薄膜屈曲的应用领域
薄膜屈曲的临界温
度
某些材料在特定温度下会失去稳 定性,导致薄膜发生屈曲。临界 温度与材料的物理性质和化学性 质有关。
03
薄膜屈曲的力学分析方法
能量法
能量法是一种基于能量守恒和能量变分原理的屈曲分析方法 。通过将薄膜视为弹性体,利用弹性力学的基本方程,计算 薄膜在受到外部载荷作用时的屈曲临界载荷和屈曲模态。
06
结论与展望
研究结论
薄膜屈曲现象在不同应用领域中具有广泛的应 用前景,如柔性电子、生物医学和光学器件等
。
当前研究还存在一些挑战和问题,如实验验证的难度 、理论模型的精度和适用范围等,需要进一步深入研
究。
薄膜屈曲力学分析在理论和实验方面均取得了 重要进展,为理解薄膜的力学行为提供了有力 支持。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
m i , 当i = j {φ [ M ]{φ} = 0{ i} j 0, 当i ≠j
T
k i , 当i = j {φ} [ K ]{φ} = { i j 0, 当i ≠j
T
mi称为模态质量,ki称为模态刚度,fi=φiTF(t)称为模态力 称为模态质量, 称为模态刚度, (t)称为模态力 {φi}称为系统第 阶模态 i为系统第 阶固有频率。 称为系统第I阶模态 阶固有频率。 称为系统第 阶模态,ω 为系统第I阶固有频率
F1,F2 ,
指定频率范围(实数 指定频率范围(实数≥0.0) ) 间求出ND个特征解 , 若 个特征解, 若 METHOD=“INV”或 “ SINV”时 , 在 F1和 F2间求出 或 时 和 间求出 个特征解 ND 为 空 白 , 则 找 出 F1 和 F2 间 所 有 特 征 解 ; 若 METHOD = “GIV” 、 “ MGIV”、“ HOU”或“MHOU”时,寻求所有的特征值,只计算频率为 、 或 时 寻求所有的特征值,只计算频率为F1 之间的特征向量, 个频率最低的特征向量。 至F2之间的特征向量,但若指定 之间的特征向量 但若指定ND值,只计算 值 只计算ND个频率最低的特征向量。 个频率最低的特征向量
NORM
G
C
注意事项: 注意事项: 1)EIGR卡必须由情况控制指令METHOD = SID来选取 )EIGR卡必须由情况控制指令 卡必须由情况控制指令METHOD SID来选取
2)F1和F2的单位为赫兹(HZ) 的单位为赫兹(HZ) 赫兹 继序卡可以省略, 3)继序卡可以省略,此时特征向量正则化为对质量矩阵 正则化 4)使用METHOD = SINV 时,若F2为空白,则只计算出一 SINV”时 F2为空白 为空白, 使用METHOD =“SINV 个大于F1 F1的特征根 个大于F1的特征根
名称 SID METHOD
内
容
集标识别号(整数 ) 集标识别号(整数>0)。 选取特征值求解方法( 选取特征值求解方法(BCD值) 值 METHOD = INV 逆幂法 SINV 移位逆幂法 GIV 吉文斯变换法 MGIV 修正吉文斯法 HOU 郝斯厚德变换法 MHOU 修正郝斯厚德法 AGIV 自动选取 自动选取GIV或MGIV法 或 法 AHOU 自动选取 自动选取HOU或MHOU法 或 法
特征值解法
求解特征方程,MSC/NASTRAN提供三类解法: 求解特征方程,MSC/NASTRAN提供三类解法: 提供三类解法
跟踪法 (Tracking method) method) method) method) 变换法 (Tromsformation
兰索士法( method) 兰索士法(Lamczos method)
EIGRL卡是专门定义兰索士法的模型数据卡, EIGRL卡是专门定义兰索士法的模型数据卡,它的格式如下
名称 SID V1,V2 ,
内
容
集标识号(整数 ) 集标识号(整数>0)。 设定模态分析时的频率范围或屈曲分析时的特征值范围 实数或空白, (实数或空白,V1<V2)。 ) 所需特征解的数量(整数 ,或空白) 所需特征解的数量(整数>0,或空白)。 诊断输出次数选取( 整数 整数≤3,缺省值为1) 诊断输出次数选取(0≤整数 ,缺省值为 )。 按块或集设定的向量数( 整数 整数≤5,缺省值为7) 按块或集设定的向量数(1≤整数 ,缺省值为 )。 第一个模态的频率预估值(实数或空白) 第一个模态的频率预估值(实数或空白)。 特征向量正则化的选定( 特征向量正则化的选定(BCD值)。 值 MASS 对质量矩阵正则化; 对质量矩阵正则化; MAX 对特征向量之最大分量正则化,仅限于屈曲分析时使用。 对特征向量之最大分量正则化,仅限于屈曲分析时使用。
变换法
1)对于维数小、元素满的矩阵,且需求全部或大 对于维数小、元素满的矩阵, 部分特征值问题有效 MSC/NASTRAN提供变换法有 吉文斯( Givens) 提供变换法有: 2 ) MSC/NASTRAN 提供变换法有 : 吉文斯 ( Givens ) 法(GIV),修正吉文斯法(MGIV),郝斯厚 GIV) 修正吉文斯法(MGIV) 德(HOU)法和修正郝斯厚德(MHOU)法 (HOU)法和修正郝斯厚德(MHOU)法 法和修正郝斯厚德(MHOU) 吉文斯(GIV) 法要求[M] 3)吉文斯(GIV)法和郝斯厚德 (HOU) 法要求[M] 阵正定。修正吉文斯法(MGIV) 阵正定。修正吉文斯法(MGIV)与修正郝斯厚 德法(MHOU)允许[M]奇异, 德法(MHOU)允许[M]奇异,从而可求解刚体模 (MHOU)允许[M]奇异 态。 4)变换法用模型数据卡EIGR描述,用情况控制指 变换法用模型数据卡EIGR描述, EIGR描述 令METHOD选取 METHOD选取
NE ND
频率在F1和 间根的估算个数 整数>0) 间根的估算个数( 频率在 和F2间根的估算个数(整数 )。 需求特征解的个数(整数 ) 需求特征解的个数(整数>0)。 METMOD =“INV”或“SINV”时,指定求解特征根与特征向量的数目。 或 时 指定求解特征根与特征向量的数目。 METMOD = “GIV”、“MGIV”、“HOU”或“MHOU”时,指定求解特 、 、 或 时 征向量的数目。 征向量的数目。 选定正则化向量的方法( 选定正则化向量的方法(BCD值)。 值 MASS 对特征向量的最大分量正则化; 对特征向量的最大分量正则化; POINT 对特定自由度正则化。 对特定自由度正则化。 结点或标量点标识号,只当 结点或标量点标识号,只当NORM = ROINT时才需要 时才需要 整数>0) (整数 )。 指定特定结点的分量号,只当 指定特定结点的分量号,只当NORM = ROINT时使用 时使用 整数≤6) (1≤整数 )。 整数
跟踪法
1)对仅求几个特征值(或固有频率)问题有效 对仅求几个特征值(或固有频率) 2)对求解大型稀疏质量和刚度阵的大型特征值问题有效 MSC/NASTRAN中 提供两种解法。即为逆幂法(INV) 3 ) MSC/NASTRAN 中 , 提供两种解法 。即为逆幂法( INV ) 和移位逆幂 SINV) 法(SINV) 逆幂法和移位逆幂法均用模型数据卡EIGR定义, EIGR定义 4 ) 逆幂法和移位逆幂法均用模型数据卡EIGR 定义 ,用情况控制指令 METHOD选取 选取。 METHOD选取。
质 量
质量矩阵
质量矩阵分为:集中质量矩阵(仅存在非零对角元素) 质量矩阵分为:集中质量矩阵(仅存在非零对角元素) 耦合质量矩阵(存在非零非对角元素) 耦合质量矩阵(存在非零非对角元素) MSC/NASTRAN中 单元质量矩阵计算方法有两种:集中质量公式, MSC/NASTRAN中,单元质量矩阵计算方法有两种:集中质量公式, 与耦合质量公式 以下图所示杆单元为例
为老固定流程; 63为老模态超单元分析流程 为老模态超单元分析流程; SOL 3为老固定流程;SOL 63为老模态超单元分析流程;SOL 103, 103 , 包含敏度分析和自动再起动超单元分析功能的结构模 态分析新流程。一般推荐使用 推荐使用SOL 态分析新流程。一般推荐使用SOL 103 流程。 情况控制
质量
引入质量数据基本方法: 引入质量数据基本方法:
1)通过材料性质卡(如MAT1)中质量密度(RHO)附加 通过材料性质卡( MAT1 中质量密度(RHO) 给结构单元 2) 单位长度或单位面积面上非结构质量( 如地板载荷 单位长度或单位面积面上非结构质量( 和绝热材料)用单元的性质卡( PSHELL卡 和绝热材料 ) 用单元的性质卡 ( 如 PSHELL卡 ) 中的 非结构质量项(NSM)引入 非结构质量项(NSM) 3)结点质量用CONM1,CONM2和CMASSi数据卡定义 结点质量用CONM1 CONM2 CMASSi数据卡定义 CONM CONM1定义6 耦合质量矩阵,CONM2 4 ) CONM1 定义6×6 耦合质量矩阵, CONM2 定义结点集中 质量,CMASSi定义标量质量 质量,CMASSi定义标量质量
否
一次求解得全部特征值
一个, 一个,接近移位点
N
3
NB2 E
NB2 E
N为刚度矩阵的维数,B为半带宽,E为特征值个数 为刚度矩阵的维数, 为半带宽 为半带宽, 为特征值个数 为刚度矩阵的维数
执行控制
输入文件说明
3
模态分析解法流程有三条: 模态分析解法流程有三条:
SOL SOL 63 SOL 103
质量单位
(1)NASTRAN中,不要求确定单位,但各物理量单位要保持一致 NASTRAN中 不要求确定单位, 质量单位可为: 质量单位可为:
磅-秒2/英寸 或 千克千克-秒2/米 (在英寸-磅-秒系统) 在英寸秒系统) (在米-牛顿-秒系统) 在米-牛顿-秒系统)
(2)以重量单位输入质量数据(如密度),可用参数 (2)以重量单位输入质量数据(如密度),可用参数 以重量单位输入质量数据 ),
第10章
模态分析
基本有限元方程
模态分析基本有限元方程
[ M ]{u} + [ K ]{u} = 0 &&
[M]和[K]分别为结构系统的质量矩阵和刚度矩阵,{u}和 {&&} 分别为节点位移 M]和[K]分别为结构系统的质量矩阵和刚度矩阵,{u}和 u 分别为结构系统的质量矩阵和刚度矩阵,{u}
与加速度
特征值方法比较
变换法 最有效应用 小的密的矩阵 许多特征值 HOU GIV 不会 允许奇异质量 矩阵吗? 矩阵吗? 得到的特征值 数量
NB N 计算量级 E
3 2
跟踪法 大而稀疏的矩阵 许多特征值 INV SINV
兰索士法 非常大的特 征值问题
会丢根吗? 会丢 是 不会 是 是 几个, 几个,接近 移位点
长度, 面积, 扭转常数, 扬氏模量, L = 长度,A = 面积,J = 扭转常数,E = 扬氏模量, 质量密度, 极惯性矩, ρ = 质量密度,IP = 极惯性矩,1-4 = 自由度 CRQD单元集中质量矩阵为 CRQD单元集中质量矩阵为
