初中数学 折叠练习题(整编版)
中考数学复习专题《折叠问题》练习题含答案

中考数学复习专题 折叠问题一、选择题1.如果将长为6 cm ,宽为5 cm 的长方形纸片折叠一次,那么这条折痕的长不可能是( A ) A .8 cm B .5 2 cm C .5.5 cm D .1 cm【解析】纸片为长方形,折痕的最大长度为对角线长,52+62=61<64=8,所以折痕长不能为8 cm.2.将抛物线y =-x 2+2x +3在x 轴上方的部分沿x 轴翻折至x 轴下方,图象的剩余部分不变,得到一个新的函数图象,那么直线y =x +b 与此新图象的交点个数的情况有( B )A .6种B .5种C .4种D .3种二、填空题3.如图,矩形纸片ABCD 中,AB =5,BC =3,先按图2操作:将矩形纸片ABCD 沿过点A 的直线折叠,使点D 落在边AB 上的点E 处,折痕为AF ;再按图3操作,沿过点F 的直线折叠,使点C 落在EF 上的点H 处,折痕为FG ,则A ,H 两点间的距离为__10__.【解析】如图3中,连结AH ,由题意可知在Rt △AEH 中,AE =AD =3,EH =EF -HF =3-2=1,∴AH =AE 2+EH 2=32+12=10.4.如图,在△ABC 中,∠ACB =90°,点D ,E 分别在AC ,BC 上,且∠CDE =∠B ,将△CDE 沿DE 折叠,点C 恰好落在AB 边上的点F 处.若AC =8,AB =10,则CD 的长为__258__. 【解析】由折叠可得,∠DCE =∠DFE =90°,∴D ,C ,E ,F 四点共圆,∴∠CDE =∠CFE =∠B ,又∵CE =FE ,∴∠CFE =∠FCE ,∴∠B =∠FCE ,∴CF =BF ,同理可得,CF =AF ,∴AF =BF ,即F 是AB 的中点,∴Rt △ABC 中,CF =12AB =5,由D ,C ,E ,F 四点共圆,可得∠DFC =∠DEC ,由∠CDE =∠B ,可得∠DEC =∠A ,∴∠DFC =∠A ,又∵∠DCF =∠FCA ,∴△CDF ∽△CF A ,∴CF 2=CD ×CA ,即52=CD ×8,∴CD =258. 三、解答题5.如图1,在等腰三角形ABC 中,AB =AC =4,BC =7.如图2,在底边BC 上取一点D ,连结AD ,使得∠DAC =∠ACD .如图3,将△ACD 沿着AD 所在直线折叠,使得点C 落在点E 处,连结BE ,得到四边形ABED .求BE 的长.解:设AE 与BD 交于点M ,∵AB =AC ,∴∠ABC =∠C ,∵∠DAC =∠ACD ,∴∠DAC =∠ABC ,∵∠C =∠C ,∴△CAD ∽△CBA ,∴CA CB =CD AC ,∴47=CD 4,∴CD =167,BD =BC -CD =337,∵∠DAM =∠DAC =∠DBA ,∠ADM =∠ADB ,∴△ADM ∽△BDA ,∴AD BD =DM DA ,即167337=DM 167,∴DM =16233×7,MB =BD -DM =332-1627×33,∵∠ABM =∠C =∠MED ,∴A 、B 、E 、D 四点共圆,∴∠ADB =∠BEM ,∠EBM =∠EAD =∠ABD ,∴△ABD ∽△MBE ,∴AB BM =BD BE ,∴BE =BM·BD AB =332-1627×33×3374=1746.如图1,将一张矩形纸片ABCD 沿着对角线BD 向上折叠,顶点C 落到点E 处,BE 交AD 于点F .(1)求证:△BDF 是等腰三角形; (2)如图2,过点D 作DG ∥BE ,交B C 于点G ,连结FG 交BD 于点O .①判断四边形BFDG 的形状,并说明理由;②若AB =6,AD =8,求FG 的长.解:(1)如图1,根据折叠,∠DBC =∠DBE ,又AD ∥BC ,∴∠DBC =∠ADB ,∴∠DBE =∠ADB ,∴DF =BF ,∴△BDF 是等腰三角形(2)①菱形,理由:∵四边形ABCD 是矩形,∴AD ∥BC ,∴FD ∥BG ,又∵FD ∥BG ,∴四边形BFDG 是平行四边形,∵DF =BF ,∴四边形BFDG 是菱形②∵AB =6,AD =8,∴BD =10.∴OB =12BD =5.设DF =BF =x ,∴AF =AD -DF =8-x.∴在Rt △ABF 中,AB 2+AF 2=BF 2,即62+(8-x )2=x 2,解得x =254,即BF =254,∴FO =BF 2-OB 2=(254)2-52=154,∴FG =2FO =152。
初中几何折叠习题(带图)精编版

图形翻折1、如图,把直角三角形纸片沿着过点B 的直线BE 折叠,折痕交AC 于点E ,欲使直角顶点C 恰好落在斜边AB 的中点上,那么∠A 的度数必须是 .2、如图,在矩形ABCD 中,,6=AB 将矩形ABCD 折叠,使点B 与点D 重合,C 落在C '处,若21::=BE AE ,则折痕EF 的长为 .3、已知△ABC 中,AB=AC ,∠BAC=120°,点D 是边AC 上一点,连BD ,若沿直线BD 翻折,点A 恰好落在边BC 上,则AD :DC= .DC BAA ’ A CBE4、如图,已知边长为6的等边三角形ABC 纸片,点E 在AC 边上,点F 在AB 边上,沿EF 折叠,使点A 落在BC 边上的点D 的位置,且ED ⊥BC,则CE 的长是( ). (A)31224- (B)24312- (C)18312- (D)31218-5、正方形纸片ABCD 中,边长为4,E 是BC 的中点,折叠正方形,使点A 与点E 重合,压平后,得折痕MN (如图)设梯形ADMN 的面积为1S ,梯形BCMN 的面积为2S ,那么1S :2S =6、如图2,把腰长为4的等腰直角三角形折叠两次后,得到一个小三角形的周长是.7、如图1,在梯形ABCD 中,AD ∥BC ,75,ABC ︒∠=将梯形沿直线EF 翻折,使B 点落在线段AD 上,记作'B 点,连结'B B 、交EF 于点O ,若'90B FC ︒∠=,则:EO FO = .A N CD BM 图2B 'OF ED C B A8、等边△OAB 在直角坐标系中的位置如图所示,折叠三角形使点B 与y 轴上的点C 重合,折痕为MN ,且CN 平行于x 轴,则∠CMN = 度.9、有一块矩形的纸片ABCD ,AB=9,AD=6,将纸片折叠,使得AD 边落在AB 边上,折痕为AE ,再将△AED 沿DE 向右翻折,AE 与BC 的交点为F ,则△CEF 的面积为 .A B A D B D BFD CE C E C10、如图,有一矩形纸片ABCD ,AB =10,AD =6,将纸片折叠,使AD 边落在AB 边上,折痕为AE ,再将△AED 以DE 为折痕向右折叠,AE 与BC 交于F ,那么△CEF 的面积是 。
初中折叠的练习题

初中折叠的练习题练习一:折叠长方形1. 折叠一张纸使两个对边平行,并用手指沿着对角线将纸折叠。
展开后纸上留下了一条明显的线。
解析:这条线是纸张对角线的痕迹。
折叠纸张时,我们将纸张沿对角线对折,使两侧的边缘完全重合。
在对角线折叠后,我们可以观察到两侧边缘的堆叠,形成一条明显的线。
练习二:折叠正方形1. 以一张方形纸为例,将其对折并展开,然后将四个顶点分别折叠至纸的中心点。
解析:这个过程中我们可以观察到纸张被分割成四块相等的小正方形,并且每个小正方形都是对称堆叠的。
这种折叠方法可以用于制作纸盒等日常用品。
练习三:折叠三角形1. 将一张纸对折,使两个对边边缘完全重合,并展开。
然后将纸的两个顶点分别折叠至纸的中心点。
解析:我们可以观察到纸的折痕形成了一个等边三角形。
在这个过程中,我们将纸的两个顶点折叠至中心点,形成了一个对称三角形。
这种折叠方法可以用于制作纸飞机等游戏工具。
练习四:折叠多边形1. 以一个等边三角形为例,将其两边的顶点向内折叠至底边的中点。
解析:在这个过程中,我们可以观察到折叠后的形状是一个小等边三角形,它嵌套在原始的等边三角形内部。
这样的折叠方法可以被应用于设计艺术、3D模型制作等方面。
练习五:折叠圆1. 以一个正方形纸为例,将其对角线相交的两个顶点折叠至纸的中心点,并展开。
解析:在这个过程中,我们可以观察到折叠后的形状是一个小圆,它完美地嵌套在原始的正方形内部。
这里展示了如何利用纸张折叠技巧来近似表示一个圆。
练习六:折叠动物1. 以一张正方形纸为例,按照特定的折叠方式,可以将其折叠成各种动物形状,例如鸟、狗等。
解析:这个练习是一个创意练习,通过特定的折叠方式,我们可以将纸张折叠成各种动物形状。
这个过程需要一定的想象力和手工技巧,可以激发创造力和动手能力。
练习七:折叠建筑1. 以一个长方形纸为例,按照特定的折叠方式,可以将其折叠成各种建筑形状,例如房屋、桥梁等。
解析:这个练习是一个设计练习,通过特定的折叠方式,我们可以将纸张折叠成各种建筑形状。
初三数学折叠练习题

初三数学折叠练习题数学是一门需要反复练习和掌握技巧的学科,特别是对于初三学生而言,数学的学习更加需要注重基础知识的巩固和运用的灵活性。
折叠练习题是一种常见的训练方法,通过将图形进行折叠来观察和推理数学问题。
下面是一些初三数学折叠练习题,希望能够帮助同学们加深对数学知识的理解和运用。
练习一:正方形对折1. 将一张正方形纸张对折,然后再对折。
最终纸张变为四个小正方形,请问每个小正方形的边长是多少?解析:我们可以通过折叠来观察和推理。
首先将正方形的上下两边对折,得到一条折痕。
然后再将左右两边对折,得到另一条折痕。
此时,纸张被折痕分成了四个小正方形,它们的边长都相等。
假设原正方形的边长为a,则第一个小正方形的边长为a/2,第二个小正方形的边长为a/2,第三个小正方形的边长也是a/2,第四个小正方形的边长也是a/2。
因此,每个小正方形的边长都是原正方形边长的一半,即a/2。
练习二:长方体的折叠2. 将一张长方形纸张对折,然后再对折,最后再对折。
最终纸张变成了一个长方体,请问纸张的长、宽、高分别是多少?解析:这个问题涉及到三次对折,我们可以通过折叠来观察和推理。
首先将纸张的上下两边对折,得到一条折痕。
然后再将左右两边对折,得到另一条折痕。
最后再将纸张的上下两边对折,得到第三条折痕。
此时,我们可以发现纸张被折痕分成了六个小矩形,它们的边长、宽、高都不相等。
假设原长方形的长为L,宽为W,则第一个小矩形的长为L/2,宽为W/2,高为W/2;第二个小矩形的长为L/2,宽为W/2,高为W/2;第三个小矩形的长为L/2,宽为W/2,高为L/2;第四个小矩形的长为L/2,宽为W/2,高为L/2;第五个小矩形的长为W/2,宽为L/2,高为W/2;第六个小矩形的长为W/2,宽为L/2,高为W/2。
因此,纸张的长、宽、高分别为L/2、W/2、L/2。
练习三:平行四边形的折叠3. 将一张平行四边形纸张对折,然后再对折,最后再对折。
初三数学折叠问题试卷

一、选择题(每题5分,共50分)1. 将一张长方形纸对折两次,折痕相交于纸的某个点,那么这个点在纸上的位置一定是:A. 纸的顶点B. 纸的中心点C. 纸的边缘点D. 无法确定2. 在折纸活动中,以下哪种折法可以使得折痕形成等边三角形?A. 将纸对折两次,折痕相交于纸的中心点B. 将纸对折一次,折痕与纸的边平行C. 将纸对折两次,折痕相互垂直D. 将纸对折一次,折痕与纸的边成45°角3. 在折纸过程中,以下哪种折法可以使得折痕形成的图形为正方形?A. 将纸对折两次,折痕相交于纸的中心点B. 将纸对折一次,折痕与纸的边平行C. 将纸对折两次,折痕相互垂直D. 将纸对折一次,折痕与纸的边成45°角4. 一个正方形纸张对折两次后,形成的折痕长度与原正方形边长的比是:A. 1:2B. 1:4C. 1:3D. 1:15. 在折纸活动中,以下哪种折法可以使得折痕形成的图形为等腰三角形?A. 将纸对折两次,折痕相交于纸的中心点B. 将纸对折一次,折痕与纸的边平行C. 将纸对折两次,折痕相互垂直D. 将纸对折一次,折痕与纸的边成45°角6. 一个矩形纸张对折两次后,形成的折痕长度与原矩形长度的比是:A. 1:2B. 1:4C. 1:3D. 1:17. 以下哪种折法可以使得折痕形成的图形为等腰梯形?A. 将纸对折两次,折痕相交于纸的中心点B. 将纸对折一次,折痕与纸的边平行C. 将纸对折两次,折痕相互垂直D. 将纸对折一次,折痕与纸的边成45°角8. 一个圆形纸张对折两次后,形成的折痕长度与原圆半径的比是:A. 1:2B. 1:4C. 1:3D. 1:19. 在折纸活动中,以下哪种折法可以使得折痕形成的图形为平行四边形?A. 将纸对折两次,折痕相交于纸的中心点B. 将纸对折一次,折痕与纸的边平行C. 将纸对折两次,折痕相互垂直D. 将纸对折一次,折痕与纸的边成45°角10. 一个三角形纸张对折两次后,形成的折痕长度与原三角形边长的比是:A. 1:2B. 1:4C. 1:3D. 1:1二、填空题(每题5分,共50分)11. 将一张正方形纸张对折两次,折痕相交于纸的中心点,那么形成的图形是______。
(完整版)中考数学几何图形折叠试题典题及解答
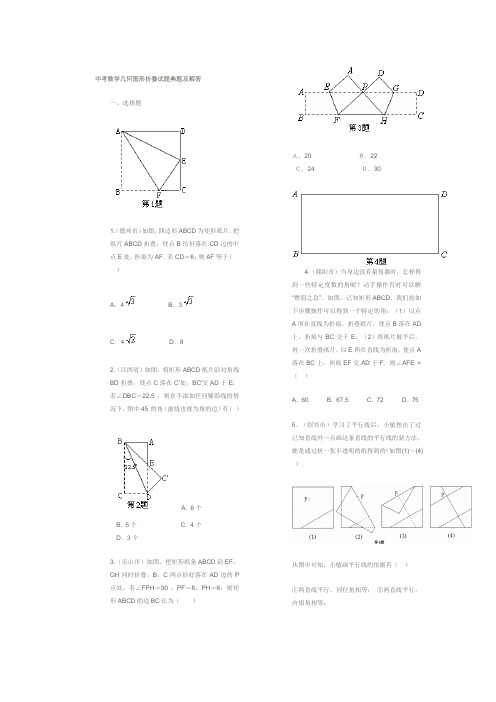
中考数学几何图形折叠试题典题及解答一、选择题1.(德州市)如图,四边形ABCD为矩形纸片.把纸片ABCD折叠,使点B恰好落在CD边的中点E处,折痕为AF.若CD=6,则AF等于()A.4B.3C.4D.82.(江西省)如图,将矩形ABCD纸片沿对角线BD折叠,使点C落在C′处,BC′交AD于E,若∠DBC=22.5°,则在不添加任何辅助线的情况下,图中45°的角(虚线也视为角的边)有()A.6个B.5个C.4个D.3个3.(乐山市)如图,把矩形纸条ABCD沿EF,GH同时折叠,B,C两点恰好落在AD边的P 点处,若∠FPH=90°,PF=8,PH=6,则矩形ABCD的边BC长为()A.20B.22C.24D.304.(绵阳市)当身边没有量角器时,怎样得到一些特定度数的角呢?动手操作有时可以解“燃眉之急”.如图,已知矩形ABCD,我们按如下步骤操作可以得到一个特定的角:(1)以点A所在直线为折痕,折叠纸片,使点B落在AD 上,折痕与BC交于E;(2)将纸片展平后,再一次折叠纸片,以E所在直线为折痕,使点A 落在BC上,折痕EF交AD于F.则∠AFE =()A.60°B.67.5°C.72°D.75°5. (绍兴市)学习了平行线后,小敏想出了过己知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如图(1)~(4)).从图中可知,小敏画平行线的依据有()①两直线平行,同位角相等;②两直线平行,内错角相等;③同位角相等,两直线平行;④内错角相等,两直线平行.A.①②B.②③C.③④D.①④6.(贵阳市)如图6-1所示,将长为20cm,宽为2cm的长方形白纸条,折成图6-2所示的图形并在其一面着色,则着色部分的面积为()A.34cm2 B.36cm2C.38cm2 D.40cm2二、填空题7.(成都市)如图,把一张矩形纸片ABCD沿E F折叠后,点C,D分别落在C′,D′的位置上,EC′交AD于点G.已知∠EFG=58°,那么∠B EG°.8. (苏州市)如图,将纸片△ABC沿DE折叠,点A落在点A′处,已知∠1+∠2=100°,则∠A的大小等于____________度.三、解答题9.(荆门市)如图1,在平面直角坐标系中,有一张矩形纸片OABC,已知O(0,0),A(4,0),C(0,3),点P是OA边上的动点(与点O、A不重合).现将△PAB沿PB翻折,得到△PDB;再在OC边上选取适当的点E,将△POE沿PE翻折,得到△PFE,并使直线PD、PF重合.设P(x,0),E(0,y),求y关于x的函数关系式,并求y的最大值;如图2,若翻折后点D落在BC边上,求过点P、B、E的抛物线的函数关系式;在(2)的情况下,在该抛物线上是否存在点Q,使△P EQ是以PE为直角边的直角三角形?若不存在,说明理由;若存在,求出点Q的坐标.10. (济宁市)如图,先把一矩形ABCD纸片对折,设折痕为MN,再把B点叠在折痕线上,得到△ABE.过B点折纸片使D点叠在直线AD上,得折痕PQ.求证:△PBE∽△QAB;你认为△PBE和△BAE相似吗?如果相似给出证明,如不相似请说明理由;如果沿直线EB折叠纸片,点A是否能叠在直线EC 上?为什么?11.(威海市)如图,四边形ABCD为一梯形纸片,AB∥CD,AD=BC.翻折纸片ABCD,使点A与点C重合,折痕为EF.已知CE⊥AB.(1)求证:EF∥BD;(2)若AB=7,CD=3,求线段EF的长.12. (烟台市)生活中,有人喜欢把传送的便条折成形状,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为2 6 cm,宽为xcm,分别回答下列问题:为了保证能折成图④的形状(即纸条两端均超出点P),试求x的取值范围.(2)如果不但要折成图④的形状,而且为了美观,希望纸条两端超出点P的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点M与点A的距离(用x表示).13. 将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′处,折痕为EF.(1)求证:△ABE≌△AD′F;(2)连接CF,判断四边形AECF是什么特殊四边形?证明你的结论.14.(孝感市)在我们学习过的数学教科书中,有一个数学活动,其具体操作过程是:第一步:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开(如图1);第二步:再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN(如图2).请解答以下问题:(1)如图2,若延长MN交BC于P,△BMP 是什么三角形?请证明你的结论.(2)在图2中,若AB=a,BC=b,a、b满足什么关系,才能在矩形纸片ABCD上剪出符合(1)中结论的三角形纸片BMP ?(3)设矩形ABCD的边AB=2,BC=4,并建立如图3所示的直角坐标系. 设直线BM′为y=kx,当∠M′BC=60°时,求k的值.此时,将△ABM′沿BM′折叠,点A是否落在EF上(E、F分别为AB、CD中点)?为什么?15.(邵阳市)如图①,△ABC中,∠ACB=90°,将△ABC沿着一条直线折叠后,使点A与点C 重合(图②).(1)在图①中画出折痕所在的直线l.设直线l 与AB,AC分别相交于点D,E,连结CD.(画图工具不限,不要求写画法)(2)请你找出完成问题(1)后所得到的图形中的等腰三角形.(不要求证明)16.(济宁市)如图,先把一矩形ABCD纸片对折,设折痕为MN,再把B点叠在折痕线上,得到△ABE.过B点折纸片使D点叠在直线AD上,得折痕PQ. 求证:△PBE∽△QAB;你认为△PBE和△BAE相似吗?如果相似给出证明,如补相似请说明理由;(3)如果直线EB折叠纸片,点A是否能叠在直线EC上?为什么?17.(临安市)如图,△OAB 是边长为的等边三角形,其中O是坐标原点,顶点B在y轴正方向上,将△OAB 折叠,使点A落在边OB上,记为A′,折痕为EF.(1)当A′E//x轴时,求点A′和E的坐标;(2)当A′E//x轴,且抛物线经过点A′和E时,求抛物线与x轴的交点的坐标;(3)当点A′在OB上运动,但不与点O、B重合时,能否使△A′EF成为直角三角形?若能,请求出此时点A′的坐标;若不能,请你说明理由.18.(南宁市)如图,在锐角△ABC中,BC=9,AH⊥BC于点H,且AH=6,点D为AB边上的任意一点,过点D作DE∥BC,交AC于点E.设△ADE的高AF为x(0<x<6),以DE为折线将△ADE翻折,所得的△A′DE与梯形DBCE重叠部分的面积记为y(点A关于DE的对称点A′落在AH所在的直线上).(1)分别求出当0<x≤3与3<x<6时,y与x 的函数关系式;(2)当x取何值时,y的值最大?最大值是多少?19.(宁夏回族自治区)如图,将矩形纸片ABCD沿对角线B D折叠,点C落在点E处,BE交AD于点F,连结AE.证明:(1)BF=DF;(2)AE∥BD.参考答案一、1.A 2.B 3.C 4.B 5.C 6.B二、7.648.50°三、9. 解:(1)由已知PB平分∠APD,PE平分∠OPF,且PD、PF重合,则∠OPE+∠APB= 90°.又∠APB+∠ABP=90°,∴∠OPE=∠PBA.∴Rt△POE∽Rt△BPA.∴.即.∴.且当x=2时,y 有最大值.由已知,△PAB、△POE均为等腰直角三角形,可得P(1,0),E(0,1),B(4,3).……6分设过此三点的抛物线为y=ax2+bx+c ,则∴y=.由(2)知∠EPB=90°,即点Q与点B重合时满足条件.直线PB为y=x-1,与y轴交于点(0,-1).将PB向上平移2个单位则过点E(0,1),∴该直线为y=x+1.由得∴Q(5,6).故该抛物线上存在两点Q(4,3)、(5,6)满足条件.10. 证明:(1)∵∠PBE+∠ABQ=180°-90°=90°,∠PBE+∠PEB=90°,∴∠ABQ=∠PEB.又∵∠BPE=∠AQB=90°,∴△PBE~△QAB.(2)∵△PBE~△QAB ,∴∵B Q=P B,∴.又∵∠ABE=∠BPE=90°,∴△PBE~△BAE.(3)点A能叠在直线EC上.由(2)得,∠AE B=∠CEB,∴EC和折痕AE重合.11. 解:(1)证明:过C点作CH∥BD,交AB的延长线于点H;连结AC,交EF于点K,则AK=CK.∵AB∥CD,∴BH=CD,BD=CH.∵AD=BC,∴AC=BD=CH.∵CE⊥AB,∴AE=EH.∴EK是△AHC的中位线.∴EK∥CH.∴EF∥BD.(2)解:由(1)得BH∥CD,EF∥BD,∴∠AEF=∠ABD.∵AB=7,CD=3,∴AH=10.∵AE=CE,AE=EH,∴AE=CE=EH=5.∵CE⊥AB,∴CH=5=BD.∵∠EAF=∠BAD,∠AEF=∠ABD,∴△AFE∽△ADB.∴.∴.12. 解:(1)由折纸过程知0<5x<26,,0<x <.(2)图④为轴对称图形,∴A M =.即点M与点A的距离是(13-x)cm.13. 证明:⑴由折叠可知:∠D=∠D′,CD=A D′,∠C=∠D′AE.∵四边形ABCD是平行四边形,∴∠B=∠D,AB=CD,∠C=∠BAD.∴∠B=∠D′,AB=AD′,∠D′AE=∠BAD,即∠1+∠2=∠2+∠3.∴∠1=∠3.∴△ABE ≌△AD′F.⑵四边形AECF是菱形.由折叠可知AE=EC,∠4=∠5.∵四边形ABCD是平行四边形,∴AD∥BC.∴∠5=∠6.∴∠4=∠6.∴AF=AE.∵AE=EC,∴AF=EC.又∵AF∥EC,∴四边形AECF是平行四边形.∵AF=AE,∴四边形AECF是菱形.14. 解:(1)△BMP是等边三角形.证明:连结AN.∵EF垂直平分AB,∴AN = BN.由折叠知AB = BN ,∴AN = AB = BN,∴△ABN为等边三角形.∴∠ABN =60°. ∴∠PBN =30°.又∵∠ABM =∠NBM =30°,∠BNM =∠A =9 0°.∴∠BPN =60°.∠MBP =∠MBN +∠PBN =60°.∴∠BMP =60°∴∠MBP =∠BMP =∠BPM =60°.∴△BMP为等边三角形 .(2)要在矩形纸片ABCD上剪出等边△BMP,则BC ≥BP.在Rt△BNP中,BN = BA =a,∠PBN =30°,∴BP =. ∴b≥. ∴a≤b .∴当a≤b时,在矩形上能剪出这样的等边△BMP.(3)∵∠M′BC =60°,∴∠ABM′=90°-60°= 30°.在Rt△ABM′中,tan∠ABM′ =. ∴tan3 0°=. ∴AM′ =.∴M′(,2). 代入y=kx中,得k== .设△ABM′沿BM′折叠后,点A落在矩形ABCD 内的点为A′.过A′作AH ⊥BC交BC于H.∵△A′BM′ ≌△ABM′,∴∠A′BM′=∠ABM′=3 0°, A′B = AB =2.∴∠A′BH=∠M′BH-∠A′BM′=30°.在Rt△A′BH中,A′H =A′B =1 ,BH=,∴.∴A'落在EF上.(图2)(图3)15.解:(1)如图.等腰三角形DAC.16.(1)证明:∵∠PBE+∠ABQ=180°-90°=90°,∠PBE+∠PEB=90°,∴∠ABQ=∠PEB.又∵∠BPE=∠AQB,∴△PBE∽△QAB.(2)∵△PBE∽△QAB,∴. ∵B Q=P B,∴.又∵∠ABE=∠BPE=90°,∴△PBE~△BAE.(3)点A能折叠在直线EC上.由(2)得,∠AEB=∠CEB,∴EC和折痕AE 重合.17. 解:(1)由已知可得∠A'OE=60o , A'E= AE.由A′E//x轴,得△OA'E是直角三角形.设A′的坐标为(0,b),则AE=A'E=b,OE=2b.∵b+2b=2+,∴b=1.∴A'、E的坐标分别是(0,1)与(,1).(2)因为A'、E在抛物线上,所以所以函数关系式为y =.由=0得,.与x轴的两个交点坐标分别是(-,0)与(,0).(3)不可能使△A'EF成为直角三角形.∵∠FA'E=∠FAE=60o,若△A'EF成为直角三角形,只能是∠A'EF=90o或∠A'FE=90o.若∠A'EF=90o,利用对称性,则∠AEF=90o, A'、E、A三点共线,O与A重合,与已知矛盾.同理若∠A'FE=90o也不可能.所以不能使△A′EF成为直角三角形.18. 解:(1)①当0<x≤3时,由折叠得到的△A'ED落在△ABC内部如图10(1),重叠部分为△A'ED.∵DE∥BC,∴∠ADE=∠B,∠AED=∠C.∴△ADE∽△ABC.∴.∴,即.又∵FA'=FA=x,∴y=DE·A'F=·x·x.∴(0<x≤3).②当3<x<6时,由折叠得到的△A'ED有一部分落在△ABC外,如图10(2),重叠部分为梯形EDPQ.∵FH=6-AF=6-x, A'H=A'F-FH=x-(6-x)=2x-6,又∵DE∥PQ,∴△A'PQ∽△A'DE.∴.∴∴.(2)当0<x≤3时,y的最大值;当3<x<6时,由,可知当x=4时,y的最大值y2=9.∵y1<y2,∴当x=4时,y有最大值y最大=9.19. 证明:(1)能正确说明∠ADB=∠EBD(或△ABF≌△EDF),∴BF=DF.(2)能得出∠AEB=∠DBE(或∠EAD=∠BD A),∴AE∥BD.。
初三折叠练习题

初三折叠练习题1. 问题描述在折纸练习中,我们使用一张矩形纸张,将其对折后再展开,然后再将其对折与前一次对折的线重合,如此往复。
则每次折叠的次数越多,纸张上出现的折痕就越多。
假设我们用N表示折叠次数,请你在此练习中回答一些相关问题。
2. 折叠练习过程初始时,我们用一张矩形纸张,宽度为W,高度为H,矩形的边界和对角线均与轴平行。
我们首先将其竖直对折,然后再展开,得到一组水平线。
接着,我们再将纸张水平对折,再展开,得到一组垂直线。
如此往复,每一次对折都会产生一组新的直线。
3. 练习题目(1) 对折N次后,纸张上共有多少条直线?(2) 在每次对折后,纸张上新增加的直线有哪些特点?4. 解答(1) 对折N次后,纸张上共有2^N-1条直线。
这是因为每次对折都会将纸张上已有的直线对折,同时产生一组新的直线。
第一次对折后,只有一条直线;第二次对折后,除了原有的直线,还会产生两条新的直线;第三次对折后,除了原有的直线,还会产生四条新的直线;以此类推,第N次对折后,除了原有的直线,还会产生2^(N-1)条新的直线。
所以总共的直线数为:总直线数 = 原有直线数 + 新增直线数= 1 + 2 + 4 + ... + 2^(N-1)= 2^N - 1(2) 在每次对折后,纸张上新增加的直线具有以下特点:- 每次对折都会在已有直线的交点处形成新的直线,这些交点称为折痕点。
- 每次对折后,新增的直线都与原有直线垂直,并且经过折痕点。
- 新增的直线在纸张上形成一组焦点,这组焦点随着对折次数的增加而变多。
5. 总结折纸练习是一种有趣的数学几何问题,通过对纸张的反复对折,我们可以观察到产生的折痕和直线的规律。
通过本次练习题,我们了解到对折N次后,纸张上共有2^N-1条直线,并且这些直线在纸张上的分布具有特殊的规律。
通过参与折纸练习,我们可以培养观察问题的能力和推理能力,同时也可以加深对几何知识的理解。
折纸练习题既有趣又有益,可以帮助我们加深对几何概念的理解,并培养数学思维的灵活性。
初二折叠重合练习题

初二折叠重合练习题练习题一:1. 将正方形A折叠成图形B,请用2D图示出该折叠过程。
2. 图形A是一个矩形,边长分别为6cm和4cm。
将图形A折叠成正方形B,请用2D图示出该折叠过程。
3. 折叠图形C,使得图形C的右半部分与左半部分完全重合。
请用2D图示出该折叠过程。
练习题二:1. 图形D是一个等腰直角三角形,底边长为8cm。
请将图形D折叠成一个等边三角形E,并用2D图示出该折叠过程。
2. 将正方体F展开成一个平面图形G,请用2D图示出该展开过程。
3. 图形H是一个五边形,在平面上无法通过折叠变化形状。
请阐述你的理由。
练习题三:1. 对称轴是指可以将一个图形平分成两部分的一条线。
请找出图形I的对称轴,并用2D图示出来。
2. 图形J是一个正方形,边长为10cm。
请用折叠的方式,使得图形J的上半部分与下半部分完全重合。
3. 图形K是一个等腰梯形,上底边长为8cm,下底边长为12cm,高为6cm。
请用折叠的方式,使得图形K的左半部分与右半部分完全重合,并用2D图示出该折叠过程。
练习题四:1. 图形L是一个长方形,长为12cm,宽为8cm。
请用折叠的方式,使得图形L的左上角与右下角完全重合。
2. 图形M是一个等腰直角三角形,直角边长为6cm,请用折叠的方式,使得图形M的直角顶点与直角边中点完全重合。
3. 图形N是一个由3个正方形拼接而成的图形。
请证明图形N的中心点与对角线起点、终点形成的直线上。
练习题五:1. 图形O是一个边长为14cm的正方形。
请按照折叠的方式,使得图形O折叠成一个长方形,并用2D图示出该折叠过程。
2. 图形P是一个边长为10cm的正方形。
请按照折叠的方式,使得图形P折叠成一个等腰直角三角形,并用2D图示出该折叠过程。
3. 图形Q是一个边长为16cm的正方形。
请按照折叠的方式,使得图形Q折叠成一个正三角形,并用2D图示出该折叠过程。
在学习几何折纸的过程中,通过练习折叠重合题目,可以帮助我们理解图形的对称性、平移性、变形等概念。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
GFEDCBA1如图,将边长为4的正方形纸片ABCD 折叠,使得点A 落在边CD 的中点E 处,折痕为FG ,点F 、G 分别在边AD 、BC 上,则折痕FG 的长度为( ) A. 25 B. 35 C. 26 D. 362.如图,在正方形ABCD 的边AB 上取一点E ,连接CE ,将△BCE 沿CE 翻折,点B 恰好与对角线AC 上的点F 重合,连接DF ,若BE =2,则△CDF 的面积是( B ) A .1 B .3 C .6D .3.如图,矩形ABCD 中,AB = 8,BC = 6,点P 为AD 边上一点,将△ABP 沿着BP 翻折至△EBP ,PE 与CD 交于点O ,且OE = OD ,则AP 的长为( ) A .4.8 B .5 C .4.5 D .44.如图,在△ABC 中,∠ABC =45°,AB =3,AD ⊥BC 于点D ,BE ⊥AC 于点E ,AE =1,连接DE ,将△AED 沿直线AE 翻折至△ABC 所在的平面内,得到△AEF ,连接DF ,过点D 作DG ⊥DE 交BE 于G ,.则四边形DFEG 的周长为( )A .8B .42C .22+4D .32+25.如图.△ABC 中.∠ABC =90°,BC =l .将△ABC 绕点B 逆时针旋转得△A 'BC '.C '恰好落在AC 边的中点处.连接AA ',取AA '的中点D ,则C 'D 的长为( )OECD ABPA.B.374C.52D.3546.如图,在△ABC中,∠ACB=90°,AC=BC=4,点D在AC上,点E在AB上,将△ADE沿直线DE翻折,点A的对称点A'落在BC上,在CD=1,则A'B'的长是()A.1B.C.D.7.如图,在△ABC中,AB=AC,∠BAC=120°,点D、E在边BC上,且∠DAE=60°.将△ADE沿AE翻折,点D的对应点是D',连接CD',若BD=4,CE=5,则DE的长为()A.92B.21C.13D.238.如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点处,两条折痕与斜边AB分别交于点E、F,则△B′DE的面积为()A.925B.1825C.1225D.24259等腰Rt△ABC,AC=BC=4,点E,F分别在边AB、BC上,将三角形沿EF翻折,使得B刚好落在AC的中点D处,则EF的长为( )A.55B.5C.25D.25E10.如图,Rt △ABC 中,∠C =90°,AC =8,BC =12,点D 为BC 边上的中点,将△ACD 沿AD 对折,使点C 落在同一平面内的点C '处,连接BC '',则BC ' 的长为( ). A .325B .325C .235D .36511 .如图,在菱形纸片ABCD 中,AB=8,∠A=60°,将菱形纸片翻折,使点A 落在CD 的中点E 处,折痕为FG.,点F 、G 分别在边AB 、AD 上,则EG 的长为( )28.5A 14.5B .4C .43D1213 如图在四边形ABCD 中,AD ∥BC,∠A=90°,∠ADC=120°,连接BD,把△ABD 沿BD 翻折,得到△BD,连接A ′C ,若AB=3,∠ABD=60°,则点D 到直线A ′C 的距离为( ) .7A 97.B 97.C 187.D F AGCEF AGD CE14.已知Rt △ABC 中,∠ACB =90°,AC =8,BC =4,D 为斜边AB 上的中点,E 是直角边AC 上的一点,连接DE ,将△ADE 沿DE 折叠至△A ′DE ,A ′E 交BD 于点F ,若△DEF 的面积是△ADE 面积的一半,则CE 的长为( )..2A B C .4D15.如图,△ABC 中,∠BAC =90°,AB =6,AC =8,点D 是BC 的中点,将△ABD ,将△ABD 沿AD 翻折得到△AED ,联结CE ,那么线段CE 的长等于( )A .125B .135C .145D .16516.如图,在Rt △ABC 中,∠ACB =90°,AC =,BC =,将边AC 沿CE 翻折,使点A 落在AB 上的点D 处,再将边BC 沿CF 翻折,使点B 落在CD 的延长线上的点B ′处,两条折痕与斜边AB 分别交于点E 、F ,则线段B ′F 的长为( ).A . 2B .3C .2D .317.如图,在Rt △ABC 中,∠ACB =90°,点D 是边AB 的中点,连结CD ,将△BCD 沿直线CD 翻折得到△ECD ,连结AE .若AC =6,CD =5,则线段AE 的长为( )12.5A 13.5B 14.5C 11.5D18、如图,矩形ABCD 中,AB =4,AD =6,点E 为BC 上一点,将△ABE 沿AE 折叠得到△AEF ,点H 为CD 上一点,将△CEH 沿EH 折叠得到△EHG ,且F 落在线段EG 上,当GF =GH 时,则BE 的长为( )..1A 3.2B .2C 5.2D19、将矩形ABCD 折叠,点A 与对角线BD 上的点G 重合,折痕BE 交AD 于点E ,点C 与对角线上的点H 重合,折痕DF 交BC 于点F .若AB =6,AD =8,则EH 的长为( ).2021 .在Rt△ABC中,∠ACB=90°,AC=3,BC=4,翻折∠C,使点C落在边AB的中点D 处,折痕为EF(E、F分别在边AC、BC上),则EF的长为(D)A.B.C.D.22.如图,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.过点D作DG∥BE,交BC于点G,连接FG交BD于点O.若AB=3,AD =4,则FG的长为()A.B.C.D.23.如图所示,ABCD为边长为1的正方形,E为BC边的中点,沿AP折叠使D点落在AE上的H处,连接PH并延长交BC于F点,则EF的长为( A )5.2A -5.2B -3C 1.4D2425、如图△ABC 中,∠ACB =90°,AC =8,BC =6,点E 是AB 中点,将△CAE 沿着直线CE 翻折,得到△CDE ,连接AD ,则线段AD 的长等于( )A .8B .C .D .1026、矩形ABCD 中,AB =3,CB =2,点E 为AB 的中点,将矩形右下角沿CE 折叠,使点B 落在矩形内部点F 位置,如图所示,则AF 的长度为( )A.B.2C.D.272829.如图,在Rt△ABC中,∠ACB=90°,AB=2,BC=2,点D为斜边AB的中点,连接CD,将△BCD沿CD翻折,使点B落在点E处,点F为直角边AC上一点,连接DF,将△ADF沿DF翻折,使点A与点E重合,则DF的长为(A).30.如图,在Rt△ACB中,∠ACB=90°,点D是边AB的中点,连接CD,将△BCD沿直线CD翻折得到△ECD,连接AE,若AC=5,CD=6.5,则线段AE的长为.31.如图,△ABC中,∠ACB=90°,BC=3,AC=4,点D是AB的中点,将△ACD沿CD翻折得到△ECD,连接AE,BE,则线段BE的长等于()A.B.C.D.232.如图,△ABC中,∠BAC=90°,AB=5,AC=12,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE,则线段CE的长等于()A.B.9C.D.33.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE使点B落在点F处,连接AF,当线段AF=AC时,BE的长为.34.如图,在Rt△ACB中,∠ACB=90°,AC=BC,点D是AB上的一个动点(不与点A,B重合),连接CD,将CD绕点C顺时针旋转90°得到CE,连接DE,DE与AC相交于点F,连接AE,若,AD=2BD,则CF等于()A.B.C.D.35.如图,等边三角形ABC边长为5、D、E分别是边AB、AC上的点,将△ADE沿DE折叠,点A恰好落在BC边上的点F处,若BF=2,则BD的长是()A.B.C.3D.236.如图,边长为2的正方形ABCD的对角线AC与BD交于点O,将正方形ABCD沿直线OM )DF折叠,点C落在对角线BD上的点E处,折痕DF交AC于点M,则(A .12BC.1- D.137.将矩形ABCD 按如图所示的方式折叠,BE ,EG ,FG 为折痕,若顶点A ,C ,D 都落在点O 处,且点B ,O ,G 在同一条直线上,同时点E ,O ,F 在另一条直线上,则ADAB的值为( )A .65BC .32D38.如图,正方形ABCD 中,6AB =,E 为AB 的中点,将ADE ∆沿DE 翻折得到FDE ∆,延长EF 交BC 于G ,FH BC ⊥,垂足为H ,连接BF 、DG .以下结论:①//BF ED ;②DFG DCG ∆≅∆;③FHB EAD ∆∆∽;④4tan 3GEB ∠=;⑤ 2.6BFG S ∆=;其中正确的个数是( )A .2B .3C .4D .539.如图,在正方形ABCD 中,E 是BC 边上的一点,4BE =,8EC =,将正方形边AB 沿AE折叠到AF ,延长EF 交DC 于G ,连接AC ,现在有如下4个结论:①45EAC ∠=︒;②FG FC =;③//FC AG ;④14GFC S ∆=.其中正确结论的个数是( )A BC DEFMO ABCDEFGOABCDEFG HA .1B .2C .3D .440.如图,在矩形ABCD 中,AB =3,AD =5,点E 在DC 上,将矩形ABCD 沿AE 折叠,点D 恰好落在BC 边上的点F 处,那么sin ∠EFC 的值为 .41.如图,在正方形ABCD 中,1BE =,将BC 沿CE 翻折,使B 点对应点刚好落在对角线AC上,将AD 沿AF 翻折,使D 点对应点刚好落在对角线AC 上,求EF = .42.如图,在矩形ABCD 中,AB =3,BC =2,H 是AB 的中点,将△CBH 沿CH 折叠,点B 落在矩形内点P 处,连接AP ,则tan ∠HAP = .43.如图,在正方形纸片ABCD 中,E 是CD 的中点,将正方形纸片折叠,点B 落在线段AE上ABCDEFXY的点G处,折痕为AF.若AD=4cm,则CF的长为cm.44.如图,矩形ABCD中,AB=36,BC=12,E为AD中点,F为AB上一点,将△AEF沿EF 折叠后,点A恰好落到CF上的点G处,则折痕EF的长是.45.如图,在矩形ABCD中,AB=1,BC=a,点E在边BC上,且BE=3α.连接AE,将△ABE5沿AE折叠,若点B的对应点B′落在矩形ABCD的边上,则a的值为.46.如图,正方形纸片ABCD的边长为12,E是边CD上一点,连接AE、折叠该纸片,使点A 落在AE上的G点,并使折痕经过点B,得到折痕BF,点F在AD上,若DE=5,则GE的长为.47.如图,在△ABC中,D是AC边上的中点,连结BD,把△BDC沿BD翻折,得到△BDC′,DC′与AB交于点E,连结AC′,若AD=AC′=2,BD=3,则点D到BC′的距离为()A.332B.3217C.7 D.1348.如图,在矩形ABCD中,AD=2.将∠A向内翻折,点A落在BC上,记为A′,折痕为DE.若将∠B沿EA′向内翻折,点B恰好落在DE上,记为B′,则AB=.4950515253545556575859 将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,3∠BAE=30°,AB=,折叠后,点C落在AD边上的C1l321S 4S 3S 2S 1处,并且点B 落在EC 1边上的B 1处.则BC 的长为( ) A .B .2C.3D .60.在直线l 上依次摆放着七个正方形(如图所示)。
