江苏省仪征市第三中学苏科版九年级下册数学课件:67用相似三角形解决问题1(共19张PPT)
合集下载
苏科版九年级数学下册第六章《相似三角形应用(1)》优课件
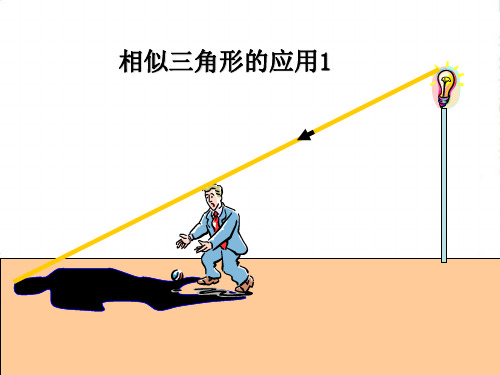
有多远吗?下面提供一种测量方法:在月圆时,
将一枚1元硬币,放在眼睛与月球之间,调整
硬币与眼睛间的距离,直到硬币刚好将月球遮
住,如果硬币与眼睛间的距离为2.72m,月球
的直径为3500km,硬币的直径为2.5cm,求
月球中心距离地球表面大约有多远?
A 视线
C OF
盲区
E
视点 D
视线
B
练习: 步枪在瞄准时的示意图如图,从 眼睛到准星的距离OE为80cm,步枪上 准星宽度AB为2mm,目标的正面宽度 CD为50cm,求眼睛到目标的距离OF。
A B 准星
A
C
O
BE
F D
1.已知如图△ABC中, ∠C=90o,BC=8cm,AC:AB=3:5,点P从点B 出发,沿BC向点C以2厘米/秒的速度移动 ,点Q从点C出发,沿CA向点A 以1厘米/ 秒的速度移动,如果P、Q分别从B、C同时 出发,经过多少秒时△CPQ∽△CBA?
A
Q
C B
拓展题
判定 2:如果一个三角形的两条边与另一个三角 形的两条边对应成比例,并且夹角相等,那么这两 个三角形相似. (两边对应成比例且夹角相等,两个三角形相似)
判定 3:如果一个三角形的三条边和另一个三角 形的三条边对应成比例,那么这两个三角形相似. (三边对应成比例,两个三角形相似)
复习
相构 造相似三角形求解 一般有以下步骤: ①审题 ②构建图形 ③利用相似解决问题
现实生活中还有许多问题我们可
以利用相似三角形的知识去解决,上 述题目只能算是沧海一粟,这就需要 我们做个有心人,从数学角度学会发 现问题,提出问题,并且尝试从不同 的角度、不同的途径去分析问题和解 决问题,不断锻炼我们的思维能力。
苏教版九年级数学下册课件:6.7 用相似三角形解决问题(1) (共14张PPT)

A
Aʹ
在平行光线的照射下, 不同物体的物高与影长成比例.
Cʹ
B
C
Bʹ
你发现的这些特点有什么利用价值?你能举 个例子吗?
例1 在阳光下,高为6 m的旗杆在地面上的 影长为4 m,在同一时刻,测得附近一座建筑物 的影长为36 m.求这座建筑物的高度.
冲一冲 再研究什么? 中心投影有什么特点?
一般的,在点光源的照射下,同一物体在不同 的位置,它的物高与影长不成比例.
4.如图,圆桌正上方的灯泡O(看成一个点)发出 的光线照射到桌面后,在地面上形成影.设桌面的半径 AC=0.8m,桌面与地面的距离AB=1m,灯泡与桌面 的距离OA=2m,求地面上形成的影的面积.
作业
1 .完成教材85页:习题1、2、3、6 . 2 .完成《学习与评价》6.7(1)(2).
§6.7 用相似三角形解决问题 (1)
连连看 你看见了什么?
它们有区别吗?
在平行光的照射下, 物体所产生的影称为平 行投影.通常,我们把 太阳光看成平行投影. 在点光源的照射下, 物体所产生的影称为中心 投影.通常,路灯、台灯、 手电筒……的光可以看成 是从一个点出发的.
试一试 研究什么?
平行投影有什么特点?
2.已知为了测量路灯CD的高度,把一根长1.5m的 竹竿AB竖直立在Байду номын сангаас平地面上.测得竹竿的影子长为1m, 然后拿竹竿向远处路灯的方向走了4m.再把竹竿竖直 立在地面上,竹竿的影长为1.8m,求路灯的高度.
C
A D B A' E B ' E '
3.如图,AB和DE是直立在地面上的两根立柱, AB=5 m,某一时刻,AB在阳光下的投影BC=4 m. (1)请你在图中画出此时DE在阳光下的投影,并简述 画图步骤. (2)在测量AB的投影长时,同时测得DE在阳光下的投 影长为6m,请你计算DE的长.
Aʹ
在平行光线的照射下, 不同物体的物高与影长成比例.
Cʹ
B
C
Bʹ
你发现的这些特点有什么利用价值?你能举 个例子吗?
例1 在阳光下,高为6 m的旗杆在地面上的 影长为4 m,在同一时刻,测得附近一座建筑物 的影长为36 m.求这座建筑物的高度.
冲一冲 再研究什么? 中心投影有什么特点?
一般的,在点光源的照射下,同一物体在不同 的位置,它的物高与影长不成比例.
4.如图,圆桌正上方的灯泡O(看成一个点)发出 的光线照射到桌面后,在地面上形成影.设桌面的半径 AC=0.8m,桌面与地面的距离AB=1m,灯泡与桌面 的距离OA=2m,求地面上形成的影的面积.
作业
1 .完成教材85页:习题1、2、3、6 . 2 .完成《学习与评价》6.7(1)(2).
§6.7 用相似三角形解决问题 (1)
连连看 你看见了什么?
它们有区别吗?
在平行光的照射下, 物体所产生的影称为平 行投影.通常,我们把 太阳光看成平行投影. 在点光源的照射下, 物体所产生的影称为中心 投影.通常,路灯、台灯、 手电筒……的光可以看成 是从一个点出发的.
试一试 研究什么?
平行投影有什么特点?
2.已知为了测量路灯CD的高度,把一根长1.5m的 竹竿AB竖直立在Байду номын сангаас平地面上.测得竹竿的影子长为1m, 然后拿竹竿向远处路灯的方向走了4m.再把竹竿竖直 立在地面上,竹竿的影长为1.8m,求路灯的高度.
C
A D B A' E B ' E '
3.如图,AB和DE是直立在地面上的两根立柱, AB=5 m,某一时刻,AB在阳光下的投影BC=4 m. (1)请你在图中画出此时DE在阳光下的投影,并简述 画图步骤. (2)在测量AB的投影长时,同时测得DE在阳光下的投 影长为6m,请你计算DE的长.
用相似三角形解决问题(课件)

B
A′
B′
02
知识精讲
建模:
如图,人的身高为O’B’=n,影长为A’B’=n,旗杆的影长为AB=m,求旗
杆OB的高度
物高 :参照物高 = 物影 :参照物影
【分析】
物高:物影=参照物高:参照物影
∵平行光,∴∠A=∠A’
O
∵∠B=∠E=90°,∴△AOB∽△A’O’B’
’’
∴ = ,∴ =
∴AC=32m+115m=147m
02
知识精讲
求不能直接测量的物体的高度,通常用“在平行光的照射下,
在同一时刻,不同物体的物高与影长成比例”的原理解决
结论公式:
物高 :参照物高 = 物影 :参照物影
或物高:物影=参照物高:参照物影
【平行投影——测高度】
知识精讲
例1、已知一直立的电线杆在地面上的影长为20m,同时,高为1.4m的测’’ ’’ ’ Nhomakorabea’
∴
= ,即OB=
O′
a
A
m
B A′ n B′
02
知识精讲
Q6:古埃及国王曾请一位学者测量金字塔的高度.当这位学者确认在阳光
下他的影长等于他的身高时(如图),要求他的助手同时测出金字塔的影
长 DB 以及金字塔底部正方形的边长,这样他就知道了金字塔的高度.他是
苏科版九年级下册第6章图形的相似
用相似三角形解决问题
Solve problems with similar triangles
教学目标
01
了解平行投影与中心投影的意义,会利用平行投影与中心
投影画图
02
理解在平行光与点光源的照射下,物体的物高与影长的关
优秀课件苏教版九年级数学下册-6.7 相似三角形的应用课件 (共23张PPT)

相似三角形的应用
相似三角 形有哪些 性质?
议一议:如何 测量学校旗杆 的高度呢?
A
友情提示:阳 光是平行线
x
D
1.5m
B
10m
C
E 1m
F
古希腊,有一位伟大的科学家叫塔列斯。 一天,希腊国王阿马西斯对他说:“你说你 什么都知道,那就请你测量一下埃及的金字 塔的高度吧!”这在当时的条件下是个大难 题,因为人很难爬上塔顶的,假若你就是当 时的科学家塔列斯,该如何测量呢? 画实物相似的平面图形
测量不能直接到达的两点间的距离, 常构造如下两种相似三角形求解。
A E D C B D A C
?
B
?
E
测量方法:
如图所示,为了测量金字塔的高度OB,先 竖一根已知长度的木棒O’B’,比较棒子的影 长A’B’与金字塔的影长AB,即可近似算出金 字塔的高度OB。
O
O’
A A’ B’
?
B
数学原理
解:由于太阳光是平行光线,因此 ∠ OAB = ∠ O’A’B’ 又因为∠ ABO = ∠ A’B’AB﹕ A’B’,
放学回家的路上,小明想起今天课上学过测量高度的 方法,他想测路边的一棵树的高度。他想了想拿出刻度尺, 如图比划起来,同学们小明这种方法能近似的算出树的高 度吗?若能,他需要量出那些线段的长度? D
A
B
C
G
H
F
E
笔直的公路需要穿过一座 小山同学们你能想办法估计隧 道的长度吗?请你设计测量方 案。
B
C
公路
E
F
A
B
C
公路
A
E
F
通过今天的学习,
你有什么收获和感想?
相似三角 形有哪些 性质?
议一议:如何 测量学校旗杆 的高度呢?
A
友情提示:阳 光是平行线
x
D
1.5m
B
10m
C
E 1m
F
古希腊,有一位伟大的科学家叫塔列斯。 一天,希腊国王阿马西斯对他说:“你说你 什么都知道,那就请你测量一下埃及的金字 塔的高度吧!”这在当时的条件下是个大难 题,因为人很难爬上塔顶的,假若你就是当 时的科学家塔列斯,该如何测量呢? 画实物相似的平面图形
测量不能直接到达的两点间的距离, 常构造如下两种相似三角形求解。
A E D C B D A C
?
B
?
E
测量方法:
如图所示,为了测量金字塔的高度OB,先 竖一根已知长度的木棒O’B’,比较棒子的影 长A’B’与金字塔的影长AB,即可近似算出金 字塔的高度OB。
O
O’
A A’ B’
?
B
数学原理
解:由于太阳光是平行光线,因此 ∠ OAB = ∠ O’A’B’ 又因为∠ ABO = ∠ A’B’AB﹕ A’B’,
放学回家的路上,小明想起今天课上学过测量高度的 方法,他想测路边的一棵树的高度。他想了想拿出刻度尺, 如图比划起来,同学们小明这种方法能近似的算出树的高 度吗?若能,他需要量出那些线段的长度? D
A
B
C
G
H
F
E
笔直的公路需要穿过一座 小山同学们你能想办法估计隧 道的长度吗?请你设计测量方 案。
B
C
公路
E
F
A
B
C
公路
A
E
F
通过今天的学习,
你有什么收获和感想?
【最新】苏科版九年级数学下册第六章《用相似三角形解决问题(1)》公开课课件.ppt

杆影长度 甲 乙 丙 通过观察,你发现了什么?
2 3
1.5 2.25
2.2 3.3
木杆 木杆长度 杆影长度 杆影长度 木杆长度
甲
2
3
1.5
乙
1.5
2.25
1.5
丙
2.2
3.3
1.5
2 31.5 2.25来自2.2 3.3在平行光线的照射下,物体所产生的影称为平行投影.
结论 在平行光的照射下,在同一时刻,
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
A
CD
B
你能说出理由吗?
C DB
AC=CD+DB
A
C
DB
如果测得金字塔的阴影DB的长为32m,金
字塔底边的长为230m,请计算出这座金字塔的
高度.
AC=CD+DB=115+32=147
如图,阳光通过窗口照到教室内,竖直窗 框在地面上留下2.1m长的影子如图所示,已知窗 框的影子DE到窗下墙脚的距离CE=3.9m,窗口 底边离地面的距离BC=1.2m,试求窗口的高度. (即AB的值)
不同物体的物高与影长成比例.
2 3
1.5 2.25
2.2 3.3
木杆 木杆长度 杆影长度 杆影长度 木杆长度
甲
2
3
1.5
乙
1.5
2.25
1.5
丙
2.2
3.3
1.5
2 31.5 2.25来自2.2 3.3在平行光线的照射下,物体所产生的影称为平行投影.
结论 在平行光的照射下,在同一时刻,
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
A
CD
B
你能说出理由吗?
C DB
AC=CD+DB
A
C
DB
如果测得金字塔的阴影DB的长为32m,金
字塔底边的长为230m,请计算出这座金字塔的
高度.
AC=CD+DB=115+32=147
如图,阳光通过窗口照到教室内,竖直窗 框在地面上留下2.1m长的影子如图所示,已知窗 框的影子DE到窗下墙脚的距离CE=3.9m,窗口 底边离地面的距离BC=1.2m,试求窗口的高度. (即AB的值)
不同物体的物高与影长成比例.
苏科版九年级数学下册第六章《相似三角形(1)》公开课课件

A
E
2
3F
1
B
D
C
解: △DEF ∽ △ABC
由三角形中位线性质,得
A
1
1
1
EF= 2 BC, DE= 2 AB, DF= 2 AC. F
E
∴ EFDE DF1 BC AB AC 2
又由三角形中位线性质,可知
B
C
D
EF∥BC, DE ∥ AB, DF ∥ AC.
∴四边形AFDE、四边形BDEF、
四边形CEFD是平行四边形
三角形相似的一种判定方法)
小试牛刀
1、如图
AB BC AC AB BC AC
且 A=A' B=B ' C=C'
则△ABC __∽__ △A'B'C'
A C
A' C'
B B'
小试牛刀
2、判断下图所示两三角形是否相似?
7
40º
5
94º
46º
8
∽
28
40º
20
94º
46º
32
小试牛刀
3、如图,DE∥BC,
ABC
相似用符号表示为
:
△ABC ∽ △ ABC
读作:△ABC相似于△ A'B'C'
注意
要把表示对应角顶点的字 母写在对应的位置上!
用符号语言表示:
C
A
B
C'
∵ ∠A= ∠A' 、∠B= ∠B' 、 ∠C=∠C'
AB BC CA A'B' B'C' C'A'
【最新】苏科版九年级数学下册第六章《相似三角形应用(1)》公开课课件.ppt
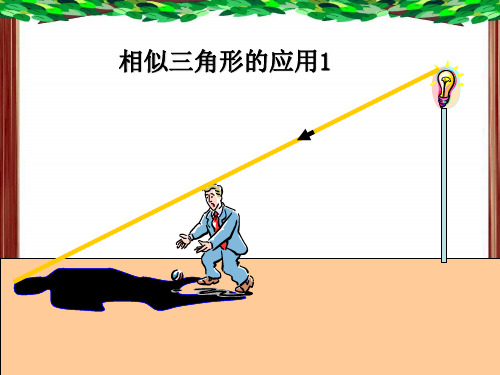
∴厚度( a - nb )÷2
路灯、台灯、手电筒的光线可以看成 是从一个点发出的。
像这样,在点光源的照射下,物体所 产生的影称为中心投影。
例4、 我侦察员孙程在距敌方200米的地方发 现敌人的一座建筑物,但不知其高度又不能靠近 建筑物测量,机灵的侦察员食指竖直举在右眼前, 闭上左眼,并将食指前后移动,使食指恰好将该 建筑物遮住。若此时眼睛到食指的距离约为 40cm,食指的长约为8cm,你能根据上述条件计 算出敌方建筑物的高度吗?请说出你的思路。
练习:小明把手臂水平向前伸直,手持 长为a的小尺竖直,瞄准小尺的两端E、F, 不断调整站立的位置,使站在点D处正好看
到旗杆的顶部和底部(如图)。如果小明 的手臂长l =40cm,小尺长a =20cm,点D 到旗杆的距离AD=40m,求旗杆的高B 度。
E a
lF
D
A
例5、 你知道月球中心距离地球表面大约
B
16m C 0.5m ┛ 1mO A (第1题)
?
┏
D
例3: 如图,已知零件的外径为a,要求它的
厚度x,需先求出内孔的直径AB,现用一个 交叉卡钳(两条尺长AC和BD相等)去量,若 OA:OC=OB:OD=n,且量得CD=b,求厚度x。
(分析:如图,要想求
O
厚度x,根据条件可知,
首先得求出内孔直径AB。
A B 准星
A
C
O
BE
F D
1.已知如图△ABC中, ∠C=90o,BC=8cm,AC:AB=3:5,点P从点B 出发,沿BC向点C以2厘米/秒的速度移动 ,点Q从点C出发,沿CA向点A 以1厘米/ 秒的速度移动,如果P、Q分别从B、C同时 出发,经过多少秒时△CPQ∽△CBA?
新苏科版九年级数学下册第六章《相似三角形应用(1)》公开课课件

像这样,在点光源的照射下,物体所 产生的影称为中心投影。
例4、 我侦察员孙程在距敌方200米的地方发 现敌人的一座建筑物,但不知其高度又不能靠近 建筑物测量,机灵的侦察员食指竖直举在右眼前, 闭上左眼,并将食指前后移动,使食指恰好将该 建筑物遮住。若此时眼睛到食指的距离约为 40cm,食指的长约为8cm,你能根据上述条件计 算出敌方建筑物的高度吗?请说出你的思路。
A
梯上点D距墙70cm,BD长 55cm,求梯子AB的长。
D
B E
C
岸选定一个目标作为点A,再在河的这一边选点B 和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视 线确定BC和AE的交点D.此时如果测得BD=120 米,DC=60米,EC=50米,求两岸间的大致距离AB.
A
例2.如图:为了估算河的宽度,我们可以在河对
判定 3:如果一个三角形的三条边和另一个三角 形的三条边对应成比例,那么这两个三角形相似. (三边对应成比例,两个三角形相似)
复习
相似三角形的性质
性质 1:相似三角形的对应边成比例,对应角相等
性质 2:相似三角形的对应高的比等于相似比
相似三角形的对应中线的比等于相似比
相似三角形的对应角平分线的比等于相似比
┏
?
D
O 1m 0.5m A ( 第 1题 )
┛
如图,已知零件的外径为a,要求它的 厚度x,需先求出内孔的直径AB,现用一个 交叉卡钳(两条尺长AC和BD相等)去量,若 OA:OC=OB:OD=n,且量得CD=b,求厚度x。
(分析:如图,要想求 厚度x,根据条件可知, 首先得求出内孔直径AB。 而在图中可构造出相似 形,通过相似形的性质, 从而求出AB的长度。)
有多远吗?下面提供一种测量方法:在月圆时, 将一枚1元硬币,放在眼睛与月球之间,调整 硬币与眼睛间的距离,直到硬币刚好将月球遮 住,如果硬币与眼睛间的距离为2.72m,月球 的直径为3500km,硬币的直径为2.5cm,求 月球中心距离地球表面大约有多远?
例4、 我侦察员孙程在距敌方200米的地方发 现敌人的一座建筑物,但不知其高度又不能靠近 建筑物测量,机灵的侦察员食指竖直举在右眼前, 闭上左眼,并将食指前后移动,使食指恰好将该 建筑物遮住。若此时眼睛到食指的距离约为 40cm,食指的长约为8cm,你能根据上述条件计 算出敌方建筑物的高度吗?请说出你的思路。
A
梯上点D距墙70cm,BD长 55cm,求梯子AB的长。
D
B E
C
岸选定一个目标作为点A,再在河的这一边选点B 和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视 线确定BC和AE的交点D.此时如果测得BD=120 米,DC=60米,EC=50米,求两岸间的大致距离AB.
A
例2.如图:为了估算河的宽度,我们可以在河对
判定 3:如果一个三角形的三条边和另一个三角 形的三条边对应成比例,那么这两个三角形相似. (三边对应成比例,两个三角形相似)
复习
相似三角形的性质
性质 1:相似三角形的对应边成比例,对应角相等
性质 2:相似三角形的对应高的比等于相似比
相似三角形的对应中线的比等于相似比
相似三角形的对应角平分线的比等于相似比
┏
?
D
O 1m 0.5m A ( 第 1题 )
┛
如图,已知零件的外径为a,要求它的 厚度x,需先求出内孔的直径AB,现用一个 交叉卡钳(两条尺长AC和BD相等)去量,若 OA:OC=OB:OD=n,且量得CD=b,求厚度x。
(分析:如图,要想求 厚度x,根据条件可知, 首先得求出内孔直径AB。 而在图中可构造出相似 形,通过相似形的性质, 从而求出AB的长度。)
有多远吗?下面提供一种测量方法:在月圆时, 将一枚1元硬币,放在眼睛与月球之间,调整 硬币与眼睛间的距离,直到硬币刚好将月球遮 住,如果硬币与眼睛间的距离为2.72m,月球 的直径为3500km,硬币的直径为2.5cm,求 月球中心距离地球表面大约有多远?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
的影长为2.1m,此时她身后一棵水杉树的影长为
10.5m,则这棵水杉树高为 (
).
A.7.5m B.8m C.14.7m D.15.75m
3.书本配套练习1. 4.书本配套练习2.
5.小明测得旗杆的影长为12米,同一时 刻为高每加呢把度1升个?.。15星旗米你米期仪。的知式一于道标上,是他秆午想小竖是不学明怎立校想很么在内测快地计量的就算上全咱算的,体们出它吗旗师了?的生杆旗影都的杆长要高的参度
A
F
C
B D
• 张明同学想利用影子测校园内的树高.他在 某一时刻测得小树高为1.5米时,其影长为 1.2米。当他测量教学楼旁一棵大树影长时, 因大树靠近教学楼,有一部分影长在墙上.经 测量,地面部分影长为6.4米,墙上影长为1.4 米,那么大树的高约为_____米
A
G
C
B D
3.皮皮欲测楼房高度,他借助一长5m的标 竿,当楼房顶部、标竿顶端与他的眼睛在 一条直线 上时,其他人测出 AB=4m,AC=12m。已知皮皮眼睛离地面1.6m. 请你帮他算出楼房的高度。
块积水处C看到塔顶的倒影,已知小明的眼部离地
面的高度DE是1.5米,塔底中心B到积水处C的距离
是40米.求塔高AB?
A
解:∵∠DEC=∠ABC=90° ∠DCE=∠ACB
∴△DEC∽△ABC
AB BC
D
CE
AB 40 1.5 2
EC
B
AB 30
答:塔高30米.
前提条件:同一时刻、同一地点
数学实验室
在学校操场上分别树立长度不同的甲,乙, 丙3根木杆,在同一时刻分别测量出3根木杆在 阳光下的影长,有关数据如下表
通过观察、计算,你发现了什么?
结论:
在平行光线的照射下,在同一时刻,不同 物体的物高与影长成比例
物高 影长
k
画在课本P114尝试1中
(1)在某一时刻,甲木杆在阳光下的影长如图, 你能画出此时乙,丙杆的影长吗?
解:设高楼的高度为x米,则
1.8 x 3 60
?
x 60 1.8
3
1.8
x 36
60米
3米
答:楼高36米.
1.在阳光下,身高1.68m的小强在地面上的影长为 2m,在同一时刻,测得旗杆在地面上的影长为 16m.求旗杆的高度(精确到0.1m).
2.身高为1.5m的小华在打高尔夫球,她在阳光下
B
D B
A
2 1
A D
A
CB
C
C
D
O
E
CA
B
B
A D
B
C
AC O
BA D D
E
C
6.7 用相似三角形解决问题(1)
光线在直线传播过程中,遇到不透明的物体, 在这个物体的后面光线不能到达的区域便产生影.
太阳光线可以看成是平行光线.
平行投影:太阳光线可以看成平行光线.像这样, 在平行光线的照射下,物体所产生的影称为平行 投影
甲
丙
乙
将这3个直角三角形平移到同一平面内,可 以得到如图的图形:
请同学们思考:如何用三角形相似的知识 说明在平行光线的照射下,不同物体的物高与 影长成比例.
A
甲
A1
丙
乙
C B1 B
例1.在同一时刻物体的高度与它的影长成正比 例,在某一时刻,有人测得一高为1.8米的竹竿
的影长为3米,某一高楼的影长为60米,那么高楼 的高度是多少米?
F
E D
A
B
C
小丽利用影长测量学校旗杆的高度.由于旗杆靠 近一个建筑物,在某一时刻旗杆影子中的一部分映在 建筑物的墙上.小丽测得旗杆AB在地面上的影长BC 为20m,在墙上的影长CD为4m,同时又测得竖立于 地面的1m长的标杆影长为0.8m,请帮助小丽求出旗 杆的高度.
3.小明要测量一座古塔的高度,从距他2米的一小
例2:张明同学想利用影子测校园内的树高.他在 某一时刻测得小树高为1.5米时,其影长为1.2米。 当他测量教学楼旁一棵大树影长时,因大树靠近 教学楼,有一部分影长在墙上.经测量,地面部分 影长为6.4米,墙上影长为1.4米,那么大树的高约 为_____米
A
C B
DE
• 张明同学想利用影子测校园内的树高.他在 某一时刻测得小树高为1.5米时,其影长为 1.2米。当他测量教学楼旁一棵大树影长时, 因大树靠近教学楼,有一部分影长在墙上.经 测量,地面部分影长为6.4米,墙上影长为1.4 米,那么大树的高约为_____米
