2019年初中数学突破中考压轴题几何模型之正方形的半角模型教案(有答案)
九年级中考几何模型之半角模型详解

中考几何模型之半角模型【模型由来】半角模型是指:共顶点的两个一大一小的角,其中小角是大角的一半。
如下图中:若小角∠EAD等于大角∠BAC的一半,我们习惯上称之为“半角模型”。
【模型思想】通过旋转变化后构造全等三角形,实线边的转化。
【基本模型】类型一、90°中夹45°(正方形中的半角模型)条件:在正方形ABCD中,E、F分别是BC、CD边上的点,∠EAF=45°,BD为对角线,交AE于M点,交AF于N点。
结论①:图1、2中,EF=BE+FD;证明:如图3中,将AF绕点A顺时针旋转90°,F点落在F’处,连接BF’,∴∠EAF’=90°-∠EAF=90°-45°=45°=∠EAF,且AE=AE,AF=AF’,∴△FAE≌△F’AE(SAS),∴EF=EF’,又∠D=∠ABF’=90°,∠ABE=90°,∴∠ABE+∠ABF’=90°+90°=180°,∴F’、B、E三点共线,∴EF’=BE+BF’=BE+DF。
结论②:图2中MN²=BM²+DN²;证明:如图4中,将AN绕点A顺时针旋转90°,N点落在N’处,连接AN’、BN’、MN’,∴∠N’AM=90°-∠EAF=90°-45°=45°=∠MAN,且AM=AM,AN=AN’,∴△MAN’≌△MAN(SAS),∴MN=MN’,又∠ADN=45°=∠ABN ’,∠ABD=45°,∴∠MBN ’=∠ABD+∠ABN ’=45°+45°=90°,∴在Rt △MBN ’中,MN ’²=BM ²+BN ’²,即MN ²=BM ²+BN ’²。
结论③:图1、2中EA 平分∠BEF ,FA 平分∠DFE 。
人教版中考数学压轴题解题模型----几何图形之半角模型(含解析)【范本模板】

几何图形之半角模型主题半角模型教学内容教学目标1。
掌握正方形的定义,弄清正方形与平行四边形、菱形、矩形的关系。
2。
掌握正方形的性质定理1和性质定理2。
3.正确运用正方形的性质解题.4。
通过四边形的从属关系渗透集合思想。
5.通过理解四种四边形内在联系,培养学生辩证观点。
知识结构正方形的性质因为正方形是特殊的平行四边形,还是特殊的矩形,特殊的菱形,所以它具有这些图形性质的综合,因此正方形有以下性质(由学生和老师一起总结)。
正方形性质定理1:正方形的四个角都是直角,四条边相等。
正方形性质定理2:正方形的两条对角线相等并且互相垂直平分,每一条对角线平分一组对角。
说明:定理2包括了平行四边形,矩形,菱形对角线的性质,一个题设同时有四个结论,这是该定理的特点,在应用时需要哪个结论就用哪个结论,并非把结论写全。
小结:(1)正方形与矩形,菱形,平行四边形的关系如上图(2)正方形的性质:①正方形对边平行。
②正方形四边相等.③正方形四个角都是直角。
④正方形对角线相等,互相垂直平分,每条对角线平分一组对角.典型例题精讲例1.如图,折叠正方形纸片ABCD ,先折出折痕BD ,再折叠使AD 边与对角线BD 重合,得折痕DG ,使2AD =,求AG .【解析】:作GM ⊥BD ,垂足为M . 由题意可知∠ADG=GDM , 则△ADG ≌△MDG . ∴DM=DA=2. AC=GM 又易知:GM=BM .而BM=BD-DM=22-2=2(2—1), ∴AG=BM=2(2—1).例2 .如图,P 为正方形ABCD 内一点,10PA PB ==,并且P 点到CD 边的距离也等于10,求正方形ABCD 的面积?【解析】:过P 作EF AB ⊥于F 交DC 于E .设PF x =,则10EF x =+,1(10)2BF x =+.由222PB PF BF =+. 可得:222110(10)4x x =++. 故6x =.216256ABCD S ==.例3。
初中数学突破中考压轴题几何模型之正方形的半角模型教案

AB CD E F 12G 正方形角含半角模型提升例1.如图,折叠正方形纸片ABCD ,先折出折痕BD ,再折叠使AD 边与对角线BD 重合,得折痕DG ,使2AD =,求AG .例2 .如图,P 为正方形ABCD 内一点,10PA PB ==,并且P 点到CD 边的距离也等于10,求正方形ABCD 的面积?例3. 如图,E 、F 分别为正方形ABCD 的边BC 、CD 上的一点,AM EF ⊥,•垂足为M ,AM AB =,则有EF BE DF =+,为什么?例 4. 如图,在正方形ABCD 的BC 、CD 边上取E 、F 两点,使45EAF ∠=,AG EF ⊥于G . 求证:AG AB =例 5.(1) 如图1,在正方形ABCD 中,点E ,F 分别在边BC ,CD 上,AE ,BF 交于点O ,90AOF ︒∠=.求证:BE CF =.(2) 如图2,在正方形ABCD 中,点E ,H ,F ,G 分别在边AB ,BC ,CD ,DA 上,EF ,GH 交于点O ,90FOH ︒∠=,4EF =.求GH 的长.【双基训练】1. 如图6,点A 在线段BG 上,四边形ABCD 与DEFG 都是正方形,•其边长分别为3cm 和5cm ,则CDE ∆的面积为________2cm .(6) (7) 2.你可以依次剪6张正方形纸片,拼成如图7所示图形.•如果你所拼得的图形中正方形①的面积为1,且正方形⑥与正方形③的面积相等,•那么正方形⑤的面积为________. 3.如图9,已知正方形ABCD 的面积为35平方厘米,E 、F 分别为边AB 、BC 上的点.AF 、CE 相交于G ,并且ABF ∆的面积为14平方厘米,BCE ∆的面积为5平方厘米,•那么四边形BEGF 的面积是________.4. 如图,A 、B 、C 三点在同一条直线上,2AB BC =。
分别以AB 、BC 为边作正方形ABEF 和正方形BCMN ,连接FN , EC 。
初中数学突破中考压轴题几何模型之正方形的半角模型教案有答案

初中数学突破中考压轴题几何模型之正方形的半角模型教案有答案 WTD standardization office【WTD 5AB- WTDK 08- WTD 2C】1.掌握正方形的定义,弄清正方形与平行四边形、菱形、矩形的关系。
2.掌握正方形的性质定理1和性质定理2。
3.正确运用正方形的性质解题。
4.通过四边形的从属关系渗透集合思想。
5.通过理解四种四边形内在联系,培养学生辩证观点。
正方形的性质因为正方形是特殊的平行四边形,还是特殊的矩形,特殊的菱形,所以它具有这些图形性质的综合,因此正方形有以下性质(由学生和老师一起总结)。
正方形性质定理1:正方形的四个角都是直角,四条边相等。
正方形性质定理2:正方形的两条对角线相等并且互相垂直平分,每一条对角线平分一组对角。
说明:定理2包括了平行四边形,矩形,菱形对角线的性质,一个题设同时有四个结论,这是该定理的特点,在应用时需要哪个结论就用哪个结论,并非把结论写全。
小结:(1)正方形与矩形,菱形,平行四边形的关系如上图(2)正方形的性质:①正方形对边平行。
②正方形四边相等。
③正方形四个角都是直角。
④正方形对角线相等,互相垂直平分,每条对角线平分一组对角。
例1.如图,折叠正方形纸片ABCD,先折出折痕BD,再折叠使AD边与对角线BD 重合,得折痕DG,使2AD=,求AG.【解析】:作GM⊥BD,垂足为M.由题意可知∠ADG=GDM,则△ADG≌△MDG.∴DM=DA=2. AC=GM又易知:GM=BM.而BM=BD-DM=22-2=2(2-1),∴AG=BM=2(2-1).例2 .如图,P为正方形ABCD内一点,10==,并且P点到CD边的距离也PA PB等于10,求正方形ABCD的面积?【解析】:过P作EF AB⊥于F交DC于E.设PF x =,则10EF x =+,1(10)2BF x =+.由222PB PF BF =+.可得:222110(10)4x x =++.故6x =.216256ABCD S ==.例3. 如图,E 、F 分别为正方形ABCD 的边BC 、CD 上的一点,AM EF ⊥,•垂足为M ,AM AB =,则有EF BE DF =+,为什么? 【解析】:要说明EF=BE+DF ,只需说明BE=EM ,DF=FM 即可,而连结AE 、AF .只要能说明△ABE ≌△AME ,△ADF ≌△AMF 即可.理由:连结AE 、AF .由AB=AM ,AB ⊥BC ,AM ⊥EF ,AE 公用, ∴△ABE ≌△AME . ∴BE=ME .同理可得,△ADF ≌△AMF . ∴DF=MF .∴EF=ME+MF=BE+DF .例4.如下图E 、F 分别在正方形ABCD 的边BC 、CD 上,且45EAF ︒∠=,试说明EF BE DF =+。
初中数学突破中考压轴题几何模型之正方形的半角模型教案、

例2.如图,分别以 的 和 为一边,在 的外侧作正方形 和正方形 ,点 是 的中点.
求证:点 到边 的距离等于 的一半.
例4.如图,四边形 为正方形, , , 与 相交于 .
求证: .
例6.设 是正方形 一边 上的任一点, , 平分 .
求证: .
例7.已知: 是边长为1的正方形 内的一点,求 的最小值.
(1)求证: ;
(2)求证: .
【纵向应用】
6. 在正方形 中, .求证:
7. 在正方形 中, . ,求证:
8. 如图13,点 为正方形 对角线 上一点, ,
求证:
9.已知:点 、 分别正方形 中 和 的中点,连接 和 相交于点 ,
于点 .
(1)求证: ;
(2)如果 ,求 的长;
(3)求证:
例1.已知:如图, 是正方形 内点, .
3.如图9,已知正方形 的面积为35平方厘米, 、 分别为边 、 上的点. 、 相交于 ,并且 的面积为14平方厘米, 的面积为5平方厘米, 那么四边形 的面积是________.
4.如图, 、 、 三点在同一条直线上, 。分别以
、 为边作正方形 和正方形 ,连接 ,
。
求证: 。
5.如图 , 是正方形. 是 上的一点, 于 , 于 .
年初中数学突破中考压轴题几何模型之正方形的半角模型教案(、)
———————————————————————————————— 作者:
———————————————————————————————— 日期:
ﻩ
正方形角含半角模型升
例1.如图,折叠正方形纸片 ,先折出折痕 ,再折叠使 边与对角线 重合,得折痕 ,使 ,求 .
人教版中考数学压轴题解题模型----几何图形之半角模型(含解析)

几何图形之半角模型主题半角模型教学内容教学目标1.掌握正方形的定义,弄清正方形与平行四边形、菱形、矩形的关系。
2。
掌握正方形的性质定理1和性质定理2。
3。
正确运用正方形的性质解题。
4。
通过四边形的从属关系渗透集合思想。
5.通过理解四种四边形内在联系,培养学生辩证观点。
知识结构正方形的性质因为正方形是特殊的平行四边形,还是特殊的矩形,特殊的菱形,所以它具有这些图形性质的综合,因此正方形有以下性质(由学生和老师一起总结).正方形性质定理1:正方形的四个角都是直角,四条边相等。
正方形性质定理2:正方形的两条对角线相等并且互相垂直平分,每一条对角线平分一组对角。
说明:定理2包括了平行四边形,矩形,菱形对角线的性质,一个题设同时有四个结论,这是该定理的特点,在应用时需要哪个结论就用哪个结论,并非把结论写全.小结:(1)正方形与矩形,菱形,平行四边形的关系如上图(2)正方形的性质:①正方形对边平行.②正方形四边相等.③正方形四个角都是直角。
④正方形对角线相等,互相垂直平分,每条对角线平分一组对角。
典型例题精讲例1.如图,折叠正方形纸片ABCD ,先折出折痕BD ,再折叠使AD 边与对角线BD 重合,得折痕DG ,使2AD =,求AG .【解析】:作GM ⊥BD ,垂足为M . 由题意可知∠ADG=GDM , 则△ADG ≌△MDG . ∴DM=DA=2. AC=GM 又易知:GM=BM .而BM=BD-DM=22-2=2(2—1), ∴AG=BM=2(2-1).例2 .如图,P 为正方形ABCD 内一点,10PA PB ==,并且P 点到CD 边的距离也等于10,求正方形ABCD 的面积?【解析】:过P 作EF AB ⊥于F 交DC 于E .设PF x =,则10EF x =+,1(10)2BF x =+.由222PB PF BF =+. 可得:222110(10)4x x =++. 故6x =.216256ABCD S ==.例3。
中考数学几何专题——半角模型(几何压轴)
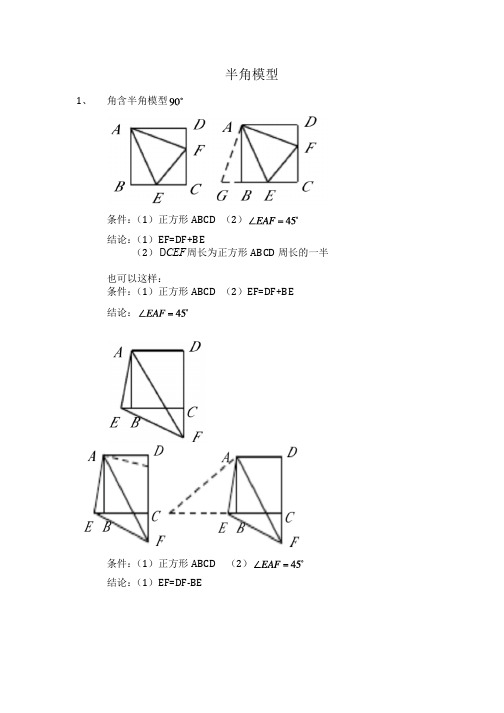
半角模型1、角含半角模型条件:(1)正方形ABCD (2)结论:(1)EF=DF+BE(2)D CEF周长为正方形ABCD周长的一半也可以这样:条件:(1)正方形ABCD (2)EF=DF+BE结论:条件:(1)正方形ABCD (2)结论:(1)EF=DF-BE条件:(1)结论:D AHE为等腰直角三角形证明:连接AC\ÐDAH=ÐCAE\D ADH相似于D ACE\DAAH=ACAE\D AHE相似于D ADC条件:(1)等腰直角D ABC(2)结论:BD2+CE2=DE2若ÐDAE旋转到D ABC外部时结论:BD2+CE2=DE2经典例题1.如图,正方形ABCD中,E、F分别在BC、DC上,且∠EAF=45°.求证:BE+DF=EF.2.如图,在正方形ABCD中,E和F分别是BC和CD上的点,AG⊥EF,∠EAF=45°,求证:AG=AD.3、已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N,AH⊥MN于点H.(1)如图①,当∠MAN绕点A旋转到BM=DN时,请你直接写出AH与AB的数量关系:;(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;(3)如图③,已知∠MAN=45°,AH⊥MN于点H,且MH=2,NH=3,求AH的长.(可利用(2)得到的结论)4、如图①△ABC是正三角形,△BDC是等腰三角形,BD=CD,∠BDC=120°,以D为顶点作一个60°角,角的两边分别交AB、AC边于M、N,连接MN.(1)探究BM、MN、NC之间的关系,并说明理由.(2)若△ABC的边长为2,求△AMN的周长.(3)若点M、N分别是AB、CA延长线上的点,其它条件不变,在图②中画出图形,并说出BM、MN、NC之间的关系.5.(2014秋•安阳校级期中)在△ABC中,∠BAC=90°,AB=AC,点D和点E均在边BC 上,且∠DAE=45°,试猜想BD.DE.EC应满足的数量关系,并写出推理过程.6.在△ABC中,∠BAC=90°,AB=AC,D、E在直线BC上,∠DAE=45°,(1)写出图中的相似三角形;(2)求证:BE•CD=2S△ABC,并探究BD、DE、CE之间的数量关系,给以证明.7.已知在△ABC中,AB=AC,点D、E在边BC上,将△ABD绕着点A旋转,得到△ACD′,接连D′E交AC于点O.(1)如图1,当△BAC=120°,△DAE=60°时,求证:DE=D′E;(2)如图2,当△DAE=45°,△BAC=90°,BD=DE时,在不舔加任何辅助线的情况下,请直接写出图2中的所有的全等三角形.8.(2014秋•通山县期中)如图1,在Rt△ABC中,∠BAC=90°,AB=AC,点D、E是BC 边上的任意两点,且∠DAE=45°.(1)将△ABD绕点A逆时针旋转90°,得到△ACF,请在图(1)中画出△ACF.(2)在(1)中,连接EF,探究线段BD,EC和DE之间有怎样的数量关系?写出猜想,并说明理由.(3)如图2,M、N分别是正方形ABCD的边BC、CD上一点,且BM+DN=MN,试求△MAN 的大小.9.△ABC的边BC在直线l上,点D,E是直线l上的两点,且BA=BD,CA=CE(1)如图1,若AB=AC,△BAC=90°,求△CAE的度数;(2)如图2,若△BAC=90°,求△CAE的度数;(3)如图3,设△BAC=α,△DAE=β,请直接写出α与β的关系式.10.(2011秋•朝阳区期末)已知,在△ABC中,∠BAC=90°,AB=AC,BC=,点D、E在BC边上(均不与点B、C重合,点D始终在点E左侧),且∠DAE=45°.(1)请在图△中找出两对相似但不全等的三角形,写在横线上,;(2)设BE=m,CD=n,求m与n的函数关系式,并写出自变量n的取值范围;(3)如图△,当BE=CD时,求DE的长;(4)求证:无论BE与CD是否相等,都有DE2=BD2+CE2.11.(2014•平谷区一模)(1)如图1,点E、F分别是正方形ABCD的边BC、CD上的点,∠EAF=45°,连接EF,则EF、BE、FD之间的数量关系是:EF=BE+FD.连结BD,交AE、AF于点M、N,且MN、BM、DN满足MN2=BM2+DN2,请证明这个等量关系;(2)在△ABC中,AB=AC,点D、E分别为BC边上的两点.△如图2,当△BAC=60°,△DAE=30°时,BD、DE、EC应满足的等量关系是;△如图3,当△BAC=α,(0°<α<90°),△DAE=时,BD、DE、EC应满足的等量关系是.[参考:sin2α+cos2α=1]12.(2015•海宁市模拟)(1)探究:如图1和2,四边形ABCD中,已知AB=AD,∠BAD=90°,点E、F分别在BC、CD上,∠EAF=45°.△如图1,若△B、△ADC都是直角,把△ABE绕点A逆时针旋转90°至△ADG,使AB与AD重合,则能证得EF=BE+DF,请写出推理过程;△如图2,若△B、△D都不是直角,则当△B与△D满足数量关系时,仍有EF=BE+DF;(2)拓展:如图3,在△ABC中,△BAC=90°,AB=AC=2,点D、E均在边BC上,且△DAE=45°.若BD=1,求DE的长.13.(2015•滑县一模)(1)问题发现如图1,点E、F分别在正方形ABCD的边BC、CD上,△EAF=45°,连接EF、则EF=BE+DF,试说明理由;(2)类比引申如图2,在四边形ABCD中,AB=AD,△BAD=90°,点E、F分别在边BC、CD上,△EAF=45°,若△B,△D都不是直角,则当△B与△D满足等量关系时,仍有EF=BE+DF;(3)联想拓展如图3,在△ABC中,△BAC=90°,AB=AC,点D、E均在边BC上,且△DAE=45°,猜想BD、DE、EC满足的等量关系,并写出推理过程.14.(2014•山西校级模拟)已知△ABC中,AB=AC,D、E是BC边上的点,将△ABD绕点A旋转,得到△ACD′,连结D′E.(1)如图1,当△BAC=120°,△DAE=60°时,求证:DE=D′E;(2)如图2,当DE=D′E时,△DAE与△BAC有怎样的数量关系?请写出,并说明理由.(3)如图3,在(2)的结论下,当△BAC=90°,BD与DE满足怎样的数量关系时,△D′EC 是等腰直角三角形?(直接写出结论,不必说明理由)。
半角模型-含答案docx
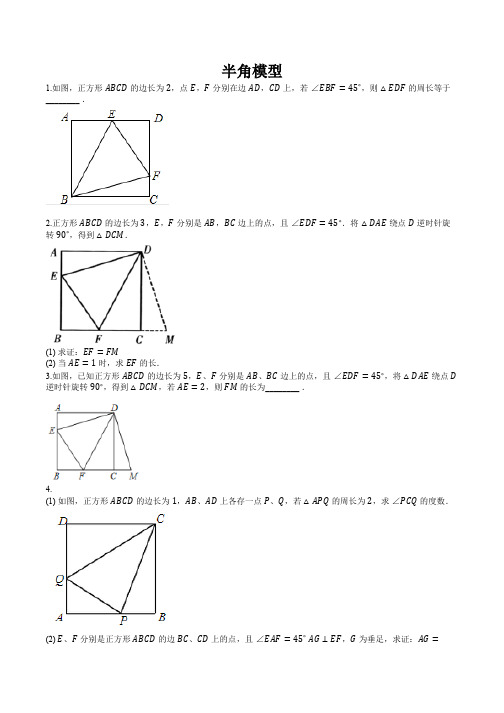
半角模型1.如图,正方形ABCD的边长为2,点E,F分别在边AD,CD上,若∠EBF=45∘,则△EDF的周长等于________ .2.正方形ABCD的边长为3,E,F分别是AB,BC边上的点,且∠EDF=45∘.将△DAE绕点D逆时针旋转90∘,得到△DCM.(1) 求证:EF=FM(2) 当AE=1时,求EF的长.3.如图,已知正方形ABCD的边长为5,E、F分别是AB、BC边上的点,且∠EDF=45∘,将△DAE绕点D 逆时针旋转90∘,得到△DCM,若AE=2,则FM的长为________ .4.(1) 如图,正方形ABCD的边长为1,AB、AD上各存一点P、Q,若△APQ的周长为2,求∠PCQ的度数.(2) E、F分别是正方形ABCD的边BC、CD上的点,且∠EAF=45∘AG⊥EF,G为垂足,求证:AG=AB.5.如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.(1) 求证:CE=CF;(2) 若点G在AD上,且∠GCE=45∘,则GE=BE+GD成立吗?为什么?6.如图,已知正方形ABCD边长为1,∠EAF=45∘,AE=AF,则有下列结论:①∠1=∠2=22.5∘②点C到EF的距离是√2−1③△ECF的周长为2④BE+DF>EF其中正确的结论是 ________.(写出所有正确结论的序号)7.如图,已知正方形ABCD的边长为8 cm,点E、F分别在边BC、CD上,∠EAF=45∘.当EF=8 cm 时,△AEF的面积是________ cm2;当EF=7 cm时,△EFC的面积是________ cm2.8.如图,正方形ABCD的边长为6,点E、F分别在AB、AD上,若CE=3√5,且∠ECF=45∘,则CF的长为 ()A.2√10 B.3√5 C.53√10D.103√59.(1) 如图,正方形ABCD的边长为1,AB、AD上各存一点P、Q,若△APQ的周长为2,求∠PCQ的度数.(2) E、F分别是正方形ABCD的边BC、CD上的点,且∠EAF=45∘,AG⊥EF,G为垂足,求证:AG= AB.10.如图,在正方形ABCD中,E是边AB上一点,点F是AD延长线上一点,且DF=BE.(1) 求证:CE=CF;(2) 若G是AD上一点,且∠GCE=45∘①证明:GE=BE+GD;②设BE=4,GE=10,求△CEG的面积.11.如图1,在正方形ABCD内作∠EAF=45∘,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.图1图2图3(1) 如图2,将△ADF绕点A顺时针旋转90∘得到△ABG.①求证:△AGE≅△AFE;②若BE=2,DF=3,求AH的长.(2) 如图3,连接BD交AE于点M,交AF于点N.请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由.12.如图(1),已知正方形ABCD中,E,F分别是BC,CD边上的点,且∠EAF=45∘,判断线段BE,EF,FD之间的数量关系,并说明理由.小明同学的想法是:已知条件比较分散,可以通过旋转变换将分散的已知条件集中在一起,于是他将△DAF绕点A顺时针旋转90∘,得到△BAH,然后通过证明三角形全等可得出结论.请你参考小明同学的思路,解决下列问题:(1) 图1中线段BE,EF,FD之间的数量关系是________;(2) 如图2,已知正方形ABCD边长为5,E,F分别是BC,CD边上的点,且∠EAF=45∘,AG⊥EF于点G,则AG的长为________,△EFC的周长为________;(3) 如图3,已知△AEF中,EAF=45∘,AG⊥EF于点G,且EG=2,GF=3,则△AEF的面积为________.13.如图,在正方形ABCD中,AB=1,E,F分别是边BC,CD上的点,连接EF、AE、AF,过A作AH⊥EF于点H.若EF=BE+DF.那么下列结论:①AE平分∠BEF②FH=FD③∠EAF=45∘④S△EAF=S△ABE+S△ADF;⑤△CEF的周长为2其中正确结论的是 ________ .14.如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45∘,将△ADC绕点A顺时针旋转90∘后,得到△AFB,连接EF,下列结论:(1)△AED≅△AEF(2)△ABE≅△ACD(3)BE+DC=DE(4)BE2+DC2=DE2其中正确结论有 () 个A.1B.2C.3D.415.如图,在△ABC中,∠BAC=90∘,AB=AC,点D、E均在边BC上,且∠DAE=45∘,猜想BD、DE、EC应满足的等量关系,并写出推理过程.16.如图,在△ABC中,AB=AC=2√2,∠BAC=90∘,点D、E都在边BC上,∠DAE=45∘,若BD= 2CE,则DE的长是 ()A.1B.3−√52C.3√5−52D.3√5−517.四边形ABCD被对角线BD分为等腰直角三角形ABD和直角三角形CBD,其中∠A和∠C都是直角,另一条对角线AC的长度为2,求四边形ABCD的面积.18.在等腰直角△ABC中,∠ACB=90∘,AC=BC.M是AB的中点,点P从B出发向点C运动,MQ⊥MP交AC于点Q.试说明△MPQ的形状和面积将如何变化.19.如图所示,△ABD是等边三角形,在△ABC中,BC=a,CA=b.问:当∠ACB为何值时,C、D两点间的距离最大?最大值是多少?20.如图所示,点D为∠ABC的平分线BD上一点,点E、F分别为∠ABC两边上的动点,且∠ABC+∠EDF=180∘.连接DE、DF,判断在E、F运动过程中,DE、DF的数量关系并证明.21.如图,P是正方形ABCD内一点,∠APB=135∘,BP=1,AP=√7,求PC的值.()A.√5B.3C.2√2D.222.点P为等腰直角三角形ABC内一点,∠ACB=90∘,PB=1,PC=2,PA=3,求∠BPC的度数.23.如图.设P是等边△ABC内的一点,且PA:PB:PC=3:4:5,求∠APB的度数.24.如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120∘,以D为顶点作一个60∘角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为 ()A.9B.8C.7D.625.△ABC是边长为1的等边三角形,△BDC是顶角为120∘的等腰三角形,∠MDN=60∘,求△AMN 的周长.26.D为等边△ABC外一点,且BD=CD,∠BDC=120∘,点M,N分别在AB,AC上,若BM+CN= MN,(1) ∠MDN= ________度;(2) 作出三角形△DMN的高DH,并证明:DH=BD;(3) 在第(2)的基础上,求证:MD平分∠BDH.27.如图,△ABC等边三角形,△BDC是顶角∠BDC=120∘的等腰三角形,以D为顶点作一个60∘角,角的两边分别交AB、AC于M、N,连接MN,若SΔBMD +SΔCND=10,则SΔDMN= ________ .28.如图,在四边形ABCD中,∠B+∠ADC=180∘,AB=AD,E、F分别是边BC、CD延长线上的点,且∠EAF=12∠BAD,求证:EF=BE−FD.29.如图,已知等边△ABC外有一点H,连接CH、BH,BH=CH且∠BHC=120∘,在AB上取点E、在AC上取点F,若∠EHF=60∘,设EH、FH分别交BC于P、Q两点,试证明以下结论:=2BC(1) CΔAEF(2) AF=2BP,AE=2CQ半角模型1.【答案】4【解析】∵四边形ABCD为正方形∴AB=BC,∠BAE=∠C=90∘∴把△ABE绕点B顺时针旋转90∘可得到△BCG,如图∴BG=AE,CG=AE,∠GBE=90∘,∠BAE=∠C=90∘∴点G在DC的延长线上∵∠EBF=45∘∴∠FBG=∠EBG−∠EBF=45∘∴∠FBG=∠FBE在△FBG和△EBF中,{BF=BF∠FBG=∠FBEBG=BE∴△FBG≌△FBE(SAS)∴FG=EF∵FG=FC+CG=CF+AE∴EF=CF+AE∴△DEF的周长=DF+DE+CF+AE=CD+AD=2+2=42.(1)【答案】证明见解析【解析】∵△DAE逆时针旋转90∘得到△DCM∴DE=DM,∠EDM=90∘∴∠EDF+∠FDM=90∘∵∠EDF=45∘∴∠FDM=∠EDF=45∘∵DF=DF∴△DEF≅△DMF∴EF=MF(2)【答案】52【解析】设EF=x∵AE=CM=1∴BF=BM−MF=BM−EF=4−x∵EB=2由勾股定理得:EB2+BF2=EF2即22+(4−x)2=x2,解得:x=523.【答案】297【解析】∵△DAE逆时针旋转90∘得到△DCM∴∠FCM=∠FCD+∠DCM=180∘∴F、C、M三点共线∴DE=DM,∠EDM=90∘∴∠EDF+∠FDM=90∘∵∠EDF=45∘∴∠FDM=∠EDF=45∘∵DF=DF∴△DEF≅△DMF∴EF=MF设EF=MF=x∵AE=CM=2,且BC=5∴BM=BC+CM=7∴BF=BM−MF=BM−EF=7−x∵EB=AB−AE=3在Rt△EBF中,由勾股定理得:EB2+BF2=EF2即32+(7−x)2=x2,解得:x=297∴FM=29 74.(1)【答案】45∘【解析】如图所示,延长AB至点E,使得BE=DQ,连接CE,证△CDQ≅△CBE,再证△CQP≅△CEP(2)【答案】证明见解析【解析】如图所示,延长FB至点Q,使得BQ=DE,连接AQ先证△ADE≅△ABQ,再证△AQF≅△AEF,利用面积法可得AB=AG5.(1)【答案】证明见解析【解析】∵四边形ABCD为正方形∴BC=CD,∠B=∠ADC=90∘在△BEC和△DFC中,{BC=CD∠B=∠CDF BE=DF∴△CBE≅△CDF(SAS)∴CE=CF(2)【答案】成立,理由见解析【解析】∵由(1)得△CBE≅△CDF∴∠BCE=∠DCF∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90∘∵∠GCE=45∘∴∠GCF=∠GCE=45∘∵CE=CF,∠GCE=∠GCF,GC=GC∴△ECG≅△FCG(SAS)∴GE=GF∴GE=DF+GD=BE+GD6.【答案】①②③【解析】∵四边形ABCD为正方形∴AB=AD,∠BAD=∠B=∠D=90∘在Rt△ABE和Rt△ADF中,{AE=AFAB=AD∴Rt△ABE≅Rt△ADF∴∠1=∠2∵∠EAF=45∘∴∠1=∠2=∠22.5∘,故①正确;连接EF、AC,它们相交于点H,如图所示:∵Rt△ABE≅Rt△ADF∴BE=DF∵BC=DC∴CE=CF∵AE=AF∴AC垂直平分EF,AH平分∠EAF∴EB=EH,FD=FH∴BE+DF=EH+HF=EF,故④错误;∴C△ECF=CE+CF+EF=CE+BE+CF+DF=CB+CD=2,故③正确;设BE=x,则EF=2x,CE=1−x∵△CEF为等腰直角三角形∴EF=√2CE,即2x=√2(1−x),解得:x=√2−1∴EF=2(√2−1)∴CH=12EF=√2−1,故②正确;故答案为①②③7.【答案】32;8【解析】如图所示,延长CB到G,使得BG=DF,连接AG∵四边形ABCD是正方形∴AB=AD,∠D=∠ABG=90∘∵BG=DF∴△ABG≅△ADF∴AG=AF,∠GAB=∠FAD∵∠EAF=45∘∴∠FAD+∠BAE=45∘∴∠GAE=∠FAE=45∘∵AE=AE∴△GAE≅△FAE∴EF=EG=8∴S△AEF=S△AEG=12×8×8=32当EF=7时,由上述结论可知:S△EFC=S正方形ABCD −2S△AEF=8×8−2×12×7×8=64−56=88.【答案】A【解析】如图,延长FD到G,使DG=BE,连接CG、EF∵四边形ABCD为正方形在△BCE与△DCG中,{CB=CD∠CBE=∠CDGBE=DG∴△BCE≅△DCG ( SAS )∴ CG=CE,∠DCG=∠BCE∴∠GCF=45∘在△GCF与△ECF中,{GC=EC∠GCF=∠ECFCF=CF∴△GCF≅△ECF ( SAS )∴ GF=EF∵ CE=3√5,CB=6∴ BE=√CE2−CB2=√(3√5)2−62=3∴ AE=3设AF=x,则DF=6−x,GF=3+(6−x)=9−x∴ EF=√AE2+x2=√9+x2∴ (9−x)2=9+x2∴ x=4,即AF=4∴ GF=5∴ DF=2∴ CF=√CD2+DF2=√62+22=2√10故选 A9.(1)【答案】45∘【解析】如图所示,将Rt△CDQ绕点C逆时针旋转90∘易证P、B、E三点共线∵AQ+QD+AP+PB=AD+AB=1+1=2∴AQ+AP+PQ=AQ+QD+AP+PB,即PQ=QD+PB=PE∵PC=PC,CQ=CE,PQ=PE∴△PQC≅△PEC(SSS)∴∠PCQ=∠PCE=45∘(2)【答案】证明见解析【解析】把△ADE绕点A顺时针旋转90∘,得△ABQ∵FA=FA,∠FAQ=∠FAE=45°,AQ=AE,∴△AFQ≅△AFE(SAS)∴AB=AG10.(1)【答案】证明见解析【解析】在正方形ABCD中,∵{BC=CD∠B=∠CDFBE=DF∴△CBE≅△CDF (SAS)∴CE=CF(2)【答案】①证明见解析;②60【解析】①∵由 (1) 得:△CBE≅△CDF∴∠BCE=∠DCF∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90∘∵∠GCE=45∘∴∠GCF=∠GCE=45∘∵{CE=CF∠GCE=∠GCFGC=GC∴△ECG≅△FCG (SAS)∴GE=GF∴GE=DF+GD=BE+GD ②由①得:GE=BE+GD∵BE=4,GE=10∴GD=6设正方形的边长为x,则AG=x−6,AE=x−4由勾股定理得:(x−6)2+(x−4)2=102解得:x1=12,x2=−2(舍去)∴正方形的边长为12∴AG=6,AE=8∴△GAE的面积为24,△CDG的面积为36,△CBE的面积为24,正方形ABCD的面积为144∴△CGE的面积为6011.(1)【答案】①见解析;②6【解析】①由旋转的性质可知:AF=AG,∠DAF=∠BAG∵四边形ABCD为正方形∴∠BAD=90∘∵∠EAF=45∘∴∠BAE+∠DAF=45∘∴∠BAG+∠BAE=45∘∴∠GAE=∠FAE在△GAE和△FAE中,{AG=AF∠GAE=∠FAEAE=AE,∴△GAE≅△FAE②∵△GAE≅△FAE,AB⊥GE,AH⊥EF∴AB=AH,GE=EF=5设正方形的边长为x,则EC=x−2,FC=x−3在Rt△EFC中,由勾股定理得:EF2=FC2+EC2即(x−2)2+(x−3)2=25,解得:x=6∴AB=6∴AH=6(2)【答案】见解析【解析】如图所示,将△ABM逆时针旋转90∘得△ADM′∵四边形ABCD为正方形∴∠ABD=∠ADB=45∘由旋转的性质可知:∠ABM=∠ADM′=45∘,BM=DM′∴∠NDM′=90∘∴NM′2=ND2+DM′2∠EAM′=90∘,∠EAF=45∘∴∠EAF=∠FAM′=45∘在△AMN和△AM′N中,{AM=AM′∠MAN=∠M′ANAN=AN∴△AMN≅△AM′N∴MN=NM′∵BM=DM′∴MN2=ND2+BM2 12.(1)【答案】EF=BE+FD【解析】△AHB≅△AFD,△AEH≅△AEF(2)【答案】5;10【解析】∵△FAE≅△HAE,AG,AB分别是△FAE与△HAE的高∴AG=AB=5∵Rt△AEG≅Rt△ABE∴EG=BE同理得:GF=DF∴△EFC的周长为BC+CD=10(3)【答案】15【解析】将△AEF置于图2中∵EG=2,GF=3∴BE=2,DF=3,EF=5设AB=x,则CE=x−2,CF=x−3在△CEF中,根据勾股定理,解得x=−1(舍去),x=6∴AG=AB=6∴S△AEF=12EF⋅AG=1513.【答案】①②③④⑤【解析】如图,延长CB到G点,使BG=DF,连接AG,则EF=EG在△ADF和△ABG中,∵AD=AB,∠D=∠ABG,DF=BG∴△ADF≅△ABG (SAS)∴∠GAB=∠FAD,AG=AF在△AEF和△AEG中,∵AG=AF,EF=EG,AE=AE∴△AEF≅△AEG (SSS)∴∠GEA=∠FEA,即AE平分∠BEF故①正确;∵∠ABE=∠AHE=90∘,∠AEB=∠AEH,AE=AE∴△ABE≅△AHE (AAS)∴BE=EH∴FH=BG=FD故②正确;∠EAF=∠GAE=∠GAB+∠BAE=∠DAF+∠BAE∴∠EAF=12∠BAD=12×90∘=45∘故③正确;∵△ABE≅△AHE (AAS),△AHF≅△ADF (HL)∴S△EAF=S△ABE+S△ADF故④正确;∵△CEF的周长=CE+CF+EF=CE+CF+BE+DF=1+1=2故⑤正确;故正确的有:①②③④⑤14.【答案】B【解析】∵△ADC绕点A顺时针旋转90∘得△AFB∴△ADC≅△AFB,∠FAD=90∘∴AD=AF∵∠DAE=45∘∴∠FAE=90∘−∠DAE=45∘∴∠DAE=∠FAE,AE为△AED和△AEF的公共边∴△AED≅△AEF∴ED=FE在Rt△ABC中,∠ABC+∠ACB=90∘∵∠ACB=∠ABF∴∠ABC+∠ABF=90∘,即∠FBE=90∘∴在Rt△FBE中,BE2+BF2=FE2∴BE+DC=DE故正确的有(1)(4)故选 B15.【答案】BD2+EC2=DE2,证明见解析【解析】如图所示,作AF⊥AE,使AF=AE∵∠DAE=∠DAF=45∘∵AD=AD∴△ADE≅△ADF∴DF=DE∵∠BAF=∠CAE=45∘−∠BAD,AB=AC∴△ABF≅△ACE∴BF=CE,∠ABF=∠ACE∴∠FBD=∠ABF+∠ABC=∠ACE+∠ABC=90∘∴BD2+EC2=BD2+BF2=DF2=DE216.【答案】D【解析】∵ΔABC中,AB=AC=2√2,∠BAC=90∘∴∠ABC=∠C=45∘由勾股定理得:BC=√AB2+AC2=4把ΔAEC绕A点旋转到ΔAFB,使AB和AC重合,连接DF则AF=AE,∠FBA=∠C=45∘,∠BAF=∠CAE∵∠DAE=45∘∴∠FAD=∠FAB+∠BAD=∠CAE+∠BAD=∠BAC−∠DAE=90∘−45∘=45∘∴∠FAD=∠DAE=45∘在ΔFAD和ΔEAD中,{AD=AD∠FAD=∠EADAF=AE∴ΔFAD≅ΔEAD(SAS)∴DF=DE,BF=EC设EC=x,则BF=x,BD=2x,DF=DE=√5x∵BC=4∴2x+√5x+x=4,解得:x=3−√5∴DE=√5x=√5(3−√5)=3√5−5故选 D17.【答案】2【解析】“对角互补”+“邻边相等”的四边形,已知对角线的长度并不能直接求面积.利用旋转可将四边形变形成我们熟悉的三角形如图:延长CD到点E,使DE=BC,连接AE易证:△ABC ≅△ADE所以S△ABC=S△ADE,AC=AE,∠BAC=∠DAE所以△ACE为等腰直角三角形,S四边形ABCD =S△ACE=12×22=218.【答案】略【解析】如图,连接CM易证△MQC ≅△MPB,所以MQ=MP 所以△MPQ为等腰直角三角形,形状不变△MPQ的面积与边MP的长度有关当点P从点B到BC中点时,面积由大变小当点P是BC中点时,三角形的面积最小当点P继续向点C运动时,面积由小变大19.【答案】∠ACB=120∘时,C、D两点间的距离最大,为a+b【解析】如图,以CD为边作等边三角形DCC′,所以CD=CC′易证△DBC ≅△DAC′,所以AC′=BC=a在△ACC′中,AC+AC′>CC′当C,A,C′三点共线时,AC+AC′=CC′=a+b所以CD的最大值为a+b此时∠ACB=∠ACD+∠BCD=∠ACD+∠AC′D=180∘−60∘=120∘20.【答案】DE=DF【解析】如图,过点D分别作BA和BC的垂线段,垂足分别为H和Q易证:△DHE ≅△DQF,所以DE=DF21.【答案】B【解析】如图,把△PBC绕点B逆时针旋转90∘得到△ABP′(点C的对应点C′与点A重合),所以,AP′=PC,BP′=BP=1,所以,△PBP′是等腰直角三角形,所以,∠P′PB=45∘,PP′=√BP2+BP′2=√12+12=√2,∵∠APB=135∘,∴∠APP′=∠APB−∠P′PB=135∘−45∘=90∘,在Rt△APP′中,AP′=√PP′2+AP2=√(√2)2+(√7)2=3,∴PC=AP′=3.22.【答案】∠BPC=135∘.【解析】如图,把△ACP绕点C逆时针旋转90∘得到△BCD,连接DP,∵△ACP绕点C逆时针旋转90∘得到△BCD,∴CP=CD=2,∠DCP=90∘,DB=PA=3,∴△CPD为等腰直角三角形,∴PD=√2PC=2√2,∠CPD=45∘,在△PDB中,PB=1,PD=2√2,DB=3,而12+(2√2)2=32,∴PB2+PD2=BD2,∴△PBD为直角三角形,∴∠DPB=90∘,∴∠BPC=45∘+90∘=135∘.23.【答案】∠APB=150∘.【解析】将ΔPBC绕点B逆时针旋转60∘得ΔDAB,则BP=BD,∠DBP=60∘,∴ΔDBP为等边三角形,∠DPB=60∘,设AD=PC=5k,DP=BP=4k,∵AP2+DP2=(3k)2+(4k)2=25k2=AD2,∴ΔADP是直角三角形,∠APD=90∘,∴∠APB=∠APD+∠DPB=150∘.24.【答案】D【解析】∵△BDC是等腰三角形,且∠BDC=120∘∴∠DBC=∠BCD=30∘∵△ABC是边长为3的等边三角形∴∠ABC=∠BAC=∠BCA=60∘∴∠DBA=∠DCA=90∘延长AB至F,使BF=CN,连接DF∴ BF =CN ,DB =DC∴ Rt △BDF ≌Rt △CDN∴ ∠BDF =∠CDN ,DF =DN∵ ∠MDN =60∘∴ ∠BDM +∠CDN =60∘∴ ∠BDM +∠BDF =60∘ ∴ ∠FDM =∠MDN =60∘∴ △DMN ≌△DMF∴ MN =MF ∴ △AMN 的周长 =AM +AN +MN =AM +MB +BF +AN =AB +AC =6故选 D25.【答案】1【解析】如图所示,延长 BD 交 AC 于 P ,延长 CD 交 AB 于 Q ,在 PC 上截取 KP =QM ,交 AC 于 P ,连接 DK∵ △BDC 是等腰三角形,且 ∠BDC =120∘ ∴ BD =CD ,∠DBC =∠DCB =30∘,∠BDQ =∠CDP =60∘ ∵ △ABC 等边三角形∴ ∠ABC =∠ACB =60∘ ∴ ∠MBD =∠PCD =30∘,CQ ⊥AB ,BP ⊥AC ∴ AQ =BQ =12AB =12,AP =PC =12AC =12在 △BDQ 和 △CDP 中,{∠QBD =∠PCDBD =CD∠BDQ =∠CDP∴ △BDQ ≌△CDP(ASA)∴ BQ =PC ,QD =PD∵ CQ ⊥AB ,BP ⊥AC∴ ∠MQD =∠DPK =90∘在 △MDQ 与 △PDK 中,{∠MQD=∠DPKQM=PK∴△MDQ≌△PDK(SAS)∴∠QDM=∠PDK,DM=DK∵∠BDQ=60∘,∠MDN=60∘∴∠QDM+∠PDN=60∘∴∠PDK+∠PDN=60∘,即∠KDN=60∘在△MDN与△KDN中,{DM=DK∠MDN=∠KDN=60∘DN=DN∴△MDN≌△KDN(SAS)∴MN=KN=NP+PK∴△AMN的周长=AM+AN+MN=AM+AN+NP+PK=AM+AN+NP+QM=AQ+AP=126.(1)【答案】60∘【解析】如图所示,将△BDM顺时针旋转120∘得到△CDE则DM=DE,∠BDM=∠CDE,BM=CE∴EN=CE+CN=BM+CN=MN∵BM+CN=MN在 △DMN 和 △DEN 中,{MN =EN DM =DE DN =DN∴△DMN ≅△DEN(SSS)∴∠MDN =∠EDN(2)【答案】证明见解析【解析】如图所示,延长 AC 至 E ,使 CE =BM ,连接 DE∵△ABC 是等边三角形∴∠ABC =∠ACB =60∘∵BD =CD ,∠BDC =120∘∴∠CBD =∠BCD =30∘∴∠ABD =∠ACD =90∘∴∠ABD =∠ECD =90∘∴△BDM ≅△CDE (SAS)∴DM =DE∵NE =NC +CE =NC +BM =MN ,DN =DN∴△DMN ≅△DEN (SSS)∴∠DNM =∠DNE∵DH ⊥MN ,DC ⊥AC∴DH =DC∵BD =DC∴DH =BD(3)【答案】证明见解析【解析】∵∠ABD =90∘,DH ⊥MN ,DH =BD ,DM =DM∴△BDM ≅△HDM∴∠BDM =∠HDM∴ MD 平分 ∠BDH27.【答案】10【解析】如图所示,延长 AB 至 K ,使 ∠KDN =∠BDC =120∘易证:△KDB≌△NDC,△DKM≌△DNM则S△DMN=S△BMD+S△CND=1028.【答案】证明见解析【解析】如图所示,在BE上截取BG,使BG=DF,连接AG∵∠B+∠ADC=180∘,∠ADF+∠ADC=180∘∴∠B=∠ADF 在△ABG和△ADF中,{AB=AD∠B=∠ADFBG=DF∴△ABG≅△ADF(SAS)∴∠BAG=∠DAF,AG=AF∴∠BAG+∠EAD=∠DAF+∠EAD=∠EAF=12∠BAD∴∠GAE=∠EAF 在△AEG和△AEF中,{AG=AF∠GAE=∠EAFAE=AE∴△AEG≅△AEF(SAS)∴EG=EF∵EG=BE−BG ∴EF=BE−FD29.(1)【答案】证明见解析【解析】如图所示,延长EB至M,使BM=CF,连接HM易证:△HCF≌△HBM(SAS),△HFE≌△HME(SAS)∴EF=BE+CF∴C△AEF=2BC(2)【答案】证明见解析【解析】如图所示,过E作ES//AC交BC于S,交HF于T由HF平分∠EFC得:△EFT为等腰三角形∴EF=ET∵△BES为等边三角形∴ST=CF,AE=CS∴△QCF≌△QST(ASA)∴QC=QS∴AE=2CQ同理可证:AF=2BP。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.掌握正方形的定义,弄清正方形与平行四边形、菱形、矩形的关系。
2.掌握正方形的性质定理1和性质定理2。
3.正确运用正方形的性质解题。
4.通过四边形的从属关系渗透集合思想。
5.通过理解四种四边形内在联系,培养学生辩证观点。
知识结构正方形的性质因为正方形是特殊的平行四边形,还是特殊的矩形,特殊的菱形,所以它具有这些图形性质的综合,因此正方形有以下性质(由学生和老师一起总结)。
正方形性质定理1:正方形的四个角都是直角,四条边相等。
正方形性质定理2:正方形的两条对角线相等并且互相垂直平分,每一条对角线平分一组对角。
说明:定理2包括了平行四边形,矩形,菱形对角线的性质,一个题设同时有四个结论,这是该定理的特点,在应用时需要哪个结论就用哪个结论,并非把结论写全。
小结:(1)正方形与矩形,菱形,平行四边形的关系如上图(2)正方形的性质:①正方形对边平行。
②正方形四边相等。
③正方形四个角都是直角。
④正方形对角线相等,互相垂直平分,每条对角线平分一组对角。
例1.如图,折叠正方形纸片ABCD ,先折出折痕BD ,再折叠使AD 边与对角线BD 重合,得折痕DG ,使2AD =,求AG .【解析】:作GM ⊥BD ,垂足为M . 由题意可知∠ADG=GDM , 则△ADG ≌△MDG . ∴DM=DA=2. AC=GM 又易知:GM=BM .而BM=BD-DM=22-2=2(2-1), ∴AG=BM=2(2-1).例2 .如图,P 为正方形ABCD 内一点,10PA PB ==,并且P 点到CD 边的距离也等于10,求正方形ABCD 的面积?【解析】:过P 作EF AB ⊥于F 交DC 于E .设PF x =,则10EF x =+,1(10)2BF x =+.由222PB PF BF =+. 可得:222110(10)4x x =++. 故6x =.216256ABCD S ==.例3. 如图,E 、F 分别为正方形ABCD 的边BC 、CD 上的一点,AM EF ⊥,•垂足为M ,AM AB =,则有EF BE DF =+,为什么?【解析】:要说明EF=BE+DF ,只需说明BE=EM ,DF=FM 即可,而连结AE 、AF .只要能说明△ABE ≌△AME ,△ADF ≌△AMF 即可.理由:连结AE 、AF .由AB=AM ,AB ⊥BC ,AM ⊥EF ,AE 公用, ∴△ABE ≌△AME . ∴BE=ME .同理可得,△ADF ≌△AMF .∴DF=MF .∴EF=ME+MF=BE+DF .例4.如下图E 、F 分别在正方形ABCD 的边BC 、CD 上,且45EAF ︒∠=,试说明EF BE DF =+。
【解析】:将△ADF 旋转到△ABC ,则△ADF ≌△ABG∴AF=AG ,∠ADF=∠BAG ,DF=BG∵∠EAF=45°且四边形是正方形,∴∠ADF ﹢∠BAE=45° ∴∠GAB ﹢∠BAE=45° 即∠GAE=45°∴△AEF ≌△AEG (SAS ) ∴EF=EG=EB ﹢BG=EB ﹢DF例 5. 如图,在正方形ABCD 的BC 、CD 边上取E 、F 两点,使45EAF ∠=,AG EF ⊥于G . 求证:AG AB =【解析】:欲证 AG=AB ,就图形直观来看,应证Rt △ABE 与Rt △AGE 全等,但条件不够. ∠EAF=45°怎么用呢?显然∠1+∠2=45°,若把它们拼在一起,问题就解决了.【证明】:把 △A FD 绕A 点旋转90°至△AHB.∵∠EAF=45°,∴∠1+∠2=45°. ∵∠2=∠3,∴∠1+∠3=45°. 又由旋转所得 AH=AF ,AE=AE. ∴ △AEF ≌△AEH.例6.(1) 如图1,在正方形ABCD 中,点E ,F 分别在边BC ,CD 上,AE ,BF 交于点O ,90AOF ︒∠=.求证:BE CF =.(2) 如图2,在正方形ABCD 中,点E ,H ,F ,G 分别在边AB ,BC ,CD ,DA 上,EF ,GH 交于点O ,90FOH ︒∠=,4EF =.求GH 的长.1.已知点E ,H ,F ,G 分别在矩形ABCD 的边AB ,BC ,CD ,DA 上,EF ,GH 交于点O ,90FOH ︒∠=,4EF =. 直接写出下列两题的答案:①如图3,矩形ABCD 由2个全等的正方形组成,求GH 的长;②如图4,矩形ABCD 由n 个全等的正方形组成,求GH 的长(用n 的代数式表示).【解析】图 3 图4 图2(1) 证明:如图1,∵ 四边形ABCD 为正方形,∴ AB =BC ,∠ABC =∠BCD =90°, ∴ ∠EAB +∠AEB =90°. ∵ ∠EOB =∠AOF =90°,∴ ∠FBC +∠AEB =90°,∴ ∠EAB =∠FBC , ∴ △ABE ≌△BCF , ∴ BE =CF . (2) 解:如图2,过点A 作AM //GH 交BC 于M ,过点B 作BN //EF 交CD 于N ,AM 与BN 交于点O /, 则四边形AMHG 和四边形BNFE 均为平行四边形, ∴ EF=BN ,GH=AM ,∵ ∠FOH =90°, AM //GH ,EF//BN , ∴ ∠NO /A =90°, 故由(1)得, △ABM ≌△BCN , ∴ AM =BN , ∴ GH =EF =4. (3) ① 8.② 4n .【双基训练】1. 如图6,点A 在线段BG 上,四边形ABCD 与DEFG 都是正方形,•其边长分别为3cm 和5cm ,则CDE ∆的面积为________2cm .(6) (7)2.你可以依次剪6张正方形纸片,拼成如图7所示图形.•如果你所拼得的图形中正方形①的面积为1,且正方形⑥与正方形③的面积相等,•那么正方形⑤的面积为________.3.如图9,已知正方形ABCD 的面积为35平方厘米,E 、F 分别为边AB 、BC 上的点.AF 、CE 相交于G ,并且ABF ∆的面积为14平方厘米,BCE ∆的面积为5平方厘米,•那么四边形BEGF 的面积是________.4. 如图,A 、B 、C 三点在同一条直线上,2AB BC =。
分别以AB 、BC 为边作正方形ABEF 和正方形BCMN ,连接FN , EC 。
求证:FN EC =。
图 2O ′NMABCDEF12GEB5.如图 ,ABCD 是正方形.G 是BC 上的一点,DE AG ⊥于 E ,BF AG ⊥于 F . (1)求证:ABF DAE △≌△;(2)求证:DE EF FB =+.【纵向应用】6. 在正方形ABCD 中,12∠=∠.求证:BE OF 21=7. 在正方形ABCD 中,12∠=∠.AE DF ⊥,求证:CE OG 21=EG CD ⊥8. 如图13,点E 为正方形ABCD 对角线BD 上一点, EF BC ⊥, 求证:AE FG ⊥9.已知:点E 、F 分别正方形ABCD 中AB 和BC 的中点,连接AF 和DE 相交于点G , GH AD ⊥于点H . 一、 求证:AF DE ⊥ ;AB C D F OEG H 12D GAE B CF 13A D E FC G B二、如果2AB=,求GH的长;三、求证:CG CD=【练习题答案】1.6cm2.2.36.3.42027cm2(面积法).4.证明:FN=EC。
证明:在正方形ABEF和正方形BCMN中,AB=BE=EF,BC=BN,∠FEN=∠EBC=90°∵AB=2BC∴EN=BC∴△FEN≌△EBC∴FN=EC。
5.略6.提示:注意到基本图形中的AE=AF.一.两次应用内角平分线定理和CE=CF可证二.过点O作OG‖DE和CO=CG,CF=CE可证.3,过点O作OH‖BE, OF= OH=BE217.提示:一条线段的一半或2倍这两者的位置关系有哪两种8.提示:延长AE交GF于点M,DC,使CH=DG,连接HF,证四边形对角互补,法2:延长FE,AE证全等三角形9.(1)略(2)45(3)作CM⊥DG,证DM=AG=0.5DG知识结构(1)定义:有一组邻边相等且有一个角是直角的平行四边形叫做正方形。
(2)特征:边:两组对边分别平行;四条边都相等;内角:四个角都是90°;对角线:对角线互相垂直;对角线相等且互相平分;每条对角线平分一组对角。
(3)主要识别方法:1:对角线相等的菱形是正方形 2:对角线互相垂直的矩形是正方形3:四边相等,有一个角是直角的四边形是正方形 4:一组邻边相等的平行四边形是正方形5:一组邻边相等且有一个角是直角的平行四边形是正方形依次连接四边形各边中点所得的四边形称为中点四边形。
不管原四边形的形状怎样改变,中点四边形的形状始终是平行四边形。
正方形的中点四边形是正方形。
15PAD PDA ︒∠=∠=.例 1. 已知:如图,P 是正方形ABCD 内点,求证:PBC ∆是正三角形.【证明】:如下图做△DGC 使与△ADP 全等,可得△PDG 为等边△,从而可得 △DGC ≌△APD ≌△CGP,得出PC=AD=DC,和∠DCG=∠PCG =150所以∠DCP=300 ,从而得出△PBC 是正三角形例 2. 如图,分别以ABC ∆的AC 和BC 为一边,在ABC ∆的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点. 求证:点P 到边AB 的距离等于AB 的一半.【证明】:过E,C,F 点分别作AB 所在直线的高EG ,CI ,FH 。
可得PQ=2EGFH。
由△EGA ≌△AIC ,可得EG=AI , 由△BFH ≌△CBI ,可得FH=BI 。
从而可得PQ=2AI BI=2AB, 从而得证。
APCDBPC GFBQADE例4. 如图,四边形ABCD 为正方形,DE AC ∥,AE AC =,AE 与CD 相交于F . 求证:CE CF =.【证明】:顺时针旋转△ADE ,到△ABG ,连接CG . 由于∠ABG=∠ADE=900+450=1350从而可得B ,G ,D 在一条直线上,可得△AGB ≌△CGB 。
推出AE=AG=AC=GC ,可得△AGC 为等边三角形。
∠AGB=300,既得∠EAC=300,从而可得∠ A EC=750。
又∠EFC=∠DFA=450+300=750.可证:CE=CF 。
例6. 设P 是正方形ABCD 一边BC 上的任一点,PF AP ⊥,CF 平分DCE ∠.求证:PA PF =.【证明】:作FG ⊥CD ,FE ⊥BE ,可以得出GFEC 为正方形。
