运筹学经典课件第1次
合集下载
Chapter01-绪论运筹学
3．注意到了工作、工人和环境之间的相互影响.
27
运筹学发展简史
Henry Ford，1863 - 1947，创造了第一条流水生 产线——汽车流水线，从而提高了整个企业的生 产效率，使成本明显降低. • 福特为了利于企业向大生产发展，进行了多方面 的标准化工作，包括：产品系列化，零件规格化，
工厂专业化，机器及工具专用化，作业专门化.
1999
2003
2006
2010
2014
2
Operations Research
Chapter 1. Introduction
第一章. 绪论
Chapter 1. Introduction
3
What is Operations Research?
Chapter 1. Introduction
4
交通控制问题
问题的确定
控制
分析问题
建立模型 软件求解 实施方案 确定解决方案 结果分析
Chapter 1. Introduction
37
运筹学的模型方法
模型的概念
模型是一件实际事物或情况的代表或抽 象。实际事物是A，若B能够真实地描述 A，则称B为A的模型
运筹学模型的一般形式
F ( X , f ( x1 , x 2 ,..., x m ; 1 , 2 ,..., n )
某些分支的研究达到当时国际水平。
35
What is Data, Model and Decision?
管理者
信息提供
模型
结论 决策
反馈
结果
执行
管理者在组织内制定决策，数据、模型与 决策的目的是在科学、符合逻辑和合理的 基础上制定决策
27
运筹学发展简史
Henry Ford，1863 - 1947，创造了第一条流水生 产线——汽车流水线，从而提高了整个企业的生 产效率，使成本明显降低. • 福特为了利于企业向大生产发展，进行了多方面 的标准化工作，包括：产品系列化，零件规格化，
工厂专业化，机器及工具专用化，作业专门化.
1999
2003
2006
2010
2014
2
Operations Research
Chapter 1. Introduction
第一章. 绪论
Chapter 1. Introduction
3
What is Operations Research?
Chapter 1. Introduction
4
交通控制问题
问题的确定
控制
分析问题
建立模型 软件求解 实施方案 确定解决方案 结果分析
Chapter 1. Introduction
37
运筹学的模型方法
模型的概念
模型是一件实际事物或情况的代表或抽 象。实际事物是A，若B能够真实地描述 A，则称B为A的模型
运筹学模型的一般形式
F ( X , f ( x1 , x 2 ,..., x m ; 1 , 2 ,..., n )
某些分支的研究达到当时国际水平。
35
What is Data, Model and Decision?
管理者
信息提供
模型
结论 决策
反馈
结果
执行
管理者在组织内制定决策，数据、模型与 决策的目的是在科学、符合逻辑和合理的 基础上制定决策
运筹学经典课件第1次
解 设x1为周一开始休息的人数 x2为周二开始休息的人数 ， ，
x6为周六开始休息的人数 x7为周日开始休息的人数 ， ，
Z表示商场的售货员人数 x1 x2 x7
求 min Z x1 x2 x7
, 约束条件 : xi为星期i日开始休息的人数i 1,2,,7 星期日 售货员人数要求: 时间 所需售货员人数 x1 x2 x3 x4 x5 28 数学模型: 星期日 28人 求 min Z x1 x2 x7 星期一 售货员人数要求: 星期一 15人 x2 x3 x4 x5 x6 15 x 星期二 x1 x2 x3 x4 24人5 28 星期三 星期二 售货员人数要求: x2 x3 x4 x5 25人 6 15 x x3 x4 x5 x6 x7 24
¤ò ¸Ð º Ò þ ¶ ý È ¥ºûó µÎÀÈ ¨¨ § £Ô£
z 工厂的总利润 目标函数：z 3x1 2 x2 5x3
¿ þ ú «Ó ¤ªä ¨Ö Ó § ¿ ì Ó ¤Ü ¦ à » ² Æ » ¸ Ê » £ «Ö £ Ã Ì » ¸ Ä Á ¬ú « » ² Æ Ò ² Æ ª² Æ ú« ûú« ¨Ö Ó § £ «Ö £ 1 2 1 430 3 0 2 460 1 4 0 420 3 2 5
星期四 19人 x x3 x4 x5 x631人 7 24 星期五 x x x x 28人 25 1 5 6 x7 星期六 4 s.t x1 x2 x5 x6 x7 19 x1 x2 : 非负约束 x3 x6 x7 31 x1 x2 x3 x4 x7 28 xi 0,,ii 1,2,,7 xi 0 1,2,,7
运筹学课件ch01s1-3
1.1 问题的提出
用数学关系式描述这个问题
设 x1 , x2分别表示计划生产 II产品的数量， I, 称它们为决策变量。
生产x1 , x2的数量多少，受资源拥有量的限制, 这是约束条件。即x1 2 x2 8;4 x1 16;4 x2 12
生产的产品不能是负值,即x1 , x2 0
a1 j x1 b1 a2 j x2 b2 X ; Pj ;b ; j 1,2 , n x b a n m mj
1.3 线性规划问题的标准型式
第1节
线性规划问题及其数学模型
线性规划是运筹学的一个重要分支。线性规划在理 论上比较成熟，在实用中的应用日益广泛与深入。特别 是在电子计算机能处理成千上万个约束条件和决策变量 的线性规划问题之后，线性规划的适用领域更为广泛了。 从解决技术问题的最优化设计到工业、农业、商业、交 通运输业、军事、经济计划和管理决策等领域都可以发 挥作用。它已是现代科学管理的重要手段之一。解线性 规划问题的方法有多种，以下仅介绍单纯形法 。 一类是（资源有限）如何合理的使用现有的劳动力、 设备、资金等资源，以得到最大的效益； 另一类是（目标一定）为了达到一定的目标，应如何 组织生产，或合理安排工艺流程，或调整产品的成分等， 以使所消耗的资源（人力、设备台时、资金、原材料等） 为最少。
(1) 用x4−x5替换x3，其中x4，x5≥0； (2) 在第一个约束不等式左端加入松弛变量x6； (3) 在第二个约束不等式左端减去剩余变量x7； (4) 令z′= −z，将求min z 改为求max z′ 即可得到该问题的标准型。
1.3 线性规划问题的标准型式
例4 例4的标准型
《运筹学》课件 第一章 线性规划
10
解：令
xi=
1， Si被选中
min z= ci xi i 1 10
0， Si没被选中
xi 5
i 1
x1 x8 1 x7 x8 1
称为技术系数
b= (b1,b2, …, bm) 称为资源系数
2、非标准型
标准型
（1）Min Z = CX
Max Z' = -CX
（2）约束条件
• “≤”型约束，加松弛变量；
松弛变量
例如： 9 x1 +4x2≤360
9 x1 +4x2+ x3=360
• “≥”型约束，减松弛变量；
例、将如下问题化为标准型
数据模型与决策 (运筹学）
课程教材：
吴育华,杜纲. 《管理科学基础》，天津大学出版社。
绪论
一、运筹学的产生与发展
运筹学（Operational Research) 直译为“运作研究”。
• 产生于二战时期 • 60年代，在工业、农业、社会等各领域得到广泛应用 • 在我国，50年代中期由钱学森等引入
Min z x1 2x2 3x3
x1 x2 x3 7
s.t
.
x1 x2 x3 3x1 x2 2
x3
2
5
x1, x2 , x3 0
解：令 Min z Max z' (z' z) ，第一个约束加松弛变量x5，
第二个约束减松弛变量x6，得标准型：
Max z' x1 2x2 +3x3
x1 x2 x3 x4 7
s.t .
x1 x2 3x1
x3 x2
x5 2 2x3 5
x1 , , x5 0
运筹学(一)ppt课件
2x3 4 3x3 6
x1 0, x2 0, x3取值无约束
解： z令 z,x1 x1,x3x3 x3 ,其x中 3 ， x3 0， 同时引入 x4和 松剩 弛余 变 x5,标 变 量准 量形式
m z x 1 a 2 x 2 x 3 x 3 3 x 3 0 x 4 0 x 5
案、措施，是问题中要确定的未知量。
2.目标函数:指问题要达到的目的要求，表示为 决策变量的函数。
3.约束条件:指决策变量取值时受到的各种可用 资源的限制，表示为含决策变量的等式或不等 式。
最新版的一般表示形式：
m ax (mm in ) 或 f ( xm ) a cz 1 x 1 c 1 cx x 21 i x 2 c 2 n x 2 ( cn x ) n c n x n
( 4 )无可行解。
目标函数为max z=3x1+x2，约束条件为
x 1 x 2 2 ; 最x 新1 版整 理ppt 2 x 2 6
库存管理。存储论应用于多种物资库存量的管理，确定某些设备的合 理的能力或容量以及适当的库存方式和库存量
运输问题。用运筹学中运输问题的方法，可以确定最小成本的运输线 路、物资的调拨、运输工具的调度以及建厂地址的选择。
人事管理。可以用运筹学方法对人员的需求和获得情况进行预测；确 定合适需要的人员编制；用指派问题对人员合理分配；用层次分析法 等方法来确定一个人才评价体系等。
数为0；
（4）第i 个约束为 型，在不等式左边减去一 个非负的变量，称为剩余变量；同时令该变量在目
标函数中的系数为0；
（5）若 ，x令0 xx
（6）若 无x约束，令 x，x其中x，
x,x0
例3：将下述线性规划模型化为标准形式：
运筹学课程讲义
运筹学课程讲义第一部分线性规划第一章线性规划的基本性质1.1 线性规划的数学模型一、线性规划问题的特点胜利家具厂生产桌子和椅子两种家具。
桌子售价50 元/个，椅子售价30 元/个。
生产桌子和椅子需木工和油漆工两种工种。
生产一个桌子需要木工4 小时，油漆工2小时。
生产一个椅子需要木工3 小时，油漆工1 小时。
该厂每月可用木工工时为120 小时，油漆工工时为50 小时。
问该厂如何组织生产才能使每月的销售收入最大？max z 50x1 30x24x1 3x2 1202x1 x2 50x1,x2 0 例：某工厂生产某一种型号的机床。
每台机床上需要 2.9m、2.1m、1.5m的轴，分别为1根、2根和1根。
这些轴需用同一种圆钢制作，圆钢的长度为74m。
如果要生产100台机床，问应如何安排下料，才能用料最省？二、数学模型的标准型1. 繁写形式2. 缩写形式3. 向量形式4. 矩阵形式若原模型中变量 x j 有上下界，如何化为非负变量？三、 任一模型如何化为标准型？1. 若原模型要求目标函数实现最大化，如何将其化为最小化问题？2. 若原模型中约束条件为不等式，如何化为等式？3. 若原模型中变量 x k 是自由变量，如何化为非负变量？1. 2 图解法该法简单直观，平面作图适于求解二维问题。
使用该法求解线性规划问题时，不必把原模型化为标准型。
一、 图解法步骤1. 由全部约束条件作图求出可行域2. 作出一条目标函数的等值线3. 平移目标函数等值线，作图求解最优点，再算出最优值 max z 5x 1 6x 2 7x 3x 1 5x 23x 3 15 5x 1 6x 210x 3 20 x 1 x 2 x 3 5x 1 0,x 2 0,x 3无约束令 x 1' x 1,x 3 x 3' x 3'',x 3' ,x 3'' 0, Z 1Z ' 1 1 min z ' 5x 1' 6x 2 7x 3' 7x 3'' 0x 5 Mx 6 1 x 1' 5x 2 1 11 3x 3' 3x 3'' x 4 x 6 15 1 5x 1' 6x 2 10x 3' 10x 3'' x 5 20 1 x ' x 1 ' II '' 54.Mx 7 x 1, x 2 , x 3, x 3, x 4 , x 5 ,x 6, x 7 0从图解法看线性规划问题解的几种情况1. 有唯一最优解2. 有无穷多组最优解3. 无可行解4. 无有限最优解（无界解）min z 6x1 4x?2x〔X2 13 最优解（1,0），最优值33x14x2 22x1, x20直观结论：1）线性规划问题的可行域为凸集，特殊情况下为无界域（但有有限个顶点）或空集；2）线性规划问题若有最优解，一定可以在其可行域的顶点上得到。
运筹学课件PPT课件
整数规划的解法
总结词
整数规划的解法可以分为精确解法和近似解法两大类。
详细描述
整数规划的解法可以分为两大类，一类是精确解法，另一类是近似解法。精确解法包括割平面法、分支定界法等， 这些方法可以找到整数规划的精确最优解。而近似解法包括启发式算法、元启发式算法等，这些方法可以找到整 数规划的近似最优解，但不一定能保证找到最优解。
模拟退火算法采用Metropolis准则来 判断是否接受一个较差解，即如果新 解的能量比当前解的能量低，或者新 解的能量虽然较高但接受的概率足够 小，则接受新解。
模拟退火算法的应用
01
模拟退火算法在旅行商问题中得到了广泛应用。通过模拟退火算 法，可以求解旅行商问题的最优解，即在给定一组城市和每对城 市之间的距离后，求解访问每个城市恰好一次并返回出发城市的 最短路径。
动态规划的解法
确定问题的阶段和状态
首先需要确定问题的阶段和状态，以便将问 题分解为子问题。
建立状态转移方程
根据问题的特性，建立状态转移方程，描述 状态之间的转移关系。
求解子问题
求解每个子问题，并存储其解以供将来使用。
递推求解
从最后一个阶段开始，通过递推方式向前求 解每个阶段的最优解。
动态规划的应用
线性规划的解法
单纯形法
01
单纯形法是求解线性规划问题的经典方法，通过迭代过程逐步
找到最优解。
对偶理论
02
对偶理论是线性规划的一个重要概念，它通过引入对偶问题来
简化求解过程。
分解算法
03
分解算法是将大规模线性规划问题分解为若干个小问题，分别
求解后再综合得到最优解。
线性规划的应用
生产计划
线性规划可以用于生产计划问题， 通过优化资源配置和生产流程， 提高生产效率和利润。
运筹学讲义第一章
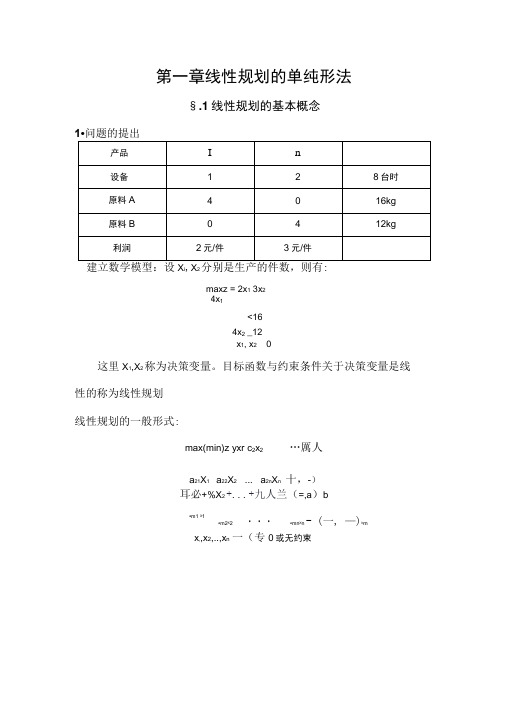
4x 1<164x 2 _12a 21X 1 a 22X 2 ... a 2n X n 十，-）b a m1 X 1第一章线性规划的单纯形法§.1线性规划的基本概念建立数学模型：设X i ,X 2分别是生产的件数，则有:maxz = 2x 1 3x 2x 1, x 2 0这里X 1,X 2称为决策变量。
目标函数与约束条件关于决策变量是线 性的称为线性规划线性规划的一般形式:max(min)z yxr c 2x 2 …厲人耳必+%X 2 +...+九人兰（=,a ）ba m2X 2 ・・・ a mn X n - (一, —)bm x ,,x 2,..,x n 一（专0或无约束2. 线性规划的标准形maxz 二C1X1 …Cn X n"a^x, +ai2x2+••• + 印*人=Ra21^ +a22x2+... + a2n x n= b2a m1 为* a m2 X2 * …+ a mn 人=b m捲_ 0,X2_0,...,X n_0特点：目标函数求极大；等式约束；变量非负。
^令c =(G,c2,…,q), X = (X1,X2，…,x n) , A = (a ij )m n，b=(九^,…,b m ) 则线性规划标准形的矩阵表达式为:max z = exAx = bx _0约定：b — 0,m ^ n,秩A=m.如何化标准形：（I）目标函数实现极大化，即min z=cx，令w--z，则m w丸；（II ）约束条件为不等式约束条件为“「不等式，则在约束条件的左端加上一个非负的松弛变量；约束条件为“ 一”不等式，则在约束条件的左端减去一个非负的松弛变量。
（III ）若存在无约束的变量X k，可令X k = Xk - x k，其中x k 一0,x'k- 0.故有 x^ -B 4b 。
由此，得到Ax -b 的一个解例1.将线性规划min z = -捲 2x 2x-i x 2 x 3 _ 2* X i — X ? + X 3 乏 1论Z0,x 2兰0,x 3无约束化为标准形。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
线性
0.6 x1 0.27x2 0.68x3 0.3x4 1
17.5 x1 7.5x2 30x4 30
x1 0，x2 0，x3 0, x4 0
问题归结为： x1，x2，x3，x4 , 使之满足以上约束条件 ， 求
并使M 0.8x1 0.5x2 0.9x3 1.5x4的值最小。
并使z 3x1 2 x2 5x3的值最大
例2 （营养搭配问题） 如果有甲、乙、丙、丁四种食品，都含 有不同成分的维生素，其含量和单价如下表所示
¬ ú Ø Î É Ë A B C ¥ Û ¨¨ § µ » £ Ô £ ¥ º µ Î Á Ë ¹ ¿ Á Ë ¹ ¿ Á Ë ¹ ¿ ¬ » 1000 0.6 17.5 0.8 Ò 1500 0.27 7.5 0.5 û ª 1750 0.68 0 0.9 ¡ ¶ 3250 0.3 30 1.5 ¿ Ë ¿ ì Ã È Ã Ì î Í è ¨ ¿ ¬µ Ð Ò Á 4000 1 30
数学模型: 求 min Z x1 x2 x7 x1 x2 x3 x4 x5 28 x2 x3 x4 x5 x6 15
解得:
x1 12, x 2 0, x3 11, x 4 5, x5 0, x6 8, x7 0. Z 0 36
x3 每天采购丙食品的数量 ， A
B x4 每天采购丁食品的数量 C ¥ µ Û ¨¨ § M 每天采购食品的费用 » £ Ô £
目标函数： M 0.8x1 0.5x2 0.9x3 1.5x4
约束条件：1000x1 1500x2 1750x3 3250x4 4000
假定所生产的三种产品都能 全部售出，问这三种产品 每天要各生产多少件才能 使得获得的利润最大？
设： x1 甲的产量 x2 乙的产量 x3 丙的产量
z 工厂的总利润
决策变量 目标函数
则有z 3x1 2x2 5x3
决策变量： x1 甲的产量 , x 2 乙的产量 , x3 丙的产量
1.1.1 线性规划模型 一、 线性规划问题举例
例1 （生产安排问题）假定某工厂生产甲、乙、丙三种产品， 每种产品都要经过三种不同的工序加工。每一件产品所需要 的加工时间（分钟）和每天对各道工序的加工能力（每天多 少分钟）以及销售各种产品的单位利润如下表所示：
¤ò ¸Ð º Ò þ ¶ ý È ¥ºûó µÎÀÈ ¨¨ § £Ô£ ¿ þ ú «Ó ¤ªä ¨Ö Ó § ¿ ì Ó ¤Ü ¦ à » ² Æ » ¸ Ê » £ «Ö £ Ã Ì » ¸ Ä Á ¬ú « » ² Æ Ò ú Æ ª² Æ ²« ûú« ¨Ö Ó § £ «Ö £ 1 2 1 430 3 0 2 460 1 4 0 420 3 2 5
解 设x1为周一开始休息的人数 x2为周二开始休息的人数 ， ，
x6为周六开始休息的人数 x7为周日开始休息的人数 ， ， Z表示商场的售货员人数
解得：x1 12, x 2 0, x3 11, x 4 5, x5 0, x6 8, x7 0. Z 0 36
例4 某工厂要做100套钢架,每套用长为2.9m,2.1m, 和1.5m的圆钢各一根,已知原料每根长7.4m, 问应如何下料,可使所用原料最省. 分析: 每根原料做一套钢架, 下角料： 0.9m 用套裁方式 下料方案：下料数
x3 x4 x5 x6 x7 24 x x x x x 25 4 5 6 7 1 s.t x1 x2 x5 x6 x7 19 x1 x2 x3 x6 x7 31 x1 x2 x3 x4 x7 28 x 0, i 1,2,,7 i
例3 福安商场是个中型的百货商场，它对售货人员的 需求经过统计分析如下所示：
时间 星期日 所需售货员 人数 28人
星期一
星期二 星期三 星期四 星期五 星期六
15人
24人 25人 19人 31人 28人
为保证售货人员充分休息， 售货人员每周工作五天，休 息两天，并要求休息的两天 是连续的，问应该如何安排 售货人员的作息，既满足了 工作的需要，又使配备的售 货人员的人数最少？
第一章 线性规划 （Linear Programming )
简记为LP
• • • • •
运筹学的一个重要分枝 研究较早 发展较快 理论较成熟 应用极为广泛
典型的线性规划的在经济管理上的应用举例: 1、合理利用线材问题: 现有一批长度一定的钢管,由于生产的需要, 要求截出不同规格的钢管若干。试问应如何 下料，既满足了生产的需要，又使得使用的 原材料钢管的数量最少。 2、配料问题： 用若干种不同价格不同成分含量的原料， 用不同的配比混合调配出一些不同价格不同 规格的产品。在原料供应量的限制和保证产 品成分的含量的前提下，如何获取最大的利润。
星期四 19人 x x3 x4 x5 x631人 7 24 星期五 x x x x 28人 25 1 5 6 x7 星期六 4 s.t x1 x2 x5 x6 x7 19 x1 x2 : 非负约束 x3 x6 x7 31 x1 x2 x3 x4 x7 28 xi 0,,ii 1,2,,7 xi 0 1,2,,7
现在我们希望每天得到的维生素不少于所规定的最低需要 量，问应该如何搭配各种食品才能使所花的费用最少？
x 解：x1 每天采购甲食品的数量 ， 2 每天采购乙食品的数量
x x3 每天采购丙食品的数量 ， 4 每天采购丁食品的数量
M 每天采购食品的费用
则有M 0.8x1 0.5x2 0.9x3 1.5x4
星期三 售货员人数要求:
x1 x4 x5 x6 x7 25
星期四 售货员人数要求:
x1 x2 x5 x6 x7 19
星期五 售货员人数要求:
x1 x2 x3 x6 x7 31
星期六 售货员人数要求:
x1 x2 x3 x4 x7 28
解 设x1为周一开始休息的人数 x2为周二开始休息的人数 ， ，
x6为周六开始休息的人数 x7为周日开始休息的人数 ， ，
Z表示商场的售货员人数 x1 x2 x7
求 min Z x1 x2 x7
, 约束条件 : xi为星期i日开始休息的人数i 1,2,,7 星期日 售货员人数要求: 时间 所需售货员人数 x1 x2 x3 x4 x5 28 数学模型: 星期日 28人 求 min Z x1 x2 x7 星期一 售货员人数要求: 星期一 15人 x2 x3 x4 x5 x6 15 x 星期二 x1 x2 x3 x4 24人5 28 星期三 星期二 售货员人数要求: x2 x3 x4 x5 25人 6 15 x x3 x4 x5 x6 x7 24
¤ò ¸Ð º Ò þ ¶ ý È ¥ºûó µÎÀÈ ¨¨ § £Ô£
z 工厂的总利润 目标函数：z 3x1 2 x2 5x3
¿ þ ú «Ó ¤ªä ¨Ö Ó § ¿ ì Ó ¤Ü ¦ à » ² Æ » ¸ Ê » £ «Ö £ Ã Ì » ¸ Ä Á ¬ú « » ² Æ Ò ² Æ ª² Æ ú« ûú« ¨Ö Ó § £ «Ö £ 1 2 1 430 3 0 2 460 1 4 0 420 3 2 5
对第一道工序，有 x1 2 x2 x3 430 对第二道工序，有 3x1 2 x3 460 对第三道工序，有 x1 4 x2 420
线性
约束条 件
且有 x1 0，x2 0，x3 0 非负性约束条件
问题归结为： x1，x2，x3，使之满足以上四个约 束条件， 求
x1 , x2 , xn 0
四、线性规划应用举例
例3 福安商场是个中型的百货商场，它对售货人员的 需求经过统计分析如下所示：
时间 星期日 星期一 星期二 所需售货员 人数 28人 15人 24人
星期三
星期四 星期五 星期六
25人
19人 31人 28人
为保证售货人员充分休息， 售货人员每周工作五天，休 息两天，并要求休息的两天 是连续的，问应该如何安排 售货人员的作息，既满足了 工作的需要，又使配备的售 货人员的人数最少？
二、线性规划模型的建立
1、建模的一般步骤：
步骤一：确定决策变量 即用变量取不同的值来表示可供选择的各种不同方案 步骤二：建立目标函数
即找到目标值与决策变量的数量关系
步骤三：确定约束条件 即决策变量所受到的外界条件的制约。 约束条件一般为决策变量的等式或不等式
要求：目标函数与约束条件均是线性的，
且目标函数只能是一个。
目标函数Biblioteka 约束方程subject to
非负约束
其中 aij , bi , c j (i 1,2, , m; j 1,2, , n) 为已知常数
决策变量
三、线性规划求解：
max （或min）z c1 x1 c2 x2 cn xn
计算机应 用软件
a11 x1 a12 x 2 a1n x n (或 ，或 ）b1 a 21 x1 a 22 x 2 a 2 n x n (或 ，或 ）b2 s.t a m1 x1 a m 2 x 2 a mn x n (或 ，或 ）bm
决策变量：
x1 每天采购甲食品的数量 ，
x2 每天采购乙食品的数量
¬úØ ÎÉË ¥º µÎ ÁË ¹¿ ÁË ¹¿ ÁË ¹¿ ¬ » 1000 0.6 17.5 0.8 Ò 1500 0.27 7.5 0.5 û ª 1750 0.68 0 0.9 ¿Ë¿ì ÃÈÃÌ îÍ訿 ¬µ Ð Ò Á 3250 4000 0.3 1 30 30 1.5 ¡ ¶