06信号与系统AB卷标准答案2
西南科技大学信号与系统2006-20007学年第2学期B答案

参考答案及评分细则西南科技大学2006——2007学年第 2 学期《信号与系统X 》期末考试试卷(B 卷)一、填空题(每小题2分,共10分)1.1 。
2.-1。
3. ωj +31。
若为“ωj +-31”,得1分。
4. 0。
5.πω16000>s 。
若为“π16000>”,或“max 2ωω>s ”,或“max 2ω>”,得2分。
若为“π16000≥”,或“max 2ωω≥s ”,或“max 2ω≥”得1分。
二、判断题(每小题2分,共10分)1.╳2.╳3.√4.╳5.√三、证明题(5分)证明: )()(ωj X t x F−→←∴)()(**ωj X t x F -−→←,)()(ωj X t x F -−→←-,)()(**ωj X t x F−→←- --------(2分) 又 )(t x 为实偶信号,即:)()()()(*t x t x t x t x -=-==*--------(1分)∴)()()()(**ωωωωj X j X j X j X =-=-=即:)(ωj X 也为实偶信号。
--------(2分)备注:证明得出仅为偶信号或仅实信号,得3分。
写出FT 定义式,正确可得分。
用定义式或其它方法求解,根据步骤与答案情况,给分。
四、绘图题(每小题6分,共18分) 1.解:)1()1()(112-++=t y t y t y ---(2分)又 系统为线性时不变系统,∴)1()1()(112-++=t x t x t x ---(2分) )(2t x 波形如右图所示。
---(2分)备注:若直接给结果图,正确给满分。
用卷积法等,根据步骤与答案情况,给分。
2.解:输出)(*)()(t h t x t y =---(2分) )1()1()(*)]1()1([-++=-++=t h t h t h t t δδ---(2分) 波形如下图所示。
---(2分)备注:若直接给结果图,正确满分。
《信号与系统》期末试卷A卷与答案.pptx

0
y(t)
1 t2 2
Tt
1 T2
1
2 t Tt
2
3T2
2
2
0
t 0 0t T
T t 2T 2T t 3T 3T t
3、(3×4 分=12 分)
j dX ( j / 2)
(1)
tx(2t) 2
d
(1t)x(1t) x(1t) tx(1t)
(2) X ( j)e j j d [X ( j)e j] jX ' ( j)e j d
(3)
t
dx(t) dt
X ( j)
dX ( j) d
第 页 4共 6 页
学海无 涯
4、(5 分)解 :
s2
1 2s 2
s2 2s 2
s2 2s 2
F (s) es 2(s 1) es (s 1)2 1
f (t) (t 1) 2e(t 1) cos(t 1)u(t 1)
学海无涯
《信号与系统》期末试卷 A 卷
班级:
学号:
姓名:
_ 成绩:
一. 选择题(共 10 题,20 分)
j( 2 )n
j( 4 )n
1、 x[n] e 3 e 3 ,该序列是
A.非周期序列 B.周期 N 3
D。
C.周期 N 3/ 8
CDCC
D. 周期 N 24
2、一连续时间系统y(t)= x(sint),该系统是
3
3
(b)若系统因果,则Re{s} 2,h(t) 1 e2tu(t)-1 et u(t) 4分
3
3
(c)若系统非稳定非因果,则Re{s} -1,h(t) 1 e2t u(t) 1 et u(t) 4分
信号与系统( A卷答案 )

淮南师范学院201 -201学年第 学期《信号与系统》A 卷参考答案及评分标准一、填空题(每题2分,共10分) 1.离散信号2.()f t 3.冲激信号或()t δ 4.可加性 5.()t δ 二、选择题(每题2分,共10分) 1. (B) 2. (C) 3. (C) 4. (A) 5. (C)三、判断题(每题2分,共10分) 1. × 2. √ 3. √ 4. √ 5. √四、简答题(每题5分,共10分)1. 简述根据数学模型的不同,列出系统常用的几种分类。
(本题5分)答:根据数学模型的不同,系统可分为4种类型. -----------------------(1分) (1) 即时系统与动态系统 -----------------------(1分) (2) 连续系统与离散系统 -----------------------(1分)(3) 线性系统与非线性系统 -----------------------(1分) (4) 时变系统与时不变系统 -----------------------(1分)2. 简述稳定系统的概念及连续时间系统时域稳定的充分必要条件。
(本题5分)答:(1)一个系统(连续的或离散的)如果对任意的有界输入,其零状态响应也是有界的则称该系统是有界输入有界输出稳定系统。
-----------------------(2分)(2)连续时间系统时域稳定的充分必要条件是()h t dt M ∞-∞≤⎰-----------------------(3分)五、计算题(每题10分,共60分) 1、如有两个序列11,0,1,2()0,k k f k +=⎧=⎨⎩ 其余 21,0,1,2()0,k f k =⎧=⎨⎩ 其余试求卷积和12()()()f k f k f k =*(本题10分)解: 1 1 1⨯ 1 2 3-------------------------- 3 3 3 2 2 21 1 1---------------------------------1 3 6 5 3 -----------------------(5分){}12()()()0,1,3,6,5,3,00f k f k f k k =*=↑= -----------------------(5分)2、求象函数2()(2)(4)sF s s s =++的拉普拉斯逆变换()f t (本题10分)解:12()24k k F S s s =+++2424s s =-+++ -----------------------(5分) 24()(24)()tt f t ee t ε--∴=-+ -----------------------(5分)3. 已知某LTI 离散系统的差分方程为()(1)2(2)2()y k y k y k f k +---=, 求单位序列响应()h k (本题10分)解:12()()2()2()Y Z Z Y Z Z Y Z F Z --+-= -----------------------(2分)()()()Y Z H Z F Z =12212z Z --=+-2222Z Z Z =+- -----------------------(2分) ()2(2)(1)H Z ZZ Z Z =+-21413132Z Z =⋅+⋅-+ -----------------------(2分) 24()3132Z ZH Z Z Z =⋅+⋅-+ -----------------------(2分)24()[(2)]()33k h k k ε=+⋅- -----------------------(2分)4. 已知02,()0,F jw ωωωω⎧<⎪=⎨>⎪⎩ ,求()F jw 的傅里叶逆变换(本题10分)解:1()()2j t f t F j e d ωωωπ+∞=-∞⎰ 0011j te d ωωωωπ=⋅-⎰ -----------------------(5分) 0011j t ejtωωωπ=⋅⋅- 02sin()t t ωπ= -----------------------(5分) 5. 已知某系统框图其中()()f t t ε= (1) 求该系统的冲激响应()h t (2) 求该系统的零状态响应()zs y t (本题10分)解:''()3'()2()4'()()y t y t y t f t f t ++=+2(32)()(41)()S S Y S S F S ++=+ -----------------------(2分)2()(41)()()(32)Y S S H S F S S S +==++ 113712S S =-⋅+⋅++ -----------------------(2分) (1) 冲激响应 2()[(3)7]()tth t e e t ε--=-⋅+ -----------------------(2分)(2) 41()()()(1)(2)zs S Y S H S F S S S S +=⋅=++ -----------------------(1分)1117132122S S S =⋅+⋅-⋅++ -----------------------(1分) 零状态响应217()(3)()22tt zs y t e e t ε--=+- -----------------------(2分)6. 如图所示的电路,写出以)(t u s 为输入,以)(t u c 为响应的微分方程。
信号与系统2006试卷A参考答案

栏 姓名
息
班级
订
信
生
专业
考
学院 装
P5
P6
G (ω)
A
A/2
A/2
−3ωm −ω m ωm 3ωm
ω
(4分,没标注扣2分)
信息工程
学号 线
栏 姓名
得
五、限选题(每题 10 分)
分
1、给定系统流图如图所示,列写状态方程与输出方程。指出 A B C D 。
e1(t)
8
1/s
4 7 7 -3
3 r(t) [通信、电子专业必做]
课程名称
适用 学院、专业、
年级
备注
集美大学试卷纸
2007—2008 学年 第 2 学期
信号与系统
试卷 A
卷别
信息工程学院 2006 级 通信工程、电子信息工程、自动化
考试 闭卷 ■ 方式 开卷 □
参考答案及评分标准
5、已知系统函数
H (s)
=
(s
1 + 1)(s
+
2)
,起始条件为: y(0− )
= 1,
∴系统完全可控、完全可观的条件是a ≠ −1且b ≠ 0。
息
班级
订
信
生
专业
考
学院 装
信息工程
P7
P8
f
(t)
=
3cos t
+
sin
⎛ ⎜⎝
5t
+
π 6
⎞ ⎟⎠
+
2
cos
⎛ ⎜⎝
8t
+
π 3
⎞ ⎟⎠
1.画出单边幅度频谱和相位谱; 2.画出双边幅度谱和相位谱。
太原理工大学信号与系统试卷A答案

太原理工大学本科课程考试参考答案与评分标准考试课程:信号与系统 学年学期:2005-2006-2 试卷类型: A 卷 考试日期:2007-1一、单项选择题(从下列各题四个备选答案中选出一个正确答案,并将其字母代号写在该题【 】内。
答案错选或未选者,该题不得分。
每小题3分,共15分。
) 1-5: CADAB 6-10: BCDBA二、填空题(将答案写在该题横线上。
前5题每小题3分,第6题6分,共21分。
)1、1+jw jw 2、()()t e t h t ε22-= 3、S e S 21-- 4、()5222++=S S S S H 5、()1122-+Z Z Z 三、计算题(请写出简明解题步骤,只有答案者得0分。
非通用符号请注明含义。
第1题10分,第2题10分,共20分)1.解:对方程两边取拉氏变换,并整理得)(6517765)0(5)0(')0()(22S F S S S S S y y Sy S Y ++++++++=--- (2分) ()11+=S S F ∴ ()()()()()()321177327++++++++=S S S S S S S S Y (2分) ∴ ()()()3425327+-+=+++=S S S S S S Y zi (1分) ()()()()322315321177+-+-+=++++=S S S S S S S S Y zf (1分) ∴ ()()t e e t y t t zi ε)45(32---= (2分)()()()t e e e t y t t t zf ε32235-----= (2分)2.解:对差分方程取单边Z 变换得()()()[]()()()[]()()Z F Z Z F Z y y Z Y Z y Z Y Z Z Y 212121221----+=-+-+--+- (2分)解得)(212121)2(2)1()21()(212211z F zz z z z y y z z Y --------++---+-+= (2分) 即 12224)(2222---++--+=z z z z z z z z z z Y ∴ 122)1)(2(4)(2+-+-=+-+=z z z z z z z z z Y zi (1分) 12312122)(--++-=z z z z z z z Y zf (1分) ∴ )(])1()2(2[)(k k y k k zi ε--= (2分))(]23)1(212[)(1k k y k k zf ε--+=+ (2分)四、看图求解题(请写出简明解题步骤,只有答案者得0分。
安徽大学信号与系统试卷及答案

安徽大学2006—2007学年第二学期 《 信号与系统 》考试试卷(A 卷)(时间120分钟)1. 系统的激励是)t (e ,响应为)t (r ,若满足dt)t (de )t (r =,则该系统为 线性、时不变、因果。
(是否线性、时不变、因果?) 2. 求积分dt )t ()t (212-+⎰∞∞-δ的值为 5 。
3. 当信号是脉冲信号f(t)时,其 低频分量 主要影响脉冲的顶部,其 高频分量 主要影响脉冲的跳变沿。
4. 若信号f(t)的最高频率是2kHz ,则t)f(2的乃奎斯特抽样频率为 8kHz 。
5. 信号在通过线性系统不产生失真,必须在信号的全部频带内,要求系统幅频特性为 一常数相频特性为_一过原点的直线(群时延)。
6. 系统阶跃响应的上升时间和系统的 截止频率 成反比。
7.若信号的3s F(s)=(s+4)(s+2),求该信号的=)j (F ωj 3(j +4)(j +2)ωωω。
8. 为使LTI 连续系统是稳定的,其系统函数)s (H 的极点必须在S 平面的 左半平面 。
9. 已知信号的频谱函数是))00(()j (F ωωδωωδω--+=,则其时间信号f(t)为01sin()t j ωπ。
10. 若信号f(t)的211)s (s )s (F +-=,则其初始值=+)(f 0 1 。
二、判断下列说法的正误,正确请在括号里打“√”,错误请打“×”。
(每小题2分,共10分)1.单位冲激函数总是满足)()(t t -=δδ ( √ )2.满足绝对可积条件∞<⎰∞∞-dt t f )(的信号一定存在傅立叶变换,不满足这一条件的信号一定不存在傅立叶变换。
( × ) 3.非周期信号的脉冲宽度越小,其频带宽度越宽。
( √ )4.连续LTI 系统的冲激响应的形式取决于系统的特征根,于系统的零点无关。
( √ )5.所有周期信号的频谱都是离散谱,并且随频率的增高,幅度谱总是渐小的。
信号与系统参考答案
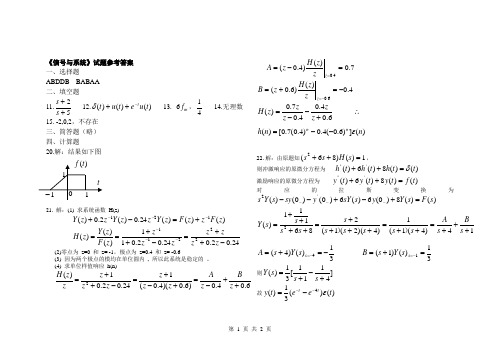
第 1 页 共 1 页《信号与系统》试题参考答案 一、选择题ABDDB BABAA 二、填空题 11.52++s s 12.)()()(t u e t u t t-++δ 13. m f 6,41 14.无理数15. -2,0,2,不存在三、简答题(略) 四、计算题20.解:结果如下图21. 解:(1) 求系统函数 H(z))()()(24.0)(2.0)(121z F z z F z Y z z Y z z Y ---+=-+ 24.02.024.02.011)()()(22211-++=-++==---z z zz z z z z F z Y z H (2)零点为 z=0 和 z= -1,极点为 z=0.4 和 z= -0.6(3) 因为两个极点的模均在单位圆内 , 所以此系统是稳定的 。
(4) 求单位样值响应 h(n)6.04.0)6.0)(4.0(124.02.01)(2++-=+-+=-++=z B z A z z z z z z z z H7.0)()4.0(4.0=-==z z z H z A4.0)()6.0(6.0-=+=-=z z z H z B6.04.04.07.0)(+--=z zz z z H ∴)(])6.0(4.0)4.0(7.0[)(n n h n n ε--=22.解:由原题知1)()86(2=++s H s s,则冲激响应的原微分方程为 )()(8)(6)('''t t h t h t h δ=++激励响应的原微分方程为 )()(8)(6)('''t f t y t y t y =++对应的拉斯变换为)()(8)0(6)(6)0()0()('2s F s Y y s sY y sy s Y s =+-+-----14)4(1(1)4)(2(1(286111)(2+++=++=++++=++++=s Bs A s s s s s s s s s s Y ))31)()4(4-=+=-=s s Y s A 31)()1(1=+=-=s s Y s B则]4111[31)(+-+=s s s Y 故)()(31)(4t e e t y tt ε---=111-)(t f t第 2 页 共 2 页23.答:(1))(2)(3)()(2s Y s sY s F s Y s--=231)()()(2++==s s s F s Y s H 对应微分方程为)()(2)(3)('"t f t y t y t y =++24.答:当0<t 时,0)(=t y当10<<t 时,⎰=⨯=t t d t y 0212)(τ 当21<<t 时,2)(=t y当32<<t 时,⎰--=+-=⨯=21)3(2)12(212)(t t t d t y τ 当3>t 时,0)(=t y注意:作题时各时段的图形。
全国2006年7月高等教育自学考试信号与系统试题及答案
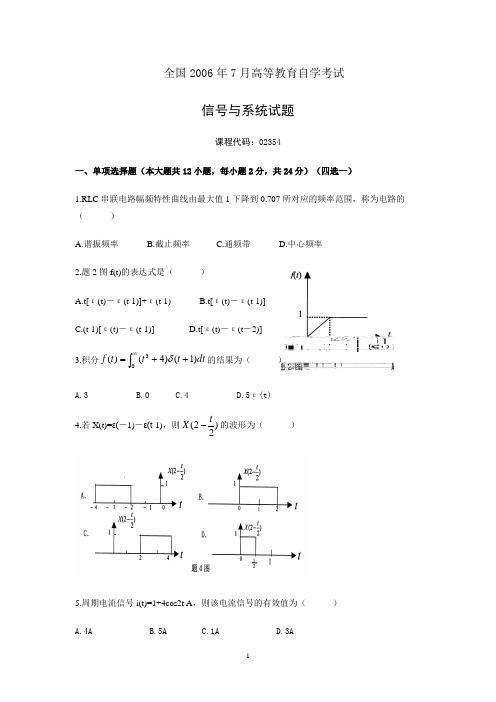
全国2006年7月高等教育自学考试信号与系统试题课程代码:02354一、单项选择题(本大题共12小题,每小题2分,共24分)(四选一)1.RLC 串联电路幅频特性曲线由最大值1下降到0.707所对应的频率范围,称为电路的( )A.谐振频率B.截止频率C.通频带D.中心频率 2.题2图f(t)的表达式是( )A.t[ε(t)-ε(t-1)]+ε(t-1)B.t[ε(t)-ε(t-1)]C.(t-1)[ε(t)-ε(t-1)]D.t[ε(t)-ε(t -2)] 3.积分⎰∞++=3)1()4()(dt t t t f δ的结果为( )A.3B.0C.4D.5ε(t) 4.若X(t)=ε(-1)-ε(t -1),则)22(t X -的波形为( )5.周期电流信号i(t)=1+4cos2t A ,则该电流信号的有效值为( ) A.4A B.5A C.1A D.3A6.用线性常系数微分方程∑∑===M k kk k Nk k k k dt t x d b dt t y d a 00)()(表征的LTI 系统,其单位冲激响应h(t)中不包括δ(t)及其导数项的条件为( )A.N=0B.M>NC.M<ND.M=N 7.已知f(t)=ε(t)-ε(t -nT),n 为任意整数,则f(t)的拉氏变换为( ) A.)1(1sT e s -- B. )1(1nsT e s -- C. )1(1ns e s-- D. )1(1nT e s-- 8.已知f(t)的象函数为1+s s,则f(t)为( ) A.1-e tB.1+e -tC.δ(t)+e tD.δ(t)-e -t9.以线性常系数微分方程表示的连续时间系统的自由响应取决于( )A.系统极点B.系统零点C.激励极点D.激励零点 10.两个有限长序列的非零序列值的宽度分别为N 和M ,则两个序列卷积所得的序列为( )A.宽度为N+M+1的有限宽度序列B.宽度为N+M-1的有限宽度序列C.宽度为N+M 的有限宽度序列D.不一定是有限宽度序列11.某一LTI 离散系统,其输入x(n)和输出y(n)满足如下线性常系数差分方程,)1(31)()1(21)(-+=--n x n x n y n y ,则系统函数H (Z )是( ) A.11211311)(--+-=Z Z Z H B. Z Z Z H 211311)(-+=C. 112131)(---+=Z Z Z H D.11211311)(---+=Z Z Z H 12.某一LTI 离散系统,它的系统函数111)(--=aZZ H ,如果该系统是稳定的,则( ) A. |a|≥1 B. |a|>1 C. |a|≤1 D. |a|<1二、填空题(本大题共12小题,每小题2分,共24分)在每小题的空格中填上正确答案 13.GCL 并联电路谐振时,流过电容和电感的电流相位相反,大小相等,其有效值都等于电源电流有效值的___________倍。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题(将唯一正确答案填入括号中,每题2分,共32分。
)1.积分dt t t e t )]()(['2δδ+⎰∞∞--等于:( D )(A )0 (B )1 (C )2 (D )3 2.序列和)2()4sin(-∑-∞=n n kn δπ等于:( C ) (A )1 (B )u(k) (C )u(k-2) (D ))2(-k δ3.已知某系统的单位样值响应)()5.1()(n u n h n =,则该系统的因果性和稳定性:( B )(A )因果,稳定 (B )因果,不稳定(C )非因果,稳定 (D )非因果,不稳定 4.dt t t t ejwt)]()([0--⎰∞∞--δδ 的结果为:( A ) (A )01jwt e -- (B )01jwt e -+ (C )01jwt e - (D )01jwt e + 5.序列卷积和)4()2()2()1(-*+--*+k k u k k u δδ等于:( B )(A ))(k δ (B ))1(-k δ (C ))1(-k u (D ))3(-k u 6.已知23)]([1-+=z z n x Z ,(2>z ),)3)(1()]([2++=z z zn x Z ,(3>z ),则)]()([21n x n x Z *为:( A )(A ))2)(1(-+z z z ,2>z (B ))2)(1(-+z z z,1>z(C ))2)(1(-+z z z ,6>z (D ))2)(1(-+z z z,3>z7.一LTI 无失真传输系统,它的幅度特性和相位特性要求为:( D )(A )幅度特性为常数,相位特性无要求 (B )幅度特性和相位特性均无要求(C )幅度特性无要求,相位特性的斜率为0t - (D )幅度特性为常数,相位特性的斜率为0t -8.若一LTI 系统输入)(1t e ,输出为)(1t r ,输入)(2t e ,输出为)(2t r ,则输入为dtt de t ae )()(21+,输出为:( C ) (A ))()(21t r t ar + (B ))()(21t r t r + (C )dt t dr t ar )()(21+(D )dtt dr t r )()(21+ 9.一理想低通滤波器的截止频率为c w ,下列信号经该滤波器滤波后信号不失真的是(cw w 32=):( B ) (A )cos2wt (B) coswt (C) coswt+cos2wt (D) cos3wt10.一LTI 系统响应的分解不对的是:( A )(A )强迫响应和瞬态响应 (B )零输入响应和零状态响应 (C )稳态响应和瞬态响应 (D )自由响应和强迫响应 11.已知一因果序列)(n f 的Z 变换式为)2)(1(12)(+++=z z z z z F ,则)(n f 的初值为:( B )(A ) 1 (B ) 0 (C )0.5 (D )2 12.若FE )()]([w F t f =,则FE )]([0t at f +为:( A )(A )a jwt e a w F a /0)(1 (B )0)(1jwt e a wF a- (C )0)(1jwt e a w F a(D )a jwt e a wF a /0)(1-13.已知1)]([2-=z zn x Z ,(1>z ),则)](3[n x Z n 为:( D ) (A )12-z z ,1>z (B )932-z z,1>z(C )12-z z ,3>z (D )932-z z,3>z14.若)()]([),()]([2211s F t f L s F t f L ==,则])()([222211dtt f d K dt t df K L +为:( C ) (A )]/)0(/)([]/)0(/)([22222111s f s s F K s f s s F K +++ (B ))]0(')0()([)]0()([22222111f sf s F s K f s sF K ++++ (C ))]0(')0()([)]0()([22222111f sf s F s K f s sF K --+-(D )]/)0(/)([]/)0(/)([22222111s f s s F K s f s s F K -+- 15.已知1)]([2-=z zn x Z ,(1>z ),则)]([2n x n Z 为:( B ) (A )2)1(2-z z (B )32)1(22-+z z z (C )32)1(-+z zz (D )12-z z 16.以下哪项陈述不是状态空间法分析系统的优点:( A )(A )特别适用于单输入单输出系统的分析 (B )特别适用于多输入多输出系统的分析(C )便于研究系统内部的一些物理量的变化规律 (D )适用于非线性时变系统的研究二、计算题17.求)12)(2(2)(2+++=s s s ss F 的拉氏逆变换。
(6分) 解:2)1(12)(+++++=s Cs B s A s F (1) 42)12(22-=-=++=s s s sA (1)41)2(41222=-=+=-=+=s s s s s ds d B (1) 2122-=-=+=s s sC (1)2)1(21424)(+-++++-=s s s s F (1) )()244()(2t u te e e t f t t t ----+-= (1)18.求方程)1()2(5.0)1(5.0)(-=---+n f n y n y n y 的单位样值相应)(n h 。
(6分)解:)()(5.0)(5.0)(121z F z z Y z z Y z z Y ---=-+ (2)2115.05.01)()()(----+==zz z z F z Y z H1325.032)(+-+-=z zz z z H (2))(])1(32)5.0(32[)(n u n h n n --= (2)19.某离散系统的差分方程表达式为)()2(2)1(3)(n f n y n y n y =-+-+,)()(n u n f =,1)1(=-y ,0)2(=-y ,试求该系统的零输入响应和零状态响应。
(12分) 解:(1)0)2(2)1(3)(=-+-+n y n y n y0232=++αα11-=α,22-=α (2)n n zi c c n y )2()1()(21-+-= (1)⎩⎨⎧+=-+-=--=-+-=----21222121121125.0)2()1(05.0)2()1(1c c c c c c c c 11=c ,42-=c (1))(])2(4)1[()(n u n y n n zi ---= (2) (2)特解为D ,则6D=1,故D=1/6 (1)61)2()1()(21+-+-=n n zs c c n y (1)⎪⎩⎪⎨⎧++=+-+-=+--=+-+-=----6125.061)2()1(0615.061)2()1(021*******211c c c c c c c c 211-=c ,342=c (2))(]61)2(34)1(21[)(n u n y n n zs +-+--= (2)20.用z 变换法解差分方程:)1()2(6)1(5)(-=-+--n f n y n y n y ,)(2)(n u n f n =,1)1(=-y ,1)2(=-y 。
(8分)解:)(])1()2()([6)]1()([5)(1121z F z z y y z Y z y z Y z z Y ----=-+-++-+- (2)2]1)([6]1)([5)(1121-=++++-----z zz z z Y z z Y z z Y (2) )3()2()123()(22--+--=z z z z z z Y 2)2(23625)(-----=z z z z z z z Y , )3(>z (2) )(])2()3(6)2(5[)(n u n n y n n n --= (2)三、综合题(共3题,共36分)0=t 以前开关位于“1”,电路已进入稳定状态,0=t 时开关从“1”倒向“2”,求电流)(t i 表示式。
(10分)解:2)0(EE R R R v c =+=- (1) 0)0(=-i (1)0>t 时的S 域等效电路如图所示: (2)sv s I sL sC c )0()()1(-=+ (2) LCs L E sL sCs Es I 1212)(2+=+=(2))()sin(2)(0t u t w LCE t i =)1(0LCw =(2)22.已知激励信号为)()(t u e t e t -=,零状态响应为)()3()(32t u e e t r t t --+-=,试求: (1)系统函数)(s H ;(2)画出系统的零极点分布图; (3)大致画出系统的幅频特性曲线。
(12分)解:(1)11)]([)(+==s t e L s E (2))3)(2(323321)]([)(+++=+++-==s s s s s t r L s R (2) 1/SCSL+-c(0-)/sV I(s))3)(2()1)(32()()()(++++==s s s s s E s R s H (2) (2)3分;(3)3分-3-2-1jwow1/40H(jw)-32123.右图是某离散系统的仿真框图,试求: (1)系统的)(z H ;(2)系统的收敛域和稳定性; (3)画出系统的零极点分布图; (4)大致画出系统的幅频特性图。
注:仿真框图中的f(n)是第一个加法器的输出,不是表示乘系数。
(14分)解:(1)⎪⎩⎪⎨⎧-+=-+--=)1(2)()()2(81)1(41)()(n f n f n y n f n f n x n f (2) )(81)(41)()(21z F z z F z z X z F --+-= 2181411)()(---+=z z z X z F (1)211181411)(2)()(2)()(-----++=+=z z z X z z X z F z z F z Y (1))41)(21()2(8141121)()()(211-++=-++==---z z z z z z z z X z Y z H (2)(2)收敛域为:21>z ;系统稳定。
(2)x(n)(3)3分(4)3分ww 802s H(e )jw w s385-1-2-10jImzo 12o 14Rez一、选择题(将唯一正确答案填入括号中,每题2分,共32分。
