泸州市中考原题07.无答案
专题07一元二次方程及应用(共30题)-2021年中考数学真题分项汇编(原卷版)【全国通用】

2021年中考数学真题分项汇编【全国通用】(第01期)专题7一元二次方程及应用(共30题)姓名:__________________ 班级:______________ 得分:_________________一、单选题1.(2021·山东临沂市·中考真题)方程256x x -=的根是( ) A .1278x x ==,B .1278x x ==-,C .1278x x =-=,D .1278x x =-=-,2.(2021·浙江丽水市·中考真题)用配方法解方程2410x x ++=时,配方结果正确的是( ) A .2(2)5x -=B .2(2)3x -=C .2(2)5x +=D .2(2)3x +=3.(2021·四川泸州市·中考真题)关于x 的一元二次方程2220x mx m m ++-=的两实数根12,x x ,满足122x x =,则2212(2)(2)x x ++的值是( )A .8B .16C . 32D .16或404.(2021·四川广安市·中考真题)关于x 的一元二次方程()22310a x x +-+=有实数根,则a 的取值范围是( )A .14a ≤且2a ≠- B .14a ≤ C .14a <且2a ≠- D .14a < 5.(2021·湖南邵阳市·中考真题)在平面直角坐标系中,若直线y x m =-+不经过第一象限,则关于x 的方程210mx x ++=的实数根的个数为( ) A .0个B .1个C .2个D .1或2个6.(2021·四川眉山市·中考真题)已知一元二次方程2310x x -+=的两根为1x ,2x ,则211252x x x --的值为( ) A .7-B .3-C .2D .57.(2021·浙江杭州市·中考真题)已知1y 和2y 均是以x 为自变量的函数,当x m =时,函数值分别为1M 和2M ,若存在实数m ,使得120M M +=,则称函数1y 和2y 具有性质P .以下函数1y 和2y 具有性质P 的是( )A .212y x x =+和21y x =--B .212y x x =+和21y x =-+C .11y x =-和21y x =-- D .11y x=-和21y x =-+8.(2021·浙江台州市·中考真题)关于x 的方程x 2-4x +m =0有两个不相等的实数根,则m 的取值范围是( ) A .m >2B .m <2C .m >4D .m <49.(2021·云南中考真题)若一元二次方程2210ax x ++=有两个不相等的实数根,则实数a 的取值范围是( ) A .1a <B .1a ≤C .1a ≤且0a ≠D .1a <且0a ≠10.(2021·山东泰安市·中考真题)已知关于x 的一元二次方程标()22120kx k x k --+-=有两个不相等的实数根,则实数k 的取值范围是( ) A .14k >-B .14k <C .14k >-且0k ≠ D .14k <0k ≠ 11.(2021·四川南充市·中考真题)已知方程2202110x x -+=的两根分别为1x ,2x ,则2122021x x -的值为( ) A .1B .1-C .2021D .2021-12.(2021·四川凉山彝族自治州·中考真题)函数y kx b =+的图象如图所示,则关于x 的一元二次方程210x bx k ++-=的根的情况是( )A .没有实数根B .有两个相等的实数根C .有两个不相等的实数根D .无法确定13.(2021·四川泸州市·中考真题)直线l 过点(0,4)且与y 轴垂直,若二次函数2222()(2)(3)2y x a x a x a a a =-+-+--+(其中x 是自变量)的图像与直线l 有两个不同的交点,且其对称轴在y 轴右侧,则a 的取值范围是( ) A .a >4 B .a >0C .0<a ≤4D .0<a <4二、填空题14.(2021·上海中考真题)若一元二次方程2230x x c -+=无解,则c 的取值范围为_________. 15.(2021·湖南岳阳市·中考真题)已知关于x 的一元二次方程260x x k ++=有两个相等的实数根,则实数k 的值为_______.16.(2021·江西中考真题)已知1x ,2x 是一元二次方程2430x x -+=的两根,则1212x x x x +-=______. 17.(2021·四川遂宁市·中考真题)如图都是由同样大小的小球按一定规律排列的,依照此规律排列下去,第___个图形共有210个小球.18.(2021·四川广安市·中考真题)一个三角形的两边长分别为3和5,第三边长是方程x 2-6x +8=0的根,则三角形的周长为_____.19.(2021·甘肃武威市·中考真题)已知关于x 的方程2x 2x m 0-+=有两个相等的实数根,则m 的值是_________.20.(2021·江苏连云港市·中考真题)已知方程230x x k -+=有两个相等的实数根,则k =____. 21.(2021·四川成都市·中考真题)若m ,n 是一元二次方程2210x x +-=的两个实数根,则242m m n++的值是______.22.(2021·浙江丽水市·中考真题)数学活动课上,小云和小王在讨论张老师出示的一道代数式求值问题: 已知实数,a b 同时满足2222,22a a b b b a +=++=+,求代数式b aa b+的值.结合他们的对话,请解答下列问题: (1)当a b =时,a 的值是__________. (2)当a b 时,代数式b aa b+的值是__________. 三、解答题23.(2021·四川南充市·中考真题)已知关于x 的一元二次方程22(21)0x k x k k -+++=. (1)求证:无论k 取何值,方程都有两个不相等的实数根.(2)如果方程的两个实数根为1x ,2x ,且k 与12x x 都为整数,求k 所有可能的值.24.(2021·浙江嘉兴市·中考真题)小敏与小霞两位同学解方程()()2333x x -=-的过程如下框:小敏:两边同除以()3x -,得33x =-, 则6x =.小霞:移项,得()()23330x x ---=, 提取公因式,得()()3330x x ---=.则30x -=或330x --=, 解得13x =,20x =.你认为他们的解法是否正确?若正确请在框内打“√”;若错误请在框内打“×”,并写出你的解答过程.25.(2021·四川遂宁市·中考真题)某服装店以每件30元的价格购进一批T恤,如果以每件40元出售,那么一个月内能售出300件,根据以往销售经验,销售单价每提高1元,销售量就会减少10件,设T恤的销售单价提高x元.(1)服装店希望一个月内销售该种T恤能获得利润3360元,并且尽可能减少库存,问T恤的销售单价应提高多少元?(2)当销售单价定为多少元时,该服装店一个月内销售这种T恤获得的利润最大?最大利润是多少元?26.(2021·浙江中考真题)今年以来,我市接待的游客人数逐月增加,据统计,游玩某景区的游客人数三月份为4万人,五月份为5.76万人.(1)求四月和五月这两个月中,该景区游客人数平均每月增长百分之几;(2)若该景区仅有,A B两个景点,售票处出示的三种购票方式如表所示:购票方式甲乙丙可游玩景点A B A和B门票价格100元/人80元/人160元/人据预测,六月份选择甲、乙、丙三种购票方式的人数分别有2万、3万和2万.并且当甲、乙两种门票价格不变时,丙种门票价格每下降1元,将有600人原计划购买甲种门票的游客和400人原计划购买乙种门票的游客改为购买丙种门票.①若丙种门票价格下降10元,求景区六月份的门票总收入;①问:将丙种门票价格下降多少元时,景区六月份的门票总收入有最大值?最大值是多少万元?27.(2021·重庆中考真题)重庆小面是重庆美食的名片之一,深受外地游客和本地民众欢迎.某面馆向食客推出经典特色重庆小面,顾客可到店食用(简称“堂食”小面),也可购买搭配佐料的袋装生面(简称“生食”小面).已知3份“堂食”小面和2份“生食”小面的总售价为31元,4份“堂食”小面和1份“生食”小面的总售价为33元.(1)求每份“堂食”小面和“生食”小面的价格分别是多少元?(2)该面馆在4月共卖出“堂食”小面4500份,“生食”小面2500份,为回馈广大食客,该面馆从5月1日起每份“堂食”小面的价格保持不变,每份“生食”小面的价格降低3a%4.统计5月的销量和销售额发现:“堂食”小面的销量与4月相同,“生食”小面的销量在4月的基础上增加5%2a ,这两种小面的总销售额在4月的基础上增加5%11a .求a 的值.28.(2021·四川乐山市·中考真题)已知关于x 的一元二次方程20x x m +-=.(1)若方程有两个不相等的实数根,求m 的取值范围;(2)二次函数2y x x m =+-的部分图象如图所示,求一元二次方程20x x m +-=的解.29.(2021·重庆中考真题)某工厂有甲、乙两个车间,甲车间生产A 产品,乙车间生产B 产品,去年两个车间生产产品的数量相同且全部售出.已知A 产品的销售单价比B 产品的销售单价高100元,1件A 产品与1件B 产品售价和为500元.(1)A 、B 两种产品的销售单价分别是多少元?(2)随着5G 时代的到来,工业互联网进入了快速发展时期.今年,该工厂计划依托工业互联网将乙车间改造为专供用户定制B 产品的生产车间.预计A 产品在售价不变的情况下产量将在去年的基础上增加a %;B产品产量将在去年的基础上减少a%,但B产品的销售单价将提高3a%.则今年A、B两种产品全部售出后总销售额将在去年的基础上增加2925a%.求a的值.30.(2021·四川泸州市·中考真题)一次函数y=kx+b(k≠0)的图像与反比例函数myx的图象相交于A(2,3),B(6,n)两点(1)求一次函数的解析式(2)将直线AB沿y轴向下平移8个单位后得到直线l,l与两坐标轴分别相交于M,N,与反比例函数的图象相交于点P,Q,求PQMN的值.。
2022年四川省泸州市中考数学试题及答案解析

2022年四川省泸州市中考数学试卷一、选择题(本大题共12小题,共36.0分)1.−√4=( )A. −2B. −12C. 12D. 22.2022年5月,四川省发展和改革委员会下达了保障性安居工程2022年第一批中央预算内投资计划,泸州市获得75500000元中央预算内资金支持,将75500000用科学记数法表示为( )A. 7.55×106B. 75.5×106C. 7.55×107D. 75.5×1073.如图是一个由6个大小相同的正方体组成的几何体,它的俯视图是( )A.B.C.D.4.如图,直线a//b,直线c分别交a,b于点A,C,点B在直线b上,AB⊥AC,若∠1=130°,则∠2的度数是( )A. 30°B. 40°C. 50°D. 70°5.下列运算正确的是( )A. a2⋅a3=a6B. 3a−2a=1C. (−2a2)3=−8a6D. a6÷a2=a36.费尔兹奖是国际上享有崇高声誉的一个数学奖项,每四年评选一次,主要授予年轻的数学家.下面数据是部分获奖者获奖时的年龄(单位:岁):29,32,33,35,35,40,则这组数据的众数和中位数分别是( )A. 35,35B. 34,33C. 34,35D. 35,347.与2+√15最接近的整数是( )A. 4B. 5C. 6D. 78.抛物线y=−12x2+x+1经平移后,不可能得到的抛物线是( )A. y=−12x2+x B. y=−12x2−4C. y=−12x2+2021x−2022 D. y=−x2+x+19.已知关于x的方程x2−(2m−1)x+m2=0的两实数根为x1,x2,若(x1+1)(x2+1)=3,则m的值为( )A. −3B. −1C. −3或1D. −1或310.如图,AB是⊙O的直径,OD垂直于弦AC于点D,DO的延长线交⊙O于点E.若AC=4√2,DE=4,则BC的长是( )A. 1B. √2C. 2D. 411.如图,在平面直角坐标系xOy中,矩形OABC的顶点B的坐标为(10,4),四边形ABEF是菱形,且tan∠ABE=43.若直线l把矩形OABC和菱形ABEF组成的图形的面积分成相等的两部分,则直线l的解析式为( )A. y=3xB. y=−34x+152C. y=−2x+11D. y=−2x+1212.如图,在边长为3的正方形ABCD中,点E是边AB上的点,且BE=2AE,过点E作DE的垂线交正方形外角∠CBG的平分线于点F,交边BC于点M,连接DF交边BC于点N,则MN的长为( )A. 23B. 56C. 67D. 1二、填空题(本大题共4小题,共12.0分)13.(−2,3)关于原点对称点的坐标是______ .14.若(a−2)2+|b+3|=0,则ab=______ .15.若方程x−3x−2+1=32−x的解使关于x的不等式(2−a)x−3>0成立,则实数a的取值范围是______.16.如图,在Rt△ABC中,∠C=90°,AC=6,BC=2√3,半径为1的⊙O在Rt△ABC内平移(⊙O可以与该三角形的边相切),则点A到⊙O上的点的距离的最大值为______.三、计算题(本大题共1小题,共6.0分)17.计算:(√3)0+2−1+√2cos45°−|−12|.四、解答题(本大题共8小题,共66.0分)18.如图,E,F分别是▱ABCD的边AB,CD上的点,已知AE=CF.求证:DE=BF.19.化简:(m2−3m+1m +1)÷m2−1m.20.劳动教育具有树德、增智、强体、育美的综合育人价值,有利于学生树立正确的劳动价值观.某学校为了解学生参加家务劳动的情况,随机抽取了m名学生在某个休息日做家务的劳动时间作为样本,并绘制了以下不完整的频数分布表和扇形统计图.根据题中已有信息,解答下列问题:劳动时间t(单位:小时)频数0.5≤t<1121≤t<1.5a1.5≤t<2282≤t<2.5162.5≤t≤34(1)m=______,a=______;(2)若该校学生有640人,试估计劳动时间在2≤t≤3范围的学生有多少人?(3)劳动时间在2.5≤t≤3范围的4名学生中有男生2名,女生2名,学校准备从中任意抽取2名交流劳动感受,求抽取的2名学生恰好是一名男生和一名女生的概率.21.某经销商计划购进A,B两种农产品.已知购进A种农产品2件,B种农产品3件,共需690元;购进A种农产品1件,B种农产品4件,共需720元.(1)A,B两种农产品每件的价格分别是多少元?(2)该经销商计划用不超过5400元购进A,B两种农产品共40件,且A种农产品的件数不超过B种农产品件数的3倍.如果该经销商将购进的农产品按照A种每件160元,B种每件200元的价格全部售出,那么购进A,B两种农产品各多少件时获利最多?22.如图,直线y=−32x+b与反比例函数y=12x的图象相交于点A,B,已知点A的纵坐标为6.(1)求b的值;(2)若点C是x轴上一点,且△ABC的面积为3,求点C的坐标.23.如图,海中有两小岛C,D,某渔船在海中的A处测得小岛C位于东北方向,小岛D位于南偏东30°方向,且A,D相距10nmile.该渔船自西向东航行一段时间后到达点B,此时测得小岛C位于西北方向且与点B相距8√2n mile.求B,D间的距离(计算过程中的数据不取近似值).24.如图,点C在以AB为直径的⊙O上,CD平分∠ACB交⊙O于点D,交AB于点E,过点D作⊙O的切线交CO的延长线于点F.(1)求证:FD//AB;(2)若AC=2√5,BC=√5,求FD的长.25.如图,在平面直角坐标系xOy中,已知抛物线y=ax2+x+c经过A(−2,0),B(0,4)两点,直线x=3与x轴交于点C.(1)求a,c的值;(2)经过点O的直线分别与线段AB,直线x=3交于点D,E,且△BDO与△OCE的面积相等,求直线DE的解析式;(3)P是抛物线上位于第一象限的一个动点,在线段OC和直线x=3上是否分别存在点F,G,使B,F,G,P为顶点的四边形是以BF为一边的矩形?若存在,求出点F的坐标;若不存在,请说明理由.答案和解析1.【答案】A【解析】解:−√4=−√22=−2.故选:A.根据算术平方根的定义判断即可.本题考查了算术平方根,掌握算术平方根的定义是解答本题的关键.2.【答案】C【解析】解:75500000=7.55×107,故选:C.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.3.【答案】C【解析】解:从物体上面看,底层有一个正方形,上层有四个正方形.故选:C.细心观察图中几何体中正方体摆放的位置,根据俯视图是从上面看到的图形判定则可.本题考查了三视图的知识,俯视图是从物体上面看所得到的图形,解答时学生易将三种视图混淆而错误地选其它选项.4.【答案】B【解析】解:如图所示,∵直线a//b,∴∠1=∠DAC,∵∠1=130°,∴∠DAC=130°,又∵AB⊥AC,∴∠BAC=90°,∴∠2=∠DAC−∠BAC=130°−90°=40°.故选:B.首先利用平行线的性质得到∠1=∠DAC,然后利用AB⊥AC得到∠BAC=90°,最后利用角的和差关系求解.本题考查平行线的性质,解答本题的关键是明确平行线的性质,求出∠DAC的度数.5.【答案】C【解析】解:A.a2⋅a3=a5,故本选项不合题意;B.3a−2a=a,故本选项不合题意;C.(−2a2)3=−8a6,故本选项符合题意;D.a6÷a2=a4,故本选项不合题意;故选:C.选项A根据同底数幂的乘法法则判断即可,同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加;选项B根据合并同类项法则判断即可,合并同类项的法则:把同类项的系数相加,所得结果作为系数,字母和字母的指数不变;选项C根据积的乘方运算法则判断即可,积的乘方法则:把每一个因式分别乘方,再把所得的幂相乘;选项D根据同底数幂的除法法则判断即可,同底数幂的除法法则:底数不变,指数相减.本题考查了同底数幂的乘除法,幂的乘方与积的乘方以及合并同类项,掌握相关运算法则是解答本题的关键.6.【答案】D【解析】解:∵35出现的次数最多,∴这组数据的众数是35,=34,把这些数从小到大排列,排在中间的两个数分别为33、35,故中位数为33+352故选:D.根据中位数和众数的定义求解可得.本题主要考查众数和中位数,求一组数据的众数的方法:找出频数最多的那个数据,若几个数据频数都是最多且相同,此时众数就是这多个数据.将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.7.【答案】C【解析】解:∵3<√15<4,而15−9>16−15,∴√15更接近4,∴2+√15更接近6,故选:C.估算无理数√15的大小,再确定√15更接近的整数,进而得出答案.本题考查估算无理数的大小,理解算术平方根的定义以及数的大小关系是正确解答的前提.8.【答案】Dx2+x+1经过平移后开口方向不变,开口大小也不变,【解析】解:∵将抛物线y=−12x2+x+1经过平移后不可能得到的抛物线是y=−x2+x+1.∴抛物线y=−12故选:D.根据抛物线的平移规律,可得答案.本题考查了二次函数图象与几何变换,由平移规律得出a不变是解题的关键.9.【答案】A【解析】解:∵方程x2−(2m−1)x+m2=0的两实数根为x1,x2,∴x1+x2=2m−1,x1x2=m2,∵(x1+1)(x2+1)=x1x2+x1+x2+1=3,∴m2+2m−1+1=3,解得:m1=1,m2=−3,∵方程有两实数根,∴Δ=(2m−1)2−4m2≥0,,即m≤14∴m2=1(不合题意,舍去),∴m=−3;故选:A.根据方程x2−(2m−1)x+m2−1=0的两实数根为x1,x2,得出x1+x2与x1x2的值,再根据x12+x22=3,即可求出m的值.本题考查了根与系数的关系及根的判别式,难度适中,关键掌握x1,x2是方程x2+px+q=0的两根时,x1+x2=−p,x1x2=q.10.【答案】C【解析】解:∵AB是⊙O的直径,∴∠C=90°,∵OD⊥AC,∴点D是AC的中点,∴OD是△ABC的中位线,BC,∴OD//BC,且OD=12设OD=x,则BC=2x,∵DE=4,∴OE=4−x,∴AB=2OE=8−2x,在Rt△ABC中,由勾股定理可得,AB2=AC2+BC2,∴(8−2x)2=(4√2)2+(2x)2,解得x=1.∴BC=2x=2.故选:C.BC,设OD=x,由垂径定理可知,点D是AC的中点,则OD是△ABC的中位线,所以OD=12则BC=2x,则OE=4−x,AB=2OE=8−2x,在Rt△ABC中,由勾股定理可得AB2= AC2+BC2,即(8−2x)2=(4√2)2+(2x)2,求出x的值即可得出结论.本题主要考查中位线的性质与判定,垂径定理,勾股定理等知识,设出参数,根据勾股定理得出方程是解题关键.11.【答案】D【解析】解:连接OB,AC,它们交于点M,连接AE,BF,它们交于点N,则直线MN为符合条件的直线l,如图,∵四边形OABC 是矩形,∴OM =BM .∵B 的坐标为(10,4),∴M(5,2),AB =10,BC =4.∵四边形ABEF 为菱形,BE =AB =10.过点E 作EG ⊥AB 于点G ,在Rt △BEG 中,∵tan∠ABE =43,∴EG BG =43,设EG =4k ,则BG =3k ,∴BE =√EG 2+BG 2=5k ,∴5k =10,∴k =2,∴EG =8,BG =6,∴AG =4.∴E(4,12).∵B 的坐标为(10,4),AB//x 轴,∴A(0,4).∵点N 为AE 的中点,∴N(2,8).设直线l 的解析式为y =ax +b ,∴{5a +b =22a +b =8,解得:{a =−2b =12,∴直线l 的解析式为y =−2x +12,故选:D.分别求出矩形OABC和菱形ABEF的中心的坐标,利用待定系数法求经过两中心的直线即可得出结论.本题主要考查了矩形和菱形的性质,中点坐标的特征,直角三角形的边角关系定理,利用待定系数法确定函数的解析式是解题的关键.12.【答案】B【解析】解:作FH⊥BG交于点H,作FK⊥BC于点K,∵BF平分∠CBG,∠KBH=90°,∴正方形BHFK是正方形,∵DE⊥EF,∠EHF=90°,∴∠DEA+∠FEH=90°,∠EFH+∠FEH=90°,∴∠DEA=∠EFH,∵∠A=∠EHF=90°,∴△DAE∽△EHF,∴ADHE =AEHF,∵正方形ABCD的边长为3,BE=2AE,∴AE=1,BE=2,设FH=a,则BH=a,∴32+a =1a,解得a=1;∵FM⊥CB,DC⊥CB,∴△DCN∽△FKN,∴DCFM =CNKN,∵BC=3,BK=1,∴CK=2,设CN=b,则NK=2−b,∴31=b2−b,解得b=32,即CN=32,∵∠A=∠EBM,∠AED=∠BME,∴△ADE∽△BEM,∴ADBE =AEBM,∴32=1BM,解得BM=23,∴MN=BC−CN−BM=3−32−23=56,故选:B.根据正方形的性质、相似三角形的判定和性质,可以求得CN和BN的长,然后根据BC=3,即可求得MN的长.本题考查正方形的性质、相似三角形的判定和性质,解答本题的关键是明确题意,利用数形结合的思想解答.13.【答案】(2,−3)【解析】解:∵点M(−2,3)关于原点对称,∴点M(−2,3)关于原点对称的点的坐标为(2,−3).故答案为(2,−3).平面直角坐标系中任意一点P(x,y),关于原点的对称点是(−x,−y),即:求关于原点的对称点,横纵坐标都变成相反数.记忆方法是结合平面直角坐标系的图形记忆.本题考查关于原点对称的点的坐标特征,这一类题目是需要识记的基础题,记忆时要结合平面直角坐标系.14.【答案】−6【解析】解:由题意得,a−2=0,b+3=0,解得a=2,b=−3,所以,ab=2×(−3)=−6.故答案为:−6.根据非负数的性质列式求出a、b的值,然后代入代数式进行计算即可得解.本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.15.【答案】a<−1【解析】解:x−3x−2+1=32−x,x−3 x−2+x−2x−2=−3x−2,2x−2x−2=0,解得:x=1,∵x−2≠0,2−x≠0,∴x=1是分式方程的解,将x=1代入不等式(2−a)x−3>0,得:2−a−3>0,解得:a<−1,∴实数a的取值范围是a<−1,故答案为:a<−1.先解分式方程,再将x代入不等式中即可求解.本题考查分式方程的解,不等式的解集,解题的关键是正确求出分式方程的解,要注意分母不能为0.16.【答案】2√7+1【解析】解:当⊙O与BC、BA都相切时,连接AO并延长交⊙O于点D,则AD为点A到⊙O上的点的距离的最大值,设⊙O与BC、BA的切点分别为E、F,连接OE、OF,则OE⊥BC,OF⊥AB,∵AC=6,BC=2√3,∴tan∠ABC=ACBC=√3,AB=√AC2+BC2=4√3,∴∠ABC=60°,∴∠OBF=30°,∴BF=OFtan∠OBF=√3,∴AF=AB−BF=3√3,∴OA=√OF2+AF2=2√7,∴AD=2√7+1,故答案为:2√7+1.连接OE、OF,根据正切的定义求出∠ABC,根据切线长定理得到∠OBF=30°,根据含30°角的直角三角形的性质、勾股定理计算,得到答案.本题考查的是切线的性质、直角三角形的性质、切线长定理,根据题意得出AD为点A到⊙O上的点的距离的最大值是解题的关键.17.【答案】解:原式=1+12+√2×√22−12=1+12+1−12=1+1=2.【解析】根据实数的运算法则,绝对值,零指数幂,负整数指数幂,特殊角的三角函数值直接计算即可.本题考查实数的运算,绝对值,零指数幂,负整数指数幂,特殊角的三角函数值,解题的关键是熟练掌握知识点,正确计算.18.【答案】证明:∵四边形ABCD是平行四边形,∴∠A=∠C,AD=CB,在△ADE和△CBF中,{AD=CB ∠A=∠C AE=CF,∴△ADE≌△CBF(SAS),∴DE=BF.【解析】根据平行四边形的性质,可以得到∠A=∠C,AD=CB,再根据AE=CF,利用SAS可以证明△ADE和△CBF全等,然后即可证明结论成立.本题考查平行四边形的性质、全等三角形的判定与性质,解答本题的关键是证明△ADE 和△CBF全等.19.【答案】解:原式=m2−3m+1+mm ÷m2−1m=m2−2m+1m ⋅m m2−1=(m−1)2m ⋅m(m+1)(m−1)=m−1m+1.【解析】先把括号部分通分并计算加法,再根据分式的乘除法法则化简即可.本题考查了分式的混合运算,掌握分式的通分以及相关乘法公式是解答本题的关键.20.【答案】80 20【解析】解:(1)m =12÷15%=80,a =80−12−28−16−4=20;故答案为:80;20;(2)640×16+480=160(人),所以估计劳动时间在2≤t ≤3范围的学生有160人;(3)画树状图为:共有12种等可能的结果,其中一名男生和一名女生的结果数为8,所以恰好抽到一名男生和一名女生的概率=812=23.(1)用A 组人数除以它所占的百分比得到m 的值,然后m 分别减去A 、C 、D 、E 组的人数得到a 的值;(2)用640乘以D 、E 组的人数所占的百分比的和即可;(3)画树状图展示所有12种等可能的结果,找出一名男生和一名女生的结果数,然后根据概率公式求解.本题考查了列表法与树状图法:利用列表法或树状图展示所有可能的结果求出n ,再从中选出符合事件A 或B 的结果数目m ,然后利用概率公式求出事件A 或B 的概率.也考查了统计图.21.【答案】解:(1)设每件A 种农产品的价格是x 元,每件B 种农产品的价格是y 元,依题意得:{2x +3y =690x +4y =720, 解得:{x =120y =150. 答:每件A 种农产品的价格是120元,每件B 种农产品的价格是150元.(2)设该经销商购进m 件A 种农产品,则购进(40−m)件B 种农产品,依题意得:{m ≤3(40−m)120m +150(40−m)≤5400,解得:20≤m≤30.设两种农产品全部售出后获得的总利润为w元,则w=(160−120)m+(200−150)(40−m)=−10m+2000.∵−10<0,∴w随m的增大而减小,∴当m=20时,w取得最大值,此时40−m=40−20=20.答:当购进20件A种农产品,20件B种农产品时获利最多.【解析】(1)设每件A种农产品的价格是x元,每件B种农产品的价格是y元,根据“购进A种农产品2件,B种农产品3件,共需690元;购进A种农产品1件,B种农产品4件,共需720元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;(2)设该经销商购进m件A种农产品,则购进(40−m)件B种农产品,利用总价=单价×数量,结合购进A种农产品的件数不超过B种农产品件数的3倍且总价不超过5400元,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,设两种农产品全部售出后获得的总利润为w元,利用总利润=每件的销售利润×销售数量,即可得出w关于m的函数关系式,再利用一次函数的性质,即可解决最值问题.本题考查了二元一次方程组的应用、一元一次不等式组的应用以及一次函数的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,找出w关于m的函数关系式.22.【答案】解:(1)∵点A在反比例函数y=12上,且A的纵坐标为6,x∴点A(2,6),x+b经过点A,∵直线y=−32∴6=−3×2+b,2∴b=9;(2)如图,设直线AB与x轴的交点为D,设点C(a,0),∵直线AB 与x 轴的交点为D ,∴点D(6,0),由题意可得:{ y =−32x +9y =12x , ∴{x 1=2y 1=6,{x 2=4y 2=3, ∴点B(4,3),∵S △ACB =S △ACD −S △BCD ,∴3=12×CD ×(6−3), ∴CD =2,∴点C(4,0)或(8,0).【解析】(1)先求出点A 坐标,代入解析式可求解;(2)先求出点D 坐标,由面积的和差关系可求CD =2,即可求解.本题是反比例函数综合题,考查一次函数的应用、反比例函数的应用等知识,解题的关键是灵活运用所学知识解决问题,学会分割法求三角形的面积.23.【答案】解:由题意得,∠CAB =∠ABC =45°,BC =8√2n mile .∴∠C =90°,∴AB =√AC 2+BC 2=√2BC =√2×8√2=16(n mile),过D 作DH ⊥AB 于H ,则∠AHD =∠BHD =90°,在Rt △ADH 中,∠ADH =30°,AD =10nmile ,cos∠ADH =DHAD ,∴AH=12AD=5nmile,DH=10⋅cos30°=10×√32=5√3,∴BH=AB−AH=11n mile,在Rt△BDH中,BD=√DH2+BH2=√(5√3)2+112=14(n mile),答:B,D间的距离是14n mile.【解析】由勾股定理求出AB过D作DH⊥AB于H,分别在Rt△ADH中和Rt△BDH中,解直角三角形即可求出BD.本题主要考查了解直角三角形的应用,正确作出辅助线构造出直角三角形是解决问题的关键.24.【答案】(1)证明:连接OD.∵DF是⊙O的切线,∴OD⊥DF,∵CD平分∠ACB,∴AD⏜=DB⏜,∴OD⊥AB,∴AB//DF;(2)解:过点C作CH⊥AB于点H.∵AB是直径,∴∠ACB=90°,∵BC=√5,AC=2√5,∴AB=√AC2+BC2=√(2√5)2+(√5)2=5,∵S△ABC=12⋅AC⋅BC=12⋅AB⋅CH,∴CH=2√5×√55=2,∴BH=√BC2−CH2=1,∴OH=OB−BH=52−1=32,∵DF//AB,∴∠COH=∠F,∵∠CHO=∠ODF=90°,∴△CHO∽△ODF ,∴CH OD =OH DF , ∴252=32DF ,∴DF =158. 【解析】(1)连接OD ,证明DF ⊥OD ,AB ⊥OD ,可得结论;(2)过点C 作CH ⊥AB 于点H.利用勾股定理求出AB ,利用面积法求出CH ,证明△CHO∽△ODF ,推出CH OD =OH DF ,由此求出DF 即可.本题属于圆综合题,考查了垂径定理,圆周角定理,平行线的判定,相似三角形的判定和性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题.25.【答案】解:(1)把A(−2,0),B(0,4)两点代入抛物线y =ax 2+x +c 中得:{4a −2+c =0c =4解得:{a =−12c =4; (2)由(2)知:抛物线解析式为:y =−12x 2+x +4,设直线AB 的解析式为:y =kx +b ,则{−2k +b =0b =4,解得:{k =2b =4, ∴AB 的解析式为:y =2x +4,设直线DE 的解析式为:y =mx ,∴2x +4=mx ,∴x =4m−2,当x =3时,y =3m ,∴E(3,3m),∵△BDO 与△OCE 的面积相等,CE ⊥OC ,∴12⋅3⋅(−3m)=12⋅4⋅42−m ,∴9m 2−18m −16=0,∴(3m +2)(3m −8)=0,∴m 1=−23,m 2=83(舍),∴直线DE的解析式为:y=−23x;(3)存在,B,F,G,P为顶点的四边形是以BF为一边的矩形有两种情况:设P(t,−12t2+t+4),①如图1,过点P作PH⊥y轴于H,∵四边形BPGF是矩形,∴BP=FG,∠PBF=∠BFG=90°,∴∠CFG+∠BFO=∠BFO+∠OBF=∠CFG+∠CGF=∠OBF+∠PBH=90°,∴∠PBH=∠OFB=∠CGF,∵∠PHB=∠FCG=90°,∴△PHB≌△FCG(AAS),∴PH=CF,∴CF=PH=t,OF=3−t,∵∠PBH=∠OFB,∴PHBH =OBOF,即t−12t2+t+4−4=43−t,解得:t1=0(舍),t2=1,∴F(2,0);②如图2,过点G作GN⊥y轴于N,过点P作PM⊥x轴于M,同①可得:NG =FM =3,OF =t −3,∵∠OFB =∠FPM ,∴tan∠OFB =tan∠FPM ,∴OB OF =FM PM ,即4t−3=3−12t 2+t+4,解得:t 1=1+√2014,t 2=1−√2014(舍), ∴F(√201−114,0); 综上,点F 的坐标为(2,0)或(√201−114,0).【解析】(1)把A(−2,0),B(0,4)两点代入抛物线y =ax 2+x +c 中列方程组解出即可;(2)利用待定系数可得直线AB 的解析式,再设直线DE 的解析式为:y =mx ,点D 是直线DE 和AB 的交点,列方程可得点D 的横坐标,根据△BDO 与△OCE 的面积相等列等式可解答;(3)设P(t,−12t 2+t +4),分两种情况:作辅助线构建相似三角形,证明三角形相似或利用等角的三角函数列等式可解答.本题是二次函数的综合题,考查了二次函数的相关性质,一次函数的相关性质,矩形的性质和判定,三角形全等的性质和判定,三角函数,解一元二次方程等知识,第三问有难度,正确作辅助线构建直角三角形是解本题的关键.。
2023年四川省泸州市中考语文真题(无答案)

2023年四川省泸州市中考语文真题学校:___________姓名:___________班级:___________考号:___________一、现代文阅读阅读下列材料,按照要求完成下面小题。
材料一①纵观历史,人类与传染病的斗争从未停止。
近几年的新冠疫情再次让人们意识到人类在传染病大流行面前是多么脆弱。
自2009年以来,世界卫生组织宣布了6起国际关注的突发公共卫生事件,除新冠疫情外,还有2009年的甲流、2014年的脊髓灰质炎和埃博拉、2016年的寨卡,以及2019年的另一起埃博拉疫情。
②为何大流行越来越多?“导致大流行发生的因素有很多,如气候变化、全球化等。
特别是对于许多新发传染病而言,人类与野生动物之间的接触越来越多,导致病原体从动物传染到人身上的可能性越来越大。
”清华大学医学院博士研究生雷雨晴解释道。
印尼某生物技术公司研发部负责人蔡金光说,缺乏准备也是疫情发展为大流行的一个重要原因,政府、卫生部门和社区之间如果没有良好的协作,那么疫情很容易演变为大流行。
③疫苗在保障公共卫生安全方面发挥着重要作用。
雷雨晴表示,目前,科学家们的目标是研发通用疫苗,例如,针对新冠病毒研发泛变种疫苗甚至是泛冠状病毒疫苗,以保护人们免受各种病毒变异株的影响。
智利某大学分子遗传学和微生物学教授苏珊·布埃诺也认为,疫苗是预防传染病最有效、最经济的方法。
她强调,加强各国的研究能力,迅速研发出能对抗新病原体的疫苗并提高疫苗生产和临床试验能力非常重要。
④针对中医如何帮助预防传染病大流行,前伊朗国家篮球队特聘随队医生祁营洲表示,过去3年,在全球许多国家暴发新冠疫情之际,中国中医药救援物资为世界各地新冠患者的治疗提供了很大帮助。
在解释中医的治病原理时,他认为中医治疗更注重改善患者身体内部的整体环境,从而增强患者自身抵抗疾病的能力。
比如说,当一个房间出现了很多害虫,中医的治疗不是一味去寻找害虫,更多的是要想办法改善房间的整体卫生条件。
2023泸州中考卷

2023泸州中考卷一、语文部分(共100分)I. 基础知识积累与运用(共30分)1. 根据拼音写汉字。
(5分)(1)lǜ shù ()(2)chóng xīn ()(3)yīn yuè ()(4)bù guì ()(5)zhì lǐ ()2. 下列词语中,没有错别字的一项是()。
(3分)A. 风驰电掣B. 鞠躬尽瘁,死而后已C. 破釜沉舟D. 砥砺前行()3. 下列句子中,成语使用不正确的一项是()。
(3分)A. 他做事总是精益求精,从不满足于现状。
B. 这部电影情节曲折,引人入胜,让人拍案叫绝。
C. 在关键时刻,他挺身而出,力挽狂澜。
D. 这个问题很简单,大家都能答得出来,无需画蛇添足。
4. 名著阅读。
(10分)(1)请简述《西游记》中孙悟空大闹天宫的原因及其结果。
(2)请简述《水浒传》中林冲被逼上梁山的过程。
5. 下列句子排序正确的一项是()。
(5分)A. ①春暖花开,阳光明媚。
B. ②小燕子从南方飞回来了。
C. ③蝴蝶在花丛中翩翩起舞。
D. ④小明和他的小伙伴们一起去公园游玩。
排序:_______6. 根据语境,补全句子。
(5分)(1) __________,山岛竦峙, __________。
(2) __________,波撼岳阳城。
(3) __________,禅房花木深。
II. 阅读理解(共40分)(一)文言文阅读(20分)阅读下面的文言文,完成相关问题。
【甲】鱼,我所欲也;熊掌,亦我所欲也。
二者不可得兼,舍鱼而取熊掌者也。
生,亦我所欲也;义,亦我所欲也。
二者不可得兼,舍生而取义者也。
生亦我所欲,所欲有甚于生者,故不为苟得也。
死亦我所恶,所恶有甚于死者,故患有所不辟也。
如使人之所欲莫甚于生,则凡可以得生者何不用也?使人之所恶莫甚于死者,则凡可以辟患者何不为也?由是则生而有不用也,由是则可以辟患而有不为也。
是故所欲有甚于生者,所恶有甚于死者。
2024年四川省泸州市中考真题试卷物理及答案

泸州市二○二四年初中学业水平考试物理试题说明:1.本次考试是物理卷,分为第一部分(选择题)和第二部分(非选择题)两部分。
第一部分第1至3页,第二部分第3至6页。
满分95分。
2.第一部分满分38分,第二部分满分57分3.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试题卷上无效。
考试结束后,将答题卡和试题卷交回。
预祝各位考生考试顺利!第一部分 选择题(共38分)注意事项:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需要改动,用橡皮擦干净后,再选涂其他答案标号。
一、选择题(本题共12小题,其中1~10题每小题3分,只有一个选项符合题目要求。
11~12题每小题4分,有多个选项符合题目要求,全部选对得4分,选对但不全得2分,有错的得0分。
共38分)物理(38分)1. 学习物理要善于发现、善于思考。
下列对你所在考场内物理量估测的数据,符合实际的是( )A. 手中一张物理试卷的厚度约为12mmB. 考场大气压强的值约为51.010PaC. 你所在考场的室内温度大约为0℃D. 考试填涂用的2B 铅笔质量约为2kg 2. 姐姐和弟弟在玩成语游戏,一些成语蕴含了生活中的物理知识,下列说法正确的是( )A. “震耳欲聋”形容声音响度很大B. “立竿见影”是光的反射形成的C. “钻木取火”是利用了热传递的方式来改变木头的内能D. “刻舟求剑”以运动的船为参照物,水底的剑是静止的3. 下列物理情境中,对功的理解正确的是( )A. 在实际生活中,利用简单机械提升重物时,可以不做额外功B. 内燃机的四个冲程中,只有做功冲程做功,其他冲程均不做功C. 力对物体做功可以改变物体的内能,电流做功也可以改变物体的内能D. 物体在竖直向上拉力作用下匀速上升,物体所受力中,只有拉力对物体做功4. 小黄在学习物理过程中提出了下列看法,其中正确的是( )A. 近视眼能看清近处的物体而看不清远处的物体,应配戴凸透镜进行矫正B. 刮大风时,能够看见工地上尘土飞扬,表明分子在不停地做无规则运动C. 保持电流、通电时间相同,探究电流产生热量与电阻的关系,采用了等效替代法D. 直导线周围平行放置一颗小磁针,通电后小磁针偏转,表明通电导体周围有磁场5. 安全用电,人人有责。
2007年泸州市中考数学试题

泸州市二OO七年初中毕业暨高中阶段学校招生统一考试数学试卷(考试时间:只完成A卷120分钟,完成A、B卷150分钟)说明:1.本次考试试卷分为A、B卷,只参加毕业考试的考生只需完成A卷,要参加升学考试的学生必须加试B卷.2.A卷分为第Ⅰ卷和第Ⅱ卷两部分,第Ⅰ卷(1至2页)为选择题,第Ⅱ(3至6页)为非选择题,满分100分;B卷(7至10页)为非选择题,满分50分.A、B卷满分共150分.3.本卷中非选择题部分的试题,除题中设计有横线的题目外,解答过程都必须有必要的文字说明、演算步骤或推理证明.A 卷第Ⅰ卷选择题(共45分)注意事项:1.第Ⅰ卷共2页,答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目填写在答题卡上.考试结束后,监考人员将试卷和答题卡一并收回.2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦擦干净后,再选涂其它答案.不能答在试卷上.一、选择题(本大题15个小题,共45分,每小题3分)在每小题给出的四个选项中,有且仅有一个是正确的,请选出并把答题卡上对应题目的正确答案标号涂黑.1.|-5|的值是A.5 B.-5 C.15D.15-2.如图1,直线l与直线a,b相交,且a∥b,∠1=800,则∠2的度数是 A.600 B.800 C.1000 D.12003.已知△ABC与△A1B1C1相似,且AB :A1B1=1 :2,则△ABC与△ABC的面积比为A.1 :1 B.1 :2C.1 :4 D.1 :84.已知函数y=,则函数自变量x的取值范围是A.x≥3 B.x>3 C.x≠3 D.x<-35.如图2所示的几何体的正视图是6.一组数据1,2,3,4,5的方差是A .1 B.2 C.3 D.47.已知⊙O 1的半径为2cm ,⊙O 2的半径为4cm ,圆心距O 1O 2为3cm ,则⊙O 1与⊙O 2的位置关系是A .外离 B.外切 C.相交 D.内切8.若关于x 的一元二次方程220x x m -+=没有实数根,则实数m 的取值是A. 1m <B. 1m >-C.1m >D.1m <-9.在同一平面内,用两个边长为a 的等边三角形纸片(纸片不能裁剪)可以拼成的四边形是A .矩形 B.菱形 C.正方形 D.梯形10.已知圆锥的母线长为5cm ,底面半径为3cm ,则它的全面积为A .230cm π B.224cm π C.215cm π D.29cm π 11.依据某校九年级一班体育毕业考试中全班所有学生成绩,制成的频数分布直方图如图3(学生成绩取整数),则成绩在21.5-24.5这一分数段的频数和频率分别是A .4,0.1 B.10, 0.1 C.10, 0.2 D.20, 0.2 12.高为2且底面为正方形的长方体的体积为30,则长方体的底面边长为A .1 B.2 C.4 D.8 13.已知函数2y ax ax =+与函数(0)ay a x=<,则它们在同一坐标系中的大致图象是14.下列命题中,正确的命题是A .边长为3,4,6的三角形是直角三角形B .三角形中各个内角的角平分线的交点是三角形的外心C .三角形中各条边的中垂线的交点是三角形的重心D .三角形的中位线平行于第三边,并且等于第三边的一半15.给出的下列计算或化简:(1)246()a a =,(2)33(3)27a a -=- (3)2124-=,(423(0).a a a =-<其中正确个数有 A .1个 B.2个 C.3个 D.4个第Ⅱ卷 非选择题(共55分)注意事项:1.用钢笔或圆珠笔直接答在试卷上.二、(本大题3个小题,共18分,每小题6分) 16.(1)计算:001()tan 453+(2)分解因式:244ax ax a -+(3)如图4是某市市区四个旅游景点示意图(图中每个小正方形的边长为1个单位长度),请以某景点为原点,建立平面直角坐标系(保留坐标系的痕迹),并用坐标表示下列景点的位置。
2023年四川省泸州市中考数学真题(含答案解析)
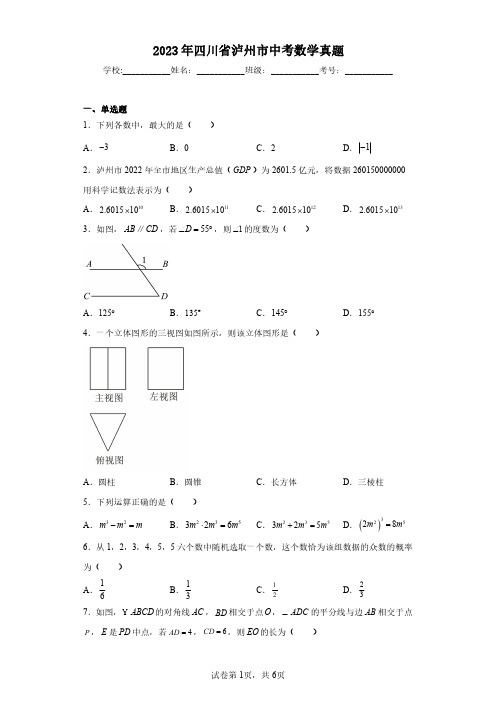
2023年四川省泸州市中考数学真题学校:___________姓名:___________班级:___________考号:___________A.125︒4.一个立体图形的三视图如图所示,则该立体图形是(A.圆柱B.圆锥5.下列运算正确的是(A.32m m m-=B.36.从1,2,3,4,5,5六个数中随机选取一个数,这个数恰为该组数据的众数的概率为()A.16B.137.如图,ABCDY的对角线P,E是PD中点,若4=ADA .1B .8.关于x 的一元二次方程A .没有实数根C .有两个不相等的实数根9.《九章算术》是中国古代重要的数学著作,该著作中给出了勾股数公式:()2212a m n =-,b =列四组勾股数中,不能..由该勾股数计算公式直接得出的是(A .3,4,5B .10.若一个菱形的两条对角线长分别是关于A .4109B .810912.已知二次函数22y ax ax =-+为正数,则a 的取值范围为(A .01a <<C .30a -<<或0<<3a 二、填空题13.8的立方根为______.14.在平面直角坐标系中,若点()2,1P -与点()2,Q m -关于原点对称,则m 的值是___________.三、解答题17.计算:(1321-+-18.如图,点B在线段19.化简:4521m mmm++⎛⎫++⎝20.某校组织全校800现随机抽取40名学生进行安全知识测试,并将测试成绩(百分制)作为样本数据进行整理、描述和分析,下面给出了部分信息.①将样本数据分成5组:并制作了如图所示的不完整的频数分布直方图;②在8090x≤<这一组的成绩分别是:89.根据以上信息,解答下列问题:(1)补全频数分布直方图;(2)抽取的40名学生成绩的中位数是___________(3)如果测试成绩达到80分及以上为优秀,试估计该校度为优秀的学生约有多少人?21.端午节是中国传统节日,人们有吃粽子的习俗.今年端午节来临之际,某商场预测A 粽子能够畅销.根据预测,每千克A 粽子节前的进价比节后多进A 粽子的数量比节后用相同金额购进的数量少(1)该商场节后每千克A 粽子的进价是多少元?(2)如果该商场在节前和节后共购进A 粽子400节前每千克20元,节后每千克16元全部售出,得利润最大?最大利润是多少?22.如图,某数学兴趣小组为了测量古树DE 底端D 在同一水平线上的点A 出发,沿斜面坡度为点B ,再沿水平方向继续前进一段距离后到达点俯角为37︒,底部D 的俯角为60︒,求古树DE 的高度3tan 374︒≈,计算结果用根号表示,不取近似值)23.如图,在平面直角坐标系xOy 与反比例函数()0my x x=>的图象相交于点(1)求k ,m 的值;(2)平行于y 轴的动直线与l 和反比例函数的图象分别交于点为顶点的四边形为平行四边形,求点24.如图,AB 是O 的直径,作O 的切线交AB 的延长线于点(1)求证:BC 平分DCF ∠;(2)G 为 AD 上一点,连接CG 交AB 于点H ,若CH 25.如图,在平面直角坐标系xOy 中,已知抛物线点A ,B ,()0,6C 三点,其对称轴为2x =.(1)求该抛物线的解析式;(2)点F 是该抛物线上位于第一象限的一个动点,直线E .①当CD CE =时,求CD 的长;②若CAD ,CDE ,CEF △的面积分别为1S ,2S ,3S ,且满足1322S S S +=,求点F 的坐标.参考答案:∴2180125D ∠=︒-∠=∴12125∠=∠=︒.故选:A .【点睛】本题主要考查了平行线的性质、是解答本题的关键.4.D∵90C ∠=︒,8AC =,BC ∴2210AB AC BC =+=∵以AD 为直径的半圆O 与∴OE BC ⊥,∵90C ∠=︒,∴90C OEB ︒∠=∠=,AC OE由题意得:此时F '落在值,设正方形ABCD 的边长为 四边形ABCD 是正方形,45F AK '∴∠=︒,P AE '∠F K AF ''⊥ ,45F AK F KA ''∴∠=∠=︒223AK a ∴=,F P K EP A '''∠=∠ ,E KP EAP '''∴△∽△,2F K KP AE AP ''∴==',12239AP AK a '∴==,729CP AC AP ''∴=-=27AP CP '∴=',∴当PE PF +取得最小值时,故答案为:27.(2)解:∵46818++=,∴第20、21个数为81、83;∴抽取的40名学生成绩的中位数是(181832+故答案为:82;(3)解:由题意可得:121080044040+⨯=(人)答:估计该校800名学生中对安全知识掌握程度为优秀的学生约有【点睛】本题考查频数分布直方图、中位数,用样本估计总体,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.21.(1)节后每千克A 粽子的进价为10元(2)节前购进300千克A 粽子获得利润最大,最大利润为则90AFB BFD ∠=∠=︒,∵斜面AB 的坡度为2:3i =,∴设2BF x =,则3AF x =,在Rt ABF 中,根据勾股定理得:即()()()22223207x x +=,解得:20x =,负值舍去,即()22040m BF =⨯=,∵BC 为水平方向,DE 为竖直方向,∴90BGD ∠=︒,∵90BFD FDG BGD ∠=∠=∠=∴四边形BFDG 为矩形,∴40m DG BF ==,∵60DCG ∠=︒,∵CF 是O 的切线,∴390OCF OCB ∠=∠+∠=︒,∵AB 是O 的直径,∴190ACB OCB ∠=∠+∠=︒,∴13∠=∠,∵AB 是O 的直径,且CD AB ⊥,∴ BCBD =,∴2A ∠=∠,∵OA OC =,∴1A ∠=∠,∴123A ∠=∠=∠=∠,∴BC 平分DCF ∠;(2)解:连接OC ,OG ,过点G 作GM AB ⊥于点∵AB 是O 的直径,且CD AB ⊥,∴132CE CD ==,1102OC OG AB ===,∴221OE OC CE =-=,∵GM AB ⊥,CD AB ⊥,∴CE GM ∥,1322S S S += ,2AD EF DE ∴+=,13DE AF ∴=,设21,262F h h h ⎛⎫-++ ⎪⎝⎭,则AH ,EG AB FH AB ⊥⊥ ,EG FH ∴∥,DEI AFB ∴∠=∠,DI EG ⊥ ,90DIE ∴∠=︒,DEI AFB ∴△∽△,112333DI AB h ∴==+,即点D 21122363EI FH h h ==-++,。
初中化学九年级全册【人教版】四川省泸州市中考试题(精校无答案)新版汇总

人教版初中化学重点知识精选化学是一门非常有意思的学科,充满了新奇的实验!人教版初中化学和你一起共同进步学业有成!第一部分选择题(共24分)一、选择题(本题共8个小题,每小题3分,共24分)化学(24分)1.下列过程中利用了物质的化学性质的是()A.液氮作制冷利B.乙炔与氧气形成高温氧炔焰C.酒精洗掉沽在试管壁上的碘D.洗洁精通过乳化作用除火油污2.分类是科学研究的重要方法,下列物质对应的类别不正确的是()选项 A B C D物质熟石灰小苏打氨气硅类别氧化物盐化合物单质3.下列说法不正确的是()A.聚乙烯塑料很难自然分解B.淀粉[(C6H10O5)n]中O和H元素质量比是8∶1C.人体需要的维生素可以从蔬菜水果中获得D.海鲜食品可用甲醛溶液浸泡以保鲜4.下图摘自元素周期表,部分信息略去。
据此判断下列叙述正确的是()A.P原子质量是30.97 B.Cl表示一个氟原子C.三种元素都是非金属元素D.三种元素在周期表中属于同一族5.下列有关说法不正确的是()A.碘、硒等微量元素对人体健康只有微小作用B.使用化肥和农药是作物增产的重要途径C.医疗上硫酸钡可用作钡餐透视D.氯化钠可用作调味品和防腐剂6.下列实验操作正确的是()A.用玻璃棒搅拌加快过滤B.用镊子取用二氧化锰C.用量筒量取液体时最后改用胶头滴管加至刻度D.实验室模拟炼铁时先加热氧化铁再通一氧化碳7.下列有关反应方程式正确,且反应前后有元素化合价升高和降低的是()A.铁和盐酸混合:2Fe+6HCl=2FeCl3+3H2↑B.碳酸铵与硫酸反应:(NH4)2CO3+H2SO4=(NH4)2SO4+H2O+CO2↑C.石英和纯碱高温:SiO2+Na2CO3 Na2SiO2+CO2↑D.磁铁矿(Fe3O4)高温下同CO:Fe3O4+4CO 3Fe+4CO28.溴酸银(AgBrO3)的溶解度随温度变化曲线如图所示,下列说法不正确的是()A.升高温度溴酸银的溶解度增大B.40℃时溴酸银易溶于水C.90℃时溴酸银溶液的溶质质量分数一定小于1.3% D.溴酸银可用降温结晶的方法从溶液中析出34.2017年5月5日,我国自主研制的大型客机C919试飞成功,这标志着我国的航空强国梦又迈出了一大步。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
泸州市二OO七年初中毕业暨高中阶段学校招生统一考试
数学试卷
(考试时间:只完成A卷120分钟,完成A、B卷150分钟)
说明:
1.本次考试试卷分为A、B卷,只参加毕业考试的考生只需完成A卷,要参加升学考试的学生必须加试B卷.
2.A卷分为第Ⅰ卷和第Ⅱ卷两部分,第Ⅰ卷(1至2页)为选择题,第Ⅱ(3至6页)为非选择题,满分100分;B卷(7至10页)为非选择题,满分50分.A、B卷满分共150分.
3.本卷中非选择题部分的试题,除题中设计有横线的题目外,解答过程都必须有必要的文字说明、演算步骤或推理证明.
A 卷
第Ⅰ卷选择题(共45分)
注意事项:
1.第Ⅰ卷共2页,答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目填写在答题卡上.考试结束后,监考人员将试卷和答题卡一并收回.
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦擦干净后,再选涂其它答案.不能答在试卷上.
一、选择题(本大题15个小题,共45分,每小题3分)在每小题给出的四个选项中,有且仅有一个是正确的,请选出并把答题卡上对应题目的正确答案标号涂黑.
1.|-5|的值是
A.5 B.-5 C.1
5
D.
1
5
-
2.如图1,直线l与直线a,b相交,且a∥b,∠1=800,则∠2的度数是 A.600 B.800 C.1000 D.1200
3.已知△ABC与△A1B1C1相似,且AB :A1B1=1 :2,则△ABC与△ABC的面积比为
A.1 :1 B.1 :2
C.1 :4 D.1 :8
4.已知函数
y=,则函数自变量x的取值范围是
A.x≥3 B.x>3 C.x≠3 D.x<-3
5.如图2所示的几何体的正视图是
6.一组数据1,2,3,4,5的方差是
A .1 B.2 C.3 D.4
7.已知⊙O 1的半径为2cm ,⊙O 2的半径为4cm ,圆心距O 1O 2为3cm ,则⊙O 1与⊙O 2的位置关系是
A .外离 B.外切 C.相交 D.内切
8.若关于x 的一元二次方程2
20x x m -+=没有实数根,则实数m 的取值是
A. 1m <
B. 1m >-
C.1m >
D.1m <-
9.在同一平面内,用两个边长为a 的等边三角形纸片(纸片不能裁剪)可以拼成的四边形是
A .矩形 B.菱形 C.正方形 D.梯形
10.已知圆锥的母线长为5cm ,底面半径为3cm ,则它的全面积为
A .230cm π B.224cm π C.215cm π D.29cm π 11.依据某校九年级一班体育毕业考试中全班所有学生成绩,制成的频数分布直方图如图3(学生成绩取整数),则成绩在21.5-24.5这一分数段的频数和频率分别是
A .4,0.1 B.10, 0.1 C.10, 0.2 D.20, 0.2 12.高为2且底面为正方形的长方体的体积为30,则长方体的底面边长为
A .1 B.2 C.4 D.8 13.已知函数2
y ax ax =+与函数(0)a
y a x
=
<,则它们在同一坐标系中的大致图象是
14.下列命题中,正确的命题是
A .边长为3,4,6的三角形是直角三角形
B .三角形中各个内角的角平分线的交点是三角形的外心
C .三角形中各条边的中垂线的交点是三角形的重心
D .三角形的中位线平行于第三边,并且等于第三边的一半
15.给出的下列计算或化简:(1)24
6
()a a =,(2)3
3
(3)27a a -=- (3)2
124
-=
,
(423(0).a a a =-<其中正确个数有 A .1个 B.2个 C.3个 D.4个
第Ⅱ卷 非选择题(共55分)
注意事项:
1.用钢笔或圆珠笔直接答在试卷上.
二、(本大题3个小题,共18分,每小题6分) 16.(1
)计算:00
()tan 453
(2)分解因式:2
44ax ax a -+
(3)如图4是某市市区四个旅游景点示意图(图中每个小正方形的边长为1个单位长度),请以某景点为原点,建立平面直角坐标系(保留坐标系的痕迹),并用坐标表示下列景点的位置。
①动物园 , ②烈士陵园 。
三、(本大题2个小题,共14分,每小题7分)
17.先将式子
2
2
11
(1)
x
x x
-
+÷化简,然后请你自选一个理想的x值求出原式的值。
18.如图5,AC是正方形ABCD的对角线,AE平分∠BAC,EF⊥AC交AC于点F。
(1)图中与线段BE相等的所有线段是;
(2)选择图中与BE相等的任意一条线段,并加以证明。
四、(本大题2个小题,共15分,19题7分,20题8分)
19.新华机械厂有15名工人,某月这15名工人加工的零件数统计如下:
(1)求这15名工人该月加工的零件数的平均数、中位数和众数; (2)
假如部门负责人把每位工人每月加工零件的任务确定为260件,你认为是否合理?为什么?如果不合理,你认为多少较为合适?
20.某市出租车计费标准如下:行驶路程不超过3千米时,收费8元;行驶路程超过3千米的部分,按每千米1.60元计费。
(1)求出租车收费y (元)与行驶路程x (千米)之间的函数关系式;
(2)若某人一次乘出租车时,付出了车费14.40元,求他这次乘坐了多少千米的路程?
五、(本大题8分)
21.某海滨浴场的海岸线可以看作直线l(如图6),有两位救生员在岸边的点A同时接到了海中的点B(该点视为定点)的呼救信号后,立即从不同的路径前往救助。
其中1号救生员从点A先跑300米到离点B最近的点D,再跳入海中沿直线游到点B救助;2号救生员先从点A跑到点C,再跳入海中沿直线游到点B救助。
如果两位救生员在岸上跑步的速度都是6米/秒,在水中游泳的速度都是2米/秒,且∠BAD=450,∠BCD=600,请问1号救生员与2号
救生员谁先到达点B?
B 卷
一、填空题(本大题5个小题,共15分,每小题3分)
1.在平面直角坐标中,已知点(3,24)P m m --在第一象限,则实数m 的取值范围是 。
2= 。
3.方程
112
62213x x
=+
--的解x= 。
4.如图7,在△ABC 中,AB=BC=2,∠ABC=900
,D 是BC 的中点,且
它关于AC 的对称点是D /,则BD /
= 。
5.若非零实数a ,b (
a ≠
b )满足2220070,20070a a b b -+=-+=,则11
a b
+= 。
二、(本大题2个小题,共14分,每小题7分)
6.在一个不透明的盒子里装着分别标有数字1,2,3,4的四个完全相同的小球,现在甲、乙两位同学做游戏,游戏规则是:“甲先从盒子里随机摸出一个小球,记下小球上的数字后放回,乙再从盒子中随机摸出一个小球,也记下球上的数字放回,则游戏结束。
若记下的数字甲比乙大,则甲获胜;若记下的数字甲不比乙大,则乙获胜”。
(1)帮树状图分析此游戏有多少种可能出现的结果; (2)该游戏规则对甲、乙双方公平吗?说明理由。
7.已知直线11
:n n l y x n n +=-
+(n 是不为零的自然数)。
当n=1时,直线1:21l y x =-+与x 轴和y 轴分别交于点A 1和B 1,设△A 1OB 1(其中O 是平面直角坐标系的原点)的面积为S 1;当n=2时,直线231
:22
l y x =-
+与x 轴和y 轴分别交于点A 2和B 2,设△A 2OB 2的面积为S 2,…, 依此类推,直线n l 与x 轴和y 轴分别交于点n n A B 和,设n n A OB ∆的面积为n S . (1) 求设△A 1OB 1的面积S 1; (2) 求1236...S S S S ++++的值.
三、(本大题9分)
8.如图8,已知AB 为⊙O 的直径,直线BC 与⊙O 相切于点B ,过A 作AD ∥OC 交⊙O 于点D ,连结CD 。
(1)求证:CD 是⊙O 的切线;
(2)若AD=2,直径AB=6,求线段BC 的长。
四、(本大题12分)
9.如图9,已知直线3
:2
l y x =及抛物线2:(0)C y ax bx c a =++≠,且抛物线C 图象上部
(2) 求直线l 与抛物线C 的交点A 、B 的坐标;
(3) 若动点M 在直线l 上方的抛物线C 上移动,求△ABM 的边AB 上的高h 的最大值。
