机械原理大作业
机械原理大作业

function [ v_Nx,v_Ny ] =v_crank(s,v_Ax,v_Ay,omiga,theta,phi) v_Nx=v_Ax-s*omiga.*sin(theta+phi); v_Ny=v_Ay+s*omiga.*cos(theta+phi); end
3>加速度计算
function [ a_Nx,a_Ny ]=a_crank(s,a_Ax,a_Ay,alph,omiga,theta,phi) a_Nx=a_Ax-alph.*s.*sin(theta+phi)-omiga.^2.*s.*cos(theta+phi);
。
1) 位置分析
将已知 P1P2 两点的坐标差表示为:
u=x2-x1,v=y2-y1
(1)
杆 l1 及 l2 投影方程式为:
l1cosθ1-l2cosθ2=u
l1sinθ1-l2sinθ2=v
(2)
消去θ1 得:vsinθ2+ucosθ2+c=0
(3)
其中: 解式(3)可得:
t(4) 式中+号和-号分别对应图 2 中 m=+1 和 m=-1 两位置。
由式(2)可得:
(5) 2) 速度分析
对 式 (2) 求 导 一 次 得 :
(6)
其中:
解式(6)可得:
(7)
其中: 3) 加速度分析
对式(6)求导一次得:
(8)
其中:
'.
解式(8)可得:
由上述式子可设计出 RRR 杆组运动分析子程序:
1>位置分析:
function[cx,cy,phi2,phi3]=s_RRR(bx,by,dx,dy,l2,l3,m,phi) d=sqrt((dx-bx).^2+(dy-by).^2); if(d>(l2+l3))|(d<abs(l2-l3))
机械原理大作业——凸轮

大作业(二)凸轮机构设计题号: 6班级:姓名:学号:同组者:成绩:完成时间:目录一凸轮机构题目要求 (1)二摆杆的运动规律及凸轮轮廓线方程 (2)三计算程序 (3)四运算结果及凸轮机构图 (9)4.1 第一组(A组)机构图及计算结果 (9)4.2 第二组(B组)机构图及计算结果 (14)4.3 第三组(C组)机构图及计算结果 (19)五心得体会 (24)第一组(A组) (24)第二组(B组) (24)第三组(C组) (24)六参考资料 (25)附录程序框图 (26)一凸轮机构题目要求(摆动滚子推杆盘形凸轮机构)题目要求:试用计算机辅助设计完成下列偏置直动滚子推杆盘形凸轮机构或摆动滚子推杆盘形凸轮机构的设计,已知数据如下各表所示。
凸轮沿逆时针方向作匀速转动。
表一摆动滚子推杆盘形凸轮机构的已知参数题号初选的基圆半径R0/mm机架长度Loa/mm摆杆长度Lab/mm滚子半径Rr/mm推杆摆角φ许用压力角许用最小曲率半径[ρamin][α1] [α2]A 15 60 55 10 24°35°70°0.3RrB 20 70 65 14 26°40°70°0.3RrC 22 72 68 18 28°45°65°0.35Rr 要求:1)凸轮理论轮廓和实际轮廓的坐标值2)推程和回程的最大压力角,及凸轮对应的转角3)凸轮实际轮廓曲线的最小曲率4)半径及相应凸轮转角5)基圆半径6)绘制凸轮理论廓线和实际廓线7)计算点数:N:72~120推杆运动规律:1)推程运动规律:等加速等减速运动2)回程运动规律:余弦加速度运动二摆杆的运动规律及凸轮轮廓线方程1)推程:1,运动规律:等加速等减速运动;2,轮廓线方程:A:等加速推程段设定推程加速段边界条件为: 在始点处 δ=0,s=0,v=0。
在终点处 h /2 s ,2/==δοδ。
整理得:⎪⎩⎪⎨⎧===^2^2/*h *4a ^2/**h *4v ^2^2/*h *2s δοωδοδωδοδ( 注意:δ的变化范围为0~δ0/2。
哈工大机械原理大作业

H a r b i n I n s t i t u t e o f T e c h n o l o g y机械原理大作业一课程名称:机械原理设计题目:连杆机构运动分析院系:机电学院班级: 1208105分析者:殷琪学号:指导教师:丁刚设计时间:哈尔滨工业大学设计说明书1 、题目如图所示机构,一只机构各构件的尺寸为AB=100mm,BC=4.28AB,CE=4.86AB,BE=8.4AB,CD=2.14AB,AD=4.55AB,AF=7AB,DF=3.32AB,∠BCE=139?。
构件1的角速度为ω1=10rad/s,试求构件2上点E的轨迹及构件5的角位移、角速度和角加速度,并对计算结果进行分析。
2、机构结构分析该机构由6个构件组成,4和5之间通过移动副连接,其他各构件之间通过转动副连接,主动件为杆1,杆2、3、4、5为从动件,2和3组成Ⅱ级RRR基本杆组,4和5组成Ⅱ级RPR 基本杆组。
如图建立坐标系3、各基本杆组的运动分析数学模型1) 位置分析2) 速度和加速度分析 将上式对时间t 求导,可得速度方程:将上式对时间t 求导,可得加速度方程:RRR Ⅱ级杆组的运动分析如下图所示 当已知RRR 杆组中两杆长L BC 、L CD 和两外副B 、D 的位置和运动时,求内副C的位置、两杆的角位置、角运动以及E 点的运动。
1) 位置方程由移项消去j ϕ后可求得i ϕ:式中,可求得j ϕ:E 点坐标方程:其中2) 速度方程两杆角速度方程为式中,点E 速度方程为3) 加速度方程两杆角加速度为式中,点E 加速度方程为RPR Ⅱ级杆组的运动分析(1) 位移方程(2)速度方程其中(3)加速度方程4、 计算编程利用MATLAB 软件进行编程,程序如下:% 点B 和AB 杆运动状态分析>>r=pi/180;w 1=10;e 1=0;l 1=100;Xa=0;Ya=0;Vax=0;Vay=0;aax=0;aay=0;f1=0:1: 360;% B 点位置Xb=Xa+l1*cos(r*f1);Yb=Ya+l1*sin(r*f1);% B点速度Vbx=Vax-w1*l1*sin(r*f1);Vby=Vay+w1*l1*cos(r*f1);% B点加速度abx=aax-l1*w1.^2.*cos(r*f1);aby=aay-l1*w1.^2.*sin(r*f1);% RRR2级杆组运动分析% 输入D点参数l2=428;l3=214;Xd=455;Yd=0;Vdx=0;Vdy=0;adx=0;ady=0;% 计算E点、2杆、3杆运动参数lbe=840;lce=486;a0=2*l2*(Xd-Xb);b0=2*l2*(Yd-Yb);c0=l2^2+(Xb-Xd).^2+(Yb-Yd).^2-l3^2;f2=2*atan((b0+sqrt(a0.^2+b0.^2-c0.^2))./(a0+c0)); % C点位置Xc=Xb+l2*cos(f2);Yc=Yb+l2*sin(f2);% 2杆、3杆运动参数计算dX=Xc-Xd;dY=Yc-Yd;for n=1:length(dX)if dX(n)>0&dY(n)>=0f3(n)=atan(dY(n)/dX(n));elseif dX(n)==0&dY(n)>0f3(n)=pi/2;elseif dX(n)<0&dY(n)>=0f3(n)=pi+atan(dY(n)/dX(n));elseif dX(n)<0&dY(n)<0f3(n)=pi+atan(dY(n)/dX(n));elseif dX(n)==0&dY(n)<0f3(n)=1.5*pi;elseif dX(n)>0&dY(n)<0f3(n)=2*pi+atan(dY(n)/dX(n));endendC2=l2*cos(f2);C3=l3*cos(f3);S2=l2*sin(f2);S3=l3*sin(f3);G1=C2.*S3-C3.*S2;w2=(C3.*(Vdx-Vbx)+S3.*(Vdy-Vby))./G1;w3=(C2.*(Vdx-Vbx)+S2.*(Vdy-Vby))./G1;G2=adx-abx+(w2.^2).*C2-(w3.^2).*C3;G3=ady-aby+(w2.^2).*S2-(w3.^2).*S3;e2=(G2.*C3+G3.*S3)./G1;% E点位置w=acos((l2^2+lbe^2-lce^2)/(2*l2*lbe));Xe=Xb+lbe*cos(f2-w);Ye=Yb+lbe*sin(f2-w);Vex=Vbx-lbe*w2.*sin(f2-w);Vey=Vby+lbe*w2.*cos(f2-w);aex=abx-lbe*(e2.*sin(f2-w)+w2.^2.*cos(f2-w));aey=aby+lbe*(e2.*cos(f2-w)-w2.^2.*sin(f2-w));% 计算杆5运动参数Xf=646.2912088;Yf=-268.9008617;l5=sqrt((Xe-Xf).^2+(Ye-Yf).^2);dX=Xe-Xf;dY=Ye-Yf;for n=1:length(dX)if dX(n)>0&dY(n)>=0f5(n)=atan(dY(n)/dX(n));elseif dX(n)==0&dY(n)>0f5(n)=pi/2;elseif dX(n)<0&dY(n)>=0f5(n)=pi+atan(dY(n)/dX(n));elseif dX(n)<0&dY(n)<0f5(n)=pi+atan(dY(n)/dX(n));elseif dX(n)==0&dY(n)<0f5(n)=1.5*pi;elseif dX(n)>0&dY(n)<0f5(n)=2*pi+atan(dY(n)/dX(n));endendw5=(-Vex.*sin(f5)+Vey.*cos(f5))./l5;a5=(-aex.*sin(f5)+aey.*cos(f5))./l5;% 画出各参数曲线figure(1);plot(Xe,Ye,'k');xlabel('Xe/\mm');ylabel('Ye/mm');grid on;title('E点位置');figure(2);plot(f1,f5,'k');xlabel('f/\circ');ylabel('f5/\circ');grid on;title('5杆角位移');figure(3);plot(f1,w5,'k');xlabel('f/\circ');ylabel('w5/rad/s');grid on;title('5杆角速度');figure(4);plot(f1,a5,'k');xlabel('f/\circ');ylabel('a5/rad/s2');gridon;title('5杆角加速度');Warning: Unable to interpret TeX string "Xe/\mm"5、计算结果图一:E点的运动轨迹图二:5杆角位移图三:5杆角速度图四:5杆角加速度6、计算结果分析由E点位置图像可看出,构件4做周期往复运动,由图二、三、四可看出,构件5的角位移、角速度、角加速度均成周期性变化。
机械原理大作业(用复数矢量法求连杆速度、加速度+c语言程序实现)

机原大作业题3-23班级:学号:姓名:指导老师:题目3-23 在图示机构中,已知原动件1以等角速度w1=10rad/s 逆时针转动,l AB =100mm , l BC =300mm ,e=30mm 。
试用复数矢量法求构件2的转角θ2、角速度w2和角加速度α2,构件3的速度v 3和加速度a 3。
(1)建立封闭矢量多边形L1+L2=L4+e (a) L1e iθ1+L2e iθ2=L4 (b)=>{L1cosθ1+L2cosθ2=L4L1sinθ1+L2sinθ2=e(c)联立可得L4=[l 22−(e −l 1sinθ1)2]1/2+l 1cosθ1 (d )θ2=arctan [e−l 1cosθ1l4−l 1cosθ1] (e)(2)速度分析将试(b)对时间t 求导,可得il 1w 1e iθ1+il 2w 2e iθ2=l 4(f) 将上式虚部和实部分开,并联解可得 l 4=v 3=−[w 1l 1sin (θ1−θ2)]/cosθ2 w 2=−l 1cosθ1l 2sinθ2w 1(3)加速度分析将式(f)对时间进行求导,可得-l1w12e iθ1+il2w2e iθ1−l2w22e iθ2=l4将上式虚部和实部分开,并联解可得w2=α2=−(w12l1sinθ1+w22l2sinθ2)/(l2cosθ2)l4=a3=[−w12l1cos(θ1−θ2)+w22l2]/ cosθ2(4)程序代码(c语言)#include<stdio.h>#include<math.h>#define pi 0.1745329#define pai 3.1415926int main(){double w1=10,l1=0.1,l2=0.3,e=0.03,j1=0,j2,w2,a2,v3,a3,l4;double j2hudu;FILE *fp;fp=fopen("d:\\jiyuandazuoye.txt","w");int i;for(i=0;i<=180;i++){l4=sqrt(fabs(l2*l2-((e-l1*sin(j1*pi))*(e-l1*sin(j1*pi)))))+l1*cos(j1*pi);j2hudu=atan((e-l1*cos(j1*pi))/(l4-l1*cos(j1*pi)));j2=pai*j2hudu;v3=-(w1*l1*sin((j1*pi-j2hudu))/cos(j2hudu));w2=-(l1*w1*cos(j1*pi))/(l2*sin(j2hudu));a2=-(w1*w1*l1*sin(j1*pi)+w2*w2*l2*sin(j2hudu))/(l2*cos(j2hudu));a3=(-w1*w1*l1*cos(pi*j1-j2hudu)+w2*w2*l2)/cos(j2hudu);fprintf(fp,"j1=%.3f l4=%.3f j2=%.3f w2=%.3f a2=%.3f v3=%.3f a3=%.3f\n",j1,l4,j2,w2,a2,v3,a3);j1+=2;}fclose(fp);return 0;}(5)图像。
哈工大机械原理大作业——齿轮——1号

Harbin Institute of Technology机械原理大作业3课程名称:机械原理设计题目:齿轮传动设计哈尔滨工业大学一、设计题目:如下图一个机械传动系统,运动运动由电动机1输入,经过机械传动系变速后由圆锥齿轮16输出三种不同转速。
选择一组传动系统的原始参数,据此设计该传动系统。
序号电机转速〔r/min〕输出轴转速〔r/min〕带传动最大传动比滑移齿轮传动定轴齿轮传动最大传动比模数圆柱齿轮圆锥齿轮一对齿轮最大传动比模数一对齿轮最大传动比模数7 1450 17 23 30 ≤2.8 ≤4.5 2 ≤4.5 3 ≤4 3二、传动比的分配计算:电动机转速n=1450r/min,输出转速n1=17r/min,n2=23 r/min,n3=30 r/min,带传动的最大传动比=2.8,滑移齿轮传动的最大传动比=4.5,圆柱齿轮传动的最大传动比=4.5,圆锥齿轮最大传动比=4。
根据传动系统的原始参数可知,传动系统的总传动比为:i1=1450/30=48.333i2=1450/23=63.043i3=1450/17=85.294传动系统的总传动比由带传动、滑移齿轮传动和定轴齿轮传动三局部实现。
设带传动的传动比为ipmax =2.8,滑移齿轮的传动比为iv1,iv2和iv3,令iv3=ivmax=4.5,那么定轴的传动比为if =85.294/(4.5*2.8)=6.769,从而iv1=48.333/〔6.769*2.8〕=2.550,iv2=3.326。
定轴齿轮每对的传动比为id==1.89。
三、滑移齿轮变速传动中每对齿轮的几何尺寸及重合度:经过计算、比拟,确定出三对滑移齿轮的齿数,其分别为:z5=17,z6=44,z 7=14,z8=47,z9=11,z10=50。
变位系数确实定:x5=x6=0; x7≥ha*(17-14)/17=0.176,取x7=0.18,x8=-0.18;x9≥ha*(17-11)/17=0.353,取x9=0.36;x10=-0.36。
机械原理大作业一(平面连杆机构的运动分析)

大作业(一)平面连杆机构的运动分析(题号:_10B_)学校:西北农林科技大学学院:机械与电子工程学院指导老师:***一.题目及原始数据;二、牛头刨床机构的运动分析方程三.计算程序框图;四.计算源程序;五.计算结果;六.运动线图及运动分析七.参考书;一、题目及原始数据;图b 所示的为一牛头刨床(Ⅲ级机构)。
假设已知各构件的尺寸如表2所示,原动件1以等角速度ω1=1rad/s 沿着逆时针方向回转,试求各从动件的角位移、角速度和角加速度以及刨头C 点的位移、速度和加速度的变化情况。
b )表2 牛头刨床机构的尺寸参数(单位:mm )要求:每三人一组,每人一个题目,每组中至少打印出一份源程序,每人计算出原动件从0゜~360゜时(N=36) 各运动变量的大小,并绘出各组对应的运动线图以及E 点的轨迹曲线。
二、牛头刨床机构的运动分析方程1)位置分析建立封闭矢量多边形由图可知错误!未找到引用源。
=3θ,故未知量有3θ、4θ、3S 、5S 。
利用两个封闭图形ABDEA和EDCGE ,建立两个封闭矢量方程,由此可得:把(式Ⅰ)写成投影方程得:⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧=+=-++=++=+h l l s l l l h s l l h s l 33445334411133441123344sin sin 0cos cos sin sin sin cos cos cos θθθθθθθθθθ(式Ⅱ)由以上各式用型转化法可求得5343 s s θθ, 23θθ=解: 211111*cos *sin b b x h l y h l θθ=+⎧⎨=+⎩4444*cos *sin d d x l y l θθ=⎧⎨=⎩3s =3sin b dx x s α-=33333)*sin *()/*cos *(/c d d b d c d d b d s x x l x l x x s y y l y l y y s αα=+=+-⎧⎪⎨=+=+-⎪⎩ 3tan c dc dy y x x θ-=-5c s x =()ae AE =444()tan *cos d c y h y l θθ+-=高斯消去法求解 2.速度分析对(式Ⅱ)求一次导数得:44433333111444333331114443335444333*sin *s '*cos *sin **sin **cos *'*sin *cos **cos **sin **sin *'0*cos **cos *0l s l l s s l l l s l l θωθθωθωθωθθωθωθωθωθωθω-+-=-⎫⎪++=⎪⎬---=⎪⎪+=⎭ (式Ⅲ)矩阵式:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----0cos cos 01sin sin 00cos cos sin 0sin sin cos 443344334433344333θθθθθθθθθθl l l l l s l s ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡'543'3s w w s =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-00cos sin 11111θθl l w (Ⅳ) 采用高斯消去法可求解(式Ⅳ)可解得角速度ω3,ω4;3.加速度分析把式Ⅳ对时间求导数得矩阵式:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----0cos cos 01sin sin 00cos cos sin 0sin sin cos 443344334433344333θθθθθθθθθθl l l l l s l s ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡''543''3s s αα = ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡----------0sin sin 00cos cos 00sin sin cos cos 0cos cos sin sin 4443334443334443333'3334443333'333θθθθθθθθθθθθw l w l w l w l w l w s s w w l w s s w +⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--00sin cos 1111111θθw l w l w(式Ⅴ)采用高斯消去法可求解(式Ⅴ)可得角加速度43αα,三.程序流程图位置分析速度分析加速度分析四、计算源程序#include<stdio.h> #include<stdlib.h> #include<math.h>#define PI 3.1415926 #define N 4#define E 0.0001 #define T 1000void Solutionangle(double [12],double ); /*迭代法求角位移*/void Solutionspeed(double [N][N],double [N],double [12],double ); /*角速度求解*/void Solutionacceleration(double [N][N],double [N][N],double [N],double [12]);/*角加速度求解*/void GaussianE(double [N][N],double [N],double [N]);/*高斯消去*/void FoundmatrixA(double [12],double [N][N]); //创建系数矩阵A void FoundmatrixB(double [12],double ,double [N]);//创建系数矩阵B void FoundmatrixDA(double [12],double [N][N]);//创建矩阵DAvoid FoundmatrixDB(double [12],double ,double [N]);//创建矩阵DB//定义全局变量double l1=180,l3=960,l4=160,h=900,h1=460,h2=110,as1=1.0;//主函数void main(){int i,j;FILE *fp;double shuju[36][12];double psvalue[12],a[N][N],da[N][N],b[N],db[N],ang1;//建立文件,并制表头if((fp=fopen("shuju","w"))==NULL){printf("Cann't open this file.\n");exit(0);}fprintf(fp,"\n L1 =%lf",l1);fprintf(fp,"\n s3 ang3 ang4 s5 "); fprintf(fp," s3' as3 as4 s5' "); fprintf(fp," s3'' aas3 aas4 s5'' \n");//计算数据并写入文件psvalue[0]=480;psvalue[1]=65*PI/180;psvalue[2]=10*PI/180;psvalue[3]=5 00;for(i=0;i<36;i++){ang1=i*PI/18;Solutionangle(psvalue,ang1);FoundmatrixB(psvalue,ang1,b);FoundmatrixA(psvalue,a);Solutionspeed(a,b,psvalue,ang1);FoundmatrixDA(psvalue,da);FoundmatrixDB(psvalue,ang1,db);Solutionacceleration(a,da,db,psvalue);for(j=1;j<3;j++)psvalue[j]=psvalue[j]*180/PI;for(j=0;j<12;j++){shuju[i][j]=psvalue[j];}fprintf(fp,"\n");for(j=0;j<12;j++)fprintf(fp,"%12.3f ",shuju[i][j]);for(j=1;j<3;j++)psvalue[j]=psvalue[j]*PI/180;for(j=0;j<4;j++)psvalue[j]+=psvalue[j+4];}fclose(fp);//输出数据for(i=0;i<36;i++){ang1=i*PI/18;printf("\n输出ang1=%d时的求解\n",i*10);printf("angle angspeed angacceleration :\n"); for(j=0;j<4;j++)printf("%lf\t",shuju[i][j]);printf("\n");for(j=4;j<8;j++)printf("%lf\t",shuju[i][j]);printf("\n");for(j=8;j<12;j++)printf("%lf\t",shuju[i][j]);printf("\n");}}/*矢量法求角位移*/void Solutionangle(double value[12],double ang1){double ae,s3,ang3,ang4,s5,t=0;s3=value[0];ang3=value[1];ang4=value[2];s5=value[3];double xb,yb,xd,yd,xc,yc;while(t<T){xb=h2+l1*cos(ang1); yb=h1+l1*sin(ang1);xd=l4*cos(ang4); yd=l4*sin(ang4);s3=sqrt((xd-xb)*(xd-xb)+(yd-yb)*(yd-yb));xc=xd+l3*(xb-xd)/s3;yc=yd+l3*(yb-yd)/s3;ang3=atan2(yc-yd,xc-xd);s5=xc;ae=sqrt(h1*h1+h2*h2);if(fabs(yc-h)<E)return;elseang4=atan((yd-yc+h)/(l4*cos(ang4)));value[0]=s3;value[1]=ang3;value[2]=ang4;value[3]=s5;while(value[1]>2*PI)value[1]-=2*PI;while(value[1]<0)value[1]+=2*PI;while(value[2]>PI)value[2]-=2*PI;while(value[2]<-PI)value[2]+=2*PI;t+=1;if(t>=T){printf("%f 迭代失败.\n",ang1*180/PI);exit(0);}}}/*角速度求解*/void Solutionspeed(double a2[N][N],double b2[N],double value[12],double ang1){double p2[N];GaussianE(a2,b2,p2);value[4]=p2[0];value[5]=p2[1];value[6]=p2[2];value[7]=p2[3];}/*角加速度求解*/void Solutionacceleration(double a3[N][N],double da3[N][N],doubledb3[N],double value[12]){int i,j;double bk[N]={0};double p3[N];for(i=0;i<N;i++){for(j=0;j<N;j++){bk[i]+=-da3[i][j]*value[4+j];}bk[i]+=db3[i]*as1;}GaussianE(a3,bk,p3);value[8]=p3[0];value[9]=p3[1];value[10]=p3[2];value[11]=p3[3];}/*高斯消去法解矩阵方程*/void GaussianE(double a4[N][N],double b4[N],double p4[N]) {int i,j,k;double a4g[N][N],b4g[N],t;for(i=0;i<N;i++)for(j=0;j<N;j++)a4g[i][j]=a4[i][j];for(i=0;i<N;i++)b4g[i]=b4[i];//施主对角线上的值尽可能大if(a4g[0][0]<a4g[1][0] && a4g[0][1]>a4g[1][1]){for(j=0;j<N;j++){t=a4g[0][j];a4g[0][j]=a4g[1][j];a4g[1][j]=t;}t=b4g[0];b4g[0]=b4g[1];b4g[1]=t;}if(a4g[2][2]<a4g[3][2] && a4g[2][3]>a4g[3][3]){for(j=0;j<N;j++){t=a4g[2][j];a4g[2][j]=a4g[3][j];a4g[3][j]=t;}t=b4g[2];b4g[2]=b4g[1];b4g[3]=t;}//初等行变换for(j=0;j<N;j++)for(i=0;i<N;i++){if(i!=j){for(k=0;k<N;k++)if(k!=j){a4g[i][k]-=a4g[i][j]/a4g[j][j]*a4g[j][k];}b4g[i]-=b4g[j]*a4g[i][j]/a4g[j][j];a4g[i][j]=0;}}for(i=0;i<N;i++)b4g[i]/=a4g[i][i];p4[0]=b4g[0];p4[1]=b4g[1];p4[2]=b4g[2];p4[3]=b4g[3];}//创建系数矩阵Avoid FoundmatrixA(double value5[12],double a5[N][N]){double s3,ang3,ang4,s5;s3=value5[0];ang3=value5[1];ang4=value5[2];s5=value5[3];a5[0][0]=cos(ang3);a5[0][1]=-s3*sin(ang3);a5[0][2]=-l4*sin(ang4);a5[1][0]=sin(ang3);a5[1][1]=s3*cos(ang3);a5[1][2]=l4*cos(ang4);a5[2][1]=-l3*sin(ang3);a5[2][2]=-l4*sin(ang4);a5[2][3]=-1;a5[3][1]=l3*cos(ang3);a5[3][2]=l4*cos(ang4);a5[0][3]=a5[1][3]=a5[2][0]=a5[3][0]=a5[3][3]=0;}//创建系数矩阵Bvoid FoundmatrixB(double value6[12],double ang1,double b6[N]){b6[0]=-l1*sin(ang1)*as1;b6[1]=l1*cos(ang1)*as1;b6[2]=b6[3]=0;}//创建矩阵DAvoid FoundmatrixDA(double value7[12],double da7[N][N]){double s3,ang3,ang4,s5,s3g,as3,as4,s5g;s3=value7[0];ang3=value7[1];ang4=value7[2];s5=value7[3];s3g=value7[4];as3=value7[5];as4=value7[6];s5g=value7[7];da7[0][0]=-as3*sin(ang3); da7[0][1]=-s3g*sin(ang3)-s3*cos(ang3)*as3; da7[0][2]=-l4*cos(ang4)*as4;da7[1][0]=as3*cos(ang3); da7[1][1]=s3g*cos(ang3)-s3*sin(ang3)*as3; da7[1][2]=-l4*sin(ang4)*as4;da7[2][1]=-l3*cos(ang3)*as3; da7[2][2]=-l4*cos(ang4)*as4;da7[3][1]=-l3*sin(ang3)*as3; da7[3][2]=-l4*sin(ang4)*as4;da7[0][3]=da7[1][3]=da7[2][0]=da7[2][3]=da7[3][0]=da7[3][3]=0;}//创建矩阵DBvoid FoundmatrixDB(double value8[12],double ang1,double db8[N]){db8[0]=-l1*as1*cos(ang1);db8[1]=-l1*as1*sin(ang1);db8[2]=db8[3]=0;}四、计算结果、数据10—B: lAB =180, lCD =960, lDE =160,h=900,h1=460,h2=135 程序运行结果:输出ang1=0时的求解angle angspeed angacceleration :504.039076 74.795444 -9.495711 409.583017198.751387 0.098628 -0.157357 -95.52202218.491125 0.270992 -0.379393 -267.416873输出ang1=10时的求解angle angspeed angacceleration :538.732197 75.993711 -11.339083 389.224179197.279713 0.138772 -0.205532 -135.726082-33.646469 0.193548 -0.180789 -197.071140输出ang1=20时的求解angle angspeed angacceleration :572.425650 77.533490 -13.505230 362.809939187.595715 0.167668 -0.223341 -165.511310-75.745240 0.141311 -0.030832 -147.198703输出ang1=30时的求解angle angspeed angacceleration :603.833542 79.322650 -15.730731 331.874448171.336235 0.189198 -0.218510 -187.964199-109.306697 0.107995 0.081095 -112.082167输出ang1=40时的求解angle angspeed angacceleration :631.929215 81.302128 -17.818172 297.500218149.836341 0.206101 -0.196427 -205.198868-136.045702 0.087401 0.168929 -86.713350输出ang1=50时的求解angle angspeed angacceleration :655.895287 83.435335 -19.612773 260.468398124.171060 0.220187 -0.160339 -218.604642-157.205807 0.075112 0.242928 -67.783866输出ang1=60时的求解angle angspeed angacceleration :675.082991 85.700444 -20.984446 221.36052195.237132 0.232630 -0.112076 -229.118402-173.614279 0.068177 0.309123 -53.324566输出ang1=70时的求解angle angspeed angacceleration :688.993808 88.084993 -21.817377 180.619839 63.810569 0.244175 -0.052735 -237.413048 -185.854285 0.064519 0.370066 -42.223597输出ang1=80时的求解angle angspeed angacceleration :697.252336 90.582388 -22.005185 138.586009 30.576581 0.255245 0.016790 -244.016229 -194.400792 0.062475 0.425589 -33.864710输出ang1=90时的求解angle angspeed angacceleration :699.596674 93.188858 -21.451254 95.514468 -3.858944 0.265988 0.095384 -249.371483 -199.694701 0.060504 0.473506 -27.864485输出ang1=100时的求解angle angspeed angacceleration :695.865633 95.900697 -20.072519 51.589105 -38.965270 0.276279 0.181437 -253.859385 -202.153581 0.057046 0.510449 -23.857448输出ang1=110时的求解angle angspeed angacceleration :685.983277 98.711634 -17.805029 6.933394-74.278772 0.285719 0.272715 -257.783709 -202.111529 0.050473 0.532809 -21.287355输出ang1=120时的求解angle angspeed angacceleration :669.950064 101.609969 -14.610191 -38.372057 -109.376771 0.293616 0.366385 -261.317271 -199.668758 0.039047 0.537342 -19.160070输出ang1=130时的求解angle angspeed angacceleration :647.841627 104.575458 -10.480584 -84.257919 -143.814604 0.298951 0.459054 -264.396466 -194.414681 0.020755 0.520667 -15.693075输出ang1=140时的求解angle angspeed angacceleration :619.821421 107.575800 -5.446130 -130.610778 -176.999389 0.300311 0.546571 -266.540129 -184.964518 -0.007020 0.476940 -7.771361输出ang1=150时的求解angle angspeed angacceleration :586.184918 110.562008 0.415063 -177.176221 -207.962526 0.295748 0.623253 -266.552595 -168.266256 -0.047758 0.393549 9.812596输出ang1=160时的求解angle angspeed angacceleration :547.454933 113.462407 6.953911 -223.398352 -235.003072 0.282665 0.680257 -262.100065 -138.903553 -0.105183 0.246327 44.899562输出ang1=170时的求解angle angspeed angacceleration :504.544302 116.176610 13.908306 -268.184887 -255.282561 0.257989 0.703480 -249.323224 -89.538230 -0.180241 0.000287 106.600867输出ang1=180时的求解angle angspeed angacceleration :458.971730 118.574668 20.844503 -309.643625 -264.764006 0.219135 0.672921 -223.057053 -14.821184 -0.265454 -0.371999 199.314672输出ang1=190时的求解angle angspeed angacceleration :413.004585 120.510406 27.115020 -344.972134 -259.172109 0.165718 0.567137 -178.419329 81.585955 -0.344194 -0.853747 314.511221输出ang1=200时的求解angle angspeed angacceleration :369.545053 121.847767 31.889429 -370.706568 -235.758436 0.099887 0.372457 -112.937479 187.297933 -0.408887 -1.378443 436.158793输出ang1=210时的求解angle angspeed angacceleration :331.798652 122.469341 34.258483 -383.133346 -193.593039 0.022078 0.086043 -25.631424 297.241960 -0.491104 -1.905920 568.696016输出ang1=220时的求解angle angspeed angacceleration :303.153821 122.219130 33.292190 -378.091293 -130.922824 -0.077456 -0.296427 88.941491 425.795050 -0.676887 -2.496336 760.311055输出ang1=230时的求解angle angspeed angacceleration :287.551415 120.753136 27.951831 -349.551698 -43.461002 -0.227868 -0.791435 247.346675 575.056468 -1.094027 -3.164335 1076.851819输出ang1=240时的求解angle angspeed angacceleration :289.100599 117.353641 17.210022 -288.265712 60.871402 -0.467341 -1.348797 462.335114 552.433286 -1.593002 -2.815597 1309.871650输出ang1=250时的求解angle angspeed angacceleration :305.894540 111.367369 2.144459 -189.884640 115.218973 -0.708552 -1.550036 642.734960 12.240677 -0.870938 0.991883 564.144526输出ang1=260时的求解angle angspeed angacceleration :323.986413 103.946293 -11.427774 -74.543748 84.395898 -0.738254 -1.089162 653.304280 -255.624069 0.384248 3.565003 -304.928302输出ang1=270时的求解angle angspeed angacceleration :335.302309 97.031096 -19.261449 33.532005 49.129286 -0.637650 -0.496091 581.357015 -130.140634 0.646045 2.981435 -447.569870输出ang1=280时的求解angle angspeed angacceleration :342.600355 91.196115 -21.943547 128.368687 38.126480 -0.532397 -0.071890 506.691297-5.585137 0.546267 1.904793 -405.499868输出ang1=290时的求解angle angspeed angacceleration :349.595686 86.317539 -21.260725 210.767956 44.168587 -0.446028 0.184434 438.002883 68.415716 0.453589 1.077375 -389.377468输出ang1=300时的求解angle angspeed angacceleration :358.607892 82.240708 -18.666754 281.194923 60.502728 -0.370112 0.316464 368.260484 116.057770 0.427245 0.460440 -415.756327输出ang1=310时的求解angle angspeed angacceleration :371.130402 78.917555 -15.254653 338.895047 84.027335 -0.293669 0.351067 291.444179 151.953756 0.455712 -0.052046 -466.454916输出ang1=320时的求解angle angspeed angacceleration :388.249233 76.393061 -11.922868 382.397984 112.840822 -0.209756 0.302612 205.717135 175.288599 0.505389 -0.486217 -511.900005输出ang1=330时的求解angle angspeed angacceleration :410.645047 74.745942 -9.416616 410.419610 143.730687 -0.119125 0.190619 115.320694 173.230815 0.523328 -0.760168 -513.913856输出ang1=340时的求解angle angspeed angacceleration :438.227350 74.001595 -8.199258 422.950752 171.284625 -0.031250 0.052211 30.029879 137.214564 0.471995 -0.783284 -454.129609输出ang1=350时的求解angle angspeed angacceleration :469.931682 74.073764 -8.319585 421.739944 190.319958 0.042754 -0.071138 -41.115003 79.001118 0.372107 -0.609234 -358.898217五.运动线图及分析θ3,θ4ω3,ω4α3,α4S3,S5V3,V5a3,a5机构运动分析:(1)、从θ3-θ1,θ4-θ1曲线图可知,3杆为摆动导杆,4杆为摇杆,(2)、从ω3-θ1、ω4-θ1容易看出:在θ1为0 o~200 o之间,3杆角速度变化较为平缓,保证刨头慢速、稳定工作;在220 o~340 o之间为回程阶段,角速度变化较快,以提高效率;4杆有4个角速度为0点,即4杆的速度方向改变了四次。
机械原理大作业1(六杆机构)
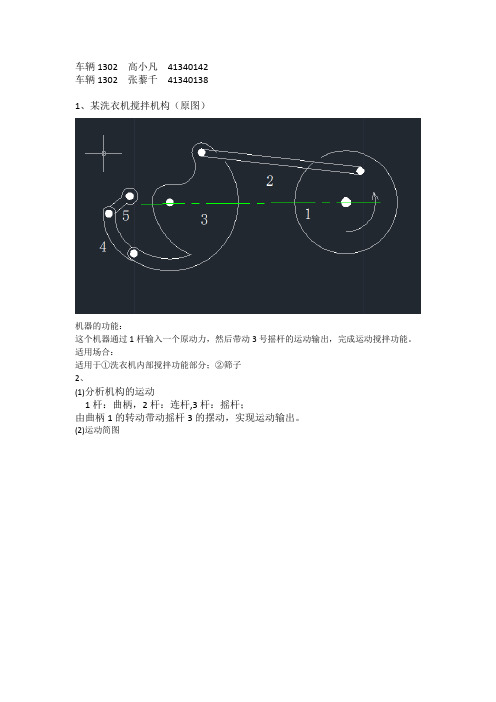
车辆1302 高小凡41340142车辆1302 张藜千413401381、某洗衣机搅拌机构(原图)机器的功能:这个机器通过1杆输入一个原动力,然后带动3号摇杆的运动输出,完成运动搅拌功能。
适用场合:适用于①洗衣机内部搅拌功能部分;②筛子2、(1)分析机构的运动1杆:曲柄,2杆:连杆,3杆:摇杆;由曲柄1的转动带动摇杆3的摆动,实现运动输出。
(2)运动简图(3)如图,该六杆机构只有一个原动件----1杆(4)自由度F=3(n-1)-2P5=3*5-2*7=1上述六杆机构的运动形式可简化为如图四杆机构的运动形式,4,5杆的运动作为摇杆3的输出机构。
3、大致测绘出构件尺寸4、确定机构所含杆组的数目和级别(拆杆组),并判断机构的级别;依次拆下4-5/2-3两个II级杆组及原动件1(II级杆组),所以该机构为II级杆组5、用图解法求出最小传动角值:由下图可知,在极限位置2时,压力角最大为70°,则最小传动角为42°6、分析该机构有无急回特性和死点位置;有急回,无死点;180+1809k 1.11180-1809θθ+===>-7、用瞬心法对机构进行运动分析上图中标出了该机构的简化四杆机构的所有瞬心P 12 P 13 P 16 P 23 P 26 P 36其中,绝对瞬心有:P 16 P 36 P 26 相对瞬心有:P 12P 13 P 23速度分析:若1的角速度为w1,则V(P12)=l1*w1V(P23)= [V(P12)/|P12P13|]*|P13P23 | w3= V(P23)/l3w6= V(P23)/| P23P26 |(1)角速度比mv=w6/w2=l1sinv/l3sinuv=0, mv=0,w6=0,此时构件1、2共线,机构处于极限位置;(2)mv=w6/w2=OP13/CP13 (瞬心P13能够用来确定速度比)上图为该机构(六杆机构)全部瞬心(15个)绝对瞬心:P16, P26,P36,P46,P56相对瞬心:P15,P25,P35,P45P14,P24,P34,P13,P23P12中间密集部分的的放大图如下图:8、用杆组法(或其他解析法)对机构进行运动分析(写出数学模型和程序框图);已知该机构的尺寸为:两个固定铰链点a,d,g的坐标分别为(0,0)(420,0)(-80,-35),曲柄原动件|ab|=100mm,连杆2长为300mm,摇杆3长150mm,杆4长100mm,杆5长50mm.经分析,该机构由一个曲柄原动件和两个RRR二级杆组组成的二级机构用杆组法搭建该机构的步奏如下:1)添加曲柄原动件ab;2)添加RRR二级杆组(2-3),杆组的两个动铰链点分别为已有铰链点b和固定铰链点d; 3)在连杆cd上添加铰链点e;4)添加RRR二级杆组(4-5),杆组的两个动铰链点分别为已有铰链点e和固定铰链点g; 5)该机构搭建完成,利用该程序可自动求出任意给定铰链点或构件的位置、速度、和加速度。
机械原理大作业一 33题

机械原理大作业(一)作业名称:机械原理设计题目:连杆机构运动分析院系:机电工程学院班级: xxxxxx设计者: xxx学号: xxxxxx指导教师: xxxxx设计时间: 6.25---7.1哈尔滨工业大学机械设计一,运动分析题目二,建立以点G为原点的固定平面直角坐标系G-x,y三,对机构进行结构分析该机构由原动件AB(Ι级组),EFG(RRRⅡ级杆组),EHK(RRRⅡ级杆组),ECD(RRRⅡ级杆组)组成。
四,各基本杆组的运动运动分析数学模型(1)原动件AB(Ⅰ级组)已知原动件AB的转角ψ1=0~2π原动件AB的角速度ω1=10rad/s原动件AB的角加速度α1=0运动副A的位置坐标 XA=0 YA=0A点与机架相连,即该点速度和加速度均为0。
运动副A的速度 VxA=0 VyA=0运动副A的加速度 aXA=0 aYA=0原动件AB长度 lAB=200mm可求出运动副B的位置坐标 XA=XA+lABcosψ1 YB=YA+lABsinψ1 运动副B的速度 vXB=vXA-ω1lABsinψ1 vYB=vYA+ω1lABcosψ1运动副B的加速度aXB=aXA-ω12lABcosψ1-α1lABsinψ1aYB=aYA-ω12lABsinψ1+α1lABcosψ1(2)ECD (RRR Ⅱ级杆组)由(1)知B 点位置坐标、速度、加速度运动副D 点位置坐标 XD=XA+lADcos ψ2 YD=YA+lADsin ψ2D 点与机架相连,即该点速度和加速度均为0。
运动副D 的速度 v X D=0 v Y D=0运动副D 的加速度 a X D=0 a Y D=0杆BC 长 lBC=800mm杆CD 长 lCD=448mm可求得BC 杆相对于X 轴正方向转角Ψ3=2arctan ()00/()0202020(C A C B A B +-++)CD 杆相对于x 轴正方向转角Ψ4=arctan ((YC-YD )/(XC-XD ))其中,A0=2lBC(XD-XB)B0=2lBC(YD-YB)C0=l 2BC+l 2BD-l 2CDl 2BD=(XD-XB)2+(YD-YB)2求导可得BC 杆ω3、α3和CD 杆ω4、α4最后求导得vXC 、vYC 以及aXC 、aYCC 的轨迹即是E 的轨迹(3)EFG (RRR Ⅱ级杆组)运动副G点位置坐标 X G=XA+lAGcosψ5 YG=YA+lAGsinψ5G点与机架相连,即该点速度和加速度均为0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机械与电子工程学院《机械原理》大作业(一)平面连杆机构的运动分析(题号:牛头刨床9A)班级:学号:姓名:同组其他人员:完成日期:目录题目、原始数据及要求 (1)一平面连杆机构运动分析方程 (1)1.1 位置方程1.2速度计算公式 (2)1.3加速度计算公式 (2)二程序 (3)2.1计算程序框图 (3)2.2计算源程序 (4)三 3.1 (一组数据Lab =200mm)计算结果 (9)3.2运动线图 (10)3.3 体会 (12)四 4.1(第二组数据Lab =150mm)计算结果 (12)4.2 运动线图 (13)4.3 体会 (15)五5.1(第三组数据Lab =220mm)计算结果 (16)5.2 运动线图 (17)5.3 体会 (21)六参考资料 (21)题目及原始数据如图所示,为一牛头刨床(Ⅲ级机构)。
假设已知各构件的尺寸如下表所示,原东件1以等角速度 ω1=1rad∕s沿着逆时针方向回转,试求各从动件的角位移、角速度和角加速度以及刨头C点位移、速度和加速度的变化。
平面连杆机构运动分析方程先建立一直角坐标系,标出各杆矢量及其方位角。
设各杆的夹角为θi,其中GE段记为s c,BD段记为s b,建立投影方程:1.1机构运动位置分析方程1.3机构运动加速度分析方程(以矩阵形式写出cosθ3 −s b sinθ3 −l4sinθ4 0sinθ3 scosθ3 l4cosθ4 00 −l3sinθ3 −θ40 l3cosθ3 lθ4−w 3sin θ3 −s b ′sin θ3−s b ω3 cos θ3−l 4ω4cos θ4 0sin θ3 s b ′cos θ3−s b ω3 sin θ3 − l 4ω4sin θ4 00 −l 3ω3 cos θ3 −l 4ω4sin θ4 00 − l 3ω3sin θ3 −l 4ω4sin θ4 034计算流程图位置分析速度分析析加速度分计算源程序#include<stdio.h>#include<stdlib.h>#include<math.h>#define PI 3.1415926#define N 4#define E 0.0001#define T 1000void Solutionangle(double [12],double ); /*迭代法求角位移*/ void Solutionspeed(double [N][N],double [N],double [12],double );/*角速度求解*/void Solutionacceleration(double [N][N],double [N][N],double [N],double [12]);/*角加速度求解*/void GaussianE(double [N][N],double [N],double [N]);/*高斯消去*/void FoundmatrixA(double [12],double [N][N]); //创建系数矩阵Avoid FoundmatrixB(double [12],double ,double [N]);//创建系数矩阵Bvoid FoundmatrixDA(double [12],double [N][N]);//创建矩阵DAvoid FoundmatrixDB(double [12],double ,double [N]);//创建矩阵DB//定义全局变量double l1=200,l3=960,l4=160,h=900,h1=500,h2=120,as1=1.0;//主函数void main(){int i,j;FILE *fp;double shuju[36][12];double psvalue[12],a[N][N],da[N][N],b[N],db[N],ang1;//建立文件,并制表头if((fp=fopen("shuju","w"))==NULL){printf("Cann't open this file.\n");exit(0);}fprintf(fp,"\n L1 =%lf",l1);fprintf(fp,"\n s3 ang3 ang4 s5 ");fprintf(fp," s3' as3 as4 s5' ");fprintf(fp," s3'' aas3 aas4 s5'' \n");//计算数据并写入文件psvalue[0]=480;psvalue[1]=65*PI/180;psvalue[2]=10*PI/180;psvalue[3]=500;for(i=0;i<36;i++){ang1=i*PI/18;Solutionangle(psvalue,ang1);FoundmatrixB(psvalue,ang1,b);FoundmatrixA(psvalue,a);Solutionspeed(a,b,psvalue,ang1);FoundmatrixDA(psvalue,da);FoundmatrixDB(psvalue,ang1,db);Solutionacceleration(a,da,db,psvalue);for(j=1;j<3;j++)psvalue[j]=psvalue[j]*180/PI;for(j=0;j<12;j++){shuju[i][j]=psvalue[j];}fprintf(fp,"\n");for(j=0;j<12;j++)fprintf(fp,"%12.3f ",shuju[i][j]);for(j=1;j<3;j++)psvalue[j]=psvalue[j]*PI/180;for(j=0;j<4;j++)psvalue[j]+=psvalue[j+4];}fclose(fp);//输出数据for(i=0;i<36;i++){ang1=i*PI/18;printf("\n输出ang1=%d时的求解\n",i*10);printf("angle angspeed angacceleration :\n");for(j=0;j<4;j++)printf("%lf\t",shuju[i][j]);printf("\n");for(j=4;j<8;j++)printf("%lf\t",shuju[i][j]);printf("\n");for(j=8;j<12;j++)printf("%lf\t",shuju[i][j]);printf("\n");}}/*矢量法求角位移*/void Solutionangle(double value[12],double ang1){double ae,s3,ang3,ang4,s5,t=0;s3=value[0];ang3=value[1];ang4=value[2];s5=value[3];double xb,yb,xd,yd,xc,yc;while(t<T){xb=h2+l1*cos(ang1); yb=h1+l1*sin(ang1);xd=l4*cos(ang4); yd=l4*sin(ang4);s3=sqrt((xd-xb)*(xd-xb)+(yd-yb)*(yd-yb));xc=xd+l3*(xb-xd)/s3;yc=yd+l3*(yb-yd)/s3;ang3=atan2(yc-yd,xc-xd);s5=xc;ae=sqrt(h1*h1+h2*h2);if(fabs(yc-h)<E)return;elseang4=atan((yd-yc+h)/(l4*cos(ang4)));value[0]=s3;value[1]=ang3;value[2]=ang4;value[3]=s5;while(value[1]>2*PI)value[1]-=2*PI;while(value[1]<0)value[1]+=2*PI;while(value[2]>PI)value[2]-=2*PI;while(value[2]<-PI)value[2]+=2*PI;t+=1;if(t>=T){printf("%f 迭代失败.\n",ang1*180/PI);exit(0);} }}/*角速度求解*/void Solutionspeed(double a2[N][N],double b2[N],double value[12],double ang1){double p2[N];GaussianE(a2,b2,p2);value[4]=p2[0];value[5]=p2[1];value[6]=p2[2];value[7]=p2[3];}/*角加速度求解*/void Solutionacceleration(double a3[N][N],double da3[N][N], double db3[N],double value[12]){int i,j;double bk[N]={0};double p3[N];for(i=0;i<N;i++){for(j=0;j<N;j++){bk[i]+=-da3[i][j]*value[4+j];}bk[i]+=db3[i]*as1;}GaussianE(a3,bk,p3);value[8]=p3[0];value[9]=p3[1];value[10]=p3[2];value[11]=p3[3];}/*高斯消去法解矩阵方程*/void GaussianE(double a4[N][N],double b4[N],double p4[N]) {int i,j,k;double a4g[N][N],b4g[N],t;for(i=0;i<N;i++)for(j=0;j<N;j++)a4g[i][j]=a4[i][j];for(i=0;i<N;i++)b4g[i]=b4[i];//施主对角线上的值尽可能大if(a4g[0][0]<a4g[1][0] && a4g[0][1]>a4g[1][1]){for(j=0;j<N;j++){t=a4g[0][j];a4g[0][j]=a4g[1][j];a4g[1][j]=t;} t=b4g[0];b4g[0]=b4g[1];b4g[1]=t;}if(a4g[2][2]<a4g[3][2] && a4g[2][3]>a4g[3][3]){for(j=0;j<N;j++){t=a4g[2][j];a4g[2][j]=a4g[3][j];a4g[3][j]=t;} t=b4g[2];b4g[2]=b4g[1];b4g[3]=t;}//初等行变换for(j=0;j<N;j++)for(i=0;i<N;i++){if(i!=j){for(k=0;k<N;k++)if(k!=j){a4g[i][k]-=a4g[i][j]/a4g[j][j]*a4g[j][k];}b4g[i]-=b4g[j]*a4g[i][j]/a4g[j][j];a4g[i][j]=0;}}for(i=0;i<N;i++)b4g[i]/=a4g[i][i];p4[0]=b4g[0];p4[1]=b4g[1];p4[2]=b4g[2];p4[3]=b4g[3];}//创建系数矩阵Avoid FoundmatrixA(double value5[12],double a5[N][N]){double s3,ang3,ang4,s5;s3=value5[0];ang3=value5[1];ang4=value5[2];s5=value5[3];a5[0][0]=cos(ang3);a5[0][1]=-s3*sin(ang3);a5[0][2]=-l4*sin(ang4);a5[1][0]=sin(ang3);a5[1][1]=s3*cos(ang3);a5[1][2]=l4*cos(ang4);a5[2][1]=-l3*sin(ang3);a5[2][2]=-l4*sin(ang4);a5[2][3]=-1;a5[3][1]=l3*cos(ang3);a5[3][2]=l4*cos(ang4);a5[0][3]=a5[1][3]=a5[2][0]=a5[3][0]=a5[3][3]=0;}//创建系数矩阵Bvoid FoundmatrixB(double value6[12],double ang1,double b6[N]){b6[0]=-l1*sin(ang1)*as1;b6[1]=l1*cos(ang1)*as1;b6[2]=b6[3]=0;}//创建矩阵DAvoid FoundmatrixDA(double value7[12],double da7[N][N]){double s3,ang3,ang4,s5,s3g,as3,as4,s5g;s3=value7[0];ang3=value7[1];ang4=value7[2];s5=value7[3];s3g=value7[4];as3=value7[5];as4=value7[6];s5g=value7[7];da7[0][0]=-as3*sin(ang3);da7[0][1]=-s3g*sin(ang3)-s3*cos(ang3)*as3;da7[0][2]=-l4*cos(ang4)*as4;da7[1][0]=as3*cos(ang3);da7[1][1]=s3g*cos(ang3)-s3*sin(ang3)*as3;da7[1][2]=-l4*sin(ang4)*as4;da7[2][1]=-l3*cos(ang3)*as3; da7[2][2]=-l4*cos(ang4)*as4;da7[3][1]=-l3*sin(ang3)*as3; da7[3][2]=-l4*sin(ang4)*as4;da7[0][3]=da7[1][3]=da7[2][0]=da7[2][3]=da7[3][0]=da7[3][3]=0; }//创建矩阵DBvoid FoundmatrixDB(double value8[12],double ang1,double db8[N]) {db8[0]=-l1*as1*cos(ang1);db8[1]=-l1*as1*sin(ang1);db8[2]=db8[3]=0;}。
