2011-2016陕西中考关于二次函数
陕西省中考数学 第三章 函数 第10讲 二次函数课件

3.(2012·陕西)在平面直角坐标系中,将抛物线y=x2-x-6向
上(下)或向左(右)平移m个单位,使平移后的抛物线恰好经过原点
,则|m|的最小值为( B )
A.1
B.2
C.3
D.6
4.(2013·陕西)已知两点A(-5,y1),B(3,y2)均在抛物线y= ax2+bx+c(a≠0)上,点C(x0,y0)是该抛物线的顶点.若y1>y2≥y0 ,则x0的取值范围是( ) B
对边只能是M′N′,∴MN∥M′N′且MN=M′N′,∴MN·NN′=16
,∴NN′=4. 当M,N,M′,N′为顶点的平行四边形是
▱MNN′M′时,将抛物线C向左或向右平移4个单位可得符合条件
的抛物线C′
M,N,M′,N′为顶点的平行四边形是
▱MNM′N′时,将抛物线C先向左或向右平移4个单位,再向下平
解:(1)∵二次函数的图象经过点A(1,0),B(3,0)两点,∴二次 函数图象的对称轴为直线x=2 (2)设二次函数的表达式为y=a(x-1)(x -3)(a≠0),当x=0时,y=3a,当x=2时,y=-a,∴点C坐标为: (0,3a),顶点D坐标为(2,-a),∴OC=|3a|,又∵A(1,0),E(2,0), ∴AO=1,EB=1,DE=|-a|=|a|,当△AOC与△DEB相似时,①假设
点,∴
-9-3b+c=0, c=3,
解得
b=-2, c=3,
故此抛物线的解析式为y
=-x2-2x+3 (2)∵由(1)知抛物线的解析式为y=-x2-2x+
3,∴当x=-2ba=-2×(--2 1)=-1时,y=4,∴M(-1,4)
(3)由题意,以点M,N,M′,N′为顶点的平行四边形的边MN的
陕西中考数学第24题二次函数专题整理
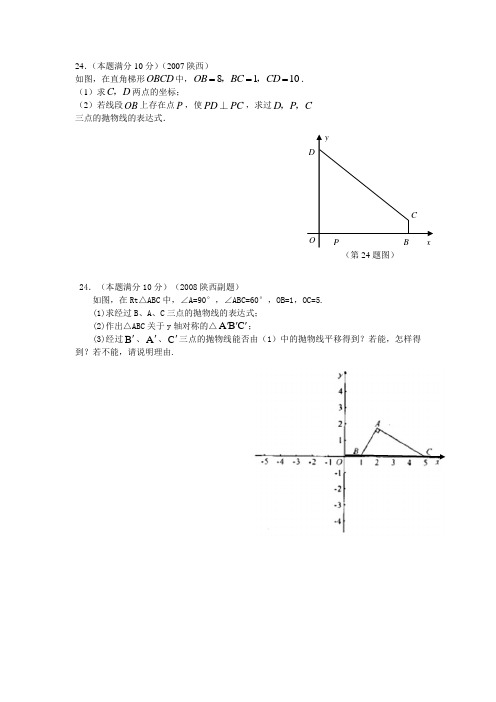
24.(本题满分10分)(2007陕西)如图,在直角梯形OBCD 中,8110OB BC CD ===,,. (1)求C D ,两点的坐标;(2)若线段OB 上存在点P ,使PD PC ⊥,求过D P C ,, 三点的抛物线的表达式.24.(本题满分10分)(2008陕西副题)如图,在Rt △ABC 中,∠A=90°,∠ABC=60°,OB=1,OC=5. (1)求经过B 、A 、C 三点的抛物线的表达式; (2)作出△ABC 关于y 轴对称的△C B A ''';(3)经过B '、A '、C '三点的抛物线能否由(1)中的抛物线平移得到?若能,怎样得到?若不能,请说明理由.DCB P O yx(第24题图)24、(本题满分10分)(2008陕西) 如图,矩形ABCD 的长、宽分别为32和1,且OB =1,点E (32,2),连接AE 、ED 。
(1)求经过A 、E 、D 三点的抛物线的表达式;(2)若以原点为位似中心,将五边形AEDCB 放大,使放大后的五边形的边长是原五边形对应边长的3倍,请在下图网格中画出放大后的五边形A ′E ′D ′C ′B ′;(3)经过A ′、E ′、D ′三点的抛物线能否由(1)中的抛物线平移得到?请说明理由。
24.(本题满分10分)(2009陕西副)如图,一条抛物线经过原点,且顶点B 的坐标(1,-1). (1)求这个抛物线的解析式;(2)设该抛物线与x 轴正半轴的交点为A ,求证:△OBA 为等腰直角三角形;(3)设该抛物线的对称轴与x 轴的交点为C ,请你在抛物线位于x 轴上方的图象上求两点E 、F ,使△ECF 为等腰直角三角形,且∠EOF=90°1 2 3 4 5 6 7AB CE DOxy16 4 2 3 57 (第24题图)24.(本题满分10分)(2009陕西)如图,在平面直角坐标系中,OB OA ⊥,且2OB OA =,点A 的坐标是(12)-,. (1)求点B 的坐标; (2)求过点A O B 、、的抛物线的表达式;(3)连接AB ,在(2)中的抛物线上求出点P ,使得ABP ABO S S =△△.24.(本题满分10分)(2010陕西副)如图,在平面直角坐标系中,△ABC 是直角三角形,且∠BAC=90°,∠ACB=30°,点A 的坐标为(0,3).(1)求点B 和点C 的坐标;(2)求经过A 、B 、C 三点的抛物线的表达式;(3)设点M 是(2)中抛物线的顶点,P 、Q 是抛物线上的两点,要使△MPQ 为等边三角形,求点P 、Q 的坐标.yOB Ax1 1(第24题图)(第24题图)24.(本题满分10分)(2009陕西)如图,在平面直角坐标系中,OB OA ⊥,且2OB OA =,点A 的坐标是(12)-,. (1)求点B 的坐标; (2)求过点A O B 、、的抛物线的表达式;(3)连接AB ,在(2)中的抛物线上求出点P ,使得ABP ABO S S =△△.24.(本题满分10分)(2010陕西副)如图,在平面直角坐标系中,△ABC 是直角三角形,且∠BAC=90°,∠ACB=30°,点A 的坐标为(0,3).(1)求点B 和点C 的坐标;(2)求经过A 、B 、C 三点的抛物线的表达式;(3)设点M 是(2)中抛物线的顶点,P 、Q 是抛物线上的两点,要使△MPQ 为等边三角形,求点P 、Q 的坐标.yOB Ax1 1(第24题图)(第24题图)(2010陕西)24.如图,在平面直角坐标系中,抛物线A (-1,0),B (3,0)C (0,-1)三点。
陕西中考数学二次函数选择填空题专题整理

(2006陕西)9.如图,抛物线的函数表达式是( ) A .22y x x =-+B .22y x x =++C .22y x x =--+D .22y x x =-++(2007陕西)8.抛物线247y x x =--的顶点坐标是( ) A .(211)-,B .(27)-,C .(211),D .(23)-,(2008陕西)10、已知二次函数2y ax bx c =++(其中a >0,b >0,c <0), 关于这个二次函数的图象有如下说法:①图象的开口一定向上;②图象的顶点一定在第四象限; ③图象与x 轴的交点至少有一个在y 轴的右侧。
以上说法正确的个数为 ( ) A .0 B .1 C .2 D .3(2008陕西副)10.若二次函数c bx ax y 2++=的图象如图所示,则a 、b 、c 间的大小关系正确的是 ( )A.a >b >cB.a <b <cC.a >c >bD.a <c <b(2009陕西)10.根据下表中的二次函数2y ax bx c =++的自变量x 与函数y 的对应值,可判断该二次函数的图象与x 轴( ).x … 1-0 1 2 … y… 1-74- 2-74- …A .只有一个交点B .有两个交点,且它们分别在y 轴两侧C .有两个交点,且它们均在y 轴同侧D .无交点(第10题(第9题(2009陕西副)9.将抛物线y=x 2-4x+3平移,使它平移后的顶点为(-2,4),则需将该抛物线 ( )A. 先向右平移4个单位,再向上平移5个单位B. 先向右平移4个单位,再向下平移5个单位C. 先向左平移4个单位,再向上平移5个单位D. 先向左平移4个单位,再向下平移5个单位(2010陕西)10.将抛物线C :y=x ²+3x-10,将抛物线C 平移到C ˋ。
若两条抛物线C,C ˋ关于直线x=1对称,则下列平移方法中正确的是 ( )A 将抛物线C 向右平移52个单位 B 将抛物线C 向右平移3个单位C 将抛物线C 向右平移5个单位D 将抛物线C 向右平移6个单位(2010陕西副)10. 若将抛物线C :1x 4-x 2y 2+=向右平移3个单位得到抛物线C ',则抛物线C 与C '一定关于某条直线对称,这条直线是 ( )A. x=23B. x=2C. x=25D. x=3(2011陕西)10、若二次函数c x x y +-=62的图像过)321,23(),,2(),,1(Y C Y B Y A +-,则321,,y y y 的大小关系正确的是A 、321y y y >>B 、231y y y >>C 、312y y y >>D 、213y y y >>(2011陕西副)10. 如果两个不同的二次函数的图象相交,那么它们的交点最多有 ( )A. 1个B. 2个C. 3个D. 4个(2012陕西)10.在平面直角坐标系中,将抛物线62--=x x y 向上(下)或向左(右)平移了m 个单位,使平移后的抛物线恰好经过原点,则m 的最小值为( )A .1B .2C .3D .6(2012陕西副)8. 如果M (x 1,y 1),N (x 2,y 2)是一次函数38y x =-图象上的两点,如果x 1+x 2=-3,那么y 1+y 2=( )A. -25B. -17C. -9D. 1(2013陕西)10.已知两点A(-5,y1),B(3,y2)均在抛物线y=ax2+bx+c(a≠0)上,点C(x0,y0)是该抛物线的顶点,若y1>y2≥y0,则x0的取值范围是()A. x0>-5B. x0>-1C.-5<x0<-1D.-2<x0<3(2013陕西副)10.若一个二次函数y=ax.2-4ax.+3(a≠0)的图象经过两点A(m+2,y1)、B(2-m,y2),则下列关系正确的是()A.y1>y2 B.y1<y2 C.y1=y2 D.y1≥y2(2014陕西)10. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )A. c>-1B. b>0C. 2a+b≠0D. 9a+c>3b第10题图(2014陕西副)10. 若a,B为非零实数,则函数y=ax+B与y=ax2+Bx在同一坐标系中的图象大致是()(2015陕西)10. 下列关于二次函数y=ax2-2ax+1(a>1)的图象与x轴交点的判断,正确的是( )A. 没有交点B. 只有一个交点,且它位于y轴右侧C. 有两个交点,且它们均位于y轴左侧D. 有两个交点,且它们均位于y轴右侧(2015陕西副)10.在平面直角坐标系中,有两条抛物线关于x轴对称,且它们的顶点相距10个单位长度.若其中一条抛物线的函数表达式为y=x2+6x+m,则m的值是()A.4或14B.4或-14C.-4或14D.-4或-14(2016陕西)10. 已知抛物线y=-x2-2x+3与x轴交于A、B两点,将这条抛物线的顶点记为C,连接AC、BC,则tan∠CAB的值为( )A.12B.55C.255D. 2(2016陕西副)10.将抛物线M:y=-13x2+2向左平移2个单位,再向上平移1个单位,得到抛物线M′.若抛物线M′与x轴交于A、B两点,M′的顶点记为C,则∠ACB=()A.45°B.60°C.90°D.120°(2017陕西)10. 已知抛物线y=x2-2mx-4(m>0)的顶点M关于坐标原点O的对称点为M′.若点M′在这条抛物线上,则点M的坐标为( )A.(1,-5)B. (3,-13)C. (2,-8)D. (4,-20)(2017陕西副)10. 已知抛物线y=x2+bx+c的对称轴为x=1,且它与x轴交于A、B两点.若AB的长是6,则该抛物线的顶点坐标为A. (1,9)B. (1,8)C. (1,-9)D. (1,-8)(2018陕西)10. 对于抛物线y=ax2+(2a-1)x+a-3,当x=1时,y>0,则这条抛物线的顶点一定在( )A.第一象限B. 第二象限C. 第三象限D. 第四象限(2018陕西副)10. 已知抛物线y=x2+(m+1)x+m,当x=1时,y>0,且当x<-2时,y 的值随x值的增大而减小,则m的取值范围是A.m>-1 B.m<3 C.-1<m≤3 D.3<m≤4(2019陕西)10.在同一平面直角坐标系中,若抛物线与关于y轴对称,则符合条件的m,n的值为A.,B. ,C. ,D. ,(2019陕西副)10.在平面直角坐标系中,将抛物线向右平移4个单位长度,平移后的抛物线与y轴的交点为,则平移后的抛物线的对称轴为A. B. C. D.(2020陕西)在平面直角坐标系中,将抛物线沿y轴向下平移3个单位.则平移后得到的抛物线的顶点一定在A.第一象限B. 第二象限C. 第三象限D. 第四象限(2020陕西副)在同一直角坐标系中,若抛物线y=mx2+2x-n与y=-6x2-2x+m-n关于x轴对称,则m,n的值为()A.m=-6,n=-3B.m=-6,n=3C.m=6,n=-3D.m=6,n=3。
2011年陕西省中考数学试题及答案(word版),推荐文档

【
】 A、2 对
B、3 对
C、4 对
D、5 对
10、若二次函数 y x2 6x c 的图像过 A(1,Y ), B(2,Y ),C(3 2,Y , 则 y , y , y 的
1
2
3)
123
大小关系是
【
】
A 、 y1 y2 y3
B 、 y1 y2 y3
C 、 y2 y1 y3
D 、 y3 y1 y2
圆锥球Βιβλιοθήκη (第二题图)圆柱A、1 个
B 、2 个
C、3 个
D、4 个
3. 我国第六次人口普查显示,全国人口为 1370536875 人,将这个总人口数(保留三个有
效数字)用科学计数法表示为
【
】
A、 1.37 109 B、1.37 107 C、1.37 108
2 4、下列四个点,在正比例函数Y X 的图像上的点是
第Ⅱ卷(非选择题 共 90 分)
二、填空题(共 6 小题,每小题 3 分,计 18 分)
11.计算: 3 2 =
.(结果保留根号)
12.如图,AC∥BD,AE 平分∠BAC 交 BD 于点 E
,若
1 640 则 1
.
13、分解因式: ab 2 4ab 4a
.
14、一商场对某款羊毛衫进行换季打折销售,若这款羊毛衫每件
(1) 根据图①、图②,计算八年级“低碳族”人数,并补全上面两个统计图;
第 3 页 共 12 页
(2) 小丽依据图①、图②提供的信息通过计算认为,与其他两个年级相比,九年级的“低 碳族”人数在本年级全体学生中所占的比例较大,你认为小丽的判断正确吗?说明理由。
20.(本题满分 8 分) 一天,数学课外活动小组的同学们,带着皮尺去测量某河道因挖沙形成的“圆锥形坑”的 深度,来评估这些坑道对河道的影响,如图是同学们选择(确保测量过程中无安全隐患) 的测量对象,测量方案如下: ①、先测出沙坑坑沿的圆周长 34.54 米; ②、甲同学直立于沙坑坑沿的圆周所在的平面上,经过适当调整自己所处的位置,当他位 于 B 时恰好他的视线经过沙坑坑沿圆周上一点 A 看到坑底 S(甲同学的视线起点 C 与点 A,点 S 三点共线),经测量:AB=1.2 米,BC=1.6 米
2011陕西中考数学试题及答案

2011陕西中考数学试题及答案一、选择题1. 计算:$3 \times (4 + 5) - 2^2 =$ (2011陕西中考)解答:首先计算括号内的加法,得到$3 \times 9 - 2^2 =$,然后计算乘法,得到$27 - 4 =$,最后计算减法,得到$23$。
因此,答案为$23$。
2. 下列各数:$\sqrt{9}$,$\frac{12}{4}$,$(-3) \times 2^2 + 5^0$和$-1.1$中,其中不是整数的是:(2011陕西中考)A. $\sqrt{9}$B. $\frac{12}{4}$C. $(-3) \times 2^2 + 5^0$D. $-1.1$解答:$\sqrt{9}=3$,$\frac{12}{4}=3$,$(-3) \times 2^2 + 5^0=-3\times 4 + 1=-11$,$-1.1$不是整数。
因此,答案是D。
3. 用$\frac{4}{9}$表示0.4,则$\frac{41}{90}$的另一种表示是:(2011陕西中考)解答:首先计算$\frac{4}{9} \times 10$,得到$\frac{40}{9}$。
然后在$\frac{40}{9}$的基础上加上$\frac{1}{9}$,得到$\frac{41}{9}$。
最后将$\frac{41}{9}$转化为分数形式,得到$\frac{41}{9}$。
因此,答案是$\frac{41}{9}$。
4. 小花去商场选购衣服,她看中了一件原价为320元的衣服,商场正在举行打折活动,全场商品打7折。
小花还是犹豫不决,她妈妈说:“你有一张价格为20元的优惠券,使用后再打折。
”小花计算了一下,最终衣服的价格是多少元?(2011陕西中考)解答:首先计算打折后衣服的价格,$320 \times 0.7=224$。
然后将优惠券价格减去衣服价格,$20-224=-204$。
因此,最终衣服的价格是负数204元。
陕西中考数学试题解析版.doc

2011年陕西省中考数学试卷一、选择题(共10小题,每小题3分,计30分.) 1、(2011•陕西)32-的倒数为( ) A . 23-B .23C .32D . 32-考点:倒数。
专题:计算题。
分析:根据倒数的意义,两个数的积为1,则两个数互为倒数,因此求一个数的倒数即用1除以这个数. 解答:解:32-的倒数为,1÷23⎛⎫- ⎪⎝⎭=3-2, 故选:A .点评:此题考查的是倒数,关键是由倒数的意义,用1除以这个数即是. 2、(2011•陕西)下面四个几何体中,同一个几何体的主视图和俯视图相同的共有( )A 、1个B 、2个C 、3个D 、4个 考点:简单几何体的三视图。
分析:主视图、俯视图是分别从物体正面和上面看,所得到的图形.解答:解:圆柱主视图、俯视图分别是长方形、圆,主视图与俯视图不相同; 圆锥主视图、俯视图分别是三角形、有圆心的圆,主视图与俯视图不相同; 球主视图、俯视图都是圆,主视图与俯视图相同;正方体主视图、俯视图都是正方形,主视图与俯视图相同. 共2个同一个几何体的主视图与俯视图相同. 故选B .点评:本题考查了几何体的三种视图,掌握定义是关键.注意所有的看到的棱都应表现在三视图中. 3、(2011•陕西)我国第六次人口普查显示,全国人口为1370536875人,将这个总人口数(保留三个有效数字)用科学记数法表示为( )A 、1.37×109B 、1.37×107C 、1.37×108D 、1.37×1010考点:科学记数法与有效数字。
分析:较大的数保留有效数字需要用科学记数法来表示.用科学记数法保留有效数字,要在标准形式a×10n中a 的部分保留,从左边第一个不为0的数字数起,需要保留几位就数几位,然后根据四舍五入的原理进行取舍.解答:解:1370536875=1.370536875×109≈1.37×109, 故选:A .点评:此题主要考查了科学记数法的表示方法,以及用科学记数法表示的有效数字的确定方法. 4、(2011•陕西)下列四个点,在正比例函数的图象上的点是( )A 、(2,5)B 、(5,2)C 、(2,﹣5)D 、(5,﹣2 考点:一次函数图象上点的坐标特征。
陕西中考数学试题解析版.doc

2011年陕西省中考数学试卷一、选择题(共10小题,每小题3分,计30分.) 1、(2011•陕西)32-的倒数为( ) A . 23-B .23C .32D . 32-考点:倒数。
专题:计算题。
分析:根据倒数的意义,两个数的积为1,则两个数互为倒数,因此求一个数的倒数即用1除以这个数. 解答:解:32-的倒数为,1÷23⎛⎫- ⎪⎝⎭=3-2, 故选:A .点评:此题考查的是倒数,关键是由倒数的意义,用1除以这个数即是. 2、(2011•陕西)下面四个几何体中,同一个几何体的主视图和俯视图相同的共有( )A 、1个B 、2个C 、3个D 、4个 考点:简单几何体的三视图。
分析:主视图、俯视图是分别从物体正面和上面看,所得到的图形.解答:解:圆柱主视图、俯视图分别是长方形、圆,主视图与俯视图不相同; 圆锥主视图、俯视图分别是三角形、有圆心的圆,主视图与俯视图不相同; 球主视图、俯视图都是圆,主视图与俯视图相同;正方体主视图、俯视图都是正方形,主视图与俯视图相同. 共2个同一个几何体的主视图与俯视图相同. 故选B .点评:本题考查了几何体的三种视图,掌握定义是关键.注意所有的看到的棱都应表现在三视图中. 3、(2011•陕西)我国第六次人口普查显示,全国人口为1370536875人,将这个总人口数(保留三个有效数字)用科学记数法表示为( )A 、1.37×109B 、1.37×107C 、1.37×108D 、1.37×1010考点:科学记数法与有效数字。
分析:较大的数保留有效数字需要用科学记数法来表示.用科学记数法保留有效数字,要在标准形式a×10n中a 的部分保留,从左边第一个不为0的数字数起,需要保留几位就数几位,然后根据四舍五入的原理进行取舍.解答:解:1370536875=1.370536875×109≈1.37×109, 故选:A .点评:此题主要考查了科学记数法的表示方法,以及用科学记数法表示的有效数字的确定方法. 4、(2011•陕西)下列四个点,在正比例函数的图象上的点是( )A 、(2,5)B 、(5,2)C 、(2,﹣5)D 、(5,﹣2 考点:一次函数图象上点的坐标特征。
陕西中考数学试题解析版.doc

2011年陕西省中考数学试卷一、选择题(共10小题,每小题3分,计30分.) 1、(2011•陕西)32-的倒数为( ) A . 23-B .23C .32D . 32-考点:倒数。
专题:计算题。
分析:根据倒数的意义,两个数的积为1,则两个数互为倒数,因此求一个数的倒数即用1除以这个数. 解答:解:32-的倒数为,1÷23⎛⎫- ⎪⎝⎭=3-2, 故选:A .点评:此题考查的是倒数,关键是由倒数的意义,用1除以这个数即是. 2、(2011•陕西)下面四个几何体中,同一个几何体的主视图和俯视图相同的共有( )A 、1个B 、2个C 、3个D 、4个 考点:简单几何体的三视图。
分析:主视图、俯视图是分别从物体正面和上面看,所得到的图形.解答:解:圆柱主视图、俯视图分别是长方形、圆,主视图与俯视图不相同; 圆锥主视图、俯视图分别是三角形、有圆心的圆,主视图与俯视图不相同; 球主视图、俯视图都是圆,主视图与俯视图相同;正方体主视图、俯视图都是正方形,主视图与俯视图相同. 共2个同一个几何体的主视图与俯视图相同. 故选B .点评:本题考查了几何体的三种视图,掌握定义是关键.注意所有的看到的棱都应表现在三视图中. 3、(2011•陕西)我国第六次人口普查显示,全国人口为1370536875人,将这个总人口数(保留三个有效数字)用科学记数法表示为( ) A 、1.37×109 B 、1.37×107 C 、1.37×108 D 、1.37×1010 考点:科学记数法与有效数字。
分析:较大的数保留有效数字需要用科学记数法来表示.用科学记数法保留有效数字,要在标准形式a×10n 中a 的部分保留,从左边第一个不为0的数字数起,需要保留几位就数几位,然后根据四舍五入的原理进行取舍.解答:解:1370536875=1.370536875×109≈1.37×109, 故选:A .点评:此题主要考查了科学记数法的表示方法,以及用科学记数法表示的有效数字的确定方法. 4、(2011•陕西)下列四个点,在正比例函数的图象上的点是( )A 、(2,5)B 、(5,2)C 、(2,﹣5)D 、(5,﹣2 考点:一次函数图象上点的坐标特征。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
09年10.根据下表中的二次函数2y ax bx c =++的自变量x 与函数y 的对应值,可判断该二次函数的图象与x 轴( ).
x …
1- 0 1 2 … y …
1- 74
- 2-
74
- …
A .只有一个交点
B .有两个交点,且它们分别在y 轴两侧
C .有两个交点,且它们均在y 轴同侧
D .无交点 24.(本题满分10分)
如图,在平面直角坐标系中,OB OA ⊥,且2OB OA =,点A 的坐标是(12)-,
. (1)求点B 的坐标;
(2)求过点A O B 、、的抛物线的表达式;
(3)连接AB ,在(2)中的抛物线上求出点P ,使得ABP ABO S S =△△.
10年10.将抛物线C :y=x ²+3x-10,将抛物线C 平移到C ˋ。
若两条抛物线C,C ˋ关于直线x=1对称,则下列平移方法中正确的是 (C )
A 将抛物线C 向右平移5
2
个单位 B 将抛物线C 向右平移3个单位
C 将抛物线C 向右平移5个单位
D 将抛物线C 向右平移6个单位
24.如图,在平面直角坐标系中,抛物线A (-1,0),B (3,0)C (0,-1)三点。
(1)求该抛物线的表达式;
(2)点Q 在y 轴上,点P 在抛物线上,要使Q 、P 、A 、B 为顶点的四边形是平行四边形求所有满足条件点P 的坐标。
11年10、若二次函数c x x y +-=62的图像过)321,23(),,2(),,1(Y C Y B Y A +-,则
321,,y y y 的大小关系是 ( )
A 、321y y y
B 、321y y y
C 、312y y y
D 、213y y y 24.(本题满分10分)
如图,二次函数x x y 3
1
322—=的图像经过△AOC 的三个顶点,其中A(-1,
m),B(n,n)
(1) 求A 、B 的坐标
(2) 在坐标平面上找点C ,使以A 、O 、B 、C 为顶点的四边形是平行四边形
①、 这样的点C 有几个?
②、
能否将抛物线x x y 3
1
322—=
平移后经过A 、C 两点,若能求出平移后经过A 、C 两点的一条抛物线的解析式;若不能,说明理由。
12年10.在平面直角坐标系中,将抛物线62--=x x y 向上(下)或向左(右)平移了m 个单位,使平移后的抛物线恰好经过原点,则m 的最小值为( ) A .1 B .2 C .3 D .6 24.(本题满分10分)
如果一条抛物线()2=++0y ax bx c a ≠与x 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”. (1)“抛物线三角形”一定是 三角形;
(2)若抛物线()2=-+>0y x bx b 的“抛物线三角形”是等腰直角三角形,求b 的值; (3)如图,△OAB 是抛物线()2=-+''>0y x bx b 的“抛物线三角形”,是否存在以原点O 为对称中心的矩形ABCD ?若存在,求出过O C D 、、三点的抛物线的表达式;若不存在,说明理由.
13年10.已知两点A (-5,1y )、B (3,2y )均在抛物线()02≠++=a c bx ax y 上,点C (0x ,0y )是该抛物线的顶点,若1y >2y ≥0y ,则0x 的取值范围是( ) A. 0x >-5 B. 0x >-1 C .-5<0x <-1 D .-2<0x <3 24.(本题满分10分)
在平面直角坐标系中,一个二次函数的图象经过A (1,0)、B (3,0)两点. (1) 写出这个二次函数图象的对称轴;
(2) 设这个二次函数图象的顶点为D ,与y 轴交于点C ,它的对称轴与x 轴交
于点E ,连接AC 、DE 和DB.当⊿AOC 与⊿DEB 相似时,求这个函数的表达式.
14年10、二次函数)0(2≠++=a c bx ax y 的图象如图所示,则下列结论正确的是( )
A 、c ˃-1
B 、b ˃0
C 、02≠+b a
D 、b c a 392〉+
x
y –1–2–3–41
2
3
4–1
–2–3–4
1
234O
24、(本题满分10分)
已知抛物线C:c bx x y ++-=2经过A(-3,0)和B(0,3)两点,将抛物线的顶点记为M,它的对称轴与x 轴的交点记为N. (1)求抛物线C 的表达式; (2)求点M 的坐标;
(3)将抛物线C 平移到抛物线C ’,抛物线C ’的顶点记为M ’、它的对称轴与x 轴的交点记为N ’。
如果点M 、N 、M ’、N ’为顶点的四边形是面积为16的平行四边形,那么应将抛物线C 怎样平移?为什么?
15年10.下列关于二次函数)>1(122a ax ax y +-=的图象与x 轴交点的判断,正确的是( )
A.没有交点
B.只有一个交点,且它位于y 轴右侧
C.有两个交点,且它们均位于y 轴左侧
D.有两个交点,且它们均位于y 轴右侧 24.(本题满分10分)在平面直角坐标系中,抛物线y=x 2+5x+4的顶点为M ,与x 轴交于A 、B 两点,与y 轴交于C 点。
(1)求点A 、B 、C 的坐标;
(2)求抛物线y=x 2+5x+4关于坐标原点O 对称的抛物线的函数表达式;
(3)设(2)中所求抛物线的顶点为M`,与x 轴交于A`、B`两点,与y 轴交
于C`点,在以A 、B 、C 、M 、A`、B`、C`、M`这八个点中的四个点为顶 点的平行四边形中,求其中一个不是菱形的平行四边形的面积。
16年
10.已知抛物线322+--=x x y 与x 轴交于A 、B 两点,将这条抛物线的定点记为C ,连接AC 、BC ,则tan ∠CAB 的值为 【 】
A.21
B. 55
C. 5
52 D. 2 24.(本题满分10分)如图,在平面直角坐标系中,点O 为坐标原点,抛物线
52++=bx ax y
经过点M (1,3)和N (3,5),与x 轴交于A 、B 两点,与y 轴交于C 点。
(1)试判断抛物线与x 轴交点的情况;
(2)平移这条抛物线,使平移后的抛物线经过A (-2,0)且与y 轴的交点为B 同时满足以A 、O 、B 为顶点的三角形是等腰直角三
角形.请写出平移的过程,并说明理由。
