陕西中考数学二次函数选择填空题专题整理
二次函数中考选择填空题专题训练

二次函数——选择填空题1、(2013陕西)已知两点),3(),,5(21y B y A -均在抛物线)0(2≠++=a c bc ax y 上,点),(00y x C 是该抛物线的顶点,若021y y y ≥>,则0x 的取值范围是( )A .50->x B.10->x C .150-<<-x D.320<<-x 考点:二次函数图象性质的应用及对称性的考查。
解析:由点),(00y x C 是该抛物线的顶点,且021y y y ≥>,所以0y 为函数的最小值,即得出抛物线的开口向上,因为021y y y ≥>,所以得出点A、B 可能在对称轴的两侧或者是在对称轴的左侧,当在对称轴的左侧时,y 随x 的增大而减小,因此0x >3,当在对称轴的两侧时,点B距离对称轴的距离小于点A 到对称轴的距离,即得0x -(-5)>3-0x ,解得10->x ,综上所得:10->x ,故选B2、(2013济宁)二次函数y=ax 2+bx+c (a ≠0)的图象如图所示,则下列结论中正确的是( )A.a>0 B.当﹣1<x<3时,y >0C .c <0ﻩD.当x ≥1时,y 随x 的增大而增大 考点:二次函数图象与系数的关系.分析:由抛物线的开口方向判断a 与0的关系,由抛物线与y轴的交点判断c 与0的关系,然后根据对称轴及抛物线与x 轴交点情况进行推理,进而对所得结论进行判断. 解答:解:A.抛物线的开口方向向下,则a <0.故本选项错误; B .根据图示知,抛物线的对称轴为x =1,抛物线与x 轴的一交点的横坐标是﹣1,则抛物线与x 轴的另一交点的横坐标是3,所以当﹣1<x<3时,y >0.故本选项正确;C.根据图示知,该抛物线与y 轴交与正半轴,则c>0.故本选项错误; D .根据图示知,当x ≥1时,y 随x 的增大而减小,故本选项错误. 故选B .点评:本题考查了二次函数图象与系数的关系.二次函数y=ax 2+bx+c 系数符号由抛物线开口方向、对称轴、抛物线与y 轴的交点抛物线与x 轴交点的个数确定. 3、(2013杭州)给出下列命题及函数y=x,y=x 2和y =①如果,那么0<a<1;②如果,那么a>1;③如果,那么﹣1<a<0;④如果时,那么a<﹣1.则()A.正确的命题是①④ﻩB.错误的命题是②③④ C.正确的命题是①②ﻩD.错误的命题只有③考点:二次函数与不等式(组);命题与定理.分析:先确定出三函数图象的交点坐标为(1,1),再根据二次函数与不等式组的关系求解即可.解答:解:易求x=1时,三个函数的函数值都是1,所以,交点坐标为(1,1),根据对称性,y=x和y=在第三象限的交点坐标为(﹣1,﹣1),①如果,那么0<a<1正确;②如果,那么a>1或﹣1<a<0,故本小题错误;③如果,那么a值不存在,故本小题错误;④如果时,那么a<﹣1正确.综上所述,正确的命题是①④.故选A.点评:本题考查了二次函数与不等式组的关系,命题与定理,求出两交点的坐标,并准确识图是解题的关键.4、(2013年江西省)若二次涵数y=ax+bx+c(a≠0)的图象与x轴有两个交点,坐标分别为(x1,0),(x2,0),且x1<x2,图象上有一点M (x0,y0)在x轴下方,则下列判断正确的是().A.a>0ﻩﻩB.b2-4ac≥0ﻩﻩC.x1<x0<x2ﻩ D.a(x0-x1)( x0-x2)<0【答案】D.【考点解剖】本题考查的是二次函数的性质,要求对二次函数的性质有比较深刻地理解,并能熟练地画函数草图作出分析.【解题思路】 抛物线与x轴有不同的两个交点,则240b ac ->,与B矛盾,可排除B 选项;剩下A 、C 、D不能直接作出正误判断,我们分a >0,a<0两种情况画出两个草图来分析(见下图).由图可知a 的符号不能确定(可正可负,即抛物线的开口可向上,也右向下),所以012,,x x x 的大小就无法确定;在图1中,a >0且有102x x x <<,则0102()()a x x x x --的值为负;在图2中,a<0且有102x x x <<,则0102()()a x x x x --的值也为负.所以正确选项为D.【解答过程】 略.【方法规律】 先排除错误的,剩下的再画图分析(数形结合) 【关键词】 二次函数 结论正误判断5、(2013四川宜宾)对于实数a、b ,定义一种运算“⊗”为:a ⊗b=a 2+ab ﹣2,有下列命题:①1⊗3=2;②方程x⊗1=0的根为:x 1=﹣2,x 2=1; ③不等式组的解集为:﹣1<x <4;④点(,)在函数y =x ⊗(﹣1)的图象上. 其中正确的是( )A.①②③④ B .①③ﻩ C .①②③ﻩ D.③④考点:二次函数图象上点的坐标特征;有理数的混合运算;解一元二次方程-因式分解法;解一元一次不等式组;命题与定理. 专题:新定义.分析:根据新定义得到1⊗3=12+1×3﹣2=2,则可对①进行判断;根据新定义由x ⊗1=0得到x 2+x ﹣2=0,然后解方程可对②进行判断;根据新定义得,解得﹣1<x<4,可对③进行判断;根据新定义得y =x ⊗(﹣1)=x 2﹣x ﹣2,然后把x =代入计算得到对应的函数值,则可对④进行判断.解答:解:1⊗3=12+1×3﹣2=2,所以①正确; ∵x ⊗1=0, ∴x 2+x ﹣2=0,∴x 1=﹣2,x 2=1,所以②正确;∵(﹣2)⊗x ﹣4=4﹣2x ﹣2﹣4=﹣2x ﹣2,1⊗x﹣3=1+x ﹣2﹣3=x﹣4, ∴,解得﹣1<x <4,所以③正确;∵y=x ⊗(﹣1)=x 2﹣x ﹣2,∴当x =时,y =﹣﹣2=﹣,所以④错误. 故选C . 点评:本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足二次函数的解析式.也考查了阅读理解能力、解一元二次方程以及解一元一次不等式组.6、(2013浙江丽水)若二次函数2ax y =的图象经过点P(-2,4),则该图象必经过点A. (2,4) B. (-2,-4) C. (-4,2) D. (4,-2)7、(2013成都市)在平面直角坐标系xOy 中,直线y=k x(k为常数)与抛物线21y 23x =-交于A,B 两点,且A点在y轴左侧,P点坐标为(0,-4),连接PA ,PB.有以下说法: ① 2PO PA PB =⋅;② 当k >0时,(PA +AO )(PB -BO)的值随k 的增大而增大;③ 当3k =-时,2BP BO BA =⋅; ④PAB 面积的最小值为46.其中正确的是___________.(写出所有正确说法的序号) 答案:③④解析:如图,无法证明△PAO ∽△POB ,故①不一定成立;对于②,取特殊值估算,知(PA+AO)(PB-BO)的值不是随k的增大而增大,也错。
中考数学专题复习:二次函数练习题(含答案)

中考数学专题复习:二次函数练习题一.选择题1.对于二次函数y=﹣x2+x﹣4,下列说法正确的是()A.图象的开口方向向上B.当>0 时,y随x的增大而增大C.当x=2时,y有最大值﹣3D.图象与x轴有两个交点2.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表所示,下列结论,其中正确的个数为()x﹣1013y﹣1353①ac<0;②当x>1时,y的值随x值的增大而减小.③当﹣1<x<3时,ax2+(b﹣1)x+c>0;④对于任意实数m,4m(am+b)﹣6b<9a总成立.A.1个B.2个C.3个D.4个3.已知二次函数y=(x﹣p)(x﹣q)+2,若m,n是关于x方程(x﹣p)(x﹣q)+2=0的两个根,则实数m,n,p,q的大小关系可能是()A.m<p<q<n B.m<p<n<q C.p<m<n<q D.p<m<q<n 4.在平面直角坐标系中,如图是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③方程ax2+bx+c=0的两根分别为﹣3和1;④b2﹣4ac >0,其中正确的命题有()A.1个B.2个C.3个D.4个5.已知点(﹣4,y1),(2,y2)均在抛物线y=x2﹣1上,则y1,y2的大小关系为()A.y1<y2B.y1>y2C.y1≤y2D.y1≥y26.如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A,B两点,与y轴交于点C,对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C,D两点,D点在x轴下方且横坐标小于3,则下列结论中正确的是()A.a﹣b+c>0B.2a+b+c<0C.x(ax+b)>a+b D.a<﹣17.若关于x的一元二次方程x2+ax+b=0的两个实数根是﹣1和3,那么对二次函数y=a(x ﹣1)2+4的图象和性质的描述错误的是()A.顶点坐标为(1,4)B.函数有最大值4C.对称轴为直线x=1D.开口向上8.如图,已知二次函数y=﹣x2+bx+c,它与x轴交于A、B,且A、B位于原点两侧,与y 的正半轴交于C,顶点D在y轴右侧的直线l:y=4上,则下列说法:①bc<0,②0<b=8<4,③AB=4,④S△ABD其中正确的结论有()A.①②B.②③C.②③④D.①②③④9.如图,抛物线y=ax2+bx与直线y=kx相交于O,A(3,2)两点,则不等式ax2+bx﹣kx <0的解集是()A.0<x<3B.2<x<3C.x<0或x>3D.x<2或x>3 10.在同一直角坐标系中分别画出函数y=x,y=x2和y=的图象,对于自变量x=a有以下命题;①如果>a>a2,那么0<a<1;②如果a2,那么a>1;③如果>a2>a,那么﹣1<a<0;④如果a2时,那么a<﹣1,则()A.正确的命题是①④B.错误的命题是②③④C.正确的命题只有①②D.错误的命题只有③二.填空题11.如图,在△ABC中,BC=12,BC上的高AH=8,矩形DEFG的边EF在边BC上,顶点D、G分别在边AB、AC上.设DE=x,矩形DEFG的面积为y,那么y关于x的函数关系式是.(不需写出x的取值范围).12.已知点P(x0,m),Q(1,n)在二次函数y=(x+a)(x﹣a﹣1)(a≠0)的图象上,且m<n下列结论:①该二次函数与x轴交于点(﹣a,0)和(a+1,0);②该二次函数的对称轴是x=;③该二次函数的最小值是(a+2)2;④0<x0<1.其中正确的是.(填写序号)13.如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3…A n,将抛物线y=x2沿直线L:y=x向上平移,得到一系列抛物线,且满足下列条件:①抛物线的顶点M1,M2,M3,…M n都在直线L:y=x上;②抛物线依次经过点A1,A2,A3…A n,则顶点M2020的坐标为.14.如图,二次函数y=x2+x﹣2的图象与x轴负半轴交于点A,与y轴负半轴交于点B.点P是线段OA上的动点,以OP为直径构造圆,连结BP交圆于点Q,连结AQ.则AQ 的最小值是.15.已知二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:①abc>0;②2a+b<0;③a ﹣b+c<0;④a+c>0;⑤b2>4ac;⑥当x>1时,y随x的增大而减小.其中正确的说法有(写出正确说法的序号)三.解答题16.如图,抛物线y=x2+bx+c与x轴交于A,C两点,与y轴交于B点,抛物线的顶点为点D,已知点A的坐标为(﹣1,0),点B的坐标为(0,﹣3).(1)求抛物线的解析式及顶点D的坐标.(2)求△ACD的面积.17.某商店经营一种文具,已知成批购进时的单价是20元.调查发现销售单价是30元时,月销售量是230件,而销售单价每上涨1元,月销售量就减少10件,且每件文具售价不能高于40元,设每件文具的销售单价上涨了x元时(x为正整数),月销售利润为y元.(1)求y与x的函数关系式;(2)每件文具的售价定为多少元时,月销售利润为2520元?(3)每件文具的售价定为多少元时可使月销售利润最大?最大的月利润是多少?18.某超市为了销售一种新型饮料,对月销售情况作了如下调查,结果发现每月销售量y(瓶)与销售单价x(元)满足一次函数关系.所调查的部分数据如表:(已知每瓶进价为4元,每瓶利润=销售单价﹣进价)单价x(元)567…销售量y(瓶)150140130…(1)求y关于x的函数表达式.(2)该新型饮料每月的总利润为w(元),求w关于x的函数表达式,并指出单价为多少元时利润最大,最大利润是多少元?(3)由于该新型饮料市场需求量较大,厂家进行了提价.此时超市发现进价提高了a元,每月销售量与销售单价仍满足第(1)问函数关系,当销售单价不超过14元时,利润随着x的增大而增大,求a的最小值.19.在平面直角坐标系中,点O(0,0),点A(﹣3,0).已知抛物线y=﹣x2+2mx+3(m 为常数),顶点为P.(1)当抛物线经过点A时,顶点P的坐标为;(2)在(1)的条件下,此抛物线与x轴的另一个交点为点B,与y轴交于点C.点Q 为直线AC上方抛物线上一动点.①如图1,连接QA、QC,求△QAC的面积最大值;②如图2,若∠CBQ=45°,请求出此时点Q坐标.20.如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.(1)求抛物线的解析式;(2)直接写出点C的坐标,并求出△ABC的面积;(3)点P是抛物线BA段上一动点,当△ABP的面积为3时,求出点P的坐标.参考答案一.选择题1.解:A、由于a=﹣<0,所以该图象的开口方向向下,故本选项说法错误.B、y=﹣x2+x﹣4=﹣(x﹣2)2﹣3,其顶点坐标是(2,﹣3),则当x<2时,y随x的增大而增大,故本选项说法错误.C、y=﹣x2+x﹣4=﹣(x﹣2)2﹣3,其顶点坐标是(2,﹣3),则当x=2时,y有最大值﹣3,故本选项说法正确.D、由于△=1﹣4×(﹣)×(﹣4)=﹣3<0,则该函数图象与x轴没有交点,故本选项说法错误.故选:C.2.解:①由图表中数据可得出:x=1时,y=5,所以二次函数y=ax2+bx+c开口向下,a<0;又x=0时,y=3,所以c=3>0,所以ac<0,故①正确;②∵二次函数y=ax2+bx+c开口向下,且对称轴为x=1.5,∴当x≥1.5时,y的值随x值的增大而减小,故②错误;③∵x=﹣1时,ax2+bx+c=﹣1,∴x=﹣1时,ax2+(b﹣1)x+c=0,∵x=3时,ax2+(b﹣1)x+c=0,且函数有最大值,∴当﹣1<x<3时,ax2+(b﹣1)x+c>0,故③正确.④将x=﹣1、y=﹣1,x=0、y=3,x=1、y=5代入y=ax2+bx+c,得,解得:,∴y=﹣x2+3x+3=﹣(x﹣)2+,可知当x=时,y取得最大值,即当x=m时,am2+bm+c≤a+b+c,变形可得4m(am+b)﹣6b≤9a,故④错误;故选:B.3.解:∵二次函数y=(x﹣p)(x﹣q)+2,∴该函数开口向上,当x=p或x=q时,y=2,∵m,n是关于x方程(x﹣p)(x﹣q)+2=0的两个根,∴p、q一定一个最大,一个最小,m、n一定处于p、q中间,故选:C.4.解:由图象可知:抛物线开口向上,对称轴为直线x=﹣1,过(1,0)点,把(1,0)代入y=ax2+bx+c得,a+b+c=0,因此①正确;对称轴为直线x=﹣1,即:﹣=﹣1,整理得,b=2a,因此②不正确;由抛物线的对称性,可知抛物线与x轴的两个交点为(1,0)(﹣3,0),因此方程ax2+bx+c =0的两根分别为﹣3和1;故③是正确的;由图可得,抛物线有两个交点,所以b2﹣4ac>0,故④正确;故选:C.5.解:把(﹣4,y1),(2,y2)分别代入抛物线y=x2﹣1得,y1=16﹣1=15,y2=4﹣1=3,∴y1>y2,故选:B.6.解:∵抛物线与y轴的交点在x轴上方,∴c>0,∵抛物线的对称轴为直线x=﹣=1,∴b=﹣2a,∴2a+b+c=2a﹣2a+c=c>0,所以B错误;∵抛物线与x轴的一个交点在点(3,0)左侧,而抛物线的对称轴为直线x=1,∴抛物线与x轴的另一个交点在点(﹣1,0)右侧,∴当x=﹣1时,y<0,∴a﹣b+c<0,所以A错误;∵x=1时,二次函数有最大值,∴ax2+bx+c≤a+b+c,∴ax2+bx≤a+b,所以C错误;∵直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,∴x=3时,一次函数值比二次函数值大,即9a+3b+c<﹣3+c,而b=﹣2a,∴9a﹣6a<﹣3,解得a<﹣1,所以D正确.故选:D.7.解:∵关于x的一元二次方程x2+ax+b=0的两个实数根是﹣1和3,∴﹣a=﹣1+3=2,∴a=﹣2<0,∴二次函数y=a(x﹣1)2+4的开口向下,对称轴为直线x=1,顶点坐标为(1,4),当x=1时,函数有最大值4,故A、B、C叙述正确,D错误,故选:D.8.解:①a<0,则b>0,c>0,故cb>0,故①错误,不符合题意;②c﹣=4,而1<c<2,故0<2<b<2<4,故正确,符合题意;③函数的表达式为:y=﹣(x﹣h)2+4,故x=h±2,故AB=x2﹣x1=4,正确,符合题意;④S=×AB×y D=8,正确,符合题意;△ABD故选:C.9.解:由ax2+bx﹣kx<0得到:ax2+bx<kx.∵抛物线y=ax2+bx与直线y=kx相交于O(0,0)和A(3,2)两点,∴关于x的不等式ax2+bx<kx的解集是0<x<3.即关于x的不等式ax2+bx﹣kx<0的解集是0<x<3.故选:A.10.解:①当0<a<1时,反比例函数的图象在最上方,一次函数的图象在中间,二次函数的图象在下方,故①正确;②当a>1或﹣1<a<0时,二次函数的图象在最上方,一次函数的图象在中间,反比例函数的图象在下方,故②错误;③当﹣1<a<0时,二次函数的图象在最上方,一次函数的图象在中间,反比例函数图象在下方,故③错误;④当a<﹣1时,二次函数的图象在最上方,反比例函数的图象在中间,一次函数的图象在最下方,故④错误;故选:B.二.填空题(共5小题)11.解:∵四边形DEFG是矩形,BC=12,BC上的高AH=8,DE=x,矩形DEFG的面积为y,∴DG∥EF,∴△ADG∽△ABC,∴,得DG=,∴y=x=+12x,故答案为:y=+12x.12.解:①∵二次函数y=(x+a)(x﹣a﹣1),∴当y=0时,x1=﹣a,x2=a+1,即该二次函数与x轴交于点(﹣a,0)和(a+1,0).故①结论正确;②对称轴为:x==.故②结论正确;③由y=(x+a)(x﹣a﹣1)得到:y=(x﹣)2﹣(a+)2,则其最小值是﹣(a+)2,故③结论错误;④当P在对称轴的左侧(含顶点)时,y随x的增大而减小,由m<n,得0<x0≤;当P在对称轴的右侧时,y随x的增大而增大,由m<n,得<x0<1,综上所述:m<n,所求x0的取值范围0<x0<1.故④结论正确.故答案是:①②④.13.解:∵抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3,…,A n,…,∴点A n的坐标为(n,n2).设点M n的坐标为(a,a),则以点M n为顶点的抛物线解析式为y=(x﹣a)2+a,∵点A n(n,n2)在抛物线y=(x﹣a)2+a上,∴n2=(n﹣a)2+a,解得:a=2n﹣1或a=0(舍去),∴M n的坐标为(2n﹣1,2n﹣1),∴M2020的坐标为(4039,4039).故答案为:(4039,4039).14.解:以OB为直径作圆E,连接AE、QE;∵y=x2+x﹣2的图象与x轴负半轴交于点A,与y轴负半轴交于点B,∴A(﹣2,0),B(0,﹣2),∴E(0,﹣1),∴AE=,∵PO是直径,∴∠PQO=90°,∴∠OQB=90°,∴Q在圆E上,在△AQE中,AQ≥AE﹣QE,∴当A、Q、E在一条直线上时,AQ取最小值,∴AQ=﹣1,故答案为﹣1.15.解:∵抛物线开口向下,∴a<0,∵抛物线的对称轴在y轴的右侧,∴a、b异号,∴b>0,∵抛物线与y轴的交点在x轴上方,∴c>0,∴abc<0,所以①错误;∵抛物线的对称轴为直线x=﹣,∴0<﹣<1,∴b<﹣2a,即2a+b<0,所以②正确;∵x=﹣1时,y>0,∴a﹣b+c>0,所以③错误;∴a+c>b,而b>0,∴a+c>0,所以④正确;∵抛物线与x轴有两个交点,∴△=b2﹣4ac>0,所以⑤正确;∵抛物线开口向下,在对称轴的右侧y随x的增大而减下,∴当x>1时,y随x的增大而减小,所以⑥正确.故选:②④⑤⑥.三.解答题(共5小题)16.解:(1)把(﹣1,0),(0,﹣3)分别代入y=x2+bx+c,得:.解得:b=﹣2,c=﹣3.故该二次函数解析式为:y=x2﹣2x﹣3;由于y=x2﹣2x﹣3=(x﹣1)2﹣4,则其顶点坐标是(1,﹣4);(2)由y=x2﹣2x﹣3知,C(0,﹣3).所以AC=4.∴S=AC•|y D|==8.△ACD∴△ACD的面积是8.17.解:(1)根据题意得:y=(30+x﹣20)(230﹣10x)=﹣10x2+130x+2300,自变量x的取值范围是:0<x≤10且x为正整数;(2)当y=2520时,得﹣10x2+130x+2300=2520,解得x1=2,x2=11(不合题意,舍去)当x=2时,30+x=32(元)答:每件文具的售价定为32元时,月销售利润恰为2520元.(3)根据题意得:y=﹣10x2+130x+2300=﹣10(x﹣6.5)2+2722.5,∵a=﹣10<0,∴当x=6.5时,y有最大值为2722.5,∵0<x≤10且x为正整数,∴当x=6时,30+x=36,y=2720(元),当x=7时,30+x=37,y=2720(元),答:每件文具的售价定为36元或37元时,每个月可获得最大利润,最大的月利润是2720元.18.解:(1)设y关于x的函数表达式为y=kx+b(k≠0)由题意得:解得:∴y关于x的函数表达式为y=﹣10x+200.(2)由题意得:w=(x﹣4)(﹣10x+200)=﹣10x2+240x﹣800=﹣10(x﹣12)2+640∵﹣10<0∴当x=12时,w有最大值640元.∴w关于x的函数表达式为w=﹣10x2+240x﹣800,单价为12元时利润最大,最大利润是640元.(3)由题意得:w=(x﹣4﹣a)(﹣10x+200)=﹣10x2+(240+10a)x﹣800二次函数的对称轴为:x=12+∵﹣10<0,当销售单价不超过14元时,利润随着x的增大而增大∴12+≥14∴a≥4∴a的最小值为4.19.解:(1)将点A坐标代入抛物线表达式并解得:m=﹣1,故抛物线的表达式为:y=﹣x2﹣2x+3…①,函数的对称轴为:x=﹣1,故点P(﹣1,4),故答案为:(﹣1,4);(2)①过点Q作y轴的平行线交AC于点N,如图1,将点A(﹣3,0)、C(0,3)的坐标代入一次函数表达式并解得:直线AC的表达式为:y=x+3,设点Q(x,﹣x2﹣2x+3),则点N(x,x+3),△QAC的面积S=QN×OA=×(﹣x2﹣2x+3﹣x﹣3)×3=﹣x2﹣x,∵﹣<0,故S有最大值为:;②如图2,设直线BQ交y轴于点H,过点H作HM⊥BC于点M,tan∠OCB==,设HM=BM=x,则CM=3x,BC=BM+CM=4x=,解得:x=,CH=x=,则点H(0,),同理可得:直线BH(Q)的表达式为:y=﹣x+…②,联立①②并解得:x=1(舍去)或﹣,故点Q(﹣,).20.解:(1)∵抛物线y=ax2+bx过A(4,0)、B(1,3)两点,∴,解得,即抛物线的解析式是y =﹣x 2+4x ;(2)∵y =﹣x 2+4x =﹣(x ﹣2)2+4,∴该函数的对称轴为直线x =2,∵B (1,3),点C 、B 关于抛物线的对称轴对称,∴点C 的坐标为(3,3),∵点A (4,0),点B (1,3),点C 的坐标为(3,3),∴△ABC 的面积是:=3;(3)设直线AB 的解析式为y =mx +n ,, 解得,∴直线AB 为y =﹣x +4,过P 点作PE ∥y 轴交AB 于点E ,P 点在抛物线y =﹣x 2+4x 的AB 段,设其坐标为(a ,﹣a 2+4a ),其中1<a <4,则点E 的坐标为(a ,﹣a +4),PE =(﹣a 2+4a )﹣(﹣a +4)=﹣a 2+5a ﹣4, S △ABP =S △PEB +S △PEA =×PE ×3=(﹣a 2+5a ﹣4)=,解得,a 1=2,a 2=3,∴点P 的坐标为(2,4)或(3,3),综上所述,当△ABP 的面积为3时,点P 的坐标为(2,4)或(3,3).。
陕西中考数学第24题二次函数专题整理
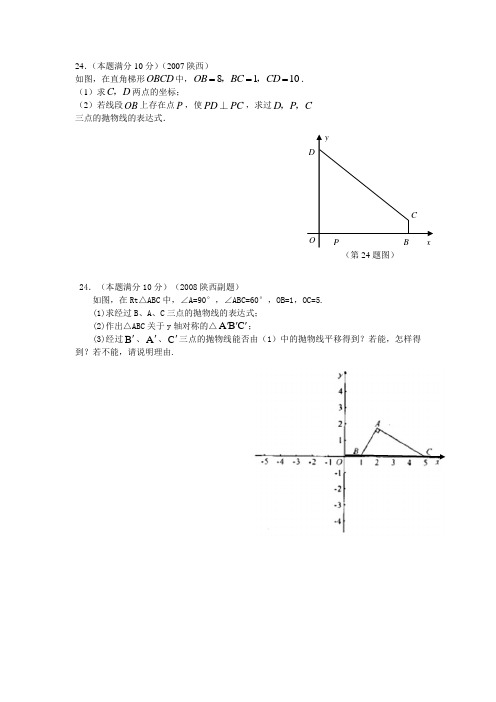
24.(本题满分10分)(2007陕西)如图,在直角梯形OBCD 中,8110OB BC CD ===,,. (1)求C D ,两点的坐标;(2)若线段OB 上存在点P ,使PD PC ⊥,求过D P C ,, 三点的抛物线的表达式.24.(本题满分10分)(2008陕西副题)如图,在Rt △ABC 中,∠A=90°,∠ABC=60°,OB=1,OC=5. (1)求经过B 、A 、C 三点的抛物线的表达式; (2)作出△ABC 关于y 轴对称的△C B A ''';(3)经过B '、A '、C '三点的抛物线能否由(1)中的抛物线平移得到?若能,怎样得到?若不能,请说明理由.DCB P O yx(第24题图)24、(本题满分10分)(2008陕西) 如图,矩形ABCD 的长、宽分别为32和1,且OB =1,点E (32,2),连接AE 、ED 。
(1)求经过A 、E 、D 三点的抛物线的表达式;(2)若以原点为位似中心,将五边形AEDCB 放大,使放大后的五边形的边长是原五边形对应边长的3倍,请在下图网格中画出放大后的五边形A ′E ′D ′C ′B ′;(3)经过A ′、E ′、D ′三点的抛物线能否由(1)中的抛物线平移得到?请说明理由。
24.(本题满分10分)(2009陕西副)如图,一条抛物线经过原点,且顶点B 的坐标(1,-1). (1)求这个抛物线的解析式;(2)设该抛物线与x 轴正半轴的交点为A ,求证:△OBA 为等腰直角三角形;(3)设该抛物线的对称轴与x 轴的交点为C ,请你在抛物线位于x 轴上方的图象上求两点E 、F ,使△ECF 为等腰直角三角形,且∠EOF=90°1 2 3 4 5 6 7AB CE DOxy16 4 2 3 57 (第24题图)24.(本题满分10分)(2009陕西)如图,在平面直角坐标系中,OB OA ⊥,且2OB OA =,点A 的坐标是(12)-,. (1)求点B 的坐标; (2)求过点A O B 、、的抛物线的表达式;(3)连接AB ,在(2)中的抛物线上求出点P ,使得ABP ABO S S =△△.24.(本题满分10分)(2010陕西副)如图,在平面直角坐标系中,△ABC 是直角三角形,且∠BAC=90°,∠ACB=30°,点A 的坐标为(0,3).(1)求点B 和点C 的坐标;(2)求经过A 、B 、C 三点的抛物线的表达式;(3)设点M 是(2)中抛物线的顶点,P 、Q 是抛物线上的两点,要使△MPQ 为等边三角形,求点P 、Q 的坐标.yOB Ax1 1(第24题图)(第24题图)24.(本题满分10分)(2009陕西)如图,在平面直角坐标系中,OB OA ⊥,且2OB OA =,点A 的坐标是(12)-,. (1)求点B 的坐标; (2)求过点A O B 、、的抛物线的表达式;(3)连接AB ,在(2)中的抛物线上求出点P ,使得ABP ABO S S =△△.24.(本题满分10分)(2010陕西副)如图,在平面直角坐标系中,△ABC 是直角三角形,且∠BAC=90°,∠ACB=30°,点A 的坐标为(0,3).(1)求点B 和点C 的坐标;(2)求经过A 、B 、C 三点的抛物线的表达式;(3)设点M 是(2)中抛物线的顶点,P 、Q 是抛物线上的两点,要使△MPQ 为等边三角形,求点P 、Q 的坐标.yOB Ax1 1(第24题图)(第24题图)(2010陕西)24.如图,在平面直角坐标系中,抛物线A (-1,0),B (3,0)C (0,-1)三点。
中考数学必考考点专题12二次函数含解析

专题12 二次函数1.二次函数的概念:一般地,自变量x 和因变量y 之间存在如下关系: y=ax 2+bx+c(a≠0,a 、b 、c 为常数),则称y 为x 的二次函数。
抛物线)0,,(2≠++=a c b a c bx ax y 是常数,叫做二次函数的一般式。
2.二次函数y=ax 2+bx+c(a ≠0)的图像与性质(1)对称轴:2b x a=-(2)顶点坐标:24(,)24b ac b a a-- (3)与y 轴交点坐标(0,c ) (4)增减性:当a>0时,对称轴左边,y 随x 增大而减小;对称轴右边,y 随x 增大而增大; 当a<0时,对称轴左边,y 随x 增大而增大;对称轴右边,y 随x 增大而减小。
3.二次函数的解析式三种形式。
(1)一般式 y=ax 2+bx+c(a ≠0).已知图像上三点或三对x 、y 的值,通常选择一般式. (2)顶点式 2()y a x h k =-+224()24b ac b y a x a a-=-+ 已知图像的顶点或对称轴,通常选择顶点式。
(3)交点式 12()()y a x x x x =--专题知识回顾已知图像与x 轴的交点坐标1x 、2x ,通常选用交点式。
4.根据图像判断a,b,c 的符号(1)a 确定开口方向 :当a>0时,抛物线的开口向上;当a<0时,抛物线的开口向下。
(2)b ——对称轴与a 左同右异。
(3)抛物线与y 轴交点坐标(0,c ) 5.二次函数与一元二次方程的关系抛物线y=ax 2+bx+c 与x 轴交点的横坐标x 1, x 2 是一元二次方程ax 2+bx+c=0(a ≠0)的根。
抛物线y=ax 2+bx+c ,当y=0时,抛物线便转化为一元二次方程ax 2+bx+c=024b ac ->0时,一元二次方程有两个不相等的实根,二次函数图像与x 轴有两个交点; 24b ac -=0时,一元二次方程有两个相等的实根,二次函数图像与x 轴有一个交点; 24b ac -<0时,一元二次方程有不等的实根,二次函数图像与x 轴没有交点。
陕西省中考数学题型分析

陕西省中考数学题型分析一、结构:一共25道题目 二、使用题型:选择题(10),填空题(6),解答题(9) 三、知识比例:数与代数、图形与几何、概率与统计分别 占42.5%,42.5%,15% 四、总体难度系数:不低于0.65五、试题比例:容易题:比较容易题:较难题:难题 =4:3:2:1(48分、36分、24分、12分)选择题 第1题:考点:四大概念——倒数、绝对值、相反数、数轴 成因:数学系的第一次扩充——加入了负数(意义) (06)1.下列计算正确的是A .123=+-B .22-=-C .9)3(3-=-⨯D .1120=-(07)1.2-的相反数为 A .2B .2-C .12 D .12- (08)1.零上13℃记作+13℃,零下2℃可记作 A .2 B .-2 C . 2℃ D .-2℃ (09)1.12-的倒数是A.2 B .2- C .12 D .12- (10)1 . 13-= A. 3 B. -3 C. 13 D. -13(11)1.23-的倒数为( ) A .32- B .32 C .23 D .23-(12)1.如果零上5 ℃记做+5 ℃,那么零下7 ℃可记作 A .-7 ℃ B .+7 ℃ C .+12 ℃ D .-12 ℃ (13)1. 下列四个数中最小的数是()A .2- B.0 C.31- D.5 每题考点及成因第2题选择题 第2题:考点:简单几何体的认识 成因:平面几何的入门知识(2011)2、下面四个几何体中,同一个几何体的主视图和俯视图 相同的共有( )A 、1个B 、2个C 、3个D 、4个(2012)2.如图,是由三个相同的小正方体组成的几何体,该几何体 的左视图是( )(2013)2.如图,下面的几何体是由一个圆柱和一个长方体组成的, 则它的俯视图是( )第3题考点:单项式或等式和不等式基本性质及其简单应用成因:数系扩充后字母体系的生成,初中学段的重要标志备考:同底数幂的乘法、同底数幂的除法、积的乘方、幂的幂运算(07)11.计算:221(3)3x y xy ⎛⎫-=⎪⎝⎭. (08)12.计算:232a ()·4a = 。
中考数学真题二次函数专项练习(带答案)

中考数学真题二次函数一、选择题1.已知点M(−4,a−2) N(−2,a) P(2,a)在同一个函数图象上.则这个函数图象可能是()A.B.C.D.2.抛物线y=ax2−a(a≠0)与直线y=kx交于A(x1,y1).B(x2,y2)两点.若x1+x2<0.则直线y= ax+k一定经过().A.第一、二象限B.第二、三象限C.第三、四象限D.第一、四象限3.设二次函数y=a(x−m)(x−m−k)(a>0,m,k是实数).则()A.当k=2时.函数y的最小值为−a B.当k=2时.函数y的最小值为−2aC.当k=4时.函数y的最小值为−a D.当k=4时.函数y的最小值为−2a4.已知二次函数y=ax2−(3a+1)x+3(a≠0).下列说法正确的是()A.点(1,2)在该函数的图象上B.当a=1且−1≤x≤3时.0≤y≤8C.该函数的图象与x轴一定有交点D.当a>0时.该函数图象的对称轴一定在直线x=32的左侧5.一个球从地面竖直向上弹起时的速度为10米/秒.经过t(秒)时球距离地面的高度h(米)适用公式h=10t-5t2.那么球弹起后又回到地面所花的时间t(秒)是()A.5B.10C.1D.2二、填空题6.在平面直角坐标系xOy中.一个图形上的点都在一边平行于x轴的矩形内部(包括边界).这些矩形中面积最小的矩形称为该图形的关联矩形.例如:如图.函数y=(x−2)2(0⩽x⩽3)的图象(抛物线中的实线部分).它的关联矩形为矩形OABC.若二次函数y=14x2+bx+c(0⩽x⩽3)图象的关联矩形恰好也是矩形OABC.则b=.三、解答题7.设二次函数y=ax2+bx+1.(a≠0.b是实数).已知函数值y和自变量x的部分对应取值如下表所示:(1)若m=4.求二次函数的表达式;(2)写出一个符合条件的x的取值范围.使得y随x的增大而减小.(3)若在m、n、p这三个实数中.只有一个是正数.求a的取值范围.8.如图.已知二次函数y=x2+bx+c图象经过点A(1,−2)和B(0,−5).(1)求该二次函数的表达式及图象的顶点坐标.(2)当y≤−2时.请根据图象直接写出x的取值范围.9.已知二次函数y=−x2+bx+c.(1)当b=4,c=3时.①求该函数图象的顶点坐标.②当−1⩽x⩽3时.求y的取值范围.(2)当x⩽0时.y的最大值为2;当x>0时.y的最大值为3.求二次函数的表达式.10.在二次函数y=x2−2tx+3(t>0)中.(1)若它的图象过点(2,1).则t的值为多少?(2)当0≤x≤3时.y的最小值为−2.求出t的值:(3)如果A(m−2,a),B(4,b),C(m,a)都在这个二次函数的图象上.且a<b<3.求m的取值范围。
中考数学二次函数填空题(难度题)含答案

《二次函数》——难度题1、从如图所示的二次函数y = ax 2+bx +c (a ≠0)的图象中,得出了下面五条信息:①ab > 0 ②a +b +c < 0 ③b +2c > 0 ④a -2b +4c > 0 ⑤32a b . 其中正确信息的序号是 ① ② ③ ④ ⑤2、如图,二次函数2y ax bx c (0≠a )的图象的顶点在第一象限,且过点(0,1)和(-1,0),下列结论:①0ab,②24b a ,③02a b c ,④01b ,⑤当1x时,0y .其中正确结论的序号是 ①②③④o x y-113、已知二次函数y =ax 2+bx+c (a ≠0)的图象如图所示,给出以下结论:①b 2>4ac ;②abc >0;③2a ﹣b =0;④8a+c <0;⑤9a+3b+c <0,其中结论正确的是①②⑤ .(填正确结论的序号)4、二次函数y= ax 2+bx+c 的图象如图所示,给出下列结论:①2a+b >0;②b >a >c ;③若﹣1<m <n <1,则m+n <a b ;④3|a |+|c |<2|b |. 其中正确的结论是 ①③④ (写出你认为正确的所有结论序号).5、二次函数y=ax 2+bx+c 图象如图,下列正确的序号为 ①③④ ①bc >0;②2a ﹣3c <0;③2a+b >0;④ax 2+bx+c =0有两个解x 1,x 2,x 1>0, x 2<0;⑤a+b+c >0;⑥当x >1时,y 随x 增大而减小.【解】①∵抛物线开口向上,∴a >0,∵对称轴在y 轴右侧,∴a ,b 异号即b <0, ∵抛物线与y 轴的交点在负半轴,∴c <0,∴bc >0,故①正确;②∵a >0,c <0,∴2a ﹣3c >0,故②错误;③∵对称轴x =﹣<1,a >0,∴﹣b <2a ,∴2a+b >0,故③正确;④由图形可知二次函数y=ax 2+bx+c 与x 轴的两个交点分别在原点的左右两侧, 即方程ax 2+bx+c=0有两个解x 1,x 2,当x 1>x 2时,x 1>0,x 2<0,故④正确; ⑤由图形可知x=1时,y=a+b+c <0,故⑤错误;⑥∵a >0,对称轴x=1,∴当x >1时,y 随x 增大而增大,故⑥错误.综上所述,正确的结论是①③④6、如图,二次函数y=ax 2+bx+c (a >0)图象的顶点为D ,其图象与x 轴的交点A 、B 的横坐标分别为﹣1,3.与y 轴负半轴交于点C ,在下面五个结论中:①2a ﹣b =0;②a+b+c >0;③c =﹣3a ;④只有当a =21时,△ABD 是等腰直角三角形;⑤使△ACB 为等腰三角形的a 值可以有四个.其中正确的结论是 ③④ .(只填序号)7、二次函数y=ax 2+bx+c (a ≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x =2,下列结论:①4a+b =0;②9a+c >3b ;③8a +7b +2c >0;④当x >﹣1时,y 的值随x 值的增大而增大.其中正确的结论有( B )A.1个B.2个C.3个D.4个8、(2014年四川)已知二次函数y=ax2+bx+c的图象如图,则下列叙述正确的是()A.a bc<0B.﹣3a+c<0 C.b2﹣4ac≥0D.将该函数图象向左平移2个单位后所得到抛物线的解析式为y=ax2+c9、二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的个数是(B)A.4个B. 3个C.2个D.1个10、二次函数bx x y +=2的图象如图,对称轴为1=x .若关于x 的一元二次方程02=-+t bx x (t 为实数)在41<<-x 的范围内有解,则t 的取值范围是 81<≤-t11、如图,已知抛物线y 1=-2x 2+2,直线y 2=2x +2,当x 任取一值时,x 对应的函数值分别为y 1、y 2.若y 1≠y 2,取y 1、y 2中的较小值记为M ;若y 1=y 2,记M = y 1=y 2.例如:当x =1时,y 1=0, y 2=4, y 1<y 2,此时M = 0. 下列判断:①当x >0时,y 1>y 2; ②当x <0时,x 值越大,M 值越小; ③使得M 大于2的x 值不存在; ④使得M = 1的x 值是 21-或22.其中正确的是 ③④12、二次函数y =ax 2+bx +c (a ≠0)图象如图,下列结论:①abc >0; ②3a +c <0; ③当m ≠1时,a +b >am 2+bm ;④a ﹣b +c >0; ⑤若ax 12+bx 1=ax 22+bx 2,且x 1≠x 2,则x 1+x 2=2.其中正确的有 xy Oy 2 y 1②③⑤( 填序号)13、如图,一条抛物线与x轴相交于A、B两点,其顶点P在折线C-D-E上移动,若点C、D、E的坐标分别为(-1,4)、(3,4)、(3,1),点B的横坐标的最小值为1,则点A的横坐标的最大值为 214、如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3…A n,….将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:①抛物线的顶点M1,M2,M3,…M n,…都在直线L:y = x上;②抛物线依次经过点A1,A2,A3…A n,….则顶点M2014的坐标为(4027,4027).2 1 - 1 O xy15、如图,抛物线y =ax 2+bx +c 的对称轴是x = 1 3,小亮通过观察得出了下面四条信息:①c <0, ②abc <0, ③a -b +c >0, ④2a -3b =0.你认为其中正确的有____①③ ____(把正确的番号填在横线上)16、二次函数y=x 2+bx 的图象如图,对称轴为直线x =1,若关于x 的一元二次方程x 2+bx ﹣t =0(t 为实数)在﹣3≤x <4的范围内有解,则t 的取值范围是﹣1≤t ≤1517、已知抛物线y =-x 2+6x -5与x 轴交于点A 、B (A 在B 的左侧),顶点为C ,CD ⊥y 轴于D ,P 是x 轴上方抛物线对称轴上一点,且S △P AD =2S △PBC ,则点P 的坐标为_)8,3()58,3(或____【方法】设点,将面积与坐标建立等量关系,用差量法求三角形面积18、已知抛物线y =ax 2+bx +c 经过A (-1,0)、B (3,0)、C (0,3)三点,顶点为D ,点P 是抛物线的对称轴上一点,以点P 为圆心的圆经过A 、B 两点,且与直线CD 相切,则点P 的坐标为_____)462,1()462,1(---或____【方法】设点坐标;三角函数;勾股定理19、已知抛物线y =x 2-2mx +4m -8的顶点为A .(1)若以A 为一个顶点作该抛物线的内接正三角形ABC (B 、C 两点都在拋物线上),则△ABC 的面积为____33______;(2)若抛物线y =x 2-2mx +4m -8与x 轴交点的横坐标均为整数,则整数m 的值为____2_____【方法】利用特殊几何形的长度角度关系,设点坐标;将点的坐标代入抛物线方程,建立方程求解。
陕西省中考数学历年(2016-2022年)真题分类汇编 二次函数

陕西省中考数学历年(2016-2022年)真题分类汇编二次函数一、单选题(共7题;共14分)1.(2分)(2016·陕西)已知抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,将这条抛物线的顶点记为C,连接AC、BC,则tan∠CAB的值为()A.12B.√55C.2√55D.2【答案】D【解析】【解答】解:令y=0,则﹣x2﹣2x+3=0,解得x=﹣3或1,不妨设A(﹣3,0),B(1,0),∵y=﹣x2﹣2x+3=﹣(x+1)2+4,∴顶点C(﹣1,4),如图所示,作CD∠AB于D.在Rt∠ACD中,tan∠CAD= CDAD=42=2,故答案为D.【分析】先求出A、B、C坐标,作CD∠AB于D,根据tan∠ACD= CDAD即可计算.本题考查二次函数与x轴交点坐标,锐角三角函数的定义,解题的关键是熟练掌握求抛物线与x轴交点坐标的方法,记住锐角三角函数的定义,属于中考常考题型.2.(2分)(2017·陕西)已知抛物线y=x2﹣2mx﹣4(m>0)的顶点M关于坐标原点O的对称点为M′,若点M′在这条抛物线上,则点M的坐标为()A.(1,﹣5)B.(3,﹣13)C.(2,﹣8)D.(4,﹣20)【答案】C【解析】【解答】y=x2﹣2mx﹣4=x2﹣2mx+m2﹣m2﹣4=(x﹣m)2﹣m2﹣4.∴点M(m,﹣m2﹣4).∴点M′(﹣m,m2+4).∴m2+2m2﹣4=m2+4.解得m=±2.∵m>0,∴m=2.∴M(2,﹣8).故答案为:C.【分析】将二次函数的解析式化成顶点式:y=x2﹣2mx﹣4=x2﹣2mx+m2﹣m2﹣4=(x﹣m)2﹣m2﹣4从而得出点M(m,﹣m2﹣4).由已知条件得出点M′(﹣m,m2+4);代入解析式求出m=±2;由m >0,得出M坐标.3.(2分)(2018·陕西)对于抛物线y=ax2+(2a-1)x+a-3,当x=1时,y>0,则这条抛物线的顶点一定在()A.第一象限B.第二象限C.第三象限D.第四象限【答案】C【解析】【解答】由题意得:a+(2a-1)+a-3>0,解得:a>1,∴2a-1>0,∴−2a−12a<0,4a(a−3)−(2a−1)24a=−8a+14a<0,∴抛物线的顶点在第三象限,故答案为:C.【分析】根据抛物线y=ax2+(2a-1)x+a-3,当x=1时,y>0,得出关于a不等式,求解得出a 的取值范围,然后根据抛物线的顶点坐标公式判断出抛物线顶点横纵坐标的正负,即可得出答案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2006陕西)9.如图,抛物线的函数表达式是( ) A .22y x x =-+
B .22y x x =++
C .22y x x =--+
D .22y x x =-++
(2007陕西)8.抛物线247y x x =--的顶点坐标是( ) A .(211)-,
B .(27)-,
C .(211),
D .(23)-,
(2008陕西)10、已知二次函数2y ax bx c =++(其中a >0,b >0,c <0), 关于这个二次函数的图象有如下说法:
①图象的开口一定向上;②图象的顶点一定在第四象限; ③图象与x 轴的交点至少有一个在y 轴的右侧。
以上说法正确的个数为 ( ) A .0 B .1 C .2 D .3
(2008陕西副)10.若二次函数c bx ax y 2++=的图象如图所示,则a 、b 、c 间的大小关系正确的是 ( )
A.a >b >c
B.a <b <c
C.a >c >b
D.a <c <b
(2009陕西)10.根据下表中的二次函数2y ax bx c =++的自变量x 与函数y 的对应值,可判断该二次函数的图象与x 轴( ).
x … 1-
0 1 2 … y
… 1-
7
4
- 2-
74
- …
A .只有一个交点
B .有两个交点,且它们分别在y 轴两侧
C .有两个交点,且它们均在y 轴同侧
D .无交点
(第10
题
(第9题
(2009陕西副)9.将抛物线y=x 2-4x+3平移,使它平移后的顶点为(-2,4),则需将该抛物线 ( )
A. 先向右平移4个单位,再向上平移5个单位
B. 先向右平移4个单位,再向下平移5个单位
C. 先向左平移4个单位,再向上平移5个单位
D. 先向左平移4个单位,再向下平移5个单位
(2010陕西)10.将抛物线C :y=x ²+3x-10,将抛物线C 平移到C ˋ。
若两条抛物线C,C ˋ关于直线x=1对称,则下列平移方法中正确的是 ( )
A 将抛物线C 向右平移5
2
个单位 B 将抛物线C 向右平移3个单位
C 将抛物线C 向右平移5个单位
D 将抛物线C 向右平移6个单位
(2010陕西副)10. 若将抛物线C :1x 4-x 2y 2+=向右平移3个单位得到抛物线C ',则抛物线C 与C '一定关于某条直线对称,这条直线是 ( )
A. x=23
B. x=2
C. x=2
5
D. x=3
(2011陕西)10、若二次函数c x x y +-=62的图像过)321,23(),,2(),,1(Y C Y B Y A +-,则
321,,y y y 的大小关系正确的是
A 、321y y y >>
B 、231y y y >>
C 、312y y y >>
D 、213y y y >>
(2011陕西副)10. 如果两个不同的二次函数的图象相交,那么它们的交点最多有 ( )
A. 1个
B. 2个
C. 3个
D. 4个
(2012陕西)10.在平面直角坐标系中,将抛物线62--=x x y 向上(下)或向左(右)平移了m 个单位,使平移后的抛物线恰好经过原点,则m 的最小值为( )
A .1
B .2
C .3
D .6
(2012陕西副)8. 如果M (x 1,y 1),N (x 2,y 2)是一次函数38y x =-图象上的两点,如果x 1+x 2=-3,那么y 1+y 2=( )
A. -25
B. -17
C. -9
D. 1
(2013陕西)10.已知两点A(-5,y1),B(3,y2)均在抛物线y=ax2+bx+c(a≠0)上,点C(x0,y0)是该抛物线的顶点,若y1>y2≥y0,则x0的取值范围是()
A. x0>-5
B. x0>-1
C.-5<x0<-1
D.-2<x0<3
(2013陕西副)10.若一个二次函数y=ax.2-4ax.+3(a≠0)的图象经过两点A(m+2,y1)、B(2-m,y
2
),则下列关系正确的是()
A.y
1
>y2 B.y1<y2 C.y1=y2 D.y1≥y2
(2014陕西)10. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
A. c>-1
B. b>0
C. 2a+b≠0
D. 9a+c>3b
第10题图
(2014陕西副)10. 若a,B为非零实数,则函数y=ax+B与y=ax2+Bx在同一坐标系中的图象大致是()
(2015陕西)10. 下列关于二次函数y=ax2-2ax+1(a>1)的图象与x轴交点的判断,正确的是( )
A. 没有交点
B. 只有一个交点,且它位于y轴右侧
C. 有两个交点,且它们均位于y轴左侧
D. 有两个交点,且它们均位于y轴右侧
(2015陕西副)10.在平面直角坐标系中,有两条抛物线关于x轴对称,且它们的顶点相距10个单位长度.若其中一条抛物线的函数表达式为y=x2+6x+m,则m的值是()
A.4或14
B.4或-14
C.-4或14
D.-4或-14
(2016陕西)10. 已知抛物线y=-x2-2x+3与x轴交于A、B两点,将这条抛物线的顶点记为C,连接AC、BC,则tan∠CAB的值为( )
A.1
2
B.
5
5
C.
25
5
D. 2
(2016陕西副)10.将抛物线M:y=-1
3
x2+2向左平移2个单位,再向上平移1个单位,得
到抛物线M′.若抛物线M′与x轴交于A、B两点,M′的顶点记为C,则∠ACB=()
A.45°
B.60°
C.90°
D.120°
(2017陕西)10. 已知抛物线y=x2-2mx-4(m>0)的顶点M关于坐标原点O的对称点为M′.若点M′在这条抛物线上,则点M的坐标为( )
A.(1,-5)
B. (3,-13)
C. (2,-8)
D. (4,-20)
(2017陕西副)10. 已知抛物线y=x2+bx+c的对称轴为x=1,且它与x轴交于A、B两点.若AB的长是6,则该抛物线的顶点坐标为
A. (1,9)
B. (1,8)
C. (1,-9)
D. (1,-8)
(2018陕西)10. 对于抛物线y=ax2+(2a-1)x+a-3,当x=1时,y>0,则这条抛物线的顶点一定在( )
A.第一象限
B. 第二象限
C. 第三象限
D. 第四象限
(2018陕西副)10. 已知抛物线y=x2+(m+1)x+m,当x=1时,y>0,且当x<-2时,y 的值随x值的增大而减小,则m的取值范围是
A.m>-1 B.m<3 C.-1<m≤3 D.3<m≤4
(2019陕西)10.在同一平面直角坐标系中,若抛物线与
关于y轴对称,则符合条件的m,n的值为
A.,
B. ,
C. ,
D. ,
(2019陕西副)10.在平面直角坐标系中,将抛物线向右平移4个单位长度,平移后的抛物线与y轴的交点为,则平移后的抛物线的对称轴为
A. B. C. D.
(2020陕西)在平面直角坐标系中,将抛物线沿y轴向下平移3个单位.则平移后得到的抛物线的顶点一定在
A.第一象限
B. 第二象限
C. 第三象限
D. 第四象限
(2020陕西副)在同一直角坐标系中,若抛物线y=mx2+2x-n与y=-6x2-2x+m-n关于x轴对称,则m,n的值为()
A.m=-6,n=-3
B.m=-6,n=3
C.m=6,n=-3
D.m=6,n=3。
