六年级数学总复习资料
小学数学六年级总复习资料

人教版小学数学总复习资料一.长度单位:1千米=1公里1千米=1000米1米=10分米1分米=10厘米1米=100厘米1厘米=10毫米1米=1000毫米二.面积单位和地积单位:1平方千米=100公顷1平方千米=1平方公里1平方千米=1000000平方米1公顷=10000平方米1平方米=100平方分米1平方分米=100平方厘米1平方米=10000平方厘米三.体积单位和容积单位:1立方米=1000立方分米1立方分米=1000立方厘米1升=1立方分米1毫升=1立方厘米1升=1000毫升1方=1立方米四.质量单位:1吨=1000千克1千克=1000克1克=1000毫克1公斤=2斤1斤=500克1两=50克五.钱的单位:1元=10角1角=10分1元=100分五.判断:任何两个长度单位之间的进率都是10.(×)任何两个面积单位之间的进率都是100.(×)。
任何两个体积单位之间的进率都是1000(×)关于时间的知识1.平年全年有365天,闰年全年有366天。
平年上半年有181天,闰年上半年有182天,任意一年的下半年都有184天。
平年的第一个季度有90天,闰年的第一个季度有91天。
平年全年有52个星期余1天,闰年全年有52个星期余2天。
平年的二月有28天,闰年的二月有29天。
2.判断平年和闰年的方法:公历年份是4的倍数,一般都是闰年;但公历年份是整百数的,必须是400的倍数,才是闰年。
3.大月的歌诀:一、三、五、七、八、十、腊,三十一天永不差。
四月、六月、九月、十一月,每个月都有30天,被称为小月。
一年有七个大月,四个小月。
4.一年有12个月,一年分为4个季度,一个季度有3个月,一个月分为上旬、中旬和下旬。
上旬和中旬都有10天,下旬可能有8天、9天、10天或11天。
5.时间换算:1星期=7天1天=24小时1小时=60分1分=60秒1时=3600秒一刻钟=15分半小时=30分 6. 求在一天里经过的时间,先用24小时计时法表示时间,然后用结束的时间—开始的时间。
小学六年级(小升初)数学总复习知识梳理+练习+答案-整数和小数的认识(部分有答案)
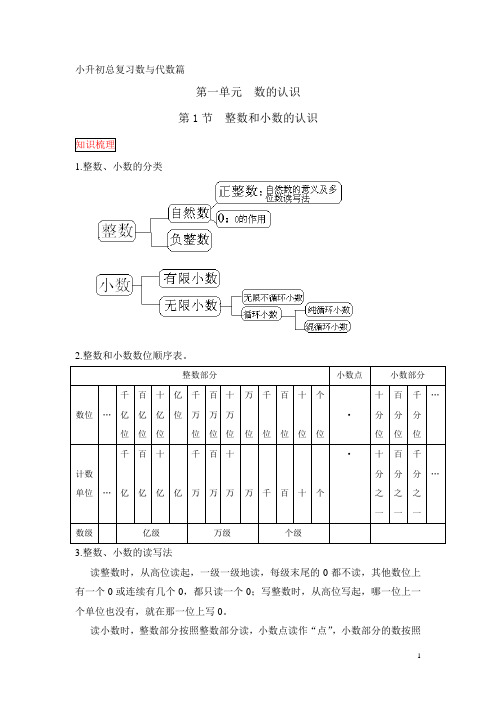
小升初总复习数与代数篇第一单元数的认识第1节整数和小数的认识知识梳理1.整数、小数的分类2.整数和小数数位顺序表。
整数部分小数点小数部分数位…千亿位百亿位十亿位亿位千万位百万位十万位万位千位百位十位个位·十分位百分位千分位…计数单位…千亿百亿十亿亿千万百万十万万千百十个·十分之一百分之一千分之一…数级亿级万级个级3.整数、小数的读写法读整数时,从高位读起,一级一级地读,每级末尾的0都不读,其他数位上有一个0或连续有几个0,都只读一个0;写整数时,从高位写起,哪一位上一个单位也没有,就在那一位上写0。
读小数时,整数部分按照整数部分读,小数点读作“点”,小数部分的数按照顺序依次读出每一位上的数;写小数时,整数部分按整数部分写,小数点写在个位右下角,然后依次写出小数部分每一个数位上的数字。
4.小数的基本性质: 在小数的末尾添上“0”或者去掉“0”,小数的大小不变。
5.大小比较:整数比大小,先看位数,位数多的数大;位数相同,从最高位看起,相同数位上的数大的那个数大;小数比大小,先比整数部分,整数部分大的这个数就大,整数部分相同的,比小数部分第一位,第一位大的这个数大,以此类推。
6.改写和省略把一个较大的数改写成以“万”或“亿”作单位,改写后的数是准确的数;把一个数根据需要省略某一位后面的尾数,省略后的数是一个近似数。
7. 小数点位置移动引起小数大小变化:小数点向右移动一位、两位、三位……原来的数就扩大到它的10倍、100倍、1000倍……反之,小数点向左移动一位、两位、三位……原来的数就缩小到它的101、1001、10001……【例1】阅读下面内容,回答问题。
2011年11月,在我国经济快速增长的拉动下,我国汽油生产总量为6899000吨,我国柴油生产总量为14132000吨,发电量达37130000万千瓦时。
(1)2011年11月我国汽油生产总量,读作:( )吨,改写成以“万吨”作单位的数是( )万吨。
小学六年级数学总复习知识考点汇总

要精心设计练习题:
甲、乙两数的和是162.8,乙数的小数点向右移 动一位就等于甲数,甲是( ),乙是( ) 。
通过此类题型,我们可以复习的知识点有: 小数点位置移动引起小数大小变化的知识。
要精心设计练习题:
将
19 27
的分子和分母减去同一个数后得
5 9
ቤተ መጻሕፍቲ ባይዱ
,减
去的这个数是( )。
通过此类题型,我们可以复习的知识点有: 分数的基本性质,约分通分的相关知识
分析余下
1、一根铁丝,第一次用去全长的1/4,第二次用去 余下的1/3,还剩60米,这根铁丝长多少米? 2、一桶油,第一次用去2.1千克,第二次用去余下 的1/4,还剩36千克,这桶油有多少千克? 3、一根铁丝,第一次用去全长的1/3多5米,第二次 用去余下的1/5少10米,这时还剩下18米,这根铁丝 长多少米?
⑴、质数与合数的辨别 ⑵ 、奇数与偶数的辨别
要精心设计练习题:
如果A=2×3×7,B=3×5×7,则A和B的最大公约数是( ), 最小公倍数是( )。
如果A=2×2×3×y,B=2×3×5×y,且A、B的最大公因数是42,那么y= ( )。
如果A=2×2×3×y,B=2×3×y×7,且A、B的最小公倍数是420,那么y=( )。
精心设计练习题:
(1)学校去年种桔树a棵,今年比去年的2倍多6棵。
今年种( )棵
(2)商店原有洗衣机 a台,现在又运进30台,现在共 有洗衣机( )台
(3)甲乙两人共同制造一批零件。甲制造a个,乙每小时制造b个,甲乙工 作了4.5小时,两人就完成了任务。这批零件共( )个。
(4)李红a天看了60页书,照这样计算,看完这本书需要b天,这本书共(
六年级数学总复习资料全

“数学总复习”复习资料(一)整数和小数1、整数和自然数像…,-3,-2,-1,0,1,2,3,…这样的数统称为(整数)。
整数的个数是(无限)的。
数物体的时候,用来表示物体个数的0,1,2,3…叫做(自然数)。
自然数整数的(一部分)。
(“1”)是自然数的单位。
最小的自然数是( 0 )。
2、小数 小数表示的就是十分之几,百分之几,千分之几……的数,一位小数可表示为十分之几的数,两位小数可表示为百分之几的数,三位小数可表示为千分之几的数 ……熟记: 51=0.2 52= 0.4 53= 0.6 54=0.8 41=0.25 43= 0.75 81= 0.125 83=0.375 85=0.625 87=0.875 小数点右边第一位是(十分位),计数单位是(十分之一);第二位是(百分位),计数单位是(百分之一)…… 小数部分有几个数位,就叫做几位小数。
如3.305是( 三 )位小数3、整数、小数的读法和写法: 读整数时注意先分级再读数。
28302006000 读作: 读小数时注意小数部分顺次读出每个数位上的数。
27.036 读作: 写数时注意写好后,一定要读一读仔细校对。
五亿零8千 写作: 三百八十点零三六 写作: 为了读写方便,常常把较大的数改写成用“万”或“亿”作单位的数。
如只要求“改写”,结果应是准确数。
768000000 =( )亿如要求“省略”万(亿)后面的尾数,结果应是近似数。
768000000≈( )亿4、小数的性质:小数的末尾添上0或者去掉0,小数的大小不变.5、小数点向右(左)移动一位、两位、三位……原来的数就扩大(缩小)10倍、100倍、1000倍……6、正数、负数0既不是正数也不是负数,0是正数和负数的分界点。
负数<0<正数 两个负数比较,负号后面的数越大这个数反而越小。
-6.8<-0.4 -2>-10(二)因数和倍数1、因数和倍数一个数的最小因数是1,最大的因数是它本身。
小学数学六年级总复习资料知识汇总

六年级数学总复习知识汇总数的意义1。
整数的含义:像-2,-1,0,1,2,3……这样的数统称整数.整数的个数是无限的。
没有最小的整数,也没有最大的整数。
自然数是整数的一部分。
2。
自然数的含义:在数物体个数的时候,用来表示物体个数的1,2,3,……叫做自然数。
一个物体也没有用0表示,自然数的个数是无限的,最小的自然数是0,没有最大的自然数。
(1)一个自然数有两方面的意义:一是表示事物得多少,称为基数;二是表示事物的次序,称为序数。
(2)0的含义:0表示一个物体也没有;表示正、负数的分界;表示起点(如0刻度);计数时0起占位作用。
(3)自然数的基本单位:任何非“0”自然数都是由若干个“1"组成的,所以“1”是自然数最基本的单位。
3。
正数和负数的含义:像1,+2,3,……这样的数叫做整数;像—3,-2,—1,……这样的数叫做负数.自然数是等于或大于0的整数,也可以说是不小于0的整数,即非负整数。
4.分数的含义:把单位“1”平均分成若干份,表示这样的一份或几份的数叫做分数。
(1)分数单位:把单位“1"平均分成若干份,表示这样一份的数就是这个分数的分数单位。
一个分数的分母是几,它的分数单位就是几分之一;分子是几,它就有几个这样的分数单位。
(注意:带分数只有化成假分数后,它的分子才能是这个带分数中含有分数单位的个数。
)(2)分数的分类:分数可以分为真分数和假分数。
真分数:分子比分母的小分数叫做真分数。
真分数小于1。
假分数:分子比分母大或分子和分母相等的分数叫做假分数。
假分数大于或者等于1。
带分数实际上就是大于1的假分数的另一种表示形式.(3)分数和除法的联系:分数的分子就是除法中的被除数,分母就是除法中的除数。
分数和比的联系:分数的分子就是比的前项,分数的分母就是比的后项。
分数和小数的联系:小数实际上就是分母是10、100、1000……的分数.(4)最简分数:分子与分母互质的分数叫做最简分数.(5)分数的基本性质:分数的分子和分母同时乘或除以相同的数(零除外),分数的大小不变。
小学数学六年级总复习资料归纳

基本概念一、整数和小数1、整数:像…,-3,-2,-1,0,1,2,3,…这样的数叫做整数。
自然数和0都是整数。
2、自然数:我们在数物体的时候,用来表示物体个数的1,2,3……叫做自然数。
一个物体也没有,用0表示。
0也是自然数。
3、小数:把整数1平均分成10份、100份、1000份…… 得到的十分之几、百分之几、千分之几…… 可以用小数表示。
一位小数表示十分之几,两位小数表示百分之几,三位小数表示千分之几……一个小数由整数部分、小数部分和小数点组成。
【小数的性质:在小数的末尾添上零或者去掉零,小数的大小不变。
】4、小数的分类纯小数:整数部分是零的小数,叫做纯小数。
例如: 0.25 、 0.368 都是纯小数。
带小数:整数部分不是零的小数,叫做带小数。
(也叫混小数) 例如: 3.25 , 5.26 都是带小数。
有限小数:小数部分的数位是有限的小数,叫做有限小数。
例如: 41.7 , 25.3 , 0.23 都是有限小数。
无限小数:小数部分的数位是无限的小数,叫做无限小数。
例如: 4.33 ……,3.1415926 ……无限不循环小数:一个数的小数部分,数字排列无规律且位数无限,这样的小数叫做无限不循环小数。
例如:π 循环小数:一个数的小数部分,有一个数字或者几个数字依次不断重复出现,这个数叫做循环小数。
例如: 3.555 …… 0.0333 …… 12.109109 …… 【循环小数一定是无限小数。
(√)】一个循环小数的小数部分,依次不断重复出现的数字叫做这个循环小数的循环节。
例如: 3.99 ……的循环节是“ 9 ” , 0.5454 ……的循环节是“ 54 ” 。
写循环小数的时候,为了简便,小数的循环部分只需写出一个循环节,并在这个循环节的首、末位数字上各点一个圆点。
如果循环节只有一个数字,就只在它的上面点一个点。
例如: 3.777 …… 简写作3.7• ,0.5302302 …… 简写作0.5302••。
六年级数学总复习知识点整理(完整版)

六年级数学总复习知识点整理(完整版)很快就小升初了,数学应该怎样复习呢?小学数学下面整理了六年级数学总复习知识点整理,供你参考。
六年级数学总复习知识点整理第一章数和数的运算一概念1 整数的意义自然数和0都是整数。
2 自然数我们在数物体的时候,用来表示物体个数的1,2,3 叫做自然数。
一个物体也没有,用0表示。
0也是自然数。
3计数单位一(个)、十、百、千、万、十万、百万、千万、亿都是计数单位。
每相邻两个计数单位之间的进率都是10。
这样的计数法叫做十进制计数法。
4 数位计数单位按照一定的顺序排列起来,它们所占的位置叫做数位。
5数的整除整数a除以整数b(b 0),除得的商是整数而没有余数,我们就说a能被b整除,或者说b能整除a 。
如果数a能被数b(b 0)整除,a就叫做b的倍数,b就叫做a 的约数(或a的因数)。
倍数和约数是相互依存的。
因为35能被7整除,所以35是7的倍数,7是35的约数。
一个数的约数的个数是有限的,其中最小的约数是1,最大的约数是它本身。
例如:10的约数有1、2、5、10,其中最小的约数是1,最大的约数是10。
一个数的倍数的个数是无限的,其中最小的倍数是它本身。
3的倍数有:3、6、9、12 其中最小的倍数是3 ,没有最大的倍数。
个位上是0、2、4、6、8的数,都能被2整除,例如:202、480、304,都能被2整除。
个位上是0或5的数,都能被5整除,例如:5、30、405都能被5整除。
一个数的各位上的数的和能被3整除,这个数就能被3整除,例如:12、108、204都能被3整除。
一个数各位数上的和能被9整除,这个数就能被9整除。
能被3整除的数不一定能被9整除,但是能被9整除的数一定能被3整除。
一个数的末两位数能被4(或25)整除,这个数就能被4(或25)整除。
例如:16、404、1256都能被4整除,50、325、500、1675都能被25整除。
一个数的末三位数能被8(或125)整除,这个数就能被8(或125)整除。
小学六年级数学总复习知识点归纳汇总

小学六年级数学总复习知识点归纳汇总小学六年级数学总复习知识点归纳1一、百分数的意义:表示一个数是另一个数的百分之几的数叫做百分数。
百分数又叫百分比或百分率,百分数不能带单位。
注意:百分数是专门用来表示一种特殊的倍比关系的,表示两个数的比。
1、百分数和分数的区别和联系:(1)联系:都可以用来表示两个量的倍比关系。
(2)区别:意义不同:百分数只表示倍比关系,不表示具体数量,所以不能带单位。
分数不仅表示倍比关系,还能带单位表示具体数量。
百分数的分子可以是小数,分数的分子只可以是整数。
注意:百分数在生活中应用广泛,所涉及问题基本和分数问题相同,分母是100的分数并不是百分数,必须把分母写成“%”才是百分数,所以“分母是100的分数就是百分数”这句话是错误的。
“%”的两个0要小写,不要与百分数前面的数混淆。
一般来讲,出勤率、成活率、合格率、正确率能达到100%,出米率、出油率达不到100%,完成率、增长了百分之几等可以超过100%。
一般出粉率在70%、80%,出油率在30%、40%。
2、小数、分数、百分数之间的互化(1)百分数化小数:小数点向左移动两位,去掉“%”。
(2)小数化百分数:小数点向右移动两位,添上“%”。
(3)百分数化分数:先把百分数写成分母是100的分数,然后再化简成最简分数。
(4)分数化百分数:分子除以分母得到小数,(除不尽的保留三位小数)然后化成百分数。
(5)小数化分数:把小数成分母是10、100、1000等的分数再化简。
(6)分数化小数:分子除以分母。
二、百分数应用题:1、求常见的百分率,如:达标率、及格率、成活率、发芽率、出勤率等求百分率就是求一个数是另一个数的百分之几。
2、求一个数比另一个数多(或少)百分之几,实际生活中,人们常用增加了百分之几、减少了百分之几、节约了百分之几等来表示增加、或减少的幅度。
求甲比乙多百分之几:(甲-乙)÷乙。
求乙比甲少百分之几:(甲-乙)÷甲。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
总复习小学数学复习资料一、概念(识记的)(一)整数1、整数:(整数=正整数+负整数+0)或(整数=自然数+负整数)2、自然数:我们在数物体的时候,用来表示物体个数的1,2,3……叫做自然数。
(自然数=奇数+偶数)或(自然数=质数+合数+1)3、计数单位:一(个)、十、百、千、万、十万、百万、千万、亿……都是计数单位。
(分数的计数单位是“分母分之一”;小数的计数单位:一位小数是0.1,两位小数是0.01,三位小数就是0.001……)4、数的整除:整数a除以整数b(b ≠0),除得的商是整数而没有余数,我们就说a能被b整除,或者说b能整除a 。
*如果数a能被数b(b ≠ 0)整除,a就叫做b的倍数,b就叫做a的约数(或a的因数)。
倍数和约数是相互依存的。
因为35能被7整除,所以35是7的倍数,7是35的约数。
*一个数的约数的个数是有限的,其中最小的约数是1,最大的约数是它本身。
例如:10的约数有1、2、5、10,其中最小的约数是1,最大的约数是10。
* 一个数的倍数的个数是无限的,其中最小的倍数是它本身。
3的倍数有:3、6、9、12……其中最小的倍数是3 ,没有最大的倍数。
*个位上是0、2、4、6、8的数,都能被2整除,例如:202、480、304,都能被2整除。
*个位上是0或5的数,都能被5整除,例如:5、30、405都能被5整除。
*一个数的各位上的数的和能被3整除,这个数就能被3整除,例如:12、108、204都能被3整除。
*能被3整除的数不一定能被9整除,但是能被9整除的数一定能被3整除。
*能被2整除的数叫做偶数,不能被2整除的数叫做奇数,0也是偶数。
自然数按能否被2 整除的特征可分为奇数和偶数。
(最小的奇数是1,最小的偶数是0)*一个数,如果只有1和它本身两个约数,这样的数叫做质数(或素数),(最小的质数是2)*一个数,如果除了1和它本身还有别的约数,这样的数叫做合数,1不是质数也不是合数,自然数除了1外,不是质数就是合数。
*把一个合数用质因数相乘的形式表示出来,叫做分解质因数。
*如果较大数是较小数的倍数,那么较大数就是这两个数的最小公倍数。
较小数就是这两个数的最大公因数。
例如:(A=8B, 则:AB的最大公因数是B,最小公倍数是A)*如果两个数是互质数,那么这两个数的积就是它们的最小公倍数。
(二)小数1、小数的意义:把整数1平均分成10份、100份、1000份……得到的十分之几、百分之几、千分之几……可以用小数表示。
2、小数的分类:纯小数有限小数小带小数纯循环小数数无限循环小数无限小数混循环小数无限不循环小数(∏)(三)分数1 、分数的意义:把单位“1”平均分成若干份,表示这样的一份或者几份的数叫做分数。
2、分数的分类:(分数=真分数+假分数)*真分数:分子比分母小的分数叫做真分数。
真分数小于1。
*假分数:分子比分母大或者分子和分母相等的分数,叫做假分数。
假分数大于或等于1。
*带分数:假分数可以写成整数与真分数合成的数,通常叫做带分数。
3、约分和通分:把一个分数化成同它相等但是分子、分母都比较小的分数,叫做约分。
(分子分母是互质数的分数,叫做最简分数。
)把异分母分数分别化成和原来分数相等的同分母分数,叫做通分。
(四)百分数:表示一个数是另一个数的百分之几的数叫做百分数,也叫做百分率或百分比。
百分数通常用"%"来表示。
百分号是表示百分数的符号。
例如:百分之75,写作:75%(五)统计图1、条形统计图:优点:很容易看出各种数量的多少。
2、折线统计图:优点:不但可以表示数量的多少,而且能够清楚地表示出数量增减变化的情况。
3、扇形统计图:优点:很清楚地表示出各部分同总数之间的关系。
(六)常见的数量关系*路程=速度×时间用 *总价=单价×数量 *工作总量=工作效率×时间(七)常用的计算公式1、长方形:c=2(a+b) s=ab2、正方形: c=4a s=a²3、三角形: s=ah/24、平行四边形: s=ah5、梯形: s=(a+b)h/26、圆: d=2r r=d/2 c=∏d c=2∏r s=∏r²7、扇形: s=n∏r²/3608、环形: s=∏(R²-r²)9、长方体: s=2(ab+ah+bh) V=sh V=abh10、正方体: S表=6a² v=a³11、圆柱: s侧=ch s表=s侧+s底×2 v=sh/312、圆锥:v= sh/3(八)、性质和规律1、商不变的规律商不变的规律:在除法里,被除数和除数同时扩大或者同时缩小相同的倍,商不变。
2、小数的性质小数的性质:在小数的末尾添上零或者去掉零小数的大小不变。
3、小数点位置的移动引起小数大小的变化小数点向右移动一位,原来的数就扩大10倍;小数点向右移动两位,原来的数就扩大100倍;小数点向右移动三位,原来的数就扩大1000倍……*小数点向左移动一位,原来的数就缩小10倍;小数点向左移动两位,原来的数就缩小100倍;小数点向左移动三位,原来的数就缩小1000倍……*小数点向左移或者向右移位数不够时,要用“0"补足位。
4、分数的基本性质:分数的分子和分母都乘以或者除以相同的数(零除外),分数的大小不变。
5、比的基本性质:比的前项和后项同时扩大或者同时缩小相同的倍,比值不变。
6、比例的基本性质:在一个比例里,两内项之积等于两外项之积,这叫比例的基本性质。
(九)、度量衡1、长度单位之间的换算* 1毫米=1000微米 * 1厘米=10 毫米 * 1分米=10 厘米* 1米=1000 毫米 * 1千米=1000 米2、面积单位的换算* 1平方厘米=100 平方毫米 * 1平方分米=100平方厘米* 1平方米=100 平方分米 * 1公倾=10000 平方米 * 1平方公里=100 公顷3、体积和容积单位换算* 1立方米=1000立方分米 * 1立方分米=1000立方厘米* 1升=1000毫升 * 1升=1立方米 * 1毫升=1立方厘米4、质量单位常用换算* 1吨=1000千克 * 1千克=1000克5、时间单位换算* 1世纪=100年 * 平年1年=365天 *闰年1年=366天 * 一、三、五、七、八、十、十二是大月大月有31 天 * 四、六、九、十一是小月小月有30天 * 平年2月有28天闰年2月有29天 * 1天= 24小时 * 1小时=60分 * 1分=60秒6、货币单位换算* 1元=10角 * 1角=10分二、方法(掌握的)(一)数的读法和写法1、整数的读法:从高位到低位,一级一级地读。
读亿级、万级时,先按照个级的读法去读,再在后面加一个“亿”或“万”字。
每一级末尾的0都不读出来,其它数位连续有几个0都只读一个零。
整数的写法:从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0。
(二)数的改写与省略一个较大的多位数,为了读写方便,常常把它改写成用“万”或“亿”作单位的数。
有时还可以根据需要,省略这个数某一位后面的数,写成近似数。
(三)数的互化1、小数化成分数:原来有几位小数,就在1的后面写几个零作分母,把原来的小数去掉小数点作分子,能约分的要约分。
2、分数化成小数:用分母去除分子。
能除尽的就化成有限小数,有的不能除尽,不能化成有限小数的,一般保留三位小数。
3、一个最简分数,如果分母中除了2和5以外,不含有其他的质因数,这个分数就能化成有限小数;如果分母中含有2和5 以外的质因数,这个分数就不能化成有限小数。
4、小数化成百分数:只要把小数点向右移动两位,同时在后面添上百分号。
5、百分数化成小数:把百分数化成小数,只要把百分号去掉,同时把小数点向左移动两位。
6、分数化成百分数:通常先把分数化成小数(除不尽时,通常保留三位小数),再把小数化成百分数。
7、百分数化成小数:先把百分数改写成分数,能约分的要约成最简分数。
(四)数的整除1、把一个合数分解质因数,通常用短除法。
先用能整除这个合数的质数去除,一直除到商是质数为止,再把除数和商写成连乘的形式。
2、求几个数的最大公约数的方法是:先用这几个数的公约数连续去除,一直除到所得的商只有公约数1为止,然后把所有的除数连乘求积,这个积就是这几个数的的最大公约数。
3、求几个数的最小公倍数的方法是:先用这几个数(或其中的部分数)的公约数去除,一直除到互质(或两两互质)为止,然后把所有的除数和商连乘求积,这个积就是这几个数的最小公倍数。
4、成为互质关系的两个数:1和任何自然数互质;相邻的两个自然数互质;当合数不是质数的倍数时,这个合数和这个质数互质;两个合数的公约数只有1时,这两个合数互质。
(五)约分和通分约分的方法:用分子和分母的公约数(1除外)去除分子、分母;通常要除到得出最简分数为止。
通分的方法:先求出原来的几个分数分母的最小公倍数,然后把各分数化成用这个最小公倍数作分母的分数。
(六)求比值和化简比求比值的方法:用比的前项除以后项,它的结果是一个数值可以是整数,也可以是小数或分数。
化简比的方法:根据比的基本性质可以把比化成最简单的整数比。
它的结果必须是一个最简比,即前、后项是互质的数。
(七)整数四则运算1、整数加法:*加数+加数=和一个加数=和-另一个加数2、整数减法:被减数-减数=差被减数=减数+差减数=被减数-差3、整数乘法:*一个因数×一个因数 =积 *一个因数=积÷另一个因数*在乘法里,0和任何数相乘都得0. 1和任何数相乘都的任何数。
4、整数除法:*被除数÷除数=商除数=被除数÷商被除数=商×除数(八)运算定律1、加法交换律: a+b=b+a 。
2、加法结合律:(a+b)+c=a+(b+c) 。
3、乘法交换律: a×b=b×a。
4、乘法结合律: (a×b)×c=a×(b×c) 。
5、乘法分配律: (a+b)×c=a×c+b×c 。
6、减法的性质: a-b-c=a-(b+c) 。
(九)运算法则1、整数加法计算法则:相同数位对齐,从低位加起,哪一位上的数相加满十,就向前一位进一。
2、整数减法计算法则:相同数位对齐,从低位加起,哪一位上的数不够减,就从它的前一位退一作十,和本位上的数合并在一起,再减。
3、整数乘法计算法则:先用一个因数每一位上的数分别去乘另一个因数各个数位上的数,用因数哪一位上的数去乘,乘得的数的末尾就对齐哪一位,然后把各次乘得的数加起来。
4、整数除法计算法则:先从被除数的高位除起,除数是几位数,就看被除数的前几位;如果不够除,就多看一位,除到被除数的哪一位,商就写在哪一位的上面。
