结构力学章节习题及参考答案
《结构力学习题集》(含答案)
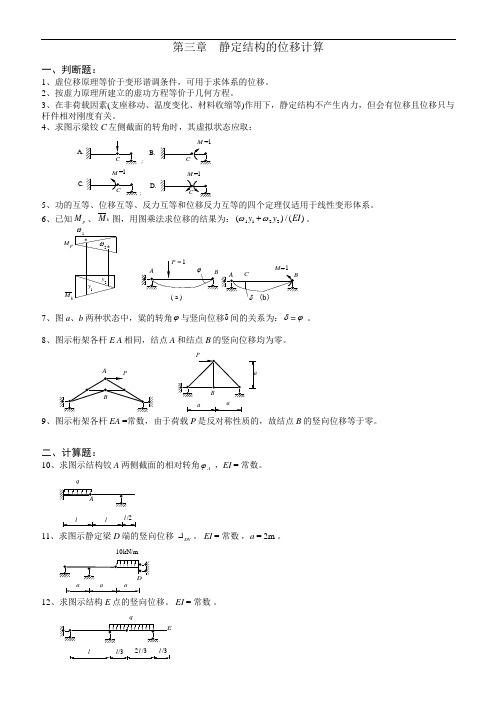
第三章 静定结构的位移计算一、判断题:1、虚位移原理等价于变形谐调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时,其虚拟状态应取:A.;;B.D.C.=1=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图,用图乘法求位移的结果为:()/()ωω1122y y EI +。
M kM p21y 1y 2**ωω( a )M =17、图a 、b 两种状态中,粱的转角ϕ与竖向位移δ间的关系为:δ=ϕ 。
8、图示桁架各杆E A 相同,结点A 和结点B 的竖向位移均为零。
Aaa9、图示桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
二、计算题:10、求图示结构铰A 两侧截面的相对转角ϕA ,EI = 常数。
qlll /211、求图示静定梁D 端的竖向位移 ∆DV 。
EI = 常数 ,a = 2m 。
a a a10kN/m12、求图示结构E 点的竖向位移。
EI = 常数 。
ll l /3/3q13、图示结构,EI=常数 ,M =⋅90kN m , P = 30kN 。
求D 点的竖向位移。
P 3m3m3m14、求图示刚架B 端的竖向位移。
q15、求图示刚架结点C 的转角和水平位移,EI = 常数 。
q16、求图示刚架中D点的竖向位移。
EI = 常数。
l/217、求图示刚架横梁中D点的竖向位移。
EI = 常数 。
18、求图示刚架中D点的竖向位移。
E I = 常数 。
qll/219、求图示结构A、B两截面的相对转角,EI = 常数 。
l/3l/320、求图示结构A 、B 两点的相对水平位移,E I = 常数。
ll21、求图示结构B 点的竖向位移,EI = 常数 。
《结构力学习题》含答案解析

第三章 静定结构的位移计算一、判断题:1、虚位移原理等价于变形谐调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时,其虚拟状态应取:A.;;B.D.C.=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图,用图乘法求位移的结果为:()/()ωω1122y y EI +。
M kM p21y 1y 2**ωω( a )M =17、图a、b两种状态中,粱的转角ϕ与竖向位移δ间的关系为:δ=ϕ。
8、图示桁架各杆E A相同,结点A和结点B的竖向位移均为零。
a a9、图示桁架各杆EA =常数,由于荷载P是反对称性质的,故结点B的竖向位移等于零。
二、计算题:10、求图示结构铰A两侧截面的相对转角ϕA,EI = 常数。
ql l l/211、求图示静定梁D端的竖向位移∆DV。
EI=常数,a= 2m 。
a a a10kN/m12、求图示结构E点的竖向位移。
EI=常数。
ll l l /32 /3/3q13、图示结构,EI=常数 ,M =⋅90kN m , P = 30kN 。
求D 点的竖向位移。
P 3m3m3m14、求图示刚架B 端的竖向位移。
q15、求图示刚架结点C 的转角和水平位移,EI = 常数 。
q16、求图示刚架中D 点的竖向位移。
EI = 常数 。
l/217、求图示刚架横梁中D点的竖向位移。
EI = 常数。
18、求图示刚架中D点的竖向位移。
EI =常数。
qll l/2219、求图示结构A、B两截面的相对转角,EI=常数。
l/23l/320、求图示结构A、B两点的相对水平位移,E I= 常数。
ll21、求图示结构B点的竖向位移,EI =常数。
l lﻩ22、图示结构充满水后,求A、B两点的相对水平位移。
《结构力学习题》(含答案解析)

《结构力学习题》(含答案解析)本页仅作为文档封面,使用时可以删除This document is for reference only-rar21year.March20 第三章 静定结构的位移计算一、判断题:1、虚位移原理等价于变形谐调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时,其虚拟状态应取:A.;; B.D.M C.=1=1=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图,用图乘法求位移的结果为:()/()ωω1122y y EI +。
M kM p 21y 1y 2**ωω( a )M =17、图a 、b 两种状态中,粱的转角ϕ与竖向位移δ间的关系为:δ=ϕ 。
8、图示桁架各杆E A 相同,结点A 和结点B 的竖向位移均为零。
Aa a9、图示桁架各杆EA =常数,由于荷载P是反对称性质的,故结点B的竖向位移等于零。
2121二、计算题:10、求图示结构铰A 两侧截面的相对转角ϕA ,EI = 常数。
q l l l /211、求图示静定梁D 端的竖向位移 ∆DV 。
EI = 常数 ,a = 2m 。
a a a 10kN/m12、求图示结构E 点的竖向位移。
EI = 常数 。
l l l /3 2 /3/3q13、图示结构,EI=常数 ,M =⋅90kN m , P = 30kN 。
求D 点的竖向位移。
P 3m 3m 3m14、求图示刚架B 端的竖向位移。
q15、求图示刚架结点C 的转角和水平位移,EI = 常数 。
q16、求图示刚架中D点的竖向位移。
EI =常数。
l ll/217、求图示刚架横梁中D点的竖向位移。
EI=常数。
18、求图示刚架中D点的竖向位移。
《结构力学习题集》(含答案)
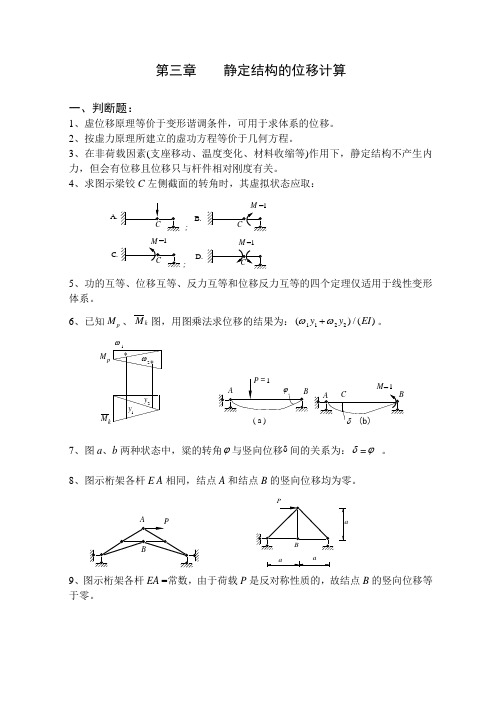
第三章 静定结构的位移计算一、判断题:1、虚位移原理等价于变形谐调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时,其虚拟状态应取:A.;; B.D.C.M =15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图,用图乘法求位移的结果为:()/()ωω1122y y EI +。
M k M p 21y 1y 2**ωω( a )M 17、图a 、b 两种状态中,粱的转角ϕ与竖向位移δ间的关系为:δ=ϕ 。
8、图示桁架各杆E A 相同,结点A 和结点B 的竖向位移均为零。
a a9、图示桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
二、计算题:10、求图示结构铰A 两侧截面的相对转角ϕA ,EI = 常数。
q l l l /211、求图示静定梁D 端的竖向位移 ∆DV 。
EI = 常数 ,a = 2m 。
a a a 10kN/m12、求图示结构E 点的竖向位移。
EI = 常数 。
l l l l /3 2 /3/3q13、图示结构,EI=常数 ,M =⋅90kN m , P = 30kN 。
求D 点的竖向位移。
P 3m 3m 3m14、求图示刚架B 端的竖向位移。
q15、求图示刚架结点C 的转角和水平位移,EI = 常数 。
16、求图示刚架中D点的竖向位移。
EI =常数。
l ll/217、求图示刚架横梁中D点的竖向位移。
EI=常数。
18、求图示刚架中D点的竖向位移。
E I = 常数。
qll l/l/2219、求图示结构A、B两截面的相对转角,EI=常数。
l/23l/320、求图示结构A、B两点的相对水平位移,E I = 常数。
ll21、求图示结构B点的竖向位移,EI = 常数。
结构力学习题及答案

结构力学习题第2章平面体系的几何组成分析2-1~2-6 试确定图示体系的计算自由度。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图2-7~2-15 试对图示体系进行几何组成分析。
若是具有多余约束的几何不变体系,则需指明多余约束的数目。
题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图题2-13图题2-14图题2-15图题2-16图题2-17图题2-18图题2-19图题2-20图题2-21图2-1 1W=2-1 9W-=2-3 3-W=2-4 2W-=2-5 1W=-2-6 4=W-2-7、2-8、2-12、2-16、2-17无多余约束的几何不变体系2-9、2-10、2-15具有一个多余约束的几何不变体系2-11具有六个多余约束的几何不变体系2-13、2-14几何可变体系为2-18、2-19 瞬变体系2-20、2-21具有三个多余约束的几何不变体系第3章静定梁和静定平面刚架的内力分析3-1 试作图示静定梁的内力图。
(a)(b)(c) (d)习题3-1图3-2 试作图示多跨静定梁的内力图。
(a)(b)(c)习题3-2图3-3~3-9 试作图示静定刚架的内力图。
习题3-3图习题3-4图习题3-5图习题3-6图习题3-7图习题3-8图习题3-9图3-10 试判断图示静定结构的弯矩图是否正确。
(a)(b)(c)(d)部分习题答案3-1 (a )m kN M B ⋅=80(上侧受拉),kN F RQB 60=,kN F L QB 60-=(b )m kN M A ⋅=20(上侧受拉),m kN M B ⋅=40(上侧受拉),kN F RQA 5.32=,kN F L QA 20-=,kN F LQB 5.47-=,kN F R QB 20=(c) 4Fl M C =(下侧受拉),θcos 2F F L QC =3-2 (a) 0=E M ,m kN M F ⋅-=40(上侧受拉),m kN M B ⋅-=120(上侧受拉)(b )m kN M RH ⋅-=15(上侧受拉),m kN M E ⋅=25.11(下侧受拉)(c )m kN M G ⋅=29(下侧受拉),m kN M D ⋅-=5.8(上侧受拉),m kN M H ⋅=15(下侧受拉) 3-3 m kN M CB ⋅=10(左侧受拉),m kN M DF ⋅=8(上侧受拉),m kN M DE ⋅=20(右侧受拉) 3-4 m kN M BA ⋅=120(左侧受拉)3-5 m kN M F ⋅=40(左侧受拉),m kN M DC ⋅=160(上侧受拉),m kN M EB ⋅=80(右侧受拉)3-6 m kN M BA ⋅=60(右侧受拉),m kN M BD ⋅=45(上侧受拉),kN F QBD 46.28=3-7 m kN M C ⋅=70下(左侧受拉),m kN M DE ⋅=150(上侧受拉),m kN M EB ⋅=70(右侧受拉) 3-8 m kN M CB ⋅=36.0(上侧受拉),m kN M BA ⋅=36.0(右侧受拉) 3-9 m kN M AB ⋅=10(左侧受拉),m kN M BC ⋅=10(上侧受拉) 3-10 (a )错误 (b )错误 (c )错误 (d )正确第4章 静定平面桁架和组合结构的内力分析4-1 试判别习题4-1图所示桁架中的零杆。
《结构力学》习题解答(内含解答图)

习题2-9试对图示体系进行几何组成分析。
习题2-9图习题2-9解答图
解:由于与基础的约束多余三个,故基础作为刚片Ⅰ。铰结△ABE为刚片Ⅱ,铰结△BCD为刚片Ⅲ。刚片Ⅰ与刚片Ⅱ是由杆FE和支撑杆A相连,虚铰在两杆的延长线的交点处,刚片Ⅰ与刚片Ⅲ是由杆GD和支撑杆C相连,虚铰在两杆的延长线的交点处,而刚片Ⅱ与刚片Ⅲ是铰B相连。此时,三铰不共线,该体系为几何不变体,且无多余约束。
结点h的隔离体上无荷载作用且为三杆结点故由平衡条件结点e的隔离体上无荷载作用且可看作为三杆结点故由平衡条件由结点g的隔离体根据平衡条件可求得由结点f的隔离体根据平衡条件可求得提高题pl2llp1pllp1vpl2llp1pllp1vbhaacefda提高题51图vanafn1ndfhadvadpnadfdhadvadhafvafnacbc提高题5
《结构力学》习题解答
第2章平面体系的几何组成分析
2.3
2.3.1基本题
习题2-1试对图示体系进行几何组成分析。
习题2-1图习题2-1解答图
解:为了便于分析,对图中的链杆和刚片进行编号,分析过程见习题2-1解答图。地基为刚片I,它与刚片Ⅱ之间用不交于一点的链杆1、2、3相连,组成几何不变部分,看作一个新刚片。此刚片与刚片Ⅲ又由不交于一点的链杆4、5、6相连,又组成几何不变体。
习题2-8试对图示体系进行几何组成分析。
习题2-8图习题2-8解答图
解:为了便于分析,对图中的链杆和刚片进行编号,分析过程见图2-21(b)。首先去掉二元体NMI、JNI,然后分析剩余部分。杆AD由固定支撑与基础联结形成一体,构成几何不变体,在此基础上增加二元体DEB、EFC、EHF形成刚片Ⅰ(注意固定铰支座与铰相同);铰结△GIJ为刚片Ⅱ;刚片I与刚片Ⅱ之间用不交于一点的杆DI、杆GI、杆HJ相连,组成几何不变体。
结构力学:第1-11章课后答案(第五版李廉锟上下册)

结构力学:第1-11章课后答案(第五版李廉锟上下册) 第一章:结构力学基本原理1.1 选择题1.(D)材料的流变效应是指在恒定的应力下长时间内所发生的持续性变形。
2.(C)结构力学是研究结构在受力作用下的平衡条件、变形特点以及保证结构安全可靠的一门学科。
3.(B)静力学是结构力学的基础和起点,为后续结构力学的学习打下了坚实的理论基础。
4.(D)载荷是指作用在结构上的外力或内力引起的结构内力。
5.(D)结构承受荷载时产生的内力只有两种,即剪力和弯矩。
1.2 计算题1.(略)1.3 解答题1.(略)第二章:静定结构的受力分析2.1 选择题1.(C)静定杆系是指感力作用下平衡的杆件系统。
2.(B)双铰支座在支座点允许的转动是绕一个垂直轴线。
3.(C)简支梁在跨中承受的弯矩最大。
4.(C)连续梁是指有多个支座并且跨度超过3倍的梁。
5.(A)当两个力的作用线相交于一点时,这两个力称为共点力。
2.2 计算题1.(略)2.3 解答题1.(略)第三章:约束结构的受力分析3.1 选择题1.(C)约束支座限制了结构的自由度。
2.(B)在平面约束条件下,三个约束就可以确定结构的静定条件。
3.(A)约束力分解是将复杂的约束力分解为多个简单的约束力。
4.(D)简支梁在跨中承受的弯矩最大。
5.(D)当两个力构成一个力偶时,它们可以合成一个力偶。
若力偶平行于结构截面,力偶不会在结构内产生剪力和弯矩。
3.2 计算题1.(略)3.3 解答题1.(略)第四章:图解法与力法4.1 选择题1.(D)作用在梁上的集中力可以用力的大小和作用点位置的乘积表示。
2.(B)变形图中每个单元代表一个约束力。
3.(C)悬臂梁上的力和矩可以通过力的图解法求解。
4.(D)力法是通过构造力平衡方程解得结构的内力。
5.(A)设计中常用的受力分析方法有解析法、图解法和力法。
4.2 计算题1.(略)4.3 解答题1.(略)第五章:静定系数法与弹性能力法5.1 选择题1.(C)在确定支座反力时,要根据结构属于静定结构、不完全静定结构还是超静定结构来决定求解的方程数。
结构力学章节习题及参考答案
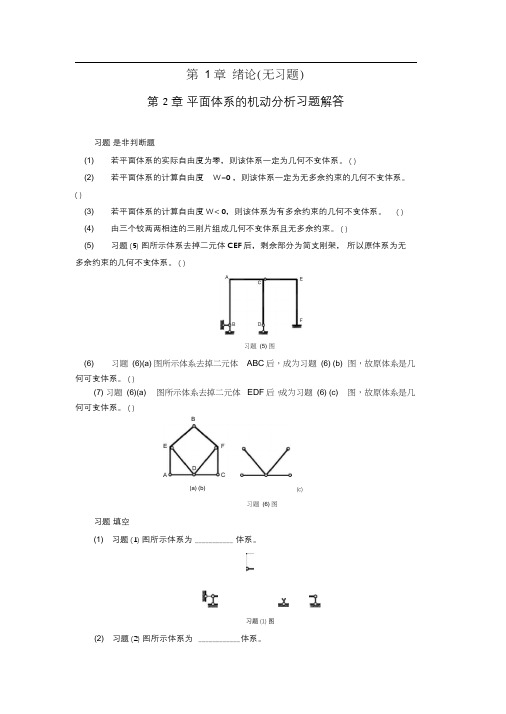
第 1 章绪论(无习题)第2 章平面体系的机动分析习题解答习题是非判断题(1) 若平面体系的实际自由度为零,则该体系一定为几何不变体系。
( )(2)若平面体系的计算自由度W=0 ,则该体系一定为无多余约束的几何不变体系。
( )(3) 若平面体系的计算自由度 W< 0,则该体系为有多余约束的几何不变体系。
( )(4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题(5) 图所示体系去掉二元体 CEF后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。
( )何可变体系。
( )何可变体系。
( )(c)习题填空(1) 习题(1) 图所示体系为___________ 体系。
习题(1) 图(2) 习题(2) 图所示体系为 ____________ 体系。
(6) 习题(6)(a) 图所示体系去掉二元体ABC后,成为习题(6) (b) 图,故原体系是几(7) 习题(6)(a) 图所示体系去掉二元体EDF后,成为习题(6) (c) 图,故原体系是几习题(5) 图B(a) (b)习题(6) 图习题 2-2(2) 图习题 (3) 图习题 对习题图所示各体系进行几何组成分析。
(3) 习题 (3) 图所示 4 个体系的多余约束数目分别为(4) 习题 (4) 图所示体系的多余约束个数为(5) 习题(5) (6) 习题(6) (7) 图所示体系的多余约束个数为习题 (5) 图图所示体系为体系,有个多余约束。
个多余约束。
习题 (7) 图所示体系为习题图(g) (h)第 3 章 静定梁与静定刚架习题解答习题 是非判断题(i) (j)(1) 在使用内力图特征绘制某受弯杆段的弯矩图时,必须先求出该杆段两端的端弯矩。
()(2) 区段叠加法仅适用于弯矩图的绘制,不适用于剪力图的绘制。
( )(3) 多跨静定梁在附属部分受竖(k)向荷载作用时,必会引起基本部分的(l) 内力。
( )(4) 习题(4) 图所示多跨静定梁中, CDE 和 EF 部分均为附属部分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题3.12图
第6章结构的位移计算习题解答
习题6.1是非判断题
(1)变形体虚功原理仅适用于弹性体系,不适用于非弹性体系。( )
(2)虚功原理中的力状态和位移状态都是虚设的。( )
(3)功的互等定理仅适用于线弹性体系,不适用于非线弹性体系。( )
(4)反力互等定理仅适用于超静定结构,不适用于静定结构。( )
(3)习题7.2(3)图所示刚架各杆的线刚度为i,欲使结点B产生顺时针的单位转角,应在结点B施加的力矩MB=______。
习题7.2(1)图习题7.2(2)图习题7.2(3)图
(4)用力矩分配法计算习题7.2(4)图所示结构(EI=常数)时,传递系数CBA=________,CBC=________。
(a)
习题3.7改正习题3.7图所示刚架的弯矩图中的错误部分。
(a)(b)(c)
(d)(e)(f)
习题3.7图
习题3.8作习题3.8图所示刚架的内力图。
(a)
(b)
习题3.8图
第4章静定拱习题解答
习题4.1是非判断题
(1)三铰拱的水平推力不仅与三个铰的位置有关,还与拱轴线的形状有关。()
(2)所谓合理拱轴线,是指在任意荷载作用下都能使拱处于无弯矩状态的轴线。()
习题4.2(1)图习题4.2(5)图
习题4.2(6)图习题4.2(7)图
习题4.2(8)图
习题6.3分别用积分法和图乘法求习题4.3图所示各指定位移CV。EI为常数。
1)求CV
习题4.3(1)图
2)求CV
习题4.3(2)图
3)求CV
习题4.3(3)图
4)求A
习题4.3(4)图
习题6.4分别用积分法和图乘法求习题4.4(a)图所示刚架C点的水平位移CH。已知EI=常数。
(3)改变荷载值的大小,三铰拱的合理拱轴线形状也将发生改变。()
习题4.2填空
(1)习题3.2(3)图所示三铰拱的水平推力FH等于。
习题3.2(3)图
习题4.3求习题3.15图所示三铰拱支反力和指定截面K的内力。已知轴线方程 。
习题3.15图
第5章静定平面桁架习题解答
习题5.1是非判断题
(1)利用结点法求解桁架结构时,可从任意结点开始。()
习题5.5图
习题7.6利用对称性,计算习题5.12图所示各结构的内力,并绘弯矩图。
习题5.12图
习题7.7画出习题5.17图所示各结构弯矩图的大致形状。已知各杆EI=常数。
习题5.17图
第8章 位移法习题解答
习题8.1确定用位移法计算习题6.1图所示结构的基本未知量数目,并绘出基本结构。(除注明者外,其余杆的EI为常数。)
习题11.1是非判断题
(1)习题8.1(1)图示结构BC杆轴力的影响线应画在BC杆上。( )
习题8.1(1)图习题8.1(2)图
(2)习题8.1(2)图示梁的MC影响线、FQC影响线的形状如图(a)、(b)所示。
(3)习题8.1(3)图示结构,利用MC影响线求固定荷载FP1、FP2、FP3作用下MC的值,可用它们的合力FR来代替,即MC=FP1y1+FP2y2+FP3y3=FR 。( )
(6)习题4.2(6)图所示拱中拉杆AB比原设计长度短了1.5cm,由此引起C点的竖向位移为________;引起支座A的水平反力为________。
(7)习题4.2(7)图所示结构,当C点有FP=1(↓)作用时,D点竖向位移等于(↑),当E点有图示荷载作用时,C点的竖向位移为________。
(8)习题4.2(8)图(a)所示连续梁支座B的反力为 ,则该连续梁在支座B下沉B=1时(如图(b)所示),D点的竖向位移 =________。
( )
(10)习题4.1(10)图所示结构的两个平衡状态中,有一个为温度变化,此时功的互等定理不成立。( )
习题4.1(7)图
习题4.1(8)图习题4.1(9)图
习题4.1(10)图
习题6.2填空题
(1)习题4.2(1)图所示刚架,由于支座B下沉所引起D点的水平位移DH=______。
(2)虚功原理有两种不同的应用形式,即_______原理和_______原理。其中,用于求位移的是_______原理。
习题8.1(3)图
(4)习题8.1(4)图中的(a)所示主梁FQC左的影响线如图(b)所示。( )
习题8.1(4)图
(5)习题8.1(5)图示梁FRA的影响线与FQA右的影响线相同。( )
习题4.4图
习题6.5习题4.5(a)图所示桁架各杆截面均为A=2×103m2,E=2.1×108kN/m2,FP=30kN,d=2m。试求C点的竖向位移 。
习题4.5图
第
习题7.1是非判断题
(1)习题5.1(1)图所示结构,当支座A发生转动时,各杆均产生内力。( )
习题5.1(1)图习题5.1(2)图
习题3.2(2)图
习题3.3作习题3.3图所示单跨静定梁的M图和 图。
(a) (b)
(c) (d)
(e) (f)
习题3.3图
习题3.4作习题3.4图所示单跨静定梁的内力图。
(c)
习题3.4图
习题3.5作习题3.5图所示斜梁的内力图。
习题3.5图
习题3.6作习题3.6图所示多跨梁的内力图。
(a)
习题3.6图
(7)习题2.1(6)(a)图所示体系去掉二元体EDF后,成为习题2.1(6) (c)图,故原体系是几何可变体系。( )
习题2.1(6)图
习题2.2填空
(1)习题2.2(1)图所示体系为_________体系。
习题2.2(1)图
(2)习题2.2(2)图所示体系为__________体系。
习题2-2(2)图
习题7.2(4)图
习题9.3用力矩分配法计算习题7.3图所示连续梁,作弯矩图和剪力图,并求支座B的反力。
(1)(2)
习题7.3图
习题9.4用力矩分配法计算习题7.4图所示连续梁,作弯矩图。
(1)(2)
习题7.4图
习题9.5用力矩分配法计算习题7.5图所示刚架,作弯矩图。
(1)(2)
习题7.5图
第11章影响线及其应用习题解答
习题8.3用位移法计算习题6.6图所示连续梁,作弯矩图和剪力图,EI=常数。
(1) (2)
习题6.6图
习题8.4用位移法计算习题6.7图所示结构,作弯矩图,EI=常数。
(1) (2)
习题6.7图
第9章渐近法习题解答
习题9.1是非判断题
(1)力矩分配法可以计算任何超静定刚架的内力。( )
(2)习题7.1(2)图所示连续梁的弯曲刚度为EI,杆长为l,杆端弯矩MBC<0.5M。( )
第1章绪论(无习题)
第2章平面体系的机动分析习题解答
习题2.1是非判断题
(1)若平面体系的实际自由度为零,则该体系一定为几何不变体系。( )
(2)若平面体系的计算自由度W=0,则该体系一定为无多余约束的几何不变体系。( )
(3)若平面体系的计算自由度W<0,则该体系为有多余约束的几何不变体系。( )
习题3.1(4)图
习题3.2填空
(1)习题3.2(1)图所示受荷的多跨静定梁,其定向联系C所传递的弯矩MC的大小为______;截面B的弯矩大小为______,____侧受拉。
习题3.2(1)图
(2)习题3.2(2)图所示风载作用下的悬臂刚架,其梁端弯矩MAB=______kN·m,____侧受拉;左柱B截面弯矩MB=______kN·m,____侧受拉。
(4)由三个铰两两相连的三刚片组成几何不变体系且无多余约束。( )
(5)习题2.1(5)图所示体系去掉二元体CEF后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。( )
习题2.1(5)图
(6)习题2.1(6)(a)图所示体系去掉二元体ABC后,成为习题2.1(6) (b)图,故原体系是几何可变体系。( )
(a) (b) (c) (d)
习题6.1图
习题8.2是非判断
(1)位移法基本未知量的个数与结构的超静定次数无关。( )
(2)位移法可用于求解静定结构的内力。( )
(3)用位移法计算结构由于支座移动引起的内力时,采用与荷载作用时相同的基本结构。( )
(4)位移法只能用于求解连续梁和刚架,不能用于求解桁架。( )
(3)用单位荷载法计算位移时,虚拟状态中所加的荷载应是与所求广义位移相应的________。
(4)图乘法的应用条件是:__________且MP与 图中至少有一个为直线图形。
(5)已知刚架在荷载作用下的MP图如习题4.2(5)图所示,曲线为二次抛物线,横梁的抗弯刚度为2EI,竖杆为EI,则横梁中点K的竖向位移为________。
(5)对于静定结构,有变形就一定有内力。( )
(6)对于静定结构,有位移就一定有变形。( )
(7)习题4.1(7)图所示体系中各杆EA相同,则两图中C点的水平位移相等。( )
(8)MP图, 图如习题4.1(8)图所示,EI=常数。下列图乘结果是正确的:
( )
(9)MP图、 图如习题4.1(9)图所示,下列图乘结果是正确的:
(3)习题2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题2.2(3)图
(4)习题2.2(4)图所示体系的多余约束个数为___________。
习题2.2(4)图
(5)习题2.2(5)图所示体系的多余约束个数为___________。
习题5.2填空
(1)习题3.2(4)图所示桁架中有根零杆。
习题3.2(4)图
习题5.3试用结点法求习题3.10图所示桁架杆件的轴力。
