九年级数学上册 21.1《二次根式》习题精选 新人教版
九年级数学二次根式总复习练习题及答案

九年级数学二次根式总复习精选练习题21.1 二次根式:1. 有意义的条件是 。
2. 当__________3. 11m +有意义,则m 的取值范围是 。
5. 在实数范围内分解因式:429__________,2__________x x -=-+=。
7. 2x =-,则x 的取值范围是 。
10. 把的根号外的因式移到根号内等于 。
12. 若1a b -+()2005_____________a b -=。
14. 下列各式一定是二次根式的是( )17. 若1a ≤ )A. (1a -B. (1a -C. (1a -D. (1a -18.=成立的x 的取值范围是( )A. 2x D. 2x≥x≠ B. 0x≥ C. 219. 的值是()A. 0B. 42-或42a-a- C. 24a- D. 24a21. 2440-+=,求xy的值。
y y22. 当a1取值最小,并求出这个最小值。
24. 已知2310-+=x x25. 已知,a b(10b-=,求20052006-的值。
a b21.2 二次根式的乘除1.最简二次根式的两个条件是:2. _____,______==。
m n3. __________==。
=。
4. 计算:_____________6. 下列各式不是最简二次根式的是()8. 对于所有实数,a b,下列等式总能成立的是()A. 2a b =+a b =+22a b =+a b =+9. -和-的大小关系是11. 计算:12. 化简:13. 把根号外的因式移到根号内:21.3 二次根式的加减1. 下列根式中,( )4. 下列根式中,是最简二次根式的是( )6. 10=,则x 的值等于( )A. 4 B. 2± C. 2 D. 4±x ,小数部分为y y -的值是( )A.310.若最简二次根式____,____a b ==。
13. 已知x y ==33_________x y xy +=。
九年级数学上册 21.1《二次根式》习题精选 新人教版

1 2 a
4. ab 、 a3b 、 是同类二次根式.…( )
3 x b
25.(a2 - mn + )÷a2b2 ;
m m m n m
b ab a b a b
1 2 2 3 3 4 99 100
1 x y x y
30.若 x,y 为实数,且 y= 1 4x + 4x 1 + .求 2 - 2 的值.
1 2 a
【提示】 a3b 、 化成最简二次根式后再判断.【答案】√.
3 x b
1
5. 8x , , 9 x2 都不是最简二次根式.( )
3 2 3 4
3. (x 1)2 = ( x 1)2 .…( )【提示】 (x 1)2 =|x-1|, ( x 1)2 =x-1(x≥
- 2 -
x2 a2 x x2 a2 x2 x x2 a2 x2 a2
1 1 1 1
29.计算(2 5 +1)( + + +…+ ).
七、选作题:(每小题 8 分,共 16 分)
x 2x x2 a2 1
28.当 x=1- 2 时,求 + + 的值.
2 y x y x
《二次根式》提高测试 答案
(一)判断题:(每小题 1 分,共 5 分)
2 2
(A) (B)- (C)-2x (D)2x
x x
a3
19.化简 ( a<0 ) 得…( )(A) a (B)- a (C)- a (D) a
15.x,y 分别为 8- 11 的整数部分和小数部分,则 2xy-y2=____________.
人教版九年级数学上册第二十一章二次根式测试题(AB)

第二十一章 二次根式测试题(A )一、选择题(每小题4分,共40分) 1、下列各等式成立的是( ) A :()255-= B ()233-=- C ()244- D 2x x =212x -x 的取值范围是( ) A :2x ≥ B :2x ≤ C :2x > D :2x >-3211a aa --=a 的取值范围是( )] A :0a ≤ B :0a < C :01a <≤ D :0a > 4、下列根式中属于最简二次根式的是( )A 21a +12C 8D 27x 5、下列计算中正确的是( )A 2222m n m n =+B 2222a b a b a b -==-C 3232⨯D ()233--624a -2a 的值为( )A :5B :6C :7D :87、已知m,n 22144m n n -+=,则m n 的值为( )A 2:14 C :12D :18、若三角形的三边分别是a,b,c ,且2(25)140a a b c ----=,则这个三角形的周长是( )A :5:453 C :455 D :4539、实数a,b 在数轴上的位置如图,那么化简2a b a - ) A :2a -b B :b C :-b D :-2a +b10、若0a >且2a x a -<<-,则化简22222x a x ax a x a +-++的结果为( )姓名班级二、填空题(每小题4分,共40分)111x -有意义,则x 的取值范围是 ;12、比较大小:--(填“>”“<”或“=” )13 ;14、已知1,a b ab -==(1)(1)a b +-= ;15是整数,则正整数a 的最小值是 ;16、计算:20082009(1(1= ;17、计算:021(3)2π---+= ;18=成立的条件是 ;19、观察分析下列数据,寻找规律:那么第10个数据是 ;20观察下列等式:1== ====规律计算:......1)= 。
九年级数学(上)第二十一章《二次根式》测试题及参考答案

九年级数学(上)《二次根式》测试题一、选择题(每小题3分,共30分)1、使式子1-x 2+x 有意义X 的取值范围是( )A 、X ≤1B 、X ≤1且X ≠-2C 、X ≠-2D X <1且X ≠-22、若代数式x x -+212有意义,则x 的取值范围是( )A 、21->x B 、4±≠x C 、0≥x D 、40≠≥x x 且 3、下列运算正确的是( ) A 、15.05.15.05.122=-=-B 、15.025.02=⨯= ≥C 、5)5(2-=-x xD 、x x x 22-=-4、下列根式中,最简二次根式是( )A 、a 25B 、22b a +C 、2aD 、5.05、已知:直角三角形的一条直角边为9,斜边长为10,则另一条直角边长为( )A 1B 19C 19D 296、若x=-3,则 ︳1-(1+X 2) ︳=( )A 1B -1C 3D -37、24n 是整数,则正整数n的最小值是( )A 4B 5C 6D 78、对于二次根式92+x ,以下说法不正确的是( )A .它是一个正数B .是一个无理数C .是最简二次根式D .它的最小值是39、下列说法错误是………………………………( ) A.962+-a a 是最简二次根式 B.4是二次根式 C.22b a +是一个非负数 D.162+x 的最小值是410、下列各式中与6是同类二次根式的是 ( ) A.36 B.12 C.32D.18二、填空题(每小题3分,共18分)11、使式子4-X 无意义的x取值是12、已知:X=2.5, 化简(X-2)2+ ︳X-4 ︳的结果是13、10xy .30yx (x>0,y>0)= 14、已知4322+-+-=x x y ,则,=xy . 15、三角形的三边长分别是20 ㎝ 45 ㎝ 40 ㎝,则这个三角形的周长为 16、观察下列各式:322322+=⨯;833833+=⨯;15441544+=⨯;……则依次第四个式子是 ;用)2(≥n n 的等式表达你所观察得到的规律应是 。
第二十一章二次根式测试题及答案(新人教版九年级上)

九年级数学第二十一章二次根式测试题(A )时间:45分钟 分数:100分一、选择题(每小题2分,共20分) 1. 下列式子一定是二次根式的是( ) A .2--x B .x C .22+x D .22-x2.若b b -=-3)3(2,则( )A .b>3B .b<3C .b ≥3D .b ≤3 3.若13-m 有意义,则m 能取的最小整数值是( ) A .m=0 B .m=1 C .m=2 D .m=34.若x<0,则xx x 2-的结果是( )A .0B .—2C .0或—2D .2 5.(2005·岳阳)下列二次根式中属于最简二次根式的是( ) A .14 B .48 C .baD .44+a 6.如果)6(6-=-∙x x x x ,那么( )A .x ≥0B .x ≥6C .0≤x ≤6D .x 为一切实数 7.(2005·湖南长沙)小明的作业本上有以下四题: ①24416a a =;②a a a 25105=⨯;③a aa a a=∙=112;④a a a =-23。
做错的题是( )A .①B .②C .③D .④ 8.化简6151+的结果为( ) A .3011 B .33030 C .30330 D .11309.(2005·青海)若最简二次根式a a 241-+与的被开方数相同,则a 的值为( ) A .43-=a B .34=a C .a=1 D .a= —1 10.(2005·江西)化简)22(28+-得( ) A .—2 B .22- C .2 D . 224- 二、填空题(每小题2分,共20分)11.①=-2)3.0( ;②=-2)52( 。
12.二次根式31-x 有意义的条件是 。
13.若m<0,则332||m m m ++= 。
14.1112-=-∙+x x x 成立的条件是 。
15.比较大小:。
16.=∙y xy 82 ,=∙2712 。
新人教版九年级数学第二十一章二次根式测试题及答案(2套)范文

一、选择题(每小题2分,共20分) 1. 下列式子一定是二次根式的是( )A .2--xB .xC .22+xD .22-x2.若b b -=-3)3(2,则( )A .b>3B .b<3C .b ≥3D .b ≤3 3.若13-m 有意义,则m 能取的最小整数值是( ) A .m=0 B .m=1 C .m=2 D .m=34.若x<0,则xx x 2-的结果是( )A .0B .—2C .0或—2D .2 5.(2005·岳阳)下列二次根式中属于最简二次根式的是( ) A .14 B .48 C .baD .44+a 8.化简6151+的结果为( ) A .3011B .33030C .30330D .11309.若最简二次根式a a 241-+与的被开方数相同,则a 的值为( ) A .43-=a B .34=a C .a=1 D .a= —1 10.(2005·江西)化简)22(28+-得( ) A .—2 B .22- C .2 D . 224- 二、填空题(每小题2分,共20分)11.①=-2)3.0( ;②=-2)52( 。
12.二次根式31-x 有意义的条件是 。
16.=∙y xy 82 ,=∙2712 。
17.计算3393aa a a-+= 。
18.23231+-与的关系是 。
19.若35-=x ,则562++x x 的值为 。
20.化简⎪⎪⎭⎫⎝⎛--+1083114515的结果是 。
11.若5-x 不是二次根式,则x 的取值范围是 。
12.已知a<2,=-2)2(a 。
13.当x= 时,二次根式1+x 取最小值,其最小值为 。
14.计算:=⨯÷182712 ;=÷-)32274483( 。
16.若433+-+-=x x y ,则=+y x 。
试求:(1)671+的值; (2)17231+的值;下列方程中是一元二次方程的是( ). A.xy +2=1 B. 09212=-+xx C. x 2=0 D.02=++c bx ax 1.配方法解方程2420x x -+=,下列配方正确的是( ) A .2(2)2x -=B .2(2)2x +=C .2(2)2x -=-D .2(2)6x -=2.若1762+--x x x 的值等于零,则x 的值是( ) A 。
九年级上第二十一章二次根式测试题参考答案.doc
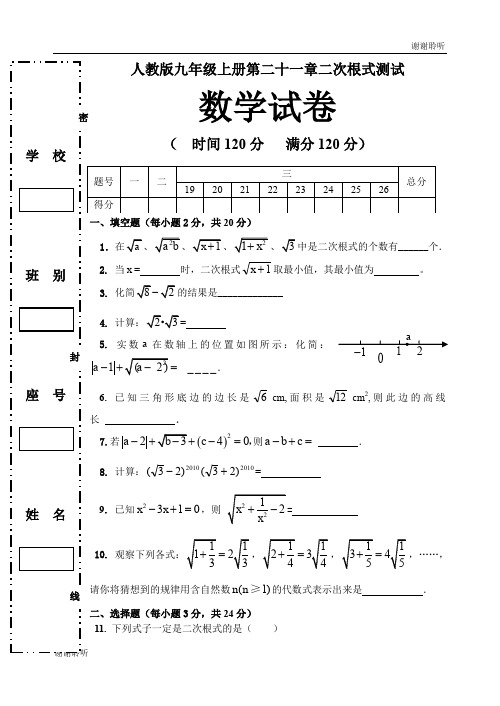
学校班别座号姓名人教版九年级上册第二十一章二次根式测试数学试卷(时间120分满分120分)一、填空题(每小题2分,共20分)1.在a、2a b、1x+、21x+、3中是二次根式的个数有______个.2.当x= 时,二次根式1+x取最小值,其最小值为。
3.化简82-的结果是_____________4.计算:23·=5.实数a在数轴上的位置如图所示:化简:21(2)______a a-+-=.6.已知三角形底边的边长是6cm,面积是12cm2,则此边的高线长.7.若()22340a b c-+-+-=,则=+-cba.8.计算:20102010)23()23(+-=9.已知2310x x-+=,则2212xx+-=10.观察下列各式:111233+=,112344+=,113455+=,……,请你将猜想到的规律用含自然数(1)n n≥的代数式表示出来是.二、选择题(每小题3分,共24分)11.下列式子一定是二次根式的是()题号一二三总分19 20 21 22 23 24 25 26得分密线封1-012aA .2--xB .xC .22+xD .22-x12. 下列二次根式中,x 的取值范围是2≥x 的是( )A .2-xB .x+2C .x -2D .1x -213. 实数a b c,,在数轴上的对应点的位置如图所示,式子①0b c +>②a b a c +>+③bc ac >④ab ac >中正确的有( )A.1个 B.2个 C.3个 D.4个14. 下列根式中,是最简二次根式的是( ) A .0.2b B . 1212a b - C. 22x y - D . 25ab15. 下列各式中,一定能成立的是( )A .22)5.2()5.2(=- B .22)(a a = C .1122-=+-x x x D .3392-∙+=-x x x16.设42-的整数部分为a ,小数部分为b ,则1a b-的值为( ) A.212-B.2 C.212+D.2-17. 把mm 1-根号外的因式移到根号内,得( ) A .m B .m -C .m --D .m -18. 若代数式22(2)(4)a a -+-的值是常数2,则a 的取值范围是( ) A.4a ≥ B.2a ≤ C.24a ≤≤ D.2a =或4a =三、解答题(76分) 19. (12分)计算:(1) 21418122-+- (2) 2)352(-2- 1- 0 1 2 3 c b a(3) 14510811253++- (4)284)23()21(01--+-⨯-20. (8分)先化简,再求值:11212222--÷+++-+x x x x x x x ,其中23-=x .21. (8分)已知:3x 22x y --+-=,求:4y x )(+的值。
九年级数学上册 21.1二次根式 同步练习 人教新课标版

21.1 二次根式一、双基整合,步步为营1.若a .2.2=2a-3成立的条件是________.3x 应满足的条件是______.4.当x>2.5.当x>1________.6.直角三角形中,一条直角边长______.7.下列各组数中,互为相反数的是( )A .-3B .│-3│与-13 C .│-3│与13D .-38 )A .B .C .-30D .309.若x 为任意数,则下列各式中成立的是( )A 2B 2C D10 )A .x 2B .±C .D .x 11.在实数范围内,把下列各式分解因式:①25x 2-7 ②2x 2-312.求下列各式的值:②二、拓广探索开发潜能13.当x_______=________.14.若,则x的取值范围是_________.15.已知x<0)A.x B.-x C.3x D.-3x16.若ab<0)A.B.C.D.17.若-3≤x≤2时,试化简│x-。
18.如图,已知等腰梯形的上下底长分别为3cm,7cm,高为4cm,求它的一条腰长,及一条对角线的长.三、智能升级,链接中考:19.实数P=________.P220.如图,在直角坐标系中,将矩形OABC沿OB对折,使点A落在点A1处,已知AB=1,则点A1的坐标是()A .32)B .3)C .(32D .(12)21.甲、乙两人计算a=5得到不同的答案.甲的解答是:=a+a-1=2a-1=2×5-1=9.乙的解答是:=a+1-a=1哪一个解答是对的?错误的解答错在哪里?为什么?参考答案:1.0 2.a≥323.x≥-3 4.-x-1 5.x-1 6. 7.D 8.B 9.A 10.B11.①((12.①5216213.≤2, -3 14.x≤0 15.•D •16.B 17.10-x18. 19.1 20.A 21.甲对,乙错.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次根式姓名 班级 学号(一)判断题:(每小题1分,共5分) 1.ab 2)2(-=-2ab .( ) 2.3-2的倒数是3+2.( )3.2)1(-x =2)1(-x .( ) 4.ab 、31b a 3、bax 2-是同类二次根式.( ) 5.x 8,31,29x +都不是最简二次根式.---( ) (二)填空题:(每小题2分,共20分) 6.当x __________时,式子31-x 有意义. 7.化简-81527102÷31225a= _. 8.a -12-a 的有理化因式是______. 9.当1<x <4时,|x -4|+122+-x x =______. 10.方程2(x -1)=x +1的解是______. 11.已知a 、b 、c 为正数,d 为负数,化简2222dc abd c ab +-=______.12.比较大小:-721_____-341. 13.化简:(7-52)2000·(-7-52)2001=_____.14.若1+x +3-y =0,则(x -1)2+(y +3)2=______.15.x ,y 分别为8-11的整数部分和小数部分,则2xy -y 2=____________.(三)选择题:(每小题3分,共15分)16.已知233x x +=-x 3+x ,则………………( )(A )x ≤0 (B )x ≤-3 (C )x ≥-3 (D )-3≤x ≤017.若x <y <0,则222y xy x +-+222y xy x ++=………………………( )(A )2x (B )2y (C )-2x (D )-2y 18.若0<x <1,则4)1(2+-xx -4)1(2-+xx 等于………………………( ) (A )x 2 (B )-x 2(C )-2x (D )2x 19.化简aa 3-(a <0)得…( )(A )a -(B )-a (C )-a -(D )a 20.当a <0,b <0时,-a +2ab -b 可变形为………………………………( )(A )2)(b a + (B )-2)(b a - (C )2)(b a -+- (D )2)(b a ---(四)在实数范围内因式分解:(每小题3分,共6分)21.9x 2-5y 2; 22.4x 4-4x 2+1. (五)计算题:(每小题6分,共24分) 23.(235+-)(235--); 24.1145--7114--732+;25.(a2m n -mabmn +m nn m )÷a 2b 2mn ;26.(a +ba abb +-)÷(b ab a ++a ab b --ab b a +)(a ≠b ).(六)求值:(每小题7分,共14分)27.已知x =2323-+,y =2323+-,求32234232y x y x y x xy x ++-的值.七、选作题:(每小题8分,共16分)28.当x =1-2时,求2222a x x a x x+-++222222ax x x a x x +-+-+221a x +的值.29.计算(25+1)(211++321++431++…+100991+).30.若x ,y 为实数,且y =x 41-+14-x +21.求x y y x ++2-xyy x +-2的值. 《二次根式》提高测试 答案(一)判断题:(每小题1分,共5分)1.ab 2)2(-=-2ab .…………………( )【提示】2)2(-=|-2|=2.【答案】×. 2.3-2的倒数是3+2.( ) 【提示】231-=4323-+=-(3+2).【答案】×.3.2)1(-x =2)1(-x .…( )【提示】2)1(-x =|x -1|,2)1(-x =x -1(x ≥1).两式相等,必须x ≥1.但等式左边x 可取任何数.【答案】×. 4.ab 、31b a 3、bax 2-是同类二次根式.…( ) 【提示】31b a 3、bax 2-化成最简二次根式后再判断.【答案】√. 5.x 8,31,29x +都不是最简二次根式.( ) 【答案】×.29x +是最简二次根式. (二)填空题:(每小题2分,共20分)6.当x __________时,式子31-x 有意义.【提示】x 何时有意义?x ≥0.分式何时有意义?分母不等于零.【答案】x ≥0且x ≠9. 7.化简-81527102÷31225a=_.【答案】-2a a .【点评】注意除法法则和积的算术平方根性质的运用. 8.a -12-a 的有理化因式是____________.【提示】(a -12-a )(________)=a 2-22)1(-a .a +12-a .【答案】a +12-a . 9.当1<x <4时,|x -4|+122+-x x =________________.【提示】x 2-2x +1=( )2,x -1.当1<x <4时,x -4,x -1是正数还是负数? x -4是负数,x -1是正数.【答案】3.10.方程2(x -1)=x +1的解是____________.【提示】把方程整理成ax =b 的形式后,a 、b 分别是多少?12-,12+.【答案】x =3+22. 11.已知a 、b 、c 为正数,d 为负数,化简2222d c ab d c ab +-=______.【提示】22d c =|cd |=-cd .【答案】ab +cd .【点评】∵ ab =2)(ab (ab >0),∴ ab -c 2d 2=(cd ab +)(cd ab -).12.比较大小:-721_________-341.【提示】27=28,43=48.【答案】<.【点评】先比较28,48的大小,再比较281,481的大小,最后比较-281与-481的大小.13.化简:(7-52)2000·(-7-52)2001=______________.【提示】(-7-52)2001=(-7-52)2000·(_________)[-7-52.] (7-52)·(-7-52)=?[1.]【答案】-7-52.【点评】注意在化简过程中运用幂的运算法则和平方差公式. 14.若1+x +3-y =0,则(x -1)2+(y +3)2=____________.【答案】40. 【点评】1+x ≥0,3-y ≥0.当1+x +3-y =0时,x +1=0,y -3=0.15.x ,y 分别为8-11的整数部分和小数部分,则2xy -y 2=____________.【提示】∵ 3<11<4,∴ _______<8-11<__________.[4,5].由于8-11介于4与5之间,则其整数部分x =?小数部分y =?[x =4,y =4-11]【答案】5.【点评】求二次根式的整数部分和小数部分时,先要对无理数进行估算.在明确了二次根式的取值范围后,其整数部分和小数部分就不难确定了. (三)选择题:(每小题3分,共15分)16.已知233x x +=-x 3+x ,则………………( )(A )x ≤0 (B )x ≤-3 (C )x ≥-3 (D )-3≤x ≤0【答案】D . 【点评】本题考查积的算术平方根性质成立的条件,(A )、(C )不正确是因为只考虑了其中一个算术平方根的意义.17.若x <y <0,则222y xy x +-+222y xy x ++=………………………( ) (A )2x (B )2y (C )-2x (D )-2y 【提示】∵ x <y <0,∴ x -y <0,x +y <0.∴222y xy x +-=2)(y x -=|x -y |=y -x .222y xy x ++=2)(y x +=|x +y |=-x -y .【答案】C . 【点评】本题考查二次根式的性质2a =|a |. 18.若0<x <1,则4)1(2+-xx -4)1(2-+xx 等于………………………( ) (A )x 2 (B )-x 2(C )-2x (D )2x 【提示】(x -x 1)2+4=(x +x 1)2,(x +x 1)2-4=(x -x 1)2.又∵ 0<x <1,∴ x +x 1>0,x -x1<0.【答案】D .【点评】本题考查完全平方公式和二次根式的性质.(A )不正确是因为用性质时没有注意当0<x<1时,x -x 1<0. 19.化简aa 3-(a <0)得………………………………………………………………( )(A )a - (B )-a (C )-a - (D )a【提示】3a -=2a a ⋅-=a -·2a =|a |a -=-a a -.【答案】C .20.当a <0,b <0时,-a +2ab -b 可变形为………………………………………( )(A )2)(b a + (B )-2)(b a - (C )2)(b a -+- (D )2)(b a --- 【提示】∵ a <0,b <0,∴ -a >0,-b >0.并且-a =2)(a -,-b =2)(b -,ab =))((b a --.【答案】C .【点评】本题考查逆向运用公式2)(a =a (a ≥0)和完全平方公式.注意(A )、(B )不正确是因为a <0,b <0时,a 、b 都没有意义. (四)在实数范围内因式分解:(每小题3分,共6分)21.9x 2-5y 2;【提示】用平方差公式分解,并注意到5y 2=2)5(y .【答案】(3x +5y )(3x -5y ).22.4x 4-4x 2+1.【提示】先用完全平方公式,再用平方差公式分解.【答案】(2x +1)2(2x -1)2.(五)计算题:(每小题6分,共24分)23.(235+-)(235--);【提示】将35-看成一个整体,先用平方差公式,再用完全平方公式.【解】原式=(35-)2-2)2(=5-215+3-2=6-215.24.1145--7114--732+;【提示】先分别分母有理化,再合并同类二次根式.【解】原式=1116)114(5-+-711)711(4-+-79)73(2--=4+11-11-7-3+7=1.25.(a 2m n -m ab mn +m n nm )÷a 2b 2m n ;【提示】先将除法转化为乘法,再用乘法分配律展开,最后合并同类二次根式. 【解】原式=(a2m n -mabmn +m nn m )·221b a nm=21b nm m n ⋅-mab 1n m mn ⋅+22b ma n n m n m ⋅ =21b-ab 1+221b a =2221b a ab a +-.26.(a +ba abb +-)÷(b ab a ++a ab b --ab b a +)(a ≠b ).【提示】本题应先将两个括号内的分式分别通分,然后分解因式并约分. 【解】原式=ba ab b ab a +-++÷))(())(()()(b a b a ab b a b a b a b b b a a a -+-+-+--=b a b a ++÷))((2222b a b a ab b a b ab b ab a a -++----=b a ba ++·)())((b a ab b a b a ab +-+-=-b a +.【点评】本题如果先分母有理化,那么计算较烦琐.(六)求值:(每小题7分,共14分)27.已知x =2323-+,y =2323+-,求32234232y x y x y x xy x ++-的值. 【提示】先将已知条件化简,再将分式化简最后将已知条件代入求值. 【解】∵ x =2323-+=2)23(+=5+26,y =2323+-=2)23(-=5-26.∴ x +y =10,x -y =46,xy =52-(26)2=1.32234232yx y x y x xy x ++-=22)())((y x y x y x y x x +-+=)(y x xy y x +-=10164⨯=652. 【点评】本题将x 、y 化简后,根据解题的需要,先分别求出“x +y ”、“x -y ”、“xy ”.从而使求值的过程更简捷. 28.当x =1-2时,求2222ax x a x x+-++222222ax x x a x x +-+-+221ax +的值.【提示】注意:x 2+a 2=222)(a x +,∴ x 2+a 2-x 22a x +=22a x +(22a x +-x ),x 2-x 22a x +=-x (22a x +-x ).【解】原式=)(2222x a x a x x-++-)(22222x a x x a x x -++-+221ax +=)()()2(22222222222x a x a x x x a x x a x x a x x -++-+++-+-=)()(22222222222222x a x a x x x a x x a x a x x x -++-+++++-=)()(222222222x a x a x x a x x a x -+++-+=)()(22222222x a x a x x x a x a x -++-++ =x 1.当x =1-2时,原式=211-=-1-2.【点评】本题如果将前两个“分式”分拆成两个“分式”之差,那么化简会更简便.即原式=)(2222x a x a x x-++-)(22222x a x x a x x -++-+221ax +=)11(2222a x x a x +--+-)11(22x x a x --++221a x +=x 1. 七、解答题:(每小题8分,共16分)29.计算(25+1)(211++321++431++…+100991+).【提示】先将每个部分分母有理化后,再计算. 【解】原式=(25+1)(1212--+2323--+3434--+…+9910099100--) =(25+1)[(12-)+(23-)+(34-)+…+(99100-)] =(25+1)(1100-)=9(25+1).【点评】本题第二个括号内有99个不同分母,不可能通分.这里采用的是先分母有理化,将分母化为整数,从而使每一项转化成两数之差,然后逐项相消.这种方法也叫做裂项相消法. 30.若x ,y 为实数,且y =x 41-+14-x +21.求x y y x ++2-xy y x +-2的值. 【提示】要使y 有意义,必须满足什么条件?].014041[⎩⎨⎧≥-≥-x x 你能求出x ,y 的值吗?].2141[⎪⎪⎩⎪⎪⎨⎧==y x 【解】要使y 有意义,必须⎩⎨⎧≥-≥-014041[x x ,即⎪⎪⎩⎪⎪⎨⎧≥≤.4141x x ∴ x =41.当x =41时,y =21.又∵x y y x ++2-x y y x +-2=2)(x y y x +-2)(xy y x - =|xy yx +|-|xy y x -|∵ x =41,y =21,∴ yx <xy.∴ 原式=x y y x +-y x x y +=2yx 当x =41,y =21时,原式=22141=2.【点评】解本题的关键是利用二次根式的意义求出x 的值,进而求出y 的。
