第2章同步电机基本方程及对称短路分析2009
电力系统暂态分析第二章

虚构电势 EQ|0|。
& &&
&
&&
&
&
Eq|0| U |0| jI d|0| xd jI q|0| xq U |0| jI d|0| xq jI q|0| xq jI d|0| (xd xq )
&&
&
&
U |0| jI|0| xq jI d|0| (xd xq ) EQ|0| jI d (xd xq )
各相磁链波形图如下:
7、定子电流表达式及波形
各相短路电流的一般表达式,当 0 为任意角度时
二、突然短路后转子励磁绕组中的电流分量
1、强制励磁电流分量 i f |0| 2、非周期自由分量 i f 3、周期自由分量 i fp
三、突然短路后转子阻尼绕组的电流分量
1、d轴阻尼绕组 (1)非周期自由分量 (2)周期自由分量
交流分量的幅值是衰减的,说明电势或阻抗是变化 的。
励磁回路电流也含有衰减的交流分量和非周期分量, 说明定子短路过程中有一个复杂的电枢反应过程。
同步发电机三相短路电流
❖ 实际电机绕组中都存在电阻,因此所有绕组的磁链都随时间变化,形 成电磁暂态过程。 ❖ 周期分量,其幅值将从起始次暂态电流逐渐衰减至稳态值; ❖ 非周期分量和倍频周期分量,它们将逐渐衰减至零。 ❖ 短路电流计算一般指起始次暂态电流或稳态短路电流计算;而其它任 意时刻短路电流工频周期分量有效值计算工程上采用运算曲线方法。
四、发电机空载情况下短路电流的表达式
1、定子绕组阻抗变化过程 2、定子电流变化过程 3、短路周期电流电流表达式
X d X d X d
I I I
t
第二章 1同步发电机的基本方程提纲
在 a、b、c 坐标上的投影表示定子三向电流瞬时值。 I m cos γ ia = − I m ib = − I m cos(γ − 120 ) ic = − I m cos(γ + 120 )
式中: γ = ω s t + γ 0
a相时间轴 −I m ω γ ic ia
0 xq 0 0 0 x aq
0 0 x0 0 0 0
xad 0 0 xf x ad 0
xad 0 0 x ad xD 0
0 xaq 0 0 0 xQ
− id − iq − i0 if iD iQ
采用标幺值后,
ψ d x d ψ q 0 ψ 0 0 = 最后得到磁链方程为: ψ f x ad ψ D x ad ψ Q 0
x d = x ad + x σ x q = x aq + xσ
式中: x = x + x d ad σ
i b = − I m cos(γ 0 − 120 0 )
0
ic = − I mcos(γ 0 + 120 )
ωs = ω r
ia = − I m cos(ωr t + γ 0 )
id = − I m cos(θ 0 - γ 0 ) i q = I m sin (θ 0 - γ 0 )
i b = − I m cos(ω r t + γ 0 − 120 )
同理有:
− sin θ − sin(θ − 120 ) − si 1 i0
ψ abc = P −1ψ dq 0 u abc = P −1u dq 0
电力系统暂态分析-第2章 同步发电机突然三相短路分析

10
电力系统暂态分析
2.2 同步发电机空载下三相短路后物理内部过程及短路电流分析
三、短路后各绕组的磁链及电流分量
1、定子绕组磁链和短路电流分量 (1)、励磁主磁通交链定子三相绕组的磁链
励磁绕组电压
励磁电流
励磁电流 i f 0 漏磁通 f 主磁路的主磁通 0
漏磁通只匝链励磁绕组,主磁通穿过气隙与定子三 相绕组匝练。
11
电力系统暂态分析
2.2 同步发电机空载下三相短路后物理内部过程及短路电流分析
(2)、短路前各相磁链
cos t 0 0 a0 ° cos t 120 b0 0 0 ° cos t 120 0 0 c0
17
电力系统暂态分析
2.2 同步发电机空载下三相短路后物理内部过程及短路电流分析
三相短路电流的表达式及波形
(7)、关于直流分量中存在倍频分量的说明
18
电力系统暂态分析
2.2 同步发电机空载下三相短路后物理内部过程及短路电流分析
2、励磁绕组磁链和短路电流分量 (1)、强制励磁电流 i f |0| 产生的磁链 短路前励磁回路中有恒定的励磁电流 i f |0| ,它由励 磁电源强制产生,定子短路后依然存在; (2)、定子三相交流电流的电枢反应 定子绕组中的三相交流电流可合成一个与转子同步旋 转的电枢反应磁动势,若忽略定子绕组电阻,该磁动势为 纯去磁的,即它穿入励磁绕组,且与主磁通方向相反,我 们用 ad 来表示,其值为常数。
第二章 同步发电机的数学模型及机端三相短路分析(第十六讲 三相短路分析及短路电流计算)

第二章同步发电机的数学模型及机端三相短路分析(回顾)第十六讲三相短路分析及短路电流计算1问题1、什么是发电机的超暂态过程、暂态过程?2、超暂态电抗、暂态电抗、同步电抗?大小关系?3、哪些绕组短路瞬间磁链不突变?4、短路电流计算时如何等值?5、为什么要计算0时刻短路电流?6、短路容量?23§1 三相短路电流的变化规律一、短路电流的组成定子abc 绕组短路电流有哪些成分?交流(周期)分量直流(非周期)分量直流分量交流分量dq0绕组电流6短路电流计算机分析结果(i d 、i q 、i 0)i d 交流分量+直流分量i q 直流分量为0i 0=0分析中关心dq0 绕组的直流分量!用标幺派克方程分析三相短路1、只需要考虑d轴方向绕组?2、d绕组直流分量衰减有什么特点?为什么?716超暂态过程结束时刻d 绕组电流值•i D =0(阻尼绕组可忽略)ψd =0,f 绕组磁链不变dI ′00(0)d d d ad f f ad d f f f f f X I X i X I X i X i ψψψ−′=−+=⎧⎪⎨′=−+==⎪⎩t E′t ′E−t t ′′′′′E E E E E−−28X adX d X f X DX qX QX aq互感为0ad qf fX E X ψ′=各电势的物理含义?磁链不突变343、假设短路前发电机为空载?,即取10=≈U E 假定各发电机内电势相角相同,且均为0,即101=°∠≈E4、在网络方面,忽略线路对地电容,变压器的励磁回路,在高压网络中忽略电阻。
线路1/2变压器1变压器2F40作业1、比较d轴超暂态电抗、暂态电抗及同步电抗的大小并从物理上解释之。
2、一台汽轮发电机其S r =15MVA,空载额定电压U r =6.3kV,在空载额定电压下发生机端三相突然短路。
已知其参数标幺值如下:s T s T s T X X X a d d d d d162.0,84.0,105.0,86.1,192.0,117.0==′=′′==′=′′设短路瞬间θa (0)=-60°。
第二章同步发电机突然三相短路分析

阻尼回路电流分量
• 一般将阻尼条构成回 路的等值绕组称为直 轴阻尼绕组D,铁芯 中涡流回路的等值绕 组称为交轴阻尼绕组
Q。
• 凸极机转子磁极上
两端短接的阻尼条和
隐极机转子铁芯中涡
流回路在正常稳态运
行时是没有电流的,
而在暂态过程中会感
生电流。
第二章同步发电机突然三相短路分 析
由图2-1:定子短路电流和励磁回路电流,在突然短 路瞬间均不突变,即三相定子电流均为零(空载), 励磁回路电流等于初始值。
第二章同步发电机突然三相短路分 析
第2节 同步发电机空载下三相短路假设 • 1、同步发电机是理想电机 • 2、暂态过程中同步发电机保持同步转速 • 3、发生短路后励磁电压恒定 • 4、短路发生在发电机的出线端口
短路电流产生的磁通
ai
a0
a
|
0
|
b i b 0 b |0 |
ci
c0
c |0 |
短路电流直 流分量产生
的磁通
主磁通交链到A相绕组的第磁二章通同仍步在发变电化机,突然三相短路分 为抵御这种变化感言析出了短路电流
短路电流 交流分量 产生的磁 通
直流
三相的直流合成为一个在空间静止的磁势,该静止的磁 势遇到的磁阻是周期变化的(因为转子的直轴和交轴的 磁阻即暂态磁阻是不同的),周期为180度电角度,频 率为两倍于基频。 因而,为产生恒定的磁链,磁势的大小随磁阻作相应的 变化,即直流电流的大小不是恒定的,而是按照两倍基 频波动。也可理解第为二章:同步直发流电机+突两然三倍相短频路交分 流
计及阻尼回路时基频交流分量初始值
右图示出计及阻尼 绕组D时,突然短 路瞬间定子电枢反 应磁通 a d 的磁路路 径。由于阻尼绕组 D也要维持其磁链
同步电机的对称运行原理

对称运行是同步电机的一种理想 运行状态,可以使得电机运行更 加稳定、效率更高,同时减小对 电网的谐波干扰。
对称运行的数学模型
同步电机的对称运行可以用数学模型 进行描述,包括电机的电压方程、磁 链方程、转矩方程等。
在对称运行状态下,同步电机的定子 电流、转子电流、气隙磁场等物理量 可以用正弦函数表示,其波形呈现出 对称分布。
对称运行的物理意义
对称运行的物理意义在于,在理想情况下,同步电机在正常 运行时,其内部各物理量分布均匀、相互协调,使得电机运 行更加高效、稳定。
对称运行可以减小同步电机的振动和噪声,提高电机的使用 寿命和可靠性。同时,对称运行还可以减小对电网的谐波干 扰,有利于电网的稳定运行。
PART 03
对称运行的特点
可靠性提高
由于电机运行平稳,各部分温升均匀,可以降低因局部过热而导致的故障率, 从而提高电机的可靠性。
PART 04
对称运行的实现方法
REPORTING
WENKU DESIGN
设计和制造过程中的对称性考虑
01
02
03
转子与定子的设计
确保转子与定子的几何形 状和尺寸完全相同,以确 保在电机运行时产生相同 的磁场和电流分布。
减排作用
对称运行有助于减少污染物排放,降低对环境的 影响。
可持续发展
对称运行与节能减排相结合,有助于实现可持续 发展目标。
THANKS
感谢观看
REPORTING
https://
绕组配置
采用对称的绕组配置,确 保在电机运行时产生的磁 通路径和电流路径对称。
质量平衡
确保电机转子的质量分布 平衡,以减少运行时的振 动和偏心。
运行过程中的对称性监测和控制
电力系统暂态分析:第二章 同步发电机突然三相短路分析1

的近似分析
• 一、同步机特点 • 1、转子是旋转的。 • 2、绕组是分散的。 • 3、存在磁饱和现象。 • 二、假设 • 1、忽略磁饱和现象,在分析中可以应用叠加原理; • 2、绕组都是对称的,即电机转子在结构上对本身的直
根据相量图可得短路前的量
•
•
•
•
•
•
E q 0 j I d 0 xad j I d 0 x E q 0 j I d 0 xd U q 0
•
•
•
•
0 j I q 0 xaq j I q 0 x 0 j I q 0 xq U d 0
隐极机
凸极机
凸极机
四、电流感应过程:原理如下: 对突然短路暂态过程进行物理分析的理论
ci c0 c 0
• a相电流所应产生的磁链包含两个分量, • 一个是恒定的,等于Ψa︱0︱ , • 一个是交变的,与Ψa 0大小相等,方向相反。
ai a0 a 0
bi b0 b 0
• 同步发电机的绕组图
2008.3
同步发电机的基本方程、参数和 等值电路
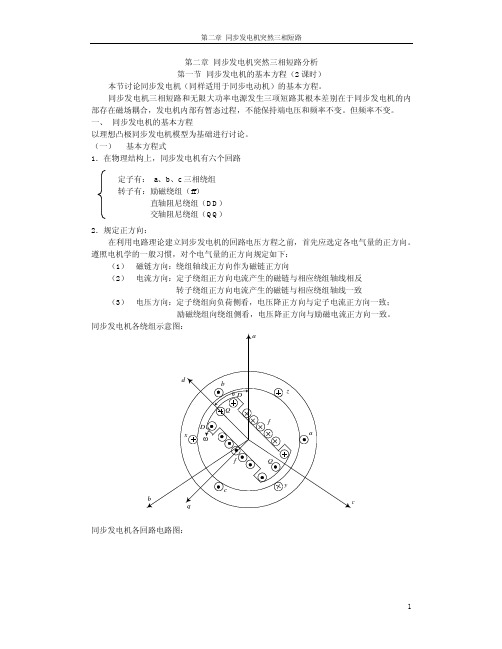
• 6绕组模型,定子abc三相绕组,励磁绕组ff,d轴
阻尼绕组DD,q轴阻尼绕组QQ • 定子各相绕组轴线的正方向为各相绕组的磁链正
方向 • 定子正电流产生负磁链,转子正电流产生正磁链 • 定子流出正电流
2008.3
同步发电机的基本方程、参数和 等值电路
• 不计饱和时
Ead ad Fad Id Eaq aq Faq Iq
•
•
•
Ead j Id xad
•
•
Eaq j Iq xaq
电力系统分析第二篇 同步发电机的基本方程

主讲教师:徐 箭 所在单位:电气工程学院
内容提要 本章将根据理想同步发电机内部的各电
磁量的关系,建立同步发电机的较为精确而 完整的数学模型,为电力系统的暂态分析准 备必要的基础知识。
《电力系统分析》 主讲人:电气工程学院 徐箭
3-1 3-2 3-3 3-6
基本前提 同步发电机的原始方程 dq0坐标系的同步发电机方程 同步电机的对称稳态运行
LfD=LDf=常数; 纵轴和横轴阻尼绕组之间的互感系数为零(因为两
绕组相互垂直),即LfQ=LQf= LDQ=LQD=0 。
《电力系统分析》 主讲人:电气工程学院 徐箭
⒋ 定子绕组和转子绕组间的互感系数
无论是凸极机还是隐极机,这些互感系数都与定子绕
组和转子绕组的相对位置有关。下面以励磁绕组和定子a
=
w2
⎡⎢⎣λmσ
+
1 4
(λad
+ λaq )⎤⎥⎦⎬⎫⎪⎪
( ) m2
=
1 2
w2
λad −λaq
⎪ ⎪⎭
《电力系统分析》 主讲人:电气工程学院 徐箭
Lab = Lba = −⎡⎣m0 + m2 cos2(α +30°)⎤⎦
定子各相绕组间的互感系数也是转子位置角的周期 函数,周期为π;
变化部分的幅值与自感系数的相等,即m2=l2; m0恒大于m2,因此定子绕组间的互感系数恒为负
《电力系统分析》 主讲人:电气工程学院 徐箭
3-1 基本前提 一、理想同步电机 二、假定正方向的选取
《电力系统分析》 主讲人:电气工程学院 徐箭
一、理想同步电机
不计磁路饱和、磁滞、涡流等的影响,即假定电机的 导磁系数为常数;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Qa q Fa sin , Fa (ia ) (2 17)
19
M Qa M aQ 0 sin
(四)转子绕组的自感系数
LFF , LDD , LQQ为常数,与 无关
(五)转子绕组间的互感系数
M FD M DF 为常数 M FQ M QF M DQ M QD 0
a Laa ia 其余电流为0 aa
Laa
aa
ia
15
• 分析结果
Laa Laa 0 Laa 2 cos(2 )
同理,
Lbb Laa0 Laa 2 cos 2( 120) (2 12)
Lcc Laa 0 Laa 2 cos 2( 120)
11
.
• 矩阵形式
. F rF u F . 0 0 D 0 . 0 Q
0 rD 0
0 iF 0 iD rQ iQ
(2 6)
简记为:
.
(2 5)
U abc abc riabc
10
(一)电压方程
2. 转子回路 F绕组
rF
uF
iF
d F u F eF riF riF dt F riF
.
eF
D绕组 Q绕组
uD D rDiD 0
.
uQ Q rQiQ 0
26
2. 电机正常稳态时,三相电流对应的通用相 量与相电流幅值相等,且以角速度ω正方 向旋转。
27
(二)通用相量的应用 1. id , iq与I、的关系
id I cos( ) iq I cos(90 ) I sin( )
0
d a
b q
c
28
2. id、iq与ia、ib、ic的关系 2 cos( ) [cos cos cos( 120) cos( 120) 3 cos( 120) cos( 120)] 2 sin( ) [sin sin sin( 120) sin( 120) 3 sin( 120) sin( 120)] 2 id I cos( ) [ I cos cos I cos( 120) cos( 120) 3 I cos( 120) cos( 120)] 2 ' [ia cos ib' cos( 120) ic' cos( 120)] 3 2 [ia cos ib cos( 120) ic cos( 120)] 3
12
(二)磁链方程 设L----自感系数,M---互感系数 以a相绕组为例
a Laaia Mabib M acic MaF iF M aDiD M aQiQ
以F绕组为例
F M Faia M Fbib M Fcic LFF iF M FDiD M FQiQ
16
(二)定子绕组间的互感系数 同学自己分析,推导出表达式 (课下完成)
M ab M ba , M ac M ca , M bc M ca M ba
ba
ia
17
• 结果如下:
M ab M ba [ M ba 0 Laa 2 cos 2( 30)] M bc M cb [M ba 0 Laa 2 cos 2( 90)] M ca M ac [ M ba 0 Laa 2 cos 2( 150)] (2 13)
35
说明: (1)电感系数均为常数; (2) Ld , Lq , L0 的含义; (3)定、转子绕组互感系数不互易。 原因:数学、物理 处理-----适当选基准值,转换为互易
1
方程(2) FDQ LRa Q i0 dq LRR iFDQ (4)
1
33
方程
0 L0i0 d Ld id M dF iF M dD iD q Lq iq M qQ iQ F M Fd id LFF iF M FD iD D M Fd id M DF iF LDD iD Q M Qq iq LQQ iQ
29
2 同理,iq [ia sin ib sin( 120) ic sin( 120)] 3 1 矩阵形式 i0 3 (ia ib ic ) i0 0.5 0.5 0.5 ia 2 id cos cos( 120) cos( 120) ib 3 iq sin sin( 120) sin( 120) ic ia Q ib (2 23) ic
d a ua ea ria ria dt a ria
b、c相
.
ra rb rc r r
ea
. .
ia
ua
ub eb rib b rib uc ec ric c ric
9
• 矩阵形式
. a r 0 0 ia u a . u 0 r 0 i b b b uc . 0 0 r ic c
6
2. 电磁量的规定正方向
定子 (1)电流 (2)电势
(3)电压
(4)正值电流产生负值磁链
(5)磁链与绕组轴线
7
2. 电磁量的规定正方向
转子 (1)d轴与磁极中心线一致,q轴超前90°; (2)ψ F与d轴方向一致;
(3)正值电流产生正值磁链;
(4)电势
(5)电压
8
一、方程形式
(一)电压方程 1. 定子回路,设 a相
18
(三)定、转子绕组间的互感系数
以
M Fa , M Da , MQa 为例
M Fa
Fa
ia
其余电流为0
Fa d Fa cos , Fa (ia )
M Fa M aF 0 cos 同理, M Da M aD 0 cos
M Qa
Qa
ia
其余电流为0
2 ia ib2 ic2 I 2 [cos2 cos2 ( 1200 ) cos2 ( 1200 )]
3 1 I [ [cos 2 cos 2( 1200 ) cos 2( 1200 )]] 2 2 3 2 I 2
2
2 2 2 2 (ia ib ic ) I 3 cos ia I
同理,可写出其他绕组的磁链方程
13
• 矩阵形式,教材P37 (2-8)
• 分块形式
abc Labc FDQ LRa
LaR iabc i (2 9) LRR FDQ
6个电压方程,6个磁链方程
14
二、电感系数
(一)定子绕组的自感系数 板书分析,以a相为例
30
即: i0 dq Qiabc iabc Q i0 dq cos sin 1 Q 1 1 cos( 120) sin( 120) 1 cos( 120) sin( 120) (2 27)
1
31
i0 dq Qiabc 1 iabc Q i0 dq 0 dq Q abc u0 dq Quabc 同理, , 1 abc Q 0 dq uabc Q 1u0 dq
4
2-1 同步电机的原始方程
• 原始方程-----根据电机电磁特性直接列写出 来的方程。
几点说明 1. 研究对象 同步电机
5
• 关于“理想电机”的假设(教材P35) (1)μ=常数,即忽略磁饱和的影响;(线性 化) (2)转子关于d轴和q轴分别对称,绕组用 集中绕组F、D、Q代替; (3)定子三相绕组空间分布对称,互差 120°,绕组用集中绕组a、b、c代替; (4)空载时,转子电流在定子绕组中感应的 电势为时间的正弦函数; (5)定、转子具有光滑的表面。
电力系统故障分析讲稿
徐玉琴
1
第2章 同步电机的基本方程和对 称故障分析
2
思路:
原始方程 (abc系统) 变系数微分方程
通用相量
Park变换
Park方程(时域、复频域形式) (dq0系统) 常系数微分方程Biblioteka 对称故障 分析、计算3
学习重点:
(1)基本概念、基本方法、park方程的由 来; (2)三相短路的计算思路 正常稳态-----park方程时域形式 故障附加状态----- park方程复域形式 时域(拉氏反变换) (3)实用计算
34
其中
L0 Laa 0 2M ab 0 3 Ld Laa 0 M ab 0 Laa 2 2 3 Lq Laa 0 M ab 0 Laa 2 2 3 3 M dF M aF 0 , M Fd M aF 0 ; M dD M aD 0 , M Dd M aD 0 ; 2 2 3 M qQ M aQ 0 , M Qq M aQ 0 2
(1) ia ib ic 0时, I、 与ia、ib、ic唯一对应 已知:I、,求ia、ib、ic ia I cos ib I cos( 1200 ) ic I cos( 1200 ) (投影)
.
j
(2 18)
24
已知:ia、ib、ic,求I、
说明: (1)abc dqo物理意义
(2)abc系统与dqo系统电磁量的对应 (3)转换矩阵不唯一
32
2-3 park方程
一、磁链方程的转换
