高三数学-2018届高三数学综合试卷(缺部分答案) 精品
2018届高三数学寒假作业 综合试卷(3)(含详细答案)

2018届高三数学寒假作业 综合试卷(3)数学Ⅰ满分160分,考试时间120分钟一、填空题:本大题共14小题,每小题5分,共计70分.1.已知集合{1,}A a =,{1,3,4}B =,且{1,3}A B = ,则实数a 的值为 .2.i 是虚数单位,复数z 满足3ii 4iz -=,则||z = . 3.对一批产品的长度(单位:毫米)进行抽样检测,样本容量为200, 右图为检测结果的频率分布直方图,根据产品标准,单件产品长 度在区间[25,30)的为一等品,在区间[20,25)和[30,35)的为 二等品,其余均为三等品,则样本中三等品的件数为 .4.某学校高三有A ,B 两个自习教室,甲、乙、丙三名同学随机选择其中一个 教室自习,则他们在同一自习教室上自习的概率为 .5.执行如图所示的流程图,会输出一列数,则这列数中的第3个数是 .6.已知双曲线C :22221(0,0)x y a b a b-=>>的一条渐近线平行于直线l :y =2x +10,且它的一个焦点在直线l 上,则双曲线C 的方程为 .7.已知等差数列{a n }的前n 项和为S n ,且2S 3-3S 2=12,则数列{a n }的公差是 . 8.已知一个圆锥的底面积为2π,侧面积为4π,则该圆锥的体积为 . 9.在平面直角坐标系中,过原点O 的直线l 与曲线2ex y -=交于不同的两点A ,B ,分别过A ,B 作x 轴的垂线,与曲线y =ln x 分别交于点C ,D ,则直线CD 的斜率为 . 10.若cos(π6-θ)=33,则cos(5π6+θ)-sin 2(θ-π6)= .11.在△ABC 中,已知AC =4,C =4π,B ∈(4π,2π),点D 在边BC 上,且AD =BD =3,则AB AD ⋅ = .12.已知圆C :x 2+y 2-2x -2y +1=0,直线l :34170x y +-=.若在直线l 上任取一点M 作圆C 的切线MA ,MB ,切点分别为A ,B ,则AB 的长度取最小值时直线AB 的方程为 .13.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,2A C =,2c =,244a b =-,则a = .14.已知函数2+1, 1,()(), 1,a x x f x x a x ⎧-⎪=⎨->⎪⎩≤ 函数()2()g x f x =- ,若函数()()y f x g x =- 恰有4个零点,则实数a 的取值范围是 .二、解答题:本大题共6小题,共计90分.解答时应写出必要的文字说明、证明过程或演算步骤. 15.(本小题满分14分) 已知向量a =3(sin ,)4x ,b =(cos x ,-1).(1)当a ∥b 时,求cos 2x -sin 2x 的值;(2)设函数f (x )=2(a +b )·b ,已知3()24f α=,(,)2απ∈π,求sin α的值.16.(本小题满分14分)已知△ABD 和△BCD 是两个直角三角形,2BAD BDC π∠=∠=,E 、F 分别是边AB 、AD 的中点,现将△ABD 沿BD 边折起到A 1BD 的位置,如图所示,使平面A 1BD ⊥平面BCD . (1)求证:EF ∥平面BCD ;(2)求证:平面A 1BD ⊥平面A 1CD ;(3)请你判断,A 1C 与BD 是否有可能垂直,做出判断并写明理由.E 17. (本小题满分14分) 如图,有一块矩形草坪ABCD,AB =100米,BC =三条小路OE 、EF 和OF ,要求O 是AB 的中点,点E 在边BC 上,点F 在边AD 上,且∠EOF =90°; (1)设∠BOE =α,试求OEF ∆的周长l 关于α的函数解析式,并求出此函数的定义域;(2)经核算,三条路每米铺设费用均为400元,试问如何设计才能使铺路的总费用最低?并求出最低总费用.18.(本小题满分16分)椭圆M :22221(0)x y a b ab+=>>的焦距为(0,2)P 关于直线y x =-的对称点在椭圆M 上.(1)求椭圆M 的方程;(2)如图,椭圆M 的上、下顶点分别为A ,B ,过点P 的直线l 与椭圆M 相交于两个不同的点C ,D .①求OC OD ⋅的取值范围;②当AD 与BC 相交于点Q 时,试问:点Q 的纵坐标是否是定值?若是,求出该定值;若不是,说明理由.19.(本小题满分16分)已知函数()1e xaf x x =-+(a ∈R ,e 为自然对数的底数) . (1)若曲线y =f (x )在点(1,f (1))处的切线平行于x 轴,求a 的值; (2)求函数f (x )的极值;(3)当a =1的值时,若直线l :y =kx -1与曲线y =f (x )没有公共点,求k 的最大值.20.(本小题满分16分)已知数列{a n }满足a 1=a (a >0,a ∈N *),a 1+a 2+…+a n -pa n +1=0(p ≠0,p ≠-1,n ∈N *).(1)求数列{a n }的通项公式a n ;(2)若对每一个正整数k ,若将a k +1,a k +2,a k +3按从小到大的顺序排列后,此三项均能构成等差数列,且公差为d k .①求p 的值及对应的数列{d k }.②记S k 为数列{d k }的前k 项和,问是否存在a ,使得S k <30对任意正整数k 恒成立?若存在,求出a 的最大值;若不存在,请说明理由.数学Ⅱ(附加题)满分40分 考试时间30分钟21.【选做题】本题包括A 、B 、C 、D 四小题,请选定其中两题,并在相应的答题区域内作答,每小题10分.若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤. B .(选修4-2:矩阵与变换) 已知矩阵1235-⎡⎤=⎢⎥-⎣⎦A . (1)求逆矩阵A -1; (2)若矩阵X 满足AX =31⎡⎤⎢⎥⎣⎦,试求矩阵X .C .选修4-4:坐标系与参数方程已知极坐标系的极点与直角坐标系的原点重合,极轴与x 轴的正半轴重合.若直线l 的极坐标方程为sin()4πρθ-=(1)把直线l 的极坐标方程化为直角坐标系方程;(2)已知P 为椭圆C :22139x y +=上一点,求P 到直线l 的距离的最小值.【必做题】第22、23题,每小题10分,共计20分.解答时应写出文字说明、证明过程或演算步骤. 22.(本小题满分10分)某地区试行高考考试改革:在高三学年中举行5次统一测试,学生如果通过其中2次测试即可获得足够学分升上大学继续学习,不用参加其余的测试,而每个学生最多也只能参加5次测试.假设某学生每次通过测试的概率都是31,每次测试时间间隔恰当,每次测试通过与否互相独立. (1)求该学生考上大学的概率.(2)如果考上大学或参加完5次测试就结束,记该生参加测试的次数为X ,求X 的分布列及X 的数学期望.23.(本小题满分10分)【16高考新课标】已知抛物线C :y 2=2x 的焦点为F ,平行于x 轴的两条直线l 1、l 2分别交C 于A 、B 两点,交C 的准线于P 、Q 两点.(1)若F 在线段AB 上,R 是PQ 的中点,证明AR ∥FQ ;(2)若△PQF 的面积是△ABF 的面积的两倍,求AB 中点的轨迹方程.2018届高三数学寒假作业 综合试卷(4)答案数学Ⅰ满分160分,考试时间120分钟一、填空题:本大题共14小题,每小题5分,共计70分.1.已知集合{1,}A a =,{1,3,4}B =,且{1,3}A B = ,则实数a 的值为 .3解:由{1,3}A B = 可知1∈A 且3∈A ,有a =3.2.i 是虚数单位,复数z 满足3ii 4iz -=,则||z = .5 解:由题意得24i 3i 43i z =+=-+,那么||5z =.3.对一批产品的长度(单位:毫米)进行抽样检测,样本容量为200,右图为检测结果的频率分布直方图,根据产品标准,单件产品长 度在区间[25,30)的为一等品,在区间[20,25)和[30,35)的为 二等品,其余均为三等品,则样本中三等品的件数为 .50 解:三等品总数[1(0,050.03750.0625)5]20050n =-++⨯⨯=.4.某学校高三有A ,B 两个自习教室,甲、乙、丙三名同学随机选择其中一个 教室自习,则他们在同一自习教室上自习的概率为 .14解:22222814P ==⨯⨯=. 5.执行如图所示的流程图,会输出一列数,则这列数中的第3个数是 .30解:A =3,N =1,输出3;A =6,N =2,输出6;A =30,N =3,输出30;则这列数中的第3个数是30.6.已知双曲线C :22221(0,0)x y a b a b -=>>的一条渐近线平行于直线l :y =2x +10,且它的一个焦点在直线l 上,则双曲线C 的方程为 .221520x y -=解:由双曲线的渐近线方程by x a =±可知b =2a ;又由题意c =5,那么a ,双曲线方程为221520x y -=. 7.已知等差数列{a n }的前n 项和为S n ,且2S 3-3S 2=12,则数列{a n }的公差是 .4解:方法1:2S 3-3S 2=112(33)3(2)312a d a d d +-+==,则d =4.方法2:因为112n S n a d n -=+,则32232S S -=2d =,得到d =4.8.已知一个圆锥的底面积为2π,侧面积为4π,则该圆锥的体积为 .解:设圆锥的底面半径为r ,母线长为l ,则22,4r rl π=π=,解得r l =h =以21133V r h=π=π⨯=.9.在平面直角坐标系中,过原点O的直线l与曲线2e xy-=交于不同的两点A,B,分别过A,B作x轴的垂线,与曲线y=ln x分别交于点C,D,则直线CD的斜率为.1解:设121(,)xA x-e,B222(,)xx-e,则由点O,A,B共线可知122212x xx x--=e e,可化为1212x xxx-=e,得到1122lnxx xx-=,故有11221212lnln lnCDxx x xkx x x x-==--1=.10.若cos(π6-θ)=33,则cos(5π6+θ)-sin2(θ-π6)=.设t=π6-θ,有cos t=33.那么cos(5π6+θ)-sin2(θ-π6)=cos(π t) sin2 t= 2+33.11.在△ABC中,已知AC=4,C=4π,B∈(4π,2π),点D在边BC上,且AD=BD=3,则AB AD⋅=.解:如图,AD=BD,∴∠DAB=∠B;∵B∈(4π,2π),∴0<∠BDA<2π.在△ACD中,AC=4,AD=3,C=4π,由正弦定理得:sin sinAD ACC ADC=∠4sin ADC=∠,∴sin∠ADC,∴cos∠BDA=13.∴21=()()3393AB AD DB DA DA DB DA DA⋅-⋅-=-⋅+=-⨯⨯+=6.12.已知圆C:x2+y2-2x-2y+1=0,直线l:34170x y+-=.若在直线l上任取一点M作圆C的切线MA,MB,切点分别为A,B,则AB的长度取最小值时直线AB的方程为.68190x y+-=解:当AB的长度最小时,圆心角∠ACB最小,设为2θ,则由cos ACCMθ=1CM=可知当θ最小时,cosθ最大,即CM最小,那么,CM⊥l,可知43AB lk k==-,设直线AB的方程为34x y m+=.又由CM=2可知,点C到直线AB的距离为12,即34125m+-=,解得192m=或92;经检验192m=,则直线AB的方程为68190x y+-=.13.在△ABC中,角A,B,C所对的边分别为a,b,c,2A C=,2c=,244a b=-,则a=.解:在△ABC中,由余弦定理24444cos2b b b C-=+-,即24(1c o s2)80b b C-++=,故228cos 80b b C -+=2sin C=,即cos C =,所以2(1)802b b b --+=,解得4b =,所以24412a b =-=,a =14.已知函数2+1, 1,()(), 1,a x x f x x a x ⎧-⎪=⎨->⎪⎩≤ 函数()2()g x f x =- ,若函数()()y f x g x =- 恰有4个零点,则实数a 的取值范围是 .解:由题意当()()y f x g x =-[]2()10f x =-=时,即方程()1f x =有4个解. 又由函数1y a x =-+与函数2()y x a =-的大致形状可知,直线1y =与函数2+1, 1,()(), 1,a x x f x x a x ⎧-⎪=⎨->⎪⎩≤的左右两支曲线都有两个交点,如下图示. 那么,有2(1)1,(1)1,(1)1a f f ->->⎧⎪⎨⎪⎩≤ ,即20,1,21,a a a a ><>-⎧⎪⎨⎪⎩或≤解得23a <≤.二、解答题:本大题共6小题,共计90分.解答时应写出必要的文字说明、证明过程或演算步骤. 15.(本小题满分14分)已知向量a =3(sin ,)4x ,b =(cos x ,-1).(1)当a ∥b 时,求cos 2x -sin 2x 的值; (2)设函数f (x )=2(a +b )·b ,已知3()24f α=,(,)2απ∈π,求sin α的值.解:(1)因为a ∥b ,所以34cos x +sin x =0,所以tan x =-34.故cos 2x -sin 2x =cos 2x -2sin x cos x sin 2x +cos 2x =1-2tan x 1+tan 2x =85.(2)223()2()222sin cos 2(cos 1)2f x x x x =+⋅=⋅+=-++a b b a b b 3sin 2cos22x x =++3)42x π++.因为3()24f α=,所以33())2424f ααπ++=,即sin()4απ+=又(,)2απ∈π,所以3444αππ5π<+<,故cos()4απ+=,所以sin sin[()])cos())4444ααααππππ=+-=+-+=+=.E16.(本小题满分14分)已知△ABD 和△BCD 是两个直角三角形,2BAD BDC π∠=∠=,E 、F 分别是边AB 、AD 的中点,现将△ABD 沿BD 边折起到A 1BD 的位置,如图所示,使平面A 1BD ⊥平面BCD . (1)求证:EF ∥平面BCD ; (2)求证:平面A 1BD ⊥平面A 1CD ;(3)请你判断,A 1C 与BD 是否有可能垂直,做出判断并写明理由. 解:(1)证明:因为E 、F 分别是边AB 、AD 的中点, 所以EF ∥BD .因为EF ⊄平面BCD ,BD ⊂平面BCD ,所以EF ∥平面BCD . (2)证明:因为平面A 1BD ⊥平面BCD , 平面A 1BD ∩平面BCD =BD , CD ⊂平面BCD , CD ⊥BD ,所以CD ⊥平面A 1BD .因为A 1B ⊂平面A 1BD ,所以CD ⊥A 1B .因为A 1B ⊥A 1D ,A 1D ∩CD =D ,所以A 1B ⊥平面A 1CD . 因为A 1B ⊂平面A 1BC ,所以平面A 1BC ⊥平面A 1CD . (3)解:结论: A 1C 与BD 不可能垂直.理由如下:假设A 1C ⊥BD ,因为CD ⊥BD ,A 1C ∩CD =C , 所以BD ⊥平面A 1CD , 因为A 1D ⊂平面A 1CD ,所以BD ⊥A 1D 与A 1B ⊥A 1D 矛盾. 故A 1C 与BD 不可能垂直.17. (本小题满分14分) 如图,有一块矩形草坪ABCD ,AB =100米,BC =三条小路OE 、EF 和OF ,要求O 是AB 的中点,点E 在边BC 上,点F 在边AD 上,且∠EOF =90°; (1)设∠BOE =α,试求OEF ∆的周长l 关于α的函数解析式,并求出此函数的定义域;(2)经核算,三条路每米铺设费用均为400元,试问如何设计才能使铺路的总费用最低?并求出最低总费用. 解:(1)Rt △BOE 中,OB =50, ∠B =90°,∠BOE =α,∴OE =50cos α. Rt △AOF 中,OA =50, ∠A =90°,∠AFO =α,∴OF =50sin α.又∠EOF =90°,∴EF==50cos sin αα, ∴505050cos sin cos sin l OE OF EF αααα=++=++即50(sin cos 1)cos sin l αααα++=.当点F 在点D 时,这时角α最小,求得此时α=π6; 当点E 在C 点时,这时角α最大,求得此时α=π3.故此函数的定义域为ππ[,]63.(2)由题意知,要求铺路总费用最低,只要求△OEF 的周长l 的最小值即可.由(1)得,50(sin cos 1)cos sin l αααα++=,ππ[,]63α∈设sin cos t αα+=,则21sin cos 2t αα-⋅=,∴250(sin cos 1)50(1)1001cos sin 12t l t t αααα+++===--. 由,5ππ7π12412α≤+≤t ≤≤11t ≤-≤,1111t ≤-,当π4α=,即BE=50时,min 1)l =,所以当BE =AE =50米时,铺路总费用最低,最低总费用为1)元.18.(本小题满分16分)椭圆M :22221(0)x y a b a b+=>>的焦距为(0,2)P 关于直线y x =-的对称点在椭圆M 上. (1)求椭圆M 的方程;(2)如图,椭圆M 的上、下顶点分别为A ,B ,过点P 的直线l 与椭圆M 相交于两个不同的点C ,D .①求OC OD ⋅的取值范围;②当AD 与BC 相交于点Q 时,试问:点Q 的纵坐标是否是定值?若是,求出该定值;若不是,说明理由.解:(1)因为点(0,2)P 关于直线y x =-的对称点为(2,0)-, 且(2,0)-在椭圆M 上,所以2a =.又2c =c =,则222431b a c =-=-=.所以椭圆M 的方程为2214x y +=.(2)①当直线l 的斜率不存在时,(0,1),(0,1)C D -,所以OC OD ⋅=-1.当直线l 的斜率存在时,设直线l 的方程为2y kx =+,1122(,),(,)C x y D x y . 222,1,4y kx x y =+⎧⎪⎨+=⎪⎩消去y 整理得22(14)16120k x kx +++=,由0∆>,可得243k >,且1212221612,1414k x x x x k k +=-=++, 所以1212OC OD x x y y ⋅=+21212217(1)2()4114k x x k x x k =++++=-++,所以1314OC OD -<⋅< ,综上13[1,)4OC OD ⋅∈- .②由题意得,AD :2211y y x x -=+,BC :1111y y x x +=-, 联立方程组,消去x 得121221233kx x x x y x x ++=-,又121243()kx x x x =-+,解得12y =-.故点Q 的纵坐标为定值12. 19.(本小题满分16分)已知函数()1e xaf x x =-+(a ∈R ,e 为自然对数的底数) . (1)若曲线y =f (x )在点(1,f (1))处的切线平行于x 轴,求a 的值;(2)求函数f (x )的极值;(3)当a =1的值时,若直线l :y =kx -1与曲线y =f (x )没有公共点,求k 的最大值. 解:(1)由()1e xa f x x =-+,得()1e x a f x '=-.又曲线y =f (x )在点(1,f (1))处的切线平行于x 轴,得f '(x )=0,即10ea-=,解得a =e . (2)()1e xaf x '=-. ①当a ≤0时,f '(x )>0,f (x )为(-∞,+∞)上的增函数,所以函数f (x )无极值. ②当a >0时,令f '(x )=0,得e x =a ,x =ln a . x ∈(-∞,ln a ),f '(x )<0;x ∈( ln a ,+∞),f '(x )>0.所以f (x )在(-∞,ln a )上单调递减,在( ln a ,+∞)上单调递增,故f (x )在x =ln a 处取得极小值,且极小值为f (ln a )=ln a ,无极大值. 综上,当a ≤0时,函数f (x )无极小值;当a >0, f (x )在x =ln a 处取得极小值ln a ,无极大值.(3)当a =1时,1()1e x f x x =-+ 令()()()()111e xg x f x kx k x =--=-+, 则直线l :y =kx -1与曲线y =f (x )没有公共点, 等价于方程g (x )=0在R 上没有实数解. 假设k >1,此时g (0)=1>1,1111()101e k g k -=-+<-, 又函数g (x )的图象连续不断,由零点存在定理,可知g (x )=0在R 上至少有一解,与“方程g (x )=0在R 上没有实数解”矛盾,故k ≤1.又k =1时,()1e xg x =>0,知方程g (x )=0在R 上没有实数解. 所以k 的最大值为1. 解法二: (1)(2)同解法一. (3)当a =1时,1()1e xf x x =-+. 直线l :y =kx -1与曲线y =f (x )没有公共点,等价于关于x 的方程111e xkx x -=-+在R 上没有实数解, 即关于x 的方程:()11ex k x -=(*)在R 上没有实数解. ①当k =1时,方程(*)可化为10e x =,在R 上没有实数解. ②当k ≠0时,方程(*)化为1e 1x x k =-.令g (x )=x e x ,则有g '(x )=(1+x )e x x e x . 令g '(x )=0,得x =-1, 当x 变化时,如下表:当x =-1时,min 1()eg x =-,同时当x 趋于+∞时,g (x )趋于+∞, 从而g (x )的取值范围为[1e -,+∞).所以当11(,)1e k ∈-∞--时,方程(*)无实数解, 解得k 的取值范围是(1-e ,1).综上,得k 的最大值为1.20.(本小题满分16分)已知数列{a n }满足a 1=a (a >0,a ∈N *),a 1+a 2+…+a n -pa n +1=0(p ≠0,p ≠-1,n ∈N *).(1)求数列{a n }的通项公式a n ;(2)若对每一个正整数k ,若将a k +1,a k +2,a k +3按从小到大的顺序排列后,此三项均能构成等差数列,且公差为d k .①求p 的值及对应的数列{d k }.②记S k 为数列{d k }的前k 项和,问是否存在a ,使得S k <30对任意正整数k 恒成立?若存在,求出a 的最大值;若不存在,请说明理由.解:(1)因为a 1+a 2+…+a n -pa n +1=0,所以n ≥2时,a 1+a 2+…+a n -1-pa n =0, 两式相减,得a n +1a n =p +1p (n ≥2),故数列{a n }从第二项起是公比为p +1p 的等比数列.又当n =1时,a 1-pa 2=0,解得a 2=ap ,从而a n =⎩⎪⎨⎪⎧a ,n =1 ,a p ⎝⎛⎭⎫p +1p n -2 ,n ≥2 .(2)①由(1)得a k +1=a p ⎝⎛⎭⎫p +1p k -1, a k +2=a p ⎝⎛⎭⎫p +1p k ,a k +3=a p ⎝⎛⎭⎫p +1p k +1,若a k +1为等差中项,则2a k +1=a k +2+a k +3,即p +1p =1或p +1p =-2,解得p =-13;此时a k +1=-3a (-2)k -1,a k +2=-3a (-2)k ,所以d k =|a k +1-a k +2|=9a ·2k -1.若a k +2为等差中项,则2a k +2=a k +1+a k +3,即p +1p=1,此时无解;若a k +3为等差中项,则2a k +3=a k +1+a k +2,即p +1p =1或p +1p =-12,解得p =-23,此时a k +1=-3a 2⎝⎛⎭⎫-12k -1,a k +3=-3a 2⎝⎛⎭⎫-12k +1,所以d k =|a k +1-a k +3|=9a 8·⎝⎛⎭⎫12k -1. 综上所述,p =-13,d k =9a ·2k -1或p =-23, d k =9a 8·⎝⎛⎭⎫12k -1.②当p =-13时,S k =9a (2k -1).则由S k <30,得a <103 2k-1, 当k ≥3时,103 2k-1 <1,所以必定有a <1,所以不存在这样的最大正整数. 当p =-23时,S k =9a 4⎣⎡⎦⎤1-⎝⎛⎭⎫12k , 则由S k <30,得a <403⎣⎡1-⎝⎛⎭⎫12k ],因为403⎣⎡⎦⎤1-⎝⎛⎭⎫12k >403,所以a =13满足S k <30恒成立;但当a =14时,存在k =5,使得a >403⎣⎡⎦⎤1-⎝⎛⎭⎫12k 即S k <30,所以此时满足题意的最大正整数a =13.数学Ⅱ(附加题)满分40分 考试时间30分钟21.【选做题】本题包括A 、B 、C 、D 四小题,请选定其中两题,并在相应的答题区域内作答,每小题10分.若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤. B .(选修4-2:矩阵与变换) 已知矩阵1235-⎡⎤=⎢⎥-⎣⎦A . (1)求逆矩阵A -1; (2)若矩阵X 满足AX =31⎡⎤⎢⎥⎣⎦,试求矩阵X .解:(1)设A -1=a b c d ⎡⎤⎢⎥⎣⎦,则a b c d ⎡⎤⎢⎥⎣⎦1235-⎡⎤⎢⎥-⎣⎦=325325a b a b c d a d +--⎡⎤⎢⎥+--⎣⎦=1001⎡⎤⎢⎥⎣⎦. ∴3125030251a b a b c d c d +=⎧⎪--=⎪⎨+=⎪⎪--=⎩解得5231a b c d =-⎧⎪=⎪⎨=-⎪⎪=⎩∴A -1=5231-⎡⎤⎢⎥-⎣⎦, (2)135231331118---⎡⎤⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦X A .C .选修4-4:坐标系与参数方程已知极坐标系的极点与直角坐标系的原点重合,极轴与x 轴的正半轴重合.若直线l的极坐标方程为sin()4πρθ-=(1)把直线l 的极坐标方程化为直角坐标系方程;(2)已知P 为椭圆C :22139x y +=上一点,求P 到直线l 的距离的最小值.解:(1)直线l的极坐标方程sin 4ρθπ⎛⎫-= ⎪⎝⎭,sin cos θρθ= 即sin cos 4ρθρθ-=,所以直线l 的直角坐标方程为40x y -+=;(2)P 为椭圆2213x y C +=:上一点,设3sin )P αα,,其中[02)α∈π,,则P 到直线l的距离d =所以当0cos(60)1α+=-时,d 的最小值为【必做题】第22、23题,每小题10分,共计20分.解答时应写出文字说明、证明过程或演算步骤. 22.(本小题满分10分)某地区试行高考考试改革:在高三学年中举行5次统一测试,学生如果通过其中2次测试即可获得足够学分升上大学继续学习,不用参加其余的测试,而每个学生最多也只能参加5次测试.假设某学生每次通过测试的概率都是31,每次测试时间间隔恰当,每次测试通过与否互相独立. (1)求该学生考上大学的概率.(2)如果考上大学或参加完5次测试就结束,记该生参加测试的次数为X ,求X 的分布列及X 的数学期望. 解:(1)记“该生考上大学”的事件为事件A ,其对立事件为A ,则 1455122()C ()()()333P A =+1455122131()1[C ()()()]333243P A ∴=-⋅+=- (2)参加测试次数X 的可能取值为2,3,4,5.P (X =2)=211()39=, 121214(3)C 33327P X ==⋅⋅⋅=, 1231214(4)C ()33327P X ==⋅⋅⋅=, 1344122(5)C ()()333P X ==⋅⋅++1627. 故X 的分布列为:1441638()234592727279E X =⨯+⨯+⨯+⨯=.答:该生考上大学的概率为131243;所求数学期望是389.23.(本小题满分10分)【16高考新课标】已知抛物线C :y 2=2x 的焦点为F ,平行于x 轴的两条直线l 1、l 2分别交C 于A 、B 两点,交C 的准线于P 、Q 两点.(1)若F 在线段AB 上,R 是PQ 的中点,证明AR ∥FQ ;(2)若△PQF 的面积是△ABF 的面积的两倍,求AB 中点的轨迹方程. 解:由题设F (12,0).设l 1:y =a ,l 2:y =b ,则ab ≠0, 且A (22a ,0),B (22b ,b ),P (-12,a ),Q (-12,b ),R (-12,2a b +).记过A 、B 两点的直线为l ,则l 的方程为2x -(a+b )y +ab =0. (1)由于F 点在线段AB 上,故1+ab =0. 记AR 得斜率为k 1,FQ 得斜率为k 2,则k 1=22211a b a b abb k a a ab a a---====-=+-, ∴AR ∥FQ .(2)设与x 轴的交点为D (x 1,0), 则2,2121211b a S x a b FD a b S PQF ABF -=--=-=∆∆. 由题设可得221211ba x ab -=--,所以01=x (舍去),11=x . 设满足条件的AB 的中点为E (x ,y ). 当AB 与x 轴不垂直时,由DE AB k k =可得)1(12≠-=+x x yb a .而y ba =+2,所以)1(12≠-=x x y . 当AB 与x 轴垂直时,E 与D 重合,所以,所求轨迹方程为12-=x y .。
2018届高三数学理科检测试题答案

2018届高三数学理科检测试题答案一、选择题:二、填空题 13.23 14. 98-15.n n 222+ 16. 2三、解答题:)cos b a C =∴由正弦定理得, …………………………2分 …………………………4分(0A ∈又,6分)由余弦定理得, 27b =+8分3,6bc =,10分的周长为5+12分18.(本小题满分12分)解:(1)设事件i A 为甲得分为i 分(1,2,3)i =,事件i B 为乙得分为i 分(1,2,3)i =则………………1分1122()5525P A =⨯= 2421311()555525P A =⨯+⨯= 25125354)(3=⨯=A P1111()5525P B =⨯= 214418()555525P B =⨯+⨯= 34416()5525P B =⨯=………………4分又甲、乙两人同时得3分为事件33B A ⋅故62519225162512)(33=⨯=⋅B A P .…………………………6分 (2)甲、乙两人得分之和ξ的可能取值为6,5,4,3,2 ………………7分6252251252)()2(11=⨯=⋅==B A P P ξ 625272512511258252)()()3(1221=⨯+⨯=⋅+⋅==B A P B A P P ξ625132251251225825112516252)()()()4(132231=⨯+⨯+⨯=⋅+⋅+⋅==B A P B A P B A P P ξ625272258251225162511)()()5(2332=⨯+⨯=⋅+⋅==B A P B A P P ξ62519225162512)()6(33=⨯=⋅==B A P P ξ …………………………10分ξ的分布列为………11分所以ξ的数学期望为481528136011523125:5625625625625625625E ξ=++++==.……………12分19.(本小题满分12分)解:(1)∵1BB ⊥平面ABCD ∴1BB ⊥AC …………2分在菱形ABCD 中,BD ⊥AC ……………4分 又1BD BB B⋂=∴AC ⊥平面1BB D ……………5分 ∵AC ⊂平面1AB C∴平面1AB C ⊥平面1BB D ……………6分(2)连接BD 、AC 交于点O ,以O 为坐标原点,以OA 为x 轴,以OD 为y 轴,如图建立空间直角坐标系.1(0,1,0),(0,1,0),(0,1,2),B D B A --………………7分11111,2)22B A BA A =⇒-,同理11(,2)2C -131(,2)22BA =,(0,2,0)BD =,11(,,2)22BC =-……………9分设平面1A BD 的法向量),,(z y x =∴10BA n BD n ⎧⋅=⎪⎨⋅=⎪⎩,则(n =- ………………10分 设平面1BDC 的法向量),,(z y x =10BD m BC m ⎧⋅=⎪⎨⋅=⎪⎩,则m = ………………11分 设二面角11A BD C --为θ,13cos 19m n m nθ⋅==……………12分 20.(本小题满分12分)解:(1)设抛物线22:2(0)C y px p =≠,则有22(0)y p x x=≠,………………1分 据此验证四个点知(3,-,(4,4)-在抛物线上,……………… 2分 易得,抛物线2C 的标准方程为22:4C y x = ………………3分椭圆22122:1(0)y x C a b a b+=>>,………………4分把点(2,0)-,代入可得:224,1a b ==………………5分所以椭圆1C 的标准方程为2214x y +=.……………6分 (2)可设2C 的焦点为F (1,0),当直线l 的斜率不存在时,直线l 的方程为1x =………………7分直线l 交椭圆1C 于点(1,M N0OM ON ≠,不满足题意. ……………8分当直线l 的斜率存在时,设直线l 的方程为(1)y k x =-, 并设1122(,),(,)M x y N x y由22(1)44y k x x y =-⎧⎨+=⎩,消去y 得, 2222(1)84(1)0k x k x k +-+-=,………………10分 于是221221224(1)8,1414k k x x x x k k -+==++2122314k y y k-=+ ①,………………11分 由OM ON ⊥得12120x x y y += ②将①代入②式,得2222224(1)340141414k k k k k k ----==+++,解得2k =±所以存在直线l 满足条件,且l 的方程为220x y --=或220x y +-=……………12分21.(本小题满分12分)解:(1)依题意:()f x 的定义域为(0,)+∞,2112()2axf x ax x x-'=-+=,当0a ≤时,()0f x '>,()f x ∴在(0,)+∞上单调递增,……………2分当0a >时,令()0f x '=,得x = ……………3分令()0f x '>,得x ∈;令()0f x '<,得)x ∈+∞,……………5分 ()f x ∴在上单调递增,在)+∞上单调递减。
2018年高考理科数学(3卷)答案详解(附试卷)
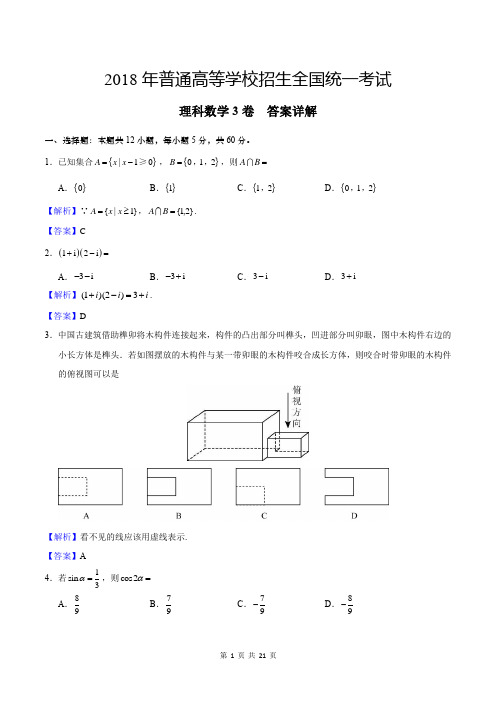
2018年普通高等学校招生全国统一考试理科数学3卷 答案详解一、选择题:本题共12小题,每小题5分,共60分。
1.已知集合,,则A .B .C .D . 【解析】∵}1|{≥=x x A ,}2,1{=B A . 【答案】C 2. A .B .C .D .【解析】i i i +=-+3)2)(1(. 【答案】D3.中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是【解析】看不见的线应该用虚线表示. 【答案】A 4.若,则 A .B .C .D . {}|10A x x =-≥{}012B =,,A B ={}0{}1{}12,{}012,,()()1i 2i +-=3i --3i -+3i -3i+1sin 3α=cos2α=897979-89-【解析】227cos212sin 199αα=-=-=. 【答案】B5.252()x x+的展开式中4x 的系数为A .10B .20C .40D .80【解析】由二项式定理得252()x x +的展开式的通项为251031552()2rr r r r rr T C x C x x --+⎛⎫== ⎪⎝⎭,由1034r -=,得2r =,∴252()x x+的展开式中4x 的系数为225240C =.【答案】C6.直线分别与轴,轴交于,两点,点在圆上,则△ABP 面积的取值范围是 A .B .C .D .【解析】如图所示,由题意可知)0,2(-A 、)0,2(-B ,∴22||=AB .过点P 作△ABP 的高PH ,由图可以看出,当高PH 所在的直线过圆心)0,2(时,高PH 取最小值或最大值. 此时高PH 所在的直线的方程为02=-+y x .将02=-+y x 代入,得到与圆的两个交点:)1,1(-N 、)1,3(M ,因此22|211|min =+-=|PM|,232|213|max =++=|PM|. 所以222221min =⨯⨯=S ,6232221max =⨯⨯=S . 20x y ++=x y A B P ()2222x y -+=[]26,[]48,⎡⎣22(2)2x y -+=图A6【答案】A7.函数的图像大致为【解析】设2)(24++-==x x y x f ,∵02)0(>=f ,因此排除A 、B ;)12(224)(23--=+-='x x x x x f ,由0)(>'x f 得22-<x 或220<<x ,由此可知函数)(x f 在),(220内为增函数,因此排除C.422y x x =-++【答案】D8.某群体中的每位成员使用移动支付的概率都为p ,各成员的支付方式相互独立,设X 为该群体的10位成员中使用移动支付的人数,4.2=DX ,)6()4(=<=x P x P ,则p= A .0.7B .0.6C .0.4D .0.3【解析】某群体中的每位成员使用移动支付的概率都为p ,看做独立重复事件,满足),10(~p B X .∵4.2=DX ,∴4.2)1(10=-p p ,解得6.0=p 或4.0=p .∵)6()4(=<=x P x P ,∴4661064410)1()1(p p C p p C -<-,解得021<-p ,即21>p . ∴6.0=p .【答案】B9.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .若△ABC 的面积为4222c b a -+,则C =A .B .C .D .【解析】由已知和△ABC 的面积公式有,4sin 21222c b a C ab -+=,解得C ab c b a sin 2222=-+.∴ C abCab ab c b a C sin 2sin 22cos 222==-+=,又∵1cos sin 22=+C C ,∴22sin cos ==C C ,4π=C . 【答案】C10.设A ,B ,C ,D 是同一个半径为4的球的球面上四点,△ABC 为等边三角形且其面积为39,则三棱锥D -ABC 体积的最大值为 A .312B .318C .324D .354【解析】如图A12所示,球心为O ,△ABC 的外心为O ′,显然三棱锥D -ABC 体积最大时D 在O′O 的延长线与球的交点.△ABC 为为等边三角形且其面积为39,因此有39432=⨯AB ,解得AB =6. △3260sin 32=⋅⨯=' AB C O ,2)32(42222=-='-='O O OC O O , 2π3π4π6π∴642=+='D O .∴ 三棱锥D -ABC 体积的最大值为31863931=⨯⨯=V .图A10【答案】B11.设F 1、F 2是双曲线C :22221(0,0)x y a b a b-=>>的左、右焦点,O 是坐标原点.过F 2作C 的一条渐近线的垂线,垂足为P .若,则的离心率为 AB.2CD【解析】双曲线C 的渐近线方程为by x a=±,即0bx ay ±=. ∴ 点F 2到渐近线的距离为b ba bc d =+=22,即b ||PF =2,∴ a b c ||PF ||OF |OP|=-=-=222222,∴ a |OP|||PF 661==,在Rt △OPF 2中,cbOF ||PF O PF ==∠||cos 222,在Rt △F 1PF 2中,bca cb |F |F ||PF ||PF |F |F ||PF O PF 4642cos 22221221221222-+=⋅-+=∠,∴ bca cbc b 464222-+=,化简得222364b a c =-,将222a c b -=代入其中得223a c =,1PF =C∴3222==ac e ,3=e .图A11【答案】C12.设0.2log 0.3a =,2log 0.3b =,则A .0a b ab +<<B .0ab a b <+<C . 0a b ab +<<D .0ab a b <<+【解析】∵0.20.20.2log 1log 0.3log 0.2<<,∴01a <<.∵221log 0.3log 2<,∴1b <-. ∴0ab <,0a b +<. ∵0.30.30.30.311=log 2log 0.2log 0.4log 0.31a b ab a b++=+=<=,0ab <,∴ab a b <+.综上所述 0ab a b <+<.【答案】B二、填空题:本题共4小题,每小题5分,共20分。
2018年全国新课标数学高考试卷及超详答案

2018年普通高等学校统一考试(宁夏卷)数学(理科)一、选择题:本大题共12小题,每小题5分,满分60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、已知函数y=2sin(ωx+φ)(ω>0)在区间[0,2π]的图像如下:那么ω=( ) A. 1B. 2C. 1/2D. 1/32、已知复数1z i =-,则221z zz -=-( ) A. 2i B. -2i C. 2 D. -23、如果等腰三角形的周长是底边长的5倍,那么它的顶角的余弦值为( ) A. 5/18B. 3/4C./2 D. 7/84、设等比数列{}n a 的公比2q =,前n 项和为n S ,则42S a =( ) A. 2 B. 4 C.152D.1725、右面的程序框图,如果输入三个实数a 、b 、c ,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入下面四个选项中的( ) A. c > xB. x > cC. c > bD. b > c6、已知1230a a a >>>,则使得2(1)1i a x -<(1,2,3)i =都成立的x 取值范围是( )A.(0,11a )B. (0,12a )C. (0,31a ) D. (0,32a ) 7、0203sin 702cos 10--=( )A. 12B. C. 2D. 8、平面向量a r ,b r共线的充要条件是( )A. a r ,b r 方向相同B. a r ,b r 两向量中至少有一个为零向量C. R λ∃∈, b a λ=r rD. 存在不全为零的实数1λ,2λ,120a b λλ+=r r r9、甲、乙、丙3位志愿者安排在周一至周五的5天中参加某项志愿者活动,要求每人参加一天且每天至多安排一人,并要求甲安排在另外两位前面。
不同的安排方法共有( ) A. 20种B. 30种C. 40种D. 60种10、由直线21=x ,x=2,曲线xy 1=及x 轴所围图形的面积为( ) A. 415 B. 417C. 2ln 21D. 2ln 211、已知点P 在抛物线y 2 = 4x 上,那么点P 到点Q (2,-1)的距离与点P 到抛物线焦点距离之和取得最小值时,点P 的坐标为( ) A. (41,-1) B. (41,1) C. (1,2) D. (1,-2)12、某几何体的一条棱长为7,在该几何体的正视图中,这条棱的投影是长为6的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a 和b 的线段,则a + b 的最大值为( )A. 22B. 32C. 4D. 52二、填空题:本大题共4小题,每小题5分,满分20分。
2018全国三卷理科数学高中高考真题包括答案.doc

精品文档2018 年普通高等学校招生全国统一考试理科数学一、选择题:本题共12 小题,每小题 5 分,共 60 分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合 A x | x 1≥ 0 , B 0 ,1,2 ,则 A BA .0B.1C.1,2D.0,1,22.1i 2 iA . 3 i B. 3 i C.3i D.3i3.中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是4.若 sin 1,则 cos2 3A .8B.7C.7 D.8 9 9 9 955. x2 2 的展开式中 x 4 的系数为xA .10 B. 20 C. 40 D. 806.直线 x y 2 0 分别与 x 轴,y轴交于A,B两点,点P在圆x22 上,则△ABP面积的取值范围2y2是A .2,6 B.4,8 C. 2 ,3 2 D. 2 2 ,3 2 7.函数y x4 x2 2 的图像大致为8.某群体中的每位成员使用移动支付的概率都为p ,各成员的支付方式相互独立,设 X 为该群体的 10 位成员中使用移动支付的人数, DX 2.4 , P X 4P X 6 ,则 pA .0.7B . 0.6C . 0.4D . 0.3222. △ABC 的内角 A , B , 的对边分别为 a , b , c ,若 △ ABC 的面积为 a bc,则 C9 C 4A . πB . πC . πD . π 234610.设 A ,B ,C , D 是同一个半径为4 的球的球面上四点, △ ABC 为等边三角形且其面积为9 3 ,则三棱锥D ABC 体积的最大值为A . 12 3B . 18 3C . 24 3D . 54 311.设 F 1 ,F 2x 2 y 20,b 0 )的左,右焦点, O 是坐标原点.过 F 2 作 C 的一条渐近线的是双曲线 C : 22 1 ( aa b垂线,垂足为 P .若 PF 16 OP ,则 C 的离心率为A . 5B . 2C . 3D . 212.设 a log 0.2 0.3 , b log 2 0.3 ,则A . a b ab 0B . ab a b 0C . a b 0 abD . ab 0 a b二、填空题:本题共 4 小题,每小题 5 分,共 20 分。
(精校版)2018年全国卷Ⅲ理数高考试题文档版(含答案)

绝密★启用前2018年普通高等学校招生全国统一考试理科数学注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{}|10A x x =-≥,{}012B =,,,则A B =A .{}0B .{}1C .{}12,D .{}012,, 2.()()1i 2i +-= A .3i --B .3i -+C .3i -D .3i +3.中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是4.若1sin 3α=,则cos 2α=A .89B .79C .79-D .89-5.522x x ⎛⎫+ ⎪⎝⎭的展开式中4x 的系数为A .10B .20C .40D .806.直线20x y ++=分别与x 轴,y 轴交于A ,B 两点,点P 在圆()2222x y -+=上,则ABP △面积的取值范围是A .[]26,B .[]48,C .232⎡⎤⎣⎦,D .2232⎡⎤⎣⎦,7.函数422y x x =-++的图像大致为8.某群体中的每位成员使用移动支付的概率都为p ,各成员的支付方式相互独立,设X 为该群体的10位成员中使用移动支付的人数, 2.4DX =,()()46P X P X =<=,则p = A .0.7B .0.6C .0.4D .0.39.ABC △的内角A B C ,,的对边分别为a ,b ,c ,若ABC △的面积为2224a b c +-,则C =A .π2B .π3C .π4D .π610.设A B C D ,,,是同一个半径为4的球的球面上四点,ABC △为等边三角形且其面积为93,则三棱锥D ABC -体积的最大值为 A .123B .183C .243D .54311.设12F F ,是双曲线22221x y C a b-=:(00a b >>,)的左,右焦点,O 是坐标原点.过2F 作C 的一条渐近线的垂线,垂足为P .若16PF OP =,则C 的离心率为 A .5B .2C .3D .212.设0.2log 0.3a =,2log 0.3b =,则A .0a b ab +<<B .0ab a b <+<C .0a b ab +<<D .0ab a b <<+二、填空题:本题共4小题,每小题5分,共20分。
高三数学-2018届高三数学质量检测题三参考答案 精品

2018届高三数学质量检测题三参考答案一、1、B 2、正确答案仅有③可推得结论成立。
3、C 4、C 5、D (33-)6、A 7、B 8、C 9、A 10、C二、11、-2018 12、22 13、⎪⎭⎫⎢⎣⎡+∞,43 14、53+。
三、 15、解:(1)由余弦定理知ab C ab ab c b a C ab b a c =∴=-+-+=cos 2,cos 2222222又------2分21cos =∴C 而0〈C 〈3ππ=∴C ------ 4分; (2)由21)24cot(=+θπ 得2)24tan(=+θπ ------ 5分344122)24(tan 1)24tan(2)2tan(2-=-⨯=+-+=+∴θπθπθπ ------ 7分 43tan =∴θ ------ 9分因为 θ为锐角54cos ,53sin ==∴θθ ------ 10分1033453215423sin 3cos cos 3sin )3sin()sin(+=⨯+⨯=+=+=+θπθπθπθC ------ 12分16、解:(1)∴+='12x y 曲线22-+=x x y 在点(1,0)处的切线的斜率为31=k因此直线1L 的方程为:)1(3-=x y ------ 3分又2L 为曲线的另一条切线,设2L 与曲线相切于点(),00y x ,2L 的斜率为2k ,则1202+=x k ,又21L L ⊥,所以1202+=x k =31-320-=∴x ------ 5分又点(00,y x )在曲线22-+=x x y 上920232)32(20-=---=∴y则直线 2L 的方程为:)32(31920+-=+x y 即2L 的方程为:3x+9y+22=0------7分 (2)由{3302293-==++x y y x 得:⎩⎨⎧=-=6125x y 即得L 1与L 2的交点M (25,61-)-------- 9分又L 1与x 轴交于点(1,0),2L 交x 轴于点B (0,322-) 1L ∴、2L 和x 轴围成的三角形的面积为∆MAB 的面积, 而12125)3221(2521=+⨯⨯=∆MAB S ------ 13分 即1L 、2L 和x 轴围成的三角形面积为12125。
2018届高三上学期期末联考数学(理)试题有答案-精品

2017—2018学年度第一学期期末联考试题高三数学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分全卷满分150分,考试时间120分钟.注意:1. 考生在答题前,请务必将自己的姓名、准考证号等信息填在答题卡上.2. 选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号,答在试卷上无效.3. 填空题和解答题用0.5毫米黑色墨水签字笔答在答题卡上每题对应的答题区域内.答在试题卷上无效.第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.把答案填在答题卡上对应题号后的框内,答在试卷上无效.1.设集合{123}A =,,,{45}B =,,{|}M x x a b a A b B ==+∈∈,,,则M 中的元素个数为A .3B .4C .5D .62.在北京召开的第24届国际数学家大会的会议,会议是根据中国古代数学家赵爽的弦图(如图)设计的,其由四个全等的直角三角形和一个正方形组成,若直角三角形的直角边的边长分别是3和4,在绘图内随机取一点,则此点取自直角三角形部分的概率为 A .125B .925C .1625D .24253.设i 为虚数单位,则下列命题成立的是A .a ∀∈R ,复数3i a --是纯虚数B .在复平面内i(2i)-对应的点位于第三限象C .若复数12i z =--,则存在复数1z ,使得1z z ∈RD .x ∈R ,方程2i 0x x +=无解4.等比数列{}n a 的前n 项和为n S ,已知3215109S a a a =+=,,则1a =A .19B .19-C .13D .13-5.已知曲线421y x ax =++在点(1(1))f --,处切线的斜率为8,则(1)f -=试卷类型:A天门 仙桃 潜江A .7B .-4C .-7D .4 6.84(1)(1)x y ++的展开式中22x y 的系数是A .56B .84C .112D .1687.已知一个空间几何体的三视图如图,根据图中标出的尺寸(单位:cm ),可得这个几何体的体积是 A .4cm 3B .5 cm 3C .6 cm 3D .7 cm 38.函数()sin()(0,0)f x A x A ωϕω=+>>的图像如图所示,则(1)(2)(3)(18)f f f f ++++的值等于ABC 2D .19.某算法的程序框图如图所示,其中输入的变量x 在1,2,3…,24 这24个整数中等可能随机产生。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018届高三数学综合试卷第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.若命题P ∶x ∈A ∪B 则?P 是A .x ∉A∩BB .x ∉A 或x ∉BC .x ∉A 且x ∉BD .x ∈A∩B2.下列各图形中,是函数图象的是3.若点A(x ,y)在第一象限,且2x+3y=6,则3322log log x y +A .有最大值1B .有最小值1C .有最大值32D .既无最大值也无最小值4.双曲线k x 2+5y 2=5的一个焦点是(0,2),则k 等于A .53B .-53CD .5.函数sin(3)cos()cos(3)cos()3633y x x x x ππππ=+--++的图象的一条对称轴的方程是 A .π12x = B .π6x = C .π12x =- D .π24x =-6.盒中有10只螺丝钉,其中有3只是坏的,现从盒中随机地抽取4只,那么310等于A .恰有2只是好的概率B .恰有1只是坏的概率C .至多2只是坏的概率D .4只全是好的概率7.甲、乙两人同时从A 地赶往B 地,甲先骑自行车到中点后改为跑步,而乙则是先跑步到中点后改为骑自行车,最后两人同时到达B 地.又知甲骑自行车比乙骑自行车的速度快,并且两人骑车速度均比跑步速度快.若某人离开A 地的距离S 与所用时间t 的函数关系可用图①~④中的某一个来表示,则甲、乙两人的图象只可能分别是A .甲是图①,乙是图②B .甲是图①,乙是图④C .甲是图③,乙是图②D .甲是图③,乙是图④8.空间四点A B C D 、、、,若直线,,AB CD AC BD AD BC ⊥⊥⊥同时成立,则A B C D 、、、四点的位置关系是A .一定共面B .一定不共面C .不一定共面D .这样的四点不存在9.函数f(x)满足f(x-1)+f(x+1)=2x 2-8x+8,f(x+1)-f(x-1)=4(x-2),且f(x-1),-12,f(x)成等差数列,则x 的值是A .2B .3C .2和3D .2和-310.已知()321233y x bx b x =++++是R 上的单调增函数,则b 的范围A .1b <-或2b >B .1b ≤-或2b ≥C .12b -<<D .12b -≤≤11.(理)131lim 3(1)3n n n n a +→∞=++,则实数a 的取值范围为 A .(-2,0) B .(-∞,-2)∪(0,+∞) C .(-4,2)D .(-∞,-4)∪(2,+∞)(文) 如右图△ABD CBD ,△ABD 为等腰三角形∠BAD =∠BCD =90°,且面ABD ⊥面BCD ,则下列4个结论中,正确结论的序号是①AC ⊥BD②△ACD 是等腰三角形 ③AB 与面BCD 成60°角 ④AB 与CD 成60°角A .①②③B .C .①③④D .②③④12.设12)310(++n (n ∈N )的整数部分和小数部分分别为I n 和F n ,则F n (F n +I n )的值为A .1B .2C .4D .与n 有关的数第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分.答案填在题中横线上.13.直线20x y m ++=按向量()1,2a =--平移后与圆22:240C x y x y ++-=相切,则实数m 的值为____________.14.设x 、y 满足约束条件310x y y x y +≤⎧⎪≤-⎨⎪≥⎩,则z =x 2+y 2的最小值是.15.“渐升数”(如34689)是指每个数字比其左边的数字大的正整数已知共有126个五位“渐升数”,若把这些数按从小到大的顺序排列,则第100个数为 16.由等式x 4+a 1x 3+a 2x 2+a 3x+a 4=(x+1)4+b 1(x+1)3+b 2(x+1)2+b 3(x+1)+b 4定义映射f:(a 1,a 2,a 3,a 4)→(b 1,b 2,b 3,b 4),则f(4,3,2,1)等于_________三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤. 17.(本题满分12分)有一块边长为6m 的正方形钢板,将其四个角各截去一个边长为x (m )的小正方形,然后焊接成一个无盖的蓄水池(不计损耗).(1)求容积V 关于自变量x 的函数,并指出其定义域; (2)指出函数V (x )的单调区间;(3)蓄水池的底边为多少时,蓄水池的容积最大?最大容积是多少?18.(本题满分12分)已知向量a = e 1-e 2,b = 4e 1+3e 2,其中e 1= (1,0),e 2= (0,1). (1)试计算a ·b ;|a +b |的值;(2)n 个向量a 1、a 2、…、a n 称为“线性相关”,如果存在n 个不全为零的实数k 1、k 2、…、k n ,使得k 1a 1+ k 2a 2+…+ k n a n =0成立,否则,则为“不线性相关”.依此定义,三个向量a 1= (-1,1),a 2= (2,1),a 3= (3,2) 是否为“线性相关”的?请说明你的判断根据;(只理科做)(3)平面上任意三个互不共线的向量a 1、a 2、a 3,一定是线性相关的吗?为什么?如图,ABC ∆中,⊥===PA a BC AC AB ,平面ABC ,且E N M a PA ,,,=分别为PC BC AB ,,的中点。
(1)求二面角A MC P --的大小; (2)求三棱锥MCB E -的体积;(3)求异面直线AE 与PN 所成角的大小。
20.(本题满分12分)已知()()1,0,1,0A B -,P 是平面上一动点,且满足PA BA PB AB ⋅=⋅ (1)求点P 的轨迹C 对应的方程;(2)已知点(),2A m 在曲线C 上,过点A 作曲线C 的两条弦,AD AE ,且,AD AE 的斜率12,k k 满足122k k ⋅=。
求证:直线DE 过定点,并求出这个定点。
21.(本小题满分12分)如图,已知斜平行六面体ABCD -A 1B 1C 1D 1中,AB =AD = 2 ,∠A 1AB =∠A 1AD =∠BAD . (1)设∠BAD =α,A 1A 与面ABCD 所成的角为β,求证:2coscos cos ααβ=;(2)设A 1A 到面B 1D 1DB 的距离为1,求二面角A 1-AD -B 的余弦.BCA 1B 1C 1D 1设集合S ={|,||<1}x x x ∈R 且.在S 中定义运算“*”,使得*1a ba b ab+=+. (1)证明:如果a ∈S ,b ∈S ,那么a *b ∈S ;(2)证明:对于S 中的任何元素a 、b 、c ,都有(a *b )*c = a *(b *c )成立;(3)试问:是否存在单位元e ,使得a *e = e *a = a ?又是否存在不变元i ,使得a *i = i *a = i .参考答案1-16 略17.(1)设蓄水池的底面边长为a ,则a =6-2x ,且蓄水池容积为2()(62)V x x x =-.由>062>0x x ⎧⎨-⎩,得()V x 定义域为(0,3).(2)322()42436,'()124836V x x x x V x x x =-+=-+.令'()V x ≥0,并注意到(0,3)x ∈知:()V x 的单调递增区间为(0,1];令'()V x ≤0,并注意到(0,3)x ∈知,()V x 的单调递减区间为[1,3].(3)令2'()1248360V x x x =-+=,得x =1(3(0,3)x =∉,舍去).此时,a = 4(m ).由()V x 单调性知,3max [()](1)16(m )V x V ==.故当底面边长为4m 时,蓄水池容积最大,最大容积为16m 3.18.(1)a = (3,0) – (0,2) = (3,-2),b = (4,0) +(0,1) =(4,1).a ·b = (3,-2) ·(4,1)=10; |a +b |=|(7,1)|= 50 = 52. (2)是“线性相关”的.令k 1(-1,1)+k 2(2,1)+k 3(3,2) = (0,0),于是k 1+2k 2+3k 3=0,且k 1+k 2+2k 3=0. 显然由以上两条件构成的方程组有不全为零的实数解(如k 1= -1,k 2= -5,k 3=3),故它们为线性相关的.(3)平面上任意三个互不共线的向量一定线性相关.由平面向量的基本定理知,平面上任意两个不共线的向量a 1、a 2均可作为向量的一组基底,并且对于平面内的任一其它向量a 3,有且仅有唯一的一对实数λ1、λ2,使a 3 = λ1a 1+λ2a 2.分别取k 1=λ1,k 2=λ2,k 3= -1,即有λ1a 1+λ2a 2- a 3 =0,也就是平面上任意三个互不共线的向量一定线性相关.19.(1)2arctg PMA =∠(2)32483218331a a a V =⋅⋅=(3)取NC 的中点K ,则AEK ∠即为异面直线AE 与PN 所成的角a AK a EK a PN a AE 413,47,27,22====, 在AEK ∆中,2814arccos=∠AEK 20.(1)设(),P x y ,则()1,PA x y =--,()1,PB x y =---,()2,0AB =-,()2,0BA =于是由PA BA PB AB ⋅=⋅()221x =+整理后得:24y x =所以点P 的轨迹C 对应的方程为24y x =(2)由(1)知()1,2M ,设221212,,,44y y D y E y ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭于是121222122221144y y k k y y --=⋅=--即()()12228y y ++= 又记12221212444DE y y k k y y y y -===+- 于是1212484y y k y y k ⎧+=⎪⎪⎨⎪⋅=-⎪⎩所以DE 直线的方程为2111244y y y x y y ⎛⎫-=- ⎪+⎝⎭即()121240x y y y y y -++=亦即()()120k x y +-+= 显然直线DE 过定点()1,2--21.(1)如图,因∠A 1AB =∠A 1AD ,A 1A =A 1A ,AB =AD ,故△A 1AB ≌△A 1AD .于是,A 1B =A 1D .故BD ⊥A 1O .因AB =AD ,故四边形ABCD 为菱形,从而BD ⊥AC .又A 1O ∩AC =O ,故BD ⊥面A 1C 1CA .于是,面ABCD ⊥面A 1C 1CA . (★)作HE ⊥AD 于E ,连A 1E ,由三垂线定AB C DA 1B 1C 1D 1O 1E FOH理得,A 1E ⊥AD .故2coscos cos 11ααβ=⋅==EA AE AE AH H A AH . (2)由(★)得,面B 1D 1DB ⊥面A 1C 1CA .作A 1F ⊥OO 1于F ,则A 1F ⊥面B 1D 1DB .故A 1F =1.在Rt △A 1O 1D 1中,A 1O 1=A 1D 1•2cos α=2cos2α.于是O 1F =αcos 21211=-F A O A .故2cos2cos cos cos 2coscos 11ααβαα=∠==F O A ,从而ααcos cos 22=.又αcos ≠0,于是αcos = 12 ,α=60º.由(1)知,∠A 1EH是二面角A 1-AD -B的平面角,于是3160tan 30tan cos 11=⋅⋅==∠AE AE E A EH EH A . 22.(1)∵a ∈S ,b ∈S ,∴|a |<1,|b |<1.∴22(1)()(1)(1) ab a b ab a b ab a b +-+=++++--22(1)(1)(1)(1)(1)(1)a b a b a b =++--=-->0.∴2()1a b ab ++<1,即|1a b ab ++|<1,也就是1a bab++∈S ,从而a *b ∈S . (2)(a *b )*c =1*1111a bca b a b c abc ab c a b ab ab ac bc c ab+++++++==+++++++,a *(b *c ) =1*1111b ca b c a b c abc bc a b c bc ab ac bca bc+++++++==+++++++, 故(a *b )*c = a *(b *c ). (3)若a *e = e *a = a ,则11a e e aa ae ea++==++,变形得(1)e a a ea +=+,从而,2a ea =,该式不能对一切满足|a |<1的实数a 恒成立,故不存在满足条件的单位元e .若a *i = i *a = i ,则11a i i ai ai ia++==++,变形得 (1)i a i ia +=+,从而,2a i a =,当1i =±时,等式对一切满足|a |<1的实数a 恒成立,故存在满足条件的不变元1i =±.。
