江西省南昌市教研室命制2014届高三交流卷(一)数学(理)试题 Word版含答案
江西省南昌市教研室命制2014届高三交流卷(二)数学(理)试题 Word版含答案

南昌市教研室命制2014届高三交流卷(二)数学(理)试题第I 卷(选择题 共60分)一、选择题:本大题共12个小题,每小题5分,共60分.每小题给出的四个选项中只有一项是符合题目要求的.1.已知全集R U =,集合{}21x A x =>,{}2340B x x x =-->,则A B ⋂=( )A .{}0x x > B .{}10x x x <->或 C .{}4x x > D .{}14x x -≤≤2.已知复数231ii--(i 是虚数单位),它的实部和虚部的和是( ) A .4 B .6 C .2 D .3 3.下列命题中是假.命题..的是 ( )A .,)1()(,342是幂函数使+-⋅-=∈∃m m xm x f m R ),0(+∞且在上递减B .有零点函数a x x x f a -+=>∀ln ln )(,02C .βαβαβαsin cos )cos(,,+=+∈∃使R ;D .,()sin(2)f x x ϕϕ∀∈=+R 函数都不是偶函数4.已知实数y x ,满足1218y y x x y ≥⎧⎪≤-⎨⎪+≤⎩,则目标函数y x z -=的最小值为( )A .5B .2-C .6D .75. “1a =”是“函数a x x f -=)(在区间[2,)+∞上为增函数”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件6.设振幅、相位、初相为方程sin()(0)y A x b A ωϕ=++>的基本量,则方程3sin(21)+4y x =-的基本量之和为 ( ) A .4B .23x +C .8D .21x +7.已知正四面体的俯视图如图所示,其中四边形ABCD 是边长为2的正方形,则这个正四面体的主视图的面积为 ( ) A .22 B .2 C .23 D .38.F 1,F 2是双曲线2222:1(,0)x y C a b b a b-=>>的左、右焦点,过左焦点F 1的直线l 与双曲线C 的左、右两支分别交于A ,B 两点,若22||:||:||3:4:5AB BF AF =,则双曲线的离心率是( )A .3B .15C .2D .139.设235111111,,a dx b dx c dx x x x ===⎰⎰⎰,则下列关系式成立的是( )A .235a b c <<B .325b a c<<C .523c a b <<D .253a c b<<10.已知()f x 是R 上的偶函数,当0x ≥时,12()22xf x x =-,又a 是函数2()ln(1)g x x x=+-的正零点,则(2)f -,()f a ,(1.5)f 的大小关系是 ( ) A .(1.5)()(2)f f a f <<- B .(2)(1.5)()f f f a -<< C .()(1.5)(2)f a f f <<-D .(1.5)(2)()f f f a <-<第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4个小题,每小题4分,共16分. 11.已知在平面直角坐标系xoy 中圆C 的参数方程为:33cos 13sin x y θθ⎧=+⎪⎨=+⎪⎩,(θ为参数),以OX 为极轴建立极坐标系,直线极坐标方程为:,0)6cos(=+πθρ则圆C 截直线所得弦长为12.右边茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中有一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率是____________.13.如图,已知||1,||3OA OB ==,OA 与OB 的夹角为56π,点C 是AOB ∆的外接圆上优孤AB 上的一个动点,则OA OC ⋅的最大值为 .14.右图是一个算法的程序框图,最后输出的W =________.15. n ⎡⎤⎣⎦表示不超过n 的最大整数.11233S ⎡⎤⎡⎤⎡⎤=++=⎣⎦⎣⎦⎣⎦,24567810S ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=++++=⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦,3910111213141521S ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=++++++=⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦,那么5S = .三、解答题:本大题共6小题,共74分. 16. (本题满分12分)已知θ为向量a 与b 的夹角,||2=a ,||1=b ,关于x 的一元二次方程2x -||a x 0+⋅=a b 有实根. (Ⅰ)求θ的取值范围;(Ⅱ)在(Ⅰ)的条件下,求函数23()sin cos 3cos 2f θθθθ=+-的最值.17.(本题满分12分)某学校实施“十二五高中课程改革”计划,高三理科班学生的化学与物理水平测试的成绩抽样统计如下表.成绩分A(优秀)、B(良好)、C(及格)三种等级,设x 、y 分别表示化学、物理成绩. 例如:表中化学成绩为B 等级的共有20+18+4=42人.已知x 与y 均为B 等级的概率为0.18. (Ⅰ) 求抽取的学生人数;(Ⅱ)若在该样本中,化学成绩的优秀率是0.3,求b a ,的值;(Ⅲ)物理成绩为C 等级的学生中,已知10≥a ,1712≤≤b , 随机变量b a -=ξ,求ξ的分布列和数学期望.18. (本题满分12分)已知公差不为零的等差数列{}n a 的前5项和为30,且2a 为1a 和4a 的等比中项. (1)求{}n a 的通项公式n a 及前n 项和n S ;(2)若数列{}n b 满足*1()n n n b S n N b n +=∈,且11b =,求数列1{}n n b +的前n 项和n T19.(本题满分12分)在三棱柱111ABC A B C -中,已知2AB BC ==,090ABC ∠=,点1A 在底面ABC 的投影为B ,且123A B =.(1)证明:平面11AA B B ⊥平面11BB C C ; (2)设P 为11B C 上一点,当29PA =时,求二面角1A AB P --的正弦值.1313xyA B C A 7 20 5 B 918 6Ca4b20.(本题满分13分)如图,设F是椭圆C:22221(0)x ya ba b+=>>的左焦点,MN为椭圆的长轴,P为椭圆C上一点,且||[2,6]PF∈.(Ⅰ)求椭圆C的方程;(Ⅱ)设点(8,0)Q-,①求证:对于任意的割线QAB,恒有AFM BFN∠=∠;②求三角形ABF∆面积的最大值.21.(本小题满分14分) 设函数2()ln ()2af x x x a =+--,a R ∈. (1)若函数()f x 在1[, 2]2上单调递增,求实数a 的取值范围; (2)求函数)(x f 的极值点.(3)设x m =为函数()f x 的极小值点,()f x 的图象与x 轴交于1212(,0),(,0)()A x B x x x <两点,且120x x m <<<,AB 中点为0(,0)C x ,比较)('x f 与0的大小.答案第I 卷(选择题 共60分)一、选择题:本大题共12个小题,每小题5分,共60分.每小题给出的四个选项中只有一项是符合题目要求的.1.已知全集R U =,集合{}21x A x =>,{}2340B x x x =-->,则A B ⋂=( )A .{}0x x > B .{}10x x x <->或 C .{}4x x > D .{}14x x -≤≤2.已知复数231ii--(i 是虚数单位),它的实部和虚部的和是( ) A .4 B .6 C .2 D .3 3.下列命题中是假命题...的是 ( )A .,)1()(,342是幂函数使+-⋅-=∈∃m m xm x f m R ),0(+∞且在上递减B .有零点函数a x x x f a -+=>∀ln ln )(,02C .βαβαβαsin cos )cos(,,+=+∈∃使R ;D .,()sin(2)f x x ϕϕ∀∈=+R 函数都不是偶函数4.已知实数y x ,满足1218y y x x y ≥⎧⎪≤-⎨⎪+≤⎩,则目标函数y x z -=的最小值为( )A .5B .2-C .6D .75. “1a =”是“函数a x x f -=)(在区间[2,)+∞上为增函数”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件6.设振幅、相位、初相为方程sin()(0)y A x b A ωϕ=++>的基本量,则方程3sin(21)+4y x =-的基本量之和为 ( ) A .4B .23x +C .8D .21x +7.已知正四面体的俯视图如图所示,其中四边形ABCD 是边长为2的正方形,则这个正四面体的主视图的面积为 ( ) A .22 B .2 C .23 D .38.F 1,F 2是双曲线2222:1(,0)x y C a b b a b-=>>的左、右焦点,过左焦点F 1的直线l 与双曲线C 的左、右两支分别交于A ,B 两点,若22||:||:||3:4:5AB BF AF =,则双曲线的离心率是( )A .3B .15C .2D .139.设235111111,,a dx b dx c dx x x x ===⎰⎰⎰,则下列关系式成立的是( )A .235a b c <<B .325b a c<<C .523c a b <<D .253a c b<<10.已知()f x 是R 上的偶函数,当0x ≥时,12()22xf x x =-,又a 是函数2()ln(1)g x x x=+-的正零点,则(2)f -,()f a ,(1.5)f 的大小关系是 ( ) A .(1.5)()(2)f f a f <<- B .(2)(1.5)()f f f a -<< C .()(1.5)(2)f a f f <<-D .(1.5)(2)()f f f a <-<第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4个小题,每小题4分,共16分.11. 已知在平面直角坐标系xoy 中圆C 的参数方程为:33cos 13sin x y θθ⎧=+⎪⎨=+⎪⎩,(θ为参数),以OX 为极轴建立极坐标系,直线极坐标方程为:,0)6cos(=+πθρ则圆C 截直线所得弦长为 2412.右边茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中有一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率是____110________.13.如图,已知||1,||3OA OB ==,OA 与OB 的夹角为56π,点C 是AOB ∆的外接圆上优孤AB 上的一个动点,则OA OC ⋅的最大值为 . 1+7214.右图是一个算法的程序框图,最后输出的W =_____22___.15. n ⎡⎤⎣⎦表示不超过n 的最大整数.11233S ⎡⎤⎡⎤⎡⎤=++=⎣⎦⎣⎦⎣⎦,24567810S ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=++++=⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦,3910111213141521S ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=++++++=⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦,那么5S = 55 .三、解答题:本大题共6小题,共74分. 16. (本题满分12分)已知θ为向量a 与b 的夹角,||2=a ,||1=b ,关于x 的一元二次方程2x -||a x 0+⋅=a b 有实根. (Ⅰ)求θ的取值范围;(Ⅱ)在(Ⅰ)的条件下,求函数23()sin cos 3cos 2f θθθθ=+-的最值. ⋅CBAO解:16.(I ) 因为θ为向量a 与b 的夹角,所[0,]θπ∈,由|a |=2,|b |=1,可得2|a |=4,⋅a b =|a ||b |cos θ. ………………3分关于x 的一元二次方程20x x -+⋅=|a |a b 有实根,则有44(12cos )0θ∆=-⋅-≥2|a |a b =,得1cos 2θ≤,所以,3πθπ⎡⎤∈⎢⎥⎣⎦.………6分 (II )23cos 3cos sin )(f 2-+=θθθθ =23)212cos (32sin 21-++θθ =)32sin(2cos 232sin 21πθϑθ+=+ ………………9分 因为π,π3θ⎡⎤∈⎢⎥⎣⎦,所以⎥⎦⎤⎢⎣⎡∈+37,32πππθ,所以sin(⎥⎦⎤⎢⎣⎡-∈+23,1)32(πθ 所以,函数的最大值为23,最小值为-1. ………………12分17. (本题满分12分)17.某学校实施“十二五高中课程改革”计划,高三理科班学生的化学与物理水平测试的成绩抽样统计如下表.成绩分A(优秀)、B(良好)、C(及格)三种等级,设x 、y 分别表示化学、物理成绩. 例如:表中化学成绩为B 等级的共有20+18+4=42人.已知x 与y 均为B 等级的概率为0.18. (Ⅰ) 求抽取的学生人数;(Ⅱ)若在该样本中,化学成绩的优秀率是0.3,求b a ,的值;(Ⅲ)物理成绩为C 等级的学生中,已知10≥a ,1712≤≤b , 随机变量b a -=ξ,求ξ的分布列和数学期望.xyA B C A 7 20 5 B 918 6Ca4b18. (本题满分12分)已知公差不为零的等差数列{}n a 的前5项和为30,且2a 为1a 和4a 的等比中项. (1)求{}n a 的通项公式n a 及前n 项和n S ; (2)若数列{}n b 满足*1()n n n b S n N b n +=∈,且11b =,求数列1{}n nb +的前n 项和n T 解:(1) 设公差为(0)d d ≠,则1121115103022()(3)a d a d a d a a d +==⎧⎧⇒⎨⎨=+=+⎩⎩,∴ 2n a n =, (1)n S n n =+; (2)由(1)11n nn b S n b n+==+, 当2n ≥时,32411231234n nn b b b b b n b b b b b -=⋅⋅⋅⋅=⋅⋅⋅⋅,∴ !n b n =,又 11b =适合上式∴ !nb n = *()n N ∈, ∴111=(1)!(1)!n n n b n n n +=-++!, ∴ 111111111()()()()11!2!2!3!3!4!!(1)!(1)!nT n n n =-+-+-++-=-++.19.(本题满分12分) 在三棱柱111ABC A B C -中,已知2AB BC ==,090ABC ∠=,点1A 在底面ABC 的投影为B ,且123A B =.(1)证明:平面11AA B B ⊥平面11BB C C ; (2)设P 为11B C 上一点,当29PA =时,求二面角1A AB P --的正弦值.1313(1)证明:∵ 1A B ⊥平面ABC ,BC ⊆平面ABC ∴ 1A B BC ⊥,在ABC ∆中,090ABC ∠=,∴ AB BC ⊥,∴ BC ⊥平面11AA B B ,BC ⊆平面11BB C C , ∴ 平面11AA B B ⊥平面11BBC C ; (2)法一:传统方法 由(1)知11B C ⊥平面11AA B B ,∴ 1PB ⊥平面11AA B B ,过点1B 作棱AB 的垂线,垂足为O ,连接OP ,则1POB ∠即为二面角1A AB P --的平面角 连接1AB ,在1ABB ∆,由余弦定理可求得128AB =,∵ 29PA =,∴ 11PB =,∴ 13OP =,∴ 113sin 13POB ∠=. 法二:向量方法 如图建立空间直角坐标系B xyz -, (2,0,0)A ,(0,2,0)A ,(0,0,23)A ,由 111(2,0,23)B A BA B =⇒-,ABCA 1B 1C 1PCA 1B 1C 1Pz yxxyOBFMNQ A 由 111(2,2,23)BC BC C =⇒-,由 1112(2,,23)(1)B C B P P λλλ=⇒->,由 292AP λ=⇒=,∴ (2,1,23)P -,设(,)n x y z =,为平面PAB 的法向量,则022300x n BA x y z n BP ⎧=⎧⋅=⎪⎪⇒⎨⎨-++=⎪⋅=⎪⎩⎩,取 (0,6,3)n =-, 由(1)知 (0,2,0)m BC ==为平面11AA B B 的法向量, ∴ 126cos ,23939n m <>=-=-,13sin ,13n m <>=.20.(本题满分13分)如图,设F 是椭圆C :22221(0)x y a b a b+=>>的左焦点,MN 为椭圆的长轴,P 为椭圆C 上一点,且||[2,6]PF ∈. (Ⅰ)求椭圆C 的方程; (Ⅱ)设点(8,0)Q -,①求证:对于任意的割线QAB ,恒有AFM BFN ∠=∠; ②求三角形ABF ∆面积的最大值.解:(Ⅰ)2211612x y +=; (Ⅱ)①易知直线AB 斜率存在.当AB 的斜率为0时,显然0AFM BFN ∠=∠=,满足题意,当AB 的斜率不为0时,设AB l : 8(0)x my m =-≠,11(,)A x y ,22(,)A x y ,由 22228(34)48144011612x my m y my x y =-⎧⎪⇒+-+=⎨+=⎪⎩. ∴ 222222248412(34)24(4)04m m m m ∆=-⨯+=->⇒>,1224834m y y m +=+,12214434y y m =+. 则121222AF BF y y k k x x +=+++1212211212(6)(6)66(6)(6)y y y my y my my my my my -+-=+=----12121226()(6)(6)my y y y my my -+=--, 又1212221444826()2603434mmy y y y m m m -+=⋅-⋅=++,∴0A F B F k k +=,从而AFM BFN ∠=∠.综合可知:对于任意的割线QAB ,恒有AFM BFN ∠=∠.②由①,22121724||||234ABF QBF QAFm S S S QF y y m ∆∆∆-=-=⋅-=+, 2222724727233163(4)162316344m m m m -==≤=-+⋅-+-,当且仅当2216344m m -=-,即2213m =±(此时适合于0>∆的条件)时取等号. ∴ 三角形ABF ∆面积的最大值是33.换元法:令24(0)m t t -=>,则 2227247272723316343162483m t m t t t-==≤=+++.21.(本小题满分14分)设函数2()ln ()2af x x x a =+--,a R ∈. (1)若函数()f x 在1[, 2]2上单调递增,求实数a 的取值范围; (2)求函数)(x f 的极值点.(3)设x m =为函数()f x 的极小值点,()f x 的图象与x 轴交于1212(,0),(,0)()A x B x x x <两点,且120x x m <<<,AB 中点为0(,0)C x ,比较)('x f 与0的大小.解:(1)21221()2()x ax f x x a x x -+'=+-=依题意得,在区间1[, 2]2上不等式22210x ax -+≥恒成立. 又因为0x >,所以12(2)a x x≤+.所以222a ≤,2a ≤所以实数a 的取值范围是(, 2]-∞.(2)2221()x ax f x x-+'=,令2()221h x x ax =-+①显然,当0a ≤时,在(0,)+∞上()0h x >恒成立,这时()0f x '>,此时,函数()f x 没有极值点; ……………………………………6分②当0a >时,(ⅰ)当0∆≤,即02a <≤时,在(0,)+∞上()0h x ≥恒成立,这时()0f x '≥,此时,函数()f x 没有极值点;(ⅱ)当0∆>,即2a >时,易知,当222222a a a a x --+-<<时,()0h x <,这时()0f x '<; 当2202a a x --<<或222a a x +->时,()0h x >,这时()0f x '>;所以,当2a >时,222a a x --=是函数()f x 的极大值点;222a a x +-=是函数()f x 的极小值点.综上,当2a ≤时,函数()f x 没有极值点;当2a >时,222a a x --=是函数()f x 的极大值点;222a a x +-=是函数()f x 的极小值点. ………9分 (3)由已知得2211122222()ln ()02()ln ()02a f x x x a a f x x x a ⎧=+--=⎪⎪⎨⎪=+--=⎪⎩两式相减,得:()112122ln ()2x x x x x a x +-+-……① 由'1()2()f x x a x =+-,得'0001()2()f x x a x =+-…………② 得①代入②,得'001201212()2()(2)f x x a x x a x x x =+-=++-+ =221222*********(1)211ln ln ()()1x x x x x x x x x x x x x x ⎡⎤-⎢⎥⎢⎥-=-+--⎢⎥+⎢⎥⎣⎦令12(0,1),x t x =∈且2222(1)()ln (01),()0,1(1)t t t t t t t t t ϕϕ--'=-<<=-<++()t ϕ∴在(0,1)上递减,()(1)0t ϕϕ∴>=120,()0x x f x '<∴<。
2014江西高考真题数学理(含解析)

的中点,则椭圆 C 的离心率为_______ 三.解答题:本大题共 6 小题,共 75 分,解答应写出文字说明、证明过程或演算步骤 π π 16. (本题满分 12 分)已知函数 f ( x) sin( x ) a cos( x 2 ) ,其中 a R, ( , ) 2 2 π (1)当 a 2, 时,求 f ( x ) 在区间 [0, π ] 上的最大值与最小值; 4 π (2)若 f ( ) 0, f ( π) 1 ,求 a, 的值. 2
4.在 △ABC 中,内角 A,B,C 所对应的边分别为 a, b, c, ,若 c 2 (a b)2 6 , C ( ) A.3 B.
π ,则 △ABC 的面积 3
9 3 2
C.
3 3 2
D. 3 3
5.一几何体的直观图如右图,下列给出的四个俯视图中正确的是(
)
俯视
A
B
C
D
左(侧)视
1
0
f ( x )dx, 则 f ( x )dx (
0
)
1 3
C.
1 3
D.1
9.在平面直角坐标系中, A, B 分别是 x 轴和 y 轴上的动点,若以 AB 为直径的圆 C 与直线
2 x y 4 0 相切,则圆 C 面积的最小值为(
A.
) D.
4 5
B.
3 4
C. (6 2 5)
cos _______
1 ,向量 a 3e1 2e1 与 b 3e1 e2 的夹角为 ,则 3
1 x2 y 2 15. 过点 M (1,1) 作斜率 为的直线与椭圆 C : 2 2 1(a b 0) 相交于 A, B , 若 M 是线段 AB 2 a b
江西省南昌市教研室命制2014届高三交流卷(六)数学(理)Word版含答案

一、选择题(每小题5分,共50分.下列每小题所给选项只有一项符合题意,请将正确答案的序号填涂在答题卡上)1、设集合A ={x |1<x <4},集合B ={x |x 2-2x -3≤0},则A ∩(∁R B )=( ). A .(1,4) B .(3,4) C .(1,3)D .(1,2)∪(3,4)2、已知i 为虚数单位,a 为实数,复数z =(1-2i)(a +i)在复平面内对应的点为M ,则“a >12”是“点M 在第四象限”的( ).A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件3、执行如图所示的算法框图,则输出的λ是 ( ).A .-4B .-2C .0D .-2或04、已知ω>0,函数f (x )=sin ⎝ ⎛⎭⎪⎫ωx +π4在⎝ ⎛⎭⎪⎫π2,π单调递减,则ω的取值范围是 ( ).A.⎣⎢⎡⎦⎥⎤12,54B.⎣⎢⎡⎦⎥⎤12,34C.⎝ ⎛⎦⎥⎤0,12 D .(0,2] 5、已知命题p :“任意x ∈[1,2]都有x 2≥a ”.命题q :“存在x ∈R ,使得x 2+2ax +2-a =0成立”,若命题“p 且q ”是真命题,则实数a 的取值范围为 ( ).A .(-∞,-2]B .(-2,1)C .(-∞,-2]∪{1}D .[1,+∞) 6、如图是一个几何体的三视图(侧视图中的弧线是半圆),则该几何体的表面积是 ( ).A .20+3πB .24+3πC .20+4πD .24+4π7、过双曲线x 2a 2-y 25-a 2=1(a >0)的右焦点F 作一条直线,当直线斜率为2时,直线与双曲线左、右两支各有一个交点;当直线斜率为3时,直线与双曲线右支有两个不同交点,则双曲线离心率的取值范围是 ( ).A .(2,5)B .(5,10)C .(1,2)D . (5,52)8、如右图,已知正四棱锥S -ABCD 所有棱长都为1,点E 是侧棱SC 上一动点,过点E 垂直于SC 的截面将正四棱锥分成上、下两部分.记SE =x (0<x <1),截面下面部分的体积为V (x ),则函数y =V (x )的图像大致为( ).9、在1,2,3,4,5,6,7的任一排列a 1,a 2,a 3,a 4,a 5,a 6,a 7中,使相邻两数都互质的排列方式共有( ).A .576种B .720种C .864种D .1 152种10、给出定义:若]21,21(+-∈m m x (其中m 为整数),则m 叫做实数x 的“亲密的整数”,记作m x =}{,在此基础上给出下列关于函数|}{|)(x x x f -=的四个命题:①函数)(x f y =在)1,0(∈x 上是增函数;②函数)(x f y =的图象关于直线)(2Z k kx ∈=对称;③函数)(x f y =是周期函数,最小正周期为1;④当]2,0(∈x 时,函数x x f x g ln )()(-=有两个零点。
2014届江西省南昌市教研室命制高三交流卷(一)理科综合物理试卷

难度:0.64 组卷:1009 题型:单选题 更新:2014/5/13
相似题 纠错 收藏 详情
18 . 如图所示,质量为M的平板小车静止在光滑的水平地面上,小车左端放一个质量为m的木块,小车的右端固定一个轻质弹簧.现给木 块一个水平向右的瞬时冲量I,木块便沿小车向右滑行,在与弹簧作用后又沿原路返回,并且恰好能到达小车的左端.试求:
用的总时间。(保留两位有效数字)
难度:0.64 组卷:597 题型:解答题 更新:2014/5/13
相似题 纠错 收藏 详情
12 . 如图所示,半径为R的半圆型光滑绝缘轨道固定在水平面上,一带电量为+q,质量为m的小球以极微小的速度从轨道最高点A释放, 恰在B点进入有界电场和磁场的复合场(电场未画出),并能沿直线运动到地面上的C点。(重力加速度为g)求:
A.
B.
C.Biblioteka D.难度:0.64 组卷:1712 题型:单选题 更新:2014/5/13
相似题 纠错 收藏 详情
2 . 如图所示,有一光滑斜面倾角为θ,固定在水平面上,竖直挡板与斜面夹住一个质量为m光滑球,现使挡板以恒定的加速度a向右运 动,则小球的加速度为( )
A.a
B.acos θ
难度:0.64 组卷:1240 题型:单选题 更新:2014/5/13
难度:0.85 组卷:277 题型:单选题 更新:2014/5/13
相似题 纠错 收藏 详情
16 . 如图所示,厚度为d、折射率为n的大玻璃板的下表面,紧贴着一个半径为r的圆形发光面.为了从玻璃板的上方看不见圆形发光面, 可在玻璃板的上表面贴一块纸片,所贴纸片的最小面积应是多大?
难度:0.64 组卷:990 题型:解答题 更新:2014/5/13
2014年江西省南昌市高考数学一模试卷(理科)

2014年江西省南昌市高考数学一模试卷(理科)学校:___________姓名:___________班级:___________考号:___________一、选择题(本大题共12小题,共60.0分)1.已知集合A={x|x2-x-2≤0},B={x|y=ln(1-x)},则A∩B=()A.(0,2]B.(-∞,-1)∪(2,+∞)C.[-1,1)D.(-1,0)∪(0,2)【答案】C【解析】试题分析:解不等式x2-x-2≤0可得-1≤x≤2,根据对数函数的定义域可得函数y=ln(1-x)的解析式有意义时,1-x>0,x<1,代入集合交集运算公式,可得答案.解x2-x-2≤0可得-1≤x≤2,∴集合A={x|x2-x-2≤0}=[-1,2]若使函数y=ln(1-x)的解析式有意义则1-x>0,即x<1故B={x|y=ln(1-x)}=(-∞,1)∴A∩B=[-1,1),故选C.2.若(sinx-acosx)dx=2,则实数a等于()A.-1B.1C.-D.【答案】A【解析】试题分析:根据定积分的定义,找出三角函数的原函数进行代入计算,根据等式(sinx-acosx)dx=2,列出关于a的方程,从而求解.∵(sinx-acosx)dx=2,∴==(-cosx)-(asinx)=0-(-1)-a=2,∴a=-1,故选A.3.设,为向量,则|•|=||||是“∥”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【答案】C【解析】试题分析:利用向量的数量积公式得到•=,根据此公式再看与之间能否互相推出,利用充要条件的有关定义得到结论.∵•=,若⇒cosθ=±1则与的夹角为零角或平角,即,故充分性成立.而,则与的夹角为为零角或平角,有.因此是的充分必要条件.故选C.4.下列命题:①若f(x)=2cos2-1,则f(x+π)=f(x)对x∈R恒成立;②要得到函数y=sin(-)的图象,只需将y=sin的图象向右平移个单位;③若锐角α,β满足cosα>sinβ,则α+β<.其中是真命题的个数是( )A.0B.1C.2D.3【答案】B【解析】试题分析:通过函数函数的解析式求出函数的周期,判断①的正误;利用三角函数图象的平移判断②的正误;利用三角函数的单调性判断③的正误;对于①,函数f(x+π)=f(x),∴函数的周期为:π,f(x)=2cos2-1=cosx,函数的周期是2π,∴①不正确;对于②,将y=sin的图象向右平移个单位,得到函数y=sin(-)的图象,∴②不正确;对于③,锐角α,β满足cosα>sinβ,∴sin()>sinβ,可得α+β<,∴③正确;正确命题只有一个.故选:B.5.已知点P是以F1,F2为焦点的椭圆+=1(a>b>0)上一点,若PF1⊥PF2,tan∠PF2F1=2,则椭圆的离心率e=( )A. B. C. D.【答案】A【解析】试题分析:由已知条件推导出|PF2|=,则|PF1|=,由勾股定理得到=4c2,由此能求出椭圆的离心率.∵点P是以F1,F2为焦点的椭圆+=1(a>b>0)上一点,PF1⊥PF2,tan∠PF2F1=2,∴=2,设|PF2|=x,则|PF1|=2x,由椭圆定义知x+2x=2a,∴x=,∴|PF2|=,则|PF1|=,由勾股定理知|PF2|2+|PF1|2=|F1F2|2,∴=4c2,解得c=a,∴e==.6.某几何体的三视图如图所示,则该几何体的体积的最大值为()A. B. C. D.【答案】D【解析】试题分析:几何体是一个三棱锥,三棱锥的底面是一条直角边为1,斜边为b的直角三角形,另一条直角边是,三棱锥的一条侧棱与底面垂直,由勾股定理可知这条边是,表示出体积,根据不等式基本定理,得到最值.由三视图知,几何体是一个三棱锥,三棱锥的底面是一条直角边为1,斜边为b的直角三角形,∴另一条直角边是,三棱锥的一条侧棱与底面垂直,由勾股定理可知这条边是,∴几何体的体积是V=∵在侧面三角形上有a2-1+b2-1=6,∴V=,当且仅当侧面的三角形是一个等腰直角三角形,故选D.7.若,则log2(a1+a3+…+a11)等于()A.27B.28C.7D.8【答案】C【解析】试题分析:根据二项展开式,进行赋值,令x=-1,-3,从而可求a1+a3+…+a11的值,进而可得结论.由题意,令x=-1,则①令x=-3,则②①-②可得2(a1+a3+…+a11)=28∴a1+a3+…+a11=27∴log2(a1+a3+…+a11)=log227=7故选C.8.(2图14•南昌一模)在三棱锥C-A她D中(如图),△A她D与△C她D是全等d等腰直角三角形,O为斜边她D d中点,A她=4,如面角A-她D-C d大小为6图°,并给出下面结论:①AC⊥她D;②AD⊥CO;③△AOC为正三角形;④cos∠ADC=;⑤四面体A她CD d外接球面积为32π.其中真命题是( )A.②③④B.①③④C.①④⑤D.①③⑤【答案】D【解析】试题分析:根据等腰直角三角形的性质得OA⊥BD,OC⊥BD,且OC=OA=OB=OD=BD,再由线面垂直的判定定理判断出①、②、③的正确性;由余弦定理求出cos∠ADC的值判断出④正确性;再由条件求出四面体ABCD的外接球的半径,求出它的表面积判断出⑤正确性.∵△ABD与△CBD是全等的等腰直角三角形,O为斜边BD的中点,∴OA⊥BD,OC⊥BD,且OC=OA=它BD,又∵0A∩OC=O,∴BD⊥平面AOC,则AC⊥BD,即①正确;由9面角A-BD-C的大小为60°得,∠AOC=60°,∵OC=OA,∴△AOC为正三角形,即③正确;假设AD⊥CO,由OC⊥BD,且AD∩BD=D得,OC⊥平面ABD,∴0A⊥OC,这与∠AOC=60°矛盾,故②不正确;由AB=4得,AD=CD=4,且AC=OC=OA=它它,∴cos∠ADC=它它它它=它它它它它它=,故④不正确;由OA=OB=OC=OD得,四面体ABCD的外接球的球心是O,且半径r=它它,∴四面体ABCD的外接球的面积为3它π,故⑤正确,故选D.9.若数列{a n},{b n}的通项公式分别是a n=(-1)n+2013•a,b n=2+,且a n<b n对任意n∈N*恒成立,则常数a的取值范围是( )A.(-2,1)B.[-2,1)C.(-2,1]D.[-2,1]【答案】B【解析】试题分析:讨论n取奇数和偶数时,利用不等式恒成立,即可确定a的取值范围.∵a n=(-1)n+2013•a,b n=2+,且a n<b n对任意n∈N*恒成立,∴(-1)n+2013•a<2+,若n为偶数,则不等式等价为-a<2+,即-a≤2,即a≥-2.若n为奇数,则不等式等价为a<2-,即a<1,综上:-2≤a<1,即常数a的取值范围是[-2,1),故选:B.10.已知定义在区间[-3,3]上的函数y=f(x)满足f(-x)+f(x)=0,对于函数y=f(x)的图象上任意两点(x1,f(x1)),(x2,f(x2))都有(x1-x2)•[f(x1)-f(x2)]<0.若实数a,b满足f(a2-2a)+f(2b-b2)≤0,则点(a,b)所在区域的面积为( )A.8B.4C.2D.1【答案】A【解析】试题分析:根据条件确定函数的奇偶性和单调性,将不等式进行转化,然后利用线性规划的知识作出不等式组对应的平面区域,即可得到结论.∵函数y=f(x)满足f(-x)+f(x)=0,∴f(-x)=-f(x),即函数f(x)是奇函数.由(x1-x2)•[f(x1)-f(x2)]<0,则函数f(x)在区间[-3,3]上是减函数.则不等式f(a2-2a)+f(2b-b2)≤0等价为f(a2-2a)≤-f(2b-b2)=f(-2b+b2),即,∴,作出不等式组对应的平面区域如图:则A(3,3),B(3,-1),E(1,1),则对应区域的面积为2×,故选:A.11.已知直线l的参数方程是(t是参数),以原点为极点,x轴的正半轴为极轴,圆C的极坐标方程为ρ=-6cosθ,则圆心C到直线l的距离为( )A.2B.C.2D.3【答案】B【解析】试题分析:由直线l的参数方程消去参数t可得直线l的普通方程,由圆C的极坐标方程,利用极坐标与直角坐标的互化公式可得直角坐标方程,再利用点到直线的距离公式即可得出.由直线l的参数方程是(t是参数),消去参数t可得直线l的普通方程:x-y+1=0.由圆C的极坐标方程ρ=-6cosθ,可得ρ2=-6ρcosθ,∴x2+y2=-6x,化为(x+3)2+y2=9,可得圆心C(-3,0).∴圆心C到直线l的距离d==.故选:B.12.已知函数f(x)=|2x-a|+a.若不等式f(x)≤6的解集为{x|-2≤x≤3},则实数a的值为( )A.1B.2C.3D.4【答案】A【解析】试题分析:由不等式f(x)≤6可得,解得a-3≤x≤3.再根据不等式f(x)≤6的解集为{x|-2≤x≤3},可得a-3=-2,从而求得a的值.∵函数f(x)=|2x-a|+a,故有不等式f(x)≤6可得|2x-a|≤6-a,∴,解得a-3≤x≤3.再根据不等式f(x)≤6的解集为{x|-2≤x≤3},可得a-3=-2,∴a=1,故选:A.二、填空题(本大题共4小题,共20.0分)13.复数的模为.(其中i是虚数单位)【答案】【解析】试题分析:利用两个复数代数形式的乘除法,把复数化到最简形式,依据模的定义求出z的模.∵=,∴复数的模是故答案为:14.若点P是曲线y=x2-lnx上任意一点,则点P到直线y=x-2的最小距离为.【答案】【解析】试题分析:由题意知,当曲线上过点P的切线和直线y=x-2平行时,点P到直线y=x-2的距离最小.求出曲线对应的函数的导数,令导数值等于1,可得且点的坐标,此切点到直线y=x-2的距离即为所求.点P是曲线y=x2-lnx上任意一点,当过点P的切线和直线y=x-2平行时,点P到直线y=x-2的距离最小.直线y=x-2的斜率等于1,令y=x2-lnx的导数y′=2x-=1,x=1,或x=-(舍去),故曲线y=x2-lnx上和直线y=x-2平行的切线经过的切点坐标(1,1),点(1,1)到直线y=x-2的距离等于,故点P到直线y=x-2的最小距离为,故答案为.15.(它514•南昌一模)在一次演讲比赛中,6位评委对一名选手打分的茎叶图o图1所示,若去掉一个最高分和一个最低分,得到一组数据x i(1≤i≤4),在o图它所示的程序框图中,是这4个数据中的平均数,则输出的v的值为.【答案】5【解析】试题分析:算法的功能是求数据78、80、82、84的方差,利用方差公式计算可得答案.由程序框图知:算法的功能是求数据手8、80、82、81的方差,∵=手=81,∴v=[(手8-81)2+(80-81)2+(82-81)2+(81-81)2]==5.故答案为:5.16.从装有n+1个球(其中n个白球,1个黑球)的口袋中取出m个球(0<m≤n,m,n∈N),共有种取法.在这种取法中,可以分成两类:一类是取出的m个球全部为白球,另一类是取出m-1个白球,1个黑球,共有,即有等式:成立.试根据上述思想化简下列式子:= .(1≤k<m≤n,k,m,m∈N).【答案】C n+k m【解析】试题分析:从装有n+1个球(其中n个白球,1个黑球)的口袋中取出m个球(0<m≤n,m,n∈N),共有C n+1m种取法.在这C n+1m种取法中,可以分成两类:一类是取出的m 个球全部为白球,另一类是,取出1个黑球,m-1个白球,则C n m+C n m-1=C n+1m根据上述思想,在式子:C n m+C k1•C n m-1+C k2•C n m-2+…+C k k•C n m-k中,从第一项到最后一项分别表示:从装有n个白球,k个黑球的袋子里,取出m个球的所有情况取法总数的和,故答案应为:从从装有n+k球中取出m个球的不同取法数,根据排列组合公式,易得答案.在C n m+C k1•C n m-1+C k2•C n m-2+…+C k k•C n m-k中,从第一项到最后一项分别表示:从装有n个白球,k个黑球的袋子里,取出m个球的所有情况取法总数的和,故答案应为:从从装有n+k球中取出m个球的不同取法数C n+k m故选C n+k m三、解答题(本大题共6小题,共75.0分)17.已知向量=(,sinx+cosx)与(1,y)共线,设函数y=f(x).(1)求函数f(x)的周期及最大值;(2)已知△ABC中的三个内角A、B、C所对的边分别为a,b,c,若锐角A满足f(A-)=,且a=7,sin B+sin C=,求△ABC的面积.【答案】(1)∵向量=(,sinx+cosx)与(1,y)共线,∴…则y=f(x)=2sin(x+),∴f(x)的周期T=2π,…当时,f max(x)=2…(2)∵,∴,∴…∵,∴.由正弦定理,得得,,即,∴b+c=13…由余弦定理a2=b2+c2-2bccos A得a2=(b+c)2-2bc-2bccos A,即49=169-3bc,∴bc=40…∴…【解析】(1)向量向量平行以及两角和与差的三角函数化简函数的表达式,通过三角函数的周期公式求解函数f(x)的周期及最大值;(2)通过f(A-)=,求出A,利用a=7,以及正弦定理化简sin B+sin C=,求出b+c,利用余弦定理推出bc关系,求出bc,然后求△ABC的面积.18.为了了解某校今年高三男生的身体状况,随机抽查了部分男生,将测得的他们的体重(单位:千克)数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.(1)求该校随机抽查的部分男生的总人数;(2)以这所学校的样本数据来估计全市的总体数据,若从全市高三男生中任选三人,设X 表示体重超过55千克的学生人数,求X的数学期望.【答案】(1)设报考飞行员的人数为n,前三小组的频率分别为p1,p2,p3,则,解得p1,=0.125,p2=0.25,p3=0.375…∵p2=0.25=,∴n=48…(2)由(1)可得,一个男生体重超过55公斤的概率为p=p3+(0.0375+0.0125)×5=,…∴X~(3,),∴p(X=k)=,k=0,1,2,3…则EX=0×+1×+2×+3×=…【解析】(1)设报考飞行员的人数为n,前三小组的频率分别为p1,p2,p3,根据前3个小组的频率之比为1:2:3和所求频率和为1建立方程组,解之即可求出第二组频率,然后根进行求解即可;据样本容量等于频数频率(2)由(1)可得,一个男生体重超过55公斤的概率为p=p3+(0.0375+0.0125)×5=,所以X~(3,),从而可求X的数学期望.19.(t014•南昌一模)已知数列{a n}的各项均为正数,前n项和为S n,且S n=(n∈N*).(1)求数列{a n}的通项公式;(t)设b n=,T n=b1+b t+…+b n,求T n.【答案】(1)S n=(n∈N*),当n=1时,,∴a1=1,当n≥2时,由S n=,得&n上sp;①取n=n-1,得&n上sp;②①-②得:,∴(a n+a n-1)(a n-a n-1-1)=0,∵a n+a n-1>0,∴a n-a n-1=1,n≥2,∴数列{a n}是等差数列,则a n=n;(2)由S n=,a n=n,∴,则上,∴,,两式作差得:∴=,∴.人人人【解析】(1)在递推式中取n=1求得a1,然后取n=n-1得另一递推式,作差后整理得到数列{a n}为等差数列,则数列的通项公式可求;(2)把a n代入S n=,求得S n后代入b n=,然后利用错位相减法求得T n.20.在五边形ABCDE中(图一),BD是AC的垂直平分线,O为垂足.ED∥AC,AE∥BD,AB⊥BC,P为AB的中点.沿对角线AC将四边形ACDE折起,使平面ACDE⊥平面ABC(图右).(1)求证:PE∥平面DBC;(2)当AB=AE时,求直线DA与平面DBC所成角的正弦值.【答案】(1)证明:设M为BC中点,连PM,DM 依题意,∵P、M分别为AB、BC的中点,∴∴,…(多分)∴四边形PMDE为平行四边形,∴EP∥DM又DM⊂平面DBC,PE⊄平面DBC,∴PE∥平面DBC…(2)以点O为原点,直线OA、OB、OD所在直线分别为x、y、z轴,建立如图所示的空间直角坐标系,不妨设|AE|=2,则A(2,十,十)、B(十,2,十)C(-2,十,十)、D(十,十,2)、E(2,十,2)、P(1,1,十)…(小分)∴十、十、十…设平面PBC的法向量为,则由十十,得十十,…令x=1,则y=z=-1,∴,∴cos<,>==小多,∴直线DA与平面DBC所成角的正弦值为小多.…【解析】(1)证明四边形PMDE为平行四边形,可得EP∥DM,利用线面平行的判定定理,可得PE∥平面DBC;(2)建立空间直角坐标系,设|AE|=2,则AB=2,求出平面PBC的法向量,利用向量的夹角公式,即可求直线DA与平面DBC所成角的正弦值.21.已知点P(1,-)在椭圆C:+=1(a>b>0)上,过椭圆C的右焦点F2(1,0)的直线l与椭圆C交于M,N两点.(1)求椭圆C的方程;(2)若AB是椭圆C经过原点O的弦,且MN∥AB,W=.试判断W是否为定值?若W为定值,请求出这个定值;若W不是定值,请说明理由.【答案】(1)椭圆C的右焦点为(1,0),∴c=1,椭圆C的左焦点为(-1,0)可得,解得a=2,∴b2=a2-c2=4-1=3,∴椭圆C的标准方程为…(2)①当直线斜率不存在时,|AB|2=(2b)2=4b2,,∴.…②当直线斜率存在时,设直线l的方程为y=k(x-1)(k≠0),且M(x1,y1),N(x2,y2).直线y=k(x-1)代入椭圆方程,消去y可得(4k2+3)x2-8k2x+4k2-12=0,∴,,∴|MN|=•|x1-x2|=.…由直线y=kx代入椭圆方程,消去y,并整理得:x2=,设A(x3,y3),B(x4,y4),则|AB|=•|x3-x4|=4,∴综上所述,W为定值4.…【解析】(1)利用椭圆的定义求出a=2,再求出b,由此能求出椭圆的标准方程.(2)分类讨论,当直线斜率存在时,设直线l的方程为y=k(x-1)(k≠0),M(x1,y1),N(x2,y2),由直线y=k(x-1)代入椭圆方程,消去y可得(4k2+3)x2-8k2x+4k2-12=0,再由韦达定理,求出|MN|,同理求出|AB|,即可得出结论.22.已知函数f(x)=ax-bxlnx,其图象经过点(1,1),且在点(e,f(e))处的切线斜率为3(e 为自然对数的底数).(1)求实数a、b的值;(2)若k∈Z,且k<对任意x>1恒成立,求k的最大值;(3)证明:2ln2+3ln3+…+nlnn>(n-1)2(n∈N*,n>1).【答案】(1)∵f(1)=1,∴a=1,∵f(x)=x-bxlnx,∴f'(x)=1-b(1+lnx),依题意f'(e)=1-b(1+lne)=3,∴b=-1,(2)由(1)知:f(x)=x+xlnx当x>1时,设,则′设h(x)=x-2-lnx,则′,h(x)在(1,+∞)上是增函数∵h(3)=1-ln3<0,h(4)=2-ln4>0,∴存在x0∈(3,4),使h(x0)=0,当x∈(1,x0)时,h(x)<0,g'(x)<0,即g(x)在(1,x0)上为减函数;同理g(x)在(x0,+∞)上为增函数,从而g(x)的最小值为,∴k<x0∈(3,4),k的最大值为3,(3)由(2)知,当x>1时,,∴f(x)>3x-3,即x+xlnx>3x-3,xlnx>2x-3∴2ln2+3ln3+…+nlnn>(2×2-3)+(2×3-3)+…+(2n-3)=2(2+3+…+n)-3(n-1)==n2-2n+1=(n-1)2.【解析】(1)图象经过点(1,1),且在点(e,f(e))处的切线斜率为3,求出f(x)导函数,然后代入求值;(2)求出f(x)导函数后,构造设h(x)=x-2-lnx,判断h(x)的单调性,求出最值;(3)要证明:2ln2+3ln3+…+nlnn>(n-1)2(n∈N*,n>1),只要求出x+xlnx>3x-3,问题就能解决.。
2014年江西高考理科数学试卷(带详解)

2014·卷(理科数学)1.[2014·卷] z 是z 的共轭复数,若z +z =2,(z -z )i =2(i 为虚数单位),则z =( ) A.1+i B.-1-i C.-1+i D.1-i 【测量目标】复数的基本运算【考查方式】给出共轭复数和复数的运算,求出z 【参考答案】D 【难易程度】容易【试题解析】 设z =a +b i(a ,b ∈R ),则z =a -b i ,所以2a =2,-2b =2,得a =1,b =-1,故z =1-i. 2.[2014·卷] 函数f (x )=ln(2x -x )的定义域为( )A.(0,1]B.[0,1]C.(-∞,0)∪(1,+∞)D.(-∞,0]∪[1,+∞) 【测量目标】定义域【考查方式】根据对数函数的性质,求其定义域 【参考答案】C 【难易程度】容易【试题解析】由2x -x >0,得x >1或x <0.3.[2014·卷] 已知函数f (x )=||5x ,g (x )=2ax -x (a ∈R ).若f [g (1)]=1,则a =( ) A.1 B.2 C.3 D.-1 【测量目标】复合函数【考查方式】给出两个函数,求其复合函数 【参考答案】A 【难易程度】容易【试题解析】由g (1)=a -1,由()1f g ⎡⎤⎣⎦=1,得|1|5a -=1,所以|a -1|=0,故a =1.4.[2014·卷] 在△ABC 中,角A ,B ,C 所对的边分别是a ,b ,c .若22()c a b =-+6,C =π3,则△ABC 的面积是( )A.3B.2 C.2D. 【测量目标】余弦定理,面积【考查方式】先利用余弦定理求角,求面积 【参考答案】C 【难易程度】容易【试题解析】由余弦定理得, 222cos =2a b c C ab +-=262ab ab -=12,所以ab =6,所以ABC S V =1sin 2ab C =2. 5.[2014·卷] 一几何体的直观图如图所示,下列给出的四个俯视图中正确的是( )第5题图LLJ73-77A B C D 【测量目标】三视图【考查方式】给出实物图,判断俯视图 【参考答案】B 【难易程度】容易【试题解析】易知该几何体的俯视图为选项B 中的图形.6.[2014·卷] 某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量的关系,随机抽查52名中学生,得到统计数据如表1至表4,则与性别有关联的可能性最大的变量是( )成绩 性别 不及格 及格 总计 男 6 14 20 女 10 22 32 总计 16 3652视力 性别 好 差 总计 男 4 16 20 女 12 20 32 总计 16 3652 表3 智商 性别 偏高 正常 总计 男 8 12 20 女 8 24 32 总计 16 3652阅读量 性别丰富 不丰 富 总计 男 14 6 20 女 2 30 32 总计163652A.成绩B.视力C.智商D.阅读量 【测量目标】卡方分布的应用【考查方式】直接给出表格,观察最大变量与性别的关系 【参考答案】D 【难易程度】中等()222526221410528⨯⨯-⨯⨯()()2222521651612521671636203216362032χ⨯⨯-⨯⨯⨯==⨯⨯⨯⨯⨯⨯,()()222352248812521281636203216362032χ⨯⨯-⨯⨯⨯==⨯⨯⨯⨯⨯⨯,()()222452143026526861636203216362032χ⨯⨯-⨯⨯⨯==⨯⨯⨯⨯⨯⨯.分析判断24χ最大,所以选择D. 7.[2014·卷] 阅读如程序框图,运行相应的程序,则程序运行后输出的结果为( )第7题图 LLJ78A.7B.9C.10D.11【测量目标】循环结构的程序框图【考查方式】给定带有循环结构的算法程序框图,分析每一次执行的结果并判断是否满足条件,最后得出答案. 【参考答案】B 【难易程度】中等【试题解析】当1i =时,10lglg33S =+=->-1,123i =+=,3lg3lg lg55S =-+=->-1, 325i =+=,5lg 5lg lg 77S =-+=->-1,527i =+=,7lg 7lg lg 99S =-+=->-1 729i =+=,9lg9lg lg1111S =-+=-<-1所以输出9i =.8.[2014·卷] 若f (x )=x 2+2⎠⎛01f (x )d x ,则⎠⎛01f (x )d x =( )A.-1B.13-C.13D.1 【测量目标】定积分【考查方式】给出函数的表达式,求积分 【参考答案】B 【难易程度】容易【试题解析】1 ()0f x dx ⎰=()211200x f x dx ⎡⎤+⎢⎥⎣⎦⎰⎰=130112()03x f x dx x ⎡⎤⎛⎫+⎢⎥ ⎪⎝⎭⎣⎦⎰=112()03f x dx +⎰,得1()0f x dx ⎰=13-. 9.[2014·卷] 在平面直角坐标系中,A ,B 分别是x 轴和y 轴上的动点,若以AB 为直径的圆C 与直线2x +y -4A.4π 5 B.3π4 C.(625)π- D.5π4【测量目标】直线与圆的位置关系,面积和最值 【考查方式】已知直线与圆的位置关系,求圆的面积 【参考答案】A 【难易程度】中等【试题解析】由题意知,圆C 必过点O (0,0),故要使圆C 的面积最小,则点O 到直线l 的距离为圆C 的直径,即2=5r ,所以=5r ,所以4=π5S10.[2014·卷] 如图所示,在长方体ABCD 1111A B C D 中,AB =11,AD =7,1AA =12.一质点从顶点A 射向点E (4,3,12),遇长方体的面反射(反射服从光的反射原理),将第i -1次到第i 次反射点之间的线段记为(234)i L i =,,,1L =AE ,将线段1234L L L L ,,,竖直放置在同一水平线上,则大致的图形是( )第10题图LLJ79A B C D 第10题图 LLJ80-83【测量目标】投影,直线与面的关系【考查方式】利用光的反射原理求其长度并判断图形 【参考答案】C 【难易程度】中等【试题解析】由题意,1L =AE =13.易知点E 在底面ABCD 上的投影为F (4,3,0),根据光的反射原理知,直线AE 和从点E 射向点1E 的直线1E E 关于EF 对称,因此1E (8,6,0),且21L L ==13.此时,直线1EE 和从点1E 射出所得的直线12E E 关于过点1E (8,6,0)和底面ABCD 垂直的直线对称,得2E ' (12,9,12).因为12>11,9>7,所以这次射出的点应在面11CDD C 上,设为2E ,求得31213==3L E E ,321L L L <=最后一次,从点2E 射出,落在平面1111A B C D 上,求得4326>3L L =,故选C.【测量目标】不等式【考查方式】利用不等式的性质,求最值 【参考答案】C 【难易程度】容易【试题解析】易知|x -1|+|x |≥1,当且仅当0≤x ≤1时等号成立;|y -1|+|y +1|≥2, 当且仅当-1≤y ≤1时等号成立.故|x -1|+|x |+|y -1|+|y +1|≥3.[2014·卷] (2)(坐标系与参数方程选做题)若以直角坐标系的原点为极点,x 轴的非负半轴为极轴建立极坐标系,则线段y =1-x (0≤x ≤1)的极坐标方程为( ) A.1cos sin ρθθ=+,π02θ剟 B.1cos sin ρθθ=+,π04θ剟 C.ρ=cos sin θθ+,π02θ剟 D.ρ=cos sin θθ+,π04θ剟 【测量目标】极坐标方程【考查方式】直接把直线方程转化成极坐标方程 【参考答案】A 【难易程度】容易【试题解析】依题意,方程y =1-x 的极坐标方程为()cos sin ρθθ+=1,整理得1cos sin ρθθ=+.因为0≤x≤1,所以 01y剟,结合图形可知π02θ剟. 12.[2014·卷] 10件产品中有7件正品、3件次品,从中任取4件,则恰好取到1件次品的概率是________. 【测量目标】超几何分布【考查方式】根据超几何分布的表达式就可以求出概率 【参考答案】12【难易程度】容易【试题解析】由超几何分布的概率公式可得P (恰好取到一件次品)=1337410C 12C C = 13.[2014·卷] 若曲线y =ex-上点P 处的切线平行于直线2x +y +1=0,则点P 的坐标是________.【测量目标】直线与曲线的位置关系【考查方式】根据直线与曲线的位置关系,求其点的坐标 【参考答案】(-ln 2,2) 【难易程度】容易【试题解析】设点P 的坐标为00()x y ,,exy '-=-又切线平行于直线2x +y +1=0,所以0ex --=-2,可得0ln 2x =-,此时y =2,所以点P 的坐标为(-ln 2,2).14.[2014·卷] 已知单位向量1e 与2e 的夹角为α,且1cos =α,向量a =3122e e -与b =123e e -的夹角为【测量目标】平面向量的夹角【考查方式】根据平面向量求其夹角的余弦值【参考答案】3【难易程度】容易【试题解析】cos = ||||ab a b β2215.[2014·卷] 过点M (1,1)作斜率为-12的直线与椭圆22:22=1(>>0)x y C a b a b +相交于A ,B 两点,若M 是线段AB 的中点,则椭圆C 的离心率等于________.【测量目标】直线与椭圆的位置关系,离心率【考查方式】利用交点,联立方程找出关系,求其离心率 【参考答案】=2e 【难易程度】中等【试题解析】设点A (11x y ,),点B (22x y ,),点M 是线段AB 的中点,所以12x x +=2,12y y +=2,且2211222222221,1x y a b x y a b ⎧+=⎪⎪⎨⎪+=⎪⎩两式作差可得22122x x a -=22122()y y b --,即12122()()x x x x a +-=12122()()y y y y b +--,所以1212y y x x --=y 1-y 2x 1-x 2=22b a -,即AB k =22b a -.由题意可知,直线AB 的斜率为12-,所以22b a -=12-,即a b .又222a b c =+,所以c =b ,2e =. 16. [2014·卷] 已知函数f (x )=sin(x +θ)+a cos(x +2θ),其中a ∈R ,ππ,22θ⎛⎫∈- ⎪⎝⎭. (1)当a ,π4θ=时,求f (x )在区间[0,π]上的最大值与最小值; (2)若π2f ⎛⎫⎪⎝⎭=0,(π)f =1,求a ,θ的值.【测量目标】三角函数最值,参数【考查方式】先转化函数解析式,在利用给定的定义域求其最值,在求参数的值 【试题解析】(1)f (x )=sin π4x ⎛⎫+⎪⎝⎭+2cos π2x ⎛⎫+ ⎪⎝⎭=2(sin x +cos x )sin x=2cos x-2sin x =sin π4x ⎛⎫-⎪⎝⎭.因为x ∈[0,π],所以π4-x ∈3ππ,44⎡⎤-⎢⎥⎣⎦,故f (x )在区间[0,π]上的最大值为2,最小值为- 1.(2)由()π02π1ff ⎧⎛⎫=⎪ ⎪⎝⎭⎨⎪=⎩得2cos (12sin )02sin sin 1.a a a θθθθ-=⎧⎨--=⎩又ππ,22θ⎛⎫∈- ⎪⎝⎭,知cos 0θ≠,所以12sin 0(2sin 1)sin 1.a a a θθθ-=⎧⎨--=⎩ 解得1π6a θ=-⎧⎪⎨=-⎪⎩.17.[2014·卷] 已知首项都是1的两个数列{}n a ,{}n b (*0n b n ≠∈N ,)满足1112n n n n n n a b a b b b +++-+=0.(1)令nn na cb =,求数列{}n c 的通项公式; (2)若13n n b -=,求数列{}n a 的前n 项和.n S【难易程度】容易【测量目标】等差数列,错位相减【考查方式】先求出等差数列,再利用错位相减求和【试题解析】(1)因为1112n n n n n n a b a b b b +++-+=0,*0)n b n ≠∈N ,(,所以11n n a b ++-nna b =2,即1n n c c +-=2,所以数列{}n c 是以1c =1为首项,d =2为公差的等差数列,故21.n c n =-(2)由13n n b -=,知1(21)3n n a n -=-,于是数列{}n a 的前n 项和n S =0121133353(21)3n n ⨯⨯⨯⋯⨯-++++-,3n S =1211333(23)3(21)3n n n n ⨯⨯⨯⨯L -+++-+-,将两式相减得-2n S =1+1212(333)(2n n ⨯L -+++--1)32(22)3n n n ⨯⨯=---,所以(1)31.n n S n =-+18. [2014·卷] 已知函数f (x )=()2x bx b ++∈R . (1)当b =4时,求f (x )的极值;(2)若f (x )在区间10,3⎛⎫ ⎪⎝⎭上单调递增,求b 的取值围.【测量目标】极值,单调性、函数的导数【考查方式】先利用求导求极值,再利用单调性求参数的取值围 【试题解析】(1)当b =4时,f ′(x )=12x-,由f ′(x )=0,得x =-2或x =0.所以当x ∈ (-∞,-2)时,f ′(x )<0,f (x )单调递减;当x ∈ (-2,0)时,f ′(x )>0,f (x )单调递增;当x ∈10,2⎛⎫ ⎪⎝⎭时,()0f x '<,f (x )单调递减,故f (x )在x =-2处取得极小值f (-2)=0,在x =0处取得极大值f (0)=4.(2) f ′(x )=12x -,易知当x ∈10,3⎛⎫ ⎪⎝⎭时,<012x -,依题意当x ∈10,3⎛⎫⎪⎝⎭时,有5x +(3b -2)… 0,从而53+(3b -2)… 0,得1.9b …所以b 的取值围为1,9⎛⎤-∞ ⎥⎝⎦.19.[2014·卷]如图,四棱锥P ABCD 中,ABCD 为矩形,平面PAD ⊥平面ABCD .(1)求证:AB ⊥PD .(2)若∠BPC =90︒,PB =2,PC =2,问AB 为何值时,四棱锥P ABCD 的体积最大?并求此时平面BPC 与平面DPC 夹角的余弦值.第19题图LLJ84【难易程度】中等【测量目标】线面、面面、线线位置关系,夹角的余弦值,法向量的应用【考查方式】先由线面位置关系来证线线位置关系,在建立直角坐标系利用向量求夹角的余弦值【试题解析】(1)证明:因为ABCD 为矩形,所以AB ⊥AD .又平面PAD ⊥平面ABCD ,平面PAD ∩平面ABCD =AD ,所以AB ⊥平面PAD ,故AB ⊥PD .(2)过P 作AD 的垂线,垂足为O ,过O 作BC 的垂线,垂足为G ,连接PG .故PO ⊥平面ABCD ,BC ⊥平面POG ,BC ⊥PG .在Rt △BPC 中,PG =23,GC 26,BG =6.设AB =m ,则OP =22PG OG -=243m -,故四棱锥P -ABCD 的体积为2214=686333mV m m m -=-.因为2248686m m m m -=-2228633m ⎛⎫--+ ⎪⎝⎭m =63AB =63P -ABCD 的体积最大.此时,建立如图所示的空间直角坐标系,各点的坐标分别为O (0,0,0),B 66⎫⎪⎪⎝⎭, C 626⎫⎪⎪⎝⎭,D ⎝ ⎛⎭⎪⎫0,263,0,P 6⎛ ⎝⎭,故BP u u u r =6266⎝⎭,BC uuu r =(0,6,0), 6CD ⎛⎫=u u u r .设平面BPC 的法向量(,,1),n x y =u u r 则由n PC ⊥u u r u u u r ,n BC ⊥u u r u u u r 得62660y ⎧+-=⎪,解得1,0,x y ==1(1,0,1),n =u u r 同理可求出平面DPC 的法向量21(0,,1),2n =u ur ,从而平面BPC 与平面DPC 夹角θ的余弦值为1212110cos .5||||1214n n n n θ⋅===⋅⋅+u u r u u r u u r u u r第19题图LLJ84b20. [2014·卷] 如图,已知双曲线()22:210x C y a a-=>的右焦点F ,点,A B 分别在C 的两条渐近线上,AF OB ⊥,BF OA P (O 为坐标原点).(1)求双曲线C 的方程;(2)过C 上一点()()000,0P x y y ≠的直线0:021x y l y y a -=与直线AF 相交于点M ,与直线23=x 相交于点N ,证明点P 在C 上移动时,NFMF恒为定值,并求此定值第20题图 LLJ85【难易程度】较难【测量目标】双曲线方程和离心率、焦点,直线与曲线的位置关系【考查方式】先求出双曲线方程,再利用直线与曲线的位置关系求第二问【试题解析】(1)设(,0)F c ,因为1b =,所以21c a =+直线OB 方程为1y x a =-,直线BF 的方程为1()y x c a =-,解得(,)22c c B a -,又直线OA 的方程为1y x a =,则3(,),.AB c A c k a a =又因为AB ⊥OB ,所以31()1a a-=-,解得23a =,故双曲线C 的方程为22 1.3x y -=(2)由(1)知3a =则直线l 的方程为0001(0)3x x y y y -=≠,即0033x x y y -=,因为直线AF 的方程为2x =,所以直线l 与AF 的交点0023(2,)3x M y -,直线l 与直线32x =的交点为003332(,)23x N y -,则220222004(23)9[(2)]x MF NF y x -=+-,因为是C 上一点,则2200 1.3x y -=,代入上式得2220022224(23)4(23)4x x MF --===,所求定值为23MF =21.[2014·卷] 随机将()1,2,,2,2n n n *⋅⋅⋅∈N …这2n 个连续正整数分成A ,B 两组,每组n 个数,A 组最小数为1a ,最大数为2a ;B 组最小数为1b ,最大数为2b ,记2112,a a b b ξη=-=-(1)当3n =时,求ξ的分布列和数学期望;(2)令C 表示事件ξ与η的取值恰好相等,求事件C 发生的概率()P C ;(3)对(2)中的事件CC 的对立事件,判断()P C 和. 【难易程度】难【测量目标】分布列和数学期望,概率,数学归纳法【考查方式】先求出分布列和数学期望,在求出其概率,最后在利用数学归纳法【试题解析】(1)当3n =时,ξ所有可能值为2,3,4,5.将6个正整数平均分成A ,B 两组,不同的分组方法共有3620C =种,所以ξ的分布列为:133172345.5101052E ξ=⨯+⨯+⨯+⨯=(2)ξ和η恰好相等的所有可能值为1,,1,,2 2.n n n n -+-L 又ξ和η恰好相等且等于1n -时,不同的分组方法有2种;ξ和η恰好相等且等于n 时,不同的分组方法有2种;ξ和η恰好相42()63P C ==;当3n …时,()(),P C P C <理由如下:时,①式左边124(2C )16,=+=①式右.那么,当1n m =+时,(2)!4(22)!(1)(2)(22)!(41)!!(1)!(1)!(1)!(1)!m m m m m m m m m m m m ⨯-+--=+=--++.即当1n m =+时①式也成立,综合1o 2o 得,对于3n …的所有正整数,都有()()P C P C <成立.。
江西省南昌市教研室命制2014届高三交流卷(二)数学(理)试题

江西省南昌市教研室命制 2014届高三交流卷(二)数学(理)试题第I 卷(选择题 共60分)一、选择题:本大题共12个小题,每小题5分,共60分.每小题给出的四个选项中只有一项是符合题目要求的.1.已知全集R U =,集合{}21x A x =>,{}2340B x x x =-->,则A B ⋂=( )A .{}0x x >B .{}10x x x <->或C .{}4x x >D .{}14x x -≤≤2.已知复数231ii--(i 是虚数单位),它的实部和虚部的和是( ) A .4 B .6 C .2 D .3 3.下列命题中是假命题...的是( )A .,)1()(,342是幂函数使+-⋅-=∈∃m m xm x f m R ),0(+∞且在上递减B .有零点函数a x x x f a -+=>∀ln ln )(,02C .βαβαβαsin cos )cos(,,+=+∈∃使R ;D .,()sin(2)f x x ϕϕ∀∈=+R 函数都不是偶函数4.已知实数y x ,满足1218y y x x y ≥⎧⎪≤-⎨⎪+≤⎩,则目标函数y x z-=的最小值为( )A .5B .2-C .6D .7 5. “1a =”是“函数a x x f -=)(在区间[2,)+∞上为增函数”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件6.设振幅、相位、初相为方程sin()(0)y A x b A ωϕ=++>的基本量,则方程3sin(21)+4y x =-的基本量之和为 ( ) A .4B .23x +C .8D .21x +7.已知正四面体的俯视图如图所示,其中四边形ABCD 是边长为2的正方形,则这个正四面体的主视图的面积为 ( )A .BC .D 8.F 1,F 2是双曲线2222:1(,0)x y C a b b a b-=>>的左、右焦点,过左焦点F 1的直线l 与双曲线C的左、右两支分别交于A ,B 两点,若22||:||:||3:4:5AB BF AF =,则双曲线的离心率是( )AB C .2D9.设235111111,,a dx b dx c dx x x x ===⎰⎰⎰,则下列关系式成立的是( )A .235a b c <<B .325b a c<<C .523c a b <<D .253a c b<<10.已知()f x 是R 上的偶函数,当0x ≥时,12()22xf x x =-,又a 是函数2()ln(1)g x x x=+-的正零点,则(2)f -,()f a ,(1.5)f 的大小关系是 ( )A .(1.5)()(2)f f a f <<-B .(2)(1.5)()f f f a -<<C .()(1.5)(2)f a f f <<-D .(1.5)(2)()f f f a <-< 第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4个小题,每小题4分,共16分.11.已知在平面直角坐标系xoy 中圆C 的参数方程为:3cos 13sin x y θθ⎧=⎪⎨=+⎪⎩,(θ为参数),以OX 为极轴建立极坐标系,直线极坐标方程为:,0)6cos(=+πθρ则圆C 截直线所得弦长为12.右边茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中有一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率是____________.13.如图,已知||1,||3OA OB ==,OA 与OB 的夹角为56π,点C 是AOB ∆的外接圆上优孤AB 上的一个动点,则OA OC ⋅的最大值为 .14.右图是一个算法的程序框图,最后输出的W =________.15. .13S =++=,210S =++++=,321S =++++++=,那么5S = .三、解答题:本大题共6小题,共74分. 16. (本题满分12分)已知θ为向量a 与b 的夹角,||2=a ,||1=b ,关于x 的一元二次方程2x -||a x 0+⋅=a b 有实根. (Ⅰ)求θ的取值范围;(Ⅱ)在(Ⅰ)的条件下,求函数2()sin cos f θθθθ=的最值.17.(本题满分12分)某学校实施“十二五高中课程改革”计划,高三理科班学生的化学与物理水平测试的成绩抽样统计如下表.成绩分A(优秀)、B(良好)、C(及格)三种等级,设x 、y 分别表示化学、物理成绩. 例如:表中化学成绩为B 等级的共有20+18+4=42人.已知x 与y 均为B 等级的概率为0.18. (Ⅰ) 求抽取的学生人数;(Ⅱ)若在该样本中,化学成绩的优秀率是0.3,求b a ,的值;(Ⅲ)物理成绩为C 等级的学生中,已知10≥a ,1712≤≤b , 随机变量b a -=ξ,求ξ的分布列和数学期望.18. (本题满分12分)已知公差不为零的等差数列{}n a 的前5项和为30,且2a 为1a 和4a 的等比中项. (1)求{}n a 的通项公式n a 及前n 项和n S ; (2)若数列{}n b 满足*1()n n n b S n N b n +=∈,且11b =,求数列1{}n nb +的前n 项和n T19.(本题满分12分)在三棱柱111ABC A B C -中,已知2AB BC ==,090ABC ∠=,点1A 在底面ABC 的投影为B ,且1A B =(1)证明:平面11AA B B ⊥平面11BB C C ;(2)设P 为11B C 上一点,当PA =1A AB P --20.(本题满分13分)如图,设F 是椭圆C :22221(0)x y a b a b+=>>的左焦点,MN 为椭圆的长轴,P 为椭圆C上一点,且||[2,6]PF ∈. (Ⅰ)求椭圆C 的方程; (Ⅱ)设点(8,0)Q -,①求证:对于任意的割线QAB ,恒有AFM BFN ∠=∠; ②求三角形ABF ∆面积的最大值.21.(本小题满分14分)设函数2()ln ()2af x x x a =+--,a R ∈. (1)若函数()f x 在1[, 2]2上单调递增,求实数a 的取值范围; (2)求函数)(x f 的极值点.(3)设x m =为函数()f x 的极小值点,()f x 的图象与x 轴交于1212(,0),(,0)()A x B x x x <两点,且120x x m <<<,AB 中点为0(,0)C x ,比较)('x f 与0的大小.参考答案第I 卷(选择题 共60分)一、选择题:本大题共12个小题,每小题5分,共60分.每小题给出的四个选项中只有一项是符合题目要求的.1.已知全集R U =,集合{}21x A x =>,{}2340B x x x =-->,则A B ⋂=( )A .{}0x x >B .{}10x x x <->或C .{}4x x >D .{}14x x -≤≤2.已知复数231ii--(i 是虚数单位),它的实部和虚部的和是( ) A .4 B .6 C .2 D .3 3.下列命题中是假命题...的是( )A .,)1()(,342是幂函数使+-⋅-=∈∃m m xm x f m R ),0(+∞且在上递减B .有零点函数a x x x f a -+=>∀ln ln )(,02C .βαβαβαsin cos )cos(,,+=+∈∃使R ;D .,()sin(2)f x x ϕϕ∀∈=+R 函数都不是偶函数4.已知实数y x ,满足1218y y x x y ≥⎧⎪≤-⎨⎪+≤⎩,则目标函数y x z -=的最小值为( )A .5B .2-C .6D .7 5. “1a =”是“函数a x x f -=)(在区间[2,)+∞上为增函数”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件6.设振幅、相位、初相为方程sin()(0)y A x b A ωϕ=++>的基本量,则方程3sin(21)+4y x =-的基本量之和为 ( ) A .4B .23x +C.8D .21x +7.已知正四面体的俯视图如图所示,其中四边形ABCD 是边长为2的正方形,则这个正四面体的主视图的面积为 ( ) A. BC. D8.F 1,F 2是双曲线2222:1(,0)x y C a b b a b-=>>的左、右焦点,过左焦点F 1的直线l 与双曲线C的左、右两支分别交于A ,B 两点,若22||:||:||3:4:5AB BF AF =,则双曲线的离心率是( )AB C .2D9.设235111111,,a dx b dx c dx x x x ===⎰⎰⎰,则下列关系式成立的是( )A .235a b c <<B .325b a c<<C .523c a b <<D .253a c b<<10.已知()f x 是R 上的偶函数,当0x ≥时,12()22xf x x =-,又a 是函数2()ln(1)g x x x=+-的正零点,则(2)f -,()f a ,(1.5)f 的大小关系是 ( )A .(1.5)()(2)f f a f <<-B .(2)(1.5)()f f f a -<<C .()(1.5)(2)f a f f <<-D .(1.5)(2)()f f f a <-< 第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4个小题,每小题4分,共16分.11. 已知在平面直角坐标系xoy 中圆C 的参数方程为:3cos 13sin x y θθ⎧=⎪⎨=+⎪⎩,(θ为参数),以OX 为极轴建立极坐标系,直线极坐标方程为:,0)6cos(=+πθρ则圆C 截直线所得弦长为12.右边茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中有一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率是____110________.13.如图,已知||1,||3OA OB ==,OA 与OB 的夹角为56π,点C 是AOB ∆的外接圆上优孤AB 上的一个动点,则OA OC ⋅的最大值为. 1214.右图是一个算法的程序框图,最后输出的W =_____22___.15..13S =++=,210S =++++=,321S =++++++=,那么5S = 55 .三、解答题:本大题共6小题,共74分. 16. (本题满分12分)已知θ为向量a 与b 的夹角,||2=a ,||1=b ,关于x 的一元二次方程2x -||a x 0+⋅=a b 有实根. (Ⅰ)求θ的取值范围;(Ⅱ)在(Ⅰ)的条件下,求函数2()sin cos f θθθθ=的最值. 解:16.(I ) 因为θ为向量a 与b 的夹角,所[0,]θπ∈,由|a |=2,|b |=1,可得2|a |=4,⋅a b =|a ||b |cos θ. ………………3分关于x 的一元二次方程20x x -+⋅=|a |a b 有实根,则有44(12cos )0θ∆=-⋅-≥2|a |a b =,得1cos 2θ≤,所以,3πθπ⎡⎤∈⎢⎥⎣⎦.………6分 (II )23cos 3cos sin )(f 2-+=θθθθ ⋅CBAO=23)212cos (32sin 21-++θθ =)32sin(2cos 232sin 21πθϑθ+=+ ………………9分 因为π,π3θ⎡⎤∈⎢⎥⎣⎦,所以⎥⎦⎤⎢⎣⎡∈+37,32πππθ,所以sin(⎥⎦⎤⎢⎣⎡-∈+23,1)32(πθ 所以,函数的最大值为23,最小值为-1. ………………12分17. (本题满分12分)17.某学校实施“十二五高中课程改革”计划,高三理科班学生的化学与物理水平测试的成绩抽样统计如下表.成绩分A(优秀)、B(良好)、C(及格)三种等级,设x 、y 分别表示化学、物理成绩. 例如:表中化学成绩为B 等级的共有20+18+4=42人.已知x 与y 均为B 等级的概率为0.18.(Ⅰ) 求抽取的学生人数;(Ⅱ)若在该样本中,化学成绩的优秀率是0.3,求b a ,的值;(Ⅲ)物理成绩为C 等级的学生中,已知10≥a ,1712≤≤b , 随机变量b a -=ξ,求ξ的分布列和数学期望.18. (本题满分12分)已知公差不为零的等差数列{}n a 的前5项和为30,且2a 为1a 和4a 的等比中项. (1)求{}n a 的通项公式n a 及前n 项和n S ; (2)若数列{}n b 满足*1()n n n b S n N b n +=∈,且11b =,求数列1{}n nb +的前n 项和n T 解:(1) 设公差为(0)d d ≠,则1121115103022()(3)a d a d a d a a d +==⎧⎧⇒⎨⎨=+=+⎩⎩,∴ 2n a n =, (1)n S n n =+;(2)由(1)11n nn b S n b n+==+, 当2n ≥时,32411231234n nn b b b b b n b b b b b -=⋅⋅⋅⋅=⋅⋅⋅⋅,∴ !n b n =,又 11b =适合上式∴!n b n = *()n N ∈, ∴111=(1)!(1)!n n n b n n n +=-++!, ∴ 111111111()()()()11!2!2!3!3!4!!(1)!(1)!n T n n n =-+-+-++-=-++.19.(本题满分12分)在三棱柱111ABC A B C -中,已知2AB BC ==,090ABC ∠=,点1A 在底面ABC 的投影为B ,且1A B =(1)证明:平面11AA B B ⊥平面11BB C C ; (2)设P 为11B C 上一点,当PA =1A AB P --的正弦值.13(1)证明:∵1A B ⊥平面ABC ,BC ⊆平面ABC∴ 1A B BC ⊥,在ABC ∆中,090ABC ∠=,∴ AB BC ⊥,∴ BC ⊥平面11AA B B ,BC ⊆平面11BB C C , ∴ 平面11AA B B ⊥平面11BBC C ; (2)法一:传统方法 由(1)知11B C ⊥平面11AA B B ,∴ 1PB ⊥平面11AA B B ,过点1B 作棱AB 的垂线,垂足为O ,连接OP ,则1P O B ∠即为二面角1A AB P--的平面角连接1AB ,在1ABB ∆,由余弦定理可求得1AB∵ PA =,∴ 11PB =,∴ OP = 1sin 13POB ∠=法二:向量方法 如图建立空间直角坐标系B xyz -,(2,0,0)A ,(0,2,0)A ,(0,0,A ,由 111(2,0,B A BA B =⇒-, 由111(2,2,BC BC C =⇒-,ABCA 1B 1C 1P C由1112(2,,1)B C B P P λλλ=⇒->,由2AP λ=⇒=,∴(2,1,P -,设(,)n x y z =,为平面PAB 的法向量,则0200x n B A x y z n B P ⎧=⎧⋅=⎪⎪⇒⎨⎨-++=⎪⋅=⎪⎩⎩,取(0,6n =-,由(1)知 (0,2,0)m BC ==为平面11AA B B 的法向量,∴c o s,9n m <>==,13sin ,13n m <>=.20.(本题满分13分)如图,设F 是椭圆C :22221(0)x y a b a b+=>>的左焦点,MN 为椭圆的长轴,P 为椭圆C 上一点,且||[2,6]PF ∈. (Ⅰ)求椭圆C 的方程; (Ⅱ)设点(8,0)Q -,①求证:对于任意的割线QAB ,恒有AFM ∠=②求三角形ABF ∆面积的最大值.解:(Ⅰ)2211612x y +=; (Ⅱ)①易知直线AB 斜率存在.当AB 的斜率为0时,显然0AFM BFN ∠=∠=,满足题意,当AB 的斜率不为0时,设AB l : 8(0)x my m =-≠,11(,)A x y ,22(,)A x y ,由 22228(34)48144011612x my m y my x y =-⎧⎪⇒+-+=⎨+=⎪⎩. ∴222222248412(34)24(4)04m m m m ∆=-⨯+=->⇒>,1224834m y y m +=+,12214434y y m =+. 则121222AF BF y yk k x x +=+++1212211212(6)(6)66(6)(6)y y y my y my my my my my -+-=+=----12121226()(6)(6)my y y y my my -+=--,又 1212221444826()2603434mmy y y y m m m -+=⋅-⋅=++,∴0AF BF k k +=,从而A F MB F N ∠=∠.综合可知:对于任意的割线QAB ,恒有AFM BFN ∠=∠.②由①,2121||||234ABF QBF QAFS S S QF y y m ∆∆∆=-=⋅-=+,72==≤=当且仅当=,即3m =±(此时适合于0>∆的条件)时取等号.∴ 三角形ABF ∆面积的最大值是33.(0)t t =>,则27272163163t t t t==≤=++ 21.(本小题满分14分)设函数2()ln ()2af x x x a =+--,a R ∈. (1)若函数()f x 在1[, 2]2上单调递增,求实数a 的取值范围; (2)求函数)(x f 的极值点.(3)设x m =为函数()f x 的极小值点,()f x 的图象与x 轴交于1212(,0),(,0)()A x B x x x <两点,且120x x m <<<,AB 中点为0(,0)C x ,比较)('x f 与0的大小.解:(1)21221()2()x ax f x x a x x -+'=+-=依题意得,在区间1[, 2]2上不等式22210x ax -+≥恒成立. 又因为0x >,所以12(2)a x x≤+.所以2a ≤a ≤所以实数a的取值范围是(,-∞.(2)2221()x ax f x x-+'=,令2()221h x x ax =-+①显然,当0a ≤时,在(0,)+∞上()0h x >恒成立,这时()0f x '>,此时,函数()f x 没有极值点; ……………………………………6分②当0a >时,(ⅰ)当0∆≤,即0a <时,在(0,)+∞上()0h x ≥恒成立,这时()0f x '≥,此时,函数()f x 没有极值点;(ⅱ)当0∆>,即a >x <<()0h x <,这时()0f x '<;当0x <<x >时,()0h x >,这时()0f x '>;所以,当a >x ()f x的极大值点;x =()f x 的极小值点.综上,当a ()f x 没有极值点;当a >2a x =是函数()f x 的极大值点;2a x =是函数()f x 的极小值点. ………9分 (3)由已知得2211122222()ln ()02()ln ()02a f x x x a a f x x x a ⎧=+--=⎪⎪⎨⎪=+--=⎪⎩两式相减,得:()112122ln()2x x x x x a x +-+-……①由'1()2()f x x a x =+-,得'0001()2()f x x a x =+-…………② 得①代入②,得 '001201212()2()(2)f x x a x x a x x x =+-=++-+ =221222*********(1)211ln ln ()()1x x x x x x x x x x x x x x ⎡⎤-⎢⎥⎢⎥-=-+--⎢⎥+⎢⎥⎣⎦令12(0,1),x t x =∈且2222(1)()ln (01),()0,1(1)t t t t t t t t t ϕϕ--'=-<<=-<++()t ϕ∴在(0,1)上递减,()(1)0t ϕϕ∴>=120,()0x x f x '<∴<。
江西省南昌市教研室命制2014届高三数学交流卷试题(一)文
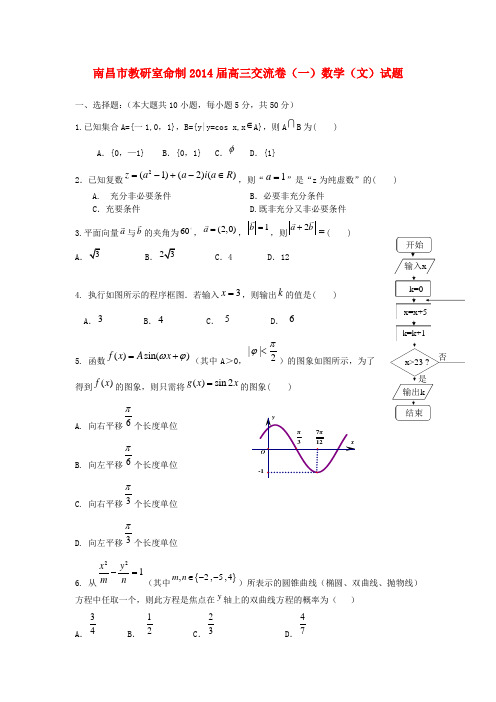
南昌市教研室命制2014届高三交流卷(一)数学(文)试题一、选择题:(本大题共10小题,每小题5分,共50分) 1.已知集合A={一1,0,1},B={y|y=cos x,x ∈A},则A B 为( )A .{0,—1}B .{0,1}C .φD .{1}2.已知复数2(1)(2)()z a a i a R =-+-∈,则“1a =”是“z 为纯虚数”的( ) A. 充分非必要条件 B .必要非充分条件C .充要条件 D.既非充分又非必要条件 3.平面向量a 与b 的夹角为60,(2,0)a =,1b =,则2a b+=( )AB. C .4 D .124. 执行如图所示的程序框图.若输入3x =,则输出k 的值是( ) A .3 B .4 C . 5 D . 65. 函数()sin()f x A x ωϕ=+(其中A >0,2||πϕ<)的图象如图所示,为了得到()f x 的图象,则只需将()sin 2g x x =的图象( )A. 向右平移6π个长度单位B. 向左平移6π个长度单位 C. 向右平移3π个长度单位 D. 向左平移3π个长度单位6. 从221x y m n -=(其中{},2,5,4m n ∈--)所表示的圆锥曲线(椭圆、双曲线、抛物线)方程中任取一个,则此方程是焦点在y 轴上的双曲线方程的概率为( )A .34B . 12 C .23D .47是结束输出k 否x>23 ?k=k+1x=x+5k=0输入x 开始7. 函数13y x x =-的图象大致为8. 四棱锥P ABCD -的顶点P 在底面ABCD 中的投影恰好是A ,其三视图如图所示,则四棱锥P ABCD -的表面积为 ( )A.2222S a a =+ B. 2223S a a =C. 2242S a a =+ D. 2233S a a =9.已知抛物线22(0)y p xp =>的焦点F 与椭圆22221(0)x y a b a b +=>>的一个焦点重合,它们在第一象限内的交点为T ,且T F 与x 轴垂直,则椭圆的离心率为( )A .212- 21- C.13- D.213-10.如图,点P 从点O 出发,分别按逆时针方向沿周长均为12的正三角形、正方形运动一周,,O P 两点连线的距离y 与点P 走过的路程x 的函数关系分别记为(),()y f x y g x ==,定义函数()()()()()()()f x f x g x h x g x f x g x ⎧⎪=⎨>⎪⎩,≤,,. 对于函数()y h x =,下列结论正确的个数是( )① (4)10h = ; ②函数()h x 的图象关于直线6x =对称; ③函数()h x 值域为013⎡⎣, ; ④函数()h x 增区间为05(,). 第10题图 A .1 B .2 C .3 D .4二、填空题(本大题共5小题,每小题5分,共25分. )OPPO11.已知数列1,,9a 是等比数列,数列121,,,9b b 是等差数列,则12ab b +的值为 .12.某校高三第一次模考中,对总分450分(含450分)以上的成绩进行统计,其频率分布直方图如图所示,若650~700分数段的人数为90,则500~550分数段的人数为_________人.13. 若关于x ,y 的不等式组10,10,10x y x ax y +-≥⎧⎪-≤⎨⎪-+≥⎩(a 为常数)所表示的平面区域的面积等于2,则a 的值为 .14. 在直角三角形ABC 中,90ACB ∠=︒,2AC BC ==,点P 是斜边AB 上的一个三等分点,则CP CB CP CA ⋅+⋅= . 15. 给出下列四个命题:①ABC ∆中,A B >是sin sin A B >成立的充要条件;②当01x x >≠且时,有1ln 2ln x x +≥;③已知n S 是等差数列{}n a 的前n 项和,若75S S >,则93S S >;④若函数)23(-=x f y 为R 上的奇函数,则函数)(x f y =的图象一定关于点)0,23(F 成中心对称.⑤函数)(cos sin cos )(23R x x x x x f ∈-+=有最大值为2,有最小值为0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
南昌市教研室命制2014届高三交流卷(一)数学(理)试题一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1设复数11z i=-,则z 的共轭复数是( )A.11i +B.1i +C.11i- D.1i -2.设p ∶22,x x q --<0∶12xx +-<0,则p 是q 的 ( ) A 充分不必要条件B 必要不充分条件C 充要条件D 既不充分也不必要3.设()f x 是定义在R 上的偶函数,且在]0,(-∞上是增函数,设412(log 7),(log 3),a f b f ==2(2)c f =,则,,a b c 的大小关系是( )A. b a c << B . a b c << C . a c b << D . c b a <<4.已知1sin 123πα⎛⎫+= ⎪⎝⎭,则7cos 12πα⎛⎫+ ⎪⎝⎭的值等于( )A.13 B. 223 C. 13- D. 223- 5.已知函数x n x m x f cos sin 2)(-=,直线3π=x 是函数)(x f 图像的一条对称轴,则=mn( ) A.332B. 3C. 332-D. 336.等差数列{}n a 中的1a 、4025a 是函数321()4613f x x x x =-+-的极值点,则22013log a =( )A .2B .3C .4D .57.过抛物线24y x =的焦点F 的直线交抛物线于A B 、两点,点O 是坐标原点,若||5AF =,则△AOB 的面积为( )A .5B .52C .32D .1788.已知函数2210()40x x f x x x a x ⎧+>⎪=⎨--+≤⎪⎩ 在点(1,2)处的切线与()f x 的图像有三个公共点,则a 的取值范围是( )A .[8,425)--+B .(425,425)---+C .(425,8]-+D .(425,8]--- 9.美不胜收的“双勾函数” 1y x x=+是一个对称轴不在坐标轴上的双曲线,它的渐近线分别是y 轴和直线y x =,其离心率e= A .2B . 21+C . 3D . 224-10若函数()y f x =图像上的任意一点P 的坐标(,)x y 满足条件|| ||y x ≥,则称函数()f x 具有性质S ,那么下列函数中具有性质S 的是 ( )A .()1x f x e =-B .()ln(1)f x x =+C .()sin f x x =D .()tan f x x = 二、选做题:请在下列两题中任选一题作答若两题都做,则按第一题评阅计分本题共5分. 11.(1)(坐标系与参数方程选做题)在直角坐标系xOy 中,以原点O 为极点, x 轴的正半轴为极轴建立极坐标系.若极坐标方程为4cos =θρ的直线与曲线⎩⎨⎧==32ty t x (t 为参数)相交于B A ,两点,则||AB =( )A.13B.14C.15D.16 11.(2)(不等式选做题)若不等式2)|2||1(|log 2≥--++m x x 恒成立,则实数m的取值范围为( )A . ]3,(--∞B . ]1,3[--C . ]3,1[-D . ]1,(--∞三、填空题:本大题共4小题,每小题5分,合计20分.12.已知向量)1,3(=a ,)1,0(-=b ,)3,(k c =,若b a 2+与c 共线,则=k _________ 13.运行如图的程序框图,输出的结果是______14.已知P 是以F 1,F 2为焦点的椭圆22221(0)x ya b a b +=>>上的任意一点,若∠PF 1F 2=α,∠PF 2F 1=β,且cos α=55,sin(α+β)=35,则此椭圆的离心率为 .15.在棱长为1的正方体ABCD —A 1B 1C 1D 1中,M 、N 分别是AC 1、A 1B 1的中点.点P 在正方体的表面上运动,则总能使MP 与BN 垂直的点P 所构成的轨迹的周长等于 .四、解答题:本大题共6小题,共75分.解答须写出文字说明、证明过程或演算步骤.16. (本小题满分12分)已知函数⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-⋅+=x x x x x f 23sin 32sin sin 2sin )(22ππ(1)若,21tan =x 求)(x f 的值;(2)求函数)(x f 最小正周期及单调递减区间.17. (本小题满分12分)PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,对人体健康和大气环境质量的影响很大。
我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某市环保局从360天的市区PM2.5监测数据中,随机抽取l5天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).(1)从这l5天的数据中任取3天的数据,记ξ表示空气质量达到一级的天数,求ξ的分布列;(2)以这l5天的PM2.5日均值来估计这360天的空气质量情况,则其中大约有多少天的空气质量达到一级.18.(本小题满分12分)如图,ABCD 是边长为3的正方形,ABCD 面⊥DE ,AF DE DE AF 3,//=,BE 与平面ABCD 所成的角为060.(1)求二面角D BE F --的的余弦值;(2)设点M 是线段BD 上一动点,试确定M 的位置,使得BEF AM 面//,并证明你的结论.19. (本小题满分12分) 设满足以下两个条件的有穷数列12,,,n a a a ⋅⋅⋅为n(n=2,3,4,,)阶“期待数列”:① 1230n a a a a ++++=;②1231n a a a a ++++=.(1)分别写出一个单调递增的3阶和4阶“期待数列”;(2)若某2k+1(*k N ∈)阶“期待数列”是等差数列,求该数列的通项公式; 20.(本小题满分13分)已知椭圆C 的中心在原点,焦点F 在x 轴上,离心率32e =,点2(2)2Q ,在椭圆C 上.(1)求椭圆C 的标准方程; (2)若斜率为k (0)k ≠的直线n 交椭圆C 与A 、B 两点,且OA k 、k 、OB k 成等差数列,点M (1,1),求ABM S ∆的最大值.21. (本小题满分14分)已知函数32()f x x x bx =-++,()ln g x a x x =+(0a ≠) (Ⅰ)若函数()f x 存在极值点,求实数b 的取值范围; (Ⅱ)求函数()g x 的单调区间;(Ⅲ)当0b =且0a >时,令(),1()(),1f x x F x g x x x <⎧=⎨-≥⎩,P (11,()x F x ),Q (22,()x F x )为曲线()y F x =上的两动点,O 为坐标原点,能否使得POQ ∆是以O 为直角顶点的直角三角形,且斜边中点在y 轴上?请说明理由.答案一.DABCC ABDDC 二.(1)D (2)D三.12 -3 13 510 14 5715 25+ 四.16所以)(x f 的单调递减区间为Z k k k ∈++],85,8[ππππ17解:(1)∵ 3,6,15===n M N ,ξ的可能值为0,1, 2,3其分布列为315396)(C C C k P kk -⋅==ξ )3 , 2 , 1 , 0(=k ………………… 3分 ξ0 1 2 3p4558445521645513545520………………… 6分(2)依题意可知,一年中每天空气质量达到一级的概率为52156==p 一年中空气质量达到一级的天数为η 则η~⎪⎭⎫ ⎝⎛52,360B , 所以14452360=⨯=ηE (天) ……………………11分一年中空气质量达到一级的天数为144天 ……………………………… 12分18(1)∵AC ⊥平面BDE ,∴平面BDE 的法向量设为(3,3,0)CA =-,∴613cos ,13||||2632n CA n CA n CA ⋅===⋅⨯,故二面角F BE D --的余弦值为1313.23211,2k k k a a a ++++++=∴(1)11,22(1)k k kd d d k k -+==+即20联立kxy y x ==+⎩⎨⎧1422易得弦AB 的长为224141k k++21当1t =时,(1,0),(1,2)OP OQ ==-则0OP OQ ⋅≠; …………11分 当1t >时,()F t =ln a t ,代入方程(*)得232ln ()0t a t t t -++= 即1(1)ln t t a=+, …………………………………12分设()(1)ln (1)h x x x x =+≥,则1()ln 10h x x x'=++>在[)1,+∞上恒成立. ∴()h x 在[)1,+∞上单调递增,从而()(1)0h x h ≥=,则值域为[)0,+∞. ∴当0a >时,方程1(1)ln t t a=+有解,即方程(*)有解. …………13分综上所述,对任意给定的正实数a ,曲线上总存在,P Q 两点,使得POQ 是以O 为直角顶点的直角三角形,且斜边中点在y 轴上. ………………14分.。
