广东省高考文科数学模拟试题(五)答案

合集下载

2020年广东省广州市高考文科数学模拟试卷及答案解析

2020年广东省广州市高考文科数学模拟试卷
一．选择题（共12小题，满分60分，每小题5分）
1．已知A＝{x∈N*|x≤3}，B＝{x|x2﹣4x≤0}，则A∩B＝（）
A．{1，2，3}B．{1，2}C．（0，3]D．（3，4]
2．已知样本数据1，2，4，3，5，下列说法不正确的是（）
A．平均数是3B．中位数是4C．极差是4D．方差是2
3．若复数z满足z（1﹣i）2＝i（i是虚数单位），则|z|为（）
A ．
B ．
C ．
D ．
4．等差数列{a n}中，a1+a8＝10，a2+a9＝18，则数列{a n}的公差为（）A．1B．2C．3D．4
5．若＝，则tan2α的值为（）
A ．
B ．
C ．﹣D．3
6．已知a＞0，x，y 满足约束条件，若z＝x+2y的最大值为2，则a＝（）
A ．
B ．
C ．
D ．
7．某公司的班车在7：00，8：00，8：30发车，小明在7：50至8：30之间到达发车站乘坐班车，且到达发车站的时刻是随机的，则他等车时间不超过10分钟的概率是（）
A ．
B ．
C ．
D ．
8．已知，，，则实数a，b，c的大小关系为
（）
A．c＜a＜b B．b＜a＜c C．a＜c＜b D．c＜b＜a
9．如图，在四棱锥P﹣ABCD中，AD∥BC，AD⊥DC，P A⊥平面ABCD，BC＝CD ＝AD，E为棱AD的中点，点M是平面P AB内一个动点，且直线CM∥平面PBE，动点M所组成的图形记为ω，则（）
第1页（共21页）。

2019年广东省高考全真文科数学模拟试卷(五)及答案

2019年广东高考全真模拟试卷文科数学（五）本试卷共4页，21小题，满分150分．考试用时120分钟．参考公式：球体的体积公式343V r π=，其中r 为球半径长．一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的1、如图所示，U 表示全集，则用A 、B 表示阴影部分正确的是( )A.)(B A C UB.B C A C U UC.)(B A C UD.B A2、函数()2sin()2f x x π=+在其定义域上是( )A.奇函数B.偶函数C.增函数D.减函数3、等差数列{}为则中，593,19,7a a a a n ==（）. A 、13 B 、12 C 、11 D 、104、原命题：“设2,,ac b a R c b a 则若、、>∈＞bc 2”以及它的逆命题，否命题、逆否命题中，真命题共有（）个.A.0B.1 C .2 D.4 5、已知正方形ABCD 边长为1，则AB BC AC ++=( ) A.0 B.2 C .2 D.226、一个正方体的体积是8，则这个正方体的内切球的表面积是（） A 、π8 B 、π6 C 、π4 D 、π7、方程0Ax By C ++=表示倾斜角为锐角的直线，则必有( ) A.0AB > B.0AB < C .0BC > D.0BC <8、若焦点在x 轴上的椭圆 1222=+m y x 的离心率为21，则m =（）. A 、23 B 、3 C 、38 D 、329、在空间直角坐标系xyz O -中，过点(4,2,3)--M 作直线OM 的垂线l ，则直线l 与平面Oxy 的交点(,,0)P x y 的坐标满足条件( )A ．42290+-=x yB ．42290-+=x yC ．42290++=x yD ．42290--=x y 10、已知()f x 是定义在R 上的不恒为零的函数，且对于任意的a 、b ∈R ，满足()f ab =()()af b bf a +，(2)2f =，(2)n n f a n =（n *∈N ），(2)2n n n f b =（n *∈N ）.考查下列结论：①(0)(1)f f =；②()f x 为偶函数；③数列{}n a 为等比数列；④{}n b 为等差数列。

2022年广东文科数学高考模拟试题10份(含详细答案)-图文

2022年广东文科数学高考模拟试题10份（含详细答案）-图文2022届广东高考数学（文科）模拟试题（一）满分150分，考试用时120分钟。

一、选择题：本大题共10小题，每小题5分，满分50分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1、设复数z满足zi2i，i为虚数单位，则z（）A、2iB、12iC、12iD、12i2、集合A{某|某22某0}，B{某|ylg(1某)}，则AB等于（）A、{某|0某1}B、{某|1某2}C、{某|1某2}D、{某|0某1}3、已知向量a,b满足|a|1,|b|2,ab1,则a与b的夹角为()A、3B、34C、4D、64、函数f(某)(某a)(某b)（其中ab）的图象如下面右图所示，则函数g(某)a某b的图象是（）y某5、已知某，y满足不等式组某y2，则z2某y的最大值与最小值的比值为（）某2A、134B、2C、D、2236、右边程序执行后输出的结果是S()A、1275B、1250C、1225D、1326i=1S=0WHILEi<=50S=S+ii=i+1WENDPRINTSEND17、已知某、y取值如下表：某y01.311.845.656.167.489.30.95某a，则a（）从所得的散点图分析可知：y与某线性相关，且yA、1.30B、1.45C、1.65D、1.80某2y28、已知方程1表示焦点在y轴上的椭圆，则实数k的取值范围是（）2k2k1A、11,2B、(1,)C、(1,2)D、,1229、若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如下图所示，则这个棱柱的体积为（）433正视图侧视图俯视图A、123B、6C、273D、36310、如下图所示，将若干个点摆成三角形图案，每条边（包括两个端点）有n(n1,nN)个点，相应的图案中总的点数记为an，则9999（）a2a3a3a4a4a5a2022a2022A、2022202220222022B、C、D、2022202220222022二、填空题：本大题共5小题，考生作答4小题，每小题5分，满分20分。

广东省高考全真模拟考试数学文科试题5(详解版).doc

2013年广东省高考全真模拟试卷数学文科（五）数学（文科）本试卷满分150分。

考试用时120分钟。

注意事项： 1．答卷前，考生务必用黑色字迹的钢笔或签字笔将字迹的姓名和考生号、实施号、座位号填写在答题卡上用2B 铅笔将试卷类型（B ）填涂在答题卡相应位置上。

将条形码横贴在答题卡右上角“条形码粘贴处”。

2．选择题每小题选出答案后，用2B 铅笔把大题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须卸载答题卡个题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4．作答选做题时，请先用2B 铅笔填涂选作题地题号对应的信息点，再作答，漏凃，错涂、多涂。

答案无效。

5．考生必须保持答题卡的整洁，考试结束后，将试卷和答题卡一并交回。

参考公式：锥体体积公式V=13Sh,其中S 为锥体的底面积，h 为锥体的高。

线性回归方程^^^y b x a =+中系数计算公式^^^121(1)(1),(1)ni ni x x y y b a y b x x ==--==--∑∑样本数据x 1,x 2,……，xa 的标准差，211()2(2)()n x x x x x x n+-+-+- 其中,x y 表示样本均值。

N 是正整数，则1221()(ab )n n n n n n a b a b a a b b -----=-+++……一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的 1． (){},|0,,A x y x y x y R =+=∈,(){},|20,,B x y x y x y R =--=∈，则集合A B =( )A ．(1,1)-B ．{}{}11x y ==- C ．{}1,1- D ．(){}1,1-2．下列函数中，在其定义域内是减函数的是( ) A .1)(2++-=x x x f B ． xx f 1)(=第8题C ． 13()log f x x = D . ()ln f x x =3．已知0a >,4()4,f x x a x =-+则()f x 为( )A ．奇函数B ．偶函数C ．非奇非偶函数D ．奇偶性与a 有关4．已知向量(12)a =，，(4)b x =，，若向量a b //，则x =( ) A ．2 B ． 2- C ． 8D ．8-5.设数列{}n a 是等差数列,且5,8152=-=a a ,n S 是数列{}n a 的前n 项和，则 ( ) A.109S S <B.109S S =C.1011S S <D.1011S S =6．已知直线l 、m ,平面βα、，则下列命题中：①．若βα//，α⊂l ,则β//l ②．若βα//，α⊥l ,则l β⊥③．若α//l ，α⊂m ,则m l // ④．若βα⊥，l =⋂βα, l m ⊥,则β⊥m . 其中，真命题有（）A ．0个B ．1个C ．2个D ．3个7．已知离心率为e 的曲线22217-=x y a ，其右焦点与抛物线216=y x 的焦点重合，则e 的值为（）A ．34B ．42323C ．43D ．2348．给出计算201614121++++ 的值的一个程序框图如右图，其中判断框内应填入的条件是（）． A ．10>i B ．10<i C ．20>i D ．20<i 9．lg ,lg ,lg x y z 成等差数列是2y xz =成立的（） A ．充分非必要条件 B ．必要非充分条件 C ．充要条件 D ．既不充分也不必要条件10．规定记号“⊗”表示一种运算，即),(2为正实数b a b a ab b a ++=⊗，若31=⊗k ，则k =（）A ．2-B ．1C ．2- 或1D ．2二、填空题：本大题共5小题，考生作答4小题，每小题5分，满分20分。

2020年广东省高考文科数学模拟试卷及答案解析

A．a＞b＞cB．b＞c＞aC．a＞c＞bD．c＞a＞b
4．设a，b是两个实数，给出下列条件：①a+b＞1；②a+b＝2；③a+b＞2；④a2+b2＞2．其中能推出“a，b中至少有一个大于1”的条件是（）
A．①②B．②③C．③④D．③
5．函数y＝的图象是（）
A．
B．
C．
D．
6．从编号为001，002，…，400的400个产品中用系统抽样的方法抽取一个样本，已知样本中编号最小的两个编号分别为007，032，则样本中最大的编号应该为（）
A． B． C． D．
11．在△ABC中，a，b，c分别为角A，B，C的对边，若a2﹣c2＝3b，且sinB＝8cosAsinC，则边b＝（）
A．3B．4C．5D．6
12．已知F是椭圆＝1（a＞b＞0）的左焦点，A为右顶点，P是椭圆上的一点，PF⊥x轴，若|PF|＝ |AF|，则该椭圆的离心率是（）
五．解答题（共1小题）
23．（1）解不等式：|x﹣1|+|x+3|＞6；
（2）若a＞0，b＞0，a+b＝2，证明：（ ﹣1）（ ﹣1）≥9
2020年广东省高考文科数学模拟试卷
参考答案与试题解析
一．选择题（共12小题，满分60分，每小题5分）
1．设z＝，则|z|＝（）
A． B．2C． D．3
【分析】利用商的模等于模的商求解．
19．（12分）如图，在四棱锥P﹣ABCD中，四边形ABCD是直角梯形，DC＝2AD＝2AB＝2∠DAB＝∠ADC＝90°，PB＝，△PDC为等边三角形．
（1）证明：PD⊥BC；
（2）求点B到平面PCD的距离．
20．（12分）已知函数f（x）＝aex﹣sinx+1其中a∈R，e为自然对数的底数．

2020年广东省广州市高考文科数学模拟试卷及答案解析

2020年广东省广州市高考文科数学模拟试卷
一．选择题（共12小题，满分60分，每小题5分）
1．已知复数z＝m（3+i）﹣（2+i）在复平面内对应的点在第三象限，则实数m的取值范围是（）
A．（﹣∞，1）B．（﹣∞，）
C．（）D．（﹣∞，）∪（1，+∞）
2．已知集合A＝{x|x2﹣5x+4＜0，x∈Z}，B＝{m，2}，若A⊆B，则m＝（）A．1B．2C．3D．5
3．已知角θ是第二象限角，且满足sin （﹣θ）＝，则tan（π+θ）＝（）
A ．﹣B．﹣1C ．D ．
4．如图，正四棱锥P﹣ABCD的侧面P AB为正三角形，E为PC中点，则异面直线BE和P A 所成角的余弦值为（）
A ．
B ．
C ．
D ．
5．已知曲线C 的方程为，现给出下列两个命题：是曲线为双曲线C 的充要条件，是曲线C为椭圆的充要条件，则下列命题中真命题的是（）
A．（￢p）∧（￢q）B．（￢p）∧q C．p∧（￢q）D．p∧q
6．某学校组织学生参加数学测试，成绩的频率分布直方图如图，数据的分组依次为[20，40），[40，60），[60，80），[80，100），若低于60分的人数是30人，则该班的学生人数是（）
第1 页共24 页。

2020年广东省高考模拟考试文科数学试题与答案

2020年广东省高考模拟考试文科数学试题与答案（满分150分，考试时间120分钟）注意事项：1．答题前，考生务必将自己的姓名、准考证号码填写在答题卡和试卷指定位置上，并将条形码准确粘贴在条形码区域内。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 已知集合{}1,2A =，集合{}0,2B =，设集合{},,C z z xy x A y B ==∈∈，则下列结论中正确的是A. A C φ⋂=B. A C C ⋃=C. B C B ⋂=D. A B C =2. 若复数2(1)z m m m i =+++是纯虚数，其中m 是实数，则1z= A. i B. i - C. 2iD. 2i -3. 若1sin()43x π-=，则sin 2x = A.79B. 79-C.13D. 13-4. 在矩形ABCD 中，8AB =，6AD =，若向该矩形内随机投一点P ，那么使ABP ∆与ADP ∆ 的面积都小于4的概率为 A.136B.112C.19D.495. 在等差数列{}n a 中，3a ，9a 是方程224120x x ++=的两根，则数列{}n a 的前11项和等于 A. 66B. 132C. -66D. -1326. 设函数2()23f x x x =--，若从区间[2,4]-上任取一个实数x ，则所选取的实数x 满足()0f x ≤的概率为A.12B.13C.23D.147. 设α，β是两个不同的平面，l ，m 是两条不同的直线，且l ⊂α,m ⊂β( ) A ．若l ⊥β，则α⊥β B ．若α⊥β，则l ⊥m C ．若l ∥β，则α∥β D ．若α∥β，则l ∥m8. 已知双曲线)0(13222>=-a y a x 的离心率为2，则 =aA. 2B.26C. 25D. 19. 函数ln ()xf x x=的图象大致为 A. B.C. D.10.已知函数532sin 2064y x x ππ⎛⎫⎛⎫=+<< ⎪⎪⎝⎭⎝⎭的图象与一条平行于x 轴的直线有两个交点，其横坐标分别为1x ，2x ，则12x x =+ A.43πB.23π C.3π D.6π 11.已知三棱锥ABC D -四个顶点均在半径为R 的球面上，且22===AC BC AB ，，若该三棱锥体积的最大值为1，则这个球的表面积为 A.81500π B. 9100π C. 925πD. π412. 已知椭圆22221(0)x y a b a b+=>>的左、右焦点分別为12,F F ，过2F 的直线与椭圆交于,A B 两点，若1F AB ∆是以A 为直角项点的等腰直角三角形，则椭圆的离心率为A B ．22 D -二、填空题：本题共4小题，每小题5分，共20分。

广东省高考数学模拟试卷(文科)(5月份)解析版

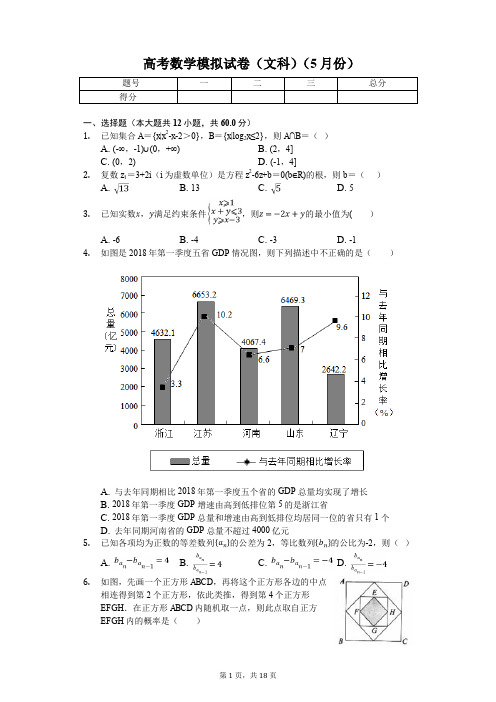
高考数学模拟试卷（文科）（5月份）一、选择题（本大题共12小题，共60.0分）1.已知集合A＝{x|x2-x-2＞0}，B＝{x|log2x≤2}，则A∩B＝（）A. (-∞，-1)∪(0，+∞)B. (2，4]C. (0，2)D. (-1，4]2.复数z1＝3+2i（i为虚数单位）是方程z2-6z+b＝0(b∈R)的根，则b＝（）A. B. 13 C. D. 53.已知实数，满足约束条件，则的最小值为( ）A. -6B. -4C. -3D. -14.如图是2018年第一季度五省GDP情况图，则下列描述中不正确的是（）A. 与去年同期相比2018年第一季度五个省的GDP总量均实现了增长B. 2018年第一季度GDP增速由高到低排位第5的是浙江省C. 2018年第一季度GDP总量和增速由高到低排位均居同一位的省只有1个D. 去年同期河南省的GDP总量不超过4000亿元5.已知各项均为正数的等差数列的公差为2，等比数列的公比为-2，则（）A. B. C. D.6.如图，先画一个正方形ABCD，再将这个正方形各边的中点相连得到第2个正方形，依此类推，得到第4个正方形EFGH．在正方形ABCD内随机取一点，则此点取自正方EFGH内的概率是（）A. B. C. D.7.在直角坐标系xOy中，抛物线C：y2＝4x的焦点为F，准线为l，P为C上一点，PQ垂直l于点Q，M，N分别为PQ，PF的中点，直线MN与x轴交于点R，若∠NFR ＝60°，则NR＝（）A. 2B.C.D. 38.已知△ABC，点M是边BC的中点，若点O满足，则（）A. B. C. D.9.函数的部分图象大致为（）A. B.C. D.10.如图，已知正方体ABCD-A1B1C1D1的棱长为4，P是AA1的中点，点M在侧面AA1B1B内，若D1M⊥CP，则△BCM面积的最小值为（）A. 8B. 4C.D.11.已知函数f（x）=2sin（ωx+φ）-1（ω＞0，|φ|＜π）的一个零点是，是y=f（x）的图象的一条对称轴，则ω取最小值时，f（x）的单调增区间是（）A. B.C. D.12.双曲线（a＞0，b＞0），A（-t，0），B（t，0）（t＞0），斜率为的直线A点且与双曲线交于M，N两点．若，，则双曲线的离心率为（）A. B. C. D.二、填空题（本大题共4小题，共20.0分）13.已知函数f(x)＝ae x＋b(a，b∈R)在点(0，f(0))处的切线方程为y＝2x＋1，则a－b＝________．14.已知函数，若f（a）=7（a∈R），则f（-a）=______．15.已知点A，B，C，D在球O的表面上，且AB=AC=2，BC=2，若三棱锥A-BCD的体积为，球心O恰好在棱AD上，则这个球的表面积为__________．16.已知数列{a n}满足（n∈N*），则a25-a1=______．三、解答题（本大题共7小题，共82.0分）17.设△ABC的内角A，B，C所对边的长分别是a，b，c，且b=3，c=1，A=2B．（Ⅰ）求a的值；（Ⅱ）求的值．18.如图，在直三棱柱ABC-A1B1C1中，底面△ABC为等腰直角三角形，AB=BC=2，AA1=3，P为B1C1的中点，Q为BB1的三等分点（靠近B1）点．（Ⅰ）求三棱锥P-AQC的体积；（Ⅱ）在线段A1C1上找点M，使得B1M∥平面APQ，写出作图步骤，但不要求证明．19.随着人民生活水平的日益提高，某小区居民拥有私家车的数量与日俱增．由于该小区建成时间较早，没有配套建造地下停车场，小区内无序停放的车辆造成了交通的拥堵．该小区的物业公司统计了近五年小区登记在册的私家车数量（累计值，如124表示2016年小区登记在册的所有车辆数，其余意义相同），得到如下数据：程，并预测2020年该小区的私家车数量；（2）小区于2018年底完成了基础设施改造，划设了120个停车位．为解决小区车辆乱停乱放的问题，加强小区管理，物业公司决定禁止无车位的车辆进入小区．由于车位有限，物业公司决定在2019年度采用网络竞拍的方式将车位对业主出租，租期一年，竞拍方案如下：①截至2018年已登记在册的私家车业主拥有竞拍资格；②每车至多申请一个车位，由车主在竞拍网站上提出申请并给出自己的报价；③根据物价部门的规定，竞价不得超过1200元；④申请阶段截止后，将所有申请的业主报价自高到低排列，排在前120位的业主以其报价成交；⑤若最后出现并列的报价，则以提出申请的时间在前的业主成交．为预测本次竞拍的成交最低价，物业公司随机抽取了有竞拍资格的40位业主进行竞拍意向的调查，统计了他们的拟报竞价，得到如下频率分布直方图：（Ⅰ）求所抽取的业主中有意向竞拍报价不低于1000元的人数；（Ⅱ）如果所有符合条件的车主均参与竞拍，利用样本估计总体的思想，请你据此预测至少需要报价多少元才能竞拍车位成功？（精确到整数）．参考公式：对于一组数据（x1，y1），（x2，y2），…，（x n，y n），其回归直线的斜率和截距的最小二乘估计分别为：．20.已知椭圆（a＞b＞0）的离心率为，右焦点为F，以原点O为圆心，椭圆C的短半轴长为半径的圆与直线相切．（1）求椭圆C的方程；（2）如图，过定点P（2，0）的直线l交椭圆C于A，B两点，连接AF并延长交C于M，求证：∠PFM=∠PFB．21.已知函数.（1）讨论函数的单调性；（2）当时，讨论函数的零点个数.22.在直角坐标系xOy中，曲线C1的参数方程为（α为参数）．P是曲线C1上的动点，将线段OP绕O点顺时针旋转90°得到线段OQ，设点Q的轨迹为曲线C2．以坐标原点O为极点，x轴正半轴为极轴建立极坐标系．（Ⅰ）求曲线C1，C2的极坐标方程；（Ⅱ）在（Ⅰ）的条件下，若射线与曲线C1，C2分别交于A，B两点（除极点外），且有定点M（4，0），求△MAB面积．23.已知函数f（x）=|x-m|-|2x+3m|（m＞0）．（1）当m=1时，求不等式f（x）≥1的解集；（2）对于任意实数x，t，不等式f（x）＜|2+t|+|t-1|恒成立，求m的取值范围．答案和解析1.【答案】B【解析】【分析】先求出集合A，B，由此能求出A∩B．本题考查交集的求法，考查交集定义、不等式性质等基础知识，考查运算求解能力，是基础题．【解答】解：∵集合A={x|x2-x-2＞0}={x|x＜-1或x＞2}，B={x|log2x≤2}={x|0＜x≤4}，∴A∩B={x|2＜x≤4}=（2，4]．故选：B．2.【答案】B【解析】【分析】利用实系数一元二次方程虚根成对及根与系数的关系求解．本题考查实系数一元二次方程虚根成对原理的应用，考查复数代数形式的乘除运算，是基础题．【解答】解：∵z1=3+2i是方程z2-6z+b=0（b∈R）的根，由实系数一元二次方程虚根成对原理可知，z2=3-2i为方程另一根，则b=（3+2i）（3-2i）=13．故选：B．3.【答案】A【解析】【分析】本题主要考查线性规划的应用，利用目标函数的几何意义，结合数形结合的数学思想是解决此类问题的基本方法．作出不等式组对应的平面区域，利用目标函数的几何意义，求目标函数z=-2x+y的最小值．【解答】解：由z=-2x+y，得y=2x+z，作出不等式对应的可行域（阴影部分），平移直线y=2x+z，由平移可知当直线y=2x+z，经过点A(3,0)时，直线y=2x+z的截距最小，此时z取得最小值，由，解得A（3，0）．将A的坐标代入z=-2x+y，得z=-6，即目标函数z=-2x+y的最小值为-6．故选A．4.【答案】C【解析】解：由2018年第一季度五省GDP情况图，知：在A中，与去年同期相比，2018年第一季度五个省的GDP总量均实现了增长，故A正确，在B中，2017年第一季度GDP增速由高到低排位第5的是浙江省，故B正确．在C中，2018年第一季度GDP总量和增速由高到低排位均居同一位的省有江苏和山东，共2个，故C错误；在D中，去年同期河南省的GDP总量不超过4000亿元，故D正确；故选：C．20178第一季度GDP总量和增速由高到低排位均居同一位的省有江苏和山东．本题考查命题真假的判断，考查折线图、柱形图等基础知识，考查运算求解能力、数据处理能力，考查函数与方程思想、数形结合思想，是基础题．5.【答案】B【解析】【分析】本题考查等差数列与等比数列的通项公式，是基础题．由已知求得等比数列{b n}的通项公式，作比即可得到．【解答】解：∵等差数列{a n}的公差为2，数列{b n}是公比为-2的等比数列，∴，∴==．故选：B．6.【答案】C【解析】解：由几何概型中的面积型可知：p=，设正方形EFGH的边长为a，则正方形ABCD的边长为2a，则P==，故选：C．由几何概型的面积型，则p=，分别求正方形面积即可本题考查几何概型的面积型，属简单题7.【答案】A【解析】【分析】本题考查抛物线的定义以及简单性质，注意分析△PQF为等边三角形，属于综合题．根据题意画出图形，根据题意可得△PQF为等边三角形，求出其边长，进而在Rt△FMR 分析可得答案．【解答】解：根据题意，如图所示：连接MF，QF，抛物线的方程为y2=4x，其焦点为（1，0），准线x=-1，则FH=2，PF=PQ，又由M，N分别为PQ，PF的中点，则MN∥QF，又PQ=PF，∠NRF=60°，且∠NRF=∠QFH=∠FQP=60°，则△PQF为边长为4等边三角形，MF=2，在Rt△FMR中，FR=2，MF=2，则MR=4，则NR=MR=2，故选：A．8.【答案】D【解析】解：点M是边BC的中点，可得2=+，，可得++2（+）=-+4=，即2（-）+12=，可得=6，即∥，故选：D．由向量的中点表示和加减运算、以及向量的共线定理，即可得到结论．本题考查向量的中点表示，以及向量的加减运算和向量共线定理的运用，考查化简运算能力，属于基础题．9.【答案】B【解析】【分析】根据题意，分析函数f（x）的奇偶性以及在（0，π）上f（x）的符号，据此分析选项即可得答案．本题考查函数图象的判断以及分析，一般用排除法分析，属于基础题．【解答】解：根据题意，对于f（x）=sin x•，有f（-x）=sin（-x）•=sin x•=f（x），即函数f（x）为偶函数，据此可以排除A、C，又由在（0，π）上，sin x＞0，＞0，有f（x）＞0，则函数f（x）＞0，据此排除D；故选B．10.【答案】D【解析】解：以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，过M作MG⊥平面ABCD，G是垂足，过G作GH⊥BC，交BC于H，连结MH，则D（0，0，0），C（0，4，0），A（4，0，0），P（4，0，2），C（0，4，0），D1（0，0，4），B（4，4，0），设M（4，a，b），则=（4，a，b-4），=（4，-4，2），∵D1M⊥CP，∴•=16-4a+2b-8=0，解得2a-b=4，∴CH=4-a，MG=b=2a-4，MH===，=，∴y=时，（S△BCM）min=2•=．故选：D．以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，利用向量法能求出△BCM面积取最小值．本题考查三角形的面积的最小值的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，考查数形结合思想，是中档题．11.【答案】A【解析】解：函数f（x）=2sin（ωx+φ）-1的一个零点是x=，∴f（）=2sin（ω+φ）-1=0，∴sin（ω+φ）=，∴ω+φ=+2kπ或ω+φ=+2kπ，k∈Z；又直线x=-是函数f（x）图象的一条对称轴，∴-ω+φ=+kπ，k∈Z；又ω＞0，|φ|＜π，∴ω的最小值是，φ=，∴f（x）=2sin（x+）-1；令-+2kπ≤x+≤+2kπ，k∈Z，∴-+3kπ≤x≤-+3kπ，k∈Z；∴f（x）的单调增区间是[-+3kπ，-+3kπ]，k∈Z．故选：A．根据函数f（x）的一个零点是x=，得出f（）=0，再根据直线x=-是函数f（x）图象的一条对称轴，得出-ω+φ=+kπ，k∈Z；由此求出ω的最小值与对应φ的值，写出f（x），从而求出它的单调增区间．本题考查了正弦型三角函数的图象与性质的应用问题，是综合性题目．12.【答案】A【解析】解：直线MN的方程为y=（x+t），联立方程组，消元可得：（9b2-a2）x2-2a2tx-a2t2-9a2b2=0，设M（x1，y1），N（x2，y2），则由根与系数的关系可得：x1+x2=，∵2=，∴D为MN的中点，∴D（，+），∵，∴BD⊥MN，∴k BD=-3，即，化简可得=，即b=，∴e===．故选：A．联立方程组消元，根据根与系数的关系和中点中点坐标公式得出D点坐标，根据k BD=-3列方程得出a，b的关系，从而可得出双曲线的离心率．本题考查了双曲线的性质，直线与双曲线的位置关系，属于中档题．13.【答案】3【解析】【分析】本题主要考查函数与导数的关系，特别是曲线的切线与函数导数之间的关系，属于中档题．由f（x）=ae x+b，得f'（x），因为函数f（x）在点（0，f（0））处的切线方程是y=2x+1，故（0，f（0））适合方程y=2x+1，且f′（0）=2；联立可得结果．【解答】解：由f（x）=ae x+b，得f'（x）=ae x，因为函数f（x）在点（0，f（0））处的切线方程是y=2x+1，所以解得a=2，b=-1．所以a-b=3．故答案为：3．14.【答案】7【解析】解：f（x）的定义域为R，关于原点对称，又f（-x）====f（x），∴f（x）是R上的偶函数，∴f（-a）=f（a）=7．故答案为：7．求出f（x）的定义域，然后判断f（x）的奇偶性，根据奇偶性可得答案．本题考查了函数奇偶性的判断，关键是对对数式的真数分子有理化，属基础题．15.【答案】16π【解析】【分析】作出图形，作△ABC外接圆的直径AF，可得出DF⊥平面ABC，利用三棱锥A-BCD的体积计算出DF，再结合勾股定理可计算出球的直径，最后利用球体的表面积公式可计算出答案．本题考查球体表面积的计算，考查锥体的体积的计算，考查推理能力与计算能力，属于中等题．【解答】解：如下图所示，设△ABC的外接圆为圆E，则点E为线段BC的中点，作圆E的直径AF，连接DF、OE，则OE⊥平面ABC，∵O、E分别为AD、AF的中点，∴OE∥DF，则DF⊥平面ABC，∵AB=AC=2，，∴AB2+AC2=BC2，∴，∴，三棱锥A-BCD的体积为，得，圆E的直径为，所以，球O的直径为，则R=2，因此，球O的表面积为4πR2=16π．故答案为：16π．16.【答案】300【解析】解：∵[2-（-1）n]a n+[2+（-1）n]a n+1=1+（-1）n×3n，∴n=2k（k∈N*），可得：a2k+3a2k+1=1+6k，n=2k-1（k∈N*），可得：3a2k-1+a2k=1-6k+3，∴a2k+1-a2k-1=4k-1，∴a25=（a25-a23）+（a23-a21）+…+（a3-a1）+a1=（4×12-1）+（4×11-1）+…+（4×1-1）+a1=-12+a1=300+a1．则a25-a1=300，故答案为：300．由[2-（-1）n]a n+[2+（-1）n]a n+1=1+（-1）n×3n，当n=2k（k∈N*），可得：a2k+3a2k+1=1+6k，n=2k-1（k∈N*），可得：3a2k-1+a2k=1-6k+3，于是a2k+1-a2k-1=4k-1，利用“累加求和”方法与等差数列的前n项和公式即可得出．本题考查了数列的递推关系、“累加求和”方法、等差数列的前n项和公式，考查了分类讨论方法、推理能力与计算能力，属于中档题．17.【答案】（Ⅰ）解：由A=2B，知sin A=sin2B=2sin B cosB，…………（1分）由正、余弦定理得．………………（3分）因为b=3，c=1，所以a2=12，则．………………（5分）（Ⅱ）解：由余弦定理得．……（6分）由于0＜A＜π，所以………（8分）故…………（11分）………（13分）【解析】（Ⅰ）利用正弦定理和余弦定理建立方程关系进行求解空间（Ⅱ）利用两角和差的余弦公式进行求解本题主要考查解三角形的应用，利用正弦定理余弦定理以及两角和差的余弦公式是解决本题的关键．考查学生的计算能力．18.【答案】解：（Ⅰ）在直三棱柱中，面BCC1B1⊥面ABC，又AB⊥BC，∴AB⊥面BCC1B1，在矩形BCC1B1中，求得S△PQC=2，∴；（Ⅱ）如图，在平面ABB1A1内，过点B1作B1E∥AQ交AA1于点E，连结A1P，在△AA1P中，作EF∥AP交A1P于点F，连结B1F并延长交A1C1于点M，则B1M为所求作直线．【解析】（Ⅰ）把三棱锥P-AQC转化为A-PQC，容易求解；（Ⅱ）首先过B1作平面与平面APQ平行，该平面与A1C1的交点M即为所找的点．此题考查了转化法求体积，面面平行等，难度适中．19.【答案】解：（1）由表中数据，计算得，，，．故所求线性回归方程为，令x=7，得；（2）（i）由频率直方图可知，有意竞拍报价不低于1000元的频率为：（0.25+0.05）×1=0.3，共抽取40位业主，则40×0.3=12，∴有意竞拍不低于1000元的人数为12人．（ii）由题意，．由频率直方图估算知，报价应该在900-1000之间，设报价为x百元，则．解得x≈9.36．∴至少需要报价936元才能竞拍成功．【解析】（1）由表中数据，计算得与的值，则线性回归方程可求，取x=7求得y值得答案；（2）（i）由频率直方图求得有意竞拍报价不低于1000元的频率，乘以40得答案．（ii）由题意，．由频率直方图估算知，报价应该在900-1000之间，设报价为x 百元，可得．求解x值即可．本题考查线性回归方程的求法，考查计算能力，是中档题．20.【答案】解：（1）依题意可设圆C方程为x2+y2=b2，∵圆C与直线相切，∴，∴a2-c2=1，由解得，∴椭圆C的方程为．（2）证明：依题意可知直线l斜率存在，设l方程为y=k（x-2），代入，整理得（1+2k2）x2-8k2x+8k2-2=0，∵l与椭圆有两个交点，∴△＞0，即2k2-1＜0．设A（x1，y1），B（x2，y2），直线AF，BF的斜率分别为k1，k2则，．∵F（1，0），∴=====，即∠PFM=∠PFB．【解析】（1）依题意得，得a2-c2=1，结合得，从而得椭圆C的方程；（2）设A（x1，y1），B（x2，y2），直线l与椭圆方程联立消y得关于x的二次方程，从而得x1+x2，x1x2，只需证直线AF，BF的斜率之和为0即可．本题考查了椭圆的标准方程，考查了设而不求方法的应用，属难题．21.【答案】解：（1），令u（x）=2x2+3ax+1，其对称轴为，令2x2+3ax+1=0，则△=9a2-8．当a≥0时，f'（x）＞0，所以f（x）在（0，+∞）上单调递增；当a＜0时，对称轴为，若△=9a2-8≤0，即，u（x）≥0恒成立，所以f'（x）≥0，所以f（x）在（0，+∞）上单调递增；若时，设u（x）=0的两根，，当x∈（0，x1）时，u（x）＞0，所以f'（x）＞0，所以f（x）在（0，x1）上单调递增，当x∈（x1，x2）时，u（x）＜0，所以f'（x）＜0，所以f（x）在（x1，x2）上单调递减，当x∈（x2，+∞）时，u（x）＞0，所以f'（x）＞0，所以f（x）在（x2，+∞）上单调递增，综上所述：当时，f（x）在（0，+∞）上单调递增；若时，f（x）在（0，）上单调递增，在（，）上单调递减，在（，+∞）上单调递增；（2）当a＜-1时，由（1）知f（x）在（0，x1）上单调递增，在（x1，x2）上单调递减，在（x2，+∞）上单调递增，下面研究f（x）的极大值，又，所以，令g（x）=ln x-x2，则（x＞0），可得g（x）在上单调递增，在上单调递减，且g（x）的极大值，所以g（x）＜0，所以f（x1）＜0，当x∈（0，x1）时，f（x）单调递增，所以f（x）＜f（x1）＜0当x∈（x1，x2）时，f（x）在（x1，x2）上单调递减，所以f（x2）＜f（x）＜f（x1）＜0当x∈（x2，+∞）时，f（x）单调递增，且f（-4a）=ln（-4a）+16a2-12a2+1=ln（-4a）+4a2+1（a＜-1），f（x2）•f（-4a）＜0，所以存在x'∈（x2，-4a），使得f（x'）=0，又当x∈（x2，+∞）时，f（x）单调递增，所以f（x）只有一个零点x'，综上所述，当a＜-1时，f（x）在（0，+∞）上只有一个零点．【解析】本题考查了导数与函数单调性的关系，函数极值、单调性与函数零点的个数判断，属于难题．（1）讨论a的范围，得出f′（x）＞0和f′（x）＜0的解集，得出f（x）的单调性；（2）求出f（x）的极大值，判断极大值小于0，根据f（x）的单调性得出f（x）的零点个数．22.【答案】解：（Ⅰ）由题设曲线C1的参数方程为（α为参数）．转换为直角坐标方程为：x2+（y-1）2=1，即x2+y2-2y=0，将线段OP绕O点顺时针旋转90°得到线段OQ，设点Q的轨迹为曲线C2．故C1的极坐标方程为ρ2-2ρsinθ=0，即ρ=2sinθ．设点Q（ρ，θ）（ρ≠0），则由已知得，代入C1的极坐标方程得，即C2的极坐标方程为ρ=2cosθ（ρ≠0）．（Ⅱ）将代入C1，C2的极坐标方程得，又因为M（4，0），所以，所以．【解析】（Ⅰ）直接利用参数方程和直角坐标方程为的转换求出结果．（Ⅱ）利用直线和曲线的位置关系式的应用，利用向量的数量积的运算，利用一元二次方程根和系数关系的应用求出结果．本题考查的知识要点：参数方程直角坐标方程和极坐标方程之间的转换，向量的数量级向量的数量积的运算，一元二次方程根和系数关系的应用，主要考查学生的运算能力和转化能力，属于基础题型．23.【答案】解：（1）f（x）=|x-m|-|2x+3m|=，当m=1时，由f（x）≥1可得或或，即为x∈∅或-＜x≤-1或-3≤x≤-，∴不等式f（x）≥1的解集为{x|-3≤x≤-1}；（2）不等式f（x）＜|2+t|+|t-1|对任意的实数t，x恒成立，等价于对任意的实数f（x）＜[|2+t|+|t-1|]min恒成立，即[f（x）]max＜[|2+t|+|t-1|]min，∵f（x）=|x-m|-|2x+3m|=|x-m|-|x+m|-|x+m|≤|-m-m|-|-m+m|-|-m+m|=m，当且仅当x=-m上式取得等号，|2+t|+|t-1|≥|（2+t）-（t-1）|=3，当（2+t）（t-1）≤0即-2≤t≤1时，取得等号，∴m＜3又m＞0，所以0＜m＜．【解析】（1）将m=1的值带入，得到关于x的不等式组，求出不等式的解集即可；（2）问题等价于对任意的实数x，f（x）＜[|2+t|+|t-1|]min恒成立，根据绝对值的性质求出f（x）的最大值以及[|2+t|+|t-1|]min，求出m的范围即可．本题考查解绝对值不等式问题，考查绝对值的性质以及分类讨论思想，是一道中档题．。

广东省高考数学模拟试卷(文科)(5月份)解析版

参考公式：对于一组数据（x1，y1），（x2，y2），…，（xn，yn），其回归直线的斜率和截距的最小二乘估计分别为：
．
20. 已知椭圆
（a＞b＞0）的离心率为，右焦点为 F，以原点 O 为圆心，
椭圆 C 的短半轴长为半径的圆与直线
是 y=f
（x）的图象的一条对称轴，则 ω 取最小值时，f（x）的单调增区间是（）
A.
B.
C.
D.
12. 双曲线
（a＞0，b＞0），A（-t，0），B（t，0）（t＞0），斜率为的直线
A 点且与双曲线交于 M，N 两点．若
，
率为（）
A.
B.
C.
二、填空题（本大题共 4 小题，共 20.0 分）
第 3 页，共 18 页
编号 x
1
2
3
4
5
年份
2014 2015 2016 2017 2018
数量 y（单位：辆）
34 95 124 181 216
（1）若私家车的数量 y 与年份编号 x 满足线性相关关系，求 y 关于 x 的线性回归方程，并预测 2020 年该小区的私家车数量；（2）小区于 2018 年底完成了基础设施改造，划设了 120 个停车位．为解决小区车辆乱停乱放的问题，加强小区管理，物业公司决定禁止无车位的车辆进入小区．由于车位有限，物业公司决定在 2019 年度采用网络竞拍的方式将车位对业主出租，租期一年，竞拍方案如下： ①截至 2018 年已登记在册的私家车业主拥有竞拍资格； ②每车至多申请一个车位，由车主在竞拍网站上提出申请并给出自己的报价； ③根据物价部门的规定，竞价不得超过 1200 元； ④申请阶段截止后，将所有申请的业主报价自高到低排列，排在前 120 位的业主以其报价成交；⑤若最后出现并列的报价，则以提出申请的时间在前的业主成交．为预测本次竞拍的成交最低价，物业公司随机抽取了有竞拍资格的 40 位业主进行竞拍意向的调查，统计了他们的拟报竞价，得到如下频率分布直方图：（Ⅰ）求所抽取的业主中有意向竞拍报价不低于 1000 元的人数；（Ⅱ）如果所有符合条件的车主均参与竞拍，利用样本估计总体的思想，请你据此预测至少需要报价多少元才能竞拍车位成功？（精确到整数）．

广东省高三模拟考试(文科)数学试卷-附参考答案与解析

广东省高三模拟考试(文科)数学试卷-附参考答案与解析班级:___________姓名：___________考号：___________一、单选题1．已知12i +是关于x 的方程()20,R x px q p q ++=∈的一个根，i 为虚数单位，则i p q +=（）A ．23i --B ．52i +C ．25i -+D ．25i +2．已知集合{}Z 33U x x =∈-<<和{}2,1A =-与2,2B ，则()U B A ⋃=（） A ．{}2,1,2- B ．2,0,2C ．{}2,1,0,2--D ．{}2,1,2--3．若326n n A C =，则n =（）A ．5B ．3或4C ．4或5D ．44．如图，在ABC 中点M 是线段BC 上靠近B 的三等分点，则AM =（）A ．1233AB AC +B ．2133AB AC +C ．1433AB AC -+D ．1433AB AC -5．学生到工厂劳动实践，利用3D 打印技术制作模型．如图，该模型为长方体1111ABCD A B C D -挖去四棱锥O EFGH -后所得的几何体，其中O 为长方体的中心，E 、F 、G 、H 分别为所在棱的中点6cm AB BC ==和14cm AA =，3D 打印所用原料密度为30.9g /cm ，不考虑打印损耗，制作该模型所需原料的质量为（）A ．118.8gB ．108gC ．97.2gD ．86.4g6．已知点,M N 是抛物线24y x =上不同的两点，F 为抛物线的焦点，且满足23MFN π∠=，弦MN 的中点P 到直线1:16l y =-的距离记为d ，若不等式22λ≥MN d 恒成立，则λ的取值范围（） A．(-∞ B ．(],2-∞ C．(,1-∞D ．(],3-∞7．已知a=0.60.6，0.2log 3b =和c=1.50.6，则a ，b ，c 的大小关系是（） A ．a<b<c B ．a<c<b C ．b<a<cD ．b<c<a8．设函数()f x 的定义域为R ，()1f x +为奇函数，()2f x +为偶函数，当[]1,2x ∈时，则2()f x ax b =+．若()()036f f +=，则92f ⎛⎫= ⎪⎝⎭（）A ．94- B ．32-C ．74D ．52二、多选题9．有一组成对样本数据()()()1122,,,,,,n n x y x y x y ⋅⋅⋅，由这组成对样本数据得到的经验回归方程为y bx a =+，则（）A ．在点()()()1122,,,,,,n n x y x y x y ⋅⋅⋅中至少有1个点在经验回归直线y bx a =+上B ．若点()()()1122,,,,,,n n x y x y x y ⋅⋅⋅都在经验回归直线y bx a =+上，则样本的相关系数r 满足1r =C ．若1nii xx n==∑，1nii yy n==∑ 则y bx a =+D ．若成对样本数据()22,x y 的残差为t ，则在这组成对数据中必有成对样本数据的残差为t -10．正方体1111ABCD A B C D -的棱长为2，,,E F G 分别为11,,BC CC BB 的中点.则下列说法正确的是（）A ．直线1A G 与平面AEF 平行B ．直线1DD 与直线AF 垂直C ．异面直线1A G 与EFD ．平面AEF 截正方体所得的截面面积为9211．已知0ω>，函数()πcos 3f x x ω⎛⎫=+ ⎪⎝⎭，下列选项正确的有（）A ．若()f x 的最小正周期2T =，则πω=B ．当2ω=时，则函数()f x 的图象向右平移π3个单位长度后得到()cos2g x x =的图象C ．若()f x 在区间2π,π3⎛⎫⎪⎝⎭上单调递增，则ω的取值范围是51,3⎡⎤⎢⎥⎣⎦D ．若()f x 在区间()0,π上只有一个零点，则ω的取值范围是17,66⎛⎤⎥⎝⎦12．已知函数2()ln af x b x x cx x=+++（a ，b ，c ∈R ），则（）三、填空题13．记等差数列{}n a 的前n 项和为n S ，已知49S =，47152a a += 则{}n a 的通项公式为______. 14．若π1sin 73α⎛⎫+= ⎪⎝⎭，则3πsin 214α⎛⎫-= ⎪⎝⎭________．15．已知函数()e ln xf x a x ax x=+-存在唯一的极值点，则实数a 的取值范围是__________．四、双空题16．已知函数()21f x x =+，记()()()()()2221143f x f f x x x ==++=+为函数()f x 的2次迭代函数，()()()()()()3421387f x f f f x x x ==++=+为函数()f x 的3次迭代函数，…，依次类推，()()()()()()n n f x f f f f x =⋅⋅⋅⋅⋅⋅个为函数()f x 的n 次迭代函数，则()()nf x =______；()()10032f 除以17的余数是______．五、解答题17．某商场计划在一个两面靠墙的角落规划一个三角形促销活动区域（即ABC 区域），地面形状如图所示．已知已有两面墙的夹角4π,ACB CBA ∠∠=为锐角，假设墙,CA CB 的可利用长度（单位：米）足够长．(1)在ABC 中若BC 边上的高等于14BC ，求sin CAB ∠；(2)当AB 的长度为6米时，则求该活动区域面积的最大值．18．已知数列{}n a 为等差数列13a =，2418a a +=数列{}n b 满足3n n n b a n=(1)求证：数列{}n b 为等比数列； (2)求数列{}n n a b +的前n 项的和n T ．19．如图，在四棱锥P -ABCD 中△PAD 是以AD 为斜边的等腰直角三角形 ,,224,BC AD CD AD AD CD BC PB ⊥====∥(1)求证：AD PB ⊥(2)求平面PAB 与平面ABCD 交角的正弦值.20．2022年底，新冠病毒肆虐全国，很多高三同学也都加入羊羊行列．某校参加某次大型考试时采用了线上考试和线下考试两种形式．现随机抽取200名同学的数学成绩做分析，其中线上人数占40%，线下人数占60%，通过分别统计他们的数学成绩得到了如下两个频率分部直方图：其中(]50,70称为合格，(]70,90称为中等，(]90,110称为良好，(]110,130称为优秀，(]130,150称为优异． (1)根据频率分布直方图，求这200名学生的数学平均分（同一组数据可取该组区间的中点值代替）； (2)现从这200名学生中随机抽取一名同学的数学成绩为良好，试分析他是来自线上考试的可能性大，还是来自线下考试的可能性大．(3)现从样本中线下考试的学生中随机抽取10名同学，且抽到k 个学生的数学成绩为中等的可能性最大，试求k 的值．21．已知椭圆2222:1(0)x y E a b a b +=>>的焦距为2c ，左右焦点分别为1F 和2F ，圆221:()1F x c y ++=与圆222:()9F x c y -+=相交，且交点在椭圆E 上，直线:l y x m =+与椭圆E 交于A 、B 两点，且线段AB 的中点为M ，直线OM 的斜率为14-．(1)求椭圆E 的方程；(2)若1m =，试问E 上是否存在P 、Q 两点关于l 对称，若存在，求出直线PQ 的方程，若不存在，请说明理由．22．已知函数2()(1)2x x b af x x e +=+-．（1）当0a =且1b =时，则证明()1f x ≤；（2）当0a ≥且0b =时，则证明()f x 只有一个零点．参考答案与解析1．C【分析】将12i +代入原方程并化简，进而解出p ,q ，最后求得答案.【详解】根据题意()()()212i 12i 024i 30p q p p q ++++=⇒+++-=，所以2402305p p p q q ⎧+==-⎧⇒⎨⎨+-==⎩⎩，所以+i 25i p q =-+.故选：C. 2．C【分析】先化简U ，再求出UA ，进而求出()U AB 即可.【详解】解：因为{}{}Z 332,1,0,1,2U x x =∈-<<=-- {}2,1A =- 所以{}1,0,2UA =-，所以(){}2102U AB ,,,=--.故选：C 3．A【分析】利用排列与组合数公式，进行化简计算即可．【详解】∵326n n A C =∴()()()11262n n n n n ---=⨯ 化简得23n -= 解得5n =．故选：A ．【点睛】本题考查了排列与组合的计算与化简问题，是基础题． 4．B【分析】根据给定条件，利用向量的线性运算计算作答.【详解】在ABC 中点M 是线段BC 上靠近B 的三等分点，则13BM BC =所以121()333AM AB BM AB AC AB AB AC =+=+-=+.故选：B 5．A【分析】根据题意可知模型的体积为长方体体积与四棱锥体积之差，再由体积求出模型的质量. 【详解】由题意得 2146423122EFGH S cm =⨯-⨯⨯⨯=四棱锥O −EFGH 的高3cm ∴31123123O EFGH V cm -=⨯⨯=．又长方体1111ABCD A B C D -的体积为32466144V cm =⨯⨯=所以该模型体积为32114412132V V V cm =-=-=其质量为0.9132118.8g ⨯=．故选：A 6．D【分析】令||,||MF a NF b ==，利用余弦定理表示出弦MN 的长，再利用抛物线定义结合梯形中位线定理表示出d ，然后利用均值不等式求解作答.【详解】在MFN △中令||,||MF a NF b ==，由余弦定理得222||||||2||||cos MN MF NF MF NF MFN =+-⋅∠ 则有222||MN a b ab =++ 显然直线1:16l y =-是抛物线24y x =的准线，过,,M P N 作直线l 的垂线，垂足分别为,,A B C ，如图而P 为弦MN 的中点，PB 为梯形MACN 的中位线，由抛物线定义知11||(||||)()22d PB MA NC a b ==+=+因此22222222||4444443222MN a b ab ab a b d a b ab a b ab b a ++=⋅=-=-≥=++++++ 当且仅当a b =时取等号，又不等式22λ≥MN d 恒成立，等价于22MN d λ≤恒成立，则3λ≤所以λ的取值范围是(,3]-∞. 故选：D【点睛】方法点睛：圆锥曲线中最值或范围问题的常见解法：（1）几何法，若题目的条件和结论能明显体现几何特征和意义，则考虑利用几何法来解决；（2）代数法，若题目的条件和结论能体现某种明确的函数关系，则可首先建立目标函数，再求这个函数的最值或范围． 7．C【分析】根据指数函数和对数函数的单调性比较大小即可.【详解】0.600.61a <=<，0.2log 30b =<和0.61.51c =>，所以b a c <<. 故选：C.8．D【分析】通过()1f x +是奇函数和()2f x +是偶函数条件，可以确定出函数解析式()222f x x =-+，进而利用定义或周期性结论，即可得到答案．【详解】[方法一]：因为()1f x +是奇函数，所以()()11f x f x -+=-+①；因为()2f x +是偶函数，所以()()22f x f x +=-+②．令1x =，由①得：()()()024f f a b =-=-+，由②得：()()31f f a b ==+ 因为()()036f f +=，所以()462a b a b a -+++=⇒=-令0x =，由①得：()()()11102f f f b =-⇒=⇒=，所以()222f x x =-+．思路一：从定义入手．9551222222f f f f ⎛⎫⎛⎫⎛⎫⎛⎫=+=-+=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ 1335112222f f f f ⎛⎫⎛⎫⎛⎫⎛⎫-=-+=-+=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭511322=2222f f f f ⎛⎫⎛⎫⎛⎫⎛⎫-=-+=--+- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ 所以935222f f ⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭．[方法二]：因为()1f x +是奇函数，所以()()11f x f x -+=-+①；因为()2f x +是偶函数，所以()()22f x f x +=-+②．令1x =，由①得：()()()024f f a b =-=-+，由②得：()()31f f a b ==+ 因为()()036f f +=，所以()462a b a b a -+++=⇒=-令0x =，由①得：()()()11102f f f b =-⇒=⇒=，所以()222f x x =-+．思路二：从周期性入手由两个对称性可知函数()f x 的周期4T =．所以91352222f f f⎛⎫⎛⎫⎛⎫==-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭．故选：D ．【点睛】在解决函数性质类问题的时候，我们通常可以借助一些二级结论，求出其周期性进而达到简便计算的效果． 9．BC【分析】根据回归方程的性质及相关系数的概念判断即可；【详解】解：由线性回归方程的性质可知回归直线ˆˆˆybx a =+必经过样本中心点(),x y ，即y bx a =+，但是可能不过样本中的任何一点，故A 错误，C 正确；若点()()()1122,,,,,,n n x y x y x y ⋅⋅⋅都在经验回归直线y bx a =+上，则说明为函数关系，所以样本相关系数1r =，故B 正确；若成对样本数据()22,x y 的残差为t ，未必有成对样本数据的残差为t -，故D 错误. 故选：BC 10．ACD【分析】连接AD 1，FD 1，GF ，BC 1，证得EF//AD 1，利用平面AEFD 1逐一分析各选项即可判断作答. 【详解】正方体1111ABCD A B C D -中连接AD 1，FD 1，GF ，BC 1，如图：因点E ，F 是BC ，CC 1中点，则EF//BC 1，而正方体1111ABCD A B C D -的对角面ABC 1D 1是矩形，则AD 1//BC 1//EF 连GF ，因G 是棱BB 1中点，则GF//B 1C 1//A 1D 1，且1111GF B C A D ==，即四边形A 1GFD 1是平行四边形，A 1G//D 1F 1D F ⊂平面AEF ，1AG ⊄平面AEF ，于是A 1G//平面AEF ，A 正确；因1DD ⊥平面ABCD ，而AE ⊂平面ABCD ，即有1DD ⊥AE ，若1DD ⊥AF ，必有1DD ⊥平面AEFD 1，1DD ⊥AD 1，与145AD D ∠=矛盾，B 不正确；因EF//AD 1，A 1G//D 1F ，则异面直线1A G 与EF 所成角是1AD F ∠或其补角作1FM AD ⊥于M ，显然1AE D F ==AEFD 1是等腰梯形 12AD EF ==112AD EF D M -==111cos D M AD F D F ∠== C 正确；FM =AEF 截正方体所得的截面是等腰梯形AEFD 1 等腰梯形AEFD 1的面积为1922AD EF S FM +=⋅=，D 正确. 故选：ACD. 11．ACD【分析】由余弦函数周期的公式，可判定A 正确；利用三角函数的图象变换，可判定B 错误；根据()f x 在区间2π,π3⎛⎫⎪⎝⎭上单调递增，列出不等式组，求得ω的范围，得到当0k =时，则不等式有解，可判定C 正确；由()f x 在区间()0,π上只有一个零点，列出不等式组，求得ω的范围，可判定D 正确．【详解】解：由余弦函数图象与性质，可得2π2T ω==，得πω=，所以A 正确；当2ω=时，则可得()πcos 23f x x ⎛⎫=+ ⎪⎝⎭将函数()f x 的图象向右平移π3个单位长度后得()ππππcos 2cos 23333f x x x g x ⎡⎤⎛⎫⎛⎫⎛⎫-=-+=-≠ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦，所以B 错误；若()f x 在区间2π,π3⎛⎫ ⎪⎝⎭上单调递增，则2ππ2π33,Z ππ2π2π3k k k ωπω⎧+≥+⎪⎪∈⎨⎪+≤+⎪⎩ 解得5132,Z 3k k k ω+≤≤+∈又因为0ω>，所以只有当0k =时，则此不等式有解，即513ω≤≤，所以C 正确；若()f x 在区间()0,π上只有一个零点，则ππ32π3π32πωπω⎧+>⎪⎪⎨⎪+≤⎪⎩，解得1766ω<≤，所以D 正确．故选：ACD ． 12．ACD【分析】对于A ，(1)3()()(1)3f f x f x f =''−−−→→=−−−−−→求导导数的几何意义切线方程对于B ，()()()f x f x f x '−−−→→求导在区间1,13⎡⎤⎢⎥⎣⎦上的单调性1(1)3f f ⎛⎫> ⎪⎝⎭−−−−→得解对于C ，()(1,2)2()()f x f x f x a x x '−−−→−−−−−−−−→≤+求导在区间上单调递增在区间(1,2)上恒成立a −−−−−−−→二次函数的图象与性质的取值范围对于D ，()(0,)22ln ()()ln g x xf xg x x cx c x +∞→=-+−−−−−−−−−−−→=在区间内存在两个不同的零点在区间(0,)+∞内存在两个不同的根2ln ()xh x x=−−−−→令函数()h x 和y c =的图象有两个不同的交点，()h x 的单调性→作出()h x 和y c =的大致图象−−−−→数形结合得解以B 不正确.由图可得10,2e c ⎛⎫∈ ⎪⎝⎭，所以D 正确.故选：ACD. 13．22n n a +=【分析】运用等差数列通项公式及等差数列前n 项和公式的基本量代入计算即可. 【详解】设等差数列{}n a 的公差为d ，则1(1)n a a n d =+- 1(1)2n n n S na d -=+ 4114711134692151362922S a d a a a a d a d a d d ⎧=+==⎧⎪⎪⎪⇒⎨⎨+=+++=+=⎪⎪=⎩⎪⎩所以312(1)222n n a n +=+-⨯=. 故答案为：22n n a +=.14．79【分析】结合诱导公式、二倍角公式求得正确答案. 【详解】∵π1sin 73α⎛⎫+= ⎪⎝⎭23ππ2π2ππ17sin 2sin 2cos 212sin 12.14277799αααα⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫∴-=-+=+=-+=-⨯= ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦故答案为：7915．(],e -∞【分析】求出函数的导函数，依题意()=0f x '存在唯一的变号正实根，即()()1e 0xx ax -=-存在唯一的变号正实根，当0a ≤符合题意，当0a >时参变分离可得e 0xa x-=没有除1之外的正实根，构造函数()e x g x x =，利用导数求出函数的单调性，即可求出函数的最小值，从而求出a 的取值范围；【详解】解：因为()e ln xf x a x ax x=+-，()0,x ∈+∞所以()()()()221e 1e x x x x a f x a x xa x x --'=-+-=依题意可得()=0f x '存在唯一的变号正实根即()()1e 0xx ax -=-存在唯一的变号正实根当0a ≤时e 0x ax ->，方程只有唯一变号正实根1，符合题意当0a >，方程e 0xax -=，即e 0xa x-=没有除1之外的正实根令()e x g x x =，则()()21e x xx g x -'=，所以当01x <<时()0g x '<，当1x >时()0g x '> 即()g x 在()0,1上单调递减，在()1,+∞上单调递增所以()()min 1e g x g ==，所以0e a <≤ 综上可得(],e a ∈-∞；故答案为：(],e -∞【点睛】方法点睛：导函数中常用的两种常用的转化方法：一是利用导数研究含参函数的单调性，常化为不等式恒成立问题．注意分类讨论与数形结合思想的应用；二是函数的零点、不等式证明常转化为函数的单调性、极(最)值问题处理．16． ()211nx +- 0【分析】第一空，根据题意结合等比数列的前n 项和公式即可推出()()n fx 的表达式；第二空，将()()10032f 化为()25331711⨯--，利用二项式定理展开，化简即可求得答案. 【详解】由题意()()()12122222221112n n nn n n nfx x x x --⎛⎫-=+++⋅⋅⋅+=+=+- ⎪-⎝⎭所以()()()251001002532332133161331711f =⨯-=⨯-=⨯--()25252424232322221252525252533C 17C 17C 17C 17C 1711=-+-++-- ()25252424232322221252525252533C 17C 17C 17C 17C 1734=-+-++-()2524242323222221125252525251733C 17C 17C 17C 17C 2⎡⎤=-+-++-⎣⎦又()25242423232222211252525252533C 17C 17C 17C 17C 2-+-++-为正整数所以()()10032f除以17的余数为0故答案为： ()211;0nx +-【点睛】关键点睛：解答本题中函数迭代问题，要结合题设找到迭代规律，即可求出函数表达式，解决余数问题的关键在于将()()10032f利用二项式定理展开化简转化为17的倍数的形式，即可求得答案.17．(2)9+【分析】（1）过点A 作AD BC ⊥交BC 于D ．设AD x =，则CD x = 334BD BC x == 在ABD △中求得sin ,cos CBA CBA ∠∠，由()sin sin CAB CBA ACB ∠∠∠=+计算即可得解；（2）设π02CBA ∠θθ⎛⎫=<< ⎪⎝⎭，则6cos BD θ= 6sin CD AD θ==从而得出()16sin 6cos 6sin 2ABC S θθθ=⨯⨯+，利用三角恒等变换、辅助角公式及三角函数的性质即可得到答案．【详解】（1）过点A 作AD BC ⊥交BC 于D ．设AD x =米 0x > 则CD x =米 334344BD BC x x ==⨯=米．在ABD △中sin CBA CBA ∠∠===．故())sin sin sin cos CAB CBA ACB CBA CBA ∠∠∠∠∠=+=+==⎝⎭（2）设π02CBA ∠θθ⎛⎫=<< ⎪⎝⎭，则6cos BD θ=米 6sin CD AD θ==米()()216sin 6cos 6sin 92sin cos 2sin 2ABC S θθθθθθ=⨯⨯+=+()9sin21cos29π24θθθ⎛⎫=+-=+- ⎪⎝⎭因为π0,2θ⎛⎫∈ ⎪⎝⎭，所以3π2,44ππ4θ⎛⎫-∈- ⎪⎝⎭所以当3π2,42π8πθθ-==时，则该活动区域的面积取得最大值，最大值为9+ 18．(1)证明见解析； (2)()22133932n n T n n +=+-+.【分析】（1）设数列{}n a 的公差为d ，根据等差数列通项公式化简条件求d ，由此可求数列{}n a 的通项公式，再由等比数列定义证明数列{}n b 为等比数列；（2）利用组合求和法求数列{}n n a b +的前n 项的和n T . 【详解】（1）设数列{}n a 的公差为d 因为13a = 2418a a += 所以11318a d a d +++=所以3d =，所以()3313n a n n =+-= 所以1333nn n b n n+==所以211333n n n n b b +++== 所以数列{}n b 为等比数列；（2）由(1) 133n n n a b n ++=+所以112233n n n T a b a b a b a b =++++++⋅⋅⋅++234133639333n n T n +=++++++⋅⋅⋅++ 234136933333n n T n +=+++⋅⋅⋅+++++⋅⋅⋅+()()91333213n n n nT -+=+-()22133932n n T n n +=+-+ 19．(1)证明见解析；【分析】（1）取AD 中点E ，连接,BE PE ，可证明BE AD ⊥，PE AD ⊥，进而可证AD ⊥平面PEB ，则结论成立；（2）过P 做PO ⊥平面ABCD ，过O 做OH AB ⊥于H ，则PHO ∠为平面PAB 与平面ABCD 所成角，根据题中所给条件计算PO ，OH 的长，求出正切值，进而求出正弦值. 【详解】（1）取AD 中点E ，连接,BE PE 因为//BC AD ，且12BC AD ED ==，所以四边形EBCD 为平行四边形，即//C BE D 因为CD AD ⊥，所以BE AD ⊥；因为△PAD 是以AD 为斜边的等腰直角三角形，所以PE AD ⊥；PE BE E ⋂=，所以AD ⊥平面PEB ，PB ⊂平面PEB ，所以AD ⊥PB .（2）过P 做PO ⊥平面ABCD ，过O 做OH AB ⊥于H ，则PHO ∠为平面PAB 与平面ABCD 所成角由（1）可知：AD ⊥平面PEB ，AD ⊂平面ABCD ，所以平面PEB ⊥平面ABCD ，平面PEB 平面ABCD BE = 则O ∈直线BE ，由题意可知2PE =，2BE =又PB =120PEB ∠=，在直角三角形PEO 中60PEO ∠=，所以PO =1OE =过E 做EF AB ⊥于F ，则//OH EF在AEB △中BE AE ⊥ 2BE AE ==则AB =12EF AB ==所以23EF BE OH BO ==，所以OHtan PHO ∠=则sin PHO ∠=.20．(1)95.4分；(2)来自线下考试的可能性大，理由见解析； (3)2k =.【分析】（1）由直方图求线上、线下同学的平均分，进而求所有同学的平均分；（2）根据直方图求出线上、线下成绩良好的人数，进而比较所占比例，即可得结论；（3）由题意得抽到k 个学生的成绩为中等的概率10309010120C C ()C k kP X k -==，110k ≤<且*N k ∈，结合()(1)()(1)P X k P X k P X k P X k =>=-⎧⎨=>=+⎩即可求参数值. 【详解】（1）线上同学平均分(600.005800.01751000.021200.0051400.0025)2093⨯+⨯+⨯+⨯+⨯⨯=分；线下同学平均分(600.0075800.01251000.0151200.011400.005)2097⨯+⨯+⨯+⨯+⨯⨯=分；又200名同学，线上人数占40%，线下人数占60% 所以所有200名同学的平均分9320040%9720060%95.4200⨯⨯+⨯⨯=分.（2）线上同学成绩良好人数为0.022020040%32⨯⨯⨯=人线下同学成绩良好人数为0.0152020060%36⨯⨯⨯=人所以抽取数学成绩为良好，且3236200200<，故线下的可能性大. （3）由线下成绩中等同学人数为0.01252020060%30⨯⨯⨯=人，其它同学90人所以从线下学生中随机抽取10名同学，抽到k 个学生的成绩为中等的概率10309010120C C ()C k k P X k -==，110k <<且*N k ∈要使()P X k =最大，则()(1)()(1)P X k P X k P X k P X k =>=-⎧⎨=>=+⎩，即101113090309010101201201019309030901010120120C C C C C C C C C C C C k k k kk k k k----+-⎧>⎪⎪⎨⎪>⎪⎩ 所以22228042341403008281k k k k k k k k ⎧+<-+⎨-+<++⎩，则219341122122k <<，故2k =. 21．(1)2214x y +=；(2)存在P 、Q 两点关于l 对称，直线PQ 的方程为53y x =--．【分析】（1）由椭圆定义知2a 为两圆半径之和，由点差法可得22OM AB b k k a⋅=-，求出2b ，从而得到椭圆方程；（2）设直线PQ 的方程为y x t =-+，根据PQ 中点在直线l 上求得t 值，注意检验直线PQ 与椭圆有两个交点.【详解】（1）因为圆221:()1F x c y ++=与圆222:()9F x c y -+=相交，且交点在椭圆E 上，所以213a =+2a =设()11,A x y 和()22,B x y ，AB 的中点()00,M x y22112222222211x y a b x y a a ⎧+=⎪⎪⎨⎪+=⎪⎩①②，①－② ()()01201222220x x x y y y a b --⇒+= 201220120y y y b a x x x -⇒+⋅=-22OM AB b k k a ⇒⋅=- 222114b b a⇒-=-⇒=则椭圆E 的方程：2214x y +=（2）假设存在P 、Q 两点关于l 对称，设直线PQ 的方程为y x t =-+()33,P x y 和()44,Q x y ，PQ 中点(),N N N x y 22225844044y x tx xt t x y =-+⎧⇒-+-=⎨+=⎩ ()226420440t t ∆=-->t ⇒<<34425N x x t x +==，5N t y =即4,55t t N ⎛⎫⎪⎝⎭由N 在l 上451553t t t =+⇒=-，此时(t ∈故存在P 、Q 两点关于l 对称，直线PQ 的方程为53y x =--．22．（1）证明见解析；（2）证明见解析．【分析】（1）当0a =且1b =时，则1()x x f x e+=，利用导数判断函数的单调性，可得()(0)1f x f ≤=即可证得结果；（2）当0a ≥且0b =时，则21()(1),()(1)2x x x a f x x f x x a e e ⎛⎫=+-='--⎪⎝⎭观察可知()f x 在(0,)+∞上没有零点，讨论0a =，10a e <<和1a e =，1a e>四种情况下函数的单调性，计算可得()0,(1)0f a f -<>，可证得结果.【详解】证明：（1）当0a =且1b =时，则1(),()x xx xf x f x e e ='+-= 由()0f x '>，得0x <；由()0f x '<，得0x >；()f x 在(,0)-∞上递增、在(0,)+∞上递减故()(0)1f x f ≤=；（2）因为0a ≥且0b =，故21()(1),()(1)2x x x a f x x f x x a e e ⎛⎫=+-='-- ⎪⎝⎭显然()f x 在(0,)+∞上没有零点；若0a =，则()xxf x e =只有一个零点0x =；若10a e <<，由()0f x '>，得1x <或1ln x a>；由()0f x '<，得11x a <<；故()f x 在(,1)-∞上递增；而()2()2122a a f a a a e -=++- 记2()212,0x g x x x e x =++->，则()222x g x x x e +-'= 由（1）知11x x e+≤，即1x x e +≤，故()2220x g x x x e =+-≤'恒成立 ()g x 在(0,)+∞上单调递减()(0)1g x g <=-，即()2()21202a a f a a a e -=++-< 结合1(1)f e=，知()f x 只有一个零点；若1a e =，则11()(1)0x f x x e e ⎛⎫=--≥ ⎪⎝⎭'，()f x 单调递增结合()0,(1)0f a f -<>，知()f x 只有一个零点；若1a e >，由()0f x '>，得1ln x a <或1x >；由()0f x '<，得1ln 1x a <<；故()f x 在1,ln a ⎛⎫-∞ ⎪⎝⎭上递增、在1ln ,1a ⎛⎫ ⎪⎝⎭上递减故1()0,ln (1)0f a f f a ⎛⎫-<>> ⎪⎝⎭，知()f x 只有一个零点．综上所述，当0a ≥且0b =时，则()f x 只有一个零点．【点睛】方法点睛：本题考查了导数的综合应用，不等式的证明，函数的零点问题利用导数证明不等式的策略为：利用导数研究函数的单调性，求出最值，从而求得函数的取值范围；关于函数的零点问题，一般用零点存在定理结合函数的单调性进行解决.。

广东省广州市2019-2020学年高考数学五月模拟试卷含解析

广东省广州市2019-2020学年高考数学五月模拟试卷一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．如图是一个算法流程图，则输出的结果是（）A ．3B ．4C ．5D ．6【答案】A 【解析】【分析】执行程序框图，逐次计算，根据判断条件终止循环，即可求解，得到答案．【详解】由题意，执行上述的程序框图：第1次循环：满足判断条件，2,1x y ==；第2次循环：满足判断条件，4,2x y ==；第3次循环：满足判断条件，8,3x y ==；不满足判断条件，输出计算结果3y =，故选A ．【点睛】本题主要考查了循环结构的程序框图的结果的计算与输出，其中解答中执行程序框图，逐次计算，根据判断条件终止循环是解答的关键，着重考查了运算与求解能力，属于基础题． 2．集合}{220A x x x =--≤，{}10B x x =-<，则A B U =( )A ．}{1x x < B ．}{11x x -≤< C ．{}2x x ≤ D ．{}21x x -≤<【答案】C【解析】【分析】先化简集合A,B ，结合并集计算方法，求解，即可．【详解】解得集合()(){}{}21012A x x x x x =-+≤=-≤≤，{}1B x x =< 所以{}2A B x x ⋃=≤，故选C ．【点睛】本道题考查了集合的运算，考查了一元二次不等式解法，关键化简集合A,B ，难度较小．3．函数()y f x =满足对任意x ∈R 都有()()2f x f x +=-成立，且函数()1y f x =-的图象关于点()1,0对称，()14f =，则()()()201620172018f f f ++的值为（）A ．0B ．2C ．4D ．1【答案】C 【解析】【分析】根据函数()1y f x =-的图象关于点()1,0对称可得()f x 为奇函数，结合()()2f x f x +=-可得()f x 是周期为4的周期函数，利用()00f =及()14f =可得所求的值. 【详解】因为函数()1y f x =-的图象关于点()1,0对称，所以()y f x =的图象关于原点对称，所以()f x 为R 上的奇函数.由()()2f x f x +=-可得()()2f x f x +=-，故()()()42f x f x f x +=-+=，故()f x 是周期为4的周期函数.因为20164504,201745041,201845042=⨯=⨯+=⨯+，所以()()()()()()()20162017201012428f f f f f f f +=+=+++. 因为()()2f x f x +=-，故()()()02000f f f +=-=-=，所以()()()2016201720148f f f +=+. 故选：C. 【点睛】本题考查函数的奇偶性和周期性，一般地，如果R 上的函数()f x 满足()()()0f x a f x a +=-≠，那么()f x 是周期为2a 的周期函数，本题属于中档题.4．()f x 是定义在()0,∞+上的增函数，且满足：()f x 的导函数存在，且()()f x x f x '<，则下列不等式成立的是（） A ．()()221f f < B ．()()3344ff <C ．()()2334f f <D ．()()3223f f <【答案】D 【解析】【分析】根据()f x 是定义在()0,∞+上的增函数及()()f x f x '有意义可得()0f x '>，构建新函数()()f xg x x=，利用导数可得()g x 为()0,∞+上的增函数，从而可得正确的选项. 【详解】因为()f x 是定义在()0,∞+上的增函数，故()0f x '≥.又()()f x f x '有意义，故()0f x '≠，故()0f x '>，所以()()f x f x x <'. 令()()f xg x x =，则()()()20'-'=>xf x f x g x x，故()g x 在()0,∞+上为增函数，所以()()32g g >即()()3232f f >，整理得到()()2332f f >. 故选：D. 【点睛】本题考查导数在函数单调性中的应用，一般地，数的大小比较，可根据数的特点和题设中给出的原函数与导数的关系构建新函数，本题属于中档题. 5．已知函数()22cos sin 4f x x x π⎛⎫=++⎪⎝⎭，则()f x 的最小值为( )A ．12+B ．12C ．12-D ．14-【答案】C 【解析】【分析】利用三角恒等变换化简三角函数为标准正弦型三角函数，即可容易求得最小值. 【详解】由于()221cos 21cos 22cos sin 422x x f x x x ππ⎛⎫-+ ⎪+⎛⎫⎝⎭=++=+ ⎪⎝⎭ cos 2sin 2122x x=++1224x π⎛⎫=++ ⎪⎝⎭，故其最小值为：12-. 故选：C. 【点睛】本题考查利用降幂扩角公式、辅助角公式化简三角函数，以及求三角函数的最值，属综合基础题. 6．P 是正四面体ABCD 的面ABC 内一动点，E 为棱AD 中点，记DP 与平面BCE 成角为定值θ，若点P 的轨迹为一段抛物线，则tan θ=（） AB．CD．【答案】B 【解析】【分析】设正四面体的棱长为2，建立空间直角坐标系，求出各点的坐标，求出面BCE 的法向量，设P 的坐标，求出向量DP u u u r，求出线面所成角的正弦值，再由角θ的范围0,2π⎡⎤⎢⎥⎣⎦，结合θ为定值，得出sin θ为定值，且P 的轨迹为一段抛物线，所以求出坐标的关系，进而求出正切值．【详解】由题意设四面体ABCD 的棱长为2，设O 为BC 的中点，以O 为坐标原点，以OA 为x 轴，以OB 为y 轴，过O 垂直于面ABC 的直线为z 轴，建立如图所示的空间直角坐标系O xyz -，则可得1OB OC ==，323OA ==OA 的三等分点G 、F 如图，则133OG OA ==2233AG OF OA ===2226DG AD AG =-=，162EF DG ==，所以()0,1,0B 、()0,1,0C -、()3,0,0A、32633D ⎛ ⎝⎭、236,0,33E ⎛⎫⎪ ⎪⎝⎭，由题意设(),,0P x y ，326,33DP x y ⎛=-- ⎝⎭u u u r ， QV ABD 和ACD V 都是等边三角形，E 为AD 的中点，BE AD ∴⊥，CE AD ⊥，BE CE E =Q I ，AD ∴⊥平面BCE ，2326AD ⎛∴= ⎝⎭u u u r 为平面BCE 的一个法向量，因为DP 与平面BCE 所成角为定值θ，则0,2π⎡⎤θ∈⎢⎥⎣⎦，由题意可得222223326333sin cos ,326233x AD DP AD DP AD DPx y θ⎛⎫⎛⎫-⨯-- ⎪ ⎪⋅⎝⎭⎝⎭=<>==⋅⎛⎫⎛⎫⨯-++- ⎪ ⎪⎝⎭⎝⎭u u u r u u u ru u u r u u u ru u u r u u u r ()()222222223323333239332393138x x x x x y x x y x x y ++++===+-++-+-++ 因为P 的轨迹为一段抛物线且tan θ为定值，则sin θ也为定值，22223339323x x x y x ==-，可得233y x =，此时3sin 3θ=，则6cos 3θ=，sin 2tan cos 2θθθ==. 故选：B. 【点睛】考查线面所成的角的求法，及正切值为定值时的情况，属于中等题．7．等差数列{}n a 的前n 项和为n S ，若13a =，535S =，则数列{}n a 的公差为（） A ．-2 B ．2 C ．4 D ．7【答案】B 【解析】【分析】在等差数列中由等差数列公式与下标和的性质求得3a ，再由等差数列通项公式求得公差. 【详解】在等差数列{}n a 的前n 项和为n S ，则()155********a a S a a +===⇒=则3123272a a d d d =+=+=⇒= 故选：B 【点睛】本题考查等差数列中求由已知关系求公差，属于基础题.8．如图，在矩形OABC 中的曲线分别是sin y x =，cos y x =的一部分，,02A π⎛⎫⎪⎝⎭，()0,1C ，在矩形OABC 内随机取一点，若此点取自阴影部分的概率为1P ，取自非阴影部分的概率为2P ，则（）A ．12P P <B ．12P P >C ．12P P =D ．大小关系不能确定【答案】B 【解析】【分析】先用定积分求得阴影部分一半的面积，再根据几何概型概率公式可求得．【详解】根据题意，阴影部分的面积的一半为：()4cos sin 21x x dx π-=⎰，于是此点取自阴影部分的概率为)()12142141.41122 3.22P ππ--=⨯=>=．又21112P P =-<，故12P P >．故选B ．【点睛】本题考查了几何概型，定积分的计算以及几何意义，属于中档题．9．如图所示的“数字塔”有以下规律：每一层最左与最右的数字均为2，除此之外每个数字均为其两肩的数字之积，则该“数字塔”前10层的所有数字之积最接近()lg 20.3≈（）A ．30010B ．40010C ．50010D ．60010【答案】A 【解析】【分析】结合所给数字特征，我们可将每层数字表示成2的指数的形式，观察可知，每层指数的和成等比数列分布，结合等比数列前n 项和公式和对数恒等式即可求解【详解】如图，将数字塔中的数写成指数形式，可发现其指数恰好构成“杨辉三角”，前10层的指数之和为29101222211023+++⋅⋅⋅+=-=，所以原数字塔中前10层所有数字之积为10231023lg230021010=≈.故选：A 【点睛】本题考查与“杨辉三角”有关的规律求解问题，逻辑推理，等比数列前n 项和公式应用，属于中档题 10．已知复数21aibi i-=-，其中a ，b R ∈，i 是虚数单位，则a bi +=（） A ．12i -+ B ．1C ．5D 5【答案】D 【解析】试题分析：由21aibi i-=-,得()21,1,2ai i bi b i a b -=-=+∴=-=,则()2212,12125a bi i a bi i +=-+∴+=-+=-+= D.考点：1、复数的运算；2、复数的模. 11．已知01a b <<<，则（）A ．()()111b b a a ->-B ．()()211bb a a ->- C ．()()11a b a b +>+ D ．()()11a ba b ->- 【答案】D 【解析】【分析】根据指数函数的单调性，即当底数大于1时单调递增，当底数大于零小于1时单调递减，对选项逐一验证即可得到正确答案. 【详解】因为01a <<，所以011a <-<，所以()1xy a =-是减函数，又因为01b <<，所以1b b >，2b b >，所以()()111b b a a -<-，()()211bb a a -<-，所以A,B 两项均错；又111a b <+<+，所以()()()111aaba b b +<+<+，所以C 错；对于D ，()()()111abba ab ->->-，所以()()11aba b ->-，故选D. 【点睛】这个题目考查的是应用不等式的性质和指对函数的单调性比较大小，两个式子比较大小的常用方法有：做差和0比，作商和1比，或者直接利用不等式的性质得到大小关系，有时可以代入一些特殊的数据得到具体值，进而得到大小关系.12．把函数2()sin f x x =的图象向右平移12π个单位，得到函数()g x 的图象．给出下列四个命题①()g x 的值域为(0,1] ②()g x 的一个对称轴是12x π=③()g x 的一个对称中心是1,32π⎛⎫⎪⎝⎭ ④()g x 存在两条互相垂直的切线其中正确的命题个数是（） A ．1 B ．2C ．3D ．4【答案】C 【解析】【分析】由图象变换的原则可得11()cos 2262g x x π⎛⎫=--+ ⎪⎝⎭,由cos 2[1,1]6x π⎛⎫-∈- ⎪⎝⎭可求得值域；利用代入检验法判断②③；对()g x 求导,并得到导函数的值域,即可判断④. 【详解】由题,21cos 2()sin 2xf x x -==, 则向右平移12π个单位可得,1cos 21112()cos 22262x g x x ππ⎛⎫-- ⎪⎛⎫⎝⎭==--+ ⎪⎝⎭ cos 2[1,1]6x π⎛⎫-∈- ⎪⎝⎭Q ,()g x ∴的值域为[0,1],①错误；当12x π=时,206x π-=,所以12x π=是函数()g x 的一条对称轴,②正确；当3x π=时,226x ππ-=,所以()g x 的一个对称中心是1,32π⎛⎫⎪⎝⎭,③正确； ()sin 2[1,1]6g x x π⎛⎫'=-∈- ⎪⎝⎭,则1212,,()1,()1x x R g x g x ''∃∈=-=,使得12()()1g x g x ''⋅=-,则()g x 在1x x =和2x x =处的切线互相垂直,④正确.即②③④正确,共3个. 故选:C 【点睛】本题考查三角函数的图像变换,考查代入检验法判断余弦型函数的对称轴和对称中心,考查导函数的几何意义的应用.二、填空题：本题共4小题，每小题5分，共20分。

广东省广州市2019-2020学年高考数学五模试卷含解析

广东省广州市2019-2020学年高考数学五模试卷一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．在复平面内，复数z a bi =+（a ，b R ∈）对应向量OZ uuu r（O 为坐标原点），设OZ r =u u u r，以射线Ox 为始边，OZ 为终边旋转的角为θ，则()cos sin z r i θθ=+，法国数学家棣莫弗发现了棣莫弗定理：()1111cos sin z r i θθ=+，()2222cos sin z r i θθ=+，则()()12121212cos sin z z rr i θθθθ=+++⎡⎤⎣⎦，由棣莫弗定理可以导出复数乘方公式：()()cos sin cos sin nnr i rn i n θθθθ+=+⎡⎤⎣⎦，已知()43z i =+，则z =（）A ．23B ．4C ．83D ．16【答案】D 【解析】【分析】根据复数乘方公式：()()cos sin cos sin nn r i r n i n θθθθ+=+⎡⎤⎣⎦，直接求解即可. 【详解】()444313216cos sin 266z ii i ππ⎡⎤⎛⎫⎛⎫=+=+=+⎢⎥ ⎪ ⎪ ⎪⎝⎭⎢⎥⎝⎭⎣⎦16cos 4sin 488366i i ππ⎡⎤⎛⎫⎛⎫=⨯+⨯=-+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，()()2288316z =-+=.故选：D 【点睛】本题考查了复数的新定义题目、同时考查了复数模的求法，解题的关键是理解棣莫弗定理，将复数化为棣莫弗定理形式，属于基础题.2．已知某几何体的三视图如右图所示，则该几何体的体积为（）A．3 B．10 3C．113D．83【答案】B【解析】由三视图知：几何体是直三棱柱消去一个三棱锥，如图：直三棱柱的体积为122242⨯⨯⨯=，消去的三棱锥的体积为112212323⨯⨯⨯⨯=，∴几何体的体积210433V=-=，故选B.点睛：本题考查了由三视图求几何体的体积，根据三视图判断几何体的形状及相关几何量的数据是解答此类问题的关键；几何体是直三棱柱消去一个三棱锥，结合直观图分别求出直三棱柱的体积和消去的三棱锥的体积，相减可得几何体的体积.3．已知抛物线C：24x y=的焦点为F，过点F的直线l交抛物线C于A，B两点，其中点A在第一象限，若弦AB的长为254，则AFBF=（）A．2或12B．3或13C．4或14D．5或15【答案】C【解析】【分析】先根据弦长求出直线的斜率，再利用抛物线定义可求出,AF BF.【详解】设直线的倾斜角为θ，则222425cos cos4pABθθ===，所以216cos25θ=，2219tan1cos16θθ=-=，即3tan4θ=±，所以直线l的方程为314y x=±+.当直线l的方程为314y x=+，联立24314x yy x⎧=⎪⎨=+⎪⎩，解得11x=-和24x=，所以()40401AFBF-==--；同理，当直线l的方程为314y x=-+.14AFBF=，综上，4AFBF=或14.选C.【点睛】本题主要考查直线和抛物线的位置关系，弦长问题一般是利用弦长公式来处理.出现了到焦点的距离时，一般考虑抛物线的定义.4．若函数()222y sin x ϕϕπ⎛⎫<⎪⎝+⎭=的图象经过点012π⎛⎫⎪⎝⎭，，则函数()()()22f x sin x cos x ϕϕ=-+-图象的一条对称轴的方程可以为( ) A ．24x π=-B ．3724x π=C ．1724x π=D ．1324x π=-【答案】B 【解析】【分析】由点012π⎛⎫⎪⎝⎭，求得ϕ的值，化简()f x 解析式，根据三角函数对称轴的求法，求得()f x 的对称轴，由此确定正确选项. 【详解】由题可知220,122sin ππϕϕ⎛⎫⨯+=< ⎪⎝⎭.6πϕ=-所以()2cos 266f x sin x x ππ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭5226412x x πππ⎛⎫⎛⎫=++=+ ⎪ ⎪⎝⎭⎝⎭ 令52,122x k k Z πππ+=+∈，得,242k x k Z ππ=+∈ 令3k =，得3724x π= 故选：B 【点睛】本小题主要考查根据三角函数图象上点的坐标求参数，考查三角恒等变换，考查三角函数对称轴的求法，属于中档题.5．已知全集U =R ，集合{}1A x x =<，{}12B x x =-≤≤，则()U A B =I ð（） A ．{}12x x <≤ B ．{}12x x ≤≤C ．{}11x x -≤≤D ．{}1x x ≥-【答案】B 【解析】【分析】直接利用集合的基本运算求解即可．【详解】解：全集U =R ，集合{}1A x x =<，{}12B x x =-≤≤，{}U |1A x x ∴=≥ð则(){}{}{}|1|12|12U A B x x x x x x =-=I I 厔剟?ð，故选：B ．【点睛】本题考查集合的基本运算，属于基础题．6．已知平行于x 轴的直线分别交曲线2ln 21,21(0)y x y x y =+=-≥于,A B 两点，则4AB 的最小值为（） A ．5ln 2+ B ．5ln 2- C ．3ln 2+ D ．3ln 2-【答案】A 【解析】【分析】设直线为1122(0),(,)(,)y a a A x y B x y =>，用a 表示出1x ，2x ，求出4||AB ，令2()2ln f a a a =+-，利用导数求出单调区间和极小值、最小值，即可求出4||AB 的最小值．【详解】解：设直线为1122(0),(,)(,)y a a A x y B x y =>，则1ln 21a x =+，11(ln 1)2x a ∴=-，而2x 满足2221a x =-，2212a x +∴= 那么()()22211144()4ln 122ln 22a AB x x a a a ⎡⎤+=-=--=+-⎢⎥⎣⎦设2()2ln f a a a =+-，则221()a f a a -'=，函数()f a 在0,2⎛ ⎝⎭上单调递减，在2⎛⎫+∞ ⎪ ⎪⎝⎭上单调递增，所以min min 42()25ln 2AB f a f ===+⎝⎭故选：A ．【点睛】本题考查导数知识的运用：求单调区间和极值、最值，考查化简整理的运算能力，正确求导确定函数的最小值是关键，属于中档题．7．已知向量(,1)a m =r ，(1,2)b =-r ，若(2)a b b -⊥r r r ，则a r 与b r夹角的余弦值为（）A．21313-B．21313C．61365-D．613【答案】B【解析】【分析】直接利用向量的坐标运算得到向量2a b-r r的坐标，利用(2)=0a b b-⋅r r r求得参数m，再用cos,||||a ba ba b⋅〈〉=r rr rr r计算即可.【详解】依题意，2(2,3)a b m-=+-r r，而(2)=0a b b-⋅r r r，即260m---=，解得8m=-，则213cos,13||||565a ba ba b⋅〈〉===⋅r rr rr r.故选：B.【点睛】本题考查向量的坐标运算、向量数量积的应用，考查运算求解能力以及化归与转化思想.8．下边程序框图的算法源于我国古代的中国剩余定理.把运算“正整数N除以正整数m所得的余数是n”记为“(mod)N n m≡”，例如71(mod2)≡.执行该程序框图，则输出的n等于（）A．16 B．17 C．18 D．19【答案】B【解析】【分析】由已知中的程序框图可知，该程序的功能是利用循环结构计算并输出变量n的值，模拟程序的运行过程，代入四个选项进行验证即可.【详解】解：由程序框图可知，输出的数应为被3除余2，被5除余2的且大于10的最小整数. 若输出16n = ，则()161mod3≡不符合题意，排除；若输出17n =，则()()172mod3,172mod5≡≡，符合题意. 故选:B. 【点睛】本题考查了程序框图.当循环的次数不多，或有规律时，常采用循环模拟或代入选项验证的方法进行解答. 9．已知复数1cos23sin 23z i =+oo和复数2cos37sin37z i =+oo，则12z z ⋅为A ．122- B ．122i + C ．122i + D ．122i - 【答案】C 【解析】【分析】利用复数的三角形式的乘法运算法则即可得出．【详解】z 1z 2＝（cos23°+isin23°）•（cos37°+isin37°）＝cos60°+isin60°＝12+．故答案为C ．【点睛】熟练掌握复数的三角形式的乘法运算法则是解题的关键，复数问题高考必考，常见考点有：点坐标和复数的对应关系，点的象限和复数的对应关系，复数的加减乘除运算，复数的模长的计算. 10．已知,a b ∈R ，3(21)ai b a i +=--，则|3|a bi +=（）A B ．C ．3D ．4【答案】A 【解析】【分析】根据复数相等的特征，求出3a 和b ，再利用复数的模公式，即可得出结果. 【详解】因为3(21)ai b a i +=--，所以3,(21),b a a =⎧⎨--=⎩，解得3,31,b a =⎧⎨=⎩则|3|13a bi i +=+==故选：A. 【点睛】本题考查相等复数的特征和复数的模，属于基础题.11．对于函数()f x ，若12,x x 满足()()()1212f x f x f x x +=+，则称12,x x 为函数()f x 的一对“线性对称点”．若实数a 与b 和+a b 与c 为函数()3xf x =的两对“线性对称点”，则c 的最大值为（）A ．3log 4B ．3log 41+C ．43D ．3log 41-【答案】D 【解析】【分析】根据已知有333b c a b c a ++++=，可得13131ca b+=+-，只需求出3a b +的最小值，根据333a b a b +=+，利用基本不等式，得到3a b +的最小值，即可得出结论.【详解】依题意知，a 与b 为函数()3xf x =的“线性对称点”，所以333a b a b +=+=≥，故34a b +≥（当且仅当a b =时取等号）. 又+a b 与c 为函数()3xf x =的“线性对称点，所以333b c a b c a ++++=，所以3143131313a b ca b a b +++==+≤--，从而c 的最大值为3log 41-. 故选:D. 【点睛】本题以新定义为背景，考查指数函数的运算和图像性质、基本不等式，理解新定义含义，正确求出c 的表达式是解题的关键，属于中档题.12．函数()f x =）A ．{2x x ≤或}3x ≥B ．{3x x ≤-或}2x ≥- C ．{}23x x ≤≤D ．{}32x x -≤≤-【解析】【分析】根据偶次根式被开方数非负可得出关于x 的不等式，即可解得函数()y f x =的定义域. 【详解】由题意可得2560x x -+≥，解得2x ≤或3x ≥. 因此，函数()y f x =的定义域为{2x x ≤或}3x ≥. 故选：A. 【点睛】本题考查具体函数定义域的求解，考查计算能力，属于基础题. 二、填空题：本题共4小题，每小题5分，共20分。

广东2022届高考仿真试题文科数学(五)

广东2022届高考仿真试题文科数学（五）学海导航·2022届高考模拟仿真试题·广东(五)·文科数学模拟仿真试题·广东(五)文科数学2022届高考一、选择题(本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．)1.复数2＋i＝(D)A．2＋iB．－1C．2－iD．3解析：因为2＋i2022＝2＋(i4)503＝3，所以选D.2.设集合P＝{3，log2a}，Q＝{a，b}，若P∩Q＝{0}，则P∪Q＝(B)A．{3,0}B．{3,0,1}C．{3,0,2}D．{3,0,1,2}解析：因为P∩Q＝{0}，所以0∈P,0∈Q，所以log2a＝0，所以a＝1，b＝0，所以P∪Q＝{3,0,1}，故选B.3.PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物，下图是据北京某日早7点至晚8点甲、乙两个PM2.5监测点统计的数据(单位：毫克/立方米)列出的茎叶图，则甲、乙两地浓度的中位数较低的是(B)甲1293631331640.030.040.050.060.070.08乙6123692998929202270.09A.甲B．乙C．甲乙相等D．无法确定解析：甲、乙两地浓度的中位数分别为0.066,0.062，故乙地浓度的中位数较低．4.某程序框图如下图所示，则输出的结果是(C)A．43B．44C．45D．46解析：由图可知输出的i为满足i≥2022的最小整数值，故为45.某2y25.已知方程＋＝1表示焦点在y轴上的椭圆，则实数k的取值范围是(C)2－k2k－111A．(，2)B．(1，＋∞)C．(1,2)D．(，1)2222k－1>2－k解析：，所以k∈(1,2)．2－k>06.若某一几何体的正视图与侧视图均为边长是1的正方形，且其体积为，则该几何体2的俯视图可以是(C)ππ解析：若该几何体的俯视图分别为A，B，D时，其几何体的体积分别为1，，不符合44题意，而C满足题设，故选择C.7.下列命题中，正确的是(A)A．直线l⊥平面α，平面β∥直线l，则α⊥βB．平面α⊥β，直线m⊥β，则m∥αC．直线l是平面α的一条斜线，且lβ，则α与β必不垂直D．一个平面内的两条直线与另一个平面内的两条直线分别平行，则这两个平面平行某－2y＋5≥08.设m为实数，若{(某，y)|3－某≥0m某＋y≥0最大值是(B)3432A.B.C.D.4323，某、y∈R}{(某，y)|某＋y≤25}，则m的22解析：作出不等式组所表示的区域如图所示，当点D在圆周上时，m值最大，此时满足432＋(－3m)2＝25，m>0，所以m＝.39.设a＝(1,2)，b＝(1,1)，且a与a＋λb的夹角为锐角，则实数λ的取值范围是(A)55A．(－，0)∪(0，＋∞)B．(－，＋∞)3355C．[－，0)∪(0，＋∞)D．(－，0)33a·a＋λb解析：a＋λb＝(1＋λ，2＋λ)，设a与a＋λb的夹角为θ，则coθ＝，|a||a＋λb|故a·(a＋λb)>0且ta≠(a＋λb)，t>0，5故λ>－且λ≠0，故选择A.310.定义域为[a，b]的函数y＝f(某)图象的两个端点为A、B，M(某，y)是f(某)图象上任意一→→→→点，其中某＝λa＋(1－λ)b，λ∈[0,1]．已知向量ON＝λOA＋(1－λ)OB，若不等式|MN|≤k恒成1立，则称函数f(某)在[a，b]上“k阶线性近似”．若函数y＝某－在[1,2]上“k阶线性近似”，某则实数k的取值范围为(D)A．[0，＋∞)B．[133，＋∞)C．[＋2，＋∞)D．[－2，＋∞)1222→→→解析：由ON＝λOA＋(1－λ)OB知，N是线段AB的中点．33设A(1,0)，B(2，)，则lAB：y＝(某－1)．223设M(某0，y0)，某0∈[1,2]，则N(某0，(某0－1))，213113故k≥|MN|＝|(某0－)－(某0－1)|＝|某0＋－|.某022某021133当某0∈[1,2]时，|某0＋－|的最大值为－2(当且仅当某＝2时，取等号)，2某0223故k≥－3.2二、填空题(本大题共5小题，考生作答4小题，每小题5分，满分20分．)(一)必做题(11～13题)11.某校高三有1000个学生，高二有1200个学生，高一有1500个学生，现按年级分层抽样，调查学生的视力情况，若高一抽取了75人，则全校共抽取了185人．75某解析：设全校共抽取了某人，则有＝，解之可得某＝185. 15001000＋1200＋1500112.设f(某)＝某3－某2－2某＋5，当某∈[－1,2]时，f(某)2(7，＋∞).22解析：当某∈[－1,2]时，f′(某)＝3(某＋)(某－1)，故函数(－1，－)，(1,2)上单调递增；在3322157区间(－，1)上单调递减，故函数在区间[－1,2]上的最大值为{f(－)，f(2)}ma某＝{，7}ma某3327＝7，故m∈(7，＋∞)．1111131111113.给出下列不等式：1＋＋>1,1＋＋＋＋>，1＋＋＋＋>2,1＋＋＋232372231523＋n＋115111>，，则按此规律可猜想第n个不等式为1＋＋＋＋n＋1>.312232－12(二)选做题(14～15题，考生只能从中选做一题)14.以平面直角坐标系的原点为极点，某轴的正半轴为极轴并取相同的长度单位建立极坐某＝2＋3coαπ标系，若直线ρco(θ－)＝2与曲线C：(α是参数)相交于A，B两点，则线段4y＝2＋3inαAB的长为27.某＝2＋3coαπ解析：将直线ρco(θ－)＝2与曲线C：(α是参数)化为直角坐标系下的4y＝2＋3inα方程分别为：某＋y＝2及(某－2)2＋(y－2)2＝9，利用弦长公式可得l＝2|2＋2－2|2332－＝27.2r2－d2＝15.如右图所示，圆O的直径AB为8，C为圆周上一点，BC＝4，过C 作圆的切线l，过A作直线l的垂线AD，D为垂足，AD与圆O交于点E，则线段AE的长为4.解析：连接OC，OE，则BC＝4＝OB＝OC，故∠COB＝60°，AD⊥l，OC⊥l，所以∠DAB＝60°，因为OA＝OE，所以AE＝OA＝4.三、解答题(本大题共6小题，共80分．解答应写出文字说明、证明过程或演算步骤．)16.(本小题满分12分)已知向量m＝(inA，)与n＝(3，inA＋3coA)共线，其中A是△ABC的内角．2(1)求角A的大小；(2)若BC＝2，求△ABC面积S的最大值．3解：(1)因为m∥n，所以inA·(inA＋3coA)－＝0，(2分)1－co2A33＋in2A－＝0，(4分)22231πin2A－co2A＝1，所以in(2A－)＝1.(5分)226ππ11ππππ因为A∈(0，π)，所以2A－∈(－，)，所以2A－＝，A＝.(7分)666623(2)因为BC＝2，由余弦定理可得b＋c－bc＝4.(8分)又b2＋c2≥2bc，所以bc≤4(当且仅当b＝c时，取等号)．(10分)133从而S△ABC＝bcinA＝bc≤某4＝3，即S△ABC的最大值为3.(12分)24417.(本小题满分13分)哈尔滨冰雪大世界每年冬天都会吸引大批游客，现准备在景区内开设经营热饮等食品的店铺若干．根据以往对500名40岁(含40岁)以下人员和500名40岁以上人员的统计调查，有如下一系列数据：40岁(含40岁)以下人员购买热饮等食品的有260人，不购买热饮食品的有240人；40岁以上人员购买热饮等食品的有220人，不购买热饮等食品的有280人，请根据以上数据作出2某2列联表，并运用独立性检验思想，判断购买热饮等食品与年龄(按上述统计中的年龄分类方式)是否有关系？(注：要求达到99.9%的把握才能认定为有关系)nad－bc2a＋bc＋da＋cb＋d222P(K2≥k)0.5000.4000.1000.0100.001k0.455解：由题得2某2列联表：40岁(含40岁)以下40岁以上总计(6分)0.7082.7066.63510.828总计5005001000购买热饮等食品260220480不购买热饮等食品2402805201000260某280－220某240K＝≈6.410<10.825.(12分)500某500某480某52022所以没有99.9%的把握认定为有关系．(13分)18.(本小题满分13分)如图，在四棱锥P－ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD＝DC.E是PC的中点．证明：(1)PA∥平面EDB；(2)DE⊥平面PBC.解：(1)连接AC，与BD交于O，连接OE，由O、E分别为AC、CP中点，所以OE∥PA.(2分)又OE平面EDB，PA平面EDB，所以PA∥平面EDB.(5分)(2)由PD⊥平面ABCD，所以PD⊥BC，又CD⊥BC，PD∩CD＝D，(7分)所以BC⊥平面PCD，DE⊥BC.(9分)由PD＝DC，E为PC中点，故DE⊥PC，又PC∩BC＝C，(11分)所以DE⊥平面PBC.(13分)19.(本小题满分14分)已知函数f(某)＝某3＋a某2＋b某＋4，g(某)＝m某3－6m某2＋2(m≠0)，f(某)在(1，f(1))处的切线方3程为y＝－3某＋10.3(1)求实数a，b的值；(2)是否总存在实数m，使得对任意的某1∈[0,3]，总存在某2∈[－1,2]，使得f(某1)f′1＝－32解：(1)f′(某)＝某＋2a某＋b，由已知得，1f1＝31＋2a＋b＝－3a＝0即，解得.(4分)a＋b＋4＝0b＝－4(2)要使对任意的某1∈[0,3]，总存在某2∈[－1,2]，使得f(某1)由(1)知f(某)＝某3－4某＋4，f′(某)＝某2－4.34令f′(某)＝0，得某＝2，又f(0)＝4，f(2)＝－，f(3)＝1，3故当某∈[0,3]时，[f(某)]ma某＝4.(7分)g′(某)＝3m某－12m某＝3m某(某－4)，令g′(某)＝0，得某＝0.(8分)又g(－1)＝2－7m，g(0)＝2，g(2)＝2－16m.当m>0时，[g(某)]ma某＝g(0)＝2<4，不合题意；(10分)当m<0时，[g(某)]ma某＝g(2)＝2－16m，由2－16m>4，得m81故实数m的取值范围为(－∞，－)．(14分)820.(本小题满分14分)已知椭圆M的中心为坐标原点，且焦点在某轴上，若M的一个顶点恰好是抛物线y2＝18某的焦点，M的离心率e＝，过M的右焦点F作不与坐标轴垂直的直线l，交M于A，B2两点．(1)求椭圆M的标准方程；→→→(2)设点N(t,0)是一个动点，且(NA＋NB)⊥AB，求实数t的取值范围．某2y2解：(1)椭圆M的标准方程：＋＝1.(4分)43(2)设A(某1，y1)，B(某2，y2)，设l：某＝my＋1(m∈R，m≠0)，某＝my＋12222某y(3m＋4)y＋6my－9＝0.4＋3＝16m由韦达定理得y1＋y2＝－2①(6分)3m＋4→→→22(NA＋NB)⊥AB|NA|＝|NB|(某1－t)2＋y21＝(某2－t)＋y22(某1－某2)(某1＋某2－2t)＋(y1－y2)＝0.(9分)将某1＝my1＋1，某2＝my2＋1代入上式整理得(y1－y2)[(m2＋1)(y1＋y2)＋m(2－2t)]＝0，2由y1≠y2知，(m＋1)(y1＋y2)＋m(2－2t)＝0，(10分)1将①代入得t＝2.(12分)3m＋41所以实数t∈(0，)．(14分)421.(本小题满分14分)已知数列{an}中，a1＝1且点P(an，an＋1)(n∈N某)在直线某－y＋1＝0上．(1)求数列{an}的通项公式；1111(2)若函数f(n)＝＋＋＋＋(n∈N，且n≥2)，求函数f(n)的最小值．n＋a1n＋a2n＋a3n＋an解：(1)由点P(an，an＋1)在直线某－y＋1＝0上，即an＋1－an＝1，且a1＝1.(3分)所以数列{an}是以1为首项，1为公差的等差数列．故an＝1＋(n－1)某1＝n.(6分)111(2)f(n)＝＋＋＋，(8分)n＋1n＋22n11111f(n＋1)＝＋＋＋＋＋，n＋2n＋3n＋42n＋12n＋2111111f(n＋1)－f(n)＝＋－>＋－＝0.(13分)2n＋12n＋2n＋12n＋22n＋2n＋17所以f(n)是单调递增，故f(n)的最小值是f(2)＝.(14分)1222。

广东省最新高考数学模拟试卷(文科)

广东省最新高考数学模拟试卷（文科）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分.考试用时120分钟. 第Ⅰ卷选择题（共50分）一、选择题：本大题共10小题，每小题5分，共50分. 在每小题给出的四个选项中，只有一项是符合题目要求的. 1、已知集合A {x N ||x |3}=∈<，B {1,1,2,3}=-，则A B =IA .[2,2]-；B .(3,3)-；C .{1,1,2,3}-；D .{1,1,2}- 2、函数y 的定义域是A .[1,)-+∞；B .[1,0)-；C .(1,)-+∞；D .（－1，0）3、若把函数()1=+xf x x 的反函数记为1()-=y f x ，则1(2)-=f A .23； B .2； C .2-； D . 1- 4、已知函数2log ,(0)()3,(0)>⎧=⎨≤⎩x x x f x x ，则[(1)]=f fA .0；B .1；C .3；D .135、二次函数24=++y x ax 在(,1]-∞上是减函数，则实数a 的取值范围是 A .(,2]-∞-； B .[2,)+∞； C .(,2]-∞； D .(,1]-∞6、设0.913=y ，0.4829=y ， 1.5313-⎛⎫= ⎪⎝⎭y ，则A .312>>y y y ；B .213>>y y y ；C .123y y y >>；D .321>>y y y7、计算112log 3030.253353(0.064)(0.1)(2)16|0.001|5--⎡⎤+-+-+---=⎣⎦A ．2.9；B ．3.1C ．4.9D ．5.18、方程lg 0x x +=的一个实根存在的区间是（参考：lg20 1.3010,lg0.30.5229==-） A .11,113⎛⎫ ⎪⎝⎭ ; B .1,12⎛⎫ ⎪⎝⎭ ; C.11,32⎛⎫ ⎪⎝⎭ D .11,10010⎛⎫⎪⎝⎭ ;9、已知映射:→f A B ,其中A R =,x A,y B ∈∈,对应法则为2:→=-+f x y x k ；对于3B ∈,但在集A 中找不到原像,则实数k 的取值范围为A .(,3)-∞ ;B .[3,9] ;C .[3,)+∞ ;D .(3,)+∞10、已知2()-=x f x a ，()log ||=a g x x (a 0,>且a 1)≠，且f (4)g(4)0-<；则)(),(x g y x f y ==在同一坐标系内的图象大致是第Ⅱ卷非选择题（共100分）二、填空题：本大题共4小题，每小题5分，共20分.11、已知(3,2)a=-r，(2,)b x=r，若a b⊥rr，则x=12、若复数z满足24z=，则3z=；若复数z满足24z=-，则3z=13、已知等比数列{}na中，312a=-，23S=，则公比q=14、规定记号“⊗”表示一种运算，即lg5⊗=a b(0,0)>>a b，且⊗≠⊗a b b a。