【数学】2010年高考真题江苏卷解析版

合集下载

江苏2010年高考数学试卷(含答案、解析)

h(x) >0，使得 f '(x) = h(x)(x 2 − ax + 1) ，则称函数 f (x) 具有性质 P(a) . (1)设函数 f (x) = h(x) + b + 2 (x > 1) ，其中 b 为实数
x +1 ①求证：函数 f (x) 具有性质 P(b)
求函数 f (x) 的单调区间
（1）估计该问题目有错，似乎为 f (x) = ln x + b + 2 (x > 1) ，则有如下解答： x +1
①
f
'( x)
=
1 x
−
b+2 (x + 1)2
=
1 x(x +1)2
(x2
− bx +1)
∵
x
> 1 时， h(x) =
1 x(x + 1)2
> 0 恒成立，
∴函数 f (x) 具有性质 P(b) ；
20)
(x
−
3(m2 − 20) )
m2 + 20
,
m2 + 80 m2 + 20
化简得
y
+
20 m2 + 20
=
−
10 m2 − 40
(x
−
3(m2 − 20) m2 + 20 )
令 y = 0 ，解得 x = 1 ，即直线 MN 过 x 轴上定点 (1,0) 。
{ } 19．（16 分）设各项均为正数的数列 {an }的前 n 项和为 Sn ，已知 2a2 = a1 + a3 ，数列 Sn 是公差为 d 的等差数列.

2010年普通高等学校招生全国统一考试数学试题(江苏卷)(含答案)

2010年江苏高考数学试题及参考答案一、填空题1、设集合A={-1,1,3}，B={a+2,a2+4},A∩B={3}，则实数a=______▲________ 答案：1；2、右图是一个算法的流程图，则输出S的值是______▲_______答案：63；3、函数y=x 2(x>0)的图像在点(a k ,a k 2)处的切线与x 轴交点的横坐标为a k+1,k 为正整数，a 1=16，则a 1+a 3+a 5=____▲_____答案：21；解答题15、（14分）在平面直角坐标系xOy 中，点A(-1,-2),B(2,3),C(-2,-1)(1)求以线段AB 、AC 为邻边的平行四边形两条对角线的长(2)设实数t 满足(OC t AB -)·OC =0，求t 的值（1）(3,5),(1,1)AB AC ==-求两条对角线长即为求||AB AC + 与||AB AC - ，由(2,6)AB AC +=，得||AB AC +=由(4,4)AB AC -=，得||AB AC -=（2）(2,1)O C =-- ，∵(OC t AB -)·OC 2AB OC tOC =- ，易求11AB OC =- ，25OC = ，所以由(OC t AB -)·OC =0得115t =-。

16、（14分）如图，四棱锥P-ABCD 中，PD⊥平面ABCD ，PD=DC=BC=1,AB=2,AB∥DC，∠BCD=900(1)求证：PC⊥BC(2)求点A 到平面PBC 的距离D CB APE（1）∵PD⊥平面ABCD ，∴PD BC ⊥，又BC C D ⊥，∴B C ⊥面P C D ，∴BC PC ⊥。

（2）设点A 到平面PBC 的距离为h ，∵A PBC P ABC V V --=,∴1133PBC ABC S h S PD ⋅=容易求出h =17、（14分）某兴趣小组测量电视塔AE 的高度H(单位m ），如示意图，垂直放置的标杆BC 高度h=4m ，仰角∠ABE=α，∠ADE=β(1)该小组已经测得一组α、β的值，tan α=1.24,tan β=1.20,,请据此算出H 的值(2)该小组分析若干测得的数据后，发现适当调整标杆到电视塔的距离d （单位m ），使α与β之差较大，可以提高测量精确度，若电视塔实际高度为125m ，问d 为多少时，α-β最大（1）∵tan AE AB α=，tan AE AD β=，∴tan 31tan 30A D A B αβ== （2）。

2010年江苏高考数学试题及答案

2010年普通高等学校招生全国统一考试江苏卷数学全解全析数学Ⅰ试题参考公式：锥体的体积公式: V 锥体=13Sh ，其中S 是锥体的底面积，h 是高。

一、填空题：本大题共14小题，每小题5分，共70分。

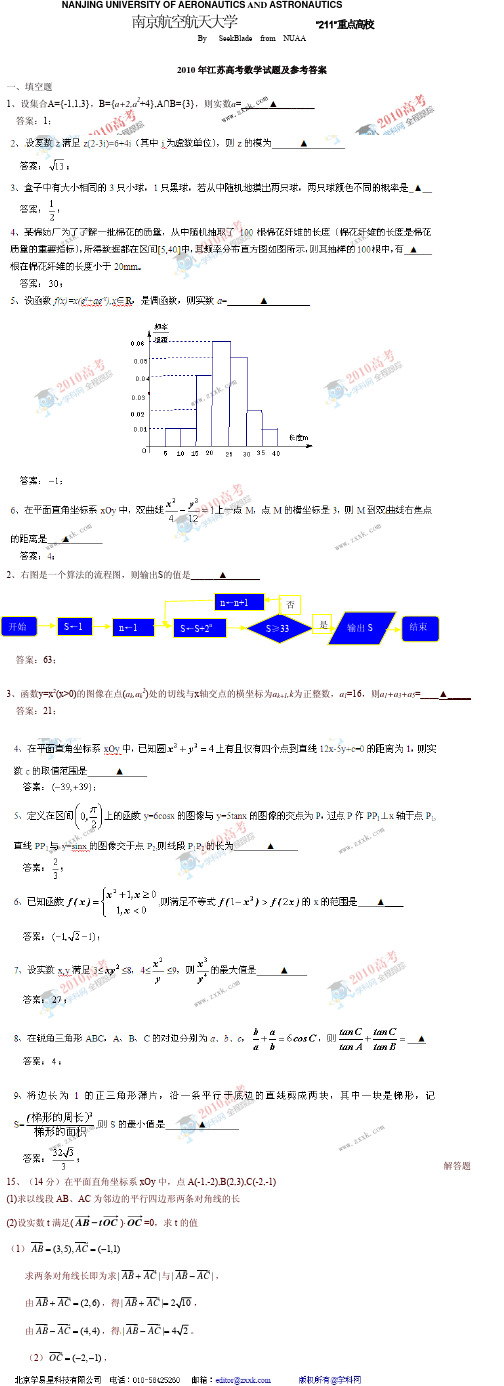
请把答案填写在答题卡相应的位．．．．．．．置上．．.1、设集合A={-1,1,3}，B={a+2,a 2+4},A ∩B={3}，则实数a =______▲_____. 2、设复数z 满足z(2-3i)=6+4i （其中i 为虚数单位），则z 的模为______▲_____.3、盒子中有大小相同的3只白球，1只黑球，若从中随机地摸出两只球，两只球颜色不同的概率是_ ▲__.4、某棉纺厂为了了解一批棉花的质量，从中随机抽取了100根棉花纤维的长度（棉花纤维的长度是棉花质量的重要指标），所得数据都在区间[5,40]中，其频率分布直方图如图所示，则其抽样的100根中，有_▲___根在棉花纤维的长度小于20mm 。

5、设函数f(x)=x(e x +ae -x )(x ∈R)是偶函数，则实数a =_______▲_________6、在平面直角坐标系xOy 中，双曲线112422=-y x 上一点M ，点M 的横坐标是3，则M 到注意事项考生在答题前请认真阅读本注意事项及各题答题要求 1.本试卷共4页，包含填空题（第1题——第14题）、解答题（第15题——第20题）。

本卷满分160分，考试时间为120分钟。

考试结束后，请将本卷和答题卡一并交回。

2.答题前，请您务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置。

3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与您本人是否相符。

4.请在答题卡上按照晤顺序在对应的答题区域内作答，在其他位置作答一律无效。

作答必须用0.5毫米黑色墨水的签字笔。

请注意字体工整，笔迹清楚。

5.如需作图，须用2B 铅笔绘、写清楚，线条、符号等须加黑、加粗。

2010年江苏高考真题(含答案)数学

2010年江苏高考数学试题一、填空题1．设集合A={-1,1,3}，B={a+2,a 2+4},A ∩B={3}，则实数a =______________ 2．设复数z 满足z （2-3i ）=6+4i （其中i 为虚数单位），则z 的模为______________3．盒子中有大小相同的3只小球，1只黑球，若从中随机地摸出两只球，两只球颜色不同的概率是___4．某棉纺厂为了了解一批棉花的质量，从中随机抽取了100根棉花纤维的长度（棉花纤维的长度是棉花质量的重要指标），所得数据都在区间[5,40]中，其频率分布直方图如图所示，则其抽样的100根中，有____根在棉花纤维的长度小于20mm 。

5．设函数f （x ）=x （e x +ae -x ）,x ∈R ，是偶函数，则实数a =________________6．在平面直角坐标系xOy 中，双曲线112422=-y x 上一点M ，点M 的横坐标是3，则M 到双曲线右焦点的距离是__________7．右图是一个算法的流程图，则输出S 的值是_____________8．函数y=x 2（x>0）的图像在点（a k ,a k 2）处的切线与x 轴交点的横坐标为a k+1,k 为正整数，a 1=16，则a 1+a 3+a 5=_________ 9．在平面直角坐标系xOy 中，已知圆422=+y x 上有且仅有四个点到直线12x-5y —c=0的距离为1，则实数c 的取值范围是___________ 10．定义在区间⎪⎭⎫⎝⎛20π,上的函数y=6cosx 的图像与y=5tanx 的图像的交点为P ，过点P 作PP 1⊥x 轴于点P 1,直线PP 1与y=sinx 的图像交于点P 2,则线段P 1P 2的长为____________D C B AP 11．已知函数21,0()1,0x x f x x ⎧+≥=⎨<⎩,则满足不等式2(1)(2)f x f x ->的x 的范围是________12．设实数x,y 满足3≤2xy ≤8，4≤y x 2≤9，则43yx 的最大值是_________13．在锐角三角形ABC ，A 、B 、C 的对边分别为a 、b 、c ，6cos b aC a b+=，则tan tan tan tan C CA B+=__ 14．将边长为1的正三角形薄片，沿一条平行于底边的直线剪成两块，其中一块是梯形，记S=梯形的面积梯形的周长）2(,则S 的最小值是______________二、解答题 15．（14分）在平面直角坐标系xOy 中，点A （-1,-2）,B （2,3）,C （-2,-1）（1）求以线段AB 、AC 为邻边的平行四边形两条对角线的长（2）设实数t 满足（AB tOC - ）·OC=0，求t 的值16．（14分）如图，四棱锥P-ABCD 中，PD ⊥平面ABCD ，PD=DC=BC=1,AB=2,AB ∥DC ，∠BCD=900（1）求证：PC ⊥BC （217．（14分）某兴趣小组测量电视塔AE 的高度H （单位m ），如示意图，垂直放置的标杆BC 高度h=4m ，仰角∠ABE=α，∠ADE=β（1）该小组已经测得一组α、β的值，tan α=1.24,tan β=1.20,,请据此算出H 的值（2）该小组分析若干测得的数据后，发现适当调整标杆到电视塔的距离d （单位m ），使α与β之差较大，可以提高测量精确度，若电视塔实际高度为125m ，问d 为多少时，α-β最大18．（16分）在平面直角坐标系xoy 中，如图，已知椭圆15922=+y x 的左右顶点为A,B ，右焦点为F ，设过点T （m t ,）的直线TA,TB 与椭圆分别交于点M ),(11y x ，),(22y x N ，其中m>0,0,021<>y y①设动点P 满足422=-PB PF ,求点P 的轨迹②设31,221==x x ，求点T 的坐标③设9=t ,求证：直线MN 必过x 轴上的一定点（其坐标与m 无关）19．（16分）设各项均为正数的数列{}n a 的前n 项和为n S ，已知3122a a a +=，数列{}nS 是公差为d 的等差数列． ①求数列{}n a 的通项公式（用d n ,表示）②设c 为实数，对满足n m k n m ≠=+且3的任意正整数k n m ,,，不等式k n m cS S S >+都成立。

2010年江苏省高考数学真题(解析版)

绝密★启用前2010年普通高等学校招生全国统一考试（江苏卷）数学注意事项考生在答题前请认真阅读本注意事项及各题答题要求1、本试卷共4页，包含填空题（第1题～第14题）、解答题（第15题～第20题）两部分。

本试卷满分160分，考试时间为120分钟。

考试结束后，请将本试卷和答题卡一并交回。

2、答题前，请您务必将自己的姓名、考试证号用书写黑色字迹的0.5毫米签字笔填写在试卷及答题卡上。

3、请认真核对监考员所粘贴的条形码上的姓名、考试证号是否与您本人的相符。

4、作答非选择题必须用书写黑色字迹的0.5毫米签字笔写在答题卡上的指定位置，在其它位置作答一律无效。

作答选择题必须用2B 铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，请用橡皮擦干净后，再选涂其它答案。

5、如有作图需要，可用2B 铅笔作答，并请加黑加粗，描写清楚。

参考公式：锥体的体积公式:V 锥体=13Sh ，其中S 是锥体的底面积，h 是高。

一、填空题：本大题共1小题，每小题5分，共70分．1、设集合A={-1,1,3}，B={a+2,a 2+4},A ∩B={3}，则实数a =______▲_____.[解析]考查集合的运算推理。

3∈B,a+2=3,a=1.2、设复数z 满足z(2-3i)=6+4i （其中i 为虚数单位），则z 的模为______▲_____.[解析]考查复数运算、模的性质。

z(2-3i)=2(3+2i),2-3i 与3+2i 的模相等，z 的模为2。

3、盒子中有大小相同的3只白球，1只黑球，若从中随机地摸出两只球，两只球颜色不同的概率是_▲__.[解析]考查古典概型知识。

3162p ==4、某棉纺厂为了了解一批棉花的质量，从中随机抽取了100根棉花纤维的长度（棉花纤维的长度是棉花质量的重要指标），所得数据都在区间[5,40]中，其频率分布直方图如图所示，则其抽样的100根中，有_▲___根在棉花纤维的长度小于20mm 。

[解析]考查频率分布直方图的知识。

2010年普通高等学校招生全国统一考试数学试卷及答案(江苏卷)

2010年江苏高考数学试题一、填空题1、设集合A={-1,1,3}，B={a+2,a 2+4},A ∩B={3}，则实数a =______▲________2、设复数z 满足z(2-3i)=6+4i （其中i 为虚数单位），则z 的模为______▲________3、盒子中有大小相同的3只小球，1只黑球，若从中随机地摸出两只球，两只球颜色不同的概率是_▲__4、某棉纺厂为了了解一批棉花的质量，从中随机抽取了100根棉花纤维的长度（棉花纤维的长度是棉花质量的重要指标），所得数据都在区间[5,40]中，其频率分布直方图如图所示，则其抽样的100根中，有_▲___根在棉花纤维的长度小于20mm 。

5、设函数f(x)=x(e x +ae -x ),x ∈R ，是偶函数，则实数a =_______▲_________O长度m组距0.050.040.030.014035302520151056、在平面直角坐标系xOy 中，双曲线112422=-y x 上一点M ，点M 的横坐标是3，则M 到双曲线右焦点的距离是___▲_______7、右图是一个算法的流程图，则输出S 的值是______▲_______8、函数y=x 2(x>0)的图像在点(a k ,a k 2)处的切线与x 轴交点的横坐标为a k+1,k 为正整数，a 1=16，则a 1+a 3+a 5=____▲_____开始 S ←1n ←1S ←S+2nS ≥33n ←n+1否输出S结束是9、在平面直角坐标系xOy 中，已知圆422=+y x 上有且仅有四个点到直线12x-5y+c=0的距离为1，则实数c 的取值范围是______▲_____ 10、定义在区间⎪⎭⎫⎝⎛20π,上的函数y=6cosx 的图像与y=5tanx 的图像的交点为P ，过点P 作PP 1⊥x 轴于点P 1,直线PP 1与y=sinx 的图像交于点P 2,则线段P 1P 2的长为_______▲_____11、已知函数⎩⎨⎧<≥+=01012x ,x ,x )x (f ,则满足不等式)x (f )x (f 212>-的x 的范围是____▲____12、设实数x,y 满足3≤2xy ≤8，4≤y x 2≤9，则43yx 的最大值是_____▲____13、在锐角三角形ABC ，A 、B 、C 的对边分别为a 、b 、c ，C cos baa b 6=+，则=+Btan Ctan A tan C tan __▲ 14、将边长为1的正三角形薄片，沿一条平行于底边的直线剪成两块，其中一块是梯形，记S=梯形的面积梯形的周长）2(,则S 的最小值是_______▲_______二、解答题15、（14分）在平面直角坐标系xOy 中，点A(-1,-2),B(2,3),C(-2,-1) (1)求以线段AB 、AC 为邻边的平行四边形两条对角线的长 (2)设实数t 满足(OC t AB -)·=0，求t 的值16、（14分）如图，四棱锥P-ABCD 中，PD ⊥平面ABCD ，PD=DC=BC=1,AB=2,AB ∥DC ，∠BCD=900 (1)求证：PC ⊥BC(2)求点A 到平面PBC 的距离DCBAPβαdDBE17、（14分）某兴趣小组测量电视塔AE 的高度H(单位m ），如示意图，垂直放置的标杆BC 高度h=4m ，仰角∠ABE=α，∠ADE=β(1)该小组已经测得一组α、β的值，tan α=1.24,tan β=1.20,,请据此算出H 的值(2)该小组分析若干测得的数据后，发现适当调整标杆到电视塔的距离d （单位m ），使α与β之差较大，可以提高测量精确度，若电视塔实际高度为125m ，问d 为多少时，α-β最大18.（16分）在平面直角坐标系xoy 中，如图，已知椭圆15922=+y x 的左右顶点为A,B ，右顶点为F ，设过点T （m t ,）的直线TA,TB 与椭圆分别交于点M ),(11y x ，),(22y x N ，其中m>0,0,021<>y y①设动点P 满足422=-PB PF ,求点P 的轨迹 ②设31,221==x x ，求点T 的坐标 ③设9=t ,求证：直线MN 必过x 轴上的一定点（其坐标与m 无关）19．（16分）设各项均为正数的数列{}n a 的前n 项和为n S ，已知3122a a a +=，数列{}nS 是公差为d 的等差数列.①求数列{}n a 的通项公式（用d n ,表示）A BO F②设c 为实数，对满足n m k n m ≠=+且3的任意正整数k n m ,,，不等式k n m cS S S >+都成立。

2010年江苏高考数学试题(含答案详解

2010 年普通高等学校招生全国统一考试江苏卷数学全解全析数学Ⅰ试题注意事项考生在答题前请认真阅读本注意事项及各题答题要求1.本试卷共 4 页，包含填空题（第 1 题——第14 题）、解答题（第15 题——第20 题）。

本卷满分160 分，考试时间为120 分钟。

考试结束后，请将本卷和答题卡一并交回。

2.答题前，请您务必将自己的姓名、准考证号用0.5 毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置。

3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与您本人是否相符。

4.请在答题卡上按照晤顺序在对应的答题区域内作答，在其他位置作答一律无效。

作答必须用0.5毫米黑色墨水的签字笔。

请注意字体工整，笔迹清楚。

5.如需作图，须用2B 铅笔绘、写清楚，线条、符号等须加黑、加粗。

6.请保持答题卡卡面清洁，不要折叠、破损。

参考公式：锥体的体积公式 : V1h 是高。

锥体= Sh，其中 S 是锥体的底面积，3一、填空题：本大题共14 小题，每小题 5 分，共 70分。

请把答案填写在答题卡相应的位．．．．．．．置上 .．．1、设集合 A={-1,1,3}，B={a+2,a 2+4},A ∩ B={3} ，则实数 a=______▲ _____.[ 解析 ] 考查集合的运算推理。

3B, a+2=3, a=1.2、设复数 z 满足 z(2-3i)=6+4i （其中 i 为虚数单位），则 z 的模为 ______ ▲_____.[ 解析 ] 考查复数运算、模的性质。

z(2-3i)=2(3+2 i), 2-3i与 3+2 i 的模相等， z 的模为 2。

3、盒子中有大小相同的 3 只白球， 1 只黑球，若从中随机地摸出两只球，两只球颜色不同的概率是 _ ▲ __.[ 解析 ] 考查古典概型知识。

p316 24、某棉纺厂为了了解一批棉花的质量，从中随机抽取了 100 根棉花纤维的长度（棉花纤维的长度是棉花质量的重要指标），所得数据都在区间[5,40] 中，其频率分布直方图如图所示，则其抽样的100 根中，有 _▲ ___根在棉花纤维的长度小于20mm。

2010年普通高等学校招生全国统一考试数学（江苏卷）（附答案-完全）

2010年普通高等学校招生全国统一考试（江苏卷）数学Ⅰ试题参考公式：锥体的体积公式：13V Sh 锥体，其中S 是锥体的底面面积，h 是高.一、填空题：本大题共14小题，每小题5分，共计70分.请把答案填写在答题卡相应位置上．．．．．．．．.1.设集合{1,1,3}A，4,22aa B ，3BA ，则实数a 的值为____▲____.1.【答案】1.【命题意图】本题考查交集的定义，对求得的集合中的元素要进行检验.【解析】由题意得1,32a a .又由342a不符合题意.经检验得1a.2.设复数z 满足(23)64z i i （i 为虚数单位），则z 的模为____▲____.2.【答案】2.【命题意图】本题考查复数有关运算及复数模的计算.【解析】由i i z 46)32(得,2)32)(32()32)(46(3246i i i i i ii z即2,2z i z.3.盒子里共有大小相同的3只白球，1只黑球.若从中随机摸出两只球，则它们颜色不同的概率是_ ▲__.3.【答案】21.【命题意图】本题考查古典概型知识.【解析】31.62p4.某棉纺厂为了解一批棉花的质量，从中随机抽测了100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标).所得数据均在区间[5,40]中，其频率分布直方图如图所示，则在抽测的100根中，有_ ▲__ 根棉花纤维的长度小于20mm.4.【答案】30.【命题意图】本题考查概率统计中频率分布直方图的有关运用,注意纵坐标是频率/组距.【解析】由频率分布直方图得棉花纤维长度小于mm 20的根数为(0.01+0.01+0.04)301005.5.设函数()()xxf x x eae (x R )是偶函数，则实数a 的值为____▲____.5.【答案】1.【命题意图】本题考查函数的奇偶性.【解析】设R xae e x g x x ,)(,由题意分析)(x g 应为奇函数(奇函数奇函数=偶函数),又R x ，0)0(g ，则,01a 所以1a .6.在平面直角坐标系xOy 中，已知双曲线221412xy上一点M 的横坐标为3，则点M 到此双曲线的右焦点的距离为____▲____. 6.【答案】4.【命题意图】本题考查求曲线上点的坐标、双曲线的焦点坐标、两点间距离公式的运用.【解析】由题意得点15,3(M ),双曲线的右焦点的坐标为(4,0)，2MF 22)015()43(=4.或用第二定义：2MF ed，2d，4MF .7.右图是一个算法流程图，则输出的S 的值是____▲____.7.【答案】63.【命题意图】本题考查算法流程图,由流程图得出S 的关系式,比较得出S 的值.【解析】由流程图得12345122222S =1+2+48+16+32=6333,即.63S 8.函数2(0)y x x的图象在点2(,)k ka a 处的切线与x 轴的交点的横坐标为1k a ，其中kN *.若116a ，则123a a a 的值是____▲____.8.【答案】21.【命题意图】考查函数的切线方程、数列的通项.【解析】在点2(,)k k a a 处的切线方程为22(),k k k y a a xa 当0y时，解得2k a x，所以1135,1641212kka a a a a .9.在平面直角坐标系xOy 中，已知圆224x y上有且只有四个点到直线1250x y c 的距离为1，则实数c 的取值范围是____▲____. 9.【答案】(13,13).【命题意图】本题考查直线与圆的位置关系.【解析】如图,圆422yx的半径为2,圆上有且仅有四个点到直线的距离为1,问题转化为原点(0,0)到直线0512cyx 的距离小于1,即1313,13,151222c c c .10.设定义在区间(0,)2上的函数y=6cosx 的图象与y=5tanx 的图象交于点P ，过点P 作x 轴的垂线，垂足为P 1，直线PP 1与函数y=sinx 的图像交于点P 2，则线段P 1P 2的长为____▲____.10.【答案】.32【命题意图】本题考查三角函数问题,由图象相交,即三角函数值相等,建立关系式,求出,32sin x结合图象,数形结合分析P 1P 2的值.xyO 0512cyx1 11【解析】由题意得x x tan 5cos 6，即x x xx xsin 5cos 6,cos sin 5cos 62，226(1sin )5sin ,6sin 5sin 60x x x x 得,32sin x结合图象分析得32sin 21P P x.11.已知函数21,0,()1,0,xx f x x则满足不等式2(1)(2)f x f x 的x 的取值范围是____▲____.11.【答案】).12,1(【命题意图】本题考查分段函数的单调性.【解析】2212,10,x x x解得121x ，所以x 的取值范围是).12,1(12.设x,y 为实数，满足3≤2xy ≤8，4≤2xy≤9，则34xy 的最大值是____▲____. 12.【答案】27.【命题意图】考查不等式的基本性质，等价转化思想.【解析】22()[16,81]xy，2111[,]83xy，322421()[2,27]xxyyxy，43yx 的最大值是27.13.在锐角△ABC 中,角A 、B 、C 的对边分别为a 、b 、c.若6cos b a C ab,则tan tan tan tan C C AB的值是▲.【答案】4.【解析】考查三角函数知识，三角形中的正、余弦定理的应用，等价转化思想.（方法一）考虑已知条件和所求结论对于角A 、B 和边a 、b 具有轮换性.当A=B 或a=b 时满足题意，此时有1cos 3C，21cos 1tan21cos 2C C C ，2tan22C .等腰三角形中，1tan tan 2tan2A BC ，tan tan tan tan C C AB=4.（方法二）226cos 6cos b a C ab Cab ab，2222222236,22a bccabab abab.2tan tan sin cos sin sin cos sin sin()1sin tan tan cos sin sin cos sin sin cos sin sin C C C B A B A C A B CABCA B C A B C A B,由正弦定理，得上式22222214113cos ()662cc cc C abab .14.将边长为1m 的正三角形薄铁皮沿一条平行于某边的直线剪成两块，其中一块是梯形，记2(s梯形的周长）梯形的面积,则s 的最小值是____▲____.【答案】3233.【解析】考查函数中的建模应用，等价转化思想.设剪成的小正三角形的边长为x ，则222(3)4(3)(01)1133(1)(1)22x x sx xx x .（方法一）利用导数求函数最小值.224(3)()13x S x x，22224(26)(1)(3)(2)()(1)3x x x x S x x 2242(31)(3)(1)3x x x 1()0,01,3S x xx.当1(0,]3x时，()0,S x 递减；当1[,1)3x 时，()0,S x 递增.故当13x时，S 取最小值3233.（方法二）利用函数的方法求最小值.令1113,(2,3),(,)32x t t t ，则2224418668331tS tttt .故当131,83xt时，S 取最小值3233.二、解答题：本大题共6小题，共计90分.请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤.15.（本小题满分14分）在平面直角坐标系xOy 中，已知点(1,2)A ，(2,3)B ，(2,1).C (1)求以线段AB 、AC 为邻边的平行四边形的两条对角线的长；(2)设实数t 满足(OC t AB)·OC =0，求t 的值.【解析】本小题主要考查平面向量的几何意义、线性运算、数量积，考查运算求解能力.满分14分.解：（1）由题设知(3,5)AB，(1,1)AC，则(2,6)A B A C ，(4,4).AB AC所以||210AB AC ，||4 2.ABAC 故所求的两条对角线长分别为42，210.（2）由题设知(2,1)OC，(32,5).ABtOCt t由()0AB tOC OC ，得(32,5)(2,1)0t t ，从而511t ，所以11.5t16.（本小题满分14分）如图，在四棱锥P-ABCD 中，PD ⊥平面ABCD ，PD=DC=BC=1，AB=2，AB ∥DC ，∠BCD=900.(1)求证：PC ⊥BC ；(2)求点A 到平面PBC 的距离.【解析】本小题主要考查直线与平面、平面与平面的位置关系，考查几何体的体积，考查空间想象能力、推理论证能力和运算能力.满分14分. 解：（1）因为PD ⊥平面ABCD ，BC 平面ABCD ，所以PD ⊥BC. 由∠BCD=900，得BC ⊥DC. 又PD DC D ，PD平面PCD ，DC平面PCD ，所以BC ⊥平面PCD.因为PC平面PCD ，所以PC ⊥BC.（2）（方法一）分别取AB 、PC 的中点E 、F ，连DE 、DF.则易证DE ∥CB ，DE ∥平面PBC ，点D 、E 到平面PBC 的距离相等. 由（1）知BC ⊥平面PCD ，所以平面PBC ⊥平面PCD.因为PD=DC ，PF=FC ，所以DF ⊥PC ，所以DF ⊥平面PBC 于F. 易知DF=22.又点A 到平面PBC 的距离等于E 到平面PBC 的距离的2倍，故点A 到平面PBC 的距离等于2.（方法二）连结AC.设点A 到平面PBC 的距离h.因为AB ∥DC ，∠BCD=900，所以∠ABC=900. 从而由AB=2，BC=1，得ABC 的面积1ABCS.由PD ⊥平面ABCD 及PD=1，得三棱锥PABC 的体积11.33ABCVSPD因为PD ⊥平面ABCD ，DC 平面ABCD ，所以PD ⊥DC.又PD=DC=1，所以222.PC PDDC由PC ⊥BC ，BC=1，得PBC 的面积2.2PBCS 由11213323PBCVShh ，得2h .因此，点A 到平面PBC 的距离为2.17.（本小题满分14分）某兴趣小组要测量电视塔AE 的高度H(单位：m).如示意图，垂直放置的标杆BC 高度h=4m ，仰角∠ABE=，∠ADE=.（1）该小组已测得一组，的值，算出了tan =1.24，tan =1.20，请据此算出H 的值；。

2010年高考数学江苏卷(word版含答案)

π 2
11．已知函数 f ( x) 是．
x 2 1， x ≥ 0 1， x0
，则满足不等式 f (1 x2 ) f (2 x) 的 x 的取值范围
12．设 x，y 为实数，满足 3≤ xy ≤8，4≤
2
x2 x3 ≤9，则 4 的最大值是 y y
．
13．在锐角 △ ABC 中，角 A、 B、 C 的对边分别为 a、 b、 c．若
b a a n t Ca n t 6 cos C ，则 a b a n t Aa n t
C B
的值是． 14．将边长为 1m 的正三角形薄铁皮，沿一条平行于某边的直线剪成两块，其中一块是梯形，记 S=
(梯形的周长) 梯形的面积
2
，则 S 的最小值是
．
二、解答题：本大题共 6 小题，共计 90 分，请在答题卡指定区域内作答，解答时应写出文．．．．．．．字说明、证明过程或演算步骤． 15．（本小题满分 14 分）在平面直角坐标系 xOy 中，已知点 A（ 1， 2），B（2，3）， C（ 2， 1）．（1）求以线段 AB、AC 为邻边的平行四边形的两条对角线的长；（2）设实数 t 满足（ AB tOC ） · OC =0，求 t 的值．
6．在平面直角坐标系 xOy 中，已知双曲线
x2 y 2 1 上一点 4 12
S≥33 Y 输出 S
M 的横坐标为 3 ，则点 M 到双曲线的右焦点的距离为． 7．右图是一个算法流程图，则输出的 S 的值是．
结束（第 7 题） 8．函数 y x （x>0）的图象在点（ak，ak2）处的切线与 x 轴的交点的横坐标为 ak+1，其中

【真题】2010年江苏省高考数学试题(含附加题+答案)

本试卷满分160分，考试时间为120分钟。

考试结束后，请将本试卷和答题卡一并交回。

2、答题前，请您务必将自己的姓名、考试证号用书写黑色字迹的0.5毫米签字笔填写在试卷及答题卡上。

3、请认真核对监考员所粘贴的条形码上的姓名、考试证号是否与您本人的相符。

4、作答非选择题必须用书写黑色字迹的0.5毫米签字笔写在答题卡上的指定位置，在其它位置作答一律无效。

作答选择题必须用2B 铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，请用橡皮擦干净后，再选涂其它答案。

5、如有作图需要，可用2B 铅笔作答，并请加黑加粗，描写清楚。

参考公式：锥体的体积公式:V 锥体=13Sh ，其中S 是锥体的底面积，h 是高。

一、填空题：本大题共1小题，每小题5分，共70分．1、设集合A={-1,1,3}，B={a+2,a 2+4},A ∩B={3}，则实数a =______▲_____.2、设复数z 满足z(2-3i)=6+4i （其中i 为虚数单位），则z 的模为______▲_____.3、盒子中有大小相同的3只白球，1只黑球，若从中随机地摸出两只球，两只球颜色不同的概率是_▲__.4、某棉纺厂为了了解一批棉花的质量，从中随机抽取了100根棉花纤维的长度（棉花纤维的长度是棉花质量的重要指标），所得数据都在区间[5,40]中，其频率分布直方图如图所示，则其抽样的100根中，有_▲___根在棉花纤维的长度小于20mm 。

5、设函数f(x)=x(e x +ae -x )(x ∈R)是偶函数，则实数a =_______▲_________6、在平面直角坐标系xOy 中，双曲线112422=-y x 上一点M ，点M 的横坐标是3，则M 到双曲线右焦点的距离是___▲_______7、右图是一个算法的流程图，则输出S 的值是______▲_______8、函数y=x 2(x>0)的图像在点(a k ,a k 2)处的切线与x 轴交点的横坐标为a k+1,k 为正整数，a 1=16，则a 1+a 3+a 5=____▲_____9、在平面直角坐标系xOy 中，已知圆422=+y x 上有且仅有四个点到直线12x-5y+c=0的距离为1，则实数c 的取值范围是______▲_____10、定义在区间⎪⎭⎫ ⎝⎛20π,上的函数y=6cosx 的图像与y=5tanx 的图像的交点为P ，过点P 作PP 1⊥x 轴于点P 1，直线PP 1与y=sinx 的图像交于点P 2,则线段P 1P 2的长为_______▲_____。

2010年江苏高考数学试卷及解析

2010年普通高等学校招生全国统一考试（江苏卷）数学Ⅰ试题参考公式：锥体的体积公式: V 锥体=13Sh ，其中S 是锥体的底面积，h 是高。

一、填空题：本大题共14小题，每小题5分，共70分。

请把答案填写在答题卡相应的位置上．．．．．．．．．.1、设集合A={-1,1,3}，B={a+2,a 2+4},A ∩B={3}，则实数a =______▲_____. [解析] 考查集合的运算推理。

3∈B, a+2=3, a=1.2、设复数z 满足z(2-3i)=6+4i （其中i 为虚数单位），则z 的模为______▲_____. [解析] 考查复数运算、模的性质。

z(2-3i)=2(3+2 i), 2-3i 与3+2 i 的模相等，z 的模为2。

3、盒子中有大小相同的3只白球，1只黑球，若从中随机地摸出两只球，两只球颜色不同的概率是_ ▲__. [解析]考查古典概型知识。

24、某棉纺厂为了了解一批棉花的质量，从中随机抽取了100根棉花纤维的长度（棉花纤维的长度是棉花质量的重要指标），所得数据都在区间[5,40]中，其频率分布直方图如图所示，则其抽样的100根中，有_▲___根在棉花纤维的长度小于20mm 。

[解析]考查频率分布直方图的知识。

100×（0.001+0.001+0.004）×5=305、设函数f(x)=x(e x +ae -x )(x ∈R)是偶函数，则实数a =_______▲_________ [解析]考查函数的奇偶性的知识。

g(x)=e x +ae -x 为奇函数，由g(0)=0，得a =－1。

6、在平面直角坐标系xOy 中，双曲线112422=-y x 上一点M ，点M 的横坐标是3，则M 到双曲线右焦点的距离是___▲_______[解析]考查双曲线的定义。

422MF e d ===，d 为点M 到右准线1x =的距离，d =2，MF=4。

7、右图是一个算法的流程图，则输出S 的值是______▲_______[解析]考查流程图理解。

2010年高考江苏数学卷试题及参考答案

2010年高考江苏数学卷试题及参考答案佚名【期刊名称】《中学数学月刊》【年(卷),期】2010(000)007【总页数】6页(P45-49,封4)【正文语种】中文参考公式:锥体的体积公式:Sh,其中S是锥体的底面面积,h是高.1.设集合A={-1,1,3},B={a+2,a2+4},A∩B={3},则实数a的值为________.2.设复数z满足z(2-3i)=6+4i(i为虚数单位)，则z的模为________.3.盒子里共有大小相同的3只白球、1只黑球.若从中随机摸出两只球，则它们颜色不同的概率是________.4.某棉纺厂为了解一批棉花的质量，从中随机抽测了100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标).所得数据均在区间[5，40]中，其频率分布直方图如图1所示，则在抽测的100根中，有根棉花纤维的长度小于20mm.5.设函数f(x)=x(ex+ae-x)(x∈R)是偶函数，则实数a的值为________.6.在平面直角坐标系xOy中，已知双曲线=1上一点M的横坐标为3，则点M到此双曲线的右焦点的距离为________.7.图2是一个算法流程图,则输出的S的值是________.8.函数y=x2(x>0)的图象在点处的切线与x轴的交点的横坐标为ak+1,其中k∈N*.若a1=16,则a1+a3+a5的值是________.9.在平面直角坐标系xOy中,已知圆x2+y2=4上有且只有四个点到直线12x-5y+c=0的距离为1,则实数c的取值范围是________.10.设定义在区间上的函数y=6cos x的图象与y=5tan x的图象交于点P,过点P 作x轴的垂线,垂足为P1,直线PP1与函数y=sin x的图象交于点P2,则线段P1P2的长为________.11.已知函数则满足不等式f(1-x2)>f(2x)的x的取值范围是________.12.设x,y为实数,满足,则的最大值是________.13.在锐角△ABC中,角A,B,C的对边分别为a,b,c.若,则的值是________.14.将边长为1m的正三角形薄铁皮沿一条平行于某边的直线剪成两块,其中一块是梯形,记,则s的最小值是________.15.(14分)在平面直角坐标系xOy中,已知点A(-1,-2),B(2,3),C(-2,-1). (1)求以线段AB,AC为邻边的平行四边形的两条对角线的长; (2)设实数t满足,求t的值.16.(14分)如图3,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°. (1)求证:PC⊥BC; (2)求点A到平面PBC的距离.17.(14分 )某兴趣小组要测量电视塔AE的高度H(单位:m),如示意图4,垂直放置的标杆BC的高度h=4m,仰角∠ABE=α,∠ADE=β. (1)该小组已测得一组α,β的值,算出了tan α=1.24,tan β=1.20,请据此算出H的值; (2)该小组分析若干测得的数据后,认为适当调整标杆到电视塔的距离d(单位:m),使α与β之差较大,可以提高测量精度.若电视塔的实际高度为125m,试问d为多少时,α-β最大?18.(16分)在平面直角坐标系xOy中,如图5,已知椭圆的左、右顶点为A,B,右焦点为F,设过点T(t,m)的直线TA，TB与此椭圆分别交于点M(x1,y1),N(x2,y2),其中m>0,y1>0,y2<0. (1)设动点P满足PF2-PB2=4，求点P的轨迹； (2)设,求点T 的坐标； (3)设t=9,求证：直线MN必过x轴上的一定点(其坐标与m无关).19.(16分)设各项均为正数的数列{an}的前n项和为Sn,已知2a2=a1+a3,数列}是公差为d的等差数列. (1)求数列{an}的通项公式(用n,d表示); (2)设c为实数,对满足m+n=3k且m≠n的任意正整数m,n,k,不等式Sm+Sn>cSk都成立,求证:c的最大值为.20.(16分)设f(x)是定义在区间(1,+∞)上的函数,其导函数为f′(x) .如果存在实数a 和函数h(x),其中h(x)对任意的x∈(1,+∞)都有h(x)>0,使得f′(x)=h(x)(x2-ax+1),则称函数f(x)具有性质P(a). (1)设函数,其中b为实数. (ⅰ)求证:函数f(x)具有性质P(b);(ⅱ)求函数f(x)的单调区间. (2)已知函数g(x)具有性质P(2).给定x1,x2∈(1,+∞),x1<x2,设m为实数,α=mx1+(1-m)x2,β=(1-m)x1+mx2,且α>1,β>1,若|g(α)-g(β)|<|g(x1)-g(x2)|,求m的取值范围.一、填空题：本题考查基础知识、基本运算和基本思想方法.1.12.23.9.(-13,13) 10.13.4 14.二、解答题15.本小题主要考查平面向量的几何意义、线性运算、数量积，考查运算求解能力. 解：(1)由题设知，则 ). 所以. 故所求的两条对角线长分别为. (2)由题设知). 由,得(3+2t,5+t)·(-2,-1)=0, 从而5t=-11,所以.16.本小题主要考查直线与平面、平面与平面的位置关系,考查几何体的体积,考查空间想象能力、推理论证能力和运算能力. 解:(1)因为PD⊥平面ABCD,BC⊂平面ABCD, 所以PD⊥BC. 由∠BCD=90°,得BC⊥DC. 又PD∩DC=D,PD⊂平面PCD, DC⊂平面PCD,所以BC⊥平面PCD. 因为PC⊂平面PCD,所以PC⊥BC.(2)连结AC.设点A到平面PBC的距离为h. 因为AB∥DC,∠BCD=90°,所以∠ABC=90°.从而由AB=2,BC=1,得△ABC的面积S△ABC=1. 由PD⊥平面ABCD及PD=1,得三棱锥P-ABC的体积 . 因为PD⊥平面ABCD,DC⊂平面ABCD,所以PD⊥DC. 又PD=DC=1,所以.由PC⊥BC,BC=1,得△PBC的面积.由,得.因此，点A到平面PBC的距离为.17.本小题主要考查解三角形、基本不等式、导数等基础知识，考查数学建模能力、抽象概括能力和解决实际问题的能力.解：(1)由及AB+BD=AD，得 , 解得.因此，算出的电视塔的高度H是124m. (2)由题设知d=AB,得.由,得,所以 , 当且仅当,即时，上式取等号.所以当时，tan(α-β)最大.因为,则,所以当时，α-β最大.故所求的d是m.18.本小题主要考查求简单曲线的方程，考查直线与椭圆的方程等基础知识，考查运算求解能力和探究问题的能力. 解：由题设得A(-3，0)，B(3，0)，F(2，0). ( 1)设点P(x,y),则PF2=(x-2)2+y2,PB2=(x-3)2+y2. 由PF2-PB2=4,得(x-2)2+y2-(x-3)2-y2=4,化简得.故所求点P的轨迹为直线.(2)由及y1>0,得,则点,从而直线AM的方程为由及y2<0,得,则点,从而直线BN的方程为.由解得所以点T的坐标为.(3)由题设知,直线AT的方程为,直线BT的方程为).点M(x1,y1) 满足得 , 因为x1≠-3,则 ,解得x1= ，从而得.点N(x2,y2)满足解得.若x1=x2,则由及m>0,得,此时直线MN的方程为x=1,过点D(1,0).若x1≠x2,则,直线MD的斜率, 直线ND的斜率,得kMD=kND,所以直线MN过D 点.因此,直线MN必过x轴上的点(1,0).19.本小题主要考查等差数列的通项、求和以及基本不等式等有关知识，考查探索、分析及论证的能力.解：(1)由题设知,,则当n≥2时, n.由2a2=a1+a3,得,解得d.故当n≥2时,an=2nd2-d2. 又a1=d2,所以数列{an}的通项公式为an=(2n-1)d2.(2)由及,得d>0,Sn=d2n2.于是,对满足题设m,n,k,m≠n,有.所以c的最大值.另一方面,任取实数.设k为偶数,令,则m,n,k符合条件,且).于是,只要9k2+4<2ak2,即当时,就有.所以满足条件的,从而.因此c的最大值为.20.本小题主要考查函数的概念、性质、图象及导数等基础知识，考查灵活运用数形结合、分类讨论的思想方法进行探索、分析与解决问题的综合能力.解：(1)(ⅰ)由,得.因为x>1时，,所以函数f(x)具有性质P(b).(ⅱ)当b≤2时，由x>1得x2-bx+1≥x2-2x+1=(x-1)2>0, 所以f′(x)>0，从而函数f(x)在区间(1，+∞)上单调递增. 当b>2时，解方程x2-bx+1=0得 .因为, 所以当x∈(1,x2)时，f′(x)<0;当x∈(x2,+∞)时，f′(x)>0;当x=x2时，f′(x)=0.从而函数f(x)在区间(1，x2)上单调递减，在区间(x2,+∞)上单调递增. 综上所述，当b≤2时，函数f(x)的单调增区间为(1，+∞)；当b>2时，函数f(x)的单调减区间为，单调增区间为.(2)由题设知，g(x)的导函数g′(x)=h(x)(x2-2x+1),其中函数h(x)>0对于任意的x∈(1,+∞)都成立，所以，当x>1时，g′(x)=h(x)(x-1)2>0,从而g(x)在区间(1，+∞)上单调递增.①当m∈(0,1)时，有α=mx1+(1-m)x2>mx1+(1-m)x1=x1,α<mx2+(1-m)x2=x2,得α∈(x1,x2)，同理可得β∈(x1,x2),所以由g(x)的单调性知g(α),g(β)∈(g(x1)，g(x2)),从而有|g(α)-g(β)|<|g(x1)-g(x2)|,符合题设.②当m≤0时，α=mx1+(1-m)x2≥mx2+(1-m)x2=x2,β=(1-m)x1+mx2≤(1-m)x1+mx1=x1,于是由α>1,β>1及g(x)的单调性知g(β)≤g(x1)<g(x2)≤g(α),所以|g(α)-g(β)|≥|g(x1)-g(x2)|,与题设不符.③当m≥1时，同理可得α≤x1,β≥x2,进而得|g(α)-g(β)|≥|g(x1)-g(x2)|,与题设不符. 因此，综合①、②、③得所求的m的取值范围为(0，1).21.[选做题]本题包括A，B，C，D四小题，请选定其中两题，若多做，则按作答的前两题评分. 解答时应写出文字说明、证明过程或演算步骤.A.选修4-1：几何证明选讲(10分) 如图9，AB是圆O的直径，D为圆O上一点，过D作圆O的切线交AB的延长线于点C.若DA=DC，求证：AB=2BC.B.选修4-2：矩阵与变换(10分) 在平面直角坐标系xOy中，已知点A(0，0)，B(-2，0)，C(-2，1).设k为非零实数，矩阵,,点A，B，C在矩阵MN对应的变换下得到的点分别为A1，B1，C1，△A1B1C1的面积是△ABC的面积的2倍，求k的值.C.选修4-4：坐标系与参数方程(10分) 在极坐标系中，已知圆ρ=2cos θ与直线3ρcos θ+4ρsin θ+α=0相切，求实数a的值.D.选修4-5：不等式选讲(10分) 设a,b是非负实数，求证).[必做题]第22题、第23题，每题10分，共计20分.解答时应写出文字说明、证明过程或演算步骤22.某工厂生产甲、乙两种产品.甲产品的一等品率为80%，二等品率为20%；乙产品的一等品率为90%，二等品率为10%.生产1件甲产品，若是一等品则获得利润4万元，若是二等品则亏损1万元；生产1件乙产品，若是一等品则获得利润6万元，若是二等品则亏损2万元.设生产各件产品相互独立. (1)记X(单位：万元)为生产1件甲产品和1件乙产品可获得的总利润，求X的分布列； (2)求生产4件甲产品所获得的利润不少于10万元的概率.23.已知△ABC的三边长都是有理数. (1)求证：cos A是有理数；(2)求证：对任意正整数n,cos nA是有理数.21.A.本题主要考查三角形、圆的有关知识，考查推理论证能力.证明：连结OD，BD.因为AB是圆O的直径, 所以∠ADB=90°,AB=2OB.因为DC是圆O的切线, 所以∠CDO=90°.又因为DA=DC,所以∠A=∠C, 于是△ADB≌△CDO,从而AB=CO, 即2OB=OB+BC,得OB=BC.故AB=2BC. B.本题主要考查图形在矩阵对应的变换下的变化特点,考查运算求解能力.解:由题设得. 由,,,可知 A1(0,0),B1(0,-2),C1(k,-2).计算得△ABC的面积是1,△A1B1C1的面积是|k|,则由题设知|k|=2×1=2.所以k的值为-2或2. C.本题主要考查曲线的极坐标方程等基础知识,考查转化问题的能力. 解:将极坐标方程化为直角坐标方程,得圆的方程为x2+y2=2x,即(x-1)2+y2=1,直线的方程为3x+4y+a=0. 由题设知,圆心(1,0)到直线的距离为1,即有, 解得a=-8,或a=2. 故a的值为-8或2. D.本题主要考查证明不等式的基本方法,考查推理论证的能力.证明:由a,b是非负实数,作差得 ).当a≥b时,,从而,得当a<b时,,从而,得 .所以).22.本题主要考查概率的有关知识,考查运算求解的能力.解:(1)由题设知,X的可能取值为10,5,2,-3,且P(X=10)=0.8×0.9=0.72,P(X=5)=0.2×0.9=0.18, P(X=2)=0.8×0.1=0.08, P(X=-3)=0.2×0.1=0.02. 由此得X的分布列为：(2)设生产的4件甲产品中一等品有n件,则二等品有4-n件.由题设知4n-(4-n)≥10,解得, 又n∈N,得n=3,或n=4.所以. 故所求概率为0.819 2.23.本题主要考查余弦定理、数学归纳法等基础知识，考查推理论证的能力与分析问题、解决问题的能力.证明：(1)由AB，BC，AC为有理数及余弦定理知cos 是有理数.(2)用数学归纳法证明cos nA和sin A·sinnA都是有理数.①当n=1时，由(1)知cos A是有理数，从而有sin A·sin A=1-cos2A也是有理数.②假设当n=k(k≥1)时，coskA和sinA·sinkA都是有理数.当n=k+1时，由cos(k+1)A=cos A·coskA-sin A·sin kA, sin A·sin(k+1)A=sinA·(sin A·cos kA+cos A·sin kA)=(sin A·sin A)·cos kA+ (sin A·sin kA)·cos A, 及①和归纳假设，知cos(k+1)A与sin A·sin(k+1)A都是有理数. 即当n=k+1时，结论成立. 综合①、②可知，对任意正整数n,cos nA是有理数.。

2010年江苏省高考数学试题真题解析(word版含理科附加题) 2

绝密★启用前2010年普通高等学校招生全国统一考试（江苏卷）数学Ⅰ试题一、填空题：本大题共14小题，每小题5分，共70分。

请把答案填写在答题卡相应的位置上．．．．．．．．．. 1、设集合A={-1,1,3}，B={a+2,a 2+4},A ∩B={3}，则实数a =______▲_____. 2、设复数z 满足z(2-3i)=6+4i （其中i 为虚数单位），则z 的模为______▲_____.3、盒子中有大小相同的3只小球，1只黑球，若从中随机地摸出两只球，两只球颜色不同的概率是_ ▲__.4、某棉纺厂为了了解一批棉花的质量，从中随机抽取了100根棉花纤维的长度（棉花纤维的长度是棉花质量的重要指标），所得数据都在区间[5,40]中，其频率分布直方图如图所示，则其抽样的100根中，有_▲___根在棉花纤维的长度小于20mm 。

5、设函数f(x)=x(e x+ae -x)(x ∈R)是偶函数，则实数a =__▲6、在平面直角坐标系xOy 中，双曲线112422=-y x 上一点M ，点M 的横坐标是3，则M 到双曲线右焦点的距离是___▲_______ 7、右图是一个算法的流程图，则输出S 的值是______▲_______8、函数y=x 2(x>0)的图像在点(a k ,a k 2)处的切线与x 轴交点的横坐标为a k+1,k 为正整数，a 1=16，则a 1+a 3+a 5=____▲_____9、在平面直角坐标系xOy 中，已知圆422=+y x 上有且仅有四个点到直线12x-5y+c=0的距离为1，则实数c 的取值范围是______▲_____ 10、定义在区间⎪⎭⎫⎝⎛20π,上的函数y=6cosx 的图像与y=5tanx 的图像的交点为P ，过点P 作PP 1⊥x 轴于点P 1，直线PP 1与y=sinx 的图像交于点P 2,则线段P 1P 2的长为_______▲_____。