SPSS多元线性回归分析报告
多元线性回归SPSS实验报告
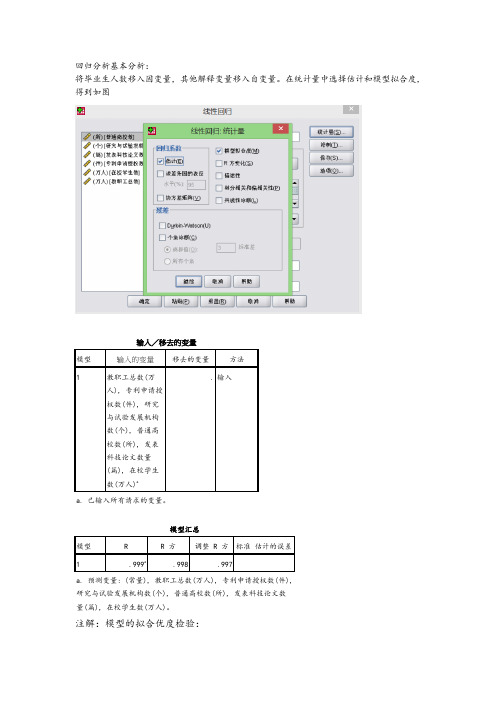
49%;可以认为:这些变量存在多重共线性。需要建立回归方程。
2.重建回归方程
模型
输入/移去的变量b
输入的变量
移去的变量
方法
1
教职工总数(万
人), 专利申请授
权数(件), 研究
b. 预测变量: (常量), 教职工总数(万人), 专利申请授权数(件), 研究与试验发展机构数(个), 普通高校数(所), 发表 科技论文数量(篇)。 c. 预测变量: (常量), 教职工总数(万人), 专利申请授权数(件), 研究与试验发展机构数(个), 发表科技论文数量(篇)。 d. 预测变量: (常量), 教职工总数(万人), 专利申请授权数(件), 发表科技论文数量(篇)。 e. 预测变量: (常量), 教职工总数(万人), 发表科技论文数量(篇)。 f. 因变量: 毕业生数(万人)
. 输入
a. 已输入所有请求的变量。
模型汇总
模型
R
R 方 调整 R 方 标准 估计的误差
1
.999a
.998
.997
a. 预测变量: (常量), 教职工总数(万人), 专利申请授权数(件), 研究与试验发展机构数(个), 普通高校数(所), 发表科技论文数 量(篇), 在校学生数(万人)。
注解:模型的拟合优度检验:
第五列:回归方程的估计标准误差=
Anovab
模型
平方和
df
均方
F
Sig.
1
回归
6
.000a
残差
7
总计
13
a. 预测变量: (常量), 教职工总数(万人), 专利申请授权数(件), 研究与试验发展机构 数(个), 普通高校数(所), 发表科技论文数量(篇), 在校学生数(万人)。 b. 因变量: 毕业生数(万人)
SPSS多元线性回归分析报告实例操作步骤

SPSS 统计分析多元线性回归分析方法操作与分析实验目的:引入1998~2008年上海市城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率和房屋空置率作为变量,来研究上海房价的变动因素。
实验变量:以年份、商品房平均售价(元/平方米)、上海市城市人口密度(人/平方公里)、城市居民人均可支配收入(元)、五年以上平均年贷款利率(%)和房屋空置率(%)作为变量。
实验方法:多元线性回归分析法软件:spss19.0操作过程:第一步:导入Excel数据文件1.open data document——open data——open;2. Opening excel data source——OK.第二步:1.在最上面菜单里面选中Analyze——Regression——Linear ,Dependent(因变量)选择商品房平均售价,Independents(自变量)选择城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率、房屋空置率;Method 选择Stepwise.进入如下界面:2.点击右侧Statistics,勾选Regression Coefficients(回归系数)选项组中的Estimates;勾选Residuals(残差)选项组中的Durbin-Watson、Casewise diagnostics默认;接着选择Model fit、Collinearity diagnotics;点击Continue.3.点击右侧Plots,选择*ZPRED(标准化预测值)作为纵轴变量,选择DEPENDNT(因变量)作为横轴变量;勾选选项组中的Standardized Residual Plots(标准化残差图)中的Histogram、Normal probability plot;点击Continue.4.点击右侧Save,勾选Predicted Vaniues(预测值)和Residuals(残差)选项组中的Unstandardized;点击Continue.5.点击右侧Options,默认,点击Continue.6.返回主对话框,单击OK.输出结果分析:1.引入/剔除变量表Variables Entered/Removed aModel Variables Entered Variables Removed Method1 城市人口密度(人/平方公里) . Stepwise (Criteria:Probability-of-F-to-enter<= .050,Probability-of-F-to-remove >=.100).2 城市居民人均可支配收入(元) . Stepwise (Criteria:Probability-of-F-to-enter<= .050,Probability-of-F-to-remove >=.100).a. Dependent Variable: 商品房平均售价(元/平方米)该表显示模型最先引入变量城市人口密度(人/平方公里),第二个引入模型的是变量城市居民人均可支配收入(元),没有变量被剔除。
spss多元线性回归研究分析

spss多元线性回归分析作者: 日期:SPSS多元线性回归分析试验在科学研究中,我们会发现某些指标通常受到多个因素的影响,如血压值除了受年龄影响之外,还受到性别、体重、饮食习惯、吸烟情况等因素的影响,用方程定量描述一个因变量y与多个自变量x1、x2、x3 之间的线性依存关系,称为多元线性回归。
有学者认为血清中低密度脂蛋白增高是引起动脉硬化的一个重要原因。
现测量30名怀疑患有动脉硬化的就诊患者的载脂蛋白A、载脂蛋白B、载脂蛋白E、载脂蛋白C、低密度脂蛋白中的胆固醇含量。
资料如下表所示。
求低密度脂蛋白中的胆固醇含量对载脂蛋白A、载脂蛋白E、载脂蛋白E、载脂蛋白C的线性回归方程。
表1 30名就诊患者资料表spss数据处理步骤:(1)打开spss输入数据后,点击“分析”—“回归”—“线性”。
然后将“低密度脂蛋白”选入因变量框,将“载脂蛋白A” “载脂蛋白E” “载脂蛋白E” “载脂蛋白C”依次选入自变量框。
方法选为“逐步”。
(2)单击“统计量”选项,原有选项基础上选择“R方变化”。
在残差中选“Durbin-Watson”,单击“继续”。
i [粘贴(E)] i ss (印11取消i L帮助(3)单击“绘制”,将“DEPENDNT ”选入“X2”中,将“*SRESID ”选入“Y 中,在标准残差图选项中选择“直方图”和“正态概率图”。
单击“继续”。
S3闵蠢墨fD):制IKDEPEHDNT T ZPRED *ZF?ESID PRESID •ADdPRED怡尺匚SID 怡口穆ESILJ呵直方便(比“正态槪率副曰继续将(3),,取卷 帮肋銭性回归册回归:圏踰点1的1厂产空所有制分團(巳(4)单击“选项”,在原有选项的基础上单击“继续”,最后单击“确定”,就完 成了。
数据处理结果如下:a.因变量低密度脂蛋白上图为统计的基本信息ca. 预测变量:(常量),载脂蛋白Bb. 预测变量:(常量),载脂蛋白B,载脂蛋白Cc. 因变量:低密度脂蛋白上图列出了模型的R、R方、调整R方。
SPSS多元回归分析报告实例
多元回归分析在大多数的实际问题中,影响因变量的因素不是一个而是多个,我们称这类回问题为多元回归分析。
可以建立因变量y与各自变量x j(j=1,2,3,…,n)之间的多元线性回归模型:其中:b0是回归常数;b k(k=1,2,3,…,n)是回归参数;e是随机误差。
多元回归在病虫预报中的应用实例:某地区病虫测报站用相关系数法选取了以下4个预报因子;x1为最多连续10天诱蛾量(头);x2为4月上、中旬百束小谷草把累计落卵量(块);x3为4月中旬降水量(毫米),x4为4月中旬雨日(天);预报一代粘虫幼虫发生量y(头/m2)。
分级别数值列成表2-1。
预报量y:每平方米幼虫0~10头为1级,11~20头为2级,21~40头为3级,40头以上为4级。
预报因子:x1诱蛾量0~300头为l级,301~600头为2级,601~1000头为3级,1000头以上为4级;x2卵量0~150块为1级,15l~300块为2级,301~550块为3级,550块以上为4级;x3降水量0~10.0毫米为1级,10.1~13.2毫米为2级,13.3~17.0毫米为3级,17.0毫米以上为4级;x4雨日0~2天为1级,3~4天为2级,5天为3级,6天或6天以上为4级。
表2-1x1 x2 x3 x4 y年蛾量级别卵量级别降水量级别雨日级别幼虫密度级别1960 1022 4 112 1 4.3 1 2 1 10 1 1961 300 1 440 3 0.1 1 1 1 4 1 1962 699 3 67 1 7.5 1 1 1 9 1 1963 1876 4 675 4 17.1 4 7 4 55 4 1965 43 1 80 1 1.9 1 2 1 1 1 1966 422 2 20 1 0 1 0 1 3 1 1967 806 3 510 3 11.8 2 3 2 28 3数据保存在“DATA6-5.SAV”文件中。
1)准备分析数据在SPSS数据编辑窗口中,创建“年份”、“蛾量”、“卵量”、“降水量”、“雨日”和“幼虫密度”变量,并输入数据。
【精品】SPSS统计实验报告多元线性回归分析

【精品】SPSS统计实验报告多元线性回归分析
本文旨在通过多元线性回归分析,深入研究X、Y、Z三个变量之间的关系,以探究这三个变量对结果的影响。
本实验中样本数量为100人,本文采用SPSS22.0计算软件进行多元线性回归分析,统计计算结果如下:
(一)检验变量X、Y、Z三个变量是否有关:
Sig.=.633。
结果显示,该值大于0.05,表明X、Y、Z三者之间没有显著统计关系;
(二)确定拟合模型:
以X、Y、Z三个变量回归拟合,得出模型为:y=1.746+0.660X+0.783Y+0.430Z。
(三)检验回归模型的有效性:
1. 回归系数的统计量检验
模型的R方为.668,该值表明,X、Y、Z三个自变量可以解释本回归模型的67.0%的变化量;
2.F检验
结果显示,f分数为20.670,Sig.=.000,结果显示,f分数小于阈值0.05,因此可以接受回归模型;
检验结果显示,当其他X、Y、Z三个自变量的条件不变的情况下,X、Y、Z三个自变量对Y的影响是有显著性的。
综上所述,本文使用SPSS22.0计算软件进行多元线性回归分析,探究X、Y、Z三个变量之间的关系。
结果显示,X、Y、Z三者之间没有显著统计关系;拟合模型为:
y=1.746+0.660X+0.783Y+0.430Z;最后,证实X、Y、Z三个自变量对Y的影响是有显著性的。
SPSS实验多元线性回归分析12

这里我们以总成绩作为因变量Y,平时成绩和期中成绩分别作为自变量X1,X2,建立的多元回归模型为:
Байду номын сангаас2,估计参数,建立回归预测模型
利用SPSS可得一下结果:
Variables Entered/Removedb
Model
Variables Entered
Variables Removed
1183.800
19
a. Predictors: (Constant),期中成绩,平时成绩
b. Dependent Variable:总成绩
注释:从表中可得拟合方程的F统计量值为7.586,相应的P值为0.000说明,拟合方程是显著的。是具有统计意义的。
Coefficientsa
Model
Unstandardized Coefficients
Method
1
期中成绩,平时成绩a
.
Enter
a. All requested variables entered.
b. Dependent Variable:总成绩
注释:根据这个表的结果我们可以初步的知道,经过检验自变量X1,X2是可以加入到准备估计的回归方程中作为变量的。
Model Summaryb
Standardized Coefficients
t
Sig.
95% Confidence Interval for B
Correlations
Collinearity Statistics
B
Std. Error
Beta
Lower Bound
Upper Bound
Zero-order
SPSS—回归—多元线性回归结果分析(二)
SPSS—回归—多元线性回归结果分析(二)2011-10-27 14:44,最近一直很忙,公司的潮起潮落,就好比人生的跌岩起伏,眼看着一步步走向衰弱,却无能为力,也许要学习“步步惊心”里面“四阿哥”的座右铭:“行到水穷处”,”坐看云起时“。
接着上一期的“多元线性回归解析”里面的内容,上一次,没有写结果分析,这次补上,结果分析如下所示:结果分析1:由于开始选择的是“逐步”法,逐步法是“向前”和“向后”的结合体,从结果可以看出,最先进入“线性回归模型”的是“price in thousands"建立了模型1,紧随其后的是“Wheelbase"建立了模型2,所以,模型中有此方法有个概率值,当小于等于0.05时,进入“线性回归模型”(最先进入模型的,相关性最强,关系最为密切)当大于等 0.1时,从“线性模型中”剔除结果分析:1:从“模型汇总”中可以看出,有两个模型,(模型1和模型2)从R2 拟合优度来看,模型2的拟合优度明显比模型1要好一些(0.422>0.300)2:从“Anova"表中,可以看出“模型2”中的“回归平方和”为115.311,“残差平方和”为153.072,由于总平方和= 回归平方和+残差平方和,由于残差平方和(即指随即误差,不可解释的误差)由于“回归平方和”跟“残差平方和”几乎接近,所有,此线性回归模型只解释了总平方和的一半,3:根据后面的“F统计量”的概率值为0.00,由于0.00<0.01,随着“自变量”的引入,其显著性概率值均远小于 0.01,所以可以显著地拒绝总体回归系数为0的原假设,通过ANOVA方差分析表可以看出“销售量”与“价格”和“轴距”之间存在着线性关系,至于线性关系的强弱,需要进一步进行分析。
结果分析:1:从“已排除的变量”表中,可以看出:“模型2”中各变量的T检的概率值都大于“0.05”所以,不能够引入“线性回归模型”必须剔除。
SPSS多元线性回归分析报告实例操作步骤
SPSS 统计分析多元线性回归分析方法操作与分析实验目的:引入1998~2008年上海市城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率和房屋空置率作为变量,来研究上海房价的变动因素。
实验变量:以年份、商品房平均售价(元/平方米)、上海市城市人口密度(人/平方公里)、城市居民人均可支配收入(元)、五年以上平均年贷款利率(%)和房屋空置率(%)作为变量。
实验方法:多元线性回归分析法软件:spss19.0操作过程:第一步:导入Excel数据文件1.open data document——open data——open;2. Opening excel data source——OK.第二步:1.在最上面菜单里面选中Analyze——Regression——Linear ,Dependent (因变量)选择商品房平均售价,Independents(自变量)选择城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率、房屋空置率;Method选择Stepwise.进入如下界面:2.点击右侧Statistics,勾选Regression Coefficients(回归系数)选项组中的Estimates;勾选Residuals(残差)选项组中的Durbin-Watson、Casewise diagnostics默认;接着选择Model fit、Collinearity diagnotics;点击Continue.3.点击右侧Plots,选择*ZPRED(标准化预测值)作为纵轴变量,选择DEPENDNT(因变量)作为横轴变量;勾选选项组中的Standardized Residual Plots(标准化残差图)中的Histogram、Normal probability plot;点击Continue.4.点击右侧Save,勾选Predicted Vaniues(预测值)和Residuals(残差)选项组中的Unstandardized;点击Continue.5.点击右侧Options,默认,点击Continue.6.返回主对话框,单击OK.输出结果分析: 1.引入/剔除变量表该表显示模型最先引入变量城市人口密度 (人/平方公里),第二个引入模型的是变量城市居民人均可支配收入(元),没有变量被剔除。
SPSS多元线性回归结果分析
SPSS多元线性回归结果分析输出下⾯三张表第⼀张R⽅是拟合优度对总回归⽅程进⾏F检验。
显著性是sig。
结果的统计学意义,是结果真实程度(能够代表总体)的⼀种估计⽅法。
专业上,p 值为结果可信程度的⼀个递减指标,p 值越⼤,我们越不能认为样本中变量的关联是总体中各变量关联的可靠指标。
p 值是将观察结果认为有效即具有总体代表性的犯错概率。
如 p=0.05 提⽰样本中变量关联有 5% 的可能是由于偶然性造成的。
即假设总体中任意变量间均⽆关联,我们重复类似实验,会发现约 20 个实验中有⼀个实验,我们所研究的变量关联将等于或强于我们的实验结果。
(这并不是说如变量间存在关联,我们可得到 5% 或 95% 次数的相同结果,当总体中的变量存在关联,重复研究和发现关联的可能性与设计的统计学效⼒有关。
)在许多研究领域,0.05 的 p 值通常被认为是可接受错误的边界⽔平。
F检验:对于多元线性回归模型,在对每个回归系数进⾏显著性检验之前,应该对回归模型的整体做显著性检验。
这就是F检验。
当检验被解释变量y t与⼀组解释变量x1, x2 , ... , x k -1是否存在回归关系时,给出的零假设与备择假设分别是H0:b1 = b2 = ... = b k-1 = 0 ,H1:b i, i = 1, ..., k -1不全为零。
⾸先要构造F统计量。
由(3.36)式知总平⽅和(SST)可分解为回归平⽅和(SSR)与残差平⽅和(SSE)两部分。
与这种分解相对应,相应⾃由度也可以被分解为两部分。
SST具有T - 1个⾃由度。
这是因为在T个变差 ( y t -), t = 1, ..., T,中存在⼀个约束条件,即 = 0。
由于回归函数中含有k个参数,⽽这k个参数受⼀个约束条件制约,所以SSR具有k -1个⾃由度。
因为SSE中含有T个残差,= y t -, t = 1, 2, ..., T,这些残差值被k个参数所约束,所以SSE具有T - k个⾃由度。
spss回归分析报告
SPSS回归分析报告1. 引言本报告旨在使用SPSS软件进行回归分析,并对分析结果进行解释和总结。
回归分析是一种用于探索自变量与因变量之间关系的统计方法。
通过对相关变量的分析,我们可以了解自变量对因变量的影响程度和方向。
2. 数据描述我们使用的数据集包含了X和Y两个变量的观测值。
X代表自变量,Y代表因变量。
数据集总共包含了N个观测值。
3. 数据处理在进行回归分析之前,我们需要对数据进行处理,包括数据清洗和变量转换。
数据清洗的目的是去除异常值和缺失值,确保数据的质量和完整性。
变量转换可以根据需要对变量进行归一化、对数化等操作,以满足回归分析的前提条件。
4. 模型建立我们选择了线性回归模型来研究自变量X对因变量Y的影响。
线性回归模型的表达式如下:Y = β0 + β1*X + ε其中,Y代表因变量,X代表自变量,β0和β1是回归系数,ε是误差项。
我们希望通过对数据进行回归分析,得到最佳的回归系数估计值。
5. 回归结果经过回归分析,我们得到了以下结果:回归方程:Y = a + b*X回归系数a的估计值为x,回归系数b的估计值为y。
回归方程可以用来预测因变量Y在给定自变量X的情况下的取值。
6. 模型评估为了评估我们建立的回归模型的拟合程度,我们使用了一些统计指标。
其中,R方(R^2)是衡量模型拟合优度的指标,它的取值范围在0到1之间,越接近1说明模型的拟合度越好。
我们得到的R方为r。
另外,我们还计算了回归系数的显著性检验。
显著性检验可以帮助我们判断回归系数是否具有统计学意义。
我们得到的显著性水平为p。
通过对这些统计指标的分析,我们可以评估回归模型的有效性和可靠性。
7. 结论通过SPSS软件进行回归分析,我们得到了自变量X对因变量Y的影响程度和方向。
根据我们的回归方程和回归系数,我们可以预测因变量Y在给定自变量X 的情况下的取值。
然而,需要注意的是,回归分析只能显示自变量和因变量之间的关系,并不能确定因果关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[]SPSS19.0实战之多元线性回归分析
(2016-08-12 20:31:47)[删除]
▼
标签:
线性回归数据(全国各地区能源消耗量与产量)来源,可点击协会博客数据挖掘栏:国数据服务中心的经济研究数据库。
1.1数据预处理
数据预处理包括的容非常广泛,包括数据清理和描述性数据汇总,数据集成和变换,数据归约,数据离散化等。
本次实习主要涉及的数据预处理只包括数据清理和描述性数据汇总。
一般意义的数据预处理包括缺失值填写和噪声数据的处理。
于此我们只对数据做缺失值填充,但是依然将其统称数据清理。
1.1.1数据导入与定义
单击“打开数据文档”,将xls格式的全国各地区能源消耗量与产量的数据导入SPSS中,如图1-1所示。
图1-1 导入数据
导入过程中,各个字段的值都被转化为字符串型(String),我们需要手动将相应的字段转回数值型。
单击菜单栏的“”-->“”将所选的变量改为数值型。
如图1-2所示:
图1-2 定义变量数据类型
1.1.2数据清理
数据清理包括缺失值的填写和还需要使用SPSS分析工具来检查各个变量的数据完整性。
单击“”-->“”,将检查所输入的数据的缺失值个数以及百分比等。
如图1-3所示:
图1-3缺失值分析能源数据缺失值分析结果如表1-1所示:
表1-1 能源消耗量与产量数据缺失值分析
SPSS提供了填充缺失值的工具,点击菜单栏“”-->“”,即可以使用软件提供的几种填充缺失值工具,包括序列均值,临近点中值,临近点中位数等。
结合本次实习数据的具体情况,我们不使用SPSS软件提供的替换缺失值工具,主要是手动将缺失值用零值来代替。
1.1.3描述性数据汇总
描述性数据汇总技术用来获得数据的典型性质,我们关心数据的中心趋势和离中趋势,根据这些统计值,可以初步得到数据的噪声和离群点。
中心趋势的量度值包括:均值(mean),中位数(median),众数(mode)等。
离中趋势量度包括四分位数(quartiles),方差(variance)等。
SPSS提供了详尽的数据描述工具,单击菜单栏的“”-->“”-->“”,将弹出如图2-4所示的对话框,我们将所有变量都选取到,然后在选项中勾选上所希望描述的数据特征,包括均值,标准差,方差,最大最小值等。
由于本次数据的单位不尽相同,我们需要将数据标准化,同时勾选上“将标准化得分另存为变量”。
图1-4 描述性数据汇总得到如表1-2所示的描述性数据汇总。
表1-2 描述性数据汇总
标准化后得到的数据值,以下的回归分析将使用标准化数据。
如图1-5所示:
图1-5 数据标准化
我们还可以通过描述性分析中的“”来得到各个变量的众数,均值等,还可以根据这些量绘制直方图。
我们选取个别变量(能源消费总量)的直方图,可以看到我们因变量基本符合正态分布。
如图1-6所示:
图1-6能源消费总量
1.2回归分析
我们本次实验主要考察地区能源消费总额(因变量)与煤炭消费量、焦炭消费量、原油消费量、原煤产量、焦炭产量、原油产量之间的关系。
以下的回归分析所涉及只包括以上几个变量,并使用标准化之后的数据。
1.2.1参数设置
1. 单击菜单栏“”-->“”-->“”,将弹出如图1-7所示的对话框,将通过选择因变量和自变量来构建线性回归模型。
因变量:标准化能源消费总额;自变量:标准化煤炭消费量、标准化焦炭消费量、标准化原油消费量、标准化原煤产量、标准化焦炭产量、标准化原油产量。
自变量方法选择:进入,个案标签使用地名,不使用权重最小二乘法回归分析—即WLS权重为空。
图1-7选择线性回归变量还需要设置统计量的参数,我们选择回归系数中的“”和其他项中的“”。
选中估计可输出回归系数B及其标准误,t值和p值,还有标准化的回归系数beta。
选中模型拟合度复选框:模型拟合过程中进入、退出的变量的列表,以及一些有关拟合优度的检验:R,R2和调整的R2, 标准误及方差分析表。
如图1-8所示:
图1-8 设置回归分析统计量
3.在设置绘制选项的时候,我们选择绘制标准化残差图,其中的正态概率图是rankit图。
同时还需要画出残差图,Y轴
选择:ZRESID,X轴选择: ZPRED。
如图1-9所示:
图1-9设置绘制左上框中各项的意义分别为:
·“DEPENDNT”因变量
·“ZPRED”标准化预测值
·“ZRESID”标准化残差
·“DRESID”删除残差
·“ADJPRED”调节预测值
·“SRESID”学生化残差
·“SDRESID”学生化删除残差
4. 许多时候我们需要将回归分析的结果存储起来,然后用得到的残差、预测值等做进一步的分析,“保存”按钮就是用来存储中间结果的。
可以存储的有:预测值系列、残差系列、距离(Distances)系列、预测值可信区间系列、波动统计量系列。
本次实验暂时不保存任何项。
5. 设置回归分析的一些选项,有:步进方法标准单选钮组:设置纳入和排除标准,可按P值或F值来设置。
在等式中包含常量复选框:用于决定是否在模型中包括常数项,默认选中。
如图1-10所示:
图1-10 设置选项
1.2.2结果输出与分析
在以上选项设置完毕之后点击确定,SPSS将输出一系列的回归分析结果。
我们来逐一贴出和分析,并根据它得到最后的回归方程以及验证回归模型。
1. 表1-3所示,是回归分析过程中输入、移去模型记录。
具体方法为:enter(进入)
表1-3 输入的变量
1.表1-4所示是模型汇总,R称为多元相关系数,R方(R2)代表着模型的拟合度。
1.我们可以看到该模型是拟合优度良好。
模型汇总
表1-4 模型汇总
3.表1-5所示是离散分析。
,F的值较大,代表着该回归模型是显著。
也称为失拟性检验。
表1-5 离散分析
4.表1-6所示的是回归方程的系数,根据这些系数我们能够得到完整的多元回归方程。
观测以下的回归值,都是具有统计学意义的。
因而,得到的多元线性回归方程:Y=0.008+1.061x1+0.087 x2+0.157 x3-0.365 x4-0.105 x5-0.017x6
(x1为煤炭消费量,x2为焦炭消费量,x3为原油消费量,x4为原煤产量,x5为原炭产量,x6为原油产量,Y是能源消费总量)
结论:能量消费总量由主要与煤炭消费总量所影响,成正相关;与原煤产量成一定的反比。
表1-6回归方程系数
5.模型的适合性检验,主要是残差分析。
残差图是散点图,如图1-11所示:
图1-11残差图
可以看出各散点随机分布在e=0为中心的横带中,证明了该模型是适合的。
同时我们也发现了两个异常点,就是省和省,这种离群点是值得进一步研究的。
还有一种残差正态概率图(rankit图)可以直观地判断残差是否符合正态分布。
如图1-12所示:
图1-12 rankit(P-P)图
它的直方图如图1-13所示:
图1-13 rankit(直方)图。
