多元线性回归SPSS实验报告
SPSS多元回归实验报告
实验八报告一、数据来源Employee data. sav 二、基本结果（1）确定自变量、因变量：）确定自变量、因变量：一般而言，因变量y与各自变量xj(j=1,2,3,…,n)之间的多元线性回归模型：之间的多元线性回归模型：其中：b0是回归常数；b k (k=1,2,3,…,n)是回归参数；e是随机误差。
是随机误差。
根据employee data.sav的数据，其中Y是当前工资salary，X1是起始资金salbegin，X2是工作经验prevexp，X3是工作时间jobtime，X4是工作种类jobcat，X5是受教育年限edcau。
（2）做出因变量与自变量的散点图：）做出因变量与自变量的散点图：从散点图可以看出因变量与各自变量之间存在线性关系。
（3）检验因变量Y是否服从正态分布的模型假定——因变量Y并没有很好地服从正态分布。
地服从正态分布。
的残差图（4）线性回归Y的残差图此标准化残差图表明，此线性回归的标准化残差呈楔形分布而非带状分布，不满足回归模型同方差的假定。
布，不满足回归模型同方差的假定。
当前薪金多元线性回归分析的残差图图当前薪金多元线性回归分析的残差图（5）通过以上检验可以看出，当前薪金并不是好的变量，对当前薪金进行Ln变换（取对数）生成新的随进变量logsale，将logsale作为因变量Y用逐步回归的方法进行回归分析：的方法进行回归分析：1）p-p图：图：较好的服从了正态分布。
发现取对数后，logY较好的服从了正态分布。
2）logY的标准化残差图：的标准化残差图：上图表明因变量Y（logsale）的标准化残差近似呈带状分布，满足模型同方差的假定。
差的假定。
3）逐步回归的判定系数：）逐步回归的判定系数：通过逐步回归，得到方程的判定系数如下表。
R²越接近1，说明回归方程解释了因变量总变异量的绝大部分比例。
本估计的回归方程有一个好的拟合，，可以认为拟合度高。
在模型5中达到0.810，且调整后的R²达到0.808，可以认为拟合度高。
多元线性回归SPSS实验报告
最终保留的回归方程的变量有:教职工总数与发表论文数 回归方程的DW检验值=1、971,表现残差序列存在正相关。说明该回归方程 没有充分说明被解释变量的变化规律,可能方程中遗漏了一些重要的解释变量
估计的标准误差=9、774。 模型二中偏F检验的概率P值=0、749,对于显著性水平0、05,接受原假设(剔除 变量的偏回归系数与0无显著性差异),认为:剔除的变量在校大学生人数的偏回归 系数与0无显著性差异。该变量对被解释变量的线性解释没有显著性贡献,不应保 留在回归方程中。 模型三中偏F检验的概率P值=0、526,对于显著性水平0、05,接受原假设(剔除 变量的偏回归系数与0无显著性差异),认为:剔除的变量普通高校数的偏回归系数 与0无显著性差异。该变量对被解释变量的线性解释没有显著性贡献,不应保留在
1
、999a 、998 、997
9、822
多元线性回归 SPSS 实验报告
输入／移去的变量
移去的变
模型 输入的变量 量
方法
1 教职工总数 (万人), 专 利申请授权 数(件), 研 究与试验发 展机构数 (个), 普通 高校数 (所), 发表 科技论文数 量(篇), 在 校学生数 (万人)a
、 输入
多元线性回归 SPSS 实验报告
注解:引入/剔除变量表 分别剔除在校学生数(万人),普通高校数(所),研究与试验发展机构数(个),专利申 请授权数(件)四个变量
模型汇总f
更改统计量
【精品】SPSS统计实验报告多元线性回归分析
【精品】SPSS统计实验报告多元线性回归分析
本文旨在通过多元线性回归分析，深入研究X、Y、Z三个变量之间的关系，以探究这三个变量对结果的影响。
本实验中样本数量为100人，本文采用SPSS22.0计算软件进行多元线性回归分析，统计计算结果如下：
（一）检验变量X、Y、Z三个变量是否有关：
Sig.=.633。
结果显示，该值大于0.05，表明X、Y、Z三者之间没有显著统计关系；
（二）确定拟合模型：
以X、Y、Z三个变量回归拟合，得出模型为：y=1.746+0.660X+0.783Y+0.430Z。
（三）检验回归模型的有效性：
1. 回归系数的统计量检验
模型的R方为.668，该值表明，X、Y、Z三个自变量可以解释本回归模型的67.0%的变化量；
2.F检验
结果显示，f分数为20.670，Sig.=.000，结果显示，f分数小于阈值0.05，因此可以接受回归模型；
检验结果显示，当其他X、Y、Z三个自变量的条件不变的情况下，X、Y、Z三个自变量对Y的影响是有显著性的。
综上所述，本文使用SPSS22.0计算软件进行多元线性回归分析，探究X、Y、Z三个变量之间的关系。
结果显示，X、Y、Z三者之间没有显著统计关系；拟合模型为：
y=1.746+0.660X+0.783Y+0.430Z；最后，证实X、Y、Z三个自变量对Y的影响是有显著性的。
SPSS实验多元线性回归分析12
这里我们以总成绩作为因变量Y，平时成绩和期中成绩分别作为自变量X1，X2，建立的多元回归模型为：
Байду номын сангаас2，估计参数，建立回归预测模型
利用SPSS可得一下结果：
Variables Entered/Removedb
Model
Variables Entered
Variables Removed
1183.800
19
a. Predictors: (Constant),期中成绩,平时成绩
b. Dependent Variable:总成绩
注释：从表中可得拟合方程的F统计量值为7.586，相应的P值为0.000说明，拟合方程是显著的。是具有统计意义的。
Coefficientsa
Model
Unstandardized Coefficients
Method
1
期中成绩,平时成绩a
.
Enter
a. All requested variables entered.
b. Dependent Variable:总成绩
注释：根据这个表的结果我们可以初步的知道，经过检验自变量X1，X2是可以加入到准备估计的回归方程中作为变量的。
Model Summaryb
Standardized Coefficients
t
Sig.
95% Confidence Interval for B
Correlations
Collinearity Statistics
B
Std. Error
Beta
Lower Bound
Upper Bound
Zero-order
SPSS—回归—多元线性回归结果分析(二)
SPSS—回归—多元线性回归结果分析（二）2011-10-27 14:44，最近一直很忙，公司的潮起潮落，就好比人生的跌岩起伏，眼看着一步步走向衰弱，却无能为力，也许要学习“步步惊心”里面“四阿哥”的座右铭：“行到水穷处”，”坐看云起时“。
接着上一期的“多元线性回归解析”里面的内容，上一次，没有写结果分析，这次补上，结果分析如下所示：结果分析1：由于开始选择的是“逐步”法，逐步法是“向前”和“向后”的结合体，从结果可以看出，最先进入“线性回归模型”的是“price in thousands"建立了模型1，紧随其后的是“Wheelbase"建立了模型2，所以，模型中有此方法有个概率值，当小于等于0.05时，进入“线性回归模型”（最先进入模型的，相关性最强，关系最为密切）当大于等 0.1时，从“线性模型中”剔除结果分析：1：从“模型汇总”中可以看出，有两个模型，（模型1和模型2）从R2 拟合优度来看，模型2的拟合优度明显比模型1要好一些（0.422>0.300）2：从“Anova"表中，可以看出“模型2”中的“回归平方和”为115.311，“残差平方和”为153.072，由于总平方和= 回归平方和+残差平方和，由于残差平方和(即指随即误差，不可解释的误差）由于“回归平方和”跟“残差平方和”几乎接近，所有，此线性回归模型只解释了总平方和的一半，3：根据后面的“F统计量”的概率值为0.00，由于0.00<0.01，随着“自变量”的引入，其显著性概率值均远小于 0.01，所以可以显著地拒绝总体回归系数为0的原假设，通过ANOVA方差分析表可以看出“销售量”与“价格”和“轴距”之间存在着线性关系，至于线性关系的强弱，需要进一步进行分析。
结果分析：1：从“已排除的变量”表中，可以看出：“模型2”中各变量的T检的概率值都大于“0.05”所以，不能够引入“线性回归模型”必须剔除。
运用SPSS建立多元线性回归模型并进行检验副本
运用S P S S建立多元线性回归模型并进行检验副本集团标准化工作小组 #Q8QGGQT-GX8G08Q8-GNQGJ8-MHHGN#计量经济学实验报告一.实验目的：1、学习和掌握用SPSS做变量间的相关系数矩阵；2、掌握运用SPSS做多元线性回归的估计；3、用残差分析检验是否存在异常值和强影响值4、看懂SPSS估计的多元线性回归方程结果；5、掌握逐步回归操作；6、掌握如何估计标准化回归方程7、根据输出结果书写方程、进行模型检验、解释系数意义和预测；二．实验步骤：1、根据所研究的问题提出因变量和自变量，搜集数据。
2、绘制散点图和样本相关阵，观察自变量和因变量间的大致关系。
3、如果为线性关系，则建立多元线性回归方程并估计方程。
4、运用残差分析检验是否存在异常值点和强影响值点。
5、通过t检验进行逐步回归。
6、根据spss输出结果写出方程，对方程进行检验（拟合优度检验、F检验和t检验）。
7、输出标准化回归结果，写出标准化回归方程。
8、如果通过检验，解释方程并应用（预测）。
三.实验要求：研究货运总量y与工业总产值x1,农业总产值x2，居民非商品支出x3,之间的关系。
详细数据见表：（1）计算出y,x1,x2,x3的相关系数矩阵。
（2）求y关于x1,x2,x3的三元线性回归方程（3）做残差分析看是否存在异常值。
（4）对所求方程拟合优度检验。
（5）对回归方程进行显着性检验。
（6）对每一个回归系数做显着性检验。
（7）如果有的回归系数没有通过显着性检验，将其剔除，重新建立回归方程，在做方程的显着性检验和回归系数的显着性检验。
（8）求标准化回归方程。
（9）求当x1=75,x2=42,x3=时y。
并给出置性水平为99%的近似预测区间。
（10）结合回归方程对问题进行一些基本分析。
四.绘制散点图或样本相关阵相关性货运总量工业总产值农业总产值居民非商品支出货运总量Pearson 相关性 1 .556 .731*.724*显着性（双侧）.095 .016 .018 N 10 10 10 10工业总产值Pearson 相关性.556 1 .155 .444 显着性（双侧）.095 .650 .171 N 10 11 11 11农业总产值Pearson 相关性.731*.155 1 .562 显着性（双侧）.016 .650 .072 N 10 11 11 11居民非商品支出Pearson 相关性.724*.444 .562 1 显着性（双侧）.018 .171 .072N 10 11 11 11*. 在水平（双侧）上显着相关。
运用SPSS建立多元线性回归模型并进行检验---副本[1]
![运用SPSS建立多元线性回归模型并进行检验---副本[1]](https://img.taocdn.com/s3/m/919a8eb504a1b0717fd5ddc7.png)
计量经济学实验报告一.实验目的：1、学习和掌握用SPSS做变量间的相关系数矩阵；2、掌握运用SPSS做多元线性回归的估计；3、用残差分析检验是否存在异常值和强影响值4、看懂SPSS估计的多元线性回归方程结果；5、掌握逐步回归操作；6、掌握如何估计标准化回归方程7、根据输出结果书写方程、进行模型检验、解释系数意义和预测；二．实验步骤：1、根据所研究的问题提出因变量和自变量，搜集数据。
2、绘制散点图和样本相关阵，观察自变量和因变量间的大致关系。
3、如果为线性关系，则建立多元线性回归方程并估计方程。
4、运用残差分析检验是否存在异常值点和强影响值点。
5、通过t检验进行逐步回归。
6、根据spss输出结果写出方程，对方程进行检验（拟合优度检验、F检验和t检验）。
7、输出标准化回归结果，写出标准化回归方程。
8、如果通过检验，解释方程并应用（预测）。
三.实验要求：研究货运总量y与工业总产值x1,农业总产值x2，居民非商品支出x3,之间的关系。
详细数据见表：（1）计算出y,x1,x2,x3的相关系数矩阵。
（2）求y关于x1,x2,x3的三元线性回归方程（3）做残差分析看是否存在异常值。
（4）对所求方程拟合优度检验。
（5）对回归方程进行显著性检验。
（6）对每一个回归系数做显著性检验。
（7）如果有的回归系数没有通过显著性检验，将其剔除，重新建立回归方程，在做方程的显著性检验和回归系数的显著性检验。
（8）求标准化回归方程。
（9）求当x1=75,x2=42,x3=3.1时y。
并给出置性水平为99%的近似预测区间。
（10）结合回归方程对问题进行一些基本分析。
四.绘制散点图或样本相关阵相关性货运总量工业总产值农业总产值 居民非商品支出货运总量Pearson 相关性1.556 .731*.724*显著性（双侧）.095.016 .018 N10 10 10 10 工业总产值Pearson 相关性.556 1.155 .444 显著性（双侧） .095 .650.171 N10 11 11 11 农业总产值Pearson 相关性.731*.155 1.562 显著性（双侧） .016 .650 .072N10 11 11 11 居民非商品支出 Pearson 相关性.724* .444 .562 1显著性（双侧）.018 .171 .072 N10111111*. 在 0.05 水平（双侧）上显著相关。
SPSS多元线性回归结果分析
SPSS多元线性回归结果分析输出下⾯三张表第⼀张R⽅是拟合优度对总回归⽅程进⾏F检验。
显著性是sig。
结果的统计学意义，是结果真实程度（能够代表总体）的⼀种估计⽅法。
专业上，p 值为结果可信程度的⼀个递减指标，p 值越⼤，我们越不能认为样本中变量的关联是总体中各变量关联的可靠指标。
p 值是将观察结果认为有效即具有总体代表性的犯错概率。
如 p=0.05 提⽰样本中变量关联有 5% 的可能是由于偶然性造成的。
即假设总体中任意变量间均⽆关联，我们重复类似实验，会发现约 20 个实验中有⼀个实验，我们所研究的变量关联将等于或强于我们的实验结果。
（这并不是说如变量间存在关联，我们可得到 5% 或 95% 次数的相同结果，当总体中的变量存在关联，重复研究和发现关联的可能性与设计的统计学效⼒有关。
）在许多研究领域，0.05 的 p 值通常被认为是可接受错误的边界⽔平。
F检验：对于多元线性回归模型，在对每个回归系数进⾏显著性检验之前，应该对回归模型的整体做显著性检验。
这就是F检验。
当检验被解释变量y t与⼀组解释变量x1, x2 , ... , x k -1是否存在回归关系时，给出的零假设与备择假设分别是H0：b1 = b2 = ... = b k-1 = 0 ,H1：b i, i = 1, ..., k -1不全为零。
⾸先要构造F统计量。
由（3.36）式知总平⽅和（SST）可分解为回归平⽅和（SSR）与残差平⽅和（SSE）两部分。
与这种分解相对应，相应⾃由度也可以被分解为两部分。
SST具有T - 1个⾃由度。
这是因为在T个变差 ( y t -), t = 1, ..., T，中存在⼀个约束条件，即 = 0。
由于回归函数中含有k个参数，⽽这k个参数受⼀个约束条件制约，所以SSR具有k -1个⾃由度。
因为SSE中含有T个残差，= y t -, t = 1, 2, ..., T，这些残差值被k个参数所约束，所以SSE具有T - k个⾃由度。
spss多元线性回归分析92134
SPSS多元线性回归分析试验在科学研究中，我们会发现某些指标通常受到多个因素的影响，如血压值除了受年龄影响之外，还受到性别、体重、饮食习惯、吸烟情况等因素的影响，用方程定量描述一个因变量y与多个自变量x1、x2、x3.......之间的线性依存关系，称为多元线性回归。
有学者认为血清中低密度脂蛋白增高是引起动脉硬化的一个重要原因。
现测量30名怀疑患有动脉硬化的就诊患者的载脂蛋白A、载脂蛋白B、载脂蛋白E、载脂蛋白Ｃ、低密度脂蛋白中的胆固醇含量。
资料如下表所示。
求低密度脂蛋白中的胆固醇含量对载脂蛋白Ａ、载脂蛋白Ｂ、载脂蛋白Ｅ、载脂蛋白Ｃ的线性回归方程。
表1 30名就诊患者资料表221101499.524.7184 2316086 5.310.8118 241121238.016.6127 251471108.518.4137 26204122 6.121.0126 27131102 6.613.4130 281701278.424.7135 291731238.719.0188 3013213113.829.2122spss数据处理步骤：（１）打开spss输入数据后，点击“分析”－“回归”－“线性”。
然后将“低密度脂蛋白”选入因变量框，将“载脂蛋白Ａ”“载脂蛋白Ｂ”“载脂蛋白Ｅ”“载脂蛋白C”依次选入自变量框。
方法选为“逐步”。
（2）单击“统计量”选项，原有选项基础上选择“R方变化”。
在残差中选“Durbin-Watson”，单击“继续”。
（3）单击“绘制”，将“DEPENDNT”选入“X2”中，将“*SRESID”选入“Y”中，在标准残差图选项中选择“直方图”和“正态概率图”。
单击“继续”。
（4）单击“选项”，在原有选项的基础上单击“继续”，最后单击“确定”，就完成了。
数据处理结果如下：输入／移去的变量a模型输入的变量移去的变量方法1载脂蛋白B.步进（准则: F-to-enter 的概率<= .050，F-to-remove 的概率>= .100）。
运用SPSS建立多元线性回归模型并进行检验
计量经济学实验报告一.实验目的：1、学习和掌握用SPSS做变量间的相关系数矩阵；2、掌握运用SPSS做多元线性回归的估计；3、用残差分析检验是否存在异常值和强影响值4、看懂SPSS估计的多元线性回归方程结果；5、掌握逐步回归操作；6、掌握如何估计标准化回归方程7、根据输出结果书写方程、进行模型检验、解释系数意义和预测；二．实验步骤：1、根据所研究的问题提出因变量和自变量，搜集数据。
2、绘制散点图和样本相关阵，观察自变量和因变量间的大致关系。
3、如果为线性关系，则建立多元线性回归方程并估计方程。
4、运用残差分析检验是否存在异常值点和强影响值点。
5、通过t检验进行逐步回归。
6、根据spss输出结果写出方程，对方程进行检验（拟合优度检验、F检验和t检验）。
7、输出标准化回归结果，写出标准化回归方程。
8、如果通过检验，解释方程并应用（预测）。
三.实验要求：研究货运总量y与工业总产值x1,农业总产值x2，居民非商品支出x3,之间的关系。
详细数据见表：（1）计算出y,x1,x2,x3的相关系数矩阵。
（2）求y关于x1,x2,x3的三元线性回归方程（3）做残差分析看是否存在异常值。
（4）对所求方程拟合优度检验。
（5）对回归方程进行显著性检验。
（6）对每一个回归系数做显著性检验。
（7）如果有的回归系数没有通过显著性检验，将其剔除，重新建立回归方程，在做方程的显著性检验和回归系数的显著性检验。
（8）求标准化回归方程。
（9）求当x1=75,x2=42,x3=3.1时y。
并给出置性水平为99%的近似预测区间。
（10）结合回归方程对问题进行一些基本分析。
四.绘制散点图或样本相关阵相关性货运总量工业总产值农业总产值 居民非商品支出货运总量Pearson 相关性1.556 .731*.724*显著性（双侧）.095.016 .018 N10 10 10 10 工业总产值Pearson 相关性.556 1.155 .444 显著性（双侧） .095 .650.171 N10 11 11 11 农业总产值Pearson 相关性.731*.155 1.562 显著性（双侧） .016 .650 .072N10 11 11 11 居民非商品支出 Pearson 相关性.724* .444 .562 1显著性（双侧）.018 .171 .072 N10111111*. 在 0.05 水平（双侧）上显著相关。
spss多元回归分析报告案例
企业管理对居民消费率影响因素的探究---以湖北省为例改革开放以来,我国经济始终保持着高速增长的趋势,三十多年间综合国力得到显著增强,但我国居民消费率一直偏低,甚至一直有下降的趋势。
居民消费率的偏低必然会导致我国内需的不足,进而会影响我国经济的长期健康发展。
本模型以湖北省1995年-2010年数据为例，探究各因素对居民消费率的影响及多元关系。
（注：计算我国居民的消费率,用居民的人均消费除以人均GDP,得到居民的消费率）。
通常来说，影响居民消费率的因素是多方面的，如:居民总收入，人均GDP，人口结构状况1（儿童抚养系数，老年抚养系数），居民消费价格指数增长率等因素。
（注：数据来自《湖北省统计年鉴》）总消费(C:亿元) 总GDP（亿元）消费率(%)1995 1095.97 2109.38 51.96 1997 1438.12 2856.47 50.35 2000 1594.08 3545.39 44.96 2001 1767.38 3880.53 45.54 2002 1951.54 4212.82 46.32 2003 2188.05 4757.45 45.99 2004 2452.62 5633.24 43.54 2005 2785.42 6590.19 42.27 2006 3124.37 7617.47 41.02 2007 3709.69 9333.4 39.75 2008 4225.38 11328.92 37.30 2009 4456.31 12961.1 34.38 2010 5136.78 15806.09 32.50一、计量经济模型分析(一)、数据搜集根据以上分析，本模型在影响居民消费率因素中引入6个解释变量。
X1:居民1.人口年龄结构一种比较精准的描述是：儿童抚养系数(0-14岁人口与 15-64岁人口的比值)、老年抚养系数(65岁及以上人口与15-64岁人口的比值〉或总抚养系数(儿童和老年抚养系数之和)。
SPSS多元线性回归分析报告实例操作步骤
SPSS多元线性回归分析报告实例操作步骤步骤1：导入数据首先，打开SPSS软件，并导入准备进行多元线性回归分析的数据集。
在菜单栏中选择"File"，然后选择"Open"，在弹出的窗口中选择数据集的位置并点击"Open"按钮。
步骤2：选择变量在SPSS的数据视图中，选择需要用于分析的相关自变量和因变量。
选中的变量将会显示在变量视图中。
确保选择的变量是数值型的，因为多元线性回归只适用于数值型变量。
步骤3：进行多元线性回归分析在菜单栏中选择"Analyze"，然后选择"Regression"，再选择"Linear"。
这将打开多元线性回归的对话框。
将因变量移动到"Dependent"框中，将自变量移动到"Independent(s)"框中，并点击"OK"按钮。
步骤4：检查多元线性回归的假设在多元线性回归的结果中，需要检查多元线性回归的基本假设。
这些假设包括线性关系、多重共线性、正态分布、独立性和等方差性。
可以通过多元线性回归的结果来进行检查。
步骤5：解读多元线性回归结果多元线性回归的结果会显示在输出窗口的回归系数表中。
可以检查各个自变量的回归系数、标准误差、显著性水平和置信区间。
同时，还可以检查回归模型的显著性和解释力。
步骤6：完成多元线性回归分析报告根据多元线性回归的结果，可以编写一份完整的多元线性回归分析报告。
报告应包括简要介绍、研究问题、分析方法、回归模型的假设、回归结果的解释以及进一步分析的建议等。
下面是一个多元线性回归分析报告的示例：标题：多元线性回归分析报告介绍：本报告基于一份数据集，旨在探究x1、x2和x3对y的影响。
通过多元线性回归分析，我们可以确定各个自变量对因变量的贡献程度，并检验模型的显著性和准确性。
研究问题：本研究旨在探究x1、x2和x3对y的影响。
SPSS统计实验报告多元线性回归分析
研究期末成绩受哪些因素影响？其影响程度的情况?班级半期成绩 期末成绩 每周学习时间 入学等级 教师等级1 85 87 42 2 1 1 98 96 45 1 1 1 74 80 35 2 1 1 87 90 40 2 1 1 86 88 38 1 2 1 75 70 353 2 1 65 67 28 3 2 1 78 72 30 2 2 1 64 70 30 3 2 1 82 75 34 1 2 1 89 86 38 1 2 2 73 77 38 2 3 2 72 68 32 2 3 2 60 65 20 3 3 2 66 61 30 3 3 2 89 93 39 2 1 2 88 88 43 1 1 2 82 80 41 1 3 2 80 85 39 2 3 2 83 85 45 2 3 2 77 80 40 3 3 297 96 50 1 1初步设定回归方程：0123y p i t ββββε=++++Descriptive StatisticsMean Std. DeviationN期末成绩 79.95 10.330 22 班级 1.50 .512 22 每周学习时间 36.91 6.768 22 半期成绩 79.55 10.294 22 入学等级 1.95 .785 22 教师等级2.05.84422表中为各因素的均值，标准差，和样本量。
表中为各因素的相关系数和P值，从表中可看出班级的相关性最低Variables Entered/Removed bModel VariablesEnteredVariablesRemoved Method1 教师等级, 入学等级, 班级, 每周学习时间, 半期成绩a . Enter采用向后剔除法，即每次剔除一个最不符合进入模型判断依据的变量，直到回归方程中不再含有不符合判断依据的自变量为止。
a. Predictors: (Constant), 教师等级, 入学等级, 班级,每周学习时间, 半期成绩b. Predictors: (Constant), 教师等级, 班级, 每周学习时间, 半期成绩c. Predictors: (Constant), 教师等级, 每周学习时间, 半期成绩d. Predictors: (Constant), 每周学习时间,半期成绩e. Predictors: (Constant), 半期成绩f. Dependent Variable: 期末成绩首先剔除了入学等级，然后剔除了班级，再次剔除了教师等级，再后剔除了每周学习时间，最后剔除半期成绩，剩下了期末成绩，从剔除顺序可知各因素对期末成绩的影响程度，入学等级最低，半期成绩最高。
spss多元回归分析实验报告
spss多元回归分析实验报告
本实验旨在探究以不同特征预测车辆燃油效率的SPSS多元回归分析。
为此，随机抽取了训练集和测试集数据集，其中训练集包括2000条记录，测试集包括301条记录。
该数据集中包括独立变量，包括：车辆排量（单位：升），车辆总重量（单位：公斤），气缸（单位：个），驱动方式（单位：RWD或FWD）和变速箱（单位：自动或手动）。
这些独立变量与响应变量（车辆燃油效率）形成了一个回归模型，并用SPSS分析软件进行多元回归计算。
结果显示，排量、总重量和气缸之间存在显著正相关，而驱动方式与变速箱对燃油效率无显著影响。
回归分析 R2为0.45,表明45%的燃油经济性是由车辆的排量、总重量和气缸决定的。
根据回归方程，可以计算出燃油效率的具体值。
从实验结果来看，回归模型能够有效地预测车辆燃油效率。
实验发现，排量，总重量和气缸对燃油效率影响最大，其中排量对燃油效率影响最大，总重量次之，气缸最小。
在改变车辆排量、总重量和气缸时，都可以影响车辆燃油效率。
虽然实验结果清晰，但也有改进的空间。
首先，研究蒙特卡罗技术可能会更好地提高模型效果。
其次，在实际应用中，还可以研究其他因素如车辆使用时间，路况等，对车辆燃油效率的影响，以及车辆燃油一般的效率等因素，最终优化车辆燃油效率。
总之，SPSS多元回归分析有助于我们更好地了解影响车辆燃油效率的因素，从而实现车辆燃油效率优化。
《应用回归分析 》---多元线性回归分析实验报告
《应用回归分析》---多元线性回归分析实验报告
二、实验步骤：
1、计算出增广的样本相关矩阵
2、给出回归方程
Y=-65.074+2.689*腰围+（-0.078*体重）3、对所得回归方程做拟合优度检验
4、对回归方程做显著性检验
5、对回归系数做显著性检验
三、实验结果分析：
1、计算出增广的样本相关矩阵相关矩阵
2、给出回归方程
回归方程：Y=-65.074+2.689*腰围+（-0.078*体重）
3、对所得回归方程做拟合优度检验
由表可知x与y的决定性系数为r2=0.800,说明模型的你和效果一般，x与y 线性相关系数为R=0.894，说明x与y有较显著的线性关系，当F=33.931，显著性Sig.p=0.000，说明回归方程显著
4、对回归方程做显著性检验
5、对回归系数做显著性检验
Beta的t检验统计量t=-6.254，对应p的值接近0，说明体重和体内脂肪比重对腰围数据有显著影响
6、结合回归方程对该问题做一些基本分析
从上面的分析过程中可以看出腰围和脂肪比重以及腰围和体重的相关性都是很大的，通过检验可以看出回归方程、回归系数也很显著。
其次可以观察到腰围、脂肪比重、体重的数据都是服从正态分布的。
spss多元回归分析的报告怎么做
spss多元回归分析的报告怎么做：怎么做回归报告分析s pss 多元线性回归spss操作spss回归分析结果解释spss多元线性回归结果篇一：SPSS多元线性回归分析实例操作步骤SPSS 统计分析多元线性回归分析方法操作与分析实验目的：引入1998~2008年上海市城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率和房屋空置率作为变量，来研究上海房价的变动因素。
实验变量：以年份、商品房平均售价（元/平方米）、上海市城市人口密度(人/平方公里)、城市居民人均可支配收入(元)、五年以上平均年贷款利率(%)和房屋空置率(%)作为变量。
实验方法：多元线性回归分析法软件：spss19.0操作过程：第一步：导入Excel数据文件1. open data document——open data——open；2. Opening excel data source——OK.第二步：1.在最上面菜单里面选中Analyze——Regression——Linear ，Dependent（因变量）选择商品房平均售价，Independents（自变量）选择城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率、房屋空置率；Method选择Stepwise.进入如下界面：2.点击右侧Statistics，勾选Regression Coefficients（回归系数）选项组中的Estimates；勾选Residuals（残差）选项组中的Durbin-Watson、Casewise diagnostics默认；接着选择Model fit、Collinearity diagnotics；点击Continue.3.点击右侧Plots，选择*ZPRED（标准化预测值）作为纵轴变量，选择DEPENDNT（因变量）作为横轴变量；勾选选项组中的Standardized Residual Plots（标准化残差图）中的Histogram、Normal probability plot；点击Continue.4.点击右侧Save，勾选Predicted Vaniues（预测值）和Residuals （残差）选项组中的Unstandardized；点击Continue.5.点击右侧Options，默认，点击Continue.6.返回主对话框，单击OK.输出结果分析：1.引入/剔除变量表该表显示模型最先引入变量城市人口密度(人/平方公里)，第二个引入模型的是变量(转载于: 写论文网:spss 多元回归分析的报告怎么做)城市居民人均可支配收入(元)，没有变量被剔除。
SPSS多元统计分析实验报告
实 验 课名称：SPSS统计分析
实验项目名称：多元线性回归分析
专 业 名 称：统计学
班 级：
学 号：
学 生 姓 名：
教 师 姓 名：
2014年12月20日
组别同组同学
实验日期2014年12月20日 实验名称多元统计分析
一、实验名称：
多元统计分析
二、实验目的和要求：
通过运用SPSS软件的多元统计分析揭示主管性格与雇员对其整体满意度之间的关系掌握多元统计分析的原理及建模过程。
六、实验结果与分析
通过以上建模和检验过程，最后得到的符合实际且具有统计意义的方程为：Y=0.78X1，即雇员对主管的满意程度只与主管处理雇员的抱怨有关，且成正相关。
七、讨论和回答问题及体会：
1.通过学习，我掌握了多元线性回归的基本原理和步骤，并学会运用SPSS软件进行处理该类问题和比较熟练地分析结果。
设随机变量y与一般变量x1,x2……xk的线性回归模型为：
y=β0+β1*x1+β2*x2+……+βk*xk+ε
其中β0，β1，β2……+βk是k+1个未知参数，β0称为回归常数，β1，β2……+βk称为回归系数，y称为被解释变量；x1,x2……xk称为解释变量。通过最小二乘法估算出各系数，并测定方程的拟合程度、检验回归方程和回归系数的显著性，得到最后的方程。
3运用SPSS软件进行多元分析对模型进行整理，比较调整的R系数、方差分析表、回归分析结果（各系数机器t检验等）、共显性检验等统计方法，得出结果。
四、实验仪器与设备：
SPSS软件、兼容SPSS软件的电脑一台、老师给的数据素材。
五、实验原理：
多元线性回归模型是一元线性回归模型的扩展，其基本原理与一员线性回归模型类似，计算公式如下：
SPSS多元线性回归分析试验
SPSS多元线性回归分析试验在科学研究中，我们会发现某些指标通常受到多个因素的影响，如血压值除了受年龄影响之外，还受到性别、体重、饮食习惯、吸烟情况等因素的影响，用方程定量描述一个因变量y与多个自变量x1、x2、x3.......之间的线性依存关系，称为多元线性回归。
有学者认为血清中低密度脂蛋白增高是引起动脉硬化的一个重要原因。
现测量30名怀疑患有动脉硬化的就诊患者的载脂蛋白A、载脂蛋白B、载脂蛋白E、载脂蛋白Ｃ、低密度脂蛋白中的胆固醇含量。
资料如下表所示。
求低密度脂蛋白中的胆固醇含量对载脂蛋白Ａ、载脂蛋白Ｂ、载脂蛋白Ｅ、载脂蛋白Ｃ的线性回归方程。
spss数据处理步骤：（１）打开spss输入数据后，点击“分析”－“回归”－“线性”。
然后将“低密度脂蛋白”选入因变量框，将“载脂蛋白Ａ”“载脂蛋白Ｂ”“载脂蛋白Ｅ”“载脂蛋白C”依次选入自变量框。
方法选为“逐步”。
（2）单击“统计量”选项，原有选项基础上选择“R方变化”。
在残差中选“Durbin-Watson”，单击“继续”。
（3）单击“绘制”，将“DEPENDNT”选入“X2”中，将“*SRESID”选入“Y”中，在标准残差图选项中选择“直方图”和“正态概率图”。
单击“继续”。
（4）单击“选项”，在原有选项的基础上单击“继续”，最后单击“确定”，就完成了。
数据处理结果如下：输入／移去的变量a模型输入的变量移去的变量方法1 载脂蛋白B . 步进（准则: F-to-enter 的概率 <= .050，F-to-remove 的概率 >= .100）。
2 载脂蛋白C . 步进（准则: F-to-enter 的概率 <= .050，F-to-remove 的概率 >= .100）。
a. 因变量: 低密度脂蛋白率越高，模型与数据的拟合程度越好。
结果显示：自变量和因变量之间的相关系数为0.733，拟合线性回归的确定性系数为0.538，经调整后的确定性系数为0.503。
SPSS多元线性回归分析报告
[]SPSS19.0实战之多元线性回归分析(2016-08-12 20:31:47)[删除]▼标签：线性回归数据（全国各地区能源消耗量与产量）来源，可点击协会博客数据挖掘栏：国数据服务中心的经济研究数据库。
1.1数据预处理数据预处理包括的容非常广泛，包括数据清理和描述性数据汇总，数据集成和变换，数据归约，数据离散化等。
本次实习主要涉及的数据预处理只包括数据清理和描述性数据汇总。
一般意义的数据预处理包括缺失值填写和噪声数据的处理。
于此我们只对数据做缺失值填充，但是依然将其统称数据清理。
1.1.1数据导入与定义单击“打开数据文档”，将xls格式的全国各地区能源消耗量与产量的数据导入SPSS中，如图1-1所示。
图1-1 导入数据导入过程中，各个字段的值都被转化为字符串型（String），我们需要手动将相应的字段转回数值型。
单击菜单栏的“”-->“”将所选的变量改为数值型。
如图1-2所示：图1-2 定义变量数据类型1.1.2数据清理数据清理包括缺失值的填写和还需要使用SPSS分析工具来检查各个变量的数据完整性。
单击“”-->“”，将检查所输入的数据的缺失值个数以及百分比等。
如图1-3所示：图1-3缺失值分析能源数据缺失值分析结果如表1-1所示：表1-1 能源消耗量与产量数据缺失值分析SPSS提供了填充缺失值的工具，点击菜单栏“”-->“”，即可以使用软件提供的几种填充缺失值工具，包括序列均值，临近点中值，临近点中位数等。
结合本次实习数据的具体情况，我们不使用SPSS软件提供的替换缺失值工具，主要是手动将缺失值用零值来代替。
1.1.3描述性数据汇总描述性数据汇总技术用来获得数据的典型性质，我们关心数据的中心趋势和离中趋势，根据这些统计值，可以初步得到数据的噪声和离群点。
中心趋势的量度值包括：均值（mean），中位数（median），众数（mode）等。
离中趋势量度包括四分位数（quartiles），方差（variance）等。
SPSS多元线性回归解析总结报告实例操作步骤
合用标准文档SPSS 统计解析多元线性回归解析方法操作与解析实验目的：引入 1998~2021年上海市城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率和房屋空置率作为变量，来研究上海房价的变动因素。
实验变量：以年份、商品房平均售价〔元 / 平方米〕、上海市城市人口密度 ( 人/平方公里 ) 、城市居民人均可支配收入 ( 元) 、五年以上平均年贷款利率 (%) 和房屋空置率 (%)作为变量。
实验方法：多元线性回归解析法软件：操作过程：第一步：导入 Excel 数据文件1. open data document —— open data —— open；2. Opening excel data source——OK.第二步：1. 在最上面菜单里面选中 Analyze —— Regression —— Linear ，Dependent 〔因变量〕选择商品房平均售价， Independents 〔自变量〕选择城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率、房屋空置率； Method 选择 Stepwise.进入以下界面：2. 点击右侧 Statistics ，勾选 Regression Coefficients 〔回归系数〕选项组中的Estimates ；勾选 Residuals 〔残差〕选项组中的 Durbin-Watson 、Casewise diagnostics 默认；接着选择 Model fit 、Collinearitydiagnotics ；点击 Continue.3.点击右侧 Plots ，选择 *ZPRED〔标准化展望值〕作为纵轴变量，选择DEPENDNT〔因变量〕作为横轴变量；勾选选项组中的 Standardized Residual Plots 〔标准化残差图〕中的Histogram 、Normal probability plot；点击 Continue.4.点击右侧 Save，勾选 Predicted Vaniues 〔展望值〕和 Residuals 〔残差〕选项组中的 Unstandardized ；点击 Continue.5. 点击右侧 Options ，默认，点击 Continue.6.返回主对话框，单击 OK.输出结果解析：1.引入 / 剔除变量表Variables Entered/Removed aModel Variables Entered Variables Removed Method1城市人口密度 ( 人/ 平方公.Stepwise (Criteria:里 )Probability-of-F-to-enter<= .050,Probability-of-F-to-remove>= .100).2城市居民人均可支配收入( 元).Stepwise (Criteria:Probability-of-F-to-enter<= .050,Probability-of-F-to-remove>= .100).a. Dependent Variable:商品房平均售价〔元/ 平方米〕该表显示模型最先引入变量城市人口密度 ( 人/ 平方公里 ) ，第二个引入模型的是变量城市居民人均可支配收入 ( 元) ，没有变量被剔除。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
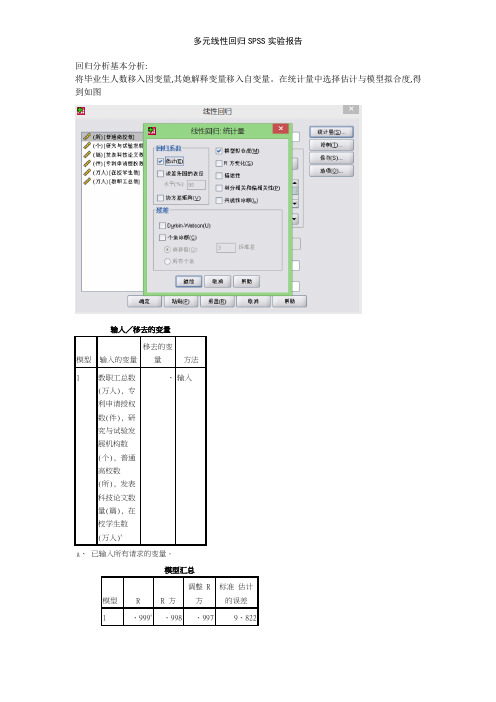
回归分析基本分析：
将毕业生人数移入因变量，其他解释变量移入自变量。
在统计量中选择估计和模型拟合度，得到如图
注解：模型的拟合优度检验：
第二列：两变量（被解释变量和解释变量）的复相关系数R=0.999。
第三列：被解释向量（毕业人数）和解释向量的判定系数R2=0.998。
第四列：被解释向量（毕业人数）和解释向量的调整判定系数R2=0.971。
在多个解释变量的时候，需要参考调整的判定系数，越接近１，说明回归方程对样本数据的拟合优度越高，被解释向量可以被模型解释的部分越多。
第五列：回归方程的估计标准误差＝9.822
回归方程的显著性检验-回归分析的方差分析表
F检验统计量的值=776.216，对应的概率p值=0.000，小于显著性水平0.05，应拒绝回归方程显著性检验原假设（回归系数与0不存在显著性差异），认为：回归系数不为0，被解释变量(毕业生人数)和解释变量的线性关系显著，可以建立线性模型。
注解：回归系数的显著性检验以及回归方程的偏回归系数和常数项的估计值第二列：常数项估计值=-544.366；其余是偏回归系数估计值。
第三列：偏回归系数的标准误差。
第四列：标准化偏回归系数。
第五列：偏回归系数T检验的t统计量。
第六列：t统计量对应的概率p值；小于显著性水平0.05，拒接原假设（回归系数与0不存在显著性差异），认为回归系数部位0，被解释变量与解释变量的线性关系是显著的；大于显著性水平0.05，接受原假设（回归系数与0不存在显著性差异），认为回归系数为0被解释变量与解释变量的线性关系不显著的。
于是，多元线性回归方程为：
ŷ=-544.366+0.032x1+0.009x2+0.001x3-0.1x5+3.046x6
回归分析的进一步分析：
1.多重共线性检验
从容差和方差膨胀因子来看，在校学生数和教职工总数与其他解释变量的多重共线性很严重。
在重新建模中可以考虑剔除该变量
注解：第二列：特征根
第三列：条件指数
从条件指数看，第3、4、5、6、7个条件指数都大于10，说明变量之间存在多重共线性。
第4-10列：各特征根解释各解释变量的方差比。
从方差比看，第5个特征根解释投入普通高校人数96%；发表科技论文数49%；可以认为：这些变量存在多重共线性。
需要建立回归方程。
2.重建回归方程
输入／移去的变量b
注解：引入/剔除变量表
分别剔除在校学生数(万人)，普通高校数(所)，研究与试验发展机构数(个)，专利申请授权数(件)四个变量
注解：利用向后筛选策略建立回归模型，经过四步完成回归方程的建立，最终模型为第五个模型，依次剔除的变量是在校学生数(万人)，普通高校数(所)，研究与试验发展机构数(个)，专利申请授权数(件)
模型五的负相关系数R=0.999。
判别系数R2=0.998.
调整判别系数R2=0.997，若将作用不显著的变量引入方程，则该系数会减少。
估计的标准误差=9.774。
模型二中偏F检验的概率P值=0.749，对于显著性水平0.05，接受原假设（剔除变量的偏回归系数与0无显著性差异），认为：剔除的变量在校大学生人数的偏回归系数与0无显著性差异。
该变量对被解释变量的线性解释没有显著性贡献，不应保留在回归方程中。
模型三中偏F检验的概率P值=0.526，对于显著性水平0.05，接受原假设（剔除变量的偏回归系数与0无显著性差异），认为：剔除的变量普通高校数的偏回归系数与0无显著性差异。
该变量对被解释变量的线性解释没有显著性贡献，不应保留在回归方程中。
模型四中偏F检验的概率P值=0.135，对于显著性水平0.05，接受原假设（剔除变量的偏回归系数与0无显著性差异），认为：剔除的变量研究与试验发展机构数(个)的偏回归系数与0无显著性差异。
该变量对被解释变量的线性解释没有显著性贡献，不应保留在回归方程中。
模型五中偏F检验的概率P值=0.304，对于显著性水平0.05，接受原假设（剔除变量的偏回归系数与0无显著性差异），认为：剔除的变量专利申请授权数(件)的偏回归系数与0无显著性差异。
该变量对被解释变量的线性解释没有显著性贡献，不应保留在回归方程中。
最终保留的回归方程的变量有：教职工总数和发表论文数
回归方程的DW检验值=1.971，表现残差序列存在正相关。
说明该回归方程没有充分说明被解释变量的变化规律，可能方程中遗漏了一些重要的解释变量。