2012启航数学三测试
2012年考研数学三真题与答案解析

2012年全国硕士研究生入学统一考试数学三试题一、选择题:1-8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项符合题目要求的,请将所选项前的字母填在答题纸...指定位置上. (1)曲线221x x y x +=-渐近线的条数为( )(A) 0 (B) 1 (C) 2 (D) 3(2)设函数2()(1)(2)()x x nx f x e e e n =--- ,其中n 为正整数,则'(0)f =( ) (A)1(1)(1)!n n --- (B)(1)(1)!n n -- (C)1(1)!n n -- (D)(1)!n n -(3)设函数()ft 连续,则二次积分22202cos d ()d f r r r πθθ=⎰⎰( )(A)2220d ()d x x y y +⎰ (B)2220d ()d x f x y y +⎰(C)222d ()d y x y x +⎰(D)22201d ()d y f x y x +⎰(4)已知级数11(1)n n α∞=-∑绝对收敛,级数21(1)n a n n∞-=-∑条件收敛,则( )(A)102a <≤(B)112a <≤ (C)312a <≤ (D)322a << (5)设1100C α⎛⎫ ⎪= ⎪ ⎪⎝⎭,2201C α⎛⎫ ⎪= ⎪ ⎪⎝⎭ ,3311C α⎛⎫ ⎪=- ⎪ ⎪⎝⎭ ,4411C α-⎛⎫ ⎪= ⎪ ⎪⎝⎭,其中1234,,,C C C C 为任意常数,则下列向量组线性相关的为( )(A)123,,ααα (B)124,,ααα (C)134,,ααα (D)234,,ααα(6) 设A 为3阶矩阵,P 为3阶可逆矩阵,且1100010002p AP -⎛⎫⎪= ⎪ ⎪⎝⎭.若P=(123,,ααα),1223(,,)ααααα=+,则1Q AQ -=( )(A)100020001⎛⎫ ⎪ ⎪ ⎪⎝⎭ (B)100010002⎛⎫ ⎪ ⎪ ⎪⎝⎭ (C)200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭ (D)200020001⎛⎫⎪ ⎪ ⎪⎝⎭(7)设随机变量X 与Y 相互独立,且都服从区间(0.1)上的均匀分布,则{}221P X Y +≤=( )(A)14 (B)12 (C)8π (D)4π (8)设1234,,,X X X X 为来自总体2(1,)N σ(σ>0)的简单随机样本,则统计量1234|2|X X X X -+-的分布为( )(A)N (0,1) (B)t(1) (C)2(1)χ (D)F(1,1)二、填空题:9-14小题,每小题4分,共24分.请将答案写在答题纸...指定位置上. (9)()1cos sin 4lim tan x xx x π-→=(10)设函数()ln ,121,1x f x x x ⎧≥⎪=⎨-<⎪⎩,()()y f f x =,则x edy dx ==(11)设连续函数(,)z f x y =满足0x y →→=则()0,1d |z =(12)由曲线4y x=和直线y x =及4y x =在第一象限中围成的平面图形的面积为 (13)设A 为3阶矩阵,3A =,*A 为A 的伴随矩阵。
2012年考研(数学三)真题试卷(题后含答案及解析)

2012年考研(数学三)真题试卷(题后含答案及解析) 题型有:1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中,只有一个选项符合题目要求。
1.曲线渐近线的条数为( ).A.0B.1C.2D.3正确答案:C2.设函数f(x)=(ex-1)(e2x-2)…(enx-n),其中n为正整数,则fˊ(0)=( ).A.(-1)n-1(n-1)!B.(-1)n(n-1)!C.(-1)n-1n!D.(-1)nn!正确答案:A3.设函数f(t)连续,则二次积分A. B. C. D. 正确答案:B4.已知级数条件收敛,则α的取值范围为( ).A.0<α≤1/2B.1/2<α≤1C.1<α≤3/2D.3/2<α<2正确答案:D5.设其中c1,c2,c3,c4为任意常数,则下列向量组线性相关的是( ).A.α1,α2,α3B.α1,α2,α4C.α1,α3,α4D.α2,α3,α4正确答案:C6.设A为3阶矩阵,P为3阶可逆矩阵,且若P=(α1,α2,α3),Q=(α1+α2,α2,α3),则Q-1AQ=( ).A. B. C. D. 正确答案:B7.设随机变量X与Y相互独立,且都服从区间(0,1)上的均匀分布,则P {X2+Y2≤1}=( ).A.1/4B.1/2C.π/8D.π/4正确答案:D8.设X1,X2,X3,X4为来自总体N(1,σ2)(σ>0)的简单随机样本,则统计量服从的分布为( ).A.N(0,1)B.t(1)C.x2(1)D.F(1,1)正确答案:B填空题9.正确答案:10.正确答案:11.正确答案:12.由曲线y=4/x和直线y=x及y=4x在第一象限中所围图形的面积为________.正确答案:如右图,阴影部分面积即为所求,由直线z:l将阴影分为两部分,则所求面积13.设A为3阶矩阵,|A|=3,A*为A的伴随矩阵,若交换A的第一行与第二行得到矩阵B,则|BA*|=_________.正确答案:根据题意,设则由题知PA=B,A为3阶矩阵,又|A|=3,所以|A*|=|A|2=9.因此|BA*|=|B||A*|=|PA||A*|=|P||A||A*|=-27.14.设A,B,C是随机事件,A,C互不相容,P(AB)=1/2,P(C)=1/2,则P(AB|C ̄)=________.正确答案:解答题解答应写出文字说明、证明过程或演算步骤。
2012考研数学三真题及答案

2012考研数学三真题及答案2012年考研数学三真题及答案2012年考研数学三真题是考研数学科目中的一道重要题目。
这道题目的出现考察了考生对于数学知识的掌握程度,也是对考生解决实际问题的能力的一种考察。
下面将对2012年考研数学三真题及答案进行详细的分析。
首先,让我们来看一下2012年考研数学三真题的具体内容。
这道题目是一个关于概率论和数理统计的问题。
题目要求考生根据给定的数据,计算出相关的概率和统计量。
通过这道题目,考生需要运用概率论和数理统计的知识,进行数据分析和计算。
接下来,我们来看一下这道题目的答案。
根据题目的要求,考生需要计算出一系列的概率和统计量。
通过对给定的数据进行分析,考生可以得出相应的答案。
在计算过程中,考生需要运用概率论和数理统计的相关公式和方法,进行数据的处理和计算。
在解答这道题目的过程中,考生需要注意以下几点。
首先,要仔细阅读题目,理解题目的要求和条件。
其次,要对给定的数据进行合理的处理和分析,找出相应的规律和关系。
然后,要运用概率论和数理统计的知识,进行计算和推导。
最后,要对计算结果进行合理的解释和说明,确保答案的准确性和可靠性。
通过解答这道题目,考生可以提高对概率论和数理统计的理解和应用能力。
同时,也可以加深对于实际问题的分析和解决能力。
这对于考生在考试中取得好成绩具有重要的意义。
除了解答这道题目,考生还可以通过其他方式来提高对概率论和数理统计的掌握程度。
可以通过阅读相关的教材和参考书籍,深入学习和理解概率论和数理统计的基本概念和方法。
可以通过做一些相关的习题和例题,加强对概率论和数理统计的实践操作能力。
可以参加一些相关的学习班和培训课程,提高对概率论和数理统计的学习效果。
总之,2012年考研数学三真题及答案是考生备考过程中的一道重要题目。
通过解答这道题目,考生可以提高对概率论和数理统计的理解和应用能力。
同时,也可以加深对于实际问题的分析和解决能力。
希望考生能够认真对待这道题目,做好相应的准备工作,取得好成绩。
2012考研数学三真题及答案解析

,
1 0
a 0 0 1
0
(Ⅰ)计算行列式 A ;
(Ⅱ)当实数 a 为何值时,方程组 Ax 有无穷多解,并求其通解.
1 0 1
(21)已知
A
0 1
1 0
1 a
,二次型
f
x1,
x2 ,
x3
xT
AT A x 的秩为 2,
0
a 1
(Ⅰ)求实数 a 的值;
(Ⅱ)求正交变换 x Qy 将 f 化为标准形.
(13)设 A 为 3 阶矩阵, A 3 , A* 为 A 的伴随矩阵。若交换 A 的第 1 行与第 2 行得矩 阵 B ,则 BA*
(14)设 A 、 B 、 C 是随机事件, A 与 C 互不相容, P( AB) 1 , P(C) 1 ,则 P( AB | C)
2
3
三、解答题:15~23 小题,共 94 分.请将解答写在答.题.纸.指定位置上.解答应写出文字说 明、证明过程或演算步骤.
0
2
0
0 0 1
(7)设随机变量 X 与 Y 相互独立,且都服从区间(0.1)上的均匀分布,则
P X 2 Y 2 1 ( )
(A) 1 4
(B) 1 2
(C) 8
(D) 4
(8)设 X1, X 2 , X 3 , X 4 为来自总体 N(1, 2 ) ( 0) 的简单随机样本,则统计量
4
2 2
2
(10)
dy dx
xe
(ln
x 1)
xe
1 e
【分析】本题主要考查复合函数求表达式及复合函数求导数。先利用分析法得到
y f ( f (x)) 的表达式,再求导数,或直接根据分段函数的定义用复合函数求导法求导
2012年考研数学三答案(完整版)
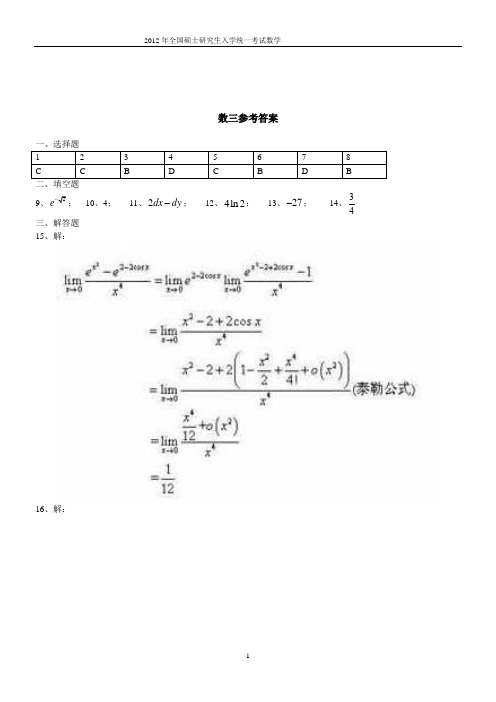
数三参考答案一、选择题二、填空题9、e; 10、4; 11、2dx dy -; 12、4ln 2; 13、27-; 14、34三、解答题 15、解:16、解:17、解:(I )(,)=20+2xx C x y ',对x 积分得:()2(,)204xC x y xD y =++再对y 求导有,()(,)6yC x yD y y ''==+ 再对y 积分有,()262yD y y c =++所以22(,)20642x y C x y x y c =++++,又(0,0)10000C =,所以10000c = 所以22(,)2061000042xyC x y x y =++++(II )x+y=50,把y=50-x 代入22(,)2061000042xyC x y x y =++++23()36115504x C x x =-+令23()361155004x C x x '⎛⎫'=-+= ⎪⎝⎭,得x=24,y=50-24=26, 这时总成本最小C (24,26)=11118万元(III )()24,26(,)32xC x y '=(万元/件) 经济意义:总产量为50件,当甲产品的产量为24时,每增加一件甲产品,则甲产品的成本增加32万元。
18、证明:令()21lncos 112x xf x x x x+=+---,()212lnsin 11x x f x x xxx+'=+----()00f '= ()()()222221411cos 1111xx f x x xxx -+''=++--+--()()222244cos 12011x x x =--≥->--所以()()00f x f ≥=即证得:()21ln cos 11112x xx x x x++≥+-<<-19、解:(I )'''()()2()0f x f x f x +-=对应的特征方程为220r r +-=,r=-2,r=1 所以()212xxf x C e C e -=+把()212xxf x C e C e -=+代入''()()2x f x f x e +=,得到()xf x e =(II )同理,当x<0时,0y ''<可知(0,0)点是曲线唯一的拐点。
2012真题数三全

2012年全国硕士研究生入学统一考试数学三试题一、选择题:1:8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项符合题目要求的,请将所选项前的字母填在答题纸...指定位置上. (1)曲线221x x y x +=-渐近线的条数为 ( )(A) 0 (B) 1 (C) 2 (D) 3 【答案】C【考点】函数图形的渐近线 【难易度】★★【详解】本题涉及到的主要知识点:(i )当曲线上一点M 沿曲线无限远离原点时,如果M 到一条直线的距离无限趋近于零,那么这条直线称为这条曲线的渐近线。
(ii )渐近线分为水平渐近线(lim ()x f x b →∞=,b 为常数)、垂直渐近线(0lim ()x x f x →=∞)和斜渐近线(lim[()()]0x f x ax b →∞-+=,,a b 为常数)。
(iii )注意:如果(1)()limx f x x→∞不存在;(2)()lim x f x a x→∞=,但lim[()]x f x ax →∞-不存在,可断定()f x 不存在斜渐近线。
在本题中,函数221x x y x +=-的间断点只有1x =±.由于1lim x y →=∞,故1x =是垂直渐近线.(而11(1)1lim lim(1)(1)2x x x x y x x →-→-+==+-,故1x =-不是渐近线).又211lim lim111x x x y x→∞→∞+==-,故1y =是水平渐近线.(无斜渐近线) 综上可知,渐近线的条数是2.故选C.(2)设函数2()(1)(2)()x x nx f x e e e n =---L ,其中n 为正整数,则'(0)f = ( ) (A) 1(1)(1)!n n --- (B)(1)(1)!n n -- (C) 1(1)!n n -- (D) (1)!n n -【答案】A【考点】导数的概念 【难易度】★★【详解一】本题涉及到的主要知识点:00000()()()limlimx x f x x f x yf x x x→→+-'==V V V V V V . 在本题中,按定义200()(0)(1)(2)()(0)lim lim 0x x nx x x f x f e e e n f x x →→----'==-L1(1)(2)[(1)](1)(1)!n n n -=-⨯-⨯⨯--=--L .故选A.【详解二】本题涉及到的主要知识点:()[()()]()()()()f x u x v x u x v x u x v x ''''==+.在本题中,用乘积求导公式.含因子1xe -项在0x =为0,故只留下一项.于是20(0)[(2)()]x x nx x f e e e n ='=--L 1(1)(2)[(1)](1)(1)!n n n -=-⨯-⨯⨯--=--L故选(A ).(3)设函数()f t 连续,则二次积分22202cos d ()d f r r r πθθ=⎰⎰( )(A)222d ()d x x y y +⎰ (B) 2220d ()d x f x y y +⎰(C)222d ()d y x y x +⎰ (D) 22201d ()d y f x y x +⎰【答案】B【考点】二重积分的计算 【难易度】★★★【详解】本题涉及到的主要知识点:(,)(cos ,sin )DDf x y d f d d σρθρθρρθ=⎰⎰⎰⎰在本题中,这是把极坐标变换下的累次积分转换为直角坐标系的累次积分.2222202cos d ()d ()DI f r r r f x y dxdy πθθ==+⎰⎰⎰⎰,D 的极坐标表示:02πθ≤≤,2cos 2r θ≤≤,02πθ⇒≤≤,22cos r r θ≤,2r ≤现转换成D 的直角坐标表示,因222x x y ≤+,224x y +≤区域D 由221(1)x y =-+,224x y +=及0x =围成,因此2220d ()d I x f x y y =+⎰.故选(B ).(4)已知级数11(1)n n α∞=-∑绝对收敛,级数21(1)n n n α∞-=-∑条件收敛,则 ( ) (A) 102α<≤(B) 112α<≤ (C) 312α<≤ (D)3 22α<< 【答案】D【考点】p 级数及其收敛性 【难易度】★★★【详解】本题涉及到的主要知识点:p 级数11p n n ∞=∑:当1p >时收敛;当1p ≤时发散.在本题中,由11(1)n n α∞=-∑绝对收敛11121 n n nα∞∞-==⇔=∑收敛⇔112α->即32α>,1211()n n nαα-→∞:又21(1) n n n α∞-=-∑条件收敛,即21(1) n n n α∞-=-∑收敛,211n n α∞-=∑发散021α⇔<-≤,即12α≤< 综上,3 22α<<.故选(D ).(5)设1100c α⎛⎫ ⎪= ⎪ ⎪⎝⎭,2201c α⎛⎫⎪= ⎪ ⎪⎝⎭,3311c α⎛⎫ ⎪=- ⎪ ⎪⎝⎭ ,4411c α-⎛⎫ ⎪= ⎪ ⎪⎝⎭ ,其中1234,,,c c c c 为任意常数,则下列向量组线性相关的为( )(A)123,,ααα (B) 124,,ααα (C)134,,ααα (D)234,,ααα【答案】C【考点】向量组的线性相关与线性无关 【难易度】★★【详解】本题涉及到的主要知识点:n 个n 维向量相关12,,,0n ααα⇔=L在本题中,显然134123011,,0110c c c ααα-=-=, 所以134,,ααα必线性相关.故选(C ).(6) 设A 为3阶矩阵,P 为3阶可逆矩阵,且1100010002P AP -⎛⎫ ⎪= ⎪ ⎪⎝⎭.若123(,,)P ααα=,1223(,,)Q αααα=+,则1Q AQ -= ( )(A) 100020001⎛⎫ ⎪ ⎪ ⎪⎝⎭ (B) 100010002⎛⎫ ⎪ ⎪ ⎪⎝⎭ (C) 200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭ (D)200020001⎛⎫⎪ ⎪ ⎪⎝⎭【答案】B【考点】矩阵的初等变换;初等矩阵 【难易度】★★★【详解】本题涉及到的主要知识点: 设A 是一个m n ⨯矩阵,对A 施行一次初等行变换,相当于在A 的左边乘以相应的m 阶初等矩阵;对A 施行一次初等列变换,相当于在A 的右边乘以相应的n 阶初等矩阵. 在本题中,由于P 经列变换为Q ,有12100110(1)001Q P PE ⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦,那么111112121212[(1)][(1)](1)()(1)Q AQ PE A PE E P AP E ----==100110011101110100120012⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=-=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦故选B.(7)设随机变量X 与Y 相互独立,且都服从区间(0.1)上的均匀分布,则{}221P X Y +≤= ( )(A)14 (B) 12 (C) 8π (D)4π【答案】D【考点】常见二维随机变量的分布 【难易度】★★【详解】本题涉及到的主要知识点:设G 是平面上的有界区域,其面积为A .若二维随机变量(,)X Y 具有概率密度1,(,),(,)0,x y G f x y A ⎧∈⎪=⎨⎪⎩其他则称(,)X Y 在G 上服从均匀分布.方法一:由条件知(,)X Y 在区域{}(,)01,01D x y x y =<<<<上服从二维均匀分布,要计算相应概率只需利用面积之比,易求得{}2214P X Y π+≤=(14圆的面积除以正方形的面积) 故选D.方法二:由条件知(,)X Y 的联合概率密度1,01,01,(,)()()0,X Y x y f x y f x f y <<<<⎧=⋅=⎨⎩其他 从而{}222222111(,)14D x y x y P X Y f x y dxdy dxdy S π+≤+≤+≤====⎰⎰⎰⎰.故选D.(8)设1234,,,X X X X 为来自总体2(1,)N σ(0)σ>的简单随机样本,则统计量1234|2|X X X X -+-的分布为 ( )(A) N (0,1) (B) t(1) (C) 2(1)χ (D)(1,1F ) 【答案】B【考点】2χ分布;t 分布【难易度】★★★★【详解】本题涉及到的主要知识点:设随机变量(0,1)X N :,2()Y n χ:,且X 与Y独立,则随机变量T =所服从的分布称为自由度为n 的t 分布,记为()T t n :.在本题中,因为2(1,)i X N σ:,所以212(0,2)X X N σ-:(0,1)N :, 234(2,2)X X N σ+:(0,1)N :,22342(2)(1)2X X χσ+-:. 又1234,,,X X X X与2342(2)2X X σ+-也相互独立,于是(1)t :,即1234(1)|2|X X t X X -+-:. 故选B.二、填空题:9:14小题,每小题4分,共24分.请将答案写在答题纸...指定位置上. (9)()1cos sin 4lim tan x xx x π-→=【答案】e【考点】两个重要极限 【难易度】★★★【详解】本题涉及到的主要知识点:1lim(1)xx e x→∞+=或10lim(1)x x x e →+=在本题中,用求1∞型极限的方法.由于111(tan 1)cos sin tan 1cos sin (tan )(1tan 1)x x xx x xx x ----=+-,而44tan 11sin cos limlim()cos sin cos cos sin x x x x xx x x x xππ→→--==--因此1cos sin 4lim(tan )x xx I x e π-→== (10)设函数(),121,1x f x x x ⎧≥⎪=⎨-<⎪⎩, ()()y f f x =,则x edy dx ==【答案】1e【考点】复合函数;复合函数求导 【难易度】★★★【详解】不必求出[()]f f x 的表达式.注意1()2f e ==,11()(ln )22x ef e x e =''==,121()(21)22x f x =''=-=于是由复合函数求导法得111[()]()()222x ex edyd f f x f fe dxdx e e ==''===⋅=(11)设连续函数(,)z f x y =满足0x y →→=则()0,1d |z =【答案】2dx dy -【考点】无穷小量的比较;全微分存在的必要条件和充分条件 【难易度】★★★★【详解】本题涉及到的主要知识点: (i )如果lim0βα=,就说β是比α高阶的无穷小,记作()o βα=. (ii )全微分存在的必要条件 如果函数(,)z f x y =在点(,)x y 可微分,则该函数在点(,)x y 的偏导数z x ∂∂、zy∂∂必定存在,且函数(,)z f x y =在点(,)x y 的全微分为z z dz x y x y ∂∂=+∂∂V V .在本题中,由于0x y →→=0011lim[(,)22]0lim (,)1x x y y f x y x y f x y →→→→⇒-+-=⇒=由连续性得(0,1)1f =.已知条件可改写成0x y →→=,由此可知(,)z f x y =在点(0,1)处可微,且()0,1d |2z dx dy =- (12)由曲线4y x=和直线y x =及4y x =在第一象限中围成的平面图形的面积为 【答案】4ln 2【考点】定积分的应用 【难易度】★★★【详解】本题涉及到的主要知识点:设()f x ,()g x 在[,]a b 连续,则由曲线()y f x =,()y g x =及直线x a =,()x b a b =<所围成的区域D 的面积为()()ba S f x g x dx =-⎰,其中曲线()y f x =,()y g x =([,])x ab ∈可以由有限个交点. 在本题中,曲线4y x=与y x =,4y x =分别交于点(2,2),(1,4). 故所围成平面图形的面积为1201431(4)()4ln 224ln 222S x x dx x dx x =-+-=+-+=⎰⎰. (13)设A 为3阶矩阵,3A =,*A 为A 的伴随矩阵。
2012考研数学三真题及答案
2012考研数学三真题及答案2012年考研数学三真题及答案一、选择题1、答案:D解析:根据题目给出的条件可以得到A,C,E,G表示的判断依据。
通过线性规划的图形可以得到B,D,F,H表示的判断依据。
因此选D。
2、答案:B解析:根据题目给出的条件可以得到A,C,G表示的判断依据。
通过线性规划的图形可以得到B,D,E,F,H表示的判断依据。
因此选B。
3、答案:C解析:根据题目给出的条件可以得到A,B,C,H表示的判断依据。
通过线性规划的图形可以得到D,E,F,G表示的判断依据。
因此选C。
4、答案:A解析:根据题目给出的条件可以得到A,B,C,D表示的判断依据。
通过线性规划的图形可以得到E,F,G,H表示的判断依据。
因此选A。
5、答案:D解析:根据题目给出的条件可以得到A,C,E,G表示的判断依据。
通过线性规划的图形可以得到B,D,F,H表示的判断依据。
因此选D。
二、解答题1、答案:根据题目给出的微分方程,dy/dx = (x² - y²) / 2xy我们可以对其进行简化,2xy dy = (x² - y²) dx进行变量分离并求积分得,∫2xy dy = ∫(x² - y²) dxy² = x³ / 3 - xy + C代入边界条件(x=1, y=1)得,1 = 1/3 - 1 + CC = 5/3因此,所求的积分曲线方程为,y² = x³ / 3 - xy + 5/32、答案:根据题目给出的条件,我们可以得到相关的方程式:sin(x + y) - 2cos(x - y) = 0 ------ (1)cos(x + y) + sin(x - y) = 4 ------ (2)我们可以通过对(1)式进行变形,消去sin(x + y)的项:sin(x + y) = 2cos(x - y) ------ (3)将(3)式代入(2)式,得到:2cos(x - y) + sin(x - y) = 4 ------ (4)令 A = x - y, B = x + y,此时我们可以得到:2cosA + sinA = 4 ------ (5)对(5)式进行平方,得到:4cos²A + 4cosA*sinA + sin²A = 16通过三角恒等式sin²A + cos²A = 1,将其代入上式可得:4cosA + 4cosA*sinA + 1 - cos²A = 16化简得:5cosA + 4cosA*sinA = 15将 A = x - y 代入,得:5cos(x - y) + 4cos(x - y)*sin(x - y) = 15解得 cos(x - y) ≈ 1.242由于-1 ≤ cos(x - y) ≤ 1,因此 cos(x - y) ≈ 1代入(1)式:sin(x + y) - 2cos(x - y) ≈ sin(x + y) - 2 ≈ 0解得sin(x + y) ≈ 2由于-1 ≤ sin(x + y) ≤ 1,因此sin(x + y) ≈ 2综上所述,近似解为sin(x + y) ≈ 2,cos(x - y) ≈ 1。
2012数学三真题+答案
2012年全国硕士研究生入学统一考试数学三试题一、选择题:1~8小题,每小题4分,共32分.(1)曲线221x xy x +=-渐近线的条数为( )(A )0 (B )1 (C )2 (D )3 (2)设函数2()(1)(2)()xxnx f x e e e n =---L ,其中n 为正整数,则'(0)f =(A )1(1)(1)!n n --- (B )(1)(1)!n n -- (C )1(1)!n n -- (D )(1)!n n -(3)设函数)(t f 连续,则二次积分rdr r f d ⎰⎰2cos 2220)(θπθ=( )(A )dy y x f y x dx x x x )(2242222022++⎰⎰-- (B )dy y x f dx x xx )(2242222+⎰⎰--(C )dy y x f y x dx x xx )(2242122222++⎰⎰--+ (D )dy y x f dx x xx )(224212022+⎰⎰--+(4)已知级数∑∞=-11sin )1(i nn n α绝对收敛,∑∞=--12)1(i n nα条件收敛,则α范围为( )(A )210≤<α (B )121≤<α (C )231≤<α (D )223≤<α (5)设1234123400110,1,1,1c c c c αααα-⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪===-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭其中1234,,,c c c c 为任意常数,则下列向量组线性相关的是( )(A )123,,ααα (B )124,,ααα (C )134,,ααα (D )234,,ααα(6)设A 为3阶矩阵,P 为3阶可逆矩阵,且1112P AP -⎛⎫⎪= ⎪ ⎪⎝⎭,()123,,P ααα=,()1223,,Q αααα=+则1Q AQ -=( )(A )121⎛⎫ ⎪ ⎪ ⎪⎝⎭ (B )112⎛⎫ ⎪ ⎪ ⎪⎝⎭ (C )212⎛⎫ ⎪ ⎪ ⎪⎝⎭ (D )221⎛⎫⎪⎪ ⎪⎝⎭(7)设随机变量X 与Y 相互独立,且都服从区间()0,1上的均匀分布,则{}221P X Y +≤( ) (A )14 (B )12 (C )8π (D )4π(8)设1234,,,X X X X 为来自总体()()21,0N σσ>的简单随机样本,则统计量12342X X XX -+-的分布( )(A )()0,1N (B )()1t (C )()21χ (D )()1,1F二、填空题:9-14小题,每小题4分,共24分. (9)()1cos sin 4lim tan x xx x π-→________。
2012年考研数学三真题与答案解析
2012年全国硕士研究生入学统一考试数学三试题一、选择题:1-8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项符合题目要求的,请将所选项前的字母填在答题纸...指定位置上. (1)曲线221x x y x +=-渐近线的条数为( )(A) 0 (B) 1 (C) 2 (D) 3(2)设函数2()(1)(2)()x x nx f x e e e n =---,其中n 为正整数,则'(0)f =( )(A)1(1)(1)!n n --- (B)(1)(1)!n n -- (C)1(1)!n n -- (D)(1)!n n -(3)设函数()f t 连续,则二次积分22202cos d ()d f r r r πθθ=⎰⎰( )(A)222d ()d x x y y +⎰(B)2220d ()d x f x y y +⎰(C)222d ()d y x y x +⎰(D)22201d ()d y f x y x +⎰(4)已知级数11(1)n n α∞=-∑绝对收敛,级数21(1)n a n n∞-=-∑条件收敛,则( )(A)102a <≤(B)112a <≤ (C)312a <≤ (D)322a << (5)设1100C α⎛⎫ ⎪= ⎪ ⎪⎝⎭,2201C α⎛⎫ ⎪= ⎪ ⎪⎝⎭ ,3311C α⎛⎫ ⎪=- ⎪ ⎪⎝⎭ ,4411C α-⎛⎫ ⎪= ⎪ ⎪⎝⎭ ,其中1234,,,C C C C 为任意常数,则下列向量组线性相关的为( )(A)123,,ααα (B)124,,ααα (C)134,,ααα (D)234,,ααα(6) 设A 为3阶矩阵,P 为3阶可逆矩阵,且1100010002p AP -⎛⎫⎪= ⎪ ⎪⎝⎭.若P=(123,,ααα),1223(,,)ααααα=+,则1Q AQ -=( )(A)100020001⎛⎫ ⎪ ⎪ ⎪⎝⎭ (B)100010002⎛⎫ ⎪ ⎪ ⎪⎝⎭ (C)200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭ (D)200020001⎛⎫⎪ ⎪ ⎪⎝⎭(7)设随机变量X 与Y 相互独立,且都服从区间(0.1)上的均匀分布,则{}221P X Y +≤=( )(A)14 (B)12 (C)8π (D)4π (8)设1234,,,X X X X 为来自总体2(1,)N σ(σ>0)的简单随机样本,则统计量1234|2|X X X X -+-的分布为( )(A)N (0,1) (B)t(1) (C)2(1)χ (D)F(1,1)二、填空题:9-14小题,每小题4分,共24分.请将答案写在答题纸...指定位置上. (9)()1cos sin 4lim tan x xx x π-→=(10)设函数(),121,1x f x x x ⎧≥⎪=⎨-<⎪⎩, ()()y f f x =,则x edy dx ==(11)设连续函数(,)z f x y =满足0x y →→=则()0,1d |z =(12)由曲线4y x=和直线y x =及4y x =在第一象限中围成的平面图形的面积为 (13)设A 为3阶矩阵,3A =,*A 为A 的伴随矩阵。
2012数学三试题及答案
2012数学三试题及答案2012年的数学三试题是一道经典的数学考题,分为多个小题。
以下是试题及答案的完整内容。
一、选择题(每小题3分,共40分)1. 已知函数f(x) = 2x^2 - 3x + 1,求f(2)的值。
答案:f(2) = 2(2)^2 - 3(2) + 1 = 92. 若a + b = 5,a - b = 1,求a的值。
答案:将两式相加:2a = 6,因此 a = 3。
3. 若log2 x = 3,求x的值。
答案:根据对数的定义,log2 x = 3可以转化为2^3 = x,因此x = 8。
4. 若三角形ABC满足AB = BC,∠ABC = 110°,求∠ACB的度数。
答案:由三角形内角和定理可得,∠ACB = 180° - ∠ABC - ∠BAC= 180° - 110° - 35° = 35°。
二、填空题(每小题4分,共40分)1. 设正实数a和b满足a + b = 10,且ab的最小值为3,则a的值为____,b的值为____。
答案:由平均值不等式可得:(a + b)/2 ≥ √ab。
代入已知条件,10/2≥ √3,得5 ≥ √3。
由此可知,a和b的取值范围为(5 - √3, 5 + √3)。
因此,a的值为5 - √3,b的值为5 + √3。
2. 若函数f(x) = a(x - 1)^2 - 1在区间[0, 2]上单调递增,则a的取值范围为____。
答案:由题意可知,函数在区间[0, 2]上单调递增,即f'(x) > 0,其中f'(x)为f(x)的导数。
对f(x)进行求导得到f'(x) = 2a(x - 1)。
根据导数的定义,当x ∈ [0, 2]时,2a(x - 1) > 0,解得 0 < a < 1。
因此,a的取值范围为0 < a < 1。
三、解答题(共20分)1. 某商店购进了若干本图书,售价79元一本。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
2012启航考研暑期特训数学三“学习效能”
诊断测试
命题说明:
1)本套试题用于暑期课程开始之前的水平测试,用以检测春季基础阶段数学课程复习的效果。
2)试题命题风格与考察重点考研真题基本一致,难度与真题持平,重点内容重点考察。
3)本套试题由启航数学教研组命制。
一单项选择题(以下各道小题,每题仅有1个正确选项,请将答案写在答题纸上相应位置;每小题4分,满分32分)。
1)lim x→0=
A) 0 B) 1 C)2 D)不存在
2)设函数f(x)在x=0处可导,且f0=0,则lim x→0x2f x−2f(x3)
x3
=
A)-2f′(0) B)- f′(0) C) f′0D) 0
3)已知x2+e2y=4,则dy
dx
=
A) −X
e2y B) y
e y
C) x D)−x2
e2y
4)已知D为圆形区域:x2+y2≤x计算二重积分I=x2+y2dxdy=
D
A) 2
3B)4
5
C)4
9
D)3
7
5) 设A为n阶非零矩阵,E为n阶非零矩阵.若A3=0,则A)E−A不可逆,E+A不可逆B)E−A不可逆,E+A可逆
2
C) E −A 可逆,E+A 可逆 D) E −A 可逆,E+A 不可逆 6)设A ,B 均为实对称矩阵,且A 与B 相似,则下列说法错误的是
A )A 与
B 合同 B ) A = B
C )rank(A)=rank(B) D) A 与B 有相同的特征值和特征向量 7)设F 1 x ,F 2(x)分别是随机变量X 1,X 2的分布函数,F x =aF 1(x)−bF 2 x ,要使F(x)是分布函数,则以下结果可能正确的是 A) a=3
5
, b=−2
5 B) a=−2
5 , b=3
5
C)a=2
3
, b=1
3
D) a=−2
3
,b =−2
3
8) 某射击运动员进行射击训练,每次射击若打中靶心则停止射击,若未打中靶心则继续射击。
已知各次射击的结果是相互独立的,且每次射击的概率是0.8,则该运动员平均射击次数为 A )1 B )1.25 C )2 D )5
二 填空题(请将以下各小题的答案写在答题纸上相应位置;每小题4分,满分24分)
9)设f x =lim t →0x(1+3t)x t
,则f ′ x =___
10)设函数f(x)= x 2+1, x ≤c
2
x
, x ≥c
在(−∞,+∞)内连续,则c=___ 11)设f(u,v)是二元可微函数,z=f(y x ,x y
),则x
∂z
∂x
−y ∂z
∂y
=____
12)幂级数 3n −(−1)n n 2
∞
n=1
x n 的收敛半径为____
13)若已知三阶矩阵A 的特征值为1,2,3,则 A −1+E =___
3
14)设随机变量X的概率密度为1
k(1+x2)
,随机变量Y=3X,则Y的概率密度为____
三)解答题(请将以下各道题目的解答过程及结果写在答题卡上相应位置;本部分满分94分)
15)求极限lim x→01+2sinx−(x+1)
xln(1+x)
16)计算不定积分
x
x
dx
17)根据a取值的不同,确定方程lnx=ax a>0实根的个数
18)设u=yf x
y +xg(y
x
),求x∂2u
∂x2
+y∂2u
∂x∂y
19)已知D区域为由:y=0,x=0,x=−2,y=2,以及x2+ y2=2y所围成的区域。
计算二重积分xdxdy
D
20)设A=121
23a+2
1a−2
,b=
1
3
,x=
x1
x2
x3
i)若齐次方程组Ax=0只有零解,求a的取值范围。
Ii)若线性方程组Ax=b无解,求a.
21)矩阵A为三阶实对称矩阵,A+E=3.已知向量α1=(1,0,1)T,α2=(0,1,1)T是线性方程组Ax=0的解. i)求矩阵A的特征值和特征向量
ii)求实对称矩阵A
4
22)已知随机变量X的概率密度为f X(x)=1
2
,−1<x<0
1
4
,0<x<2
0,其它
,令
Y=X2.
i) 求随机变量Y的概率密度f Y(y)
ii)求随机变量Y的期望E(Y)和方差D(Y)
23)设随机变量(X,Y)的概率密度为
f(x,y)=1,y<x,0<x<1
0,其它
i)求Y的边缘概率密度f Y(y)
ii)随机变量X,Y是否相互独立?请说明理由
5
2012启航暑期特训学习效能诊断测试答题卡(数学三)
姓名_______ 报考院校专业_________ __联系电话______________ 电子邮箱____ _________ 一.选择题(本大题共8小题,每小题4分,满分32分)
二.填空题(本大题共6小题,每小题4分,满分24分)
9.________ 10.________ 11._________
12.________ 13.________14._________
三.解答题(本大题共6小题,满分94分,解答题写出必要的文字说明、推演步骤)
15、(本题10分)
6
16、(本题11分)
17、(本题10分)
18、(本题10分)
7
19、(本题11分)
20、(本题10分)
21、(本题11分)
8
22、(本题11分)
23、(本题10分)。
