(完整版)机械原理与机械设计-上册-范元勋-课后答案
《机械原理》课后习题附答案
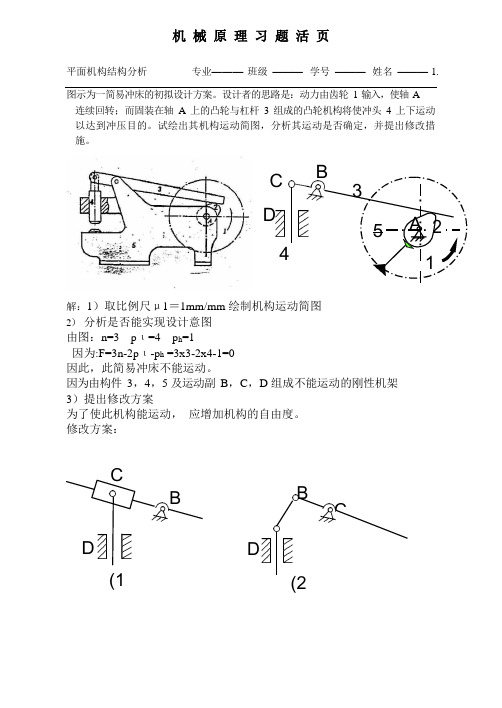
CB D BC平面机构结构分析专业———班级———学号———姓名——— 1.图示为一简易冲床的初拟设计方案。
设计者的思路是：动力由齿轮1 输入，使轴A连续回转；而固装在轴A 上的凸轮与杠杆3 组成的凸轮机构将使冲头4 上下运动以达到冲压目的。
试绘出其机构运动简图，分析其运动是否确定，并提出修改措施。
C B 35 A 24 1解：1）取比例尺μ1＝1mm/mm 绘制机构运动简图2）分析是否能实现设计意图由图：n=3 pι=4 p h=1因为:F=3n-2pι-p h =3x3-2x4-1=0因此，此简易冲床不能运动。
因为由构件3，4，5 及运动副B，C，D 组成不能运动的刚性机架3）提出修改方案为了使此机构能运动，应增加机构的自由度。
修改方案：D(1 (2DG7D 64C EF9 38B 2 A122如图所示为一小型压力机。
图中齿轮 1与偏心轮 1’为同一构件，绕固定轴心 o 连续转动。
在齿轮 5上开有凸轮凹槽，摆杆 4上的滚子 6嵌在凹槽中，从而使摆杆 4 绕 C 轴上下摆动。
同时，又通过偏心轮 1’、连杆 2、滑杆 3使 C 轴上下移动。
最后通过在摆杆 4的叉槽中的滑块 7和铰链 G 使冲头 8实现冲压运动。
试绘制其机构运动简图，并计算自由度。
b)解：计算该机构的自由度n=7， p ι=9， p h =2 F=3n-2p e -p h =3x7-2x8-2=13. 试计算下列二图所示齿轮连杆组合机构的自由度。
图中相切的圆周表示一对齿轮传动的节圆；凡局部自由度、复合铰链和虚约束均需明确指出。
解：a ）解n=4 P ι=5 Ph=1F=3x4-2x5-1=134 C A复合铰链1a)BD 5b）解：n＝6 Pι=7 Ph=3F＝3×6－2×7－3＝14.试计算下列二图所示压榨机的自由度。
图a 中，左右两半完全对称；图b 中，CD = FI = KL = KM = FJ = CE，LI =KF = MJ = JE = FC = ID。
(完整版)机械设计课后习题答案
第一章绪论（1）1-2 现代机械系统由哪些子系统组成, 各子系统具有什么功能？（2）答: 组成子系统及其功能如下:（3）驱动系统其功能是向机械提供运动和动力。
（4）传动系统其功能是将驱动系统的动力变换并传递给执行机构系统。
第二章执行系统其功能是利用机械能来改变左右对象的性质、状态、形状或位置, 或对作业对象进行检测、度量等, 按预定规律运动, 进行生产或达到其他预定要求。
第三章控制和信息处理系统其功能是控制驱动系统、传动系统、执行系统各部分协调有序地工作, 并准确可靠地完成整个机械系统功能。
第四章机械设计基础知识2-2 什么是机械零件的失效？它主要表现在哪些方面？答：（1）断裂失效主要表现在零件在受拉、压、弯、剪、扭等外载荷作用时, 由于某一危险截面的应力超过零件的强度极限发生的断裂, 如螺栓的断裂、齿轮轮齿根部的折断等。
（2）变形失效主要表现在作用在零件上的应力超过了材料的屈服极限, 零件产生塑性变形。
（3）表面损伤失效主要表现在零件表面的腐蚀、磨损和接触疲劳。
2-4 解释名词: 静载荷、变载荷、名义载荷、计算载荷、静应力、变应力、接触应力。
答: 静载荷大小、位置、方向都不变或变化缓慢的载荷。
变载荷大小、位置、方向随时间变化的载荷。
名义载荷在理想的平稳工作条件下作用在零件上的载荷。
计算载荷计算载荷就是载荷系数K和名义载荷的乘积。
静应力不随时间变化或随时间变化很小的应力。
变应力随时间变化的应力, 可以由变载荷产生, 也可由静载荷产生。
（1）2-6 机械设计中常用材料选择的基本原则是什么？（2）答：机械中材料的选择是一个比较复杂的决策问题, 其基本原则如下：①材料的使用性能应满足工作要求。
使用性能包含以下几个方面:②力学性能③物理性能④化学性能①材料的工艺性能应满足加工要求。
具体考虑以下几点:②铸造性③可锻性④焊接性⑤热处理性⑥切削加工性①力求零件生产的总成本最低。
主要考虑以下因素:②材料的相对价格③国家的资源状况④零件的总成本2-8 润滑油和润滑脂的主要质量指标有哪几项？答: 衡量润滑油的主要指标有: 粘度（动力粘度和运动粘度）、粘度指数、闪点和倾点等。
机械原理课后答案
习题解答第一章绪论1-1 答：1 ）机构是实现传递机械运动和动力的构件组合体。
如齿轮机构、连杆机构、凸轮机构、螺旋机构等。
2 ）机器是在组成它的实物间进行确定的相对运动时，完成能量转换或做功的多件实物的组合体。
如电动机、内燃机、起重机、汽车等。
3 ）机械是机器和机构的总称。
4 ）a. 同一台机器可由一个或多个机构组成。
b. 同一个机构可以派生出多种性能、用途、外型完全不同的机器。
c. 机构可以独立存在并加以应用。
1-2 答：机构和机器，二者都是人为的实物组合体，各实物之间都具有确定的相对运动。
但后者可以实现能量的转换而前者不具备此作用。
1-3 答：1 ）机构的分析：包括结构分析、运动分析、动力学分析。
2 ）机构的综合：包括常用机构设计、传动系统设计。
1-4 略习题解答第二章平面机构的机构分析2－1 ～2－5 （答案略）2-6(a) 自由度F＝1 (b) 自由度F＝1(c) 自由度F＝12-7题2 －7 图F ＝3 × 7 －2 × 9 －2 ＝12 -8a) n ＝7 ＝10 ＝0 F ＝3×7－2×10 ＝1b) B 局部自由度n ＝3 ＝3 ＝2 F＝3×3 －2×3－2＝1c) B 、D 局部自由度n ＝3 ＝3 ＝2 F＝3×3 －2×3－2 ＝1d) D( 或C) 处为虚约束n ＝3 ＝4 F＝3×3 －2×4＝1e) n ＝5 ＝7 F＝3×5－2×7＝1f) A 、B 、C 、E 复合铰链n ＝7 ＝10 F ＝3×7－2×10 ＝1g) A 处为复合铰链n ＝10 ＝14 F ＝3×10 －2×14＝2h) B 局部自由度n ＝8 ＝11 ＝1 F ＝3×8－2×11－1 ＝1i) B 、J 虚约束C 处局部自由度n ＝6 ＝8 ＝1 F ＝3×6 －2×8－1＝1j) BB' 处虚约束A 、C 、D 复合铰链n ＝7 ＝10 F ＝3×7－2×10＝1 k) C 、D 处复合铰链n＝5 ＝6 ＝2F ＝3×5－2×6－2 ＝1l) n ＝8 ＝11 F ＝3×8－2×11 ＝2m) B 局部自由度I 虚约束4 杆和DG 虚约束n ＝6 ＝8 ＝1 F ＝3×6－2×8－1 ＝12-9a) n ＝3 ＝4 ＝1 F ＝3 × 3 －2 × 8 －1 ＝0 不能动。
机械原理课后习题答案
第四章课后习题4—12图示为一曲柄滑块机构的三个位置，F为作用在活塞上的力转动副A及B上所画的小圆为摩擦圆，试决定在此三个位置时作用在连杆AB上的作用力的真实方向（构件重量及惯性力略去不计）。
解：上图中构件2受压力。
因在转动副A处2、1之间的夹角∠OAB在逐渐减小，故相对角速度ω21沿顺时针方向，又因2受压力，故FR12应切于摩擦圆的下方；在转动副B处，2、3之间的夹角∠OBA在逐渐增大，相对角速度ω23也沿顺时针方向，故FR32应切于摩擦圆的上方。
R32解：上图构件2依然受压力。
因在转动副A处2、1之间的夹角∠OAB逐渐减小，故相对角速度ω21沿顺时针方向，又因2受压力，故F R12应切于摩擦圆的下方；在转动副B处，2、3之间的夹角∠OBA逐渐减小，故相对角速度ω23沿逆时针方向，F R32应切于摩擦圆的下方。
解：上图构件2受拉力。
因在转动副A处2、1之间的夹角∠OAB在逐渐增大，故相对角速度ω21沿顺时针方向，又因2受拉力，故FR12应切于摩擦圆的上方；在转动副B处，2、3之间的夹角∠OBA逐渐减小，故相对角速度ω23沿顺时针方向，FR32应切于摩擦圆的下方。
4-13 图示为一摆动推杆盘形凸轮机构，凸轮1沿逆时针方向回转，F为作用在推杆2上的外载荷，试确定凸轮1及机架3作用给推杆2的总反力FR12及FR32方位（不考虑构件的重量及惯性力，解：经受力分析，FR12的方向如上图所示。
在FR12的作用下，2相对于3顺时针转动，故FR32应切于摩擦圆的左侧。
补充题1 如图所示，楔块机构中，已知γ＝β＝60°，Q ＝1000N 格接触面摩擦系数f ＝0.15，如Q 为有效阻力，试求所需的驱动力F 。
解:对机构进行受力分析,并作出力三角形如图。
对楔块1，R 21R310F F F ++=由正弦定理有21sin(602sin(90R F F ϕϕ+-=））o o ① 对楔块2，同理有R12R320Q F F ++=sin(90sin(602ϕϕ+-=））o o ②sin(602sin(602F Q ϕϕ+=⋅-））o o且有2112R R F F = ，8.53arctgf ϕ＝＝o ③联立以上三式，求解得F ＝1430.65N2 如图示斜面机构，已知：f （滑块1、2与导槽3相互之间摩擦系数）、λ（滑块1的倾斜角）、Q （工作阻力，沿水平方向），设不计两滑块质量，试确定该机构等速运动时所需的铅重方向的驱动力F 。
机械原理课后习题答案部分
第二章2-1 何谓构件何谓运动副及运动副元素运动副是如何进行分类的答：参考教材5~7页;2-2 机构运动简图有何用处它能表示出原机构哪些方面的特征答：机构运动简图可以表示机构的组成和运动传递情况,可进行运动分析,也可用来进行动力分析;2-3 机构具有确定运动的条件是什么当机构的原动件数少于或多于机构的自由度时,机构的运动将发生什么情况答：参考教材12~13页;2-5 在计算平面机构的自由度时,应注意哪些事项答：参考教材15~17页;2-6 在图2-22所示的机构中,在铰链C、B、D处,被连接的两构件上连接点的轨迹都是重合的,那么能说该机构有三个虚约束吗为什么答：不能,因为在铰链C、B、D中任何一处,被连接的两构件上连接点的轨迹重合是由于其他两处的作用,所以只能算一处;2-7 何谓机构的组成原理何谓基本杆组它具有什么特性如何确定基本杆组的级别及机构的级别答：参考教材18~19页;2-8 为何要对平面高副机构进行“高副低代"“高副低代”应满足的条件是什么答：参考教材20~21页;2-11 如图所示为一简易冲床的初拟设计方案;设计者的思路是：动力由齿轮1输入,使轴 A连续回转；而固装在轴A上的凸轮2与杠杆3组成的凸轮机构将使冲头上下运动以达到冲压目的;试绘出其机构运动简图,分析其是否能实现设计意图并提出修改方案;解：1取比例尺绘制机构运动简图;2分析其是否可实现设计意图;F=3n- 2P l +P h –p’ -F’=3×3-2×4+1-0-0=0此简易冲床不能运动,无法实现设计意图;3修改方案;为了使此机构运动,应增加一个自由度;办法是：增加一个活动构件,一个低副;修改方案很多,现提供两种;※2-13图示为一新型偏心轮滑阎式真空泵;其偏心轮1绕固定轴心A转动,与外环2固连在一起的滑阀3在可绕固定轴心C转动的圆柱4中滑动;当偏心轮按图示方向连续回转时可将设备中的空气吸入,并将空气从阀5中排出,从而形成真空;1试绘制其机构运动简图；2计算其自由度;解：1取比例尺作机构运动简图如图所示;2 F=3n-2p1+p h-p’-F’=3×4-2×4+0-0-1=12-14 解：1绘制机构运动简图1）绘制机构运动简图F=3n-2P l +P h –p’-F’=3×5-2×7+0-0-0=12）弯曲90o 时的机构运动简图※2-15试绘制所示仿人手型机械手的食指机构的机构运动简图以手掌8作为相对固定的机架,井计算自由度;解：1取比倒尺肌作机构运动简图；2计算自由度1⨯=-F210⨯73=2-17 计算如图所示各机构的自由度;aF=3n- 2P l +P h–p’-F’=3×4-2×5+1 -0-0=1A处为复合铰链bF=3n-2P l +P h–p’-F’=3×7-2×8+2-0-2=12、4处存在局部自由度cp’= 2P l ’+P h ’-3n’=2×10+0-3×6=2,F=3n-2P l +P h–p’-F’=3×11-2×17+0-2-0=1C、F、K 处存在复合铰链,重复部分引入虚约束※2-21图示为一收放式折叠支架机构;该支架中的件1和5分别用木螺钉连接于固定台板1’和括动台板5’上．两者在D处铰接,使活动台板能相对于固定台极转动;又通过件1,2,3,4组成的铰链四杆机构及连杆3上E点处的销子与件5上的连杆曲线槽组成的销槽连接使活动台板实现收放动作;在图示位置时,虽在活动台板上放有较重的重物．活动台板也不会自动收起,必须沿箭头方向推动件2,使铰链B,D重合时．活动台板才可收起如图中双点划线所示;现已知机构尺寸l AB=l AD=90 mm；l BC=l CD=25 mm,其余尺寸见图;试绘制该机构的运动简图,并计算其自由度;解：F=3n-2p1+p b-p’-F’=3×5-2×6+1-0-1=12-23 图示为一内燃机的机构简图,试计算其自由度,并分析组成此机构的基本杆组;有如在该机构中改选EG为原动件,试问组成此机构的基本杆组是否与前有所不同;解：1计算自由度F=3n-2P l +P h–p’-F’=3×7-2×10+0-0-0=12拆组3EG 为原动件,拆组2-24 试计算如图所示平面高副机构的自由度,并在高副低代后分析组成该机构的基本杆组;1、解：1计算自由度F=3n-2P l +P h –p ’-F ’=3×5-2×6+1-0-1=12从结构上去除局部自由度、虚约束、多余的移动副、转动副如图2所示 3高副低代如图3所示 4拆组如图4所示 2、解：1计算自由度F=3n-2P l +P h –p ’-F ’=3×-2×9+1-0-1=12从结构上去除局部自由度、虚约束、多余的移动副、转动副如图b 所示 3高副低代如图c 所示 4拆组如图d 所示第三章3—1 何谓速度瞬心相对瞬心与绝对瞬心有何异同点 答：参考教材30~31页;3—2 何谓三心定理何种情况下的瞬心需用三心定理来确定 答：参考教材31页;※3-3机构中,设已知构件的尺寸及点B 的速度v B 即速度矢量pb,试作出各机构在图示位置时的速度多边形;※3-4 试判断在图示的两机构中．B 点足否都存在哥氏加速度又在何位置哥氏加速度为零怍出相应的III 级组II 级组II 级组II 级组机构位置图;并思考下列问题;1什么条件下存在氏加速度2根椐上一条．请检查一下所有哥氏加速度为零的位置是否已全部找出;3图 a 中,a kB2B3=2ω2v B2B3对吗为什么;解：1图 a 存在哥氏加速度,图 b 不存在;2由于a kB2B3==2ω2v B2B3故ω3,v B2B3中只要有一项为零,则哥氏加速度为零;图 a 中B 点到达最高和最低点时构件1,3．4重合,此时v B2B3=0,当构件1与构件3相互垂直．即_f=；点到达最左及最右位置时ω2=ω3=0．故在此四个位置无哥氏加速度;图 b 中无论在什么位置都有ω2=ω3=0,故该机构在任何位置哥矢加速度都为零; 3对;因为ω3≡ω2;3-5 在图示的曲柄滑块机构中,已知mm l mm l mm l mm l DE BD A AB 40,50,100,30C ====,曲柄以等角速度s rad /101=ω回转,试用图解法求机构在︒=451ϕ位置时,点D 、E 的速度和加速度以及构件2的角速度和角加速度;解：1以选定的比例尺l μ作机构运动简图（2）速度分析AB)(m/s 3.01⊥==AB B l v ωBCBCv v v v v C C C B C B C //32322⊥∨∨+=+=？方向：？0？大小：？根据速度影像原理,作BC BD bc bd //2=求得点d,连接pd;根据速度影像原理,作BDE bde ∆≈∆求得点e,连接pe,由图可知)(/r 2/m/s,175.0m/s,173.0,m/s 23.0223232顺时针s ad l bc c c v pe v pd v BC v v C C v E v D ========μωμμμ （3）加速度分析A)(B m/s 3221→==AB B l a ω根据速度影像原理作BC BD c b d b /''/''2=求得点'd ,连接''d p ;根据速度影像原理,作BDE e d b ∆≈'''∆求得点e ',连接e p '',由图可知)(/36.8//,m/s 8.2'',m/s 64.2''2'2'22222顺时针s rad l c n l a e p a d p a BC a BC B C a E a D =======μαμμτ 3-6 在图示机构中,设已知各构件的尺寸,原动件1以等角速度1ω顺时针方向转动,试用图解法求机构在图示位置时构件3上C 点速度和加速度比例尺任选;abc3-7 在图示机构中,已知mm l mm l mm l mm l mm l BC CD EF A AE 50,75,35,40,70B =====,曲柄以等角速度s rad /101=ω回转,试用图解法求机构在︒=501ϕ位置时,C 点的速度c v 和加速度c a ; 解：1以选定的比例尺l μ作机构运动简图;速度分析m/s 72.0m/s,4.01111====AF F AB B l v l v ωω AFAF EFv v v v F F F F F //15145⊥⊥∨+==方向：大小：v d 用速度影响法求2速度分析CD ED v v v CDD C ⊥⊥∨+=方向：大小： BC AB v v v CBB C ⊥⊥∨+=方向：大小：3加速度分析)(m/s 2.7A),(B m/s 42211221A F l a l a AF F AB B →==→==ωω AFA F v a a a a a F F rF F k F F F F F ///21511515145→→∨++==方向：大小：ω EFEF l a a a a a EFEF n E F E F F ⊥→++==方向：大小：2444450ωτa d 用加速度影像法求CD D C l a a a a CDCDnCD D C ⊥→∨∨++=方向：大小：23ωτ CBB C l a a a a CB CBnCB B C ⊥→∨∨++=方向：大小：22ωτ 2m/s 3''=⋅=a C c p a μ3-8 在图示凸轮机构中,已知凸轮1以等角速度s rad /101=ω转动,凸轮为一偏心圆,其半径︒====90,50,15,251B ϕmm l mm l mm R AD A ;试用图解法求构件2的角速度2ω和角加速度2α; 解：1以选定的比例尺l μ作机构运动简图;2速度分析：将机构进行高副低代,其替代机构如图b 所示;m/s 15.0141===AB B B l v v ωCDAB BD v v v B B B B //4242⊥⊥∨+=方向：大小：？？)(/3.2//222逆时针s rad l pb l v BD v BD B ===μω3加速度分析A)m/s(B 5.12141→===AB B B l a a ω其中,）（顺时针222222222242242rad/s 9.143/''/,m/s 286.0,m/s 746.02=======BD a BD D B BD n D B B B k B B l b n l a l a v a μαωωτ 3-11 试求图示机构在图示位置时的全部瞬心; 解：a 总瞬心数：4×3/2=6对P 13：P 12、P 23、P 13在同一直线上, P 14、P 34、P 13在同一直线上 对P 24:P 23、P 34、P 24在同一直线上,P 12、P 14、P 24在同一直线上 d 总瞬心数：4×3/2=6对P 13：P 12、P 23、P 13在同一直线上, P 14、P 34、P 13在同一直线上 对P 24:P 23、P 34、P 24在同一直线上,P 12、P 14、P 24在同一直线上※3-12 标出图示的齿轮一连杆组合机构中所有瞬心,并用瞬心法求齿轮1与齿轮3的传动比ω1/ω3; 解：1瞬新的数目：K=NN-1/2=66-1/2=152)为求ω1/ω3需求3个瞬心P 16、P 36、P 13的位置,3)ω1/ω3= P 36P 13/P 16P 13=DK/AK,由构件1、3在K 点的速度方向相同,可知ω3与ω1同向;3-13 在图示四杆机构中,s rad mm l mm l CD AB /10,90,602===ω,试用瞬心法求：1当︒=165ϕ时点C 的速度C v ；当︒=165ϕ时构件3的BC 线上或其延长线上速度最小的一点E 的位置及其速度大小；3当0=C v 时ϕ角之值有两解;解：1以选定的比例尺l μ作机构运动简图（2）因P 24为构件2、4的顺心,则m/s 4.0rad/s 5.4424242242424=⋅==⋅=⋅=CD C D P A P l v DP AP l l ωωωω，对P 24:P 23、P 34、P 24在同一直线上,P 12、P 14、P 24在同一直线上（3）因构件3的BC 线上速度最小的点到绝对瞬心P 13的距离最近,故从P 13作BC 线的垂线交于E 点; 对P 13：P 12、P 23、P 13在同一直线上, P 14、P 34、P 13在同一直线上,故m/s 357.0131321313133313=⋅⋅=⋅⋅⋅=⋅⋅=⋅=E P B P l E P u B P v E P l v ABl l B l E P E ωμμωω（4）若0=C v ,则04=ω,DP AP l l DP A P 24242242424⋅=⋅=ωωω若024=A P ,则P 24与P 12重合,对P 24:P 23、P 34、P 24在同一直线上,P 12、P 14、P 24在同一直线上 若024=A P ,则A 、B 、C 三点共线;︒=⋅-++︒=︒=⋅-+=6.226)2arccos(1804.26)2arccos(22222221212211ADAC D C AD AC AD AC D C AD AC ϕϕ， ※3-15 在图示的牛头刨机构中,l AB =200 mnl,l CD =960 mm,l DE =160 mm, h=800mm,h 1=360mm,h 2=120mm;设曲柄以等角速度ω1=5 rad ／s ．逆时针方向回转．试以图解法求机构在φ1=135o 位置时．刨头点的速度v C ;sm AP v v P P P l p c l /24.1,,)2(151********===μωμ出瞬心利用顺心多边形依次定所示作机构运动简图，如图（1）以:解。
机械原理课后习题答案
inva )
=6.8mm
分度圆半径r=mz/2=10*18/2=90mm
齿槽宽：ea=2π ra/z-sa
分度圆齿厚s=π m/2=15.7mm
=28.1mm
齿顶圆半径ra=r+ha*m=90+10=100mm
基圆半径rb=rcosα=90cos200=84.57mm
inv200=0.0148
齿顶圆压力角
第2章 平面机构的结构分析
2-7：计算自由度，指出所有的复合铰链、局部自由度和虚约束，判定运动 是否确定； 解：自由度：
a) F=3n-2PL-PH=3*3-2*4=1；确定 b) F=3n-2PL-PH=3*6-2*8=2；不确定 c) F=3n-2PL-PH=3*4-2*5-1=1；确定 d) F=3n-2PL-PH=3*4-2*5-1=1；确定
从而lAB+lBC, lBC-lAB可求得,最后确定lAB和lBC； 设计步骤：
①取一点A，并定D点； ②以D为圆心，作圆； 根据CD摆角15°定C1，C2点； ③ 量取lAC1,lAC2
lAB+lBC=430 lBC-lAB=348
C2 15° 15°C1
B A
lAB=41
A
B1
D
lBC=389
B2
虚约束
局部自由度
复合铰链
a)
b)
c)
d)
机械原理 作业
第2章 平面机构的结构分析
2-8：计算自由度；确定机构所含杆组的数目与级别；确定机构级别。画出 瞬时替代机构； 解：自由度：
a) F=3n-2PL-PH=3*7-2*10=1；Ⅱ级 b) F=3n-2PL-PH=3*6-2*8-1=1；Ⅲ级
机械原理课后习题答案
《机械原理》课后习题答案第2章（P27）2-2 计算下列机构的自由度，如遇有复合铰链、局部自由度、虚约束等加以说明。
（a）n=3，p l=3 F=3*3-2*3=3（b）n=3，p l=3，p h=2 F=3*3-2*3-2=1 （B处有局部自由度）（c）n=7，p l=10 F=3*7-2*10=1（d）n=4，p l=4，p h=2 F=3*4-2*4-2=2 （A处有复合铰链）（e）n=3，p l=4 F=3*3-2*4=1 （A或D处有虚约束）（f）n=3，p l=4 F=3*3-2*4=1 （构件4和转动副E、F引入虚约束）（g）n=3，p l=5 F=(3-1)*3-(2-1)*5=1 （有公共约束）（h）n=9，p l=12，p h=2 F=3*9-2*12-2=1 （M处有复合铰链，C处有局部自由度）2-3 计算下列机构的自由度，拆杆组并确定机构的级别。
（a）n=5，p l=7 F=3*5-2*7=1由于组成该机构的基本杆组的最高级别为Ⅱ级杆组，故此机构为Ⅱ级机构。
（b）n=5，p l=7 F=3*5-2*7=1此机构为Ⅱ级机构。
（c）n=5，p l=7 F=3*5-2*7=1拆分时只须将主动件拆下，其它构件组成一个Ⅲ级杆组，故此机构为Ⅲ级机构。
2-4 验算下列运动链的运动是否确定，并提出具有确定运动的修改方案。
（a）n=3，p l=4，p h=1 F=3*3-2*4-1=0 该运动链不能运动。
修改方案如下图所示：（b）n=4，p l=6 F=3*4-2*6=0 该运动链不能运动。
修改方案如下图所示：或第3章（P42）3-2 下列机构中，已知机构尺寸，求在图示位置时的所有瞬心。
（a）（b）（c）(a) v3=v P13=ω1P14P13μl3-6 在图示齿轮连杆机构中，三个圆互作纯滚，试利用相对瞬心P13来讨论轮1与轮3的传动比i13。
第5章（P80）5-2 一铰接四杆机构（2）机构的两极限位置如下图：（3）传动角最大和最小位置如下图：5-3题略解：若使其成为曲柄摇杆机构，则最短杆必为连架杆，即a 为最短杆。
机械原理课后习题答案.pdf
[解]
（1）取μι作机构运动简图；
μl
=
0.002
m mm
C3
lBC =
l
2 AB
+
l
2 AC
−
l AB
⋅ lAB
⋅ cos135
= 302 + 1002 − 30 ×100 × cos135 = 123 (mm)
B
D
2
1 ω1
A
ϕ1
4
E
（2）速度分析 取C为重合点：C( C2, C3)
vB → vC 2 → vD ,vE → ω2
p(c3)
ω2
2
D
c2
2) 求aC2
aC 2 = aB
+ aCn 2B
+
at C 2B
=
aC 3
+
aCk
2C 3
+ aCr 2C 3
方向： B→A C→B ⊥CB
0 ⊥CБайду номын сангаас向下 ∥BC e
大小： √ √
?
0√
?
E
d
b
其中:
an C 2B
= ω2 2
lBC
=
2.02
4
C P34
1
A P12
题3-1 试求图示各机构在图示位置时全部瞬心。
b) P13
P34 B
3
P 23 →∞
2
P12
A
4
C P14→∞
P24
1
题3-1 试求图示各机构在图示位置时全部瞬心。
c)
P13 P14 C
4
→∞ P 34
M
vM
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
VC VD VCD VB VCB
P→d ⊥CD P→b ⊥CB
pd v ? 1 lAB
?
VC
v pc 0.45m s
4
VCD lCD
8.7 rad s ，
3
VF3 lFE
pf3 lFE
20.3，逆
5
VCB lCB
1rad
s ，顺
求加速度
根据影像法求 aD、aB
aF1 aF3 aD aD aC aB
习题 1.画出图示平面机构的运动简图，并计算其自由度。
(a)
(b)
(c)
1-6自动倾卸机构
3、计算图示平面机构的自由度；机构中的原动件用圆弧箭 头表示。
中文书2—5颚式破碎机 已知xD=260mm, yD=480mm, xG=400mm, yG=200mm,
lAB LCE 100 mm, lBC LBE 500 mm, lCD 300 mm, lEF 400 mm, lGF 685 mm, lBC LBE 500 mm
1 45, 1 30rad / s, 逆时针
求：5 , 5
解：1）求速度 VB VC VE VF 5
VC VB VCB
⊥CD ⊥AB ⊥CB ？ ω1lAB ？
根据速度影像求 VE
VF VE VFE
⊥GF P→e ⊥FE ？ Pev ？
5
fp v
lGF
1.7 rad s 将pf
VB1 VB2 构件2与构件3在B处形成重合点
求加速度
待求点 B3 为动点，求 VB3
VB3 VB2 VB3B2
//导路 ⊥AB ⊥导路
？
1 lAB
？
aB3
aB2
ar B3B2
//导路 B→A ⊥导路
？ 12 lAB ？
aB2 202 lAB 400 0.05 20 m s2
作加速度多边形：
移至F点知顺时针
2）求加速度 aB aC aE aF 5 加速度影像法求 aE
aCn aCt aB aCnB aCt B
C→D ⊥CD B→A C→B ⊥CB
BC CE BE b'c' c'e' b'e'
VC2 lCD
? 12 lAB
VC2B lCB
?
求得e΄
aFn aFt aE aFnE aFt E
a
d '
2 4
lCD
？
aC a c' 9.5mm,lBD=50mmllDE=40mm,φ1=45º,等角 速度ω1=10rad/s,求E、D的速度和加速度,构件3的角 速度和角加速度.
解：（1）选取l 0.002米/mm作机构运动简图。
（2）解题步骤为：VB VC2 (VD ,VE )及aB aC2 (aD , aE )
解题思路： VB1 VB2 构件2与构件3在B处形成重合点
待求点 B3 为动点，求 VB3
VB3 VB2 VB3B2
//导路 ⊥AB ⊥导路
？
1 lAB
？
VB2 1 lAB 20 0.05 1m s 取v作速度多边形VB3 v pb3 0.72
方向水平向左
求加速度 aB3
aB3
aB2
根据速度影像求 VE
VF VE VFE
⊥GF P→e ⊥FE
？ Pev ？
5
fp v
lGF
1.7 rad s 将pf
移至F点知顺时针
2）求加速度 aB aC aE aF 5 加速度影像法求 aE
aCn aCt aB aCnB aCt B
C→D ⊥CD B→A C→B ⊥CB
BC CE BE b'c' c'e' b'e'
F→G ⊥FG π→e΄ F→E ⊥FE
VF2 lFG
? e' a
VF2E lFE
?
5
aFt lFG
f '" f ' a
lFG
22 rad s2
将 f "' f '移至F知5逆时针
中文书：2－9已知曲柄长度l1=0.05m ,角速度ω1＝20rad/s,图解法确定 该机构在1＝45º时导杆3的速度v3与角速度a3.
VC2 lCD
? 12 lAB
VC2B lCB
?
求得e΄
aFn aFt aE aFnE aFt E
F→G ⊥FG π→e΄ F→E ⊥FE
VF2 lFG
? e' a
VF2E lFE
?
5
aFt lFG
f '" f ' a
lFG
22 rad s2
将 f "' f '移至F知5逆时针
2-9
VB2 1 lAB 20 0.05 1m s 取v作速度多边形VB3 v pb3 0.72
aB3 a b3' 14 m s
方向水平向左
2-10
VB
1
l
方向
AB
AB
VF1 VF3 VD VC
VB VC
VF3 VF1 VF3F1
⊥FE ⊥FA ∥AF ? 1 lAF ?
根据速度 影像法求 VD
ar B3B2
//导路 B→A ⊥导路
？ 12 lAB ？
aB2 202 lAB 400 0.05 20 m s2
作加速度多边形：
aB3 a b3' 14 m s
方向水平向左
3-3
当滑块 C至左极限和右极限位置时,曲柄与连杆在两共线位置, 曲柄在两位置的极位夹角θ=0,K=1,滑块的压力角在0~αmax 之间变化.
aFn 3 aFt 3 aF1 aF 3F1 aFk 3F1
F→E ⊥FE F→A ∥AF ⊥f1f3
VF21 lFE
？ 12 lFA
？ 21VF 3F1
aC aB aCnB aCt B aD aCnD aCt D
B→A C→B ⊥CB π→d’ C→D ⊥CD
12 lAB 52 lBC ？
(3）求VD ,VE，3。
VB l AB 1 0.0310 0.3米/秒
取pb
45毫米表示VB，则v
0.3 45
0. 0067 米毫/米秒 。
由VC2 V BVC2B VC3 VC2C3 求VC3
AB, C2B // C2B
pb bc2
c3c2
式中VC3 0
作速度多边形pbc2,然后按速度影象法，作Δbec2∽ΔBEC得 e点，再从e点作ed⊥bc2得d点，则 VE=(pe)μv=26×0.0067=0.1742m/s指向如图。 VD=(pd)μv=34×0.0067=0.2278m/s指向如图
max
arcsin a b
11.5
sin e 0.25 14.47
ba
' 4.88
K
180 180
4.88 4.88
1.056
sin ' e 0.1667 ' 9.5
ba
2—5
解：1）求速度 VB VC VE VF 5
VC VB VCB
⊥CD ⊥AB ⊥CB ？ ω1lAB ？