平行线与三角形内角和的综合应用每日一题及答案

合集下载

八年级数学上册平行线与三角形内角和的综合应用(习题及答案)(人教版)

）
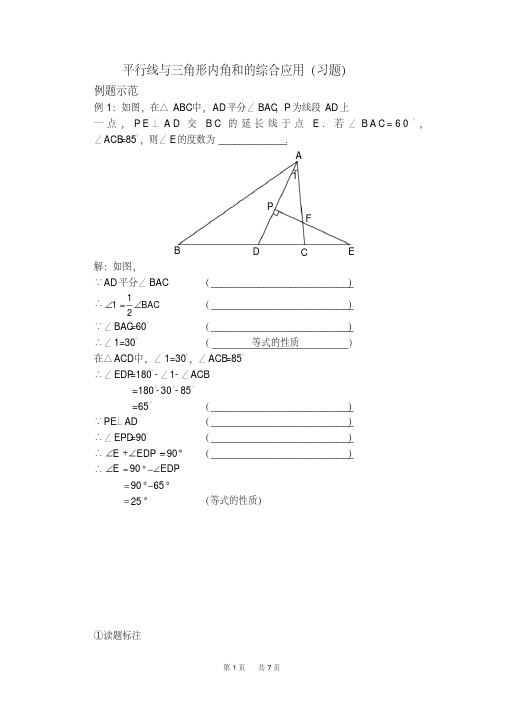
在△ ACD中，∠ 1=30°，∠ ACB=85°
∴∠ EDP=180°- ∠1- ∠ACB
=180°- 30°- 85°
=65°
（ __________________________）_
∵PE⊥ AD
（ __________________________）_
∴∠ EPD=90°
（ __________________________）_
证自明的“基本事实” ，可以当做已知的大前提来进行使用．而其中的三条，
是我们在几何证明中不经意间多次用到的，下面对它们来进行简单的解释．
当我们证明时，会遇到如下的推理：
∵a=b，b=c
∴a=c
在这个推理过程中，我们很容易就理解它的正确性，但往往不知道它的依据
是什么．其实，它的依据就是欧几里得公理体系中 5 条公理中的第一条：“（1）
∴∠ A+∠ C=90°（等量代换）
这里推理的依据就是第一条公理，我们把它简记为 “等量代换”．“等量代换”
第5页共7页
A
D
B
C
第3页共7页
6. 已知：如图， AB∥CD，∠ BAE=∠DCE=45°．求证：∠ E=90°．
A
B
1 E
Байду номын сангаас
2
C
D
7. 已知：如图， EF⊥BC， DE⊥AB，∠ B=∠ADE．求证： AD∥EF． A
E
B
F
D
C
第4页共7页
思考小结
1. 在证明过程中：（1）由平行可以想 ________相等、 __________相等、 ________互补；
=180°- 30°- 85°

平行线与三角形内角和的综合应用(讲义)

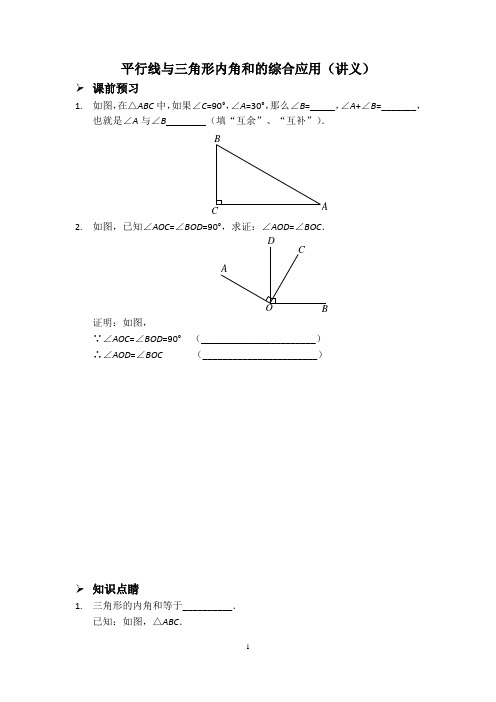
平行线与三角形内角和的综合应用（讲义）➢ 课前预习1. 如图，在△ABC 中，如果∠C =90°，∠A =30°，那么∠B =_____，∠A +∠B =_______，也就是∠A 与∠B ________（填“互余”、“互补”）．ABC2. 如图，已知∠AOC =∠BOD =90°，求证：∠AOD =∠BOC ．DCB OA证明：如图，∵∠AOC =∠BOD =90° （_______________________） ∴∠AOD =∠BOC （_______________________）➢ 知识点睛1. 三角形的内角和等于__________．已知：如图，△ABC ．求证：∠BAC +∠B +∠C =180°．A MBC12N证明：_______，___________________________． ∵MN ∥BC （已作） ∴∠B =∠1，∠C =∠2（_______________________）∵∠BAC+∠1+∠2=180°（_______________________） ∴∠BAC +∠B +∠C =180°（_______________________）2. 直角三角形两锐角___________．➢ 精讲精练1. 如图，在△ABC 中，∠A =50°，∠C =72°，BD 是△ABC 的一条角平分线，则∠ABD=__________．DAC FED C BA第1题图第2题图2. 如图，在△ABC 中，∠B =∠C ，E 是AC 上一点，ED ⊥BC ，DF ⊥AB ，垂足分别为D ，F ．若∠AED =140°，则∠C =_____，∠BDF =______，∠A =______．3. 如图，AE ∥BD ，∠1=110°，∠2=30°，则∠C =______．21EDCB A FDAEB第3题图第4题图4. 如图，AD ∥BC ，AB ∥CD ，E 在CB 的延长线上，EF 经过点A ，∠C =50°，∠FAD =60°，则∠EAB =_______．5. 如图，在△ABC 中，CD 平分∠ACB 交AB 于点D ，过点D 作DE ∥BC 交AC 于点E ．若∠A =75°，∠ADE =35°，则 ∠EDC =_________．6. 如图，在△ABC 中，∠B =40°，∠BAC =68°，AD ⊥BC 于点D ，求∠DAC 的度数．解：如图，在△ABC 中，∠B =40°，∠BAC =68°（已知） ∴∠C =180°-______-______ =180°-_____-_____=______（_______________________） ∵AD ⊥BC （已知）∴∠ADC =90°（垂直的定义） ∴∠C +_____=90°（直角三角形两锐角互余）∴∠DAC =90°-______=90°-______=______（_______________________）7. 如图，在Rt △ABC 中，∠ACB =90°，CD ⊥AB ，垂足为D ．求证：∠A =∠BCD ．证明：如图， ∵∠ACB =90°（已知）∴∠A +_____=90°（直角三角形两锐角互余） ∵CD ⊥AB （已知）ABDABCDEDCBA∴∠CDB =90°（垂直的定义）∴_____+∠B =90°（______________________） ∴∠A =∠BCD （______________________）8. 如图，在△ABC 中，∠C =90°，点D 是边AC 上一点，DE ∥BC ，∠1=60°，求∠A 的度数．ADE1BC9. 如图，BD ∥AE 交△ABC 的边AC 于点F ，∠CAE =95°，∠CBD =30°，求∠C 的度数．AB CDEF10.如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，AF平分∠CAB交CD于点E，交BC于点F．求证：∠1=∠2．【参考答案】➢课前预习1.60°，90°，互余2.已知，同角的余角相等➢知识点睛1.180°如图，过点A作MN∥BC两直线平行，内错角相等平角的定义等量代换2.互余➢精讲精练1.29°21FEDCB A2.50°，40°，80°3.40°4.70°5.35°6.解：如图，在△ABC中，∠B=40°，∠BAC=68°（已知）∴∠C=180°-∠B-∠BAC=180°-40°-68°=72°（三角形的内角和等于180°）∵AD⊥BC（已知）∴∠ADC=90°（垂直的定义）∴∠C+∠DAC=90°（直角三角形两锐角互余）∴∠DAC=90°-∠C=90°-72°=18°（等式的性质）7.证明：如图，∵∠ACB=90°（已知）∴∠A+∠B=90°（直角三角形两锐角互余）∵CD⊥AB（已知）∴∠CDB=90°（垂直的定义）∴∠BCD+∠B=90°（直角三角形两锐角互余）∴∠A=∠BCD（同角的余角相等）8.解：如图，∵DE∥BC（已知）∴∠1=∠B（两直线平行，同位角相等）∵∠1=60°（已知）∴∠B=60°（等量代换）∵∠C=90°（已知）∴∠A+∠B=90°（直角三角形两锐角互余）∴∠A=90°-∠B=90°-60°=30°（等式的性质）9.解：如图，∵BD∥AE（已知）∴∠CFD=∠CAE（两直线平行，同位角相等）∵∠CAE=95°（已知）∴∠CFD=95°（等量代换）∴∠CFB =180°-∠CFD=180°-95°=85°（平角的定义）在△CBF 中，∠CBD =30°，∠CFB =85°（已知） ∴∠C =180°-∠CBD -∠CFB =180°-30°-85°=65°（三角形的内角和等于180°） 10. 证明：如图，∵∠ACB =90°（已知）∴∠CAF +∠2=90°（直角三角形两锐角互余） ∵CD ⊥AB （已知）∴∠EDA =90°（垂直的定义）∴∠DAE +∠AED =90°（直角三角形两锐角互余） ∵AF 平分∠CAB （已知）∴∠CAF =∠DAE （角平分线的定义） ∴∠2=∠AED （等角的余角相等） ∵∠1=∠AED （对顶角相等） ∴∠1=∠2（等量代换）平行线与三角形内角和的综合应用（随堂测试）1. 已知：如图，AB ∥CD ，∠ABF =120°，CE ⊥BF ，垂足为E ，则∠ECF =___________．ABC D EF2. 已知：如图，在△ABC 中，∠B =40°，AD 平分∠BAC 交BC 于点D ，DE ∥BA 交AC 于点E ，∠ADE =40°，求∠C 的度数．EDC BA【参考答案】1.30°2.解：如图，∵DE∥BA（已知）∴∠BAD=∠ADE（两直线平行，内错角相等）∵∠ADE=40°（已知）∴∠BAD=40°（等量代换）∵AD平分∠BAC（已知）∴∠BAC=2∠BAD=2×40°=80°（角平分线的定义）在△ABC中，∠B=40°，∠BAC=80°（已知）∴∠C=180°-∠B-∠BAC=180°-40°-80°=60°（三角形的内角和等于180°）。

平行线与三角形内角和的综合应用作业及答案

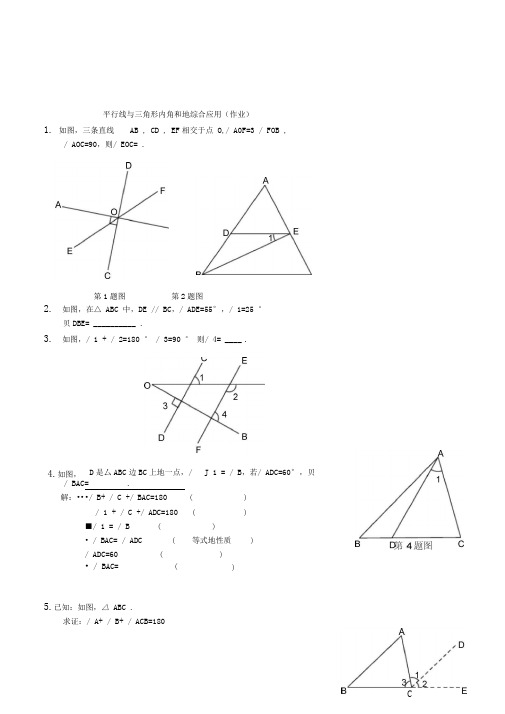
平行线与三角形内角和地综合应用（作业）1. 如图，三条直线 AB , CD , EF 相交于点 O ,/ A0F=3 / FOB ,/ AOC=90，则/ EOC= .2. 如图，在△ ABC 中，DE // BC ，/ ADE=55°，/ 1=25 °贝DBE= __________ .3. 如图，/ 1 + / 2=180 ° / 3=90 ° 则/ 4= ____ .5.已知：如图，△ ABC .求证：/ A+ / B+ / ACB=180C 第2题图4.如图， D 是厶ABC 边BC 上地一点，/ J 1 = / B ，若/ ADC=60°，贝U / BAC= .解：•• •/ B+ / C +/ BAC=180 ()/ 1 + / C +/ ADC=180 ()■/ 1 = / B ( )• / BAC= / ADC ( 等式地性质 )/ ADC=60 ( )• / BAC= ( )第1题图证明：作 BC 地延长线 CE ,过点C 作CD // AB ,•/ CD // AB•••/ A= / 1 / B= / 2 •••/ 1 + Z 2+ / 3=180° •••/ A+ / B+ / ACB=180 ( ( )(( ))) 第5题6.已知如图， AB // CD ，/ BAE= / DCE=45° ./ E=90° . •/ AB // CD ( )+ =180 ( )•••/ BAE= 7 D C E=45 ( )• 7 1+45°+ 7 2+45° =即7 1 + 7 2= ( )•••/ E=180° - (/ 1+ / 2)=180 °-90 °=90 ° ( )7.已知：如图，/ 1 = / ACB ，/ 2=7 3.求证：CD // HF.证明：•••7 1= 7 ACB ( )• // ( )• 7 2=• 7 2=7 3 ( )'• 7 3= ( )•• // ( )【参考答案】1. 45°2. 30°3. 90°4. 60 °三角形三个内角地和是 180。

三角形内角和综合习题精选(含答案)

...三角形内角和综合习题精选一．解答题（共12小题）1．如图（1），△ABC中，AD是角平分线，AE⊥BC于点E．（1）．若∠C=80°，∠B=50°，求∠DAE的度数．（2）．若∠C＞∠B，试说明∠DAE=（∠C﹣∠B）．（3）．如图（2）若将点A在AD 上移动到A´处，A´E⊥BC于点E．此时∠DAE变成∠DA´E，（2）中的结论还正确吗？为什么？2．如图，DB是△ABC的高，AE是角平分线，∠BAE=26°，求∠BFE的度数．3．如图，AD为△ABC的中线，BE为三角形ABD中线，（1）∠ABE=15°，∠BAD=35°，求∠BED的度数；（2）在△BED中作BD边上的高；（3）若△ABC的面积为60，BD=5，则点E到BC边的距离为多少？4．如图，在△ABC中，AD平分∠BAC，P为线段AD上的一个动点，PE⊥AD交直线BC于点E．（1）若∠B=35°，∠ACB=85°，求∠E的度数；（2）当P点在线段AD上运动时，猜想∠E与∠B、∠ACB的数量关系，写出结论无需证明．5．（1）如图1，有一块直角三角板XYZ放置在△ABC上，恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C．△ABC中，∠A=30°，则∠ABC+∠ACB= _________ ，∠XBC+∠XCB= _________ ．（2）如图2，改变直角三角板XYZ的位置，使三角板XYZ的两条直角边XY、XZ仍然分别经过B、C，那么∠ABX+∠ACX的大小是否变化？若变化，请举例说明；若不变化，请求出∠ABX+∠ACX的大小．6．如图1，△ABC中，∠A=50°，点P是∠ABC与∠ACB平分线的交点．（1）求∠P的度数；（2）猜想∠P与∠A有怎样的大小关系？（3）若点P是∠CBD与∠BCE平分线的交点，∠P与∠A又有怎样的大小关系？（4）若点P是∠ABC与∠ACF平分线的交点，∠P与∠A又有怎样的大小关系？【（2）、（3）、（4）小题只需写出结论，不需要证明】8．如图，A、B两点同时从原点O出发，点A以每秒x个单位长度沿x轴的负方向运动，点B以每秒y个单位长度沿y轴的正方向运动．（1）若|x+2y﹣5|+|2x﹣y|=0，试分别求出1秒钟后A、B两点的坐标；（2）设∠BAO的邻补角和∠ABO的邻补角的平分线相交于点P，问：点A、B在运动的过程中，∠P的大小是否会发生变化？若不发生变化，请求出其值；若发生变化，请说明理由；（3）如图，延长BA至E，在∠ABO的内部作射线BF交x轴于点C，若∠EAC、∠FCA、∠ABC的平分线相交于点G，过点G作BE的垂线，垂足为H，试问∠AGH和∠BGC的大小关系如何？请写出你的结论并说明理由．9．如图所示，点E 在AB 上，CE ，DE 分别平分∠BCD ，∠ADC ，∠1+∠2=90°，∠B=75°，求∠A 的度数．10．如图，∠AOB=90°，点C 、D 分别在射线OA 、OB 上，CE 是∠ACD 的平分线，CE 的反向延长线与∠CDO 的平分线交于点F．（1）当∠OCD=50°（图1），试求∠F ．（2）当C 、D 在射线OA 、OB 上任意移动时（不与点O 重合）（图2），∠F 的大小是否变化？若变化，请说明理由；若不变化，求出∠F ．11．如图，△ABC 中，AE 、BF 是角平分线，它们相交于点O ．（∠ABC ＞∠C ），（1）试说明∠BOA=90°+∠C；（2）当AD 是高，判断∠DAE 与∠C 、∠ABC 的关系，并说明理由．12．已知△ABC 中，∠BAC=100°．（1）若∠ABC 和∠ACB 的角平分线交于点O ，如图1所示，试求∠BOC 的大小；（2）若∠ABC 和∠ACB 的三等分线（即将一个角平均分成三等分的射线）相交于O ，O 1，如图2所示，试求∠BOC 的大小；（3）如此类推，若∠ABC 和∠ACB 的n 等分线自下而上依次相交于O ，O 1，O 2…，如图3所示，试探求∠BOC 的大小与n 的关系，并判断当∠BOC=170°时，是几等分线的交线所成的角．答案与评分标准一．解答题（共12小题）1．如图（1），△ABC中，AD是角平分线，AE⊥BC于点E．（1）．若∠C=80°，∠B=50°，求∠DAE的度数．（2）．若∠C＞∠B，试说明∠DAE=（∠C﹣∠B）．（3）．如图（2）若将点A在AD 上移动到A´处，A´E⊥BC于点E．此时∠DAE变成∠DA´E，（2）中的结论还正确吗？为什么？考点：三角形的角平分线、中线和高；角平分线的定义；垂线；三角形内角和定理。

八年级平行线、三角形内角和答案

B EAC F平行线、三角形内角和定理一、基本知识1.平行线性质：两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补。

平行线判定：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行。

3.三角形内角和定理：三角形三个内角的和等于180°。

直角三角形两锐角互余；四边形的内角和等于360°。

三角形的一个外角等于和它不相邻的两个内角的和；三角形的外角大于和它不相邻的任何一个内角。

二、训练题1.下列说话正确的是（ B ）A 、互补的两个角一定是邻补角B 、同一平面内，b // a, c // a,则b//cC 、同一平面内，,,.a c b c a b ⊥⊥⊥则D 相等的角一定是对顶角。

2.如图1，∠1=∠2，则有（ A ）A 、 EB//CF,B 、 AB//CF,C 、 EB//CD,D 、 AB//CD,3.如图2，已知∠1=80°， m//n, 则∠4=（ A ） A 、100°, B 、70° C 、80°, D 、60°,4.如图3，AB//EF,BC//DE, ∠B=40°，则∠E=（ C ）A 、90°,B 、120°C 、140°,D 、360°,5.如图4，点E 在AC 的延长线上，下列条件中能判断AB//CD 的是（ A ） A 、∠1=∠2, B 、∠3=∠4 C 、∠D=∠DCE D ∠D+∠ACD=180°6.如图5，AB//CD//EF, ∠ABE=38°，∠ECD=100°,则∠BEC=（ A ） A 、42°, B 、32° C 、62°, D 、38°,7.如图6，AE//CD, DE 平分∠ADC ，∠EAD=50°则∠DEA= 65° 。

三角形内角和综合习题精选(含答案)

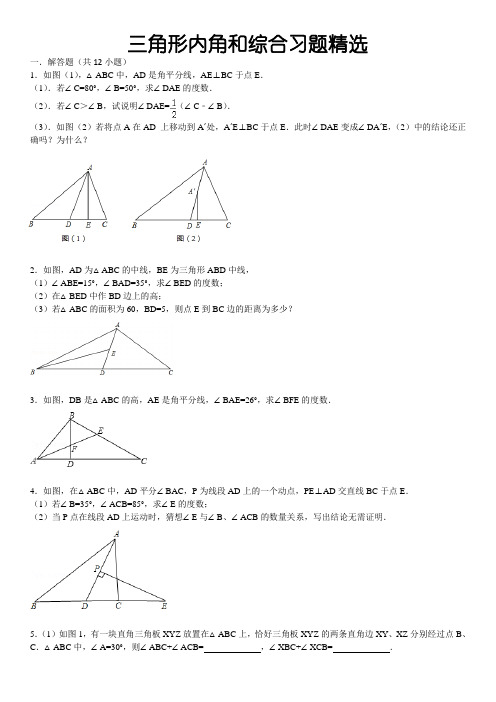
三角形内角和综合习题精选一．解答题（共12小题）1．如图（1），△ABC中，AD是角平分线，AE⊥BC于点E．（1）．若∠C=80°，∠B=50°，求∠DAE的度数．（2）．若∠C＞∠B，试说明∠DAE=（∠C﹣∠B）．（3）．如图（2）若将点A在AD 上移动到A´处，A´E⊥BC于点E．此时∠DAE变成∠DA´E，（2）中的结论还正确吗？为什么？2．如图，AD为△ABC的中线，BE为三角形ABD中线，（1）∠ABE=15°，∠BAD=35°，求∠BED的度数；（2）在△BED中作BD边上的高；（3）若△ABC的面积为60，BD=5，则点E到BC边的距离为多少？3．如图，DB是△ABC的高，AE是角平分线，∠BAE=26°，求∠BFE的度数．4．如图，在△ABC中，AD平分∠BAC，P为线段AD上的一个动点，PE⊥AD交直线BC于点E．（1）若∠B=35°，∠ACB=85°，求∠E的度数；（2）当P点在线段AD上运动时，猜想∠E与∠B、∠ACB的数量关系，写出结论无需证明．5．（1）如图1，有一块直角三角板XYZ放置在△ABC上，恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C．△ABC中，∠A=30°，则∠ABC+∠ACB=_________，∠XBC+∠XCB=_________．（2）如图2，改变直角三角板XYZ的位置，使三角板XYZ的两条直角边XY、XZ仍然分别经过B、C，那么∠ABX+∠ACX的大小是否变化？若变化，请举例说明；若不变化，请求出∠ABX+∠ACX的大小．6．如图1，△ABC中，∠A=50°，点P是∠ABC与∠ACB平分线的交点．（1）求∠P的度数；（2）猜想∠P与∠A有怎样的大小关系？（3）若点P是∠CBD与∠BCE平分线的交点，∠P与∠A又有怎样的大小关系？（4）若点P是∠ABC与∠ACF平分线的交点，∠P与∠A又有怎样的大小关系？【（2）、（3）、（4）小题只需写出结论，不需要证明】7．如图，已知△ABC中，∠B=∠E=40°，∠BAE=60°，且AD平分∠BAE．（1）求证：BD=DE；（2）若AB=CD，求∠ACD的大小．8．如图，A、B两点同时从原点O出发，点A以每秒x个单位长度沿x轴的负方向运动，点B以每秒y个单位长度沿y轴的正方向运动．（1）若|x+2y﹣5|+|2x﹣y|=0，试分别求出1秒钟后A、B两点的坐标；（2）设∠BAO的邻补角和∠ABO的邻补角的平分线相交于点P，问：点A、B在运动的过程中，∠P的大小是否会发生变化？若不发生变化，请求出其值；若发生变化，请说明理由；（3）如图，延长BA至E，在∠ABO的内部作射线BF交x轴于点C，若∠EAC、∠FCA、∠ABC的平分线相交于点G，过点G作BE的垂线，垂足为H，试问∠AGH和∠BGC的大小关系如何？请写出你的结论并说明理由．9．如图所示，点E在AB上，CE，DE分别平分∠BCD，∠ADC，∠1+∠2=90°，∠B=75°，求∠A的度数．10．如图，∠AOB=90°，点C、D分别在射线OA、OB上，CE是∠ACD的平分线，CE的反向延长线与∠CDO的平分线交于点F．（1）当∠OCD=50°（图1），试求∠F．（2）当C、D在射线OA、OB上任意移动时（不与点O重合）（图2），∠F的大小是否变化？若变化，请说明理由；若不变化，求出∠F．11．如图，△ABC中，AE、BF是角平分线，它们相交于点O．（∠ABC＞∠C），（1）试说明∠BOA=90°+∠C；（2）当AD是高，判断∠DAE与∠C、∠ABC的关系，并说明理由．12．已知△ABC中，∠BAC=100°．（1）若∠ABC和∠ACB的角平分线交于点O，如图1所示，试求∠BOC的大小；（2）若∠ABC和∠ACB的三等分线（即将一个角平均分成三等分的射线）相交于O，O1，如图2所示，试求∠BOC 的大小；（3）如此类推，若∠ABC和∠ACB的n等分线自下而上依次相交于O，O1，O2…，如图3所示，试探求∠BOC的大小与n的关系，并判断当∠BOC=170°时，是几等分线的交线所成的角．答案与评分标准一．解答题（共12小题）1．如图（1），△ABC中，AD是角平分线，AE⊥BC于点E．（1）．若∠C=80°，∠B=50°，求∠DAE的度数．（2）．若∠C＞∠B，试说明∠DAE=（∠C﹣∠B）．（3）．如图（2）若将点A在AD 上移动到A´处，A´E⊥BC于点E．此时∠DAE变成∠DA´E，（2）中的结论还正确吗？为什么？考点：三角形的角平分线、中线和高；角平分线的定义；垂线；三角形内角和定理。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

平行线与三角形内角和地综合应用（每日一题）
1. 如图，在△ ABC 中，D 为BC 边上一点，DF丄AB 于F, ED// AC,/ A=Z B. 求证：/ EDF=/
BDF.
2. 已知：如图，AD丄BC, EF丄BC,/仁/2 .求证：AB/ DG.
r
3. 在厶ABC中，/ ACB=90 , E是BC边上地一点，过C作CF丄AE,垂足为F,过B作
BD丄BC,交CF地延长线于D.若/ EAC=25°,求/ D地度数.
4. 已知：如图，AC EF相交于点O,/ E=/ F,/仁/ 2. 求证：AB // DG.
5. 已知：如图，AD// EF, BF// DG,/ A=Z B=Z G=35° 求/
EFG地度数.
【参考答案】
1•证明：如图,
已知 )
Z FED +Z EDF =Z B+Z BDF=90°( 直角三角形两锐角互余 )
等角地余角相等
•Z ACB=90°
Z D=90°- Z DCB =90 - 25°
等式性质
4.证明：如图，
•Z E=Z F
DE// AC • / A =Z FED • / B =Z FED
已知 ) 两直线平行，同位角相等 ) 已知 ) 等量代换即：Z CAB=Z DCA 等式性质 ) • AB / DG ( 内错角相等，两直线平行 ) 5.证明：如图，
• Z A=Z B=35° ( 已知 ) •Z ACB=18°0-Z A-Z B
=180°-35 °-
35° =110°
三角形地三个内角地和等于 180°) •Z DCF=Z ACB (
对顶角相等 ) 已知
( •Z 1+Z CAE =Z 2+Z FCA • DF 丄 AB • / EDF=Z BDF 2.证明：如图，
•/ EF ± BC •••/ B+Z 1=90 •/ AD 丄 BC •Z 2+ Z CDG=9°0
已知 ) 直角三角形两
锐角互余
已知 )
垂直地性质
•Z B=Z CDG
• AB / DG
3.解：如图，
•/ CF 丄 AE 已知 ) 等角地余角相等 ( 同位角相等，两直线平行已知 •Z EAC +Z ACD=9°0
) 直角三角形两锐角互余即 Z DCB+Z ACD=90
已知 Z DCB=Z EAC
Z EAC=25°
等角地余角相等已知 Z DCB = 25°
BD 丄 BC
Z D+Z DCB=9°0
) 等量代换已知 ) 直角三角形两锐角互余 = 65 • AE / FC 内错角相等，两直线平行 •Z CAE =FCA 两直线平行，内错角相等
已知
•Z 1=Z 2
/ DCF=11O ( 等量代换)
BF// DG ( 已知)
/ D+Z DCF=180 ( 两直线平行，同旁内角互补 ) / D=70 ( 等式性质)
AD/ EF ( 已知)
Z D=Z FEG ( 两直线平行，同位角相等 )
Z FEG=70°( 等量代换)
Z G=35°( 已知)
Z EFG=180-Z FEG-Z G
=180 -70 °-3°5 °
=75°(三角形地三个内角地和等于180 °)。

平行线与三角形内角和的综合应用每日一题及答案

最新平行线与三角形内角和的综合应用每日一题目及答案

八年级数学上册平行线与三角形内角和的综合应用(习题及答案)(人教版)

平行线与三角形内角和的综合应用(讲义)

平行线与三角形内角和的综合应用作业及答案

最新平行线与三角形内角和(计算(人教版

三角形内角和综合习题精选(含答案)

八年级平行线、三角形内角和答案

三角形内角和综合习题精选(含答案)