直角三角形练习题精选
直角三角形的性质练习题

直角三角形的性质练习题一、选择题1. 在直角三角形ABC中,角A为90°,且满足AB = 3,AC = 4,BC = 5,那么∠B的度数是:A) 30°B) 45°C) 60°D) 90°2. 直角三角形PQR中,∠P = 90°,PR = 5,RQ = 12,那么∠Q的度数是:A) 30°B) 45°C) 60°D) 90°3. 若一个直角三角形的一个锐角的度数是30°,那么另一个锐角的度数是:A) 30°B) 45°C) 60°D) 90°4. 若三角形ABC是直角三角形,其中∠A = 90°,AB = 8,AC = 15,则BC的长度为:A) 7B) 9C) 17D) 245. 直角三角形XYZ中,∠X = 90°,XY = 5,YZ = 12,则∠Y的正弦值是:A) 5/12B) 12/13C) 5/13D) 12/5二、填空题1. 直角三角形ABC中,∠C = 90°,AC = 7,BC = 24,则AB的长度为 ________。
2. 设直角三角形XYZ中,∠Y = 90°,XY = 6,则YZ的长度为________。
3. 直角三角形PQR中,PR = 5,RQ = 12,则∠P的度数为________。
4. 若直角三角形ABC中,∠B = 90°,AB = 14,则AC的长度为________。
5. 若直角三角形XYZ中,∠Y = 90°,XY = 9,则∠Z的度数为________。
三、解答题1. 已知直角三角形ABC,其中∠A = 90°,AB = 5,AC = 12,求BC的长度。
解析:根据直角三角形的性质,可使用勾股定理求解。
根据勾股定理,若AC、BC、AB分别表示直角三角形ABC的三条边的长度,则有AC² = AB² + BC²。
解直角三角形练习题

解直角三角形练习题一、选择题1. 在直角三角形中,若一个锐角的度数是45°,则另一个锐角的度数是()A. 45°B. 135°C. 90°D. 45°或135°2. 若直角三角形的两条直角边分别为3和4,则斜边的长度为()A. 5B. 6C. 7D. 83. 在直角三角形中,若斜边长为10,一直角边长为6,则另一直角边长为()A. 8B. 9C. 10D. 124. 已知直角三角形的斜边长为10,一个锐角的度数为30°,则该三角形的面积是()A. 25B. 30C. 50D. 100二、填空题1. 在直角三角形中,若一个锐角的度数是60°,则另一个锐角的度数是______。
2. 若直角三角形的两条直角边分别为5和12,则斜边的长度是______。
3. 在直角三角形中,若斜边长为13,一直角边长为5,则另一直角边长为______。
4. 已知直角三角形的斜边长为10,一个锐角的度数为45°,则该三角形的面积是______。
三、解答题1. 在直角三角形ABC中,∠C=90°,∠A=30°,AC=6,求BC和AB的长度。
2. 在直角三角形DEF中,∠F=90°,DF=5,EF=12,求∠D和∠E 的度数。
3. 已知直角三角形的斜边长为15,一个锐角的度数为60°,求该三角形的面积。
4. 在直角三角形XYZ中,∠Y=90°,∠X=45°,ZY=8,求XY和XZ的长度。
5. 已知直角三角形的斜边长为10,一直角边长为6,求另一直角边长及两个锐角的度数。
6. 在直角三角形LMN中,∠N=90°,∠L=30°,LN=9,求LM和MN的长度。
7. 已知直角三角形的面积为24,斜边长为10,求两个直角边的长度。
8. 在直角三角形PQR中,∠Q=90°,∠P=60°,PQ=8,求PR和QR的长度。
解直角三角形练习题

解直角三角形1、在△ABC 中,∠C =90°,tan A =13,则sin B =________ 2、已知在Rt ABC △中,390s i n 5C A ∠==°,,则t a n B =______3、在Rt △ABC 中,∠ACB =900,CD ⊥AB 于D ,BC=7,BD =5,则sinB = ,cosA = ,sinA = ,tanA = 。
4、在△ABC 中,∠C =900,CD ⊥AB 于D ,∠ACD =α,若tan α=23,则sinB =________5、△ABC 中,∠C =900,CD 是AB 上的高,则CD ∶CB=( )A 、sinAB 、cosAC 、tanAD 、cotA 6、A 、B 、C 是△ABC 的三个内角,则2sin B A +等于( )A 、2cosC B 、2sin C C 、C cosD 、2cos B A +7、如图,小明要测量河内小岛B 到河边公路l 的距离,在A 点测得30BAD ∠=°,在C 点测得60BCD ∠=°,又测得50AC =米,则小岛B 到公路l 的距离为_______米.7题 8题 9题8、将宽为2的长方形纸条折叠成如图的形状,那么折痕PQ =______9、如图,在矩形ABCD 中,DE ⊥AC 于E ,∠EDC ∶∠EDA=1∶3,且AC=10,则DE 的长度是_________10、如图,沿AE 折叠矩形纸片ABCD ,使点D 落在BC 边的点F 处.已知8AB =,10BC =,AB=8,则tan EFC ∠=________10题 11题11、坐标系中,将矩形OABC 沿OB 对折,使A 落在1A 处,已知OA =1AB =,则1A 的坐标是 。
12、如图,在等腰直角ABC ∆中,90C ∠=︒,6AC =,D 为AC 上一点,若1tan 5DBA ∠= ,则AD 的长为_____13、Rt ABC ∆中,90C ∠=︒,D 是直角边AC 上的点,且2AD DB a ==,15A ∠=︒,则BC = . 14、矩形ABCD 中,E 、F 、G 、H 分别为AB 、BC 、CD 、DA 的中点,若4tan 3AEH ∠=,四边形EFGH 的周长为40,则矩形ABCD 的面积为 ______________.12题 13题 14题 15、三角形ABC 中,∠A =60°,AB =6 cm ,AC =4 cm ,则△ABC 的面积是_________16、如图,矩形ABCD 中,AB >AD ,AB=a ,AN 平分∠DAB,DM⊥AN 于点M ,CN⊥AN 于点N .则DM+CN=________(用含a 的式子表示)17、等边三角形ABC 中,D 、E 分别为AB 、BC 上的点,AD BE =,AE 与CD 交于F ,AG CD ⊥于G , 则AG AF= . 18、如图,小阳发现电线杆AB 的影子落在土坡的坡面CD和地面BC 上,量得CD=8•米,BC=20米,CD 与地面成30°角,且此时测得1米的影长为2米,则电线杆的高度为____________16题 17题 18题19、ABC ∆中,0|t a n 3|)2c o s 2(2=-+-B A,则C ∠=______20.等腰三角形一腰上的高与腰长之比为2:1,则等腰三角形顶角的度数为________21、等腰三角形腰上的高等于底上的高的一半,则底角的余弦值为______.22、等腰三角形的三边长分别为1、1、3,则它的底角为_______23、在菱形ABCD 中,60ABC ∠=︒,AC=4,则BD 的长是 ______24、如图,ABC ∆中,AB AC =,BD AC ⊥于D ,6BC =,12DC AD =,则cos C =____. 25、如图,在ABC ∆中,090=∠C ,52=AC ,BAC ∠的平分线交BC 于D ,且3154=AD ,则BAC ∠tan=______24题25题26、今年入夏以来,松花江哈尔滨段水位不断下降,达到历史最低水位,一条船在松花江某水段自西向东沿直线航行,在A 处测得航标C 在北偏东60°方向上,前进100米到达B 处,又测得航标C 在北偏东45°方向上,如图9,在以航标C 为圆心,120米长为半径的圆形区域内有浅滩,如果这条船继续前进,是否有被浅滩阻碍的危险?27.某校九年级某班开展数学活动,小明和小军合作用一副三角板测量学校的旗杆,小明站在B 点测得旗杆顶端E 点的仰角为45°,小军站在点D 测得旗杆顶端E 点的仰角为30°,已知小明和小军相距(BD )6米,小明的身高(AB )1.5米,小军的身高(CD )1.75米,求旗杆的高EF 的长.(结果精确到0.1,≈1.41,≈1.73)28.如图,一楼房AB 后有一假山,其坡度为i=1:,山坡坡面上E 点处有一休息亭,测得假山坡脚C 与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E 点的俯角为45°,求楼房AB 的高.(注:坡度i 是指坡面的铅直高度与水平宽度的比)29.在中俄“海上联合—2014”反潜演习中,我军舰A 测得潜艇C 的俯角为300.位于军舰A 正上方1000米的反潜直升机B 侧得潜艇C 的俯角为680.试根据以上数据求出潜艇C 离开海平面的下潜深度.(结果保留整数。
直角三角形练习题及答案

直角三角形练习题及答案一、选择题1. 直角三角形中,直角边长分别为3厘米和4厘米,斜边长是多少?A. 5厘米B. 6厘米C. 7厘米D. 8厘米2. 在直角三角形ABC中,∠C=90°,AC=5,BC=12,求AB的长度。
A. 13B. 15C. 20D. 263. 直角三角形的两条直角边分别为a和b,斜边为c,根据勾股定理,正确的表达式是:A. a² + b² = cB. a² + b² = c²C. a² - b² = cD. a² + c² = b二、填空题4. 直角三角形的斜边长为13,一条直角边长为5,另一条直角边的长度是________。
5. 如果直角三角形的一条直角边长为x,另一条直角边长为2x,斜边长为3x,那么x的值是________。
三、解答题6. 已知直角三角形的两条直角边分别为6厘米和8厘米,求斜边的长度。
7. 一个直角三角形的斜边长为10厘米,一条直角边长为6厘米,求另一条直角边的长度。
8. 直角三角形的高为4厘米,底为6厘米,求斜边的长度。
答案:一、选择题1. A2. B3. B二、填空题4. 12厘米5. 3三、解答题6. 根据勾股定理,斜边长度为√(6²+8²)=√(36+64)=√100=10厘米。
7. 根据勾股定理,另一条直角边的长度为√(10²-6²)=√(100-36)=√64=8厘米。
8. 根据勾股定理,斜边长度为√(4²+6²)=√(16+36)=√52厘米。
以上练习题及答案旨在帮助学生加深对直角三角形及其性质的理解,通过实际计算来掌握勾股定理的应用。
直角三角形专题练习
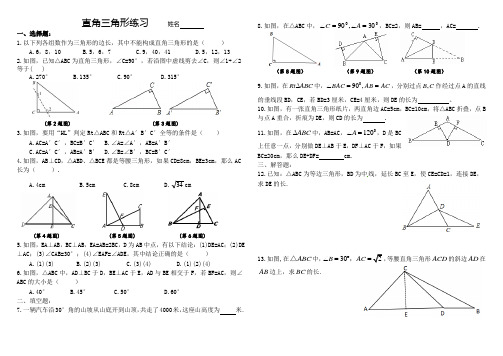
直角三角形练习姓名一、选择题:1.以下列各组数作为三角形的边长,其中不能构成直角三角形的是()A.6,8,10B.5,6,7C.9,40,41D.5,12,132.如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )A.270°B.135°C.90°D.315°(第2题图) (第3题图)3.如图,要用“HL”判定Rt△ABC和Rt△A′B′C′全等的条件是()A.AC=A′C′,BC=B′C′B.∠A=∠A′,AB=A′B′C.AC=A′C′,AB=A′B′D.∠B=∠B′,BC=B′C′4.如图,AB⊥CD,△ABD、△BCE都是等腰三角形,如果CD=8cm,BE=3cm,那么AC长为().A.4cmB.5cmC.8cmD.34cm(第4题图) (第5题图) (第6题图)5.如图,EA⊥AB,BC⊥AB,EA=AB=2BC,D为AB中点,有以下结论:(1)DE=AC;(2)DE ⊥AC;(3)∠CAB=30°;(4)∠EAF=∠ADE。
其中结论正确的是()A.(1)(3)B.(2)(3)C.(3)(4)D.(1)(2)(4)6.如图,△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,若BF=AC,则∠ABC的大小是()A.40°B.45°C.50°D.60°二、填空题:7.一辆汽车沿30°角的山坡从山底开到山顶,共走了4000米,这座山高度为米.8.如图,在△ABC中,0030,90=∠=∠AC,BC=2,则AB= ,AC= .(第8题图)(第9题图)(第10题图)9.如图,在Rt ABC∆中,090,BAC AB AC∠==,分别过点,B C作经过点A的直线的垂线段BD,CE,若BD=3厘米,CE=4厘米,则DE的长为。
10.如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,点B 与点A重合,折痕为DE,则CD的长为 .11.如图,在ABC∆中,AB=AC,0120A∠=,D是BC上任意一点,分别做DE⊥AB于E,DF⊥AC于F,如果BC=20cm,那么DE+DF= cm.三、解答题:12.已知:△ABC为等边三角形,BD为中线,延长BC至E,使CE=CD=1,连接DE,求DE的长.13.如图,在ABC△中,302B AC∠=︒=,,等腰直角三角形ACD的斜边AD在AB边上,求BC的长.B14.如图,AD 是∠BAC 的角平分线,DE ⊥AB ,DF ⊥AC ,BD = CD 。
第一章直角三角形练习题

第一章直角三角形练习题A. 基础概念1. 若直角三角形的两个直角边长分别为3cm和4cm,求斜边的长度。
2. 在直角三角形中,如果一个锐角的度数是30°,求另一个锐角的度数。
3. 若直角三角形的斜边长为10cm,一个锐角为60°,求该锐角所对的直角边长度。
4. 判断下列哪个选项不能构成直角三角形的三边长:(A)3, 4,5 (B)5, 12, 13 (C)8, 15, 17 (D)6, 8, 115. 在直角三角形中,如果斜边上的中线等于斜边的一半,那么这个三角形是什么三角形?B. 特殊角的三角函数1. 已知直角三角形中,一个锐角为45°,求该角的正弦值。
2. 若直角三角形的一个锐角为30°,求该角的余弦值。
3. 在直角三角形中,如果斜边长为2,一个锐角为60°,求该角的正切值。
4. 已知直角三角形的斜边长为10,一个锐角的正弦值为1/2,求这个锐角的度数。
5. 在直角三角形中,如果一个锐角的余弦值等于它的正切值,求这个锐角的度数。
C. 三角函数的应用1. 一个灯塔距离海岸线3公里,从灯塔顶部看到一艘船在正北方向,船与灯塔的水平距离为2公里,求船距离海岸线的距离。
2. 在直角三角形中,斜边长为13cm,一个锐角的正切值为3/4,求这个锐角的余弦值。
3. 一座山的高度为1800米,测得山顶与地面上某点的角度为15°,求该点到山顶的水平距离。
4. 在直角三角形中,如果一个锐角的正弦值和余弦值相等,求这个锐角的度数。
5. 一个旗杆的高度为15米,在旗杆顶部系一条绳子,绳子另一端固定在地面上,绳子长度为20米,求绳子与地面的夹角度数。
D. 三角形的边长关系1. 若直角三角形的斜边长为c,一个直角边长为a,求另一个直角边长b(用勾股定理表示)。
2. 已知直角三角形的一个直角边长为8cm,斜边长为10cm,求另一个直角边长。
3. 在直角三角形中,如果一个锐角的正弦值为0.6,斜边长为15cm,求这个锐角所对的直角边长度。
(完整版)初中解直角三角形练习题

解直角三角形练习题一、 真空题: 1、 在Rt △ABC 中,∠B =900,AB =3,BC =4,则sinA= 2、在Rt △ABC 中,∠C =900,AB =,35cm BC cm=则SinA= cosA= 3、Rt △ABC 中,∠C =900,SinA=54,AB=10,则BC =4、α是锐角,若sin α=cos150,则α= 若sin53018\=0.8018,则cos36042\=5、 ∠B 为锐角,且2cosB -1=0则∠B =6、在△ABC 中,∠C =900,∠A ,∠B ,∠C 所对的边分别为a ,b ,c ,a =9,b =12,则sinA= sinB=7、 Rt △ABC 中,∠C =900,tanA=0.5,则cotA= 8、 在Rt △ABC 中,∠C =900,若b a 32=则tanA= 9.等腰三角形中,腰长为5cm ,底边长8cm ,则它的底角的正切值是10、若∠A 为锐角,且tan 2A+2tanA -3=0则∠A = 11、Rt △ABC 中,∠A =600,c=8,则a = ,b = 12、在△ABC 中,若32=c ,b =3,则tanB= ,面积S = 13、在△ABC 中,AC :BC =1:3,AB =6,∠B = ,AC = BC = 14、在△ABC 中,∠B =900,AC 边上的中线BD =5,AB =8,则tanACB=二、选择题1、在Rt △ABC 中,各边的长度都扩大2倍,那么锐角A 的正弦、余弦值 ( )A 、都扩大2倍B 、都扩大4倍C 、没有变化D 、都缩小一半2、若∠A 为锐角,且cotA <3,则∠A ( )A 、小于300B 、大于300C 、大于450且小于600D 、大于600 3、在Rt △ABC 中,已知a 边及∠A ,则斜边应为 ( ) A 、asinA B 、A a sin C 、acosA D 、Aa cos 4、等腰三角形底边与底边上的高的比是2:3,则顶角为( ) A 、600 B 、900 C 、1200 D 、15005、在△ABC 中,A ,B 为锐角,且有sinA =cosB ,则这个三角形是( )A 、等腰三角形B 、直角三角形C 、钝角三角形D 、锐角三角形6、有一个角是300的直角三角形,斜边为1cm ,则斜边上的高为( )A 、41cmB 、21cmC 、43cmD 、23cm三、求下列各式的值1、sin 2600+cos 26002、sin600-2sin300cos3003. sin300-cos 24504. 2cos450+|32-|5. 0045cos 360sin 2+ 6. 130sin 560cos 300-7. 2sin 2300·tan300+cos600·cot300 8. sin 2450-tan 2300四、解答下列各题1、在Rt △ABC 中,∠C =900,,AB =13,BC =5, 求sinA, cosA, tanA, cotA2. 在Rt △ABC 中,∠C =900,若1312sin =A 求cosA, sinB, cosB3. 在Rt △ABC 中,∠C =900,b=17, ∠B=450,求a, c 与∠A四、根据下列条件解直角三角形。
完整版初中解直角三角形练习题

解直角三角形练习题一、真空题:0 sinA= =90 ,AB =3,BC=4,则中,∠1、在Rt△ABCB0 AB90=,2、在Rt △ABC中,∠C=,5cmBC?3cm cosA= 则SinA=40=ABC中,∠C=90,SinA=,AB=10,则3、BCRt△5\00,sin53=0.8018α=cos1518,则α=若sin4、α是锐角,若\0则cos3642=2cosB-1=0则∠B=、5∠B为锐角,且0,ba,,∠A,∠B,∠C所对的边分别为6、在△ABC中,∠C=90 sinB= sinA= c,a=9,b=12,则0则cotA= 7、Rt△ABC中,∠C=90 ,tanA=0.5,0ba?32 90 ,若tanA= 则C8、在Rt△ABC中,∠=,则它的底角的正切值,底边长8cm9.等腰三角形中,腰长为5cm 是2A=为锐角,且tan A+2tanA-3=0则∠10、若∠A0,b=△11、RtABC中,∠A=60c=8,,则a=32c?,面积中,若S=,b=3,则tanB= ABC12、在△3,AB=6,∠B=,AC=BCABC13、在△中,AC:=1:0,AC边上的中线BD=5中,∠14、在△ABC B=90,AB =BC=8,则tanACB=1二、选择题的正弦、A2倍,那么锐角1、在Rt△ABC中,各边的长度都扩大)余弦值(4倍2倍B、都扩大A、都扩大D、都缩小一半C、没有变化3),则∠A 2、若∠A为锐角,且cotA(<0 0000 60DB、大于30、大于 C45、大于且小于60A、小于30)(△3、在RtABC中,已知a边及∠A,则斜边应为aa、 C、、AasinA B、 acosA D A sin A cos3),则顶角为( 4、等腰三角形底边与底边上的高的比是2 :0000、150120 D、60 B、90 C、A,则这个三角形是=cosBsinA中,A,B为锐角,且有5、在△ABC )(、直角三角形、等腰三角形BA 、锐角三角形C、钝角三角形D0)30则斜边上的高为的直角三角形,斜边为1cm,(、6有一个角是1133、DcmC、cm、B、Acm cm42422三、求下列各式的值02000202、sin60cos30sin1、-602sin30+cos 60 020032?| 2cos45|+ 45 4. 3. sin30-cos060cos30045?3cos2sin60 6. 5. 01?30sin5 000020202 45-tan7. 2sintan3030·+cos6030·cot30 8. sin四、解答下列各题0=,=中,∠△、在1RtABCC90,AB135=,BC,sinA, cosA, tanA, cotA 求3120cosA, sinB, cosB ,若=90求C2. 在Rt△ABC中,∠?sin A13A a, c=C90与∠,b=17, ∠B=45,求△3. 在RtABC中,∠00中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B
C A
30° 1.下列长度的三条线段,能组成直角三角形的是( )
A .1cm ,3 cm ,3cm
B .2cm ,3 cm ,4 cm
C .4cm ,6 cm ,8cm
D .5cm ,12 cm ,13cm
2、如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了 步路(假设2步为1米),却踩伤了花草.
3.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A 、B 、C 、D 的边长分别是3、5、2、3,则最大正方形E 的面积是( ) A .13 B .26 C .47 D .944.如图,已知△ABC 为直角三角形,∠C =90°,若沿图中虚线剪去∠C ,则∠1+∠2等于_______. 5.如图,△ABC 中,∠C =90°,AC =3,∠B =30°,点P 是BC 边上的动点,则AP 长不可能是( ) (A )3.5 (B )4.2 (C )5.8 (D )7
6、某楼梯的侧面视图如图所示,其中4AB =米,30BAC ∠=°,90C ∠=°,因某种活动要求铺设红色地毯,则在AB 段楼梯所铺地毯的长度应为 .
7. 某市在“旧城改造”中计划在市内一块如图的三角形空地上移植某种草皮以美化环境,已知这种草皮每平方米售价a 元,则购买这种草皮至少需要( )A .450a 元 B .225a 元 C .150a 元 D .300a 元
8.将一个有45度角的三角板的直角顶点放在一张宽为3cm 的纸带边沿上,另一个顶点在纸带的另一边沿上,测
得三角板的一边与纸带的一边所在的直线成30度角,如图(3),则三角板的最大边的长为( ) A. 3cm B. 6cm C. 32cm D. 62cm
9、如图所示,A 、B 、C 分别表示三个村庄,AB =1000米,BC =600米,AC =800米,在社会主义新农村建设中,为了丰富群众生活,拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P 的位置应在( )A .AB 中点
B .B
C 中点 C .AC 中点
D .∠C 的平分线与AB 的交点
10.如图是油路管道的一部分,延伸外围的支路恰好构成一个直角三角形,两直角边分别为6m 和8m.按照输油中心O 到三条支路的距离相等来连接管道,则O 到三条支路的管道总长(计算时视管道为线,中心O 为点)是( )A 2m B. 3m C. 6m D. 9m
图3
A 'C
B
A
D
E
11.如图,已知ABC △中,45ABC ∠=,4AC =,H 是高AD 和BE 的交点,则线段BH 的长度为( )
A .6
B .4
C .23
D .5
12.如图,CD 是Rt△ABC 斜边上的高,将△BCD 沿CD 折叠,B•点恰好落在AB 的中点E 处,则∠A 等于( )
A .25°
B .30°
C .45°
D .60°
13.如图3,在△ABC 中,∠C=90°,BC=6,D,E 分别在AB,AC 上,将△ABC 沿DE 折叠,使点A 落在点A ′处,若A ′为CE 的中点,则折痕DE 的长为( )A .
2
1
B .2
C .3
D .4
14.如图,在Rt △ABC 中,∠C =90°,BC =6cm ,AC =8cm ,按图中所示方法将△BCD 沿BD 折叠,使点C 落在AB 边的C ′点,那么△ADC ′的面积是 .
15、如图,将等腰直角三角形ABC 绕点A 逆时针旋转15°后得到△AB′C′,若AC=1,则图中阴影部分的面积为 ( )A .
33 B .36
C .3
D .33 16. 如图,ABC △是等腰直角三角形,BC 是斜边,将ABP △绕点A 逆时针旋转后,能与ACP '△重合,如果3AP =,那么PP '的长等于( )A .32 B .23
C .42
D .33
17. 如图,每个小正方形的边长为1,A 、B 、C 是小正方形的顶点,则∠ABC 的度数为( )
A .90°
B .60°
C .45°
D .30° 18、如图,在Rt△ABC 内有边长分别为,,a b c 的三个正方形,则,,a b c 满足的 关系式是_____________.
19、已知△ABC 中,AB =17,AC =10,BC 边上的高AD =8, 则边BC 的长为( )
A .21
B .15
C .6
D .以上答案都不对
C
B
A
D
C
B
A
E H
O
20.图甲是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的。
在Rt△ABC 中,若直角边AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图乙所示的“数学风车”,则这个风车的外围周长(图乙中的实线)是______________。
21、如图所示的圆柱体中底面圆的半径是
2
π
,高为2,若一只小虫从A 点出发沿着圆柱体的侧面爬行到C 点,则小虫爬行的最短路程是 (结果保留根号).
22. 含30角的直角三角板ABC (30B ∠=)绕直角顶点C 沿逆时针方向旋转角α(90α∠<),再沿A ∠的对边翻折得到A B C ''△,AB 与B C '交于点M ,A B ''与BC 交于点N ,A B ''与AB 相交于点E .(1)求证:ACM A CN '△≌△.(2)当30α∠=时,找出ME 与MB '的数量关系,并加以说明.
23.拼图填空:剪裁出若干个大小、形状完全相同的直角三角形,三边长分别记为a 、b 、c ,如图①.(1)拼图一:分别用4张直角三角形纸片,拼成如图②③的形状,观察图②③可发现,图②中两个小正方形的面积之和_______ (填“大于”、“小于”或“等于”)图③中小正方形的面积,用关系式表示为________ .(2)拼图二:用4张直角三角形纸片拼成如图④的形状,观察图形可以发现,图中共有__________个正方形,它们的面积之间的关系是________ ,用关系式表示为_____ .(3)拼图三:用8个直角三角形纸片拼成如图⑤的形状,图中3个正方形的面积之间的关系是_____ ____ ,用关系式表示________ . ① ② ③
a c
b
A
E B M C A 'N
B '。
