解直角三角形的应用典型习题(方位角)
课时练习：解直角三角形的应用(方位角问题)
方位角问题知识点一 与方位角有关的问题1．如图，B 点在A 点的南偏西 或 ；A 点在B 点的北偏东 或 ． 2．如图，小明从A 地沿北偏东030方向走1003m 到B 地，再从B 地向正南方向走200m 到C 地，此时小明离A 地 m ．3．两座灯塔A 和B 与海洋观测站的距离相等,灯塔A 在观测站的北偏东40°,灯塔B 在观测站的南偏东60°,那么灯塔A 在灯塔B 的（ ）. A.北偏东10° B.南偏东10° Ｃ.北偏西10° Ｄ.南偏西20°4．小明同学在东西方向的沿江大道A 处，测得江中灯塔P 在北偏东60°方向上，在A 处正东400米的B 处，测得江中灯塔P 在北偏东30°方向上，则灯塔P 到沿江大道的距离为___________米．5．如图，小明同学在东西方向的环海路A 处，测得海中灯塔P 在北偏东60°方向上，在A 处东500m 的B 处，测得海中灯塔P 在北偏东30°方向上，则灯塔P 到环海路的距离PC ＝ m ．（用根号表示） 技能点一 利用方位角解决与航海、航空有关的实际问题6．如图，客轮在海上以30km/h 的速度由B 向C 航行，在B 处测得灯塔A 的方位角为北偏东80，测得C 处的方位角为南偏东25，航行1小时后到达C 处，在C 处测得A 的方位角为北偏东20，则C 到A 的距离是（ ）. A ．156kmB ．152kmC ．15(62)+kmD ．5(632)+km7．如图，一艘轮船以每小时20海里的速度沿正北方向航行，在A 处测得灯塔C 在北偏西30°方向，轮船航行2小时后到达B 处，PA B C30°60°北第5题图030第2题图40第1题图 北东ABC第6题图 第7题图在B 处测得灯塔C 在北偏西60°方向．当轮船到达灯塔C 的正东方向的D 处时，求此时轮船与灯塔C 的距离．（结果保留根号）技能点二 解决底部不能到达的测量问题8．燕尾槽的横断面是等腰梯形．如图是一燕尾槽的横断面，其中燕尾角B 是55，外口宽AD 是16cm ，燕尾槽的深度是6cm ，求它的里口宽BC (精确到cm ．9．某电视发射塔BC ，为稳固塔身，周围拉有钢丝地锚线（如图线段AB ），若AB =60m ，并且AB 与地面成45°角，欲升高发射塔的高度到CB /，同时原地锚线仍使用，若塔升高后使地锚线与地面成60°角，求电视发射塔升高了多少米（即BB /的高度）（精确到0.01m ）.参考答案1．040 西偏南050 040 东偏北050第8题图A /ACBB / 第9题图2．100 3．C4．5．6．D7．轮船与灯塔C 的距离为8．作AE BC DF BC ⊥⊥，，垂足分别为E ，F ，在Rt ABE △中，tan AEB BE=，∴ tan AE BE B ==6tan55．∴6221624.4tan55BC BE AD =+=⨯+≈（cm ）．答：燕尾槽的里口宽BC 约为24.4cm ．9．解：在Rt △ACB 中，因为∠BAC=450，AB=60m ，所以BC=AB·sin ∠BAC=60×sin450=302（m ）．在Rt △A /B /C 中，A /B /=60m ，∠B /A /C=600，所以B /C=A /B /·sin600=60×33023=（m ）．所以电视塔升高的高度： BB /=B /C-BC。
解直角三角形的应用(2方位角)
倍 速 课 时 学 练
三、解答题(共 40 分)
4 9．(12 分)如图所示，MN 表示某引水工程的一段设计路线，从 M 到 N 的走向为南偏东
30°，在 M 的南偏东 60°方向上有一点 A，以 A 为圆心，500 m 为半径的圆形区域为居民 区，取 MN 上另一点 B，测得 BA 的方向为南偏东 75° ，已知 MB＝ 400 m，通过计算回答， 如果不改变方向，输水路线是否会穿过居民区？
利用解直角三角形的知识解决实际问题的一般过程是：
（1）将实际问题抽象为数学问题（画出平面图形，转化
为解直角三角形的问题）； （2）根据条件的特点，适当选用锐角三角形函数等去
解直角三角形；
倍 速 课 时 学 练
（3）得到数学问题的答案； （4）得到实际问题的答案．
B
当海轮到达位于灯塔P的南偏东34°方向时，它距离灯塔P大约130.23海里
练习1
倍 速 课 时 学 练
倍 速 课 时 学 练
2. 海中有一个小岛A，它的周围8海里内有暗礁，渔船跟踪鱼群由 西向到航行，在B点测得小岛A在北偏东60°方向上，航行12海里 到达D点，这时测得小岛A在北偏到30°方向上，如果渔船不改变 航线继续向东航行，有没有触礁的危险？
倍 速 课 时 学 练
解：依题意得：∠AMN＝30°，∠ABN＝45°，过点 A 作 AC⊥MN 于点 C，在 Rt△ AC ABC 中， tan∠ABC＝ ， ∴BC＝AC， 由 MB＝MC－BC， 得 3AC－AC＝400， ∴AC＝200( 3 BC ＋1)≈546＞500，∴不改变方向，输水路线不会穿过居民区．
F
30°
3x AF tan 30 tan ABF BF 12 x
解直角三角形的应用-方向角问题-初中数学习题集含答案
一．填空题（共 5 小题） 1．（2018 秋•顺义区期末）轮船从 B 处以每小时 50 海里的速度沿南偏东 30 方向匀速航行，在 B 处观测灯塔 A 位于
南偏东 75 方向上，轮船航行半小时到达 C 处，在观测灯塔 A 北偏东 60 方向上，则 C 处与灯塔 A 的距离是 海里．
2．（2019 秋•东城区校级期中）如图，某货船以 24 海里 / 时的速度从 A 处向正东方向的 D 处航行，在点 A 处测得某 岛 C 在北偏东 60 的方向．该货船航行 30 分钟后到达 B 处，此时测得该岛在北偏东 30 的方向上．则货船在航行中 离小岛 C 的最短距离是 ．
3．（2017 春•西城区校级期中）如图，在点 A 测得某岛 C 在北偏东 60 方向上，且距 A 点18 3 海里，某船以每小时 36 海里的速度从点 A 向正东方向航行，航行半小时后到达 B 点，此时测得岛 C 在北偏东 30 方向上，已知该岛周围 16 海里内有暗礁． B 点与 C 岛的距离是 B 点暗礁区域 （填内或外）
7．（2016•延庆县一模）如图，甲船在港口 P 的南偏西 60 方向，距港口 86 海里的 A 处，沿 AP 方向以每小时 15 海 里的速度匀速驶向港口 P ．乙船从港口 P 出发，沿南偏东 45 方向匀速驶离港口 PC 2x ，现两船同时出发，2 小 时后乙船在甲船的正东方向．求乙船的航行速度．（结果精确到个位，参考数据： 2 1.414 ， 3 1.732 ， 5 2.236)
【分析】根据题中所给信息，求出 BCA 90 ，再求出 CBA 45 ，从而得到 ABC 为等腰直角三角形，然后根据 解直角三角形的知识解答．
【解答】解：根据题意，得 1 2 30 ， Q ACD 60 ， ACB 30 60 90 ， CBA 75 30 45 ， ABC 为等腰直角三角形， Q BC 50 0.5 25 ， AC BC 25 （海里）． 故答案为：25．
解直角三角形方位角问题
小结:
1.在解直角三角形及应用时经常接触到的一些概念
2.实际问题向数学模型的转化 3.解直角三角形的边角关系
成功就是99%的汗水， 加上1%的灵感。 ------爱迪生
如图，我校九（4）班的一个学习小组进行测量 孤山高度的实践活动。部分同学在山脚点A测得 山腰上一点D的仰角为30°，并测得AD的长度为 180米；另一部分同学在山顶点B测得山脚点A的 俯角为45°，山腰点D的俯角为60°。请你帮助 他们计算出小山的高度BC（计算过程和结果都 B H 不取近似值）。
A 60° B
12 30° 30°
D
F
3. 外国船只，除特许外，不得进入我国海洋 100海里以内的区域，如图，设A、B是我们的观 察站，A和B 之间的距离为150海里，海岸线是 过A、B的一条直线，一外国船只在P点，在A点 测得p点在北偏东600，同时在B点测得p点在北 偏西450， ，问此时是否要向外国船只发出警 告，令其退出我国海域. P
A
D
B
4.如图，MN表示某引水工程的一段设计路线，从M到N 的走向为南偏东30°，在M的南偏东60°方向上有一点 A，以A为圆心、500m为半径的圆形区域为居民区。取 MN上的另一点B，测得BA的方向为南偏东75°。已知 MB＝400m，通过计算回答，如果不改变方向，输水管 道是否会穿过居民区。
5.由于过度采伐森林和破坏植被，我国部分地区频 频遭受沙尘暴侵袭。近日，A城气象局测得沙尘暴 中心在A城的正南方向240km的B处，以每小时 12km的速度向北偏东30°方向移动，距沙尘暴中 心150km的范围为受影响区域。 1）A城是否受到这次沙尘暴的 影响，为什么？ （2）若A城受这次沙尘暴的影响， 那么遭受影响的时间有多长？
60° P C A
25.4 解直角三角形的应用(2)
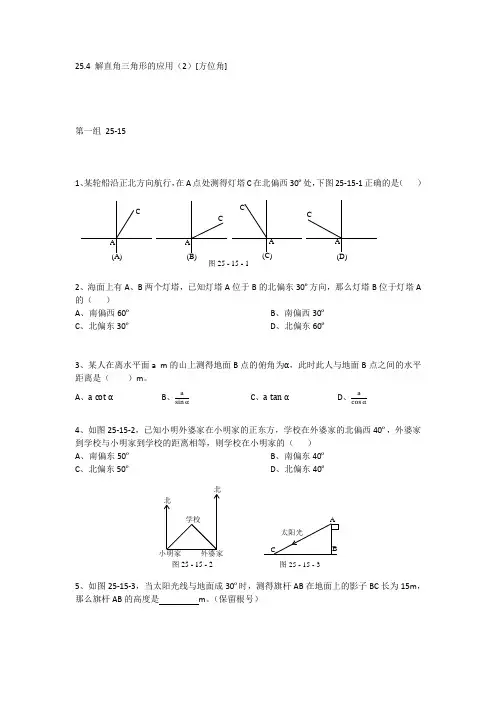
25.4 解直角三角形的应用（2）[方位角]第一组 25-151、某轮船沿正北方向航行，在A 点处测得灯塔C 在北偏西30º处，下图25-15-1正确的是（ ）2、海面上有A 、B 两个灯塔，已知灯塔A 位于B 的北偏东30º方向，那么灯塔B 位于灯塔A 的（ ）A 、南偏西60ºB 、南偏西30ºC 、北偏东30ºD 、北偏东60º3、某人在离水平面a m 的山上测得地面B 点的俯角为α，此时此人与地面B 点之间的水平距离是（ ）m 。
A 、a cot α B 、a sin αC 、a tan αD 、acos α4、如图25-15-2，已知小明外婆家在小明家的正东方，学校在外婆家的北偏西40º，外婆家到学校与小明家到学校的距离相等，则学校在小明家的（ ） A 、南偏东50º B 、南偏东40º C 、北偏东50º D 、北偏东40º5、如图25-15-3，当太阳光线与地面成30º时，测得旗杆AB 在地面上的影子BC 长为15m ，那么旗杆AB 的高度是 m 。
（保留根号）图 25 - 15 - 1(D)A CA C CA CA 图 25 - 15 - 2小明家学校北北图 25 - 15 - 3BA太阳光C6、某人从A 点出发，向北偏东45º方向走到B 点，再从B 点出发，向南偏西15º方向走到C 点，那么∠ABC= 。
7、如图25-15-4，点B 在点A 北偏西30º方向，且AB=5km ，点C 在点B 北偏东60º方向，且BC=12km ，则A 到C 的距离是 。
8、如图25-15-5，一轮船以每小时20海里的速度沿正东方向航行，上午8时，该船在A 处测得某灯塔位于它的北偏东30º的B 处，上午9时行至C 处，测得灯塔恰好在它的正北方向，此时它与灯塔的距离是 海里。
解直角三角形的应用(方位角)
解直角三角形的应用1.居民小区有一朝向为正南方向的居民楼（如图），该居民楼的一楼是高6米的小区超市，超市以上是居民住房.在该楼的前面15米处要盖一栋高20米的新楼.当冬季正午的阳光与水平线的夹角为32°时.（1）该超市以上的居民住房采光是否有影响？请说明理由。
（2）若要使超市采光不受影响，两楼应相距多少米？（结果保留整数）2.学校准备在相距5km的A、B两地之间修筑一条笔直的公路，经测量，在A地的北偏东60°、B地的北偏西45°方向的C处有一个半径为1.8km的湖泊，计划修筑的这条公路是否会穿过湖泊？请说明理由。
3．如图，海上有一灯塔P，在它周围的3海里处有暗礁，一艘客轮以9海里/时的速度由西向东航行，航行到A处测得P在它的北偏东60︒方向，继续航行20分钟后，到达B处又测得灯塔P在它的北偏东45︒方向，若该客轮不改变方向，继续前行有无触礁的危险？请说明理由。
4.如图，有两条公路OM、ON相交成30°角，沿公路OM方向80m的A处有一所小学，当拖拉机沿ON方向行驶时，路两旁50m的范围内会受到噪音的影响，已知拖拉机的速度为18km/h，那么拖拉机沿ON方向行驶将给小学带来噪音影响的时间有多长？5.如图，A城气象部门测得今年第九号台风上午8时在A城南偏东22.5°的海面B点生成，并以每小时640千米的速度向正北方向移动，上午10时测得台风中心移到了A城南偏东45°方向，若台风中心140千米的范围内将受台风影响，则A城是否会受九号台风影响？请说明理由。
6．根据气象观测，距沿海某城市A的正南方向220千米B处有一台风中心，其中的最大风力为12级，每远离台风中心20千米，风力就会减弱一级，台风中心现正以15千米/小时的速度沿北偏东30°方向往C移动，但台风中心风力不变，若城市所受风力达到或超过四级，则称为受台风影响。
（1）该城市是否会受到台风的影响？请说明理由。
解直角三角形第三课时(方位角)
A
N1
NБайду номын сангаас
D X
C
24海里
B
答：货轮无触礁危险。
课堂检测：1、.海中有一个小岛A，它的周围8海里范 围内有暗礁，渔船跟踪鱼群由西向东航行，在B点测得 小岛A在北偏东60°方向上，航行12海里到达D点，这 时测得小岛A在北偏东30°方向上，如果渔船不改变航 线继续向东航行，有没有触礁的危险？
A
B
12
D
F
2、王英同学从A地沿北偏西60º 方向走100m到B地， 再从B地向正南方向走200m到C地，此时王英同 学离A地多少距离？
北 E B 西 D
100m 600
东 A
200m
南 C
1、解直角三角形的关键是找到与已知和未知相关联
的直角三角形，当图形中没有直角三角形时，要通过 作辅助线构筑直角三角形（作某边上的高是常用的辅 助线）；当问题以一个实际问题的形式给出时，要善 于读懂题意，把实际问题化归为直角三角形中的边角 关系。 2、一些解直角三角形的问题往往与其他知识联系， 所以在复习时要形成知识结构，要把解直角三角形作 为一种工具，能在解决各种数学问题时合理运用。
解直角三角形的应用（第三课时）
方位角问题
北
西
东
南
方位角
指南或指北的方向线与目标方向线构成小于 900的角,叫做方位角. 如图：点A在O的北偏东30° 点B在点O的南偏西45°（西南方向）
北 30° A
西
O 45°
东
B
南
探究一例3. 如图，一艘海轮位于灯塔P的北偏东
65°方向，距离灯塔80海里的A处，它沿正南方向航行 一段时间后，到达位于灯塔P的南偏东34°方向上的B 处，这时，海轮所在的B处距离灯塔P有多远？ （精确 到0.01海里）
解直角三角形 的应用(方位角)
D
450
B
拓展提高
今年5、6月份，某省各地、市普遭暴雨袭击，某市抗洪抢险救 援队伍在B处接到报告，有受灾群众被困于一座水淹的楼顶A处， 情况危急，救援队伍在B处测 得A在B的北偏东600的方向上， 队伍决定分成两组，第一组马上下水游向A处救人，同时第二组 从陆地往正东方向奔跑120米到达C处,再从C处下水游向A处救 人，已知A在C的北偏东300的方向上，且救援人员在水中游泳 的速度为每秒1米，在陆地上奔跑的速度为每秒4米，试问那组 先到处?请说明理由。
∴ EF = 2CE = 2 x 90 = 180 M ∴ A城受到沙尘暴影响的时间为 180÷12 = 15小时 答：A城将受到这次沙尘暴影响， 影响的时间为15小时。 B E A C F
例4：我市准备在相距2千米的A、B两工厂间修一条笔直的公路， 但在A地的北偏东600方向，B地的北偏西450方向的C处，有一个半 径为0.6千米的圆形住宅小区，问修公路时，这个小区是否有 居民 需要搬迁？（参考数据：2 1.41, 3 1.73 ） C 600
解直角三角形的应用(1)
1、解直角三角形的思想
B
c a C
模型思想
2、解直角三角形的依据 ⑴ 三边之间的关系 ⑵ 锐角之间的关系 ⑶ 边角之间的关系 A
b
a2＋b2＝c2（勾股定理）；
∠ A＋ ∠ B＝ 90º
a b a sin A , cos A , tan A , c c b
特殊角： 30°，45°，60°角的正弦、余弦、正切值.
例3
解:
过A作AC⊥BM,垂足为C, 在Rt△ABC中， ∠B = 30°, 1 1 ∴AC= 2 AB = x 240 = 120 2 ∵AC = 120 < 150 ∴A城受到沙尘暴影响 M A C
【浙教版】2022年九年级(上)期末复习培优提分专项训练：解直角三角形的应用(方位角问题)(原卷)
【浙教版】2022年九年级（上）期末复习培优提分专项训练解直角三角形的应用（方位角问题）1．（2022·浙江宁波·一模）如图，某渔船沿正东方向以10海里／小时的速度航行，在A处测得岛C在北偏东60°方向，1小时后渔船航行到B处，测得岛C在北偏东30°方向，已知该岛周围9海里内有暗礁．参考数据：√3≈1.732，sin75°≈0.966，cos75°≈0.259．(1)B处离岛C有多远？如果渔船继续向东航行，有无触礁危险？(2)如果渔船在B处改为向东偏南15°方向航行，有无触礁危险？2．（2022·浙江宁波·九年级专题练习）我国海域辽阔，渔业资源丰富，如图，现有渔船以18√2km/ℎ的速度在海面上沿正东方向航行，当行至A处时，发现它的东南方向有一灯塔B，船续向东航行30min后达到C处，发现灯塔B在它的南偏东15°方向．(1)求此时渔船与灯塔B的距离．(2)若渔船继续向东行驶，还要行驶多少千米与B的距离达到最小值．（参考数据：sin75°≈0.97，cos75°≈0.26，tan75°≈3.73）3．（2022·浙江宁波·一模）如图，C岛在A岛的北偏东45°方向，在B岛的北偏西25°方向．(1)直接写出∠ACB的度数是；(2)测量发现∠BAC=20°，A岛与C岛之间的距离AC=20海里，求A岛与B岛之间的距离．（结果精确到0.1海里）（参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36）4．（2021·浙江丽水·一模）如图，某海岸边有B，C两个码头，C码头位于B码头的正东方向，距离B码头60海里．甲、乙两船同时从A岛出发，甲船向位于A岛正北方向的B码头航行，乙船向位于A岛北偏东30°方向的C码头航行，当甲船到达距离B码头45海里的E 处时，乙船位于甲船北偏东60°方向的D处，求此时乙船与C码头之间的距离．（结果保留根号）5．（2022·浙江·一模）小明在A点测得C点在A点的北偏西75°方向，并由A点向南偏西45°方向行走到达B点测得C点在B点的北偏西45°方向，继续向正西方向行走2km后到达D 点，测得C点在D点的北偏东22.5°方向，求A，C两点之间的距离．（结果保留0.1km．参数数据√3≈1.732）6．（2022·浙江金华·一模）某海域有A，B两个岛屿，B岛在A岛北偏西30°方向上，距A岛120海里．有一艘船从A岛出发，沿东北方向行驶一段距离后，到达位于B岛南偏东75°方向的C处．(1)求∠BCA的度数．(2)求BC的长．7．（2022·浙江宁波·九年级期末）如图，某渔船向正东方向以14海里/时的速度航行，在A处测得小岛C在北偏东70∘方向，2小时后渔船到达B处，测得小岛C在北偏东45∘方向，已知该岛周围20海里范围内有暗礁．（参考数据：sin70∘≈0.94,cos70∘≈0.34,tan70∘≈2.75,√2≈1.41）(1)求B处距离小岛C的距离（精确到0.1海里）；(2)为安全起见，渔船在B处向东偏南转了25∘继续航行，通过计算说明船是否安全？8．（2021·浙江·杭州外国语学校九年级阶段练习）阅读下列材料，并解决问题．如图（1），在锐角△ABC中，∠A，∠B，∠C的对边分别是a，b，c，过点A作AD∠BC于点D，则sinB=ADc ，sinC=ADb，即AD＝c sin B，AD＝b sin C．于是c sin B＝b sin C，即bsinB=csinC．同理有：csinC =asinA，asinA=bsinB，所以asinA=bsinB=csinC．即在一个三角形中，各边和它所对角的正弦的比相等．在锐角三角形中，若已知三个元素（至少有一条边），运用上述结论就可以求出其余三个未知元素．（1）如图（2），一货轮在B处测得灯塔A在货轮的北偏东15°的方向上，随后货轮以80海里/时的速度向正东方向航行，半小时后到达C处，此时又测得灯塔A在货轮的北偏西30°的方向上，求此时货船距灯塔A的距离AC．（2）在（1）的条件下，试求75°的正弦值．（结果保留根号）9．（2020·浙江衢州·九年级期末）某社会实践活动小组实地测量河两岸互相平行的一段河的宽度，在河的南岸边点A处，测得河的北岸边点B在其北偏东45°方向，然后向西走50m 到达C点，测得点B在点C的北偏东60°方向，如图．（1）求∠CBA的度数；（2）求这段河的宽度．（结果精确到1m）10．（2022·重庆·四川外国语大学附属外国语学校九年级期中）期中测试临近学生都在紧张的复习中，小甘和小西相约周末去图书馆复习，如图，小甘从家A地沿着正东方向走900m 到小西家B地，经测量图书馆C地在B地的北偏东15°，C地在A地的东北方向．(1)求AC的距离：(2)两人准备从B地出发，实然接到疾控中心通知，一名确诊的新冠阳性患者昨天经过了C 地，并沿着C地南偏东22°走了1800m到达D地，根据相关要求，凡是确诊者途径之处800m 区域以内都会划为管控区，问：小西家会被划为管控区吗？请说明理由（参考数据：√3≈1.73,√2≈1.41,√6≈2.45,sin37°≈0.6,cos37°≈0.8,tan37°≈0.75）．11．（2021·河南·辉县市太行中学九年级期中）如图，一位自行车爱好者沿宿鸭湖湖边正东方向笔直的公路BC骑行，在B地测得湖中小岛上某建筑物A在北偏东45°方向，行驶12min 后到达C地，测得建筑物A在北偏西60°方向，如果此自行车爱好者的速度为60km/h，求建筑物A到公路BC的距离．（结果保留根号）【分母有理化：√3+1=√3−1(√3+1）)(√3-−1)=√3−12】12．（2022·上海市民办新复兴初级中学九年级期中）如图，一艘海岸巡逻快艇在基地A的正东方向，且距A地13海里的B处巡逻．突然接到基地A命令，要该快艇前往C岛，接送一名病人到基地A的医院救治．已知C岛在基地A的南偏东α的方向，且在B处南偏东β的方向，巡逻快艇从B处出发，平均每小时行驶30海里，需要多少时间才能把病人送到基地A的医院？（参考数据：tanα=158，sinβ=45）13．（2022·山东青岛·九年级期中）九年级二班学生到某劳动教育实践基地开展实践活动，当天，他们先从基地门口A处向正北方向走了220米，到达菜园B处锄草，再从B处沿正西方向走了200米，到达果园C处采摘水果，再向南偏东37°方向走了200米，到达手工坊D处进行手工制作，最后从D处回到门口A处．(1)求从手工坊D处回到门口A处的距离．(2)求从手工坊D处回到门口A处的方位角．[参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75]14．（2022·重庆一中九年级阶段练习）公园大门A的正东方向原本有一条通往湖心小岛B的景观步道AB，但为了让市民朋友多角度欣赏公园景色，市政府决定新修一条景观步道通往湖心小岛B，新步道从A出发通向C地，C位于A的北偏西45°方向，AC=800米，再从C 地到达湖心小岛B，其中C位于B的北偏西60°方向，甲工程队以每天60米的速度进行单独施工，2天后，为了加快工程进度，乙工程队以每天90米的速度加入项目建设，直到两队起完成景观步道的修建．（参考数据：√2≈1.4）(1)求A、B两地的距离（结果保留根号）；(2)新的景观步道能否在15天内完成？请说明理由．15．（2022·山东·济南市大学城实验学校九年级阶段练习）如图，三角形花园ABC紧邻湖泊，四边形ABDE是沿湖泊修建的人行步道．经测量，点C在点A的正东方向，AC=200米．点E在点A的正北方向．点B，D在点C的正北方向，BD=100米．点B在点A的北偏东30°，点D在点E的北偏东45°．(1)求步道DE的长度（精确到个位）；(2)点D处有直饮水，小红从A出发沿人行步道去取水，可以经过点B到达点D，也可以经过点E到达点D．请计算说明他走哪一条路较近？（参考数据：√2≈1.4，√3≈1.7）16．（2022·上海·九年级专题练习）如图，在东西方向的海岸线l上有长为300米的码头AB，在码头的最西端A处测得轮船M在它的北偏东45°方向上；同一时刻，在A点正东方向距离100米的C处测得轮船M在北偏东22°方向上．（参考数据：sin22°≈0.375，cos22°≈0.927，tan22°≈0.404，√3≈1.732．）(1)求轮船M到海岸线l的距离；（结果精确到0.01米）(2)如果轮船M沿着南偏东30°的方向航行，那么该轮船能否行至码头AB靠岸？请说明理由．17．（2022·上海·九年级专题练习）如图，在航线l的两侧分别有两个灯塔A和B，灯塔A到航线l的距离为AC=3千米，灯塔B到航线l的距离为BD=4千米，灯塔B位于灯塔A南偏东60°方向．现有一艘轮船从位于灯塔B北偏西53°方向的N（在航线l上）处，正沿该航线自东向西航行，10分钟后该轮船行至灯塔A正南方向的点C（在航线l上）处．（参考数据：√3≈1.73，sin53°≈0.80，cos53°≈0.60，tan53°≈1.33）(1)求两个灯塔A和B之间的距离；(2)求该轮船航行的速度（结果精确到0.1千米/小时）．18．（2022·重庆八中九年级阶段练习）如图，在竖直的海岸线上有长为68米的码头AB，现有一艘货船在点P处，从码头A处测得货船在A的东南方向，若沿海岸线向南走30米后到达点C，在C处测得货船在C的南偏东75°方向．（参考数据：√2≈1.41，√3≈1.73，√6≈2.45）(1)求货船到A的距离（结果精确到1米）；(2)若货船从点P出发，沿着南偏西60°的方向行驶，请问该货船能否行驶到码头所在的线段AB上？请说明理由．19．（2022·四川·仁寿县黑龙滩镇光相九年制学校九年级期末）小明周未与父母一起到眉山湿地公园进行数学实践活动，在A处看到B，C处各有一棵被湖水隔开的银杏树.他在A处测得B在西北方向，C在北偏东30°方向.他从A处走了20米到达B处，又在B处测得C在北偏东60°方向．(1)求∠C的度数；(2)求两棵银杏树B，C之间的距离．（结果保留根号）20．（2022·广东·广州市越秀区育才实验学校二模）如图，我国一艘海监执法船在南海海域进行常态化巡航，在A处测得北偏东30°方向距离为40海里的B处有一艘可疑船只正在向正东方向航行，我海监执法船便迅速沿北偏东75°方向前往监视巡查，经过一段时间在C处成功拦截可疑船只．求我海监执法船前往监视巡查的过程中行驶的路程（即AC长）？（结果精确到0.1海里，√3≈1.732，√2≈1.414，√6≈2.449）21．（2021·山东·泰安市泰山区大津口中学九年级阶段练习）如图，在一笔直的海岸线l上有AB两个观测站，A在B的正东方向，AB=2（单位：km）．有一艘小船在点P处，从A测得小船在北偏西60°的方向，从B测得小船在北偏东45°的方向．(1)求点P到海岸线l的距离；(2)小船从点P处沿射线AP的方向航行一段时间后，到点C处，此时，从B测得小船在北偏西15°的方向．求点C与点B之间的距离．（上述两小题的结果都保留根号）22．（2022·湖南湘潭·八年级期末）如图，一艘渔船以30海里/h的速度由西向东追赶鱼群，在A处测得小岛C在船的北偏东60°方向；40min后，渔船行至B处，此时测得小岛C在船的北偏东30°方向．已知以小岛C为中心，周围10海里以内有暗礁，问这艘渔船继续向东追赶鱼群是否有触礁的危险？23．（2022·黑龙江·哈尔滨市风华中学校九年级阶段练习）如图，海中有一个小岛A，它周围8n mile 内有暗礁. 渔船跟踪鱼群由西向东航行，在B点测得小岛A在北偏东60∘方向上，航行12n mile 到达D点，这时测得小岛A在北偏东30∘方向上．如果渔船不改变航线继续向东航行，有没有触礁的危险？24．（2022·黑龙江·大庆市祥阁学校九年级期中）为了维护我国海域安全，某巡逻艇从码头A 出发向东航行40海里后到达B处，再从B处沿北偏东30°方向行驶40海里到达C处，然后沿北偏西60°方向航行到D处，发现码头A在正南方向．求此时巡逻艇与码头A的距离．(结果保留根号）25．（2022·四川资阳·中考真题）小明学了《解直角三角形》内容后，对一条东西走向的隧道AB进行实地测量．如图所示，他在地面上点C处测得隧道一端点A在他的北偏东15°方向上，他沿西北方向前进100√3米后到达点D，此时测得点A在他的东北方向上，端点B在他的北偏西60°方向上，（点A、B、C、D在同一平面内）(1)求点D与点A的距离；(2)求隧道AB的长度．（结果保留根号）26．（2022·重庆市江津中学校八年级阶段练习）某海域有一小岛P，在以P为圆心，半径r 为10(3+√3)海里的圆形海域内有暗礁．一海监船自西向东航行，它在A处测得小岛P位于北偏东60°的方向上，当海监船行驶20√5海里后到达B处，此时观测小岛P位于B处北偏东45°方向上．(1)求A、P之间的距离AP；(2)若海监船由B处继续向东航行是否有触礁危险？请说明理由．27．（2022·重庆市第三十七中学校九年级阶段练习）海洋安全预警系统为海洋安全管理起到了巨大作用，某天海洋监控中心收到信息，在A的北偏西60°方向的120海里的C处，疑似有海盗船在沿CB方向行驶，C在B的北偏西30°方向上，监控中心向A正西方向的B处海警船发出指令，海警船立即从B出发沿BC方向行驶，在距离A为60√2海里的D处拦截到该可疑船只．(1)求点A到直线CB的距离；(2)若海警船的速度是30海里/小时，那么海警船能否在1小时内拦截到可疑船只？请说明理由．（结果保留一位小数，参考数据：√3≈1.73）28．（2021·河南·油田十中九年级阶段练习）如图，是学生小金家附近的一块三角形绿化区的示意图；为增强体质，他每天早晨都沿着绿化区周边小路AB，BC，CA跑步（小路的宽度不计），观测得点B在点A的南偏东30°方向上，点C在点A的南偏东60°的方向上，点B 在点C的北偏西75°方向上，AC间距离为400米．小金沿三角形绿化区的周边小路跑一圈共跑了多少米？（结果精确到1米，参考数据：√2≈1.4，√3≈1.7）29．（2022·贵州安顺·中考真题）随着我国科学技术的不断发展，5G移动通信技术日趋完善．某市政府为了实现5G网络全覆盖，2021~2025年拟建设5G基站3000个，如图，在斜坡CB上有一建成的5G 基站塔AB ，小明在坡脚C 处测得塔顶A 的仰角为45°，然后他沿坡面CB 行走了50米到达D 处，D 处离地平面的距离为30米且在D 处测得塔顶A 的仰角53°．（点A 、B 、C 、D 、E 均在同一平面内，CE 为地平线）（参考数据：sin53°≈45，cos53°≈35，tan53°≈43）(1)求坡面CB 的坡度；(2)求基站塔AB 的高．30．（2022·辽宁丹东·中考真题）如图，我国某海域有A ，B ，C 三个港口，B 港口在C 港口正西方向33.2nmile （nmile 是单位“海里”的符号）处，A 港口在B 港口北偏西50°方向且距离B 港口40nmile 处，在A 港口北偏东53°方向且位于C 港口正北方向的点D 处有一艘货船，求货船与A 港口之间的距离．（参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.19，sin53°≈0.80，cos53°≈0.60，tan53°≈1.33．）。
解直角三角形应用(方位角、仰角、俯角)[1]
![解直角三角形应用(方位角、仰角、俯角)[1]](https://img.taocdn.com/s3/m/45a0d012c281e53a5902ff04.png)
1PC B B解直角三角形应用题（方位角、仰角、俯角）1、 如图海岛A 四周20海里内为暗礁区，一艘货轮由东向西航行，在B 处见岛A 在北偏西60°，航行24海里岛C 见岛A 在北偏西302、 国外船只除特许外不得进入我国海洋100海里内航行，如图设A 、B 是我们的观察站，A和B 之间的距离是157.73海里，海岸线是过A 、B 的一条直线，一外国船只在P 点，在A 点测得∠BAP=45°，同时在B 点测得∠ABP=60°，问此时是否要向外国船只发出警告令其退出我国领海。
3、 小明同学从A 地沿北偏西60°方向走100米到达B 地，再从B 的沿正南方向走200米到达C 地，此时小明同学离A 地多远？4、 海中有一个小岛A ，它的周围8海里范围内有暗礁，渔船跟踪鱼群由西向东航行，在B 点测得小岛A 在北偏东60°方向上，航行12海里到达D 点，这时测得小岛A 在北偏东30°方向上，如果渔船不改变航线继续向东航行，有没有触礁的危险？5、为建设“宜居宜业宜游”山水园林式城市，某市正在对城区某河段进行区域性景观打造. 如图，某施工单位为测得某河段的宽度，测量员先在河对岸边取一点A ，再在河这边沿河取 两点B C 、，在点B 处测得点A 在北偏东30°方向上，在点C 处测得点A 在西北方向上，量 得BC 长为200米.请你求出该河段的宽度（结果保留根号）.6、放风筝是大家喜爱的一种运动．星期天的上午小明在大洲广场上放风筝．如图他在A 处时不小心让风筝挂在了一棵树的树梢上，风筝固定在了D 处．此时风筝线AD 与水平线的夹角为30°． 为了便于观察．小明迅速向前边移动边收线到达了离A 处7米的B 处，此时风筝线BD 与水平线的夹角为45°．已知点A 、B 、C 在冋一条直线上，∠ACD=90°．请你求出小明此吋所收回的风筝线的长度是多少米？（本题中风筝线均为线段，≈1.414≈1.732．最后结果精确到1米）第 1 页2LP 地面A7、去年某省将地处A 、B 两地的两所大学合并成一所综合性大学，为了方便A 、B 两地师生的交往，学校准备在相距2千米的A 、B 两地之间修筑一条笔直公路（即图中的线段AB ），经测量，在A 地的北偏东60°方向，B 地向西偏北45°方向的C 处有一个半径为0.7千米的公园，问计划修筑的这条公路会不会穿过公园？为什么？8、 在山顶上D 处由一铁塔，在塔顶B 处测得地面一点A 的俯角为60°，在塔底D 测得点A的俯角为45°，已知塔高BD=30米，求山高CD 。
九年级数学上册4.4解直角三角形的应用第3课时与方位角有关的应用问题练习湘教版
第3课时与方位角有关的应用问题基础题知识点与方位角有关的应用问题1．如图，某海监船和一渔船同时从点A动身，海监船沿正北方向MN航行，渔船往北偏东60°方向以40海里/时的速度航行，渔船半小时后抵达B处，现在渔船恰好在海监船的正东方向，则现在渔船与海监船的距离为( )A．20海里B．103海里C．202海里D．30海里2．如图，某人从O点沿北偏东30°的方向走了20米抵达A点，B在O点的正东方，且在A 的正南方，则现在AB间的距离是________米．(结果保留根号)3．如图，C、D是两个村落，别离位于一个湖的南、北两头A和B的正东方向上，且D位于C的北偏东30°方向上，且CD＝6 km，则AB＝________km.4．(长春中考)如图，海面上B、C两岛别离位于A岛的正东和正北方向，一艘船从A岛动身，以18海里/时的速度向正北方向航行2小时抵达C岛，现在测得B岛在C岛的南偏东43°.求A、B两岛之间的距离．(结果精准到海里，参考数据：sin43°≈，cos43°≈，tan43°≈5．(湘西中考)钓鱼岛自古以来就是中国的神圣领土，为宣誓主权，我海监船编队受命在钓鱼岛周围海域进行维权活动，如图，一艘海监船以30海里/时的速度向正北方向航行，海监船在A处时，测得钓鱼岛C在该船的北偏东30°方向上，航行半小时后，该船抵达点B处，发觉现在钓鱼岛C与该船距离最短．(1)请在图中作出该船在点B处的位置；(2)求钓鱼岛C到B处的距离．(结果保留根号)6．(宜宾中考)如图，某市对位于笔直公路AC上两个小区A、B的供水线路进行优化改造．供水站M在笔直公路AD上，测得供水站M在小区A的南偏东60°方向，在小区B的西南方向，小区A、B之间的距离为300(3＋1)米，求供水站M别离到小区A、B的距离．(结果可保留根号)中档题7．(滨湖区校级二模)某人从A处动身沿北偏东30°方向走了100米抵达B处，再沿北偏西60°方向走了100米抵达C处，则他从C处回到A处至少要________米．8．(昭通中考)小亮一家在一湖泊中游玩，湖泊中有一孤岛，妈妈在孤岛P处观看小亮与爸爸在湖中划船(如图所示)．小船从P处动身，沿北偏东60°方向划行200米到A处，接着向正南方向划行一段时刻到B处．在B处小亮观测到妈妈所在的P处在北偏西37°的方向上，这时小亮与妈妈相距多少米(精准到1米)？(参考数据：sin37°≈，cos37°≈，tan37°≈，2≈，3≈9．(邵阳中考)一艘参观游船从口岸A以北偏东60°的方向出港参观，航行80海里至C处时发生了侧翻沉船事故，当即发出了求救信号，一艘在口岸正东方向的海警船接到求救信号，测得事故船在它的北偏东37°方向，马上以40海里每小时的速度前去救援，求海警船抵达事故船C处所需的大约时刻．(温馨提示：sin53°≈，cos53°≈10．如图，在东西方向的海岸线MN上有A、B两艘船，均收到已触礁搁浅的船P的求救信号，已知船P在船A的北偏东58°方向，船P在船B的北偏西35°方向，AP的距离为30海里．(参考数据：sin32°≈，cos32°≈，sin55°≈，cos55°≈(1)求船P到海岸线MN的距离(精准到海里)；(2)若船A、船B别离以20海里/时、15海里/时的速度同时动身，匀速直线前去救援，试通过计算判断哪艘船先抵达船P处．综合题11．(苏州中考改编)如图，口岸A在观测站O的正东方向，OA＝4 km，某船从口岸A动身，沿北偏东15°方向航行一段距离后抵达B处，现在从观测站O处测得该船位于北偏东60°的方向，求该船航行的距离(即AB的长)．参考答案基础题1．B4.由题意得，AC＝18×2＝36(海里)，∠ACB＝43°.在Rt△ABC中，∵∠A＝90°，∴AB＝AC·tan∠ACB＝36×≈(海里)，故A、B两岛之间的距离约为海里．5.(1)如图所示.(2)AB＝30×＝15(海里)，由题意知CB⊥AB，在Rt△ABC中，∠BAC＝30°，tan∠BAC＝BC AB，∴BC＝AB·tan∠BAC＝AB·tan30°＝15×33＝53(海里)．答：钓鱼岛C到B处的距离为53海里．6.过点M作MN⊥AB于N，设MN＝x米．在Rt△AMN中，∵∠ANM＝90°，∠MAN＝30°，∴MA＝2MN＝2x，AN＝3MN＝3x.在Rt△BMN中，∵∠BNM＝90°，∠MBN＝45°，∴BN＝MN＝x，MB＝2MN＝2x.∵AN＋BN＝AB，∴3x＋x＝300(3＋1)．∴x＝300.∴MA＝2x＝600，MB＝2x＝300 2.故供水站M到小区A的距离是600米，到小区B的距离是3002米．中档题7．100 28.过P作PC⊥AB于C.在Rt△APC中，AP＝200 m，∠ACP＝90°，∠PAC＝60°，∴PC ＝200×sin60°＝200×32＝100 3.∵在Rt △PBC 中，sin37°＝PC PB， ∴PB ＝PCsin37°＝错误!≈288(m)．答：小亮与妈妈相距约288米． 9.过点C 作CD ⊥AB 交AB 延长线于D.在Rt △ACD 中，∵∠ADC ＝90°，∠CAD ＝30°，AC ＝80海里，∴CD ＝12AC ＝40海里．在Rt △CBD 中，∵∠CDB ＝90°，∠CBD ＝90°－37°＝53°，∴BC ＝CDsin ∠CBD≈错误!＝50(海里)．∴海警船抵达事故船C 处所需的时刻大约为：50÷40＝54(小时)．答：海警船抵达事故船C 处所需时刻约为54小时．10.(1)过点P 作PD ⊥A B 于点D.由题意，得∠PAB ＝90°－58°＝32°，∠PBD ＝90°－35°＝55°，AP ＝30，在Rt △ADP 中，sin ∠PAD ＝PDAP ，得PD ＝AP·sin∠PAD ＝30×sin32°≈.答：船P 到海岸线MN 的距离约为海里． (2)在Rt △BDP 中，sin ∠PBD ＝PDBP，∴BP ＝PDsin ∠PBD ＝错误!≈，A 船需要时刻为错误!＝(小时)，B 船需要时刻为错误!≈(小时)． ∵＞，∴B 船先抵达P 处．答：B 船先抵达P 处． 综合题11．过点A 作AD ⊥OB 于D.在Rt △AOD 中，∵∠ADO ＝90°，∠AOD ＝30°，OA ＝4， ∴AD ＝OA·sin∠AOD ＝2.在Rt △ABD 中，∵∠ADB ＝90°，∠B ＝∠CAB －∠AOB ＝75°－30°＝45°， ∴BD ＝AD ＝2.∴AB ＝2AD ＝22，即该船航行的距离(即AB 的长)为2 2 km.。
解直角三角形的应用(方位角)
当堂练习
1、海中有一个小岛A，它的周围8海里内有暗礁，鱼 船跟踪鱼群由西向东航行。在B点测得小岛A在北偏 东60°方向上，航行12海里到达点D，这时测得小岛A 在北偏东30°方向上，如果鱼船不改变航线继续向东 航行，有没有触礁的危险？
A
B D
当堂练习
2、如图，某船以29.8海里/时的速度向正北方向航 行，在A处测得灯塔C在该船的北偏东32°方向上， 半小时后该船航行到点B处，发现此时灯塔C与船 的距离最短。 (1)在图上标出点B的位置； (2)求灯塔C到B处的距离(精确到0.1海里)。
复习
如图，在高为300m的山顶上，测得一 建筑物顶端与底端的俯角分别为30°和 60°，求该建筑物的高。
A C
300m
BD
方位角的定义：
指北或指南方向线与目标方向线所 成的小于90°的角叫做方位角。
认识方位角
北 D E
45° 45°
西
C
O
F
B南
（1）正东，正南，正西，正北
射线OA OB OC OD H（2）西北方向:_射__线__O_E___
探究
例题：如图，一艘海轮位于灯塔P的北偏东65°方向 ，距离灯塔80海里的A处，它正沿着正南方向航行一 段时间后，到达位于灯塔P的南偏东34°方向上的B处 ，这时，海轮所在的B处距离灯塔P有多远？
北
A
P
C
B
小结
解直角三角形的应用：
(1)将实际问题抽象为数学问题(画出平面 图形，转化为解直角三角形的问题)； (2)根据条件的特点，适当选用锐角三角 函数等知识去解直角三角形； (3)得到数学问题答案； (4)得到实际问题答案；
北 P东
A
当堂练习
第6课 解直角三角形的应用——方位角(课时作业)
第6课解直角三角形的应用（二）方向角（作业）1．如图，某渔船在海面上朝正东方向匀速航行，在A处观测到灯塔M在北偏东60° 方向上，且AM＝100海里，那么该船继续航行多少海里可使渔船到达离灯塔最近的位置．2．如图，一艘轮船以每小时10海里的速度沿正北方向航行，在A处测得灯塔C在北偏西30°方向，轮船航行2小时后到达B处，在B处测得灯塔C在北偏西60°方向．当轮船到达灯塔C的正东方向的D处时，求此时轮船与灯塔C的距离．(结果保留根号)3．如图，一艘海轮位于灯塔P的北偏东30°方向，距离灯塔80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，这时，海轮所在的B处与灯塔P的距离为多少海里．(结果保留根号)4．如图，在东西方向的海岸线MN 上有A 、B 两艘船，均收到已触礁搁浅的船P 的求救信号，已知船P 在船A 的北偏东60°方向，船P 在船B 的北偏西35°方向，AP 的距离为30海里．求PB 的长．(精确到0.1海里，参考数据：sin 35°≈0.57，cos 35°≈0.82)5. 如图，海平面上灯塔O 方圆100千米范围内有暗礁，一艘轮船自西向东航行，在点A 处测得灯塔O 在北偏东60°方向，继续航行100千米后，在点B 处测得灯塔O 在北偏东37°方向．请判断，为了避免触礁，这艘轮船是否要改变航向？(参考数据：sin 37°≈0.6， cos 37°≈0.80，tan 37°≈0.75，√3≈1.73)6.一艘轮船以每小时10海里的速度在B 点沿正南方向航行，在灯塔A 处测得B 在北偏东26°方向，轮船航行2小时后到达C 处，在A 处测得C 在北偏东45°方向，当轮船到达灯塔A 的正东方向D 时，求此时轮船与灯塔A 的距离. (参考数据：sin 26°≈0.4， cos 26°≈0.9，tan 37°≈0.5)CA。
解直角三角形(方位角)
海中有一个小岛A，它的周围8海里范围 内有暗礁，渔船跟踪鱼群由西向东航行，在B点 测得小岛A在北偏东60°方向上，航行12海里到 达D点，这时测得小岛A在北偏东30°方向上， 如果渔船不改变航线继续向东航行，有没有触 礁的危险？
A
30° 60°
B
12
D
F
1. 海中有一个小岛A，它的周围8海里内有暗礁，渔船跟踪鱼群由西向到航 行，在B点测得小岛A在北偏东60°方向上，航行12海里到达D点，这时测 得小岛A在北偏到30°方向上，如果渔船不改变航线继续向东航行，有没有 触礁的危险？ 解：由点A作BD的垂线 交BD的延长线于点F，垂足为F，∠AFD=90° A 由题意图示可知∠DAF=30° 设DF= x , AD=2x 60° 则在Rt△ADF中，根据勾股定理
课前热身
1．(2004年· 宁夏)在倾斜角为30°的山坡上种树，要求相 邻两棵树间的水平距离为3米，那么，相邻两棵树间的坡 面距离为 2 3 米.
B A C
2．如图所示，某地下车库的入口处有斜坡AB，其坡度 i=1∶1.5，且AB= 13 m. C
A
2m
B
五、（2003.哈尔滨）今年入夏以来，松花江哈尔滨段 水位不断下降，达到历史最低水位，一条船在松花江 某段自西向东沿直线航行，在A处测得航标C在北偏东 60°方向上，前进100米到达B处，又测得航标C在北 偏东45°方向上，在以航标C为圆心，120米长为半径 的圆形区域内有浅滩，如果这条船继续前进，是否有 被浅滩阻碍的危险？
C
合作与探究
一轮船以30海里/时的速度由南向北航 行，在A处看见灯塔S在船的北偏东30°方 向上，半小时后航行到B处，看见灯塔S在 船的东北方向，求灯塔S与B的距离。
解直角三角形方位角问题
市一中
九年级数学组
你还记得方位角吗？
Hale Waihona Puke D 40° O 45°A
20°
30° C B
例1、 今年入夏以来，松花江哈尔滨段水
位不断下降，达到历史最低水位．一条船 在松花江某水段自西向东沿直线航行，在 A处测得航标C在北偏东60°的方向 上．前进100米到达B处，又测得航标C在 北偏东45°方向上（如图4）．在以航标C 为圆心，120米长为半径的圆形区域内有 浅滩．如果这条船继续前进，是否有被浅 滩阻碍的危险？（ 3 ≈1.73）．
60 2 30 6 30 2
答:O,B的距离为 60 2 m, A,B的距离为 (30 6＋30 2 ) m.
C
30 2
60
图2
如图3，海中有一小岛P，在其距8海里 范围内有暗礁，一轮船自西向东航行， 它在A处时测得小岛P位于北偏东60°， 且A、P之间的距离为16海里，若轮船继 续向东方向航行，请计算轮船有无触礁 的危险，如有危险，轮船自A处开始至 少沿东偏南多少度方向航行，才能安全 通过这一海域．
解：如图1，过点S作AB的垂线，交直线 AB于点C，得到Rt△SBC与Rt△SAC． 由题意知∠SBC=45°，∠SAC=75°－45°=30°． 设SC＝x海里，在Rt△SBC中，BC=SC= x． 在Rt△SAC中，∵tan∠SAC= SC ， AC
SC ∴AC= tan SAC
12 ∵AC－BC=AB，∴ 3 x－x=30× ，∴x≈8.2＞8． 60
AP 16 2
∴∠PAC＝45°，从而知∠BAC＝15°． 故轮船自A开始，至少应沿东偏南15°的方向航行，才 能安全通过此海域．
1．（南充）如图4，一艘轮船由海平面上A地出发向南偏西40º 的方 向行驶40海里到达B地，再由B地向北偏西10º 的方向行驶40海里 到达C地，则A、C两地相距（ ）． （A）30海里 （B）40海里 （C）50海里 （D）60海里 C 北 A 北
解直角三角形的应用-方向角问题专题练习
解直角三角形的应用-方向角问题一、选择题（共20小题）1、如图所示，渔船在A处看到灯塔C在北偏东60°方向上，渔船正向东方向航行了12海里到达B处，在B处看到灯塔C在正北方向上，这时渔船与灯塔C的距离是（）A、12海里B、6海里C、6海里D、4海里2、如图，小明为了测量其所在位置A点到河对岸B点之间的距离，沿着与AB垂直的方向走了m米，到达点C，测得∠ACB=α，那么AB等于（）A、m•sinα米B、m•tanα米C、m•cosα米D、米3、如图，小明要测量河内小岛B到河边公路l的距离，在A点测得∠BAD=30°，在C点测得∠BCD=60°，又测得AC=50米，则小岛B到公路l的距离为（）米．A、25B、25C、D、25+254、如图，小雅家（图中点O处）门前有一条东西走向的公路，经测得有一水塔（图中点A 处）在她家北偏东60度500m处，那么水塔所在的位置到公路的距离AB是（）A、250mB、250mC、mD、250m5、如图，为了测量河两岸A，B两点的距离，在与AB垂直的方向上取点C，测得AC=a，∠ACB=a，那么AB等于（）A、a•sinαB、a•cosαC、a•tanαD、a•cotα6、如图，为了测量河的宽度，王芳同学在河岸边相距200m的M和N两点分别测定对岸一棵树P的位置，P在M的正北方向，在N的北偏西30°的方向，则河的宽度是（）A、200mB、mC、mD、100m7、如图，为了测量两岸A、B两点的距离，在河的一岸与AB垂直的方向上取一点C，测得AC=b，∠ACB=а，那么AB等于（）A、b•tanаB、b•cotаC、b•sinаD、b•cosа8、如图，为了确定一条小河的宽度BC，可在点C左侧的岸边选择一点A，使得AC⊥BC，若测得AC=a，∠CAB=θ，则BC=（）A、asinθB、acosθC、atanθD、acotθ9、如图，沿AC方向开山修路，为了加快施工进度，要在小山的另一边同时施工，从AC 上的一点B，取∠ABD=145°，BD=500米，∠D=55度．要使A，C，E成一直线．那么开挖点E离点D的距离是（）A、500sin55°米B、500cos55°米C、500tan55°米D、500cot55°米10、如图，为了测量一河岸相对两电线杆A，B间的距离，在距A点15米的C处（AC⊥AB）测得∠ACB=50°，则A，B间的距离应为（）A、15sin50°米B、15tan50°米C、15tan40°米D、15cos40°米11、上午9时，一条船从A处出发，以每小时40海里的速度向正东方向航行，9时30分到达B处（如图）．从A、B两处分别测得小岛M在北偏东45°和北偏东15°方向，那么在B 处船与小岛M的距离为（）A、20海里B、20海里C、15海里D、20海里12、如图，已知一渔船上的渔民在A处看见灯塔M在北偏东60°方向，这艘渔船以28海里/时的速度向正东方向航行，半小时后到达B处，在B处看见灯塔M在北偏东15°方向，此时灯塔M与渔船的距离是（）A、7海里B、14海里C、7海里D、14海里13、如图，为了测量河两岸A、B两点的距离，在与AB垂直的方向点C处测得AC=a，∠ACB=α，那么AB等于（）A、a•sinαB、a•tanαC、a•cosαD、14、为了确定一条河的宽度AB，可以在点B一侧的岸边选择一点C，使得CB⊥AB，若测得∠ACB=30°，量得BC=60m，那么河宽AB为（）A、20mB、40mC、30mD、60m15、如图为了测量一条小河的宽度BC，可在点C的左侧岸边选择一点A使AC⊥BC，若量得AC=a，∠BAC=θ，那么宽度BC为（）A、asinθB、acosθC、atanθD、条件不足，无法计算16、如图，为测河两岸两抽水泵A，B的距离，在距B点25m的C处（BC⊥BA）测得∠BCA=50°，则A，B间的距离为（）A、25tan50°mB、mC、25sin50°mD、25cos50°m17、如图，学校在小明家北偏西30°方向，且距小明家6千米，那么学校所在位置A点坐标为（）A、（3，3）B、（﹣3，﹣3）C、（3，﹣3）D、（﹣3，3）18、如图，上午9时，一条船从A处出发以20海里/小时的速度向正北航行，11时到达B 处，从A、B望灯塔C，测得∠NAC=36°，∠NBC=72°，那么从B处到灯塔C的距离是（）海里．A、20B、36C、72D、4019、海军军事演习中，有三艘船在同时刻向指挥所报告：A船说B船在它的正东方向，C 船在它的北偏东55°方向；B船说C船在它的北偏西35°方向；C船说它在A船的距离比它到B船的距离远40海里，则AB的距离为（sin35°=0.5736，cos35°=0.8192，tan35°=0.7002，cot35°=1.428）（）A、182.8海里B、162.8海里C、133.4海里D、93.4海里20、上午9时，一船从A处出发，以每小时40海里的速度向正东方向航行，9时30分到达B处，如图所示，从A，B两处分别测得小岛M在北偏东45°和北偏东15°方向，那么B 处与小岛M的距离为（）A、20海里B、20海里C、15海里D、20海里二、填空题（共5小题）21、在一自助夏令营活动中，小明同学从营地A出发，要到A地的北偏东60°方向的C处，他先沿正东方向走了200m到达B地，再沿北偏东30°方向走，恰能到达目的地C（如图），那么，由此可知，B、C两地相距_________m．22、如图，小明从A地沿北偏东30°方向走100m到B地，再从B地向正南方向走200m到C地，此时小明离A地_________m．23、小明同学在东西方向的沿江大道A处，测得江中灯塔P在北偏东60°方向上，在A处正东400米的B处，测得江中灯塔P在北偏东30°方向上，则灯塔P到沿江大道的距离为_________米．24、如图，一轮船由南向北航行到O处时，发现与轮船相距40海里的A岛在北偏东33°方向．已知A岛周围20海里水域有暗礁，如果不改变航向，轮船_________（填“有”或“没有”）触暗礁的危险．（可使用科学记算器）25、王英同学从A地沿北偏西60°方向走100米到B地，再从B地向正南方向走200米到C 地，此时王英同学离A地的距离是_________米．三、解答题（共5小题）26、在一次课外实践活动中，同学们要测湘江河的宽度．如图1所示，小明先在河西选定建筑物A，并在河东岸的B处观察，此时视线BA在河岸BE所成的夹角∠ABE=32°，小明沿河岸BE走了400米到C处，再观察A，此时视线CA与河岸所成的夹角∠ACE=64°．（1）请你根据以上数据，帮助小明计算出湘江河的宽度（结果精确到0.1米）．（2）求出湘江河宽后，小明突发奇想，欲求B的正对岸建筑物的高度MN（如图2所示），现测得小明的眼睛与地面的距离（FB）是1.6m，看建筑物顶部M的仰角（∠MFG）是8°，BN为湘江河宽，求建筑物的高度MN（结果精确到0.1米）．（提示：河的两岸互相平行；参考数值：sin32°≈0.530；cos32°≈0.848；tan32°≈0.625；sin64°≈0.900；cos64°≈0.438；tan64°≈2.050；sin8°≈0.139；cos8°≈0.990；tan8°≈0.141）27、如图所示，若河岸的两边平行，河宽为900米，一只船由河岸的A处沿直线方向开往对岸的B处，AB与河岸的夹角是60°，船从A到B处需时间2分钟，求该船的速度．28、如图，某船由西向东航行，在点A测得小岛O在北偏东60°，船航行了10海里后到达点B，这时测得小岛O在北偏东45°，船继续航行到点C时，测得小岛O恰好在船的正北方，求此时船到小岛的距离．29、五一期间，小红到美丽的世界地质公园湖光岩参加社会实践活动，在景点P处测得景点B位于南偏东45°方向；然后沿北偏东60°方向走100米到达景点A，此时测得景点B正好位于景点A的正南方向，求景点A与B之间的距离．（结果精确到0.1米）30、喜欢数学的小伟沿笔直的河岸BC进行数学实践活动，如图，河对岸有一水文站A，小伟在河岸B处测得∠ABD=45°，沿河岸行走300米后到达C处，在C处测得∠ACD=30°，求河宽AD．（最后结果精确到1米．已知：≈1.414，≈1.732，≈2.449，供选用）。
解直角三角形应用——方向角2
《方位角》练习题（2）班级：姓名：1．如图，禁渔期间，我渔政船在A处发现正北方向B处有一艘可疑船只，测得A、B两处距离为99海里，可疑船只正沿南偏东53°方向航行．我渔政船迅速沿北偏东27°方向前去拦截，2小时后刚好在C处将可疑船只拦截．求该可疑船只航行的速度．（参考数据：sin27°≈，cos27°≈，tan27°≈，sin53°≈，cos53°≈，tan53°≈）2．如图，湖中的小岛上有一标志性建筑物，其底部为A，某人在岸边的B处测得A在B的北偏东30°的方向上，然后沿岸边直行4公里到达C处，再次测得A在C的北偏西45°的方向上（其中A、B、C 在同一平面上）．求这个标志性建筑物底部A到岸边BC的最短距离．3．如图，轮船从点A处出发，先航行至位于点A的南偏西15°且与点A相距100km的点B处，再航行至位于点B的北偏东75°且与点B相距200km的点C处．（1）求点C与点A的距离（精确到1km）；（2）确定点C相对于点A 的方向．（参考数据：≈1.414，≈1.732）4．某海域有A、B、C三艘船正在捕鱼作业，C船突然出现故障，向A、B两船发出紧急求救信号，此时B船位于A船的北偏西72°方向，距A船24海里的海域，C船位于A船的北偏东33°方向，同时又位于B船的北偏东78°方向．（1）求∠ABC的度数；（2）A船以每小时30海里的速度前去救援，问多长时间能到出事地点．（结果精确到0.01小时）．（参考数据：≈1.414，≈1.732）5．一艘观光游船从港口A以北偏东60°的方向出港观光，航行80海里至C处时发生了侧翻沉船事故，立即发出了求救信号，一艘在港口正东方向的海警船接到求救信号，测得事故船在它的北偏东37°方向，马上以40海里每小时的速度前往救援，求海警船到大事故船C处所需的大约时间．（温馨提示：sin53°≈0.8，cos53°≈0.6）6．如图，位于A处的海上救援中心获悉：在其北偏东68°方向的B处有一艘渔船遇险，在原地等待营救．该中心立即把消息告知在其北偏东30°相距20海里的C处救生船，并通知救生船，遇险船在它的正东方向B处，现救生船沿着航线CB前往B处救援，若救生船的速度为20海里/时，请问：救生船到达B处大约需要多长时间？（结果精确到0.1小时：参考数据：sin38°≈0.62，cos38°≈0.79，sin22°≈0.37，cos22°≈0.93，sin37°≈0.60，cos37°≈0.80）7．如图，一艘海轮在A点时测得灯塔C在它的北偏东42°方向上，它沿正东方向航行80海里后到达B处，此时灯塔C在它的北偏西55°方向上．（1）求海轮在航行过程中与灯塔C的最短距离（结果精确到0.1）；（2）求海轮在B处时与灯塔C的距离（结果保留整数）．（参考数据：sin55°≈0.819，cos55°≈0.574，tan55°≈1.428，tan42°≈0.900，tan35°≈0.700，tan48°≈1.111）8．中考英语听力测试期间，需要杜绝考点周围的噪音．如图，点A是某市一中考考点，在位于A考点南偏西15°方向距离125米的C处有一消防队．在听力考试期间，消防队突然接到报警电话，告知在位于C点北偏东75°方向的F点处突发火灾，消防队必须立即赶往救火．已知消防车的警报声传播半径为100米，若消防车的警报声对听力测试造成影响，则消防车必须改进行驶，试问：消防车是否需要改道行驶？请说明理由．（取1.732）9．钓鱼岛自古以来就是中国领土．中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测．如图，E、F为钓鱼岛东西两端．某日，中国一艘海监船从A点向正北方向巡航，其航线距离钓鱼岛最近距离CF=海里，在A点测得钓鱼岛最西端F在点A的北偏东30°方向；航行22海里后到达B点，测得最东端E在点B的东北方向（C、F、E在同一直线上）．求钓鱼岛东西两端的距离．（，，结果精确到0.1）10．如图，一艘海上巡逻船在A地巡航，这时接到B地海上指挥中心紧急通知：在指挥中心北偏西60°方向的C地，有一艘渔船遇险，要求马上前去救援．此时C地位于A北偏西30°方向上，A地位于B地北偏西75°方向上，A、B两地之间的距离为12海里．求A、C两地之间的距离（参考数据：≈1.41，≈1.73，≈2.45，结果精确到0.1）11．如图，我国渔政船在钓鱼岛海域C处测得钓鱼岛A在渔政船的北偏西30°的方向上，随后渔政船以80海里/小时的速度向北偏东30°的方向航行，半小时后到达B处，此时又测得钓鱼岛A在渔政船的北偏西60°的方向上，求此时渔政船距钓鱼岛A的距离AB．（结果保留小数点后一位，其中≈1.732）12．2014年3月8日凌晨，马来西亚航空公司吉隆坡飞北京的MH370航班在起飞一个多小时后在雷达上消失，至今没有被发现踪迹．飞机上有239名乘客，其中154名是中国同胞．中国政府启动了全面应急和搜救机制，派出多艘中国舰船在相关海域进行搜救．如图，某日在南印度洋海域有两艘自西向东航行的搜救船A，B，B船在A船的正东方向，且两船保持20海里的距离，某一时刻两船同时测得在A的东北方向，B的北偏东15°方向有疑似物C，求此时疑似物C与搜救船A，B的距离各是多少（结果保留根号）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1.如下图，某船以每小时36海里的速度向正东方向航行，在点A 测得某岛C 在北偏东60°方向上，航行半小时后到达点B 测得该岛在北偏东30°方向上，已知该岛周围16海里内有暗礁。
（1）说明点B 是否在暗礁区域内；（2）若继续向东航行有无触礁的危险？请说明理由。
2.如图，海岛A 四周20海里周围内为暗礁区，一艘货轮由东向西航行，在B 处见岛A 在北偏西60˚，航行24海里到C ，见岛A 在北偏西15˚，货轮继续向西航行，有无触礁的危险
3.如图所示，
A 、
B 两城市相距
100km ．现计划在这两座城市间修筑一条高速公路（即线段
AB ），经测
量，森林保护中心P 在A 城市的北偏东30°和B 城市的北偏西45°的方向上．已知森林保护区的范围在
以P 点为圆心，50km 为半径的圆形区域内．请问计划修筑的这条高速公路
会不会穿越保护区．为什么？（参考数据：
3 1.7322 1.414≈，≈）
4.为打击索马里海盗，保护各国商船的顺利通行，我海军某部奉命前往该海域执行护航任务．某天我护航
舰正在某小岛A 北偏西45°并距该岛20海里的B 处待命．位于该岛正西方向C 处的某外国商船遭到海盗袭击，船长发现在其北偏东60°的方向有我军护航舰（如图所示），便发出紧急求救信号．我护航舰接警后，立即沿BC 航线以每小时60海里的速度前去救援．问我护航舰需多少分钟可以到达该商船所在的位置C 处？（结果精确到个位）
5.如图，某天然气公司的主输气管道从A 市的东偏北30°方向直线延伸，测绘员在A 处测得要安装天然气的M 小区在A 市东偏北60°方向，测绘员沿主输气管道步行2000米到达C 处，测得小区M 位于C 的北偏西60°方向，请你在主输气管道上寻找支管道连接点N ，使到该小区铺设的管道最短，并求AN 的长.
6.如图，A 城气象台测得台风中心在A 城的正西方300千米处，以每小时10千米的速度向北偏东60º
的BF 方向移动，距台风中心200千米的范围内是受这次台风影响的区域。
（1） 问A 城是否会受到这次台风的影响？为什么？（2） 若A 城受到这次台风的影响，那么A 城遭受这次台风影响的时间有多长？
7． 在东西方向的海岸线l 上有一长为1km 的码头MN （如图），在码头西端M 的正西19．5 km 处有一观察站A ．某时刻测得一艘匀速直线航行的轮船位于 A 的北偏西30°,且与A 相距40km 的B 处；经过1小时20分钟，又测得该轮船位于A 的北偏东60°，且与A 相距83km 的C 处．（1）求该轮船航行的速度（保留精确结果）； （2）如果该轮船不改变航向继续航行，那么轮船能否正
好行至码头MN 靠岸？请说明理由．
A
B
F E P
45°
30° N
M 东
北
B
C
A
l。