《线性系统理论基础》第三章作业及答案
自控 第三章答案

第三章 线性系统的时域分析与校正习题及答案3-1 已知系统脉冲响应t 25.1e 0125.0)t (k -=,试求系统闭环传递函数)s (Φ。
解 [])25.1s /(0125.0)t (k L )s (+==Φ3-2 设某高阶系统可用下列一阶微分方程)t (r )t (r )t (c )t (c T +τ=+∙∙近似描述,其中,1)T (0<τ-<。
试求系统的调节时间s t 。
解 设单位阶跃输入ss R 1)(=当初始条件为0时有:1Ts 1s )s (R )s (C ++τ=1Ts T s 1s 11Ts 1s )s (C +τ--=⋅++τ=∴ T/t e T T 1)t (h )t (c -τ--== T)0(h τ=,1)(h =∞,20TT )]0(h )(h [05.0τ-=-∞=∆求 s tT/t s s eTT 1)0(h )]0(h )(h [95.0)t (h -τ--=+-∞=/10.95(1)s t TT eTTTτττ---=-+/0.05s t Te-=ln0.053T s t T ∴=-=3-3 一阶系统结构如图所示。
要求单位阶跃输入时调节时间4.0t s ≤s (误差带为5%),稳态 输出为2,试确定参数21k ,k 的值。
解 由结构图写出闭环系统传递函数1k k s k 1k k s k sk k 1sk )s (212211211+=+=+=Φ闭环增益2k 1k 2==Φ, 得:5.0k 2=令调节时间4.0k k 3T 3t 21s ≤==,得:15k 1≥。
3-4 在许多化学过程中,反应槽内的温度要保持恒定, 下图(a )和(b )分别为开环和闭环温度控制系统结构图,两种系统正常的K 值为1。
解 (1)对(a )系统:1s 1011s 10K )s (G a +=+=, 时间常数 10T =632.0)T (h = (a )系统达到稳态温度值的63.2%需要10秒;对(b )系统:1s 10110101100101s 10100)s (b +=+=Φ, 时间常数 10110T =632.0)T (h = (b )系统达到稳态温度值的63.2%需要0.099秒。
线性系统理论复习题纲
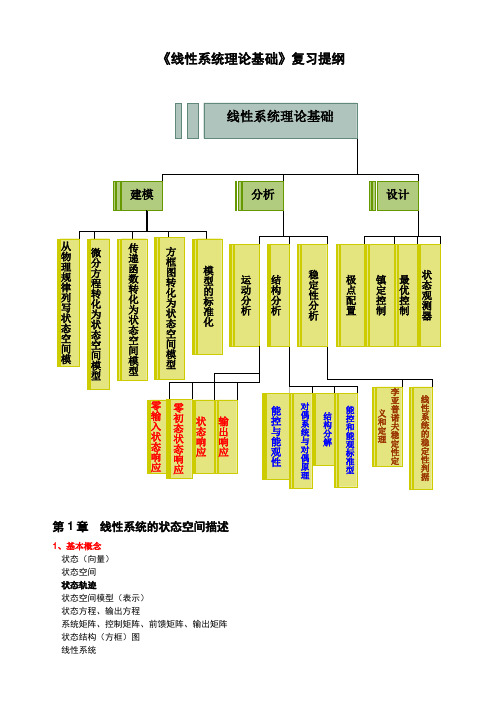
《线性系统理论基础》复习提纲第1章线性系统的状态空间描述1、基本概念状态(向量)状态空间状态轨迹状态空间模型(表示)状态方程、输出方程系统矩阵、控制矩阵、前馈矩阵、输出矩阵状态结构(方框)图线性系统时不变(定常)系统、时变系统连续时间系统、离散时间系统 状态线性变换矩阵的特征值、矩阵的特征向量 对角线标准型、约当标准型 模态标准型 正则型矩阵 范德蒙矩阵 传递函数矩阵2、知识要点%%知识点1:根据物理规律建立状态空间模型♦ 简单机械系统 ♦简单电气系统参考例题:例2.1.1,例2.1.2(P8)%%知识点2:微分方程模型转化为状态空间模型♦微分方程中不含输入导数项给定 ()(1)110n n n y a ya y a y bu --++++=&L ,选取状态向量12(1)n n x y x y x y -⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦&M M , 则有状态方程: 1122011010010n n n x x x x u x a a a x b -⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦⎣⎦&&M O M M M&L输出方程: []⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n x x x y M Λ21001 例2.1.3 (注意:方框图在没有要求时可以不画出) ♦微分方程中包含输入函数导数项,且m n <给定()(1)()(1)110110n n m m n m m ya y a y a yb u b u b u b u ----++++=++++&&L L ,m n <,将其转化为()(1)110()(1)110n n n m m m m y a y a y a y u y b yb y b y b y ----⎧++++=⎪⎨=++++⎪⎩&%%%%L &%%%%L ,选取状态向量12(1)n n x yx y x y-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦%&%M M %,则有状态方程 120110100101n n x x u x a a a -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦&&M O M M &L 输出方程 12011[,,,,0,,0]m n m n x x y b b b x --⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦L L 123M例2.1.4 ♦ 微分方程中包含输入函数导数项,且n m =若()(1)()(1)110110n n n n n n n ya y a y a yb u b u b u b u ----++++=++++&&L L ,让n y y b u =-%,则转化为如下微分方程的形式()(1)(1)(1)110111100()()()n n n n n n n n n y a y a y a y b a b u b a b u b a b u -----++++=-++-+-%%%%&L L 。
《线性系统理论基础》第三章作业及答案

第三章作业及答案3.1 判断下列系统的能控性和能观测性。
2) []x y u x x 111,100041020122-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=解:2C 012000101Q bAbA b -⎡⎤⎢⎥⎡⎤==⎣⎦⎢⎥⎢⎥-⎣⎦,2c rankQ n =<∴ 系统是状态不完全能控的2111101121o c Q cA cA -⎡⎤⎡⎤⎢⎥⎢⎥==--⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦,o 2rankQ n =<∴ 系统是状态不完全能观测的。
3.2 判断下列系统的能控性和能观测性。
1) []x y u x x 101,101300040002=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=2) x y u x x⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=01011000,1110000130000200001000113) []x y u x x 101,110200020012=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=4) x y u x x ⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=610321,029331100050005解:由系统能控和能观测性判据:1)A 为对角标准型,且对角元素互不相同,B 阵有全零元素的行,所以系统是不完全能控;C 阵中有全零元素的列,故系统是不完全能观测的。
2)1100100100000001A B C=0020011010000311⎡⎤⎡⎤⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦A 为约旦标准型,且各约旦块对角元素不相同,第一个约旦块最后一行对应到B 阵中的相应行为全零元素行,所以系统是不完全能控的;而各约旦块第一列对应到C 阵无全零元素列,所以系统是完全能观测的。
3)A =210020002⎡⎤-⎢⎥-⎢⎥⎢⎥-⎣⎦ B =011⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦C =[]101A 为约旦标准型,但两个约旦块元素相同,课本上给出的由标准型判定系统能控、能观测的定理不再适用,因此要采用能控性判别矩阵和能观测性判别矩阵来判断。
线性系统理论

Linear Systems Theory: A Structural Decomposition Approach线性系统理论: 结构分解法Ben M. Chen (陈本美)新加坡国立大学Zongli Lin(林宗利)美国弗吉尼亚大学Yacov Shamash (雅科夫 司马诩)美国纽约州立大学石溪分校此书献给我们的家人前两位作者谨以这中译版献给他们的母校 厦门大学目录绪论1 导论和预览1.1 背景1.2 各章预览1.3 符号和术语2 数学基础2.1 导论2.2 矢量空间和子空间2.3 矩阵代数和特性2.3.1 行列式、逆和求导2.3.2 秩、特征值和约当型2.3.3 特殊矩阵2.3.4 奇异值分解2.4 范数2.4.1 矢量范数2.4.2矩阵范数2.4.3 连续时间信号范数2.4.4 离散时间信号范数2.4.5 连续时间系统范数2.4.6 离散时间系统范数3 线性系统理论复习3.1 导论3.2 动态响应3.3 系统稳定性3.4 可控性和可观性3.5 系统可逆性3.6 常态秩、有限零点和无限零点3.7 几何子空间3.8 状态反馈和输出馈入的特性3.9 练习4 无驱动和/或无检测系统的分解4.1 导论4.2 自治系统4.3 无驱动系统4.4 无检测系统4.5 练习5. 正则系统的分解5.1 导论5.2 SISO系统5.3 严格正则系统5.4 非严格正则系统5.5 结构化分解特性的证明5.6 系统矩阵的Kronecker型和Smith型5.7 离散时间系统5.8 练习6 奇异系统的分解6.1 导论6.2 SISO奇异系统6.3 MIMO描述系统6.4 定理6.3.1的证明和性质6.5 离散时间奇异系统6.6 练习7 双线性变换的结构化映射7.1 导论7.2 连续到离散时间系统的映射7.3 离散时间到连续时间系统的映射7.4 定理7.2.1的证明7.5 练习8 系统因子分解8.1 导论8.2 严格正则系统8.3 非严格正则系统8.4 离散时间系统8.5 练习9 通过选择传感器/执行器实现的结构配置9.1 导论9.2 同时有限和无限零点结构配置9.2.1 SISO系统9.2.2 MIMO系统9.3 完全结构配置9.4 练习10 通过状态反馈实现的时间尺度和特征结构配置10.1 导论10.2 连续时间系统10.2.1 设计步骤和基本特性10.2.2 控制、控制和干扰解耦10.3 离散时间系统10.3.1设计步骤和基本特性10.3.2 控制、控制和干扰解耦10.4 练习11 通过静态输出反馈实现的干扰解耦11.1 导论11.2 左可逆系统11.3 一般的多变量系统11.4 练习12 软件工具箱12.1 导论12.2 m-函数描述12.2.1 自治系统的分解12.2.2 无驱动和无检测系统的分解12.2.3 正则系统的分解和特性12.2.4 矢量空间的运算12.2.5 奇异系统的分解和特性12.2.6 系统分解12.2.7 通过选择传感器/执行器实现结构配置12.2.8 具有特征结构配置的状态反馈控制12.2.9 通过静态输出反馈实现干扰解耦参考文献索引前言系统的结构特性对我们理解以状态空间表示的线性系统起着重要作用。
第三章习题答案1

(6)用双线性变换公式将转换成 = 3-15 一个数字系统的抽样频率为1000,已知该系统受到频率为100的噪 声干扰,现设计一带阻滤波器去掉该噪声。要求3的带边频率为95 和105,阻带衰减不小于14,阻带的下边和上边频率分别为99和 101。 解: (1)确定带阻滤波器技术指标:因为,所以得出: , , 通带内最大衰减,阻带内最小衰减。 (2)确定相应模拟滤波器技术指标。为计算简单,设。 == == == == 阻带中心频率 = 带阻带宽 =- 将以上边界频率对归一化,得到相应归一化带阻边界频率: = , = =, = = (3)由归一化带阻指标确定相应模拟归一化低通技术指标。 归一化阻带截止频率为:
点) 负肩峰(C 点) 过渡带宽度为 利用MATLAB演示其结果如题3-16图所示: N=21;a=(N-1)/2;Wc=0.5*pi; n=[0:1:(N-1)]; m=n-a+eps;避免被零除 hd=sin(Wc*m)./(pi*m); [H1,W]=freqz(hd,1); figure(1); subplot(211); stem(n,hd);xlabel('n');ylabel('h(n)'); subplot(212); plot(W/pi,20*log10(abs(H1)/max(H1))); xlabel('频率');ylabel('幅频响应');
题3-16图 加矩形窗时的脉冲响应及其频谱图
3-17 试用窗函数法设计一个第一类线性相位FIR数字高通滤波器,已 知 ,,,对于矩形窗,过渡带宽度为。 (1)确定的长度;(2)求的表达式;(3)? 解: (1) 偶数,取=65 (2)
(3) 3-18 用矩形窗设计线性相位数字低通滤波器,理想滤波器传输函数 为: (1)求出相应的理想低通滤波器的单位脉冲响应。 (2)求出用矩形窗函数法设计的FIR滤波器的表达式。 解:(1) (2)为满足线性相位条件,要求,为矩形窗函数的长度。加矩形 窗函数得。 。 3-19 用矩形窗设计线性相位高通滤波器,逼近滤波器传输函数为 = (1) 求出相应于理想低通的单位脉冲响应; (2) 求出矩形窗设计法的表达式,确定与之间的关系; (3) 的取值有什么限制?为什么? 解: (1) 直接IDTFT[]计算: = = = = = = 表达式中第2项正好是截止频率为的理想低通滤波器的单位脉冲 相应。而对应于一个线性相位全通滤波器:
北航线性系统理论完整版答案

1-1 证明:由矩阵 可知A 的特征多项式为nn n n n n n n n n nn n n n a a a a a a a a a a a a a a a a a a a a a a a A I ++++++=+++++=+++=++=+=-+λλλλλλλλλλλλλλλλλλλλλλλ1-3-32-21-11-3-3122-2-1-n 13-n 2-n 21-1n 12-n 1-n 12-n 1-n n1- )1(-)1(- 00 0 1- )1(-)1(- 0 00 1-1 0 1- 0 0 0 1-若i λ是A 的特征值,则所以[]Ti i 1-n i 2 1 λλλ 是属于i λ的特征向量。
1-7 解:由于()ττ--t e t g =,,可知当τ<t 时,()0≠τ,t g ,所以系统不具有因果性。
又由于()()0 ,,ττ-=t g t g ,所以系统是时不变的。
1-8 解:容易验证该系统满足齐次性与可加性,所以此系统是线性的。
由于()()t 0t ⎩⎨⎧>≤-=-=ααββαβαt u t u P u Q P 而()()⎩⎨⎧+>+≤-=⎩⎨⎧>≤=βαβαβααβαβ t 0 t t 0 t t u t u Q u P Q ,故u P Q u Q P αββα≠,所以系统是时变的。
又因为()()()()()⎩⎨⎧>≤=⎩⎨⎧>≤=ααααα,,T T t u t u P u P P T T min t 0 min t t 0 t 而()()()()()()()⎩⎨⎧>≤=⎩⎨⎧>≤=ααααα,,,,T T t u T T t u P u P P P T T T min t 0 min t min t 0 min t ,故()()u P P P u P P T T T αα=,所以系统具有因果性。
1-11 解:由题设可知,()τ-t g 随τ变化的图如下所示。
线性系统理论第三章(1)

第三章 线性时不变系统的标准形与最小阶实现把系统动态方程化为等价的简单而典型的形式,对于揭示系统代数结构的本质特征,以及系统的分析与设计将会带来很大的方便,因此利用等价变换化系统动态方程为标准形的问题成为线性系统理论中的一个重要课题。
在第一章中已经指出,动态方程等价变换的矩阵P 是由状态空间基底的选取来决定的。
因此常把构造P 阵的问题化为选取状态空间适当基底的问题来讨论。
由于所给的条件不同和选取基底的方法不同,从而可以得到各种不同形式的标准形。
在实际实用中,常是根据所研究问题的需要而决定采用什么样的标准形。
本章所介绍的几种标准形,是以后讨论极点配置和观测器设计等问题时要用到的。
实现问题,也是线性系统理论的重要课题之一。
这是因为:状态空间方法在系统设计和计算上都是以动态方程为基础的,为了应用这些方法,我们需要把传递函数阵用动态方程予以实现,特别是在有些实际问题中,由于系统物理过程比较复杂,通过分析的方法来建立它的动态方程十分困难,甚至不可能,这时可能采取途径之一就是先确定输入输出间的传递函数阵,然后根据传递函数阵来确定系统的动态方程。
其次,复杂系统的设计往往希望能在模拟计算机或数字计算机上仿真,以便在构成物理系统之前就能检查它的特性,系统的动态方程描述则比较便于仿真,例如在模拟机上指定积分器的输出作为变量,就很容易仿真系统。
在实际应用中,动态方程实现也提供了运算放大器电路综合传递函数的一个方法。
每一个可实现的传递函数阵,可以有无限多个实现。
我们感兴趣的是这些实现中维数最小的实现,即最小阶实现。
在实用中,最小阶实现在网络综合和系统仿真时,所用到的元件和积分器最少,从经济和灵敏度的角度来看是必要的。
关于有理函数阵的最小阶实现问题,定理2—20及定理2—21是基本的,本章则着重于构成最小阶实现的方法。
§3—1系统的标准形关于等价变换 等价变换的关系A PAPB PBC CP 11,,--===其中P 为坐标变换阵,即有x Px =。
《线性系统理论》作业参考答案6

可控可观,
>
5-9(2) 解:由题得系统的传递函数为
2 G (s) 0 s 3 1 1 0 2 1 0 1 s 1 0 1 s 1
1
0 1 0
2 0 s 5s 2 2 0 ( s s 1)( s 3 ) 2s 3 1 2 s s 1
注:本题也可以按照课本上介绍的方法做,答案不唯一。
注:本题也可以按照书上提供的第一种方法做。
-82 -40.5 128 62
( s5
2 2
d1 1 1 0 d2 1 1 0 经计算得 , E lim sG 1 ( s ) 1 1 E 2 lim sG 2 ( s ) 2 s 1 s
1 1 3 x 2 1 3 1 3 v 。 1 3
2 1 1 u Kx Hv E Fx E v 4
注:这只是其中一种方法,不唯一。 (3)在第二问的基础上做,由于 等于-1,-2, -3,即可配置。 5-11 本题中,系统有耦合,p+q -1=2+2-1=3<n=4,故不能用静态反馈来配置系统极点,本题 只能用设计动 态输出反 馈补偿器的 方法, 设 计一个一 维的动态输 出反馈补 偿器,使得 p+q+2l-1=5>4 式成立。对此五维系统,可增设一个需要配置的极点(如 -5 或-6)用待定系数 法解 K 的各参数。以上只是大体思路,本题计算繁琐且 K 阵不唯一。 ,故只需令以上三个根
1 1 E 为非奇异阵,所以系统可以用反馈解耦。 2 1
1
C1 A d 1 1 6 F d 2 1 C A 2 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章作业及答案3.1 判断下列系统的能控性和能观测性。
2) []x y u x x111,100041020122-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=解:2C 01200011Q bAbA b -⎡⎤⎢⎥⎡⎤==⎣⎦⎢⎥⎢⎥-⎣⎦,2c rankQ n =< ∴ 系统是状态不完全能控的 2111101121o c Q cA cA -⎡⎤⎡⎤⎢⎥⎢⎥==--⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦,o 2rankQ n =< ∴ 系统是状态不完全能观测的。
3.2 判断下列系统的能控性和能观测性。
1) []x y u x x101,101300040002=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=2) x y u x x⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=01011000,111000013000020*********3) []x y u x x101,110200020012=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=4) x y u x x⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=610321,029331100050005解:由系统能控和能观测性判据:1)A 为对角标准型,且对角元素互不相同,B 阵有全零元素的行,所以系统是不完全能控;C 阵中有全零元素的列,故系统是不完全能观测的。
2)1100100100000001A B C =00200111000311⎡⎤⎡⎤⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦A 为约旦标准型,且各约旦块对角元素不相同,第一个约旦块最后一行对应到B 阵中的相应行为全零元素行,所以系统是不完全能控的;而各约旦块第一列对应到C 阵无全零元素列,所以系统是完全能观测的。
3)A =210020002⎡⎤-⎢⎥-⎢⎥⎢⎥-⎣⎦ B =011⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦C =[]11A 为约旦标准型,但两个约旦块元素相同,课本上给出的由标准型判定系统能控、能观测的定理不再适用,因此要采用能控性判别矩阵和能观测性判别矩阵来判断。
2C 014124124Q bAbA b -⎡⎤⎢⎥⎡⎤==-⎣⎦⎢⎥⎢⎥-⎣⎦,2c rankQ n =< ∴ 系统是状态不完全能控的 2101212444o c Q cA cA ⎡⎤⎡⎤⎢⎥⎢⎥==--⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦,o 2rankQ n =< ∴ 系统是状态不完全能观测的。
4)500A 050001⎡⎤-⎢⎥=-⎢⎥⎢⎥⎣⎦ 13B 3920⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦123C 016⎡⎤=⎢⎥⎣⎦A 为对角标准型,但有对角元素相同的情况;同上题,课本上给出的由标准型判定系统能控、能观测的定理不再适用,因此要采用能控性判别矩阵和能观测性判别矩阵来判断。
2C 135152575391545752252220Q BABA B --⎡⎤⎢⎥⎡⎤==--⎣⎦⎢⎥⎢⎥⎣⎦,2c rankQ n =<∴ 系统是状态不完全能控的21230165103056255030256o C Q C A C A ⎡⎤⎢⎥⎢⎥⎡⎤⎢⎥--⎢⎥==⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎢⎥⎣⎦ ,o 3rankQ n == ∴ 系统是状态完全能观测的。
3.3 给定系统 []x y u x c b a x01,100=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=求:1) 确定使系统完全能控时待定系数的取值范围; 2) 确定使系统完全能观测时待定系数的取值范围;3) 确定使系统既能控又能观测时待定系数的取值范围。
解:1) 系统能控性矩阵为[]Cb Q b A b 10⎡⎤==⎢⎥⎣⎦若使系统完全能控,则要求rank C Q =2,⇒即b 0≠。
2) 系统可测性矩阵为o c 10Q cA ab ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦若使系统完全能观测,则要求能观性矩阵o rankQ 2=,即o Q =b ,⇒b 0≠ 3) 若要使系统状态既能控又能观,则要求rank C Q =2且o rankQ 2=,⇒b 0≠3.5 给定离散时间系统 [])(110)()(101)(011220001)1(k x k y k u k x k x =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=+ 判定系统的能控性和能观测性。
解:系统能控性判别矩阵为2C111Q h G h G h 022113⎡⎤⎢⎥⎡⎤==--⎣⎦⎢⎥⎢⎥-⎣⎦因为rank C Q =3=n ,所以系统完全可控。
系统能观测性判别矩阵 为o 2c 011Q cG 132cG 146⎡⎤⎡⎤⎢⎥⎢⎥==--⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦因为o rankQ 3==n ,所以系统完全能观。
3.7 已知系统 1)[]x y u x x011,102101110221=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----= 试分别判断其能控性。
如完全能控,将其化为能控标准型,如不完全能控,则找出它的能控子系统。
解: 2C 244Q bAbA b 012131--⎡⎤⎢⎥⎡⎤==⎣⎦⎢⎥⎢⎥-⎣⎦rank C Q =3,系统完全可控,利用x P x =求能控标准型。
()32s 122det sI A det 0s 11s s s 31s 1+⎡⎤⎢⎥-=+-=+++⎢⎥⎢⎥--⎣⎦所以 1a 1= 2a 1= 3a 3= 构造F 阵:n-1n-2121n-2n-311a a a 1a a 1111a a 1F a 1011010010a 11⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦C 244111622P Q F 012110310131100341----⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦10.05560.55560.1111P0.16670.66670.33330.50001.00000---⎡⎤⎢⎥=--⎢⎥⎢⎥⎣⎦化为能控标准型后的系统矩阵如下: 110A P AP 001311-⎡⎤⎢⎥==⎢⎥⎢⎥---⎣⎦10P b 01b -⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦[]cP=312c =--3.8 对3.7题判断其能观测性。
如完全能观测,将其化为能观测标准型,如不完全能观测,则找出它的能观测子系统。
解:1)O2c 110Q cA 131cA 052⎡⎤⎡⎤⎢⎥⎢⎥==---⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦rank O Q =3,所以系统完全可观测,利用x Qx =求能观测标准型。
构造O111110033Q FQ 11013102110052110-⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥==---=--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦系统化为能观标准型的各矩阵为:103A Q AQ10-1011--⎡⎤⎢⎥==⎢⎥⎢⎥-⎣⎦03323Q b 021*******b --⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥==--=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦[]1Q =01c c -=3.9 已知系统 []x y u x x101,100102322001=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=- 试对其进行结构分解。
解:2C 000Q bAbA b 039111⎡⎤⎢⎥⎡⎤==⎣⎦⎢⎥⎢⎥⎣⎦rank C Q =2<3,所以系统不完全可控。
构造变换阵C 001T 030110⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⇒ 1C 10131T 003100-⎡⎤-⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦10.11110.33331Q0.11110.333300.22220.33330--⎡⎤⎢⎥=-⎢⎥⎢⎥--⎣⎦经C x T x =等价变换后: 1C C 80232A =T A T 133001-⎡⎤--⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦1C 1T b 00b -⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦[]C c c T 111== 能控子系统:[]c c N C c c80213xx x u 13203y 11x ⎡⎤-⎢⎥-⎡⎤⎡⎤=++⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦=C O 11rankQ rank 1211⎡⎤==<⎢⎥⎣⎦,所以系统能控部分不完全能观测。
构造非奇异变换阵,对能控部分进行能观测性结构分解:O 111T 01⎡⎤=⎢⎥⎣⎦(注意:变换阵不唯一,例如可取O 111T 10⎡⎤=⎢⎥⎣⎦) 不能控子系统:N C N C N C N Cxx y x ==显然是能观测的,不需要分解,21O T =。
令 1211001001O O O T T T ⎡⎤⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦ 111001001O T --⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦将能控性结构分解后的系统作变换 O x T x =,得能观测性结构分解11022123001O OA T AT --⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎣⎦100O b T b ⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦ []1101O c c T -==即系统结构标准分解后,三个状态变量分别为能控能观测、能控不能观测和不能控能观测的。
[],,,,,,,,,10212120300111C O C O C N O C N O N C O N C O C O C N O N C O xx x x ux x x y x x -⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦⎣⎦⎣⎦⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦(注意:变换阵O 1T 不唯一,最终的变换阵O T 不唯一,结构分解后的结果不唯一。
例如取O 111T 10⎡⎤=⎢⎥⎣⎦,求得1211010001O O O T T T ⎡⎤⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦11011001O T -⎡⎤⎢⎥⇒=-⎢⎥⎢⎥⎣⎦,(很多同学分解不完全,完全的结构分解既要进行能控分解,还要进行能观测分解。
)3.10 求下面传递函数的能控型实现、能观测型实现和约旦型实现。
1216716174)(232+++++=s s s s s s G解:1)能控性实现是指实现以后的系统完全能控,能控标准型表示的系统一定能控,故是一种能控性实现。
[]01000010********174x x u y x⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦=2)能观测性实现是指实现以后的系统完全能观测,能观测标准型表示的系统一定能观测,故是一种能观测性实现。
[]001216101617017401xx uy x-⎡⎤⎡⎤⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦=3)令传递函数分母32716120s s s +++=,求得系统特征根1232;3λλλ==-=-,有重根,则该系统可进行约旦标准形实现。
可进行约旦标准形实现的传递函数(设1个重根,j 重)可写为: ()()()1j 11122n jj-112n11C C C C C G s s s s s s λλλλλ=+++++-----其中:11(i 1)j 1i 1s i i 1C limG (s)(s )(i 1)!s C lim G (s)(s )x dd λλλλ-→→⎡⎤=-⎣⎦-=-本题中,由上述计算,得()()2231232G s s s s -=+++++则该系统约旦标准形实现为:[]210002010031231xx u y x-⎡⎤⎡⎤⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦=-(注意:特征根与求得的系数在实现中的位置关系)3.11 求下列系统的最小实现。
