索洛模型1
索罗增长模型
第一章索洛经济增长模型The Solow Growth Model基本内容1 索洛模型的基本假定2 离散时间的索洛模型3离散时间索洛模型的过渡过程4连续时间的索洛模型5连续时间索洛模型的过渡过程6持久增长7带技术进步的索洛模型8比较动态分析1 索洛模型的基本假定● 一个分析经济增长和各国收入差异的基本框架.● 其核心假定是新古典总的生产函数.家庭与生产 I● 封闭经济,唯一的最终产品.● 离散时间，t = 0, 1, 2, ....● 该经济里有众多的家庭，暂时假定家庭没有优化行为.● 这也是索罗模型与新古典增长模型的主要区别.● 为了简化，假定各个家庭相同，可以用代表性家庭来表示.家庭与生产II● 假定家庭的储蓄率外生● 所有厂商具有相同的生产函数，可以用代表性厂商表示.● 对该经济中的唯一最终产品，生产函数为(1)Y T F K t L t A t()[(),(),()]●假定资本与最终产品相同（比如玉米）,用于生产更多的产品.●()A t可以理解为技术.●主要假定: 技术是免费的; 具有非竞争性与非排他性.关键假设1Assumption 1 (连续性, 可微性, 边际产出为正且递减, 规模报酬不变) 生产函数3:F R R ++→ 关于 K 与 L 二阶连续可微, 且满足2222()()(,,)0 (,,)0()()(,,)0 (,,)0K L KK LL F F F K L A F K L A K L F F F K L A F K L A K L ∂⋅∂⋅≡>≡>∂∂∂⋅∂⋅≡<≡<∂∂ 同时, F 关于K 与 L 规模报酬不变.● 假定 F 关于K 与 L 规模报酬不变，即关于这两个变量线性齐次.复习定义 假定K 为整数，如果对任意的R λ+∈与K z R ∈，有(,,)(,,)m g x y z g x y z λλλ=，那么函数2:K g R R ++→为x R ∈与y R ∈的m 次齐次函数.定理 (欧拉定理Euler 's Theorem ) 假定函数2:K g R R ++→为x R ∈与y R ∈的m 次齐次函数，偏导数分别是x g 与y g ，那么对任意的x R ∈，y R ∈以及K z R ∈，有()()(),, ,,,,x y mg x y z g x y z x g x y z y =+同时，,(),x g x y z 与,(),y g x y z 是关于x 与y 的1m -次齐次式.市场结构与市场出清 I●假定市场是竞争的, 因此也可认为是竞争一般均衡模型. ●家庭拥有劳动, 供给无弹性.●经济中的劳动（力）,)L t , 无论在什么价格下，劳动的供给量均为()L t .●劳动力市场出清条件:())L t L t =上式对所有的t 均成立 , ()L t 劳动需求 (也可视为就业水平). ●一般来说, 互补松弛条件的表述更为准确.●记 t 时期的工资率为 w (t), 于是劳动力市场出清条件可表示为()()),0(L t L t w t ≤≥ and (()()) (0)L t L t w t =-市场结构与市场出清II●假设 1 与竞争的劳动力市场意味着工资率必须严格为正. ●家庭拥有资本，并将其出租给厂商.●记t 期的资本租赁价格()R t .●资本市场出清条件:()()s d K t K t =LHS-家庭的行为决定；RHS-厂商的行为决定●假定家庭拥有的初始资本存量为()0K●()P t 为t 时期最终产品的价格, 将其标准化为1.●利率r(t)●折旧率δ●家庭得到的实际回报()() r t R t δ=-.厂商优化厂商优化 I●考虑代表性厂商的最大化问题:0)0,()([()()()],()()()(),.L t K t max F K t L t A t w t L t R t K t ≥≥--●注意:●上述最大化问题中的变量是总量.●在F 前面没有系数, 这是因为最终产品的价格已正规化为1.●假定要素市场完全竞争: 在厂商看来，()w t 与()R t 是给定的.●凹的问题,因为F 是凹的.厂商优化 II●由于 F 可微, 一阶条件（FOC ）为:()[()()()],,,L w t F K t L t A t = (2)()[()()()] ,.,K R t F K t L t A t = (3)●在(2) 与(3)中, ()K t 与()L t 分别表示厂商对资本和劳动的需求量.●实际上，可以通过(2)与(3)求解()K t 与 ()L t ,它们是资本租赁价格()R t 和工资率()w t 的函数.厂商优化 III命题 假定假设1成立，那么均衡时厂商的利润为0，()()( )()() .Y t w t L t R t K t =+●证明: 可直接从欧拉定理得到（注意到1m =,即规模报酬不变）.关键假设2假设2 (Inada conditions) F 满足 Inada 条件0 0 0 ()() K K K K lim F and lim F for all L all A →→∞⋅=∞⋅=> 00 0 ()() L L L L lim F and lim F for all L all A →→∞⋅=∞⋅=> ●保证内点解.生产函数Figure: Production functions and the marginal product of capital. The example in Panel A satisfies the Inada conditions in Assumption 2, while the example in Panel B does not.2 离散时间Solow 模型Solow模型的动态过程描述 I●K的折旧率为 , 于是1 1()((() ),)K t K t I t δ+=-+ (4) 其中， ()I t 是t 阶段的投资.●对于封闭经济, 产出等于消费与储蓄（投资）之和 ,()()()Y t C t I t =+ (5) ●注意，该模型没有家庭效用的最大化问题，因此此处难以讨论社会福利等方面的话题.Solow 模型的动态过程描述II●由于经济是封闭的 (同时不考虑政府支出)，于是.()()()()S t I t Y t C t ==-●假定家庭的储蓄率是常数，则()(),S t sY t =(6) 1()()()C t s Y t =-(7) ●于是资本供给（家庭的行为决定储蓄率s ）可表示为()()( 1 1 )()()()().s K t K t S t K t sY t δδ=-+=-+Solow 模型的动态过程描述 III●资本的供求相等 ()().s K t K t =●同时也有劳动力市场供求相等 ()().L t L t =●结合 (1) 与 (4), 可得 Solow 增长模型的动态方程: ()[()()1 ,, 1.()]()()K t sF K t L t A t K t δ+=+- (8) ●非线性差分方程.●Solow 增长模型的均衡由该方程以及 ()(())()L t or L t and A t 来刻画.定义均衡 I●没有家庭优化, 但仍然有厂商最大化行为以及要素市场的出清.定义 在Solow 模型中，对于给定的序列 {}0()(),t L t A t ∞= 以及初始资本存量()0K , {}0,,,()()()(,)()t K t Y t C t w t R t ∞=是资本、产出、消费、工资率、租赁价格的均衡路径，其中()K t 满足 (8), ()Y t 由(1)给出, ()C t 由 (7)给出, ()w t 与 ()R t 分别由 (2) 与 (3)给出.●注意，均衡是沿着时间的整条路径，而不是静态的点.不考虑人口增长与技术进步时的均衡不考虑人口增长与技术进步时的均衡I●进一步假定（稍后放松假定）:●没有人口增长;假定总人口为常数 L > 0， 即() L t L =. ●假定没有技术进步，即() A t A =.●定义资本-劳动比率（人均资本）为 ((,))K t k t L ≡(9)●利用规模报酬不变, 人均产出) ()(/y t Y t L ≡可表示为,1, ()()(() ).K t y t F A L f k t ⎡⎤=⎢⎥⎣⎦≡ (10)不考虑人口增长与技术进步时的均衡 II ●注意()f k 依赖于A, 本可以将生产函数写成,()f k A ;但由于A 是常数，因此可以假定 A = 1.●由欧拉定理0 ()(())()(())()(())0.R t f k t w t f k t k t f k t -'=>'=> (11) ●由假设1可知（11）中的要素价格均为正.例子: Cobb-Douglas 生产函数 I●一类特殊的生产函数，但应用很广泛:1()[()()()]()( ,,,01)Y t F K t L t A t AK t L t ααα-==<<●满足假设1和 2.●两边同时除以()L t ,()() y t Ak t α=●由 (11)可得(1)()()()()Ak t R t Ak t k t ααα--∂==∂ ●由欧拉定理,()()() 1.()()()w t y t R t k t Ak t αα==--例子: Cobb ‐Douglas 生产函数II●或者直接从 Cobb-Douglas 生产函数有,()111()()() () ,R t AK t L t Ak t ααααα----==()()()()()()1 1 ,w t AK t L t A t k ααααα-=-=-直接可验证满足欧拉定理.不考虑人口增长与技术进步时的均衡 不考虑人口增长与技术进步时的均衡I●将 (8)的两端同时除以 L 可得人均量的表达式:()(()1 1).)(()k t sf k t k t δ+=+- (12) 定义 稳态均衡（steady-state equilibrium ）* ()k t k =.该经济将趋于该稳态均衡(但在有限时间不能到达).稳态人均资本不考虑人口增长与技术进步时的均衡 II●上图实线代表 (12)，虚线是45 线.●它们的（正的）交点*k 表示稳态人均资本 **.()f k k s δ=(13)●注意到还有另一交点0k =,因为已经假定0(0)f =.●忽略该稳态值:●如果资本不是必不可少的（essential ）, ()0f 可能大于0 0k =可能变为稳态均衡点●本交点,即使存在，也不稳定。
索洛进步模型1
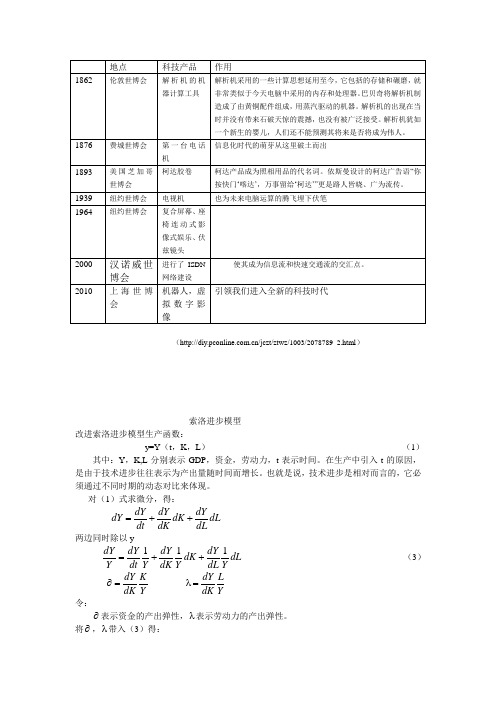
（/jczt/ztwz/1003/2078789_2.html ）索洛进步模型改进索洛进步模型生产函数：y=Y （t ，K ，L ） （1）其中：Y ，K,L 分别表示GDP ，资金，劳动力，t 表示时间。
在生产中引入t 的原因，是由于技术进步往往表示为产出量随时间而增长。
也就是说，技术进步是相对而言的，它必须通过不同时期的动态对比来体现。
对（1）式求微分，得：dL dLdY dK dK dY dt dY dY ++= 两边同时除以ydL YdL dY dK Y dK dY Y dt dY Y dY 111++= （3） Y K dK dY =∂ YL dK dY = 令：∂表示资金的产出弹性， 表示劳动力的产出弹性。
将∂， 带入（3）得：dLdY dK dK dt Y dt dY Y dY +∂+=1 以差分代替微分，并令1=∆t ，（4）式变为LL K K dt Y dt dY Y Y ∆+∆∂+=∆β1 (5) 上式表明，总产出的增长速度Y Y ∆可以分解成三项：第一项dt Ydt dY a 1= 其中dtdY 表示K 和L 都不变的情况项GDP Y 的增长（这种增长可以归于因科技进步产生的）。
第二项表示资金增长产生的弹性系数给产值带来的增长率。
第三项表示有劳动增长率产生的弹性系数给产值带来的增长率。
令y=Y Y ∆，k=KK ∆，l=L L ∆。
它们分别表示GDP ，资金和劳动的平均增长速度，（假设劳动力始终不变）则有l=L L ∆=0 于是（5）变为：y=a+∂k+βla=y-∂k+βl式中a 为科技进步率；y 为GDP 的增长速度 因此得到科技对经济的作用%100⨯=ya E模型求解：由假设（假设劳动力始终不变）可得：l=0即a=y-∂k按国家发改委根据我国国情推荐∂=0.2——0.3 ， =0.7——0.8则：a=y-0.3k。
索洛模型
本存量折旧率为 5% ，人口增长率为 1% ， 储蓄率为10%。 求：（1）均衡时本国的人均资本存量、 人均产出及人均消费水平。 （2）黄金律稳态时的人均资本量和人均 产出以及储蓄率水平。
2017/4/7 中国矿业大学管理学院 徐建博 32
二、 技术进步的影响
前面的研究一直基于一个假定，即技术水平不变，在此条 件下考虑资本、劳动的变化对经济增长的影响。 事实上，现实中技术的发展日新月异，对劳动生产率的提 高起到了积极的推动作用。所以，我们有必要把技术进步引 入索洛模型。
2017/4/7 中国矿业大学管理学院 徐建博 1
经济增长理论——索罗模型 第一节 资本积累
一. 基本假设条件 （1）劳动力和技术水平保持不变。
（2）两部门经济（居民和生产者）： Y=C+I 。 （3）生产函数规模不变 Y= F（K，L） 规模收益不变：λY= F（λK,λL） （4）储蓄函数S = sY，s----储蓄率, 0≤s ≤1
(1)y=k 0.5
MPK=dy/dk=1/2K -0.5 . 求出k=25,y=5
(2)
2017/4/7
s f（k）=δk, 5s=0.25,
中国矿业大学管理学院 徐建博
s=0.5
24
第三节 人口增长与技术进步
前面的分析表明，高储蓄能提高一个经济的稳 态资本存量和产出。在原来资本水平较低时，有 更多的发展空间，促进经济增长。但资本积累本 身不能带来持续的经济增长。 要解释一个经济的持续增长就必须扩展基本的 索洛模型，即把原来没有考虑的两个因素：人口 增长和技术进步引入模型。因为现实当中，一个 国家的人口或技术总是在不断变化的。
索洛简介
1956 年 , 麻省理工学院 (MIT) 的教授罗伯特 • 索洛 写了一篇有关经济均衡增长路径的文章，这篇文章 第一次引入了长期经济增长模型，又被称做“新古 典增长模型”（建立在凯恩斯以前的经济学家所使 用的古典模型基础上的）。 为此，索洛获得了1987年的诺贝尔经济学奖。 索洛对经济增长考察是从资本积累开始的。 索洛模型基本思路：先让劳动力和技术保持不变， 然后逐步放宽假设（劳动力的变化和技术进步）研 究经济增长。
索洛模型
利用上面的结果，i = sy = sf(k)
对于任何一个给定的资本存量k，生产函数y=f(k)决 定了经济生产多少产出
12
2、资本存量的增长与稳定状态
资本存量是决定产出的关键因素
有两个因素影响资本存量的变动：投资和折旧
投资指用于新工厂和设备的支出，它引起资本存量增
加
折旧指原有资本的磨损，它引起资本存量减少
k
投资与折旧
sf(k)
k3 k*
人均资本 k
24
k>
* k
类似地，假定经济的初始资本水平高于稳定状态。
在这种情况下，投资小于折旧：资本的磨损快于更替。 资本存量将减少，又一次向稳定状况的水平趋近 一旦资本存量达到了稳定状态，投资等于折旧，资本 存量增加或减少的压力都不存在
25
3、向稳态接近：一个数字例子
设定 z = 1/N，则有 Y/N = F (K/N , 1)
定义: y = Y/N = 每个工人的产出 k = K/N = 每个工人的资本量
y = F (k, 1) y = f(k)
其中 f(k)= F (k, 1)
8
生产函数
人均产出， y
生产函数表示 人均资本量k如 何决定人均产 出y=f(k)。生产 函数的斜率是 资本的边际产 量：如果k增加 1单位，y增加 MPK单位
34
• 图a显示人均收入的时间路径。储蓄率上升导致人均资本上
升，从而增加了人均产量，直到达到新的均衡为止。 y y0 O
t0 t1 t
G增长率
t0 t1
n t
• 图b显示总产量的时间路径。储蓄率的增加导致资本积累，
索洛增长模型
在A点的左边，sy曲线比（n+g+δ）k
线高，这表明储蓄高于资本广化的需 要，会导致人均资本k的提高，从而使 产出增加，k会不断向kA靠近，直到最 终用于资本广化的储蓄等于全部储蓄， 而人均占有的资本数量保持不变，经 济增长达到稳定状态。 在A点的右边，情况完全相反。
当经济处于资本深化阶段时，产出的增长
y
人均产出和增长率随时间变化的轨迹
y00 gFra bibliotekt0t1
t
0
t
上图的上半部分显示了人均产出水平
的时间路径。储蓄率的提高增加了人 均资本占有量从而人均产量提高，直 到达到新的稳定状态。 下半部分则显示了人均产量增长率的 时间路径。储蓄率的增加会导致资本 积累，实现人均产量水平的暂时性较 高增长，但是随着资本积累，人均产 量的增长率最终会回落到人口增长率 水平。
由于K / AL k , L/ L n, A/ A g , K sY (t ) K (t ),则， sY (t ) K (t ) Y (t ) k (t ) k (t )n k (t ) g s k (t ) nk(t ) gk(t ) A(t ) L(t ) A(t ) L(t ) 应用Y / AL f (k ), 有 k (t ) sf (k (t )) (n g )k (t )
索罗模型的定量含义
前面我们对储蓄率变动 对增长产生的水平影响 的解释如果成立，取决 于经济体系从前一个均 衡增长向后一个均衡增 长路径收敛的速度，如 果 需要上百年的时间才能 最终收敛，那么这种水 平 效应的认识就毫无意义 。下面我们将对这一过 程 作定量化分析。
储蓄率上升对产量的影 响
索洛模型
仍然从资本积累的角度来研究。
则一年中资本的变化量（新增的资本量）
为
Δk = i-δk- nk=i-（δ+n）k = s f（k）-（δ+n）k
2013-8-4
中国矿业大学管理学院 徐建博
27
3. 人口增长后稳态的变化
现在，考虑了人口的变动，稳态点就会有变化。 稳态时， s f（k）=（δ+n）k （δ+n）k称为“平衡投资”，即存在折旧和人 口增长的情况下，新增投资必须至少等于它， 才能使资本存量保持不变，达到稳态。 说明：经济处于稳态时， “平衡投资”投资一部分
2013-8-4 中国矿业大学管理学院 徐建博 1
经济增长理论——索罗模型 第一节 资本积累
一. 基本假设条件 （1）劳动力和技术水平保持不变。
（2）两部门经济（居民和生产者）： Y=C+I 。 （3）生产函数规模不变 Y= F（K，L） 规模收益不变：λY= F（λK,λL） （4）储蓄函数S = sY，s----储蓄率, 0≤s ≤1
尽管高的储蓄率可带来高的经济增长速度，但高的资本数 量和高产出，其实并不是一个经济所追求的目标。人们的目 标是长期中的消费福利。 高储蓄是以低消费为代价的。因此，选择最佳稳态，应该 以高消费作为选定稳态的标准。
一. 假设条件
1. 索洛模型成立 2. 储蓄率s可以调整； 3. 目标：未来消费水平最高。
2013-8-4 中国矿业大学管理学院 徐建博 15
查阅资料并利用索洛经济增长模型解释：
（1） 我国经济最近几年增长速度都很高，会不会一直这 么高下去？ （2） 日本和德国是两个成功的经济增长事例。二战期间 摧毁了两国的大量资本存量。但是，战后的几十年中，这两 个国家经历了最迅速的增长。在1948年到1972年间，日本 每年人均产出为8.2%，德国的每年人均产出增长率为5.7%。 相比之下，美国每年的人均产出增长率仅为2.2%。 为什么战后的日本、德国的经济会得到高速的增长？
第一章-索洛增长模型
第一章 索洛增长模型一、索洛模型的介绍与一些前提假设条件该模型是经济学家传统上用于分析经济增长的主要模型。
几乎对于所有有关增长的分析而言，索洛模型是其起点。
理解该模型实质上便是理解增长理论。
但该模型也存在缺陷：它不能解释不同时间上人均产出的巨大增长，也无法解释地域上不同人均产出的巨大差距。
（按边际产品取得收益的传统途径）。
()((),()())Y t F K t A t L t =假设：（1）生产函数关于两个自变量是规模报酬不变的，即资本与有效劳动是规模报酬不变的((,)(,),0)F cK cAL cF K AL c =∀≥；（2）除资本、劳动与知识以外的其他投入是相对不重要的，特别地，模型忽略了土地与其他自然资源。
规模报酬不变的假设可以让我们利用紧凑形式的生产函数进行分析：当11/,(,)(,)(,1)(,)K c AL F cK cAL cF K AL F F K AL AL AL ==⇒=，其中，KAL是单位有效劳动的资本量，1(,)F K AL AL 是单位有效劳动的产出。
定义Kk AL=，/y Y AL =，及(,1)y F k =()y f k ⇒=，即把单位有效劳动的产出写成单位有效劳动的资本量的函数。
[人均收入：/(/)()Y L A Y AL Af k ==]紧凑型生产函数()f k 假定满足(0)0f =，'()0f k >，''()0f k <。
因为：'(,)(/)(,)/(/)(1/)F K AL ALf K AL F K AL K ALf K AL AL =⇒∂∂='()f k = '()0f k >，''()0f k <的假设意味着资本的边际产品为正，但它随每单位有效劳动的资本量的增加而下降。
另()f •被假设满足稻田条件：''0lim (),lim ()0k k f k f k →→∞=∞=，其意思是在资本存量充分小量资本的边际产品是十分大的，而当资本存量变大时，资本的边际产品变得十分小。
索洛模型中文译文(1、2部分)
索洛模型关于经济增长理论的一篇贡献罗伯特M索洛第一部分引言所有理论依赖于不太真实的假设，这就是理论之所以成理论。
成功的理论的艺术，是用这样一种方式来做不可避免的简化假设，用这种方法最后总结过不会很敏感。
一个决定性的假设是结论显著依赖着的假设，并且决定性假设是相当可靠真实的，这点很重要。
当一个理论的结论明显地由一个特定的假设产生，而这个假设是可疑的，那么结果也是可疑的。
我想论证一些此类的东西对于哈罗德—多马经济增长模型是正确的。
哈罗德—多马思路最具特点且有力的结论是：即使是在长期当中，经济体系至多是在一种刃锋平衡状态。
关键参数有，储蓄率、资本产出比率、劳动力增长率。
任何由绝对中心的滑动，其结果将是失业率的增长或长期通胀。
在哈罗德体系中，关于平衡的最重要的问题归结于无技术改变前提下，依赖于劳动力增长的“自然增长率”，以及基于家庭与工厂储蓄投资习惯的“保证增长率”之间的比较。
但保证增长率与自然增长率的基本矛盾最终源于要素比例固定这一决定性假设，在生产中，劳动力与资本没有替代的可能。
如果放弃这个假设，那么不稳定的均衡的刀锋概念也就随之而去了。
其实，这一点也不奇怪，系统中一部如此完全的刚性，会限定另一部分缺少弹性。
哈罗德—多马模型的一个显著特点是它坚持用一般的短期工具来研究长期问题。
人们通常认为长期是新古典主义分析的领土，边际分析的领域。
但哈罗德和多马用乘数，投资增加系数，资本系数来讨论长期。
这篇文章的大部分用于一个接受除了固定要素比例外所有哈罗德—多马模型假设的长期模型。
但我忍为单个的合成商品，在标准的新古典主义经典条件下，是由劳动力和资本共同制造的。
对于外因决定劳动力增长率，系统进行细微调节来适应，以观察哈罗德不稳定是否出现。
在这个新古典主义经典调整过程中，价格—工资—利率反应扮演着重要的角色，因此也会对它们进行分析。
还会稍微放松一些其他的刚性的假设条件，来观测性质改变引起的结果：允许模糊技术改变和一个利率弹性的储蓄时间表。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1
预备知识：技术进步的类型
Y=F(K,AL)（哈罗德型，资本增进型） Y=F(AK,L)（索洛型，劳动增进型） Y=AF(K,L)（希克斯型，同等密集型）
2
新古典经济增长模型的提出
由美国经济学家R·Solow(索洛)和T·Swan(斯 旺)提出,即Solow- Swan Model
33
1.储蓄率变化的影响方向分析
snew
k
ne
w
y new
snew f (k )
(n g )k sold f (k )
kold
k
ne
w
k
34
变化的路径：
k
•
k 0 k
k
为实际投资
•
k 0 k
(g n ) 曲线上任一
点与原点连
sf (k) / k 接直线的斜
率，随k增加
k
而降低。
31
（三）参数变化的影响
索洛模型中，主要参数有：
n, g, , s
政策最有可能影响的是储蓄率
32
（三）参数变化的影响
1.储蓄率增加的影响方向分析（定性）； 2.储蓄率增加的影响程度分析（定量）； 3.最优储蓄率——资本的黄金规则水平。 分三个角度来观察： 1.旧的稳态点 2.新的稳态点 3.由旧稳态点到新稳态点的动态调整过程
等于常数，人口和知识呈指数增长。
15
（二）模型的动态学
k的动态变化
kt dk d K t AtLt
dt
dt
Kt At Lt
K t
At Lt 2
AtLt
Lt At
Kt At Lt
K t At Lt
Lt Lt
K t At Lt
At At
sY t K t At Lt
ktn ktg
(n g )，c * f
s
0
当k* f
k *gold ，f
'(k *(s, n, g, )) p
(n g )，c * p
s
0
42
3. 储蓄率的变动——资本的黄金律水平
c
储蓄率提高，消费减少（资
本高于黄金律水平）
t0
t
43
3. 储蓄率的变动——资本的黄金律水平
储蓄率降低，消费增加（资
c
sf kt n g kt
16
（二）模型的动态学
索洛模型的核心公式：
kt sf kt n g kt
单位有效劳动的资本存量的变化等于两项之：
sf k： 单位有效劳动的平均投资
n g k：t持平投资，使k保持现有水平所必
需的投资
17
经济解释
k&(t)=sf(k(t))-(n+g+ )k(t)
边际报酬递减
满足稻田(Inada)条件：
lim f k
k 0
lim f k 0
k
保证经济增长路径不发散
8
（一）模型的基本假定
f( k)
k
9
注释：新古典生产函数
第一，每种投入的边际产品为正且递减。 第二，规模报酬不变。 第三，稻田条件：
满足这三个条件的 生产函数被称为新 古典生产函数。
35
随时间变化的路径：
k
•
k 0 k
当储蓄率一次性提高，k的增 长速度在最开始达到最大，之 后开始减少，直至到新的稳态 处为0.
(g n)
s2 f (k) / k s1 f (k) / k
k1
k
2
k
36
储蓄率增加的影响方向分析
储蓄率的一个永久增加： 导致k在一定时期上升，保持在一个较高水平； ➢ 在短期内会改变Y、K的增长率，长期无影响； ➢ 造成Y/L增长率的暂时性增长；
形式： F K ,1 1 FK, AL
AL AL
y f k
y为单位有效劳动的平均产量； k为单位有效劳动的平均资本量。
其中：有效劳动AL，有效劳动人均资本k=K/AL， 有效劳动人均产量y=Y/AL，总产量Y=AL·f(k)
7
（一）模型的基本假定
进一步假设：
f k 0
f k 0
12
（一）模型的基本假定
劳动和知识的进化，使得有效劳动数量 在增长，其增长率为：
d A(t)L(t) dt A(t)L(t) A(t)L(t) A(t) L(t) g n
A(t ) L(t )
A(t ) L(t )
A(t) L(t)
13
（一）模型的基本假定
3.资本的增长（投资）：
Kt sY t K t
i=sgf(k)
i=s1f(k)
0
k1*
k
g
k2*
k
47
（四）收敛问题
收敛速度 绝对收敛与相对收敛
48
收敛速度
•
定义k的增长率 k/ k sf (k) / k (n g ) k •
当sf (k(t))>(n g )k(t)时，k(t)>0；
•
当sf (k(t))<(n g )k(t)时，k(t)<0；
产量取决于三个变量：资本、劳动、知识； A和L以相乘形式影响Y
5
（一）模型的基本假定
规模报酬不变
FcK,cL cFK, L c 0
这意味着：
a 经济规模足够大（专业化收益已被穷尽）； b 其他因素，如自然资源等不重要。
6
（一）模型的基本假定
根据规模报酬不变假设，可以将生产函数写成密集
52
xt xt
2.储蓄率增加的影响程度分析
x(t) 的增长路径：
xt x0et
写成k的形式：
k t k * e 1K k* ng t k 0 k *
53
绝对收敛与相对收敛
对索洛模型的收敛性的实证检验（样本 的同质性与异质性），产生绝对收敛与 相对收敛的概念。
是索洛模型的基本微分方程， 它表明k&(t)是k的方程。 含义说明：人均实际投资sf(k(t)) 用于两个方面：一是“资本的深化”， 即k&(t)，二是“资本的广化”（持平投资），
即（n+g+）k(t)。 18
（二）模型的动态学
每单位有效劳动 平均投资
n g kt
sf k
k*
k
19
（二）模型的动态学
11
（一）模型的基本假定
投入品的指数增长： 假设时间t是连续的（非离散的） （1）劳动力的增长：•
L(t) / L(t) [dL(t) / dt] / L(t) n （2）知识的增长：A• (t) / A(t) [dA(t) / dt] / A(t) g
其中n为人口增长率，g为技术进步率，均为外 生参数，表示不变增长速度
dt L(t) L(t) L(t) L(t)
L(t)
L(t)
L(t)
人均产出（劳动生产率）以技术进步率g增长。
注意区分人均产出与人均有效劳动产出。
28
平衡增长路径
在索洛模型中，无论从任何一点出发， 经济向平衡增长路径收敛，在平衡增长 路径上，每个变量的增长率都是常数， 且是外生决定的。特别是，在该路径上， 人均产出的增长率仅取决于技术进步率。
49
结论
k s • f '(k) f (k) k/ k p 0 k
经济体低于稳态越多，将会增长越快；经 济体高于稳态越多，将会增长越慢。
50
收敛速度：定量分析
收敛速度：k以多快的速度趋近于k*。
k kk
在k k *处，对kk 作一阶泰勒级数近似：
k
kk
k
k k*
k
k
*
kk sf k * n g
k的相图（三维空间在平面的投影）
•
k (t )
k
与上图联 系起来
k*
k
20
稳态
定义“稳态”：一种其中各种变量 都以不变速度增长的情况，即k&(t)=0。
当sf(k(t))f (n+g+ )k(t)时，k&(t)f 0（资本存量增加） 当sf(k(t))p (n+g+ )k(t)时，k&(t)p 0（资本存量减少） 当sf(k(t))＝(n+g+ )k(t)时，k&(t)＝0
Solow模型就是要通过改变资本-产量比来考 虑技术进步对经济增长的作用。
3
索洛模型
（一）模型的基本假定 （二）模型的动态学 （三）参数变化的影响 （四）收敛问题 （五）模型的主要结论
4
（一）模型的基本假定
1.关于生产函数的假定
Y t F K t , At Lt K t ：资本存量； At ：知识水平； Lt ：劳动力
29
变量
含义
平衡增长速度
备注证明
K
资本存量
n+g
k=K/AL
绝
L
劳动力
n
对
A
知识或技术
g
量
AL
有效劳动
n+g
总产出
F(cK,cAL)=cF(K,
Y
n+g
AL)
C
总消费
n+g
C=(1-s)Y
有效劳动的平均资
k(K/AL) 本
0
K/L
人均资本
g
相
有效劳动的人均产
y=f(k)=Y/AL
y(Y/AL)
出
0
对
Y/L
人均产出
g
量
有效劳动的人均消
c=(1-s)f(k)
c(C/AL)