最值与轨迹问题专题

合集下载

初中数学精讲隐圆模型(线段最值和轨迹问题)

几何模型11——隐圆问题在初中数学中利用隐圆解决平面几何问题大致分为三类，第一类是定点加定长构造圆形，第二类是定弦定角，第三类是从动模型之轨迹为圆也就是常说的“瓜豆原理”，在初中数学当中构造定弦定角构造圆形在压轴题当中经常出现，定弦定角构造圆形圆形中一般求一个定点到一动点线段长度的最小值问题的时候一般涉及定弦定角问题。

定弦定角解决问题的步骤：（1）让动点动一下，观察另一个动点的运动轨迹，发现另一个动点的运动轨迹为一段弧（2）找不变的张角（很多时候一般是找出张角的补角），（补角一般为60︒、45︒）（3）找张角所对的定弦，根据三点确定隐形圆，确定圆心位置（4）计算隐形圆的半径（5）圆心与所求线段上定点的距离可以求出来（6）最小值等于圆心到定点之间的距离减去半径例1.如图，在矩形纸片ABCD中，AB＝2，AD＝3，点E是AB的中点，点F是AD边上的一个动点，将△AEF沿EF所在直线翻折，得到△A′EF，求A′C的长的最小值变式1.如图，在矩形ABCD中，AB＝2，AD＝，点E为AB中点，点F为AD 边上从A到D运动的一个动点，连接EF，将△AEF沿EF折叠，点A落在点G处，在运动的过程中，求点G运动的路径长（1）直径所对的圆周角是直角．构造思路：一条定边所对的角始终为直角，则直角顶点轨迹是以定边为直径的圆或圆弧．图形释义：例2.如图，半径为4的⊙O 中，CD 为直径，弦AB ⊥CD 且过半径OD 的中点，点E 为⊙O 上一动点，CF ⊥AE 于点F ．当点E 从点B 出发顺时针运动到点D 时，求点F 所经过的路径长变式1.如图，在正方形ABCD 中，AB ＝2，动点E 从点A 出发向终点D 运动，同时动点F 从点D 出发向终点C 运动，点E ，F 的运动速度相同，当它们到达各自的终点时停止运动．运动过程中线段AF ，BE 相交于点P ，求线段DP 长的最小值变式2.如图，E ，F 是正方形ABCD 的边AD 上两个动点，满足AE =DF ．连接CF 交BD 于点G ，连接BE 交AG 于点H ．若正方形的边长为2，则线段DH 长度的最小值是．P PA BOP变式3.如图，在菱形ABCD 中，∠ABC ＝60°，AB ＝4，点E 是AB 边上的动点，过点B 作直线CE 的垂线，垂足为F ，当点E 从点A 运动到点B 时，求点F 的运动路径长变式4.如图，Rt △ABC 中，AB ⊥BC ，AB ＝6，BC ＝4，P 是△ABC 内部的一个动点，且满足∠P AB ＝∠PBC ，则线段CP 长的最小值为（）（2）定边对定角在“定边对直角”问题中，依据“直径所对的圆周角是直角”，关键性在于寻找定边、直角，而根据圆周角定理：同圆或等圆中，同弧或等弧所对的圆周角都相．定边必不可少，而直角则可一般为定角．例如，AB 为定值，∠P 为定角，则A点轨迹是一个圆．∠P 度数也是特殊角，比如30°、45°、60°、120°，下分别作对应的轨迹圆．例3.如图，△ABC 是等边三角形，边长为6，E 、F 分别是BC 、AC 上的动点，且CE ＝AF ，连接AE 、BF 交于点G ，求CG 最小值60°120°O P ABO120°120°P ABP PAB P30°O 60°BAP 90°45°ABO P变式2.如图，△ABC为等边三角形，AB＝3．若P为△ABC内一动点，且满足∠P AB＝∠ACP，求线段PB长度的最小值变式3.边三角形ABC的边长为6，在AC，BC边上各取一点E，F，连接AF，BE相交于点P．AF＝BE，当点E从点A运动到点C时，试求点P经过的路径长．例4.如图，半径为2cm，圆心角为90°的扇形OAB的弧AB上有一运动的点P，从点P向半径OA引垂线PH交OA于点H．设△OPH的内心为I，当点P在弧AB上从点A运动到点B时，求内心I所经过的路径长变式1.如图，AB是⊙O的直径，M、N是（异于A、B）上两点，C是上一动点，∠ACB的角平分线交⊙O于点D，∠BAC的平分线交CD于点E．当点C从点M运动到点N时，则C、E两点的运动路径长的比是．变式2.如图，半径为4的⊙O中，弦AB的长度为4，点C是劣弧上的一个动点，点D是弦AC的中点，点E是弦BC的中点，连接DE、OD、OE．（1）求∠AOB的度数；（2）当点C沿着劣弧从点A开始，逆时针运动到点B时，求△ODE的外心P所经过的路径的长度；例5.如图，AC＝3，BC＝5，且∠BAC＝90°，D为AC上一动点，以AD为直径作圆，连接BD交圆于E点，连CE，则CE的最小值为（）16A．213+C．5D．13-B．29变式1.如图，△ABC中，AC＝3，BC＝24，∠ACB＝45°，D为△ABC内一动点，⊙O为△ACD的外接圆，直线BD交⊙O于P点，交BC于E点，弧AE＝CP，则AD的最小值为（）A．1B．2C．2D．241-4例6.如图，P 是圆O 上一个动点，A 为定点，连接AP ，以AP 为一边作等边△APQ ．考虑：当点P 在圆O 上运动时，Q 点轨迹是？【分析】Q 点满足（1）∠PAQ=60°；（2）AP=AQ ，故Q 点轨迹是个圆：考虑∠PAQ=60°，可得Q 点轨迹圆圆心M 满足∠MAO=60°；考虑AP=AQ ，可得Q 点轨迹圆圆心M 满足AM=AO ，且可得半径MQ=PO ．即可确定圆M 位置，任意时刻均有△APO ≌△AQM ．例7.如图，正方形ABCD 中，25AB ，O 是BC 边的中点，点E 是正方形内一动点，OE=2，连接DE ，将线段DE 绕点D 逆时针旋转90°得DF ，连接AE 、CF ．求线段OF 长的最小值．【解析】E 是主动点，F 是从动点，D 是定点，E 点满足EO=2，故E 点轨迹是以O 为圆心，2为半径的圆．答案为52-2 变式1.如图，已知在扇形AOB 中，OA ＝3，∠AOB ＝120º，C 是在上的动点，以BC 为边作正方形BCDE ，当点C 从点A 移动至点B 时，求点D 运动的路径长？OPA Q60°MQAPOO AB CD E F O A B C D EF M变式2.如图，AB为⊙O的直径，C为⊙O上一点，其中AB＝2，∠AOC＝120°，P为⊙O上的动点，连AP，取AP中点Q，连CQ，则线段CQ的最大值为____________．变式3.如图，在等腰Rt△ABC中，AC＝BC＝22，点P在以斜边AB为直径的半圆上，M为PC的中点，当半圆从点A运动至点B时，点M运动的路径长为________．。

轨迹法在最值问题中的应用

又Ａ（，）Ｄ（ｃｃ，ｃ０，２，）直线０ｃ，２，）Ｆ（即点，直雎与圆的得（，）为Ｆ线椭ｃ鲁詈＿＿故
点、轴长为６的椭圆上．长注意到焦距Ｃ＝ＡＤＣ一
：
２．ｃ
注本题若用常规法计算量较大，对计算能
ｚ＋ｙ一４（［ｚ一６＋ｙ］），
整理得（４ｙ一１．以Ａ到Ｂ边的ｚ一）＋６所Ｄ
解法２常规法）设Ｂ＝则Ａ（Ｃ：ｚ，＝Ｃ一√ ，２且Ｘ＋２＞ √ ．，２＋＞２解得２√ ２Ｅ√ Ｙ，（２— １＜）Ｘ＜２√ （２＋１．）又设ＡＣＢ一０则，
・
４・０
中学数学月刊
２１年第１０１Ｏ期
轨迹法在最值问题中的应用
张青（苏省苏州中学江２５０）１０７
本文将通过三个例题来讨论轨迹法在最值问题中的应用．为叙述方便，我们先介绍一下阿波
思路审视此题
椭圆上顶点Ａ作右准线ｌ的垂线，足为Ｄ，垂线段
Ｄ与椭圆的交点是Ｍ．问：否存在，ＴＦ试是使Ａ
—
Ｔ成立？若存在，出２的值；不存在，Ｍ求若试
思路审视此题的
的常规思路是先求出直
ｚ。
一
｛７
一ｚ，以Ｐ所Ｃ＋Ｐ一６所以Ｐ点在以Ｃ，Ｄ．Ｄ为焦

中考数学几何动点运动轨迹及最值专题讲义

2020春中考数学几何动点运动轨迹及最值专题讲义一、动点运动轨迹——直线型（动点轨迹为一条直线，利用“垂线段最短”）Ⅰ．当一个点的坐标以某个字母的代数式表示，若可化为一次函数，则点的轨迹是直线；1．在平面直角坐标系中，点P的坐标为（0，2），点M的坐标为39(1,)44m m−−−(其中m为实数)，当PM 的长最小时，m的值为__________．2．如图，在平面直角坐标系中，A(1，4)，B(3，2)，C(m，－4m＋20)，若OC恰好平分四边形．．．OACB．．．．的面积，求点C的坐标．Ⅱ．当某一动点到某条直线的距离不变时，该动点的轨迹为直线；3．如图，矩形ABCD中，AB＝6，AD＝8，点E在边AD上，且AE：ED＝1：3．动点P从点A出发，沿AB运动到点B停止．过点E作EF⊥PE交射线BC于点F，设M是线段EF的中点，则在点P运动的整个过程中，点M运动路线的长为_________.【变式1】如图，矩形ABCD中，AB＝6，AD＝8，点E在边AD上，且AE：ED＝1：3．动点P从点A出发，沿AB运动到点B停止．过点E作EF⊥PE交边BC或CD于点F，设M是线段EF的中点，则在点P运动的整个过程中，点M运动路线的长为___________.ABDCEFPMABDCEFPMyxBAO【变式2】如图，在矩形ABCD 中，点P 在AD 上，AB ＝2，AP ＝1，E 是AB 上的一个动点，连接PE ，过点P 作PE 的垂线，交BC 于点F ，连接EF ，设EF 的中点为G ，当点E 从点B 运动到点A 时，点G 移动的路径的长是_________.【变式3】在矩形ABCD 中，AB ＝4，AD ＝6，P 是AD 边的中点，点E 在AB 边上，EP 的延长线交射线CD于F 点，过点P 作PQ ⊥EF ，与射线BC 相交于点Q ．（1）如图1，当点Q 在点C 时，试求AE 的长；（2）如图2，点G 为FQ 的中点，连结PG ． ①当AE ＝1时，求PG 的长；②当点E 从点A 运动到点B 时，试直接写出线段PG 扫过的面积．变式3图14．如图，C 、D 是线段AB 上两点，且AC ＝BD ＝16AB ＝1，点P 是线段CD 上一个动点，在AB 同侧分别作等边△P AE 和等边△PBF ，M 为线段EF 的中点。

最值问题2-轨迹法

最值问题2－轨迹法一．轨迹法：（Made by MrH）1．标志特点：遇“动点”，找轨迹2．考点：①两点之间线段最短；②点到直线垂线段最短3．轨迹类型：①直线轨迹；②圆轨迹；二．轨迹找法：（Made by MrH）1．直线轨迹：①直接看出；②瓜豆原理；③夹角定位法；（1）主要说明：“夹角定位法”如图1，l为定直线，A为l上一定点，B为动点，且AB与直线l夹角为定值，则B点的轨迹为直线l'．【示例】如图2所示，等腰△ABC中，AB＝AC，∠B＝30°，D为BC上一动点，以AD为边在右侧作等腰△ADE，AD＝AE，∠BAC＝∠DAE，则动点E的轨迹为？解析：①易证△ABD≌△ACE（SAS）∴∠ACE＝30°，即E点轨迹为直线②根据瓜豆原理，E点可以看做是D点绕A点旋转120°得到的点，则E的轨迹为BC绕点A旋转120°的线段．2．轨迹为圆：①一中同长（定义）；②定角对定边（一般为90°）③瓜豆原理（1）一中同长：如图3，动点A到定点O的距离为定值，则A点的轨迹为以O为圆心的圆．【示例】如图4，矩形ABCD中，AD＝1，AB＝5，E为AB上一动点，连接DE并将△ADE沿着DE翻折得到△DEF，则F点的轨迹为？解析：∵AD＝DF＝1,∴F是以D为圆心，1为半径的圆，由于E点从A运动到B，分析起始位置和终止位置，F的轨迹不完整，是一段弧线．（2）定角对定边：“一般为90°”如图5，A为动点，满足∠A＝90°，且∠A所对的边BC长度一定，则A点轨迹为以BC为直径的圆，圆心为BC的中点．三．基本模型：（Made by MrH）1．点线轨迹：“点到直线垂线段最短”→斜≥垂如图6，A为定点，C为直线l上一动点，则AC≥AB（垂线）由此可推论：“斜≥垂”2．点圆轨迹：如图1，A为定点，B为动点（轨迹为以定点O为圆心的圆），求AB的最大值与最小值．解析：两边之差＜第三边＜两边之和∴d－r≤AB≤d＋r即AB最大值为d＋r，最小值为d－r3．线线轨迹：如图2，直线l1∥l2，A、B分别为l1、l2上的两个动点，求AB的最小值．解析：“斜≥垂”∴AB≥AC，即AB最小值为AC4．线圆轨迹：如图3，A为圆O上动点，B为直线l上动点，则AB≥CD．Made By HuangTao2019.2.17MrH老大笔记。

《解析几何》第5讲圆的最值与轨迹问题

第八章
平面解析几何
第4课时圆的最值与轨迹问题
第八章
平面解析几何
2 2 例题1.实数x,y满足x +y -4x+1=0.
(1) 求y-x的最值．
(2) 求y/x的最值．
(3)求x2+y2的最值．
栏目导引
第八章
平面解析几何
y －b (1) 形如 u＝型的最值问题， x－a 可转化为过点(a， b)和点(x， y)的直线的斜率． (2) 形如 t＝ax＋by 型的最值问题，可转化为动直线的截距． (3) 形如(x－a) ＋(y－b) 型的最值问题，可转化为动点到定点的距离平方．
栏目导引
第八章
平面解析几何
解析：圆 x2＋ y2＋ 2x－4y＋ 1＝ 0 的圆心为(－1， 2)，半径 r ＝ 2. 因为直线被截得的弦长为 4，则圆心在直线 2ax－ by＋ 2＝ 0 上，所以－ 2a－2b＋ 2＝ 0，即 a＋ b＝ 1. a＋b 2 1 1 所以 ab≤ ( ) ＝，当且仅当 a＝ b＝时取等号． 2 4 2 1 故 (ab)max＝ . 4
栏目导引
2
2
第八章
平面解析几何
例题2.已知点A(2,0)在圆x2＋y2＝4上， B(1,1)在圆内，P，Q为圆上的动点． (1)求线段AP中点的轨迹方程； (2)若PQ 经过点B，求线段PQ中点的轨迹方程． (3)若∠PBQ＝90°,求线段PQ中点的轨迹方程．
栏目导引
第八章
平面解析几何
求与圆有关的轨迹常采用以下方法： (1)直接法：直接根据题目提供的条件列出方程． (2)定义法：根据圆、直线等定义列方程． (3)几何法：利用圆的几何性质列方程． (4)代入法：找到要求点与已知点的关系，代入已知点满足的关系式等．

轨迹问题

轨迹演示（2）
D
F C B
A
解答图
E
E
F
C B
A
D
例4.在△ABC中，∠ACB＝90°，∠B＝60°，
AC＝6，点D是直线AC上一动点，连接BD，
连接BD，以BD为边作等边△BDE(B、D、E逆
时针排列），连接CE，当线段CE的长度最小
时，求线段CD的长度
B
E
CD
A
轨迹演示（1）
轨迹演示（2）
轨迹问题（2）
湖北省水果湖第二中学游民主
例1.如图，在△ABC中，AB=AC,BC＝a，D、E 分别为AB、AC上的点，且AD＝CE，求DE最小值.
轨迹演示（1）
轨迹演示（2）
轨迹演示（3）
例2.如图,已知△ABC中，∠ACB＝90°， ∠BAC＝30°，AB＝4，点D为直线AB上一动点,将线段CD绕点C逆时针旋转60°得到线段 CE,连接ED、BE，当BE最小时，求线段AD的值.
E
C
B
DA
轨迹演示（1）
轨迹演示（2）
解答图
E
C G
C G
BFAD来自DBF
A
E
a a
例3.在△ABC中，∠ACB＝90°，∠B＝60°， AB＝4，点D是直线BC上一动点，连接AD，直线AD的右侧作等边△ADE，连接CE，当线段CE的长度最小时，求线段CD的长度.
E F
C
B
A
D
轨迹演示（1）
B F
D
C EM
A
解答图
E B
F C MD A
E
B F
CM A
D

2021秋季创新班第十三讲-轨迹最值综合解析

3 3 2021 秋季初三创新班第十三讲补充题轨迹问题综合1．如图，等边∆ABC 边长为2，射线AM//BC，P是射线AM 上一动点(P不与A点重合），∆APC 的外接圆交BP 于Q ，则AQ 长的最小值为【解析】解：过点B 作BD ⊥直线AP ，垂足为D ，过点C 作CE ⊥直线AP ，垂足为E ，连接QC ，如图，则有BD / /CE ．AP / / BC ，∠BDE = 90︒，∴四边形BCED 是矩形，∴∠DBC =∠ECB = 90︒．∆ABC 是等边三角形，∴AB =AC =BC = 2 ，∠ABC =∠ACB = 60︒，∴∠DBA =∠ECA = 30︒，∴AD = 1，AE = 1 ，∴BD =，CE =．设AP =x ，则DP =x + 1 ，EP =x -1 ．在Rt∆BDP 中，BP2 =BD2 +DP2 = 3 + (x +1)2 =x2 + 2x +4 ．在Rt∆CEP 中，CP2 =CE2 +EP2 = 3 + (x -1)2 =x2 - 2x+ 4 ．AM / / BC ，∴∠APB =∠CBP ．∠APB =∠ACQ ，∴∠ACQ =∠CBP ．∠QAC =∠CPB ，xx3∴∆AQC∽∆PCB ，∴AQ=PC，∴AQ = 2 ⨯PC，AC PB∴2PC2PBx2 - 2x + 4 4xAQ = 4 ⨯= 4 ⨯PB2x2 + 2x + 4= 4 ⨯ (1 -x2 + 2x + 4)= 4 ⨯ (1 -4x + 2 +4x) = 4 -(16，-2)2 + 6当-2= 0 即x = 2 时，AQ2 取到最小值为4，此时AQ =2 3．3 3方法二：如图，易知∠PQC =∠PAC =∠ACB = 60︒，∴∠BQC = 120︒，∴点Q 的运动轨迹是BC ，∴当AQ ⊥BC 时，AQ 的长最小，设AQ 交BC 于G ，此时AG =，OG =1BQ =1AQ ，2 2∴AQ 的最小值为2 3，3xx33O'C2 +AC242 + 322．如图，∆ABC ，AC = 3 ，BC = 4 ，∠ACB = 60︒，过点A 作BC 的平行线l ，P 为直线l 上一动点，O 为∆APC 的外接圆，直线BP 交O 于E 点，则AE 的最小值为【解析】解：如图，连接CE ．AP / / BC ，∴∠PAC =∠ACB = 60︒，∴∠CEP =∠CAP = 60︒，∴∠BEC = 120︒，∴点E 在以O'为圆心，O'B 为半径的BC 上运动，连接OA 交BC 于E'，此时AE'的值最小．此时O 与O'交点为E'．= 120︒∴BC 所对圆周角为60︒，∴∠BOC = 2 ⨯ 60︒= 120︒，△BO'C 是等腰三角形，BC = 4 ，∴O'B =O'C = 4 ，∠ACB = 60︒，∠BCO'= 30︒，∴∠ACO'= 90︒∴O'A === 5 ，∴AE'=O'A -O'E'= 5 - 4 = 1 ．∠BE'C2 2 2 ⎨ ⎩3．如图，扇形 AOD 中， ∠AOD = 90︒ ， OA = 6 ，点 P 为弧 AD 上任意一点（不与点 A 和 D 重合）， PQ ⊥ OD 于Q ，点 I 为∆OPQ 的内心，过O ， I 和 D 三点的圆的半径为r ．则当点 P 在弧 AD 上运动时， r 的值满足( )A． 0 < r < 3B． r = 3 C． 3 < r < 3 D． r = 3 【解析】解：如图，连OI ， PI ， DI ，的内心为 I ，∴∠IOP = ∠IOD ， ∠IPO = ∠IPH ，∴∠PIO = 180︒ - ∠IPO - ∠IOP = 180︒ - 1 (∠HOP + ∠OPH ) ， 2而 PH ⊥ OD ，即∠PHO = 90︒ ，∴∠PIO = 180︒ - 1 (∠HOP + ∠OPH ) = 180︒ - 1 (180︒ - 90︒) = 135︒ ， 2 2⎧IO = IO 在 ∆OPI 和∆ODI 中， ⎪∠POI = ∠DOI ，∴∆OPI ≅ ∆ODI (SAS ) ，∴∠DIO = ∠PIO = 135︒ ，⎪OD = OP所以点 I 在以OD 为弦，并且所对的圆周角为135︒ 的一段劣弧上；过 D 、 I 、O 三点作 O ' ，如图，连O 'D ， O 'O ，在优弧 DO 取点 P ' ，连 P 'D ， P 'O ，∠DIO = 135︒ ，∴∠DP 'O = 180︒ - 135︒ = 45︒ ，∴∠DO 'O = 90︒ ，而OD = 6 ，∴OO ' = DO ' = 3 ，∴r 的值为3 ．2∆OPH2 y 2 +12 y 2 +1 y 2 + 1 4 2 2 24．如图，∆ABC 在直角坐标系中， AB = AC ， A (0 ，2 2) ，C (1, 0) ，D 为射线 AO 上一点，一动点 P 从 A 出发，运动路径为 A → D → C ，点 P 在 AD 上的运动速度是在CD 上的 3 倍，要使整个运动时间最少，则点 D 的坐标应为【解析】解：假设 P 在 AD 的速度为 3，在CD 的速度为 1，设 D 坐标为(0, y ) ，则 AD = 2 - y ， CD = = ，∴设t = 2 2 - y+ ，3 等式变形为： t + 1 y - 2 2 = 3 3，则t 的最小值时考虑 y 的取值即可， ∴t 2 + ( 2 y - )t + (1 y - )2 = y 2 + 1 ，3 3 3 3∴ 8 y 2 + ( 4 2 - 2 t ) y - t 2 + 4 2 t + 1 = 0 ， 9 9 3 3△ = ( 4 2 - 2 t )2 - 4 ⨯ 8 (-t 2 + 4 2 t + 1) 0 ， 9 3 9 3∴t 的最小值为 3 ，∴ y = 2， 4 ∴点 D 的坐标为(0, 2 ) ， 4 解法二：假设 P 在 AD 的速度为3V ，在CD 的速度为1V ，总时间t = AD + CD = 1 ( AD + CD ) ，要使t 最小，就要 AD + CD 最小，3V V V 3 3因为 AB = AC = 3 ，过点 B 作 BH ⊥ AC 交 AC 于点 H ，交OA 于 D ，易证∆ADH ∽∆ACO ，所以 AC = AD = 3 ，所以 AD = DH ，因为∆ABC 是等腰三角形，所以 BD = CD ，所以OC DH 3要 AD + CD 最小，就是要 DH + BD 最小，就要 B 、 D 、 H 三点共线就行了．因为 3∆AOC ∽∆BOD ，所以 AO = OC ，即 2 2 = 1 ，所以OD = 2 ，所以点 D 的坐标应为(0, OB OD 2 ) ． 41 OD 4y 2 + 1TH 2 +CH2 7 - 1 2 25．如图， AB 是 O 的直径， AB = 2 ，∠ABC = 60︒ ，P 是 O 上一动点，D 是 AP 的中点，连接CD ，则CD 的最小值为．【解析】解：如图，取OA 是中点T ，连接CT ，DT ，OP ，OC ，过点C 作CH ⊥ AB 于 H ．OB = OC ， ∠OBC = 60︒ ，∴ ∆OBC 是等边三角形，CH ⊥ OB ，∴OH = HB = 1 ， CH = 2 3OH = 3 ，2AT = TO = 1 ， AD = DP ，2∴ DT = 1 OP = 1 ，2 2在Rt ∆CTH 中， TH = OT + OH = 1 ，CH = 3 ，2 ∴CT = =∴CD CT - DT ，= 7 ， 2 ∴CD， ∴CD 的最小值为 7 - 1．2 212 + ( 3 )2 23 ⎨ ⎩6．如图，扇形OAB 中，∠AOB = 60︒ ，OA = 3 ，点C 是 AB 上一动点，CD / /OB 交OA 于 D ，I 是∆COD 的内心，则 BI 的最小值为．【解析】解：CD / /OB ，∴∠CDA = ∠BOA = 60︒ ，∴∠CDO = 120︒ ，I 是 ∆COD 的内心，∴∠OIC = 1 (180︒ - ∠ODC ) = 90︒ + 1 ⨯120︒ = 150︒ ． ∠IOC = ∠IOA ， 2 2⎧OA = OC 在∆OIA 和∆OIC 中， ⎪∠IOA = ∠IOC ，⎪OI = OI ∴∆OIA ≅ ∆OIC (SAS ) ，∴∠OIA = ∠OIC = 150︒ ，又OA = 3 ，∴ I 在以O ' 为圆心， O 'A 为半径的弧OA 上运动，如图所示：连接OI 、 AI 、CI ，在优弧OA 上取点 E ，连接OE 、 AE 、OO ' 、O 'A 、O 'B ， ∴∠E = 180︒ - 150︒ = 30︒ ，∴∠OO 'A = 2∠E = 60︒ ，O 'O = O 'A ，∴△ OO 'A 是等边三角形，∴O 'A = OA = 3 ， ∠O 'OA = 60︒ = ∠AOB ，∴OO ' = OB ， ∠O 'OB = 120︒ ，∴OA ⊥ O 'B ， ∠OO 'B = 30︒ ， O 'D =3 OO ' = 3 3 ， 2 2∴O 'B = 2O 'D == 3 ，当B 、I 、O'三点共线时，BI 的最小值为O'B -O'F = 3 - 3 ；3故答案为： 3 - 3 ．7．如图，抛物线 y = x 2 - 2x - 3 与 x 轴交于 A 、 B 两点，过 B 的直线交抛物线于 E ，且tan ∠EBA= 4 ，有一只蚂蚁从A 出发，先以 1 单位 / s 的速度爬到线段 BE 上的点 D 处，再3以 1.25 单位 / s 的速度沿着 DE 爬到 E 点处觅食，则蚂蚁从 A 到 E 的最短时间是 s ．【解析】解：过点 E 作 x 轴的平行线，再过 D 点作 y 轴的平行线，两线相交于点 H ，如图，EH / / AB ，∴∠HEB = ∠ABE ，∴ tan ∠HED = tan ∠EBA = DH = 4 ，EH 3设 DH = 4m ， EH = 3m ，则 DE = 5m ，∴蚂蚁从 D 爬到 E 点的时间= 5x 1.25= 4(s ) 若设蚂蚁从 D 爬到 H 点的速度为 1 单位 / s ，则蚂蚁从 D 爬到 H 点的时间= 4m = 4(s ) ， 1∴蚂蚁从 D 爬到 E 点所用的时间等于从 D 爬到 H 点所用的时间相等，∴蚂蚁从 A 出发，先以 1 单位 / s 的速度爬到线段 BE 上的点 D 处，再以 1.25 单位/ s 的速度沿着 DE 爬到 E 点所用时间等于它从 A 以 1 单位 / s 的速度爬到 D 点，再从 D 点以 1 单位/ s3⎨ 速度爬到 H 点的时间，作 AG ⊥ EH 于G ，则 AD + DH AH AG ， ∴ AD + DH 的最小值为 AG 的长，当 y = 0 时， x 2 - 2x - 3 = 0 ，解得 x = -1 ， x = 3 ，则 A (-1, 0) ， B (3, 0) ， 1 2 直线 BE 交 y 轴于C 点，如图，在Rt ∆OBC 中， tan ∠CBO = CO = 4 ，∴OC = 4 ，则C (0, 4) ，OB 3 设直线 BE 的解析式为 y = kx + b ， ⎧3k + b = 0⎧k =-4 把 B (3, 0) ， C (0, 4) 代入得⎨⎩b = 4 ，解得⎪ 3 ，⎪⎩b = 4∴直线 BE 的解析式为 y = - 4 x + 4 ， 3 ⎧ y = x 2 - 2x - 3 ⎧x =- 7 解方程组⎪ 得⎧x = 3 或⎪ 3 ，则 E 点坐标为(- 7 ， 64) ，∴ AG = 64 ， ⎨ y = - 4 x + 4 ⎨ y = 0 ⎨ 64 3 9 9 ⎪⎩ 3 ⎩ ⎪ y = ⎪⎩ 964 ∴蚂蚁从 A 爬到G 点的时间= 9 = 64 (s ) ， 1 9即蚂蚁从 A 到 E 的最短时间为 64 s ． 9故答案为 64 ．98．等边三角形 ABC 的边长为 6，在 AC ， BC 边上各取一点 E ， F ，连接 AF ， BE 相交于点 P ．（1）若 AE = CF ；①求证：AF =BE ，并求∠APB 的度数；⎨ ⎩②若 AE = 2 ，试求 AP 的值；（2）若 AF = BE ，当点 E 从点 A 运动到点C 时，试求点 P 经过的路径长．【解析】（1）①证明：∆ABC 为等边三角形，∴ AB = AC ， ∠C = ∠CAB = 60︒ ，在∆ABE 和∆CAF 中，⎧ AB = AC ⎪∠BAE = ∠ACF ，⎪ AE = CF ∴∆ABE ≅ ∆CAF (SAS ) ，∴ AF = BE ， ∠ABE = ∠CAF ．又 ∠APE = ∠BPF = ∠ABP + ∠BAP ，∴∠APE = ∠BAP + ∠CAF = 60︒ ．∴∠APB = 180︒ - ∠APE = 120︒ ．② ∠C = ∠APE = 60︒ ， ∠PAE = ∠CAF ，∴ ∆APE ∽∆ACF ，∴ AP = AE ，即 AP = 2 ，所以 AP AC AF 6 AF（2）①如图 1 所示：当 AE = CF 时，点 P 的路径是一段弧．由题目不难看出当 E 为 AC 的中点的时候，点 P 经过弧 AB 的中点，此时∆ABP 为等腰三角又 AE = CF ，AF AF = 123BC 2 - BH 2 62 - 32 3 1 4 3π = 2 3π 2 3 3 3 形，且∠ABP = ∠BAP = 30︒ ，∴∠AOB = 120︒ ，∴OA = 2 ．∴点 P 的路径是l = n π r = 120π ⨯= 4 3π ． 180 180 3②如图 2 所示，当 AE = BF 时，过点C 作CH ⊥ AB 垂足为H ．点 P 的路径就是过点C 向 AB 作的垂线段 HC 的长度．等边三角形 ABC 的边长为 6， CH ⊥ AB ．∴ BH = 3 ．∴点 P 的路径CH = = = 3 ．③如图 3 所示：AG = 1 AB = ． 2OA = 0B ， CA = CB ，∴OC 垂直平分 AB ．又 ∠AOB = 120︒ ，∴ ∠AOG = 60︒ ．∴OD = AD tan 30︒ = 3 ⨯ 3 =3 3 ． O A = 2OD = 2 ．又 AB = 6 ，2 33 3 3 3 3 3 3 3 3 ∴ DG = OG - OD = 2 - = ．∴GC = 3 - = 2 ．所以点 P 经过的轨迹= AG + GC= 2 3π+ 2 3 ．3 ④如图4 所示：由③可知： DG = ， BG = AG =2 3π ．3所以点 P 经过的轨迹= BG + DG = 2 3π + 3 ．3综上所述，点 P 经过的轨迹的长度为 4 3π 或3 或 2 3π + 2 3 或 2 3π + ．3 3 39．如图，在∆ACE 中，CA = CE ，∠CAE = 30︒ ， O 经过点C ，且圆的直径 AB 在线段 AE 上．（1）试说明CE 是 O 的切线；（2）若∆ACE 中 AE 边上的高为h ，试用含h 的代数式表示 O 的直径 AB ；（3）设点 D 是线段 AC 上任意一点（不含端点），连接OD ，当 1 CD + OD 的最小值为 6 时， 2求 O 的直径 AB 的长．【解析】解：（1）连接OC ，如图 1，3CA = CE ， ∠CAE = 30︒ ，∴∠E = ∠CAE = 30︒ ， ∠COE = 2∠A = 60︒ ，∴ ∠OCE = 90︒ ，∴CE 是 O 的切线；（2）过点C 作CH ⊥ AB 于 H ，连接OC ，如图 2，由题可得CH = h ．在Rt ∆OHC 中， CH = OC sin ∠COH ，∴ h = OC sin 60︒= 3OC ，2∴OC = 2h = 2 3 h ，3∴ AB = 2OC = 4 3h ；3（3）作OF 平分∠AOC ，交 O 于 F ，连接 AF 、CF 、DF ，如图 3，3 3 则∠AOF = ∠COF = 1 ∠AOC = 1 (180︒ - 60︒) = 60︒ ． 2 2OA = OF = OC ，∴ ∆AOF 、 ∆COF 是等边三角形，∴ AF = AO = OC = FC ，∴四边形 AOCF 是菱形，∴根据对称性可得 DF =DO ．过点 D 作 DH ⊥ OC 于H ，OA = OC ，∴∠OCA = ∠OAC = 30︒ ，∴ DH = DC sin ∠DCH = DC sin 30︒ = 1 DC ， 2∴ 1 CD + OD = DH + FD ． 2根据垂线段最短可得：当 F 、 D 、 H 三点共线时， DH + FD （即 1 CD + OD ) 最小， 2此时 FH = OF sin ∠FOH = 3 OF = 6 ， 2则OF = 4 ， AB = 2OF = 8 3 ．∴当 1 CD + OD 的最小值为 6 时， O 的直径 AB 的长为8 ． 210．如图，已知点 A (2, 0) ， B (0, 2) ， C (4, 0) ， D (3, 2) ， P 是∆AOB 外第一象限内的一个动点，且保持∠APB = 135︒ ，求2PD + PC 的最小值．【解析】解：如图，取一点T (1, 0) ，连接OP ， PT ， TD ．OT22 + 22 2A (2,0) ，B (0, 2) ，C (4, 0) ，∴OA = OB = 2 ， OC = 4 ，以O 为圆心OA 为半径作 O ，在优弧 AB 上取一点Q ，连接QB ，QA ，∠Q = 1∠AOB = 45︒ ， ∠APB = 135︒ ，2 ∴∠Q + ∠APB = 180︒ ，∴ A ， P ， B ， Q 四点共圆，∴OP = OA == 2OP = 2 ， OT = 1 ， OC = 4 ，∴OP 2 = OC ，∴ OP= OT ，OC OP = ∠POC ，∴ ∆POT ∽∆COP ，∴ PT = OP= 1 ，PC OC 2 ∴ PT = 1PC ，2 ∴ 2PD + PC = 2(PD + 1PC ) = 2(PD + PT ) ，2， DT = = 2 ，∴2PD + P C 4 2 ，∴ 2PD + PC 的最小值为4 2 ，∠POT PD + PT DT11．如图，矩形 ABCD 中，AB=4,BC=6，点 P 是边 AD 上一动点，E 为PE 的中点，F 是PB 上一点，且满足 EF=ED，连接 AF，当点 P 在AD 上运动的过程中，AF 长的最小值为：12．如图，边长为 2 的正方形 ABCD 中，P 是CD 上一动点，E 是AP 上一点，且 BE=AB，∠EBC的平分线交射线 AP 于 F，则△ABF 的面积最大值为：13．如图，半径为 2cm 的圆O 上有一运动的点 P，从点 P 向直径 AB 引垂线 PH 交AB 于点H，设△OPH 的内心为 I，当点 P 在圆 O 上从点 A 绕一周运动回 A 时，内心 I 所经过的路径长为：。

(完整版)立体几何中的轨迹问题(总结+讲义+练习),推荐文档

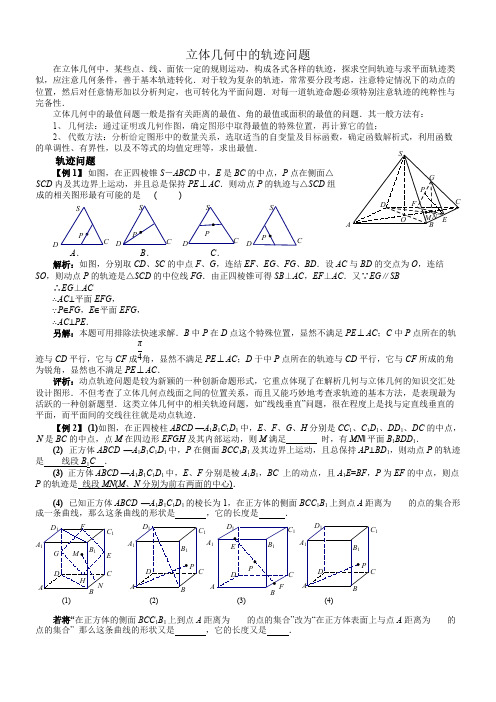
立体几何中的轨迹问题在立体几何中，某些点、线、面依一定的规则运动，构成各式各样的轨迹，探求空间轨迹与求平面轨迹类似，应注意几何条件，善于基本轨迹转化．对于较为复杂的轨迹，常常要分段考虑，注意特定情况下的动点的位置，然后对任意情形加以分析判定，也可转化为平面问题．对每一道轨迹命题必须特别注意轨迹的纯粹性与完备性．立体几何中的最值问题一般是指有关距离的最值、角的最值或面积的最值的问题．其一般方法有：1、几何法：通过证明或几何作图，确定图形中取得最值的特殊位置，再计算它的值；2、代数方法：分析给定图形中的数量关系，选取适当的自变量及目标函数，确定函数解析式，利用函数的单调性、有界性，以及不等式的均值定理等，求出最值．轨迹问题【例1】如图，在正四棱锥S－ABCD中，E是BC的中点，P点在侧面△SCD内及其边界上运动，并且总是保持PE AC．则动点P的轨迹与△SCD组⊥成的相关图形最有可能的是( )D DA．B．C．解析：如图，分别取CD、SC的中点F、G，连结EF、EG、FG、BD．设AC与BD的交点为O，连结SO，则动点P的轨迹是△SCD的中位线FG．由正四棱锥可得SB⊥AC，EF⊥AC．又∵EG∥SB ∴EG⊥AC∴AC⊥平面EFG，∵P∈FG，E∈平面EFG，∴AC⊥PE．另解：本题可用排除法快速求解．B中P在D点这个特殊位置，显然不满足PE AC；C中P点所在的轨⊥迹与CD平行，它与CF成角，显然不满足PE AC；D于中P点所在的轨迹与CD平行，它与CF所成的角π4⊥为锐角，显然也不满足PE AC．⊥评析：动点轨迹问题是较为新颖的一种创新命题形式，它重点体现了在解析几何与立体几何的知识交汇处设计图形．不但考查了立体几何点线面之间的位置关系，而且又能巧妙地考查求轨迹的基本方法，是表现最为活跃的一种创新题型．这类立体几何中的相关轨迹问题，如“线线垂直”问题，很在程度上是找与定直线垂直的平面，而平面间的交线往往就是动点轨迹．【例2】(1)如图，在正四棱柱ABCD —A1B1C1D1中，E、F、G、H分别是CC1、C1D1、DD1、DC的中点，N是BC的中点，点M在四边形EFGH及其内部运动，则M满足时，有MN∥平面B1BDD1．(2)正方体ABCD—A1B1C1D1中，P在侧面BCC1B1及其边界上运动，且总保持AP⊥BD1，则动点P的轨迹是线段B1C．(3)正方体ABCD —A1B1C1D1中，E、F分别是棱A1B1，BC上的动点，且A1E=BF，P为EF的中点，则点P的轨迹是线段MN(M、N分别为前右两面的中心)．(4)已知正方体ABCD—A1B1C1D1的棱长为1，在正方体的侧面BCC1B1上到点A距离为的点的集合形成一条曲线，那么这条曲线的形状是，它的长度是．1ACC1AE1AA1A1(1)(2)(3)(4)若将“在正方体的侧面BCC1B1上到点A距离为的点的集合”改为“在正方体表面上与点A距离为的点的集合”那么这条曲线的形状又是，它的长度又是．A【例3】(1)(04北京)在正方体ABCD -A 1B 1C 1D 1中，P 是侧面BB 1C 1C 内一动点，若P 到直线BC 与直线C 1D 1的距离相等，则动点P 的轨迹所在的曲线是 ( D )A ．A 直线B ．圆C ．双曲线D ．抛物线变式：若将“P 到直线BC 与直线C 1D 1的距离相等”改为“P 到直线BC 与直线C 1D 1的距离之比为1：2(或2：1)”，则动点P 的轨迹所在的曲线是椭圆 (双曲线)．(2)(06北京)平面α的斜线AB 交α于点B ，过定点A 的动直线l 与AB 垂直，且交α于点C ，则动点C 的轨迹是 (A )A ．一条直线B ．一个圆C ．一个椭圆D ．双曲线的一支解：设l 与l 是其中的两条任意的直线，则这两条直线确定一个平面，且斜线AB 垂直这个平面，由过平面外一点有且只有一个平面与已知直线垂直可知过定点A 与AB 垂直所有直线都在这个平面内，故动点C 都在这个平面与平面α的交线上，故选A ．(3)已知正方体ABCD —A 1B 1C 1D 1的棱长为1，M 在棱AB 上，且AM =，点P 到直13线A 1D 1的距离与点P 到点M 的距离的平方差为1，则点P 的轨迹为抛物线．(4)已知正方体ABCD —A 1B 1C 1D 1的棱长为3，长为2的线段MN 点一个端点M 在DD 1上运动，另一个端点N 在底面ABCD 上运动，则MN 的中点P 的轨迹与正方体的面所围成的几何体的体积为．π6【例4】(04重庆)若三棱锥A -BCD 的侧面ABC 内一动点P 到底面BCD 的距离与到棱AB 的距离相等，则动点P 的轨迹与△ABC 组成图形可能是：( D )BAB CD 【例5】四棱锥P -ABCD ，AD ⊥面PAB ，BC ⊥面PAB ，底面ABCD 为梯形，AD =4，BC =8，AB =6，∠APD =∠CPB ，满足上述条件的四棱锥的顶点P 的轨迹是()A ．圆B ．不完整的圆C ．抛物线D ．抛物线的一部分分析：∵AD ⊥面PAB ，BC ⊥平面PAB ∴AD ∥BC 且AD ⊥PA ，CB ⊥PB ∵∠APD =∠CPB ∴tanAPD =tanCPB∴=AD PA CBPB ∴PB =2PA在平面APB 内，以AB 的中点为原点，AB 所在直线为x 轴建立平面直角坐标系，则A (-3，0)、B (3，0)，设P (x ，y )(y ≠0)，则(x -3)2+y 2=4[(x +3)2+y 2](y ≠0)即(x +5)2+y 2=16(y ≠0)∴P 的轨迹是(B)1AA 3A立体几何中的轨迹问题（教师版）1．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 与到直线B 1C 1的距离相等，则动点P 所在曲线的形状为（D ）．A ．线段B ．一段椭圆弧C ．双曲线的一部分D ．抛物线的一部分简析本题主要考查点到直线距离的概念，线面垂直及抛物线的定义．因为B 1C 1面AB 1，所以⊥PB 1就是P 到直线B 1C 1的距离，故由抛物线的定义知：动点的轨迹为抛物线的一段，从而选D ．2．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为2：1，则动点P 所在曲线的形状为（B ）．A ．线段B ．一段椭圆弧C ．双曲线的一部分D ．抛物线的一部分3．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为1：2，则动点P 所在曲线的形状为（C ）．A ．线段B ．一段椭圆弧C ．双曲线的一部分D ．抛物线的一部分4．在正方体ABCD-A 1B 1C 1D 1中，E 为AA 1的中点，点P 在其对角面BB 1D 1D 内运动，若EP 总与直线AC 成等角，则点P 的轨迹有可能是（A ）．A ．圆或圆的一部分B ．抛物线或其一部分C ．双曲线或其一部分D ．椭圆或其一部分简析由条件易知：AC 是平面BB 1D 1D 的法向量，所以EP 与直线AC 成等角，得到EP 与平面BB 1D 1D 所成的角都相等，故点P 的轨迹有可能是圆或圆的一部分．5．已知正方体的棱长为a ，定点M 在棱AB 上（但不在端点A ，B 上），点P 是平面ABCD A B C D -1111ABCD 内的动点，且点P 到直线的距离与点P 到点M 的距离的平方差为a 2，则点P 的轨迹所在曲线为A D 11（A ）．A ．抛物线B ．双曲线C ．直线D ．圆简析在正方体中，过P 作PF AD ，过F 作FE A 1D 1，垂足分别为F 、E ，ABCD A B C D -1111⊥⊥连结PE ．则PE 2=a 2+PF 2，又PE 2-PM 2=a 2，所以PM 2=PF 2，从而PM ＝PF ，故点P 到直线AD 与到点M 的距离相等，故点P 的轨迹是以M 为焦点，AD 为准线的抛物线．6．在正方体中，点P 在侧面BCC 1B 1及其边界上运动，总有AP BD 1，则动点P 的轨迹ABCD A B C D -1111⊥为__________．简析在解题中，我们要找到运动变化中的不变因素，通常将动点聚焦到某一个平面．易证BD 1面ACB 1，所以满足BD 1AP 的所有点P 都在一个平面ACB 1上．而已知条件中的点P 是在侧面BCC 1B 1及⊥⊥其边界上运动，因此，符合条件的点P 在平面ACB 1与平面BCC 1B 1交线上，故所求的轨迹为线段B 1C ．本题的解题基本思路是：利用升维，化“动”为“静”，即先找出所有点的轨迹，然后缩小到符合条件的点的轨迹．7．在正四棱锥S-ABCD 中，E 是BC 的中点，点P 在侧面SCD 内及其边界上运动，总有PE AC ，则动点∆⊥P 的轨迹为_______________．答案线段MN （M 、N 分别为SC 、CD 的中点）8．若A 、B 为平面的两个定点，点P 在外，PB ，动点C （不同于A 、B ）在内，且PC AC ，则αα⊥αα⊥动点C 在平面内的轨迹是________．（除去两点的圆）9．若三棱锥A —BCD 的侧面ABC 内一动点P 到底面BCD 的距离与到棱AB 的距离相等，则动点P 的轨迹与ABC 组成的图形可能是：（D ）∆A A A AB C B C B C B C A B C D简析动点P 在侧面ABC 内，若点P 到AB 的距离等于到棱BC 的距离，则点P 在的内角∠ABC 平分线上．现在P 到平面BCD 的距离等于到棱AB 的距离，而P 到棱BC 的距离大于P 到底面BCD 的距离，于是，P 到棱AB 的距离小于P 到棱BC 的距离，故动点P 只能在的内角平分线与AB 之间的区域∠ABC 内．只能选D ．10．已知P 是正四面体S-ABC 的面SBC 上一点，P 到面ABC 的距离与到点S 的距离相等，则动点P 的轨迹所在的曲线是（B ）． A ．圆B ．椭圆 C ．双曲线D ．抛物线解题的要领就是化空间问题为平面问题，把一些重要元素集中在某一个平面内，利用相关的知识去解答，象平面几何知识、解析几何知识等．11．已知正方体的棱长为1，在正方体的侧面上到点A 距离为的点的轨迹形ABCD A B C D -1111BCC B 11233成一条曲线，那么这条曲线的形状是_________，它的长度为__________．12．已知长方体中，，在线段BD 、上各有一点P 、Q ，PQ 上有一点ABCD A B C D -1111AB BC ==63,A C 11M ，且，则M 点轨迹图形的面积是．PM MQ =2提示轨迹的图形是一个平行四边形．13．已知棱长为3的正方体中，长为2的线段MN 的一个端点在上运动，另一个端点ABCD A B C D -1111DD 1N 在底面ABCD 上运动，求MN 中点P 的轨迹与正方体的面所围成的几何体的体积．14．已知平面平面，直线，点，平面、间的距离为4，则在内到点P 的距离为5且到直//αβl α⊂l P ∈αββ线的距离为的点的轨迹是（）l 29A ．一个圆B ．两条平行直线C ．四个点D ．两个点简析：如图，设点P 在平面内的射影是O ，则OP 是、的公垂线，OP=4．在βαβ点的轨迹是四个点，故选C ．16．在四棱锥中，面PAB ，面PAB ，底面ABCD 为梯形，AD=4，BC=8，AB=6，ABCD P -⊥AD ⊥BC ，满足上述条件的四棱锥的顶点P 的轨迹是（）CPB APD ∠=∠A ．圆B ．不完整的圆C ．抛物线D ．抛物线的一部分简析：因为面PAB ，面PAB ，所以AD//BC ，且．⊥AD ⊥BC ︒=∠=∠90CBP DAP 又，8BC ,4AD ,CPB APD ==∠=∠由于点P 不在直线AB 上，故此轨迹为一个不完整的圆，选B ．17．如图，定点A 和B 都在平面内，定点P C 是内异于A 和B α,PB ,α⊥α∉α的动点．且，那么动点C 在平面内的轨迹是（）AC PC ⊥αA ．一条线段，但要去掉两个点B ．一个圆，但要去掉两个点C ．一个椭圆，但要去掉两个点D ．半圆，但要去掉两个点简析：因为，且PC 在内的射影为BC ，所以，即．所以点C 的轨迹是PC AC ⊥αBC AC ⊥︒=∠90ACB 以AB 为直径的圆且去掉A 、B 两点，故选B ．18．如图，在正方体中，P 是侧面内一动点，若P 到直线1111D C B A ABCD -1BC BC 与直线的距离相等，则动点P 的轨迹所在的曲线是（）11D C A ．直线B ．圆C ．双曲线D ．抛物线简析：因为P 到的距离即为P 到的距离，所以在面内，P 到定点11D C 1C 1BC 的距离与P 到定直线BC 的距离相等．由圆锥曲线的定义知动点P 的轨迹为抛物线，故选D ．1C 19．已知正方体的棱长为1，点P 是平面AC 内的动点，若点P 到直线的距离等于点1111D C B A ABCD -11D A P 到直线CD 的距离，则动点P 的轨迹所在的曲线是（）A ．抛物线B ．双曲线C ．椭圆D ．直线简析：如图4，以A 为原点，AB 为x 轴、AD 为y 轴，建立平面直角坐标系．设P （x ，y ），作于E 、于F ，连结EF ，易知AD PE ⊥11D A PF ⊥建议收藏下载本文，以便随时学习！1x |EF ||PE ||PF |2222+=+=又作于N ，则．依题意，CD PN ⊥|1y ||PN |-=|PN ||PF |=故动点P 的轨迹为双曲线，选B ．20．如图，AB 是平面的斜线段，A 为斜足，若点P 在平面内运动，使得△ABP a a 的面积为定值，则动点P 的轨迹是（）（A ）圆（B ）椭圆（C ）一条直线（D ）两条平行直线分析：由于线段AB 是定长线段，而△ABP 的面积为定值，所以动点P 到线段AB 的距离也是定值．由此可知空间点P 在以AB 为轴的圆柱侧面上．又P 在平面内运动，所以这个问题相当于一个平面去斜切一个圆柱(AB 是平面的斜线段)，得到的切痕是椭圆．P 的轨迹就是圆柱侧面与平面的交线．a 21．如图，动点在正方体的对角线上．过点作垂直于平面的直线，与正P 1111ABCD A B C D -1BD P 11BB D D 方体表面相交于．设，，则函数的图象大致是（）M N ，BP x =MN y =()y f x=ABCD MN P A 1B 1C 1D 1分析：将线段MN 投影到平面ABCD 内，易得y 为x 一次函数．22．已知异面直线a ，b 成角，公垂线段MN 的长等于2，线段AB 两个端点A 、B 分别在a ，b 上移动，且︒60线段AB 长等于4，求线段AB 中点的轨迹方程．图5简析：如图5，易知线段AB 的中点P 在公垂线段MN 的中垂面上，直线、为平面内过MN 的中α'a 'b α点O 分别平行于a 、b 的直线，于，于，则，且P 也为的中点．'a 'AA ⊥'A 'b 'BB ⊥'B P 'B 'A AB =⋂'B 'A 由已知MN=2，AB=4，易知得．,2AP ,1'AA ==32'B 'A =则问题转化为求长等于的线段的两个端点、分别在、上移动时其中点P 的轨迹．现以32'B 'A 'A 'B 'a 'b 的角平分线为x 轴，O 为原点建立如图6所示的平面直角坐标系．'OB 'A ∠图6设，，)y ,x (P n |'OB |,m |'OA |==则)n 21,n 23('B ),m 21,m 23('A -)n m (41y ),n m (43x -=+=222)32()n m (41)n m (43=++-消去m 、n ，得线段AB 的中点P 的轨迹为椭圆，其方程为．1y 9x 22=+点评：例5和例6分别将立体几何与解析几何中的双曲线与椭圆巧妙地整合在一起，相互交汇和渗透，有利于培养运用多学科知识解决问题的能力．立体几何中的轨迹问题1．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 与到直线B 1C 1的距离相等，则动点P 所在曲线的形状为（）A ．线段B ．一段椭圆弧C ．双曲线的一部分D ．抛物线的一部分2．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为2：1，则动点P 所在曲线的形状为（） A ．线段 B ．一段椭圆弧 C ．双曲线的一部分 D ．抛物线的一部分3．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为1：2，则动点P 所在曲线的形状为（） A ．线段 B ．一段椭圆弧 C ．双曲线的一部分 D ．抛物线的一部分4．在正方体ABCD-A 1B 1C 1D 1中，E 为AA 1的中点，点P 在其对角面BB 1D 1D 内运动，若EP 总与直线AC 成等角，则点P 的轨迹有可能是（） A ．圆或圆的一部分 B ．抛物线或其一部分 C ．双曲线或其一部分 D ．椭圆或其一部分5．已知正方体的棱长为a ，定点M 在棱AB 上（但不在端点A ，B 上），点P 是平面ABCD A B C D -1111ABCD 内的动点，且点P 到直线的距离与点P 到点M 的距离的平方差为a 2，则点P 的轨迹所在曲线为（ A D 11）A ．抛物线B ．双曲线C ．直线D ．圆6．若三棱锥A —BCD 的侧面ABC 内一动点P 到底面BCD 的距离与到棱AB 的距离相等，则动点P 的轨迹与ABC 组成的图形可能是（ ∆）A A AB C B C B C B CA B C D7．已知P 是正四面体S-ABC 的面SBC 上一点，P 到面ABC 的距离与到点S 的距离相等，则动点P 的轨迹所在的曲线是（） A ．圆B ．椭圆 C ．双曲线D ．抛物线8．已知平面平面，直线，点，平面、间的距离为4，则在内到点P 的距离为5且到直//αβl α⊂l P ∈αββ线的距离为的点的轨迹是（l 29）A ．一个圆B ．两条平行直线C ．四个点D ．两个点9．在四棱锥中，面PAB ，面PAB ，底面ABCD 为梯形，AD=4，BC=8，AB=6，ABCD P -⊥AD ⊥BC ，满足上述条件的四棱锥的顶点P 的轨迹是（）CPB APD ∠=∠A ．圆B ．不完整的圆C ．抛物线D ．抛物线的一部分10．如图，定点A 和B 都在平面内，定点P C 是内异于A 和B α,PB ,α⊥α∉α的动点．且，那么动点C 在平面内的轨迹是（）AC PC ⊥αA ．一条线段，但要去掉两个点B ．一个圆，但要去掉两个点C ．一个椭圆，但要去掉两个点D ．半圆，但要去掉两个点11．已知正方体的棱长为1，点P 是平面AC 内的动点，若点P 到直线的距离等于点1111D C B A ABCD -11D A P 到直线CD 的距离，则动点P 的轨迹所在的曲线是（）A ．抛物线B ．双曲线C ．椭圆D ．直线12．如图，AB 是平面的斜线段，A 为斜足，若点P 在平面内运动，使得△ABP a a 的面积为定值，则动点P 的轨迹是（）A ．圆B ．椭圆C ．一条直线D ．两条平行直线13．如图，动点在正方体的对角线上．过点作垂直于平面的直线，与正P 1111ABCD A B C D -1BD P 11BB D D 方体表面相交于．设，，则函数的图象大致是（）M N ，BP x =MN y =()y f x =ABCD MN P A 1B 1C 1D 114．在正方体中，点P 在侧面BCC 1B 1及其边界上运动，总有AP BD 1，则动点P 的轨迹ABCD A B C D -1111⊥为________．15．在正四棱锥S-ABCD 中，E 是BC 的中点，点P 在侧面SCD 内及其边界上运动，总有PE AC ，则动点∆⊥P 的轨迹为_______________．16．若A 、B 为平面的两个定点，点P 在外，PB ，动点C （不同于A 、B ）在内，且PC AC ，则αα⊥αα⊥动点C 在平面内的轨迹是________．17．已知正方体的棱长为1，在正方体的侧面上到点A 距离为的点的轨迹形ABCD AB C D -1111BCC B 11233成一条曲线，那么这条曲线的形状是_________，它的长度为__________．18．已知长方体中，，在线段BD 、上各有一点P 、Q ，PQ 上有一点ABCD A B C D -1111AB BC ==63,A C 11M ，且，则M 点轨迹图形的面积是．PM MQ =219．已知棱长为3的正方体中，长为2的线段MN 的一个端点在上运动，另一个端点ABCD A B C D -1111DD 1N 在底面ABCD 上运动，则MN 中点P 的轨迹与正方体的面所围成的几何体的体积是．20．已知异面直线a ，b 成角，公垂线段MN 的长等于2，线段AB 两个端点A 、B 分别在a ，b 上移动，且︒60线段AB 长等于4，求线段AB 中点的轨迹方程．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

❖共线类最值问题✧单动点共线最值
1、如图,正△ABC得边长为2,过点B得直线l⊥AB,
且△ABC与△A′BC′关于直线l对称,D为线段BC′上一动点,则AD+CD得最小值就是()
2.如
图Rt△ABC中,AB=BC=4,D为BC得中点,在AC边上存在一点E,连接ED,EB,则△BDE周长得最小值为()
A.5
2 B.3
2 C.2
5
2+ D.2
3
2+
3、已知菱形OABC在平面直角坐标系得位置如图所示,顶点A(5,0),OB=45,点P就是对角线OB上得一个动点,D(0,1),当CP+DP最短时,点P得坐标为( )
A、(0,0)
B、(1,2
1
) C、(5
6
,5
3
) D、(7
10
,7
5
)
A.4
B.2
3 C.3
2 D.3
2+
4、如图,已知在矩形ABCD 中,AB=4,BC=2,点M,E 在AD 上,点F 在边AB 上,并且DM=1,现将△AEF 沿着直线EF 折叠,使点A 落在边CD 上得点P 处,则当PB+PM 得与最小时,ME 得长度为( )
A.31
B.94
C.32
D.9
5
✧ 多动点最值 1．如图,已知等边△ABC 得边长为8,点D 为AC 得中点,点E 为BC 得中点,点P 为BD 上一动点,则PE+PC 得最小值为( )
A.3
B.24
C.32
D.34
2．如图,已知正比例函数y=kx(k ＞0)得图象与x 轴相交所成得锐角为70°,定点A 得坐标为(0,4),P 为y 轴上得一个动点,M 、N 为函数y=kx(k ＞0)得图象上得两个动点,则AM+MP+PN 得最小值为( )
A.2
B.4sin40°
C.32
D.4sin20°(1+cos20°+sin20°cos20°)
✧ 动线段类型
1、如图,矩形ABCD 中,AB=4,BC=8,E 为CD 边得中点,点P 、Q 为BC 边上两个动点,且PQ=2,当BP=________时,四边形APQE 得周长最小.
2．如图,已知平面直角坐标系,A 、B 两点得坐标分别为A(2,-3),B(4,-1).若C(a,0),D(a+3,0)就是x 轴上得两个动点,则当a=___________时,四边形ABDC 得周长最短.
✧ 翻折衍生得圆弧轨迹问题
1、如图,在边长为2得菱形ABCD 中,∠A=60°,点M 就是AD 边得中点,点N 就是AB 边上一动点,将△AMN 沿MN 所在得直线翻折得到△A′MN,连结A′C,则A′C 长度得最小值就是( )
A.7
B.17-
C.3
D.2
2、已知正方形ABCD 得边长为3,E 就是BC 上一点,BE=3,Q 就是CD 上一动点,将△CEQ 沿直线EQ 折叠后,点C 落在点P 处,连接PA,点Q 从点C 出发,沿线段CD 向点D 运动,当PA 得长度最小时,CQ 得长为( )
A.333-
B.33-
C.23
D.3
3、如图,菱形ABCD 得边AB=8,∠B=60°,P 就是AB 上一点,BP=3 , Q 就是CD 边上一动点,将梯形APQD 沿直线PQ 折叠,A 得对应点为A ′。

当CA ′得长度最小时, CQ 得长为( )
A.5
B.7
C.8
D.2
13
✧ 定长线段辅助类
1、(2014•北塘区校级一模)如图,∠MON=90°,矩形ABCD得顶点A、B分别在边OM,ON上,AB=4,BC=1.当点B在边ON上运动时,点A随之在边OM上运动,运动过程中矩形ABCD得形状保持不变,则点D到点O得最大距离就是__________、
2、(2015春•成都校级期末)在平面直角坐标系xOy中,点A、B分别在x轴、y轴得正半轴上运动,点M 为线段AB得中点.点D、E分别在x轴、y轴得负半轴上运动,且DE=AB=10.以DE为边在第三象限内作正方形DGFE,则线段MG长度得最大值为_________、
垂线段最短类型
1、(2013•宝应县二模)如图,在Rt△ABC中,∠C=90°,∠ABC=45°,AB=6,点D在AB边上,点E在BC边上(不与点B、C重合).若DA=DE,则AD得取值范围就是________
2、(2016成都中考)如图,面积为6得平行四边形纸片ABCD中,AB＝3,∠BAD＝45°,按下列步骤进行裁剪与拼图、
第一步:如图①,将平行四边形纸片沿对角线BD剪开,得到△A BD与△BCD纸片,再将△ABD纸片沿AE剪开(E为BD上任意一点),得到△ABE与△ADE纸片;
第二步:如图②,将△ABE纸片平移至△DCF处,将△ADE纸片平移至△BCG处;
第三步:如图③,将△DCF纸片翻转过来使其背面朝上置于△PQM处(边PQ与DC重合,△PQM与△DCF在CD同侧),将△BCG纸片翻转过来使其背面朝上置于△PRN处(边PR与BC重合,△PRN与△BCG 在BC同侧)。

则由纸片拼成得五边形PMQRN中,对角线MN长度得最小值为_______、
3. (2012成都中考)如图,长方形纸片ABCD中,AB=8cm,AD=6cm,按下列步骤进行裁剪与拼图:
第一步:如图①,在线段AD上任意取一点E,沿EB,EC剪下一个三角形纸片EBC(余下部分不再使用);
第二步:如图②,沿三角形EBC得中位线GH将纸片剪成两部分,并在线段GH上任意取一点M,线段BC上任意取一点N,沿MN将梯形纸片GBCH剪成两部分;
第三步:如图③,将MN左侧纸片绕G点按顺时针方向旋转180°,使线段GB与GE重合,将MN右侧纸片绕H点按逆时针方向旋转180°,使线段HC与HE重合,拼成一个与三角形纸片EBC面积相等得四边形纸片.(注:裁剪与拼图过程均无缝且不重叠)
则拼成得这个四边形纸片得周长得最小值=______________,最大值=_____________。

❖轨迹类问题复习
1、(圆弧轨迹) 如图,在等腰Rt△ABC中,AC＝BC＝2
2,点P在以斜边AB为直径得半圆上,M为PC得中点.当点P沿半圆从点A运动至点B时,点M运动得路径长就是( )
A．π2B.π
C.2
2 D.2
2.(线段轨迹)已知Rt△ABC,∠ACB=90°,AC=BC=4,点O就是AB中点,点P、Q分别从点A、C出发,沿AC、CB以每秒1个单位得速度运动,到达点C、B后停止.连接PQ、点D就是PQ中点,连接CD并延长交AB于点E.
(1)试说明:△POQ就是等腰直角三角形;
(2)设点P、Q运动得时间为t秒,试用含t得代数式来表示△CPQ得面积S,并求出S得最大值;
(3)如图2,点P在运动过程中,连接EP、EQ,问四边形PEQC就是什么四边形,并说明理由;
(4)求点D运动得路径长(直接写出结果).。