【长沙中考数学试题及答案】2010
2010年长沙市初中毕业模拟考试试卷(4)答案.doc

2010年长沙市初中毕业模拟考试试卷(4)参考答案一 . 单项选择题(本题共8个小题,每小题3分,满分24分)二、填空题(本题共8个小题,每小题3分,满分24分) 9、 -1 10、 2 11、20112、等或423+-=+-=x y x y (答案不唯一)13、090 14、 3 15、 2或10 16、 ()22+n n三、解答题(本题共6个小题,每小题6分,满分36分) 17.解:原式=()1212--- ……………………3分=121+- ……………………5分 =22-……………………6分18. 解:原式=xy xy x x y 222x +-÷- ……………………2分 =()2y x x x y x -∙- ……………………3分 =yx -1……………………4分 当2009=x ,2010=y 时,原式=1201020091-=- ……………………6分19. 解: 解不等式①得2<x ……………………2分解不等式②得1-≥x ……………………4分 ∴ 12x -≤< ……………………5分∴ 所求不等式组的整数解为:-1. 0. 1 . ……………………6分20. 解:∵ ∠AED=∠ABD-∠BDE=1500-600 =900……………………2分 ∴ 在Rt △BDE 中 BD DEBDE =∠cos ……………………3分 19060cos 380cos 0==∠∙=BDE BD DE ……………………5分答:开挖点E 要离D 处190米,才正好使A 、C 、E 三点在同一直线.…………6分95 9085 80 75 70分数/分竞聘人ABC21.解:(1)90;补充后的图如下:……………………………………………2分(2)A :30035105⨯=% B :30040120⨯=% C :3002575⨯=% …………4分 (3)A :854903105392.5433⨯+⨯+⨯=++(分)B :954803120398433⨯+⨯+⨯=++(分)C :90485375384433⨯+⨯+⨯=++(分)所以,B 能竞聘成功.………………………………6分22. 解:⑴ ADC S ∆= 6 2cm ………………2分⑵ 若AOB COD S S ∆∆=,则ACD DBA ∆≅∆,………………3分 证明:∵COD AOB S S ∆∆= ∴CB CD A A S S ∆∆= ………………4分 ∴ B 、D 到AC 的距离相等 ∴ BD ∥AC ………………5分 ∵ AB ∥CD ∴ ABCD 是平行四边形 ∴ACD DBA ∆≅∆ ………………6分 四、解答题(本题共2个小题,每小题8分,满分16分) 23. 解.(1)设A 市投资“改水工程”年平均增长率是x ,则 2600(1)1176x +=.………………4分解之,得0.4x = 或 2.4x =-(不合题意,舍去).所以,A 市投资“改水工程”年平均增长率为40%.………………6分 (2)600+600×1.4+1176=2616(万元).A 市三年共投资“改水工程”2616万元. ………………8分24.解:(1)连结OE.∵DF 切半圆于E ,∴∠OEF=90°,在正方形ABCD 中,AB=AD ,∠DAF=90°,∴∠OEF=∠DAF.又∵∠F 为公共角, ∴△OEF ∽△DAF. ………………2分∴21===AB OE DA OE AF EF .即AF=2EF. ………………3分 ∵DF 切半圆O 于E ,∴EF 2=FB ·FA=BF ·2EF ,∴EF=2BF=8,AF=2EF=16.∴AB=AF -BF=12,FO=21AB+BF=21×12+4=10.在Rt △OEF 中, cos ∠F=54108==FO EF .…………………………5分 (2)连结AE ,∵DF 切半圆于E ,∴∠EAF=∠BEF.∵∠F=∠F ,∴△BEF ∽△EAF. ∴21168===AF EF EA BE . ……………………………6分 设BE=k(k >0),则AE=2k ,∵AB 为半圆O 的直径,∴∠AEB=90°. 在Rt △AEB 中,AE 2+BE 2=AB 2,(2k )2+k 2=122,∴BE=k=5512. ……………………8分 五、解答题(本题共2个小题,每小题10分,满分20分) 25.解:(1)根据图形:0∶00-20∶00之间气站每小时增加的储气量为:(238-30)÷20=10.4(米3/小时)………(2分)(2)设气站每小时进气量为a 米3,每小时供气量为b 米3, 根据题意,得423030,(204)()238230a a b =-⎧⎨--=-⎩ 解得:50,49.5a b =⎧⎨=⎩ ……(4分)在20∶00-24∶00只打开供气阀门,到24:00时,气站的储气量为238-4×49.5=40,即当24x = 时,40y =;又当20x =时,238y =……(5分) 设20∶00-24∶00时,y 与x 的函数关系式为y kx m =+,则 2440,20238k m k m +=⎧⎨+=⎩ 解得:49.51228k m =-⎧⎨=⎩………………………(7分)所以,49.51228y x =-+ (2024)x ≤≤图形如图所示………………………(8分) (3)68小时, 2583米 ……………(10分)26.解:(1)根据题意,得 10,22550.2b c b c ⎧-++=⎪⎪⎨⎪-++=⎪⎩ 解得3,5.2b c =⎧⎪⎨=-⎪⎩ ……………(2分)∴215322y x x =-+-=21(3)22x --+∴顶点C 的坐标为(3,2).……………(3分) (2)①∵CD=DB=AD=2,CD⊥AB, ∴∠DCB=∠CBD=45°.……………(4分) ⅰ)若CQ=CP ,则∠PCD=12∠PCQ=22.5°. ∴当α=22.5°时,△CPQ 是等腰三角形.……………(5分) ⅱ)若CQ=PQ ,则∠CPQ=∠PCQ=45°,此时点Q 与D 重合,点P 与A 重合.∴当α=45°时,△CPQ 是等腰三角形.……………(6分)ⅲ)若PC=PQ , ∠PCQ=∠PQC=45°,此时点Q 与B 重合,点P 与D 重合.∴α=0°,不合题意.∴当α=22.5°或45°时,△CPQ 是等腰三角形.………(7分) ② 连接AC ,∵AD=CD=2,CD⊥AB,∴∠ACD=∠CAD=45,=8分)ⅰ)当045α<≤时,∵∠ACQ=∠ACP+∠PCQ=∠ACP+45°. ∠BPC=∠ACP+∠CAD=∠ACP+45°.∴∠ACQ=∠BPC. 又∵∠CAQ=∠PBC=45°, ∴△ACQ∽△BPC.∴AQ ACBC BP=.∴AQ·BP=AC·BC==8 ……………(9分) ⅱ)当4590α<<时,同理可得AQ·BP=AC·BC=8 ∴8s t=.……………(10分)。
10年长沙中考数学答案

2010年长沙市初中毕业学业水平考试试卷数学参考答案及评分标准一、选择题(本题共8个小题,每小题3分,共24分)请将你认为正确的选项的代号填在答题卡上.题号1 2 3 4 5 6 7 8 答案C C C A C B CD 二、填空题(本题共8个小题,每小题3分,共24分) 9.3 10.8×106 11.153.5 12.|a |>|b |13.m <1 14.120 15.6 16.50三、解答题(本题共6个小题,每小题6分,共36分)17.原式=133123+⨯- …………………………………………………3分 =12……………………………………………………………6分 18.原式=(3)(3)13(3)x x x x x +--+ ……………………………………………2分 =1x……………………………………………………………4分 当13x =时,原式=3 …………………………………………………6分 19.解:∵在Rt △ADB 中,∠BDA =45°,AB =3 ∴DA =3 …………2分 在Rt △ADC 中,∠CDA =60°∴tan60°=CA AD∴CA =33 …………4分 ∴BC=CA -BA =(33-3)米答:路况显示牌BC 的高度是(33-3)米 ………………………6分20.解:(1) 或用列表法 …………3分(2)P (小于6)=816=12………………………………………………………6分 21.解:(1)如图C 1(-3,2)…………………3分(2)如图C 2(-3,-2) …………………6分开始 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 2 4 6 8 3 6 9 12 48 12 16或22.(1)证明:∵四边形ABCD 是正方形∴BC =CD ,∠ECB =∠ECD =45°又EC =EC …………………………2分∴△ABE ≌△ADE ……………………3分(2)∵△ABE ≌△ADE∴∠BEC =∠DEC =12∠BED …………4分 ∵∠BED =120°∴∠BEC =60°=∠AEF ……………5分∴∠EFD =60°+45°=105° …………………………6分四、解答题(本题共2个小题,每小题8分,共16分)23.解:(1)设平均每次降价的百分率是x ,依题意得 ………………………1分5000(1-x )2= 4050 ………………………………………3分 解得:x 1=10% x 2=1910(不合题意,舍去) …………………………4分 答:平均每次降价的百分率为10%. …………………………………5分(2)方案①的房款是:4050×100×0.98=396900(元) ……………………6分方案②的房款是:4050×100-1.5×100×12×2=401400(元) ……7分∵396900<401400∴选方案①更优惠. ……………………………………………8分24.证明:连BD ∵ BD AD =∴∠A =∠ABD ∴AD =BD …………………2分∵∠A +∠C =90°,∠DBA +∠DBC =90°∴∠C =∠DBC ∴BD =DC∴AD =DC ………………………………………………………4分(2)连接OD ∵DE 为⊙O 切线 ∴OD ⊥DE …………………………5分 ∵ BD AD =,OD 过圆心 ∴OD ⊥AB又∵AB ⊥BC ∴四边形FBED 为矩形∴DE ⊥BC ……………………6分 ∵BD 为Rt △ABC 斜边上的中线∴BD =DC ∴BE =EC =DE∴∠C =45° …………………………………………………7分 ∴sin ∠C =22………………………………………………………………8分五、解答题(本题共2个小题,每小题10分,共20分)25.解:(1)∵一次函数过原点∴设一次函数的解析式为y =kx∵一次函数过(1,-b ) ∴y =-bx ……………………………3分(2)∵y =ax 2+bx -2过(1,0)即a +b =2 …………………………4分 由2(2)2y bx y b x bx =-⎧⎨=-+-⎩得 ……………………………………5分 22(2)20ax a x +--=① ∵△=224(2)84(1)120a a a -+=-+>∴方程①有两个不相等的实数根∴方程组有两组不同的解∴两函数有两个不同的交点. ………………………………………6分(3)∵两交点的横坐标x 1、x 2分别是方程①的解 ∴122(2)24a a x x a a--+== 122x x a -= ∴2121212()4x x x x x x -=+-=22248164(1)3a a a a-+=-+ 或由求根公式得出 ………………………………………………………8分 ∵a >b >0,a +b =2 ∴2>a >1 令函数24(1)3y a =-+ ∵在1<a <2时y 随a 增大而减小. ∴244(1)312a <-+< ……………………………………………9分 ∴242(1)323a <-+< ∴12223x x <-< ………………10分26.解:(1) ∵CQ =t ,OP =2t ,CO =8 ∴OQ =8-t ∴S △OPQ =212(8)24222t t t t -=-+ (0<t <8) …………………3分 (2) ∵S 四边形OPBQ =S 矩形ABCD -S △P AB -S △CBQ =11882828(822)22t t ⨯-⨯-⨯⨯-=322 ………… 5分 ∴四边形O PBQ 的面积为一个定值,且等于322 …………6分(3)当△OPQ 与△P AB 和△QPB 相似时, △QPB 必须是一个直角三角形,依题意只能是∠QPB =90°又∵BQ 与AO 不平行 ∴∠QPO 不可能等于∠PQB ,∠APB 不可能等于∠PBQ ∴根据相似三角形的对应关系只能是△OPQ ∽△PBQ ∽△ABP ………………7分 ∴828822t t t-=-解得:t =4 经检验:t =4是方程的解且符合题意(从边长关系和速度)此时P (42,0)∵B (82,8)且抛物线214y x bx c =++经过B 、P 两点, ∴抛物线是212284y x x =-+,直线BP 是:28y x =- …………………8分 设M (m , 28m -)、N (m ,212284m m -+)∵M 在BP 上运动 ∴4282m ≤≤ ∵2112284y x x =-+与228y x =-交于P 、B 两点且抛物线的顶点是P ∴当4282m ≤≤时,12y y > ………………………………9分 ∴12MN y y =-=21(62)24m --+ ∴当62m =时,MN 有最大值是2 ∴设MN 与BQ 交于H 点则(62,4)M 、(62,7)H ∴S △BHM =13222⨯⨯=32∴S △BHM :S 五边形QOPMH =32:(32232)-=3:29 ∴当MN 取最大值时两部分面积之比是3:29. …………………10分。
湖南省长沙市2010年中考语文试卷(word版,含答案)

2010年长沙市初中毕业学业水平考试试卷语文注意事项:1、答题前,请考生先将自己的姓名、准考证号填写清楚,并认真核对条形码上的姓名、准考证号、考室和座位号;2、必须在答题卡上答题,在草稿纸、试题卷上答题无效;3.答题时,请考生注意各大题题号后面的答题提示;4、请勿折叠答题卡,保持字体工整、笔迹清晰、卡面清洁;5、答题卡上不得使用涂改液、潦改胶和贴纸;6.本学科考试时量120分钟,满分120分。
一、基础知识积累及其运用(12分)1.下列词语中加点字的注音完全正确的一项是A.妖娆.(ráo) 愧怍.(zà) 中流砥.柱(dǐ)B.惬.意(xiá) 萌.庇(yìn) 相形见绌.(chū)C.点缀.(zhuì)潮汛.(xùn) 孜.孜不倦(zī)D.静谧.(bì) 追溯.(shuò) 问心无愧.(kuì)2.下列词语中没有错别字的一项是A.慷概细腻美不胜收炯乎不同B.嘹亮孕育尽态极妍各得其所C.拮局斑澜一泄千里锐不可当D.祈祷推祟物竟天择随机应变3.结合语境,选出下列句子中加点词语解释有误的一项A.我们希望看到一个落英缤纷、屋舍俨然..、民风淳朴的都市桃花源。
(俨然:形容庄严。
) B.“我们所做的一切都是要让人民生活得更加幸福、更有尊严,让社会更加公正、更加和谐”。
温总理的话语像和煦..的春风温暖了人们的心。
(和煦:温暖。
)C.知识是形成新创意..的素材。
但这并不是说,光凭知识就能拥有创造性。
(创意:创造性的见解或意见。
)D.教育要得到长足的发展,一方面需要各级领导的重视,全社会的支持;另一方面也需要教育部门加强内部改革,增强造血..功能。
(造血:比喻部门、组织、单位等从内部挖掘潜力,增强自身的实力。
)4.选出下列句子中投有语病的一句A.继北京奥运会之后,在21世纪初又举办了一次全球盛会——上海世博会。
B.为了防止校园安全问题不再发生,各个学校都加强了安全保卫工作。
2010年长沙市中考数学模拟试卷(三)

2010年长沙市中考数学模拟试卷(三)(总分:120 分考试时间: 120分钟)一、选择题(共8题,24分)1. 函数的自变量的取值范围是()A. B.C. D.2. 下列运算正确的是()A. B. C.· D.3. 如图所示,在平面直角坐标系中,点的坐标分别为和.月牙①绕点顺时针旋转90°得到月牙②,则点的对应点的坐标为()A.B.C.D.4. 如图是某商场一楼与二楼之间的手扶电梯示意图.其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8 m,则乘电梯从点B到点C上升的高度h 是()A. m B.4 m C. m D.8 m5. 二次函数的图象如图所示,则一次函数与反比例函数在同一坐标系内的图象大致为()6. 在下图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心可能是()A.点A B.点B C.点C D.点D7. 在一个不透明的口袋中,装有若干个除颜色不同其余都相同的球,如果口袋中装有3个红球且摸到红球的概率为,那么口袋中球的总数为()A.12个B.9个C.6个D.3个8. 如图①,在直角梯形中,动点从点出发,沿,运动至点停止.设点运动的路程为,的面积为,如果关于的函数图象如图②所示,则的面积是()A.3 B.4 C.5 D.6二、填空题(共8题,24分)9. 16的平方根是.10. 不等式的解集是.11. 因式分解:12. 如果关于的方程(为常数)有两个相等的实数根,那么.13. 如图,已知,∠1=130o,∠2=30o,则∠C= .14. 如图,为半圆的直径,延长到点,使,切半圆于点,点是弧AC上和点不重合的一点,则的度数为.(圆的性质、切线的性质、解三角形)15. 在平面直角坐标系中,直线与两坐标轴围成一个.现将背面完全相同,正面分别标有数1、2、3、、的5张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数作为点P的横坐标,将该数的倒数作为点P的纵坐标,则点P落在内的概率为.16. 动手操作:在矩形纸片中,.如图所示,折叠纸片,使点落在边上的处,折痕为.当点在边上移动时,折痕的端点也随之移动.若限定点分别在边上移动,则点在边上距B点可移动的最短距离为.三、计算题(共6题,36分)17. 计算:18. 先化简,再求值:,其中.19. 如图,两点在函数的图象上.(1). 求的值及直线的解析式;(2). 如果一个点的横、纵坐标均为整数,那么我们称这个点是格点,请直接写出图中阴影部分(不包括边界)所含格点的个数.20. 解不等式组:,并将其解集在数轴上表示出来.21. 如图,⊙O的直径AB=4,C为圆周上一点,AC=2,过点C作⊙O的切线l,过点B 作l的垂线BD,垂足为D,BD与⊙O交于点E.(1). 求∠AEC的度数;(2). 求证:四边形OBEC是菱形.22. 省教委在推进课堂教学改革的过程中,为了切实减轻学生的课业负担,对义务教育阶段低年级学生原则上要求老师不布置课外作业,九年级学生每天的课外作业总时间不得超过1小时(学生阅读、自学除外):为了了解各校情况,县教委对其中40个学校九年级学生课外完成作业时间调研后进行了统计,并根据收集的数据绘制了下面两幅不完整的统计图,请你根据图中提供的信息,解答下面的问题:(1). 计算出学生课外完成作业时间在30~45分钟的学校对应的扇形圆心角;(2). 将图中的条形图补充完整;(3). 计算出学生课外完成作业时间在60~75分钟的学校占调研学校总数的百分比.四、解答题(共4题,36分)23. 已知:如图,在平面直角坐标系中,直线AB分别与轴交于点B、A,与反比例函数的图象分别交于点C、D,轴于点E,.(1). 求该反比例函数的解析式;(2). 求直线AB的解析式24. 2009年4月7日,国务院公布了《医药卫生体制改革近期重点实施方案(2009~2011年》,某市政府决定2009年投入6000万元用于改善医疗卫生服务,比2008年增加了1250万元.投入资金的服务对象包括“需方”(患者等)和“供方”(医疗卫生机构等),预计2009年投入“需方”的资金将比2008年提高30%,投入“供方”的资金将比2008年提高20%.(1). 该市政府2008年投入改善医疗卫生服务的资金是多少万元?(2). 该市政府2009年投入“需方”和“供方”的资金各多少万元?(3). 该市政府预计2011年将有7260万元投入改善医疗卫生服务,若从2009~2011年每年的资金投入按相同的增长率递增,求2009~2011年的年平均增长率.25. 已知某种水果的批发单价与批发量的函数关系如图(1)所示.(1). 请说明图中①、②两段函数图象的实际意义;(2). 写出批发该种水果的资金金额w(元)与批发量n(kg)之间的函数关系式;在下图的坐标系中画出该函数图象;指出金额在什么范围内,以同样的资金可以批发到较多数量的该种水果.(3). 经调查,某经销商销售该种水果的日最高销量与零售价之间的函数关系如图(2)所示,该经销商拟每日售出60kg以上该种水果,且当日零售价不变,请你帮助该经销商设计进货和销售的方案,使得当日获得的利润最大.26. 如图所示,将矩形沿折叠,使点恰好落在上处,以为边作正方形,延长至,使,再以、为边作矩形.(1). 试比较、的大小,并说明理由.(2). 令,请问是否为定值?若是,请求出的值;若不是,请说明理由.(3). 在(2)的条件下,若为上一点且,抛物线经过、两点,请求出此抛物线的解析式.(4). 在(3)的条件下,若抛物线与线段交于点,试问在直线上是否存在点,使得以、、为顶点的三角形与相似?若存在,请求直线与轴的交点的坐标;若不存在,请说明理由.。
2010-2023历年初中毕业升学考试(湖南长沙卷)数学

2010-2023历年初中毕业升学考试(湖南长沙卷)数学第1卷一.参考题库(共10题)1.等于()A.2B.C.D.2.使得函数值为零的自变量的值称为函数的零点。
例如,对于函数,令y=0,可得x=1,我们就说1是函数的零点。
己知函数 (m为常数)。
(1)当=0时,求该函数的零点;(2)证明:无论取何值,该函数总有两个零点;(3)设函数的两个零点分别为和,且,此时函数图象与x轴的交点分别为A、B(点A在点B左侧),点M在直线上,当MA+MB最小时,求直线AM的函数解析式。
3.计算:= .4.下列长度的三条线段,能组成三角形的是()A.1、l、2B.3、4、5C.1、4、6D.2、3、75.如图,在△ABC中,AB=5cm,AC=3cm,BC的垂直平分线分别交AB、BC于D、E,则△ACD的周长为 cm.6.已知,求的值。
7.正五边形的每一个内角都等于.8.分解因式:=____________。
9.菱形的两条对角线的长分别是6cm和8cm,则菱形的周长是__________cm.10.张经理到老王的果园里一次性采购一种水果,他俩商定:张经理的采购价y(元/吨)与采购量x(吨)之间函数关系的图象如图中的折线段ABC所示(不包含端点A,但包含端点C).(1)求y与x之间的函数关系式;(2)已知老王种植水果的成本是2 800元/吨,那么张经理的采购量为多少时,老王在这次买卖中所获的利润w最大?最大利润是多少?第1卷参考答案一.参考题库1.参考答案:A2.参考答案:(1)当=0时,该函数的零点为和。
(2)令y=0,得△=∴无论取何值,方程总有两个不相等的实数根。
即无论取何值,该函数总有两个零点。
(3)依题意有,由解得。
∴函数的解析式为。
令y=0,解得∴A(),B(4,0)作点B关于直线的对称点B’,连结AB’,则AB’与直线的交点就是满足条件的M点。
易求得直线与x轴、y轴的交点分别为C(10,0),D(0,10)。
2010年全国中考数学试题汇编专题三整式.doc

一、选择题1.(2010安徽省中中考)计算x x ÷)2(3的结果正确的是…………………………()A )28x B )26x C )38x D )36x 【答案】A 2.(2010广东广州,3,3分)下列运算正确的是()A .-3(x -1)=-3x -1B .-3(x -1)=-3x +1C .-3(x -1)=-3x -3D .-3(x -1)=-3x +3【答案】D 3.(2010广东广州,8,3分)下列命题中,正确的是()A .若a ·b >0,则a >0,b >0B .若a ·b <0,则a <0,b <0C .若a ·b =0,则a =0,且b =0D .若a ·b =0,则a =0,或b =0【答案】D 4.(2010江苏南京)34a a ⋅的结果是A.4a B.7a C.6a D.12a 【答案】B5.(2010江苏盐城)下列说法或运算正确的是A .1.0×102有3个有效数字B .222)(b a b a −=−C .532a a a =+D .a 10÷a 4=a 6【答案】D6.(2010辽宁丹东市)图①是一个边长为()m n +的正方形,小颖将图①中的阴影部分拼成图②的形状,由图①和图②能验证的式子是()图①图②第4题图A.22()()4m n m n mn +−−=B.222()()2m n m n mn +−+=C.222()2m n mn m n −+=+D.22()()m n m n m n +−=−【答案】B 7.(2010浙江金华)如果33−=−b a ,那么代数式b a 35+−的值是(▲)A .0B .2C .5D .8【答案】D8.(2010山东日照)由m (a +b +c )=ma +mb +mc ,可得:(a +b )(a 2-ab +b 2)=a 3-a 2b +ab 2+a 2b-ab 2+b 3=a 3+b 3,即(a +b )(a 2-ab +b 2)=a 3+b 3.我们把等式①叫做多项式乘法的立方公式。
2010-2023历年初中毕业升学考试(湖南长沙卷)数学

2010-2023历年初中毕业升学考试(湖南长沙卷)数学第1卷一.参考题库(共12题)1.请写出一个大于1且小于2的无理数:.2.如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、BC、CA的中点,若CD=5cm,则EF= cm.(第16题) (第17题) (第18题)3.如图是每个面上都有一个汉字的正方体的一种展开图,那么在原正方体的表面上,与汉字“美"相对的面上的汉字是()A.我B.爱C.长D.沙4.如图,CD是△ABC的外角∠ACE的平分线,AB∥CD,∠ACE=100°,则∠A=__ __________。
5.等于()A.2B.C.D.6.下列二次函数中,图象以直线x=2为对称轴、且经过点(0,1)的是( ) A.y=(x-2)2+1B.y=(x+2)2+1C.y=(x-2)2-3D.y=(x+2)2-37.一名同学想用正方形和圆设计一个图案,要求整个图案关于正方形的某条对角线对称,那么下列图案中不符合要求的是( )A B C D8.分解因式:=____________。
9.已知,求的值。
10.如图,抛物线y=x2+1与双曲线y=的交点A的横坐标是1,则关于x的不等式+ x2+1<0的解集是( )A.x>1B.x<-1C.0<x<1D.-1<x<011.“珍惜能源从我做起,节约用电人人有责”.为了解某小区居民节约用电情况,物业公司随机抽取了今年某一天本小区l0户居民的日用电量,数据如下:用户序号12345678910日用电量(度)4.44.05.05.63.44.83.45.24.04.2(1)求这组数据的极差和平均数;(2)已知去年同一天这10户居民的平均日用电量为7.8度,请你估计,这天与去年同日相比,该小区200户居民这一天共节约了多少度电?12.若a>b,则( )A.a>-bB.a<-bC.-2a>-2bD.-2a<-2b第1卷参考答案一.参考题库1.参考答案:(答案不唯一)2.参考答案:53.参考答案:C4.参考答案:505.参考答案:A6.参考答案:C7.参考答案:D考点:轴对称图形.分析:轴对称图形是针对一个图形而言的,是一种具有特殊性质图形,被一条直线分割成的两部分沿着对称轴折叠时,互相重合.解:A、图象关于对角线所在的直线对称,两条对角线都是其对称轴;故符合要求;B、图象关于对角线所在的直线对称,两条对角线都是其对称轴;故符合要求;C、图象关于对角线所在的直线对称,有一条对称轴;故符合要求;D、图象关于对角线所在的直线不对称;故不符合要求;故选D.8.参考答案:9.参考答案:410.参考答案:D11.参考答案:(1)极差:2.2 平均数:4.4(2)这10户居民这一天平均每户节约:7.8-4.4="3.4" (度)∴总数为:3.4×200=680(度)考点:用样本估计总体;算术平均数;极差.分析:(1)根据极差和平均数的概念求解即可,极差是指一组数据中最大数据与最小数据的差.(2)先求出这10户居民这一天平均每户节约的度数,再用样本估计总体的方法求出该小区200户居民这一天共节约了多少度电.解:(1)这组数据中,日用电量最多的是5.6,最少的是3.4,∴极差=5.6-3.4=2.2,平均数=(4.4+4.0+5.0+5.6+3.4+4.8+3.4+5.2+4.0+4.2)÷10=4.4;(2)这10户居民这一天平均每户节约:7.8-4.4=3.4(度)∴总数为:3.4×200=680(度).12.参考答案:D。
2010年部分省市中考数学试题分类汇编 压轴题(五)及答案
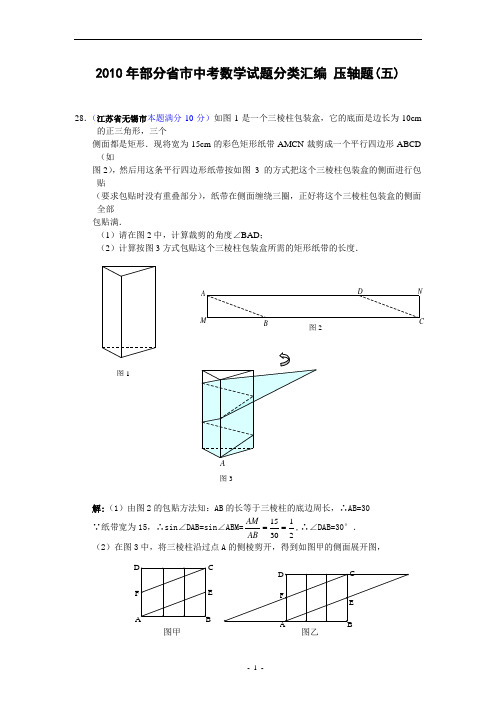
2010年部分省市中考数学试题分类汇编压轴题(五)28.(江苏省无锡市本题满分10分)如图1是一个三棱柱包装盒,它的底面是边长为10cm 的正三角形,三个侧面都是矩形.现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD (如图2),然后用这条平行四边形纸带按如图3 的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.(1)请在图2中,计算裁剪的角度∠BAD;(2)计算按图3方式包贴这个三棱柱包装盒所需的矩形纸带的长度.解:(1)由图2的包贴方法知:AB的长等于三棱柱的底边周长,∴AB=30∵纸带宽为15,∴sin∠DAB=sin∠ABM=151302AMAB==,∴∠DAB=30°.(2)在图3中,将三棱柱沿过点A的侧棱剪开,得到如图甲的侧面展开图,C 图甲图1图3A将图甲种的△ABE 向左平移30cm ,△CDF 向右平移30cm ,拼成如图乙中的平行四边形ABCD ,此平行四边形即为图2中的平行四边形ABCD 由题意得,知:BC=BE+CE=2CE=2×cos 30CD =︒∴所需矩形纸带的长为MB+BC=30·cos30°+cm .28.(江苏省宿迁市 本题满分12分)已知抛物线c bx x y ++=2交x 轴于)0,1(A 、)0,3(B ,交y 轴于点C ,其顶点为D .(1)求b 、c 的值并写出抛物线的对称轴; (2)连接BC ,过点O 作直线BC OE ⊥交抛物线的对称轴于点E .求证:四边形ODBE 是等腰梯形; (3)问Q 抛物线上是否存在点Q ,使得△OBQ 的面积等于四边形ODBE 的面积的31?若存在,求出点Q 的坐标;若不存在,请说明理由.解:(1)求出:4-=b ,3=c ,抛物线的对称轴为:x=2 ……3分(2) 抛物线的解析式为342+-=x x y ,易得C 点坐标为(0,3),D 点坐标为(2,-1) 设抛物线的对称轴DE 交x 轴于点F ,易得F 点坐标为(2,0),连接OD ,DB ,BE ∵∆OBC 是等腰直角三角形,∆DFB 也是等腰直角三角形,E 点坐标为(2,2), ∴∠BOE= ∠OBD=45 ∴OE ∥BD∴四边形ODBE 是梯形 ………………5分在ODF Rt ∆和EBF Rt ∆中,(第28题)(第28题2)OD=5122222=+=+DF OF ,BE=5122222=+=+FB EF∴OD= BE∴四边形ODBE 是等腰梯形 ……………7分(3) 存在, ……8分 由题意得:29332121=⨯⨯=⋅=DE OB S ODBE 四边形 ………………9分 设点Q 坐标为(x ,y ), 由题意得:y y OB S OBQ 2321=⋅=三角形=23293131=⨯=ODBE S 四边形 ∴1±=y当y=1时,即1342=+-x x ,∴ 221+=x , 222-=x ,∴Q 点坐标为(2+2,1)或(2-2,1) …………11分 当y=-1时,即1342-=+-x x , ∴x=2, ∴Q 点坐标为(2,-1)综上所述,抛物线上存在三点Q 1(2+2,1),Q 2 (2-2,1) ,Q 3(2,-1) 使得OBQ S 三角形=ODBE S 四边形31. ………………12分EFQ 1 Q 3Q 226.(湖南省长沙市)如图,在平面直角坐标系中,矩形OABC 的两边分别在x 轴和y轴上,OA =cm , OC=8cm ,现有两动点P 、Q 分别从O 、C 同时出发,P 在线段OA 上沿OAcm 的速度匀速运动,Q 在线段CO 上沿CO 方向以每秒1 cm 的速度匀速运动.设运动时间为t 秒. (1)用t 的式子表示△OPQ 的面积S ;(2)求证:四边形OPBQ 的面积是一个定值,并求出这个定值;(3)当△OPQ 与△P AB 和△QPB 相似时,抛物线214y x bx c =++经过B 、P 两点,过线段BP 上一动点M 作y 轴的平行线交抛物线于N ,当线段MN 的长取最大值时,求直线MN 把四边形OPBQ 分成两部分的面积之比.解:(1) ∵CQ =t ,OPt ,CO =8 ∴OQ =8-t∴S △OPQ=21(8)222t t -=-+(0<t <8) …………………3分 (2) ∵S 四边形OPBQ =S 矩形ABCD -S △PAB -S △CBQ=1188)22⨯⨯-⨯⨯=………… 5分 ∴四边形O PBQ 的面积为一个定值,且等于 …………6分(3)当△OPQ 与△P AB 和△QPB 相似时, △QPB 必须是一个直角三角形,依题意只能是∠QPB =90°又∵BQ 与AO 不平行 ∴∠QPO 不可能等于∠PQB ,∠APB 不可能等于∠PBQ ∴根据相似三角形的对应关系只能是△OPQ ∽△PBQ ∽△ABP ………………7分8=解得:t =4经检验:t =4是方程的解且符合题意(从边长关系和速度) 此时P(0)∵B (8)且抛物线214y x bxc =++经过B 、P 两点, 第26题图∴抛物线是212284y x x =-+,直线BP 是:28y x =- …………………8分 设M (m , 28m -)、N (m ,212284m m -+)∵M 在BP 上运动 ∴4282m ≤≤ ∵2112284y x x =-+与228y x =-交于P 、B 两点且抛物线的顶点是P ∴当4282m ≤≤时,12y y > ………………………………9分 ∴12MN y y =-=21(62)24m --+ ∴当62m =时,MN 有最大值是2 ∴设MN 与BQ 交于H 点则(62,4)M 、(62,7)H ∴S △BHM =13222⨯⨯=32 ∴S △BHM :S 五边形QOPMH =32:(32232)-=3:29 ∴当MN 取最大值时两部分面积之比是3:29. ……10分28.(南京市8分)如图,正方形ABCD 的边长是2,M 是AD 的中点,点E 从点A 出发,沿AB 运动到点B 停止,连接EM 并延长交射线CD 于点F ,过M 作EF 的垂线交射线BC 于点G ,连结EG 、FG 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
BOACO AC B第8题图二0一0年长沙市初中毕业学业水平考试试卷数 学一、选择题(在下列各题的四个选项中,只有一项是符合题意的。
请在答题卡中填涂符合题意的选项。
本题共8个小题,每小题3分,共24分) 1.4的平方根是A .2B .2C .±2D .2± 2.函数11y x =+的自变量x 的取值范围是 A .x >-1 B .x <-1 C .x ≠-1 D .x ≠1 3.一个几何体的主视图、左视图、俯视图的图形完全相同,它可能是 A .三棱锥 B .长方体 C .球体 D .三棱柱 4.下列事件是必然事件的是A .通常加热到100℃,水沸腾;B .抛一枚硬币,正面朝上;C .明天会下雨;D .经过城市中某一有交通信号灯的路口,恰好遇到红灯.5.下列每一组数据中的三个数值分别为三角形的三边长,不能构成直角三角形的是A .3、4、5B .6、8、10C .3、2、5D .5、12、136.已知⊙O 1、⊙O 2的半径分别是12r =、24r =,若两圆相交,则圆心距O 1O 2可能取的值是 A .2 B .4 C .6D .87.下列计算正确的是A .2242a a a +=B .2(2)4a a =C .333⨯=D .1232÷=8.如图,在⊙O 中,OA =AB ,OC ⊥AB ,则下列结论错误的是A .弦AB 的长等于圆内接正六边形的边长 B .弦AC 的长等于圆内接正十二边形的边长 C . AC BC= D .∠BAC =30°二、填空题(本题共8个小题,每小题3分,共24分) 9.-3的相反数是 .10.截止到2010年5月31日,上海世博园共接待8 000 000人,用科学记数法表示是 人.11.如图,O 为直线AB 上一点,∠COB =26°30′,则∠1= 度.12.实数a 、b 在数轴上位置如图所示,则| a |、| b |的大小关系是 .a ob C B A O O A B C 1yx -O 第13题图 第12题图 第11题图 .··.13.已知反比例函数1my x-=的图象如图,则m 的取值范围是 . 14.已知扇形的面积为12π,半径等于6,则它的圆心角等于 度. 15.等腰梯形的上底是4cm ,下底是10 cm ,一个底角是60︒,则等腰梯形的腰长是 cm .16.2010年4月14日青海省玉树县发生7.1级大地震后,湘江中学九年级(1)班的60名同学踊跃捐款.有15人每人捐30元、14人每人捐100元、10人每人 捐70元、21人每人捐50元.在这次每人捐款的数值中,中位数是 .三、解答题(本题共6个小题,每小题6分,共36分) 17.计算:1023tan 30(2010)π-︒+--18.先化简,再求值:2291()333x x x x x ---+ 其中13x =.19.为了缓解长沙市区内一些主要路段交通拥挤的现状,交警队在一些主要路口设立了交通路况显示牌(如图).已知立杆AB 高度是3m ,从侧面D 点测得显示牌顶端C 点和底端B 点的仰角分别是60°和45°.求路况显示牌BC 的高度. 20.有四张完全一样的空白纸片,在每张纸片的一个面上分别写上1、2、3、4.某同学把这四张纸片写有字的一面朝下,先洗匀随机抽出一张,放回洗匀后,再随机抽出一张.求抽出的两张纸片上的数字之积小于6的概率.(用树状图或列表法求解)21.△ABC 在平面直角坐标系中的位置如图所示.A 、B 、C 三点在格点上.(1)作出△ABC 关于y 轴对称的△A 1B 1C 1,并写出点C 1的坐标;(2)作出△ABC 关于原点O 对称的△A 2B 2C 2,并写出点C 2的坐标.EBD A C F AFDE B C第19题图第21题图yx22.在正方形ABCD 中,AC 为对角线,E 为AC 上一点,连接EB 、ED . (1)求证:△BEC ≌△DEC ;(2)延长BE 交AD 于F ,当∠BED =120°时,求∠EFD 的度数.四、解答题(本题共2个小题,每小题8分,共16分)23.长沙市某楼盘准备以每平方米5000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望.为了加快资金周转,房地产开发商对价格经过两次下调后,决定以每平方米4050元的均价开盘销售.(1)求平均每次下调的百分率;(2)某人准备以开盘均价购买一套100平方米的房子.开发商还给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,送两年物业管理费.物业管理费是每平方米每月1.5元.请问哪种方案更优惠?24.已知:AB 是O 的弦,D 是 AB 的中点,过B 作AB 的垂线交AD 的延长线于C . (1)求证:AD =DC ;(2)过D 作⊙O 的切线交BC 于E ,若DE =EC ,求sin C .五、解答题(本题共2个小题,每小题10分,共20分)25.已知:二次函数22y ax bx =+-的图象经过点(1,0),一次函数图象经过原点和点(1,-b ),其中0a b >>且a 、b 为实数.(1)求一次函数的表达式(用含b 的式子表示); (2)试说明:这两个函数的图象交于不同的两点;(3)设(2)中的两个交点的横坐标分别为x 1、x 2,求| x 1-x 2 |的范围.26.如图,在平面直角坐标系中,矩形OABC 的两边分别在x 轴和y 轴上,82OA = cm , OC=8cm ,现有两动点P 、Q 分别从O 、C 同时出发,P 在线段OA 上沿OA 方向以每秒2 cm 的速度匀速运动,Q 在线段CO 上沿CO 方向以每秒1 cm 的速度匀速运动.设运动时间为t 秒. (1)用t 的式子表示△OPQ 的面积S ;(2)求证:四边形OPBQ 的面积是一个定值,并求出这个定值;(3)当△OPQ 与△PAB 和△QPB 相似时,抛物线214y x bx c =++经过B 、P 两点,过线段BP 上一动点M 作y 轴的平行线交抛物线于N ,当线段MN 的长取最大值时,求直线MN 把四边形OPBQ 分成两部分的面积之比.第22题图B ECD A O OADB EC第24题图BA PxCQOy 第26题图2010年长沙市初中毕业学业水平考试试卷数学参考答案及评分标准一、选择题(本题共8个小题,每小题3分,共24分)请将你认为正确的选项的代号填在答题卡上.题号 1 2 3 4 5 6 7 8答案C C C A C B C D二、填空题(本题共8个小题,每小题3分,共24分)9.3 10.8×10611.153.5 12.|a |>|b | 13.m <1 14.120 15.6 16.50 三、解答题(本题共6个小题,每小题6分,共36分)17.原式=133123+⨯- …………………………………………………3分 =12……………………………………………………………6分 18.原式=(3)(3)13(3)x x x x x +--+……………………………………………2分 =1x ……………………………………………………………4分 当13x =时,原式=3 …………………………………………………6分19.解:∵在Rt △ADB 中,∠BDA =45°,AB =3 ∴DA =3 …………2分 在Rt △ADC 中,∠CDA =60°∴tan60°=CAAD∴CA =33 …………4分 ∴BC=CA -BA =(33-3)米答:路况显示牌BC 的高度是(33-3)米 ………………………6分 20.解:(1)或用列表法 …………3分(2)P (小于6)=816=12………………………………………………………6分 21.解:(1)如图C 1(-3,2)…………………3分 (2)如图C 2(-3,-2) …………………6分22.(1)证明:∵四边形ABCD 是正方形 ∴BC =CD ,∠ECB =∠ECD =45°又EC =EC …………………………2分开1 2 3 41 2 3 1 2 3 1 2 3 1 2 3 1 2 3 4 2 4 6 8 3 6 9 12 4 8 12∴△ABE ≌△ADE ……………………3分 (2)∵△ABE ≌△ADE ∴∠BEC =∠DEC =12∠BED …………4分 ∵∠BED =120°∴∠BEC =60°=∠AEF ……………5分 ∴∠EFD =60°+45°=105° …………………………6分四、解答题(本题共2个小题,每小题8分,共16分)23.解:(1)设平均每次降价的百分率是x ,依题意得 ………………………1分5000(1-x )2= 4050 ………………………………………3分 解得:x 1=10% x 2=1910(不合题意,舍去) …………………………4分 答:平均每次降价的百分率为10%. …………………………………5分 (2)方案①的房款是:4050×100×0.98=396900(元) ……………………6分方案②的房款是:4050×100-1.5×100×12×2=401400(元) ……7分 ∵396900<401400∴选方案①更优惠. ……………………………………………8分24.证明:连BD ∵ BD AD =∴∠A =∠ABD ∴AD =BD …………………2分∵∠A +∠C =90°,∠DBA +∠DBC =90°∴∠C =∠DBC ∴BD =DC∴AD =DC ………………………………………………………4分 (2)连接OD ∵DE 为⊙O 切线 ∴OD ⊥DE …………………………5分∵ BD AD =,OD 过圆心 ∴OD ⊥AB又∵AB ⊥BC ∴四边形FBED 为矩形∴DE ⊥BC ……………………6分 ∵BD 为Rt △ABC 斜边上的中线∴BD =DC ∴BE =EC =DE∴∠C =45° …………………………………………………7分 ∴sin ∠C =22………………………………………………………………8分五、解答题(本题共2个小题,每小题10分,共20分)25.解:(1)∵一次函数过原点∴设一次函数的解析式为y =kx∵一次函数过(1,-b ) ∴y =-bx ……………………………3分 (2)∵y =ax 2+bx -2过(1,0)即a +b =2 …………………………4分 由2(2)2y bxy b x bx =-⎧⎨=-+-⎩得 ……………………………………5分22(2)20ax a x +--=① ∵△=224(2)84(1)120a a a -+=-+>∴方程①有两个不相等的实数根∴方程组有两组不同的解∴两函数有两个不同的交点. ………………………………………6分 (3)∵两交点的横坐标x 1、x 2分别是方程①的解∴122(2)24a a x x a a--+==122x x a -= ∴2121212()4x x x x x x -=+-=22248164(1)3a a a a-+=-+ 或由求根公式得出 ………………………………………………………8分∵a >b >0,a +b =2 ∴2>a >1令函数24(1)3y a=-+ ∵在1<a <2时y 随a 增大而减小.∴244(1)312a<-+< ……………………………………………9分∴242(1)323a<-+< ∴12223x x <-< ………………10分26.解:(1) ∵CQ =t ,OP =2t ,CO =8 ∴OQ =8-t∴S △OPQ =212(8)24222t t t t -=-+ (0<t <8) …………………3分 (2) ∵S 四边形OPBQ =S 矩形ABCD -S △PAB -S △CBQ=11882828(822)22t t ⨯-⨯-⨯⨯-=322 ………… 5分 ∴四边形O PBQ 的面积为一个定值,且等于322 …………6分(3)当△OPQ 与△PAB 和△QPB 相似时, △QPB 必须是一个直角三角形,依题意只能是∠QPB=90°又∵BQ 与AO 不平行 ∴∠QPO 不可能等于∠PQB ,∠APB 不可能等于∠PBQ ∴根据相似三角形的对应关系只能是△OPQ ∽△PBQ ∽△ABP ………………7分 ∴828822t tt-=-解得:t =4经检验:t =4是方程的解且符合题意(从边长关系和速度) 此时P (42,0)∵B (82,8)且抛物线214y x bx c =++经过B 、P 两点, ∴抛物线是212284y x x =-+,直线BP 是:28y x =- …………………8分 设M (m , 28m -)、N (m ,212284m m -+)∵M 在BP 上运动 ∴4282m ≤≤∵2112284y x x =-+与228y x =-交于P 、B 两点且抛物线的顶点是P∴当4282m ≤≤时,12y y > ………………………………9分 ∴12MN y y =-=21(62)24m --+ ∴当62m =时,MN 有最大值是2 ∴设MN 与BQ 交于H 点则(62,4)M 、(62,7)H ∴S △BHM =13222⨯⨯=32 ∴S △BHM :S 五边形QOPMH =32:(32232)-=3:29∴当MN 取最大值时两部分面积之比是3:29. …………………10分。
